Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-27T09:48:59.018Z Has data issue: false hasContentIssue false
  • English
  • Français

A van der Waals contact-bond model for low-dimensional nanoscale carbon materials based on the quasi-continuum method

Published online by Cambridge University Press:  09 December 2019

Xiangyang Wang ,
Huibo Qi ,
Zhongyu Sun  and
Lifen Hu
Xiangyang Wang*
Affiliation:
School of Transportation, Ludong University, Yantai, Shandong 264025, China
Huibo Qi
Affiliation:
School of Transportation, Ludong University, Yantai, Shandong 264025, China
Zhongyu Sun
Affiliation:
School of Transportation, Ludong University, Yantai, Shandong 264025, China
Lifen Hu
Affiliation:
School of Transportation, Ludong University, Yantai, Shandong 264025, China
*
a)Address all correspondence to this author. e-mail: wxy017@126.com
Get access

Abstract

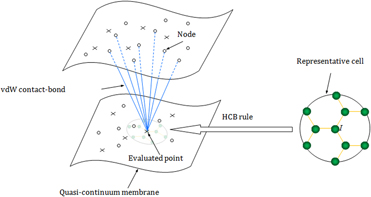
In order to develop an efficient and accurate quasi-continuum approach for contact problems of low-dimensional nanoscale carbon materials, a van der Waals contact-bond model is proposed in this study. This method can involve the important information of nano- and micro-structures, such as the bonded carbon atom interactions and the long-range van der Waals effect, which is usually homogenized and neglected in continuum methods. The degree of freedom of the atomic systems can be reduced dramatically; therefore, the model is beneficial for rapid simulations and large-scale computations of carbon nano-components. The so-called higher-order Cauchy–Born rule is used to establish the geometrically consistent constitutive model, and a meshless local Petrov–Galerkin-based computational framework is constructed for the mechanical responses of carbon nanoscale systems. The stiffness matrix is derived analytically, and the incremental governing equation is solved with the Newton–Raphson iteration method. Consequently, this method is much faster than order-N2 approaches such as molecular dynamic simulation.

Keywords

nanoscale contact behaviorsquasi-continuum methodhigher-order Cauchy–Born rulemeshless computational scheme
Type
Article
Information
Journal of Materials Research , Volume 34 , Issue 24 , 30 December 2019 , pp. 4011 - 4023
Copyright
Copyright © Materials Research Society 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Choi, W.B., Bae, E., Kang, D., Chae, S., Cheong, B., and Ko, J.: Aligned carbon nanotubes for nanoelectronics. Nanotechnol 15, 512 (2004).CrossRefGoogle Scholar
Lau, K.T., Chipara, M., Ling, H.Y., and Hui, D.: On the effective elastic moduli of carbon nanotubes for nanocomposite structures. Composites, Part B 35, 95 (2004).CrossRefGoogle Scholar
Barros, E.B., Jorio, A., Samsonidze, G.G., Capaz, R.B., Souza Filho, A.G., Mendes Filho, J., Dresselhaus, G., and Dresselhaus, M.S.: Review on the symmetry-related properties of carbon nanotubes. Phys. Rep. 431, 261 (2006).CrossRefGoogle Scholar
Lau, K.T., Gu, C., and Hui, D.: A critical review on nanotube and nanotube/nanoclay related polymer composite materials. Composites, Part B 37, 425 (2006).CrossRefGoogle Scholar
Tombler, T.W., Zhou, C., Alexseyev, L., Kong, J., Dai, H., Liu, L., Jayanthi, C.S., Tang, M., and Wu, S.Y.: Reversible electromechanical characteristics of carbon nanotubes under local-probe manipulation. Nature 405, 769 (2000).CrossRefGoogle ScholarPubMed
Liu, B., Jiang, H., Johnson, H.T., and Huang, Y.: The influence of mechanical deformation on the electrical properties of single wall carbon nanotubes. J. Mech. Phys. Solids 52, 1 (2004).CrossRefGoogle Scholar
Jiang, H., Liu, B., Huang, Y., and Hwang, K.C.: Thermal expansion of single wall carbon nanotubes. ASME J. Eng. Mater. Technol. 126, 265 (2004).CrossRefGoogle Scholar
Yakobson, B.I., Brabec, C.J., and Bernholc, J.: Structural mechanics of carbon nanotubes: From continuum elasticity to atomistic fracture. J. Comput.-Aided Mater. Des. 3, 173 (1996).CrossRefGoogle Scholar
Yakobson, B.I., Campbell, M.P., Brabec, C.J., and Bernholc, J.: High strain rate fracture and C-chain unraveling in carbon nanotubes. Comput. Mater. Sci. 8, 341 (1997).CrossRefGoogle Scholar
Liew, K.M., He, X.Q., and Wong, C.H.: On the study of elastic and plastic properties of multi-walled carbon nanotubes under axial tension using molecular dynamics simulation. Acta Mater. 52, 2521 (2004).CrossRefGoogle Scholar
Liew, K.M., Wong, C.H., He, X.Q., Tan, M.J., and Meguid, S.A.: Nanomechanics of single and multi-walled carbon nanotubes. Phys. Rev. B 69, 115429 (2004).CrossRefGoogle Scholar
Hernandez, E., Goze, C., Bernier, P., and Rubio, A.: Elastic properties of C and BxCyNz composite nanotubes. Phys. Rev. Lett. 80, 4502 (1998).CrossRefGoogle Scholar
Zhang, K. and Tadmor, E.B.: Energy and moiré patterns in 2D bilayers in translation and rotation: A study using an efficient discrete–continuum interlayer potential. Extreme Mech. Lett. 14, 16 (2017).CrossRefGoogle Scholar
Zhang, K. and Tadmor, E.B.: Structural and electron diffraction scaling of twisted graphene bilayers. J. Mech. Phys. Solids 112, 225 (2018).CrossRefGoogle Scholar
Aitken, Z.H. and Huang, R.: Effects of mismatch strain and substrate surface corrugation on morphology of supported monolayer graphene. J. Appl. Phys. 107, 123531 (2010).CrossRefGoogle Scholar
Zhang, K. and Arroyo, M.: Understanding and strain-engineering wrinkle networks in supported graphene through simulations. J. Mech. Phys. Solids 72, 61 (2014).CrossRefGoogle Scholar
Hu, N., Nunoya, K., Pan, D., Okabe, T., and Fukunaga, H.: Prediction of buckling characteristics of carbon nanotubes. Int. J. Solids Struct. 44, 6535 (2007).CrossRefGoogle Scholar
Liu, B., Huang, Y., Jiang, H., Qu, S., and Hwang, K.C.: The atomic-scale finite element method. Comput. Methods Appl. Mech. Eng. 193, 1849 (2004).CrossRefGoogle Scholar
He, X.Q., Kitipornchai, S., Wang, C.M., and Liew, K.M.: Modeling of van der Waals force for infinitesimal deformation of multi-walled carbon nanotubes treated as cylindrical shells. Int. J. Solids Struct. 42, 6032 (2005).CrossRefGoogle Scholar
Lu, W.B., Wu, J., Jiang, L.Y., Huang, Y., Hwang, K.C., and Liu, B.: A cohesive law for multi-wall carbon nanotubes. Philos. Mag. 87, 2221 (2007).CrossRefGoogle Scholar
Sears, A. and Batra, R.C.: Buckling of multiwalled carbon nanotubes under axial compression. Phys. Rev. B 73, 085410 (2006).CrossRefGoogle Scholar
Timesli, A., Braikat, B., Jamal, M., and Damil, N.: Prediction of the critical buckling load of multi-walled carbon nanotubes under axial compression. C. R. Mec. 345, 158 (2017).CrossRefGoogle Scholar
Guo, X., Wang, J.B., and Zhang, H.W.: Mechanical properties of single-walled carbon nanotubes based on higher order Cauchy–Born rule. Int. J. Solids Struct. 43, 1276 (2006).CrossRefGoogle Scholar
Guo, X., Liao, J.B., and Wang, X.Y.: Investigation of the thermo-mechanical properties of single-walled carbon nanotubes based on the temperature-related higher order Cauchy–Born rule. Comput. Mater. Sci. 51, 445 (2012).CrossRefGoogle Scholar
Wang, X.Y. and Guo, X.: Numerical simulation for finite deformation of single-walled carbon nanotubes at finite temperature using temperature-related higher order Cauchy–Born rule based quasi-continuum model. Comput. Mater. Sci. 55, 273 (2012).CrossRefGoogle Scholar
Sun, Y.Z. and Liew, K.M.: The buckling of single-walled carbon nanotubes upon bending: The higher order gradient continuum and mesh-free method. Comput. Methods Appl. Mech. Eng. 197, 3001 (2008).CrossRefGoogle Scholar
Wang, X.Y. and Guo, X.: Quasi-continuum model for the finite deformation of single-layer graphene sheets based on the temperature-related higher order Cauchy–Born rule. J. Comput. Theor. Nanosci. 10, 154 (2013).CrossRefGoogle Scholar
Wang, X.Y., Wang, J.B., and Guo, X.: Finite deformation of single-walled carbon nanocones under axial compression using a temperature-related multiscale quasi-continuum model. Comput. Mater. Sci. 114, 244 (2016).CrossRefGoogle Scholar
Wang, X.Y., Guo, X., and Su, Z.: A quasi-continuum model for human erythrocyte membrane based on the higher order Cauchy–Born rule. Comput. Methods Appl. Mech. Eng. 268, 284 (2014).CrossRefGoogle Scholar
Xiang, P. and Liew, K.M.: Predicting buckling behavior of microtubules based on an atomistic-continuum model. Int. J. Solids Struct. 48, 1730 (2011).CrossRefGoogle Scholar
Arroyo, M. and Belytschko, T.: An atomistic-based finite deformation membrane for single layer crystalline films. J. Mech. Phys. Solids 50, 1941 (2002).CrossRefGoogle Scholar
Arroyo, M. and Belytschko, T.: Nonlinear mechanical response and rippling of thick multiwalled carbon nanotubes. Phys. Rev. Lett. 91, 215505 (2003).10.1103/PhysRevLett.91.215505CrossRefGoogle ScholarPubMed
Arroyo, M. and Belytschko, T.: Finite element methods for the non-linear mechanics of crystalline sheets and nanotubes. Int. J. Numer. Methods Eng. 59, 419 (2004).CrossRefGoogle Scholar
Wang, X.Y. and Guo, X.: Quasi-continuum contact model for the simulation of severe deformation of single-walled carbon nanotubes at finite temperature. J. Comput. Theor. Nanosci. 10, 810 (2013).CrossRefGoogle Scholar
Gao, H. and Klein, P.: Numerical simulation of crack growth in an isotropic solid with randomized internal cohesive bonds. J. Mech. Phys. Solids 46, 187 (1998).CrossRefGoogle Scholar
Atluri, S.N. and Zhu, T.: A new Meshless Local Petrov-Galerkin (MLPG) approach in computational mechanics. Comput. Mech. 22, 117 (1998).CrossRefGoogle Scholar
Atluri, S.N. and Zhu, T.: A new meshless local Petrov–Galerkin (MLPG) approach to nonlinear problems in computer modeling and simulation. Comput. Model. Simul. Eng. 3, 187 (1998).Google Scholar
Brenner, D.W.: Empirical potential for hydrocarbons for use in simulating the chemical vapor deposition of diamond films. Phys. Rev. B 42, 9458 (1990).CrossRefGoogle ScholarPubMed
Lennard-Jones, J.E.: The determination of molecular fields: From the variation of the viscosity of a gas with temperature. Proc. R. Soc. 106, 441 (1924).CrossRefGoogle Scholar
Girifalco, L.A., Hodak, M., and Lee, R.S.: Carbon nanotubes, buckyballs, ropes, and a universal graphitic potential. Phys. Rev. B 62, 13104 (2000).CrossRefGoogle Scholar
Lancaster, P. and Salkauskas, K.: Surfaces generated by moving least squares methods. Math. Comput. 37, 141 (1981).CrossRefGoogle Scholar
Iijima, S., Brabec, C., Maiti, A., and Bernholc, J.: Structural flexibility of carbon nanotubes. J. Chem. Phys. 104, 2089 (1996).CrossRefGoogle Scholar