Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Lewandowski, R
and
Lenkowska, A
2017.
Steady-state response of systems with fractional dampers.
IOP Conference Series: Materials Science and Engineering,
Vol. 251,
Issue. ,
p.
012091.
Lewandowski, Roman
and
Wielentejczyk, Przemysław
2017.
Nonlinear vibration of viscoelastic beams described using fractional order derivatives.
Journal of Sound and Vibration,
Vol. 399,
Issue. ,
p.
228.
Duan, Jun-Sheng
Cheng, Cui-Ping
and
Chen, Lian
2017.
A comparison study of steady-state vibrations with single fractional-order and distributed-order derivatives.
Open Physics,
Vol. 15,
Issue. 1,
p.
809.
Duan, Jun-Sheng
and
Baleanu, Dumitru
2018.
Steady periodic response for a vibration system with distributed order derivatives to periodic excitation.
Journal of Vibration and Control,
Vol. 24,
Issue. 14,
p.
3124.
Duan, Lingjie
and
Duan, Junsheng
2018.
A Generalized Constitutive Equation with Distributed Order Derivative for Viscoelastic SolidA Generalized Constitutive Equation with Distributed Order Derivative for Viscoelastic Solid.
International Journal of Materials, Mechanics and Manufacturing,
Vol. 6,
Issue. 3,
p.
191.
Duan, Jun-Sheng
and
Qiu, Xiang
2018.
Stokes’ second problem of viscoelastic fluids with constitutive equation of distributed-order derivative.
Applied Mathematics and Computation,
Vol. 331,
Issue. ,
p.
130.
Duan, Jun-Sheng
and
Xu, Yun-Yun
2019.
Vibration Equation of Fractional Order Describing Viscoelasticity and Viscous Inertia.
Open Physics,
Vol. 17,
Issue. 1,
p.
850.
Yin, Yue
and
Wang, Luyao
2020.
Research on personal financial data storage medium system based on fractional order calculus encryption algorithm.
Chaos, Solitons & Fractals,
Vol. 131,
Issue. ,
p.
109459.
Li, Yu
and
Duan, Jun-Sheng
2020.
The periodic response of a fractional oscillator with a spring-pot and an inerter-pot.
Journal of Mechanics,
Vol. 37,
Issue. ,
p.
108.
Duan, Jun-Sheng
and
Chen, Lian
2020.
Oscillatory shear flow between two parallel plates for viscoelastic constitutive model of distributed-order derivative.
International Journal of Numerical Methods for Heat & Fluid Flow,
Vol. 30,
Issue. 3,
p.
1137.
Liu, Xiaohan
and
Shi, Guangfeng
2020.
Residual stress detection of welded parts based on excitation vibration response.
International Journal of Advanced Robotic Systems,
Vol. 17,
Issue. 1,
Duan, Jun-Sheng
and
Hu, Di-Chen
2021.
Vibration Systems with Fractional-Order and Distributed-Order Derivatives Characterizing Viscoinertia.
Fractal and Fractional,
Vol. 5,
Issue. 3,
p.
67.
Huang, Lewei
Xiao, Changwang
Cao, Mingyue
and
Li, Xuran
2025.
Fractal damping optimization (FDO): A novel metaheuristic algorithm inspired by fractional-order vibration systems.
Journal of Computational Methods in Sciences and Engineering,
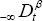 . First we investigated the response to the harmonic excitation in the form of complex exponential function. The amplitude-frequency relation and phase-frequency relation were derived. The effect of the fractional derivative term on the stiffness and damping was discussed. For the case of periodic excitation, we decompose the periodic excitation into a superposition of harmonic excitations by using the Fourier series, and then utilize the results for harmonic excitations and the principle of superposition, where our adopted tactics avoid appearing a fractional power of negative numbers to overcome the difficulty in fractional case. Finally we demonstrate the proposed method by three numerical examples.
. First we investigated the response to the harmonic excitation in the form of complex exponential function. The amplitude-frequency relation and phase-frequency relation were derived. The effect of the fractional derivative term on the stiffness and damping was discussed. For the case of periodic excitation, we decompose the periodic excitation into a superposition of harmonic excitations by using the Fourier series, and then utilize the results for harmonic excitations and the principle of superposition, where our adopted tactics avoid appearing a fractional power of negative numbers to overcome the difficulty in fractional case. Finally we demonstrate the proposed method by three numerical examples.
