Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-28T20:23:07.887Z Has data issue: false hasContentIssue false
  • English
  • Français

A Derivation of Stiffness and Damping Coefficients for Short Hydrodynamic Journal Bearings with Pseudo-Plastic Lubricants

Published online by Cambridge University Press:  14 October 2020

Zhuxin Tian Open the ORCID record for Zhuxin Tian [Opens in a new window]  and
Runchang Chen
Zhuxin Tian*
Affiliation:
School of Mechanical Engineering, Hubei University of Arts and Science, Xiangyang, PR China State Key Lab of Digital Manufacturing Equipment and Technology, Huazhong University of Science and Technology, Wuhan, PR China
Runchang Chen
Affiliation:
School of Mechanical Engineering, Hubei University of Arts and Science, Xiangyang, PR China State Key Lab of Digital Manufacturing Equipment and Technology, Huazhong University of Science and Technology, Wuhan, PR China
*
*Corresponding author (zhuxintian1987@sina.com)
Get access

Abstract

A new derivation considering the non-linear terms has been proposed to calculate stiffness and damping coefficients for short hydrodynamic journal bearings lubricated with pseudo-plastic fluids. The proposed method has relaxed the constraint of small perturbation method applicable to only small values of non-Newtonian factor α. An analytical solution is also given. The non-linear Reynolds equation is solved with a more reasonable boundary condition ∂p*/∂z* = 0 at the location of z*=0 while the analytical pressure distribution is obtained by seven-point Gauss-Legendre integral formula. When the non-dimensional non-Newtonian factor α is small, the stiffness and damping coefficients of computed by the proposed method can agree well with those from small perturbation method, which could verify the proposed derivation. As for large non-dimensional non-Newtonian factor α, the stiffness coefficients 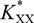$K_{XX}^*$ , 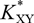$K_{XY}^*$ and 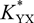$K_{YX}^*$ as well as the damping coefficients 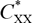$C_{XX}^*$ , 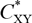$C_{XY}^*$ and 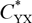$C_{YX}^*$ decrease with the increasing of non-dimensional non-Newtonian factor α. The significance of the derivation is that it can relax the constraint of small α and simplify the computation process.

Keywords

Stiffness and damping coefficientsShort journal bearingsPseudo-plastic fluidsnon-Newtonian factor
Type
Research Article
Information
Journal of Mechanics , Volume 36 , Issue 6 , December 2020 , pp. 943 - 953
Copyright
Copyright © 2020 The Society of Theoretical and Applied Mechanics

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Khonsari, M. M. and Chang, Y. J., “Stability boundary of non-linear orbits within clearance circle of journal bearings”. Journal of Vibration and Acoustics, 115, pp. 303-307 (1993).CrossRefGoogle Scholar
Huang, Y., Tian, Z., Chen, R. and Cao, H., “A simpler method to calculate instability threshold speed of hydrodynamic journal bearings”. Mechanism and Machine Theory, 108, pp. 209-216 (2017).CrossRefGoogle Scholar
Lund, J. W. and Thomsen, K. K., “A calculation method and data for the dynamic coefficients of oil lubricated journal bearings: topics in fluid journal bearing and rotor bearing system design and optimization”. ASME, 1, pp. 1–28 (1978).Google Scholar
Jang, G. H. and Kim, Y. J., “Calculation of dynamic coefficients in a hydrodynamic bearing considering five degrees of freedom for a general rotor-bearing system”. Journal of Tribology, 121, pp. 499-505 (1999).CrossRefGoogle Scholar
Crooijmans, M. T., Brouwers, H. J. and Van Campen, D. H., “Limit cycle predictions of a nonlinear journal-bearing system”. Journal of Engineering for Industry, 112, pp. 168-171 (1990).CrossRefGoogle Scholar
Wang, J. K. and Khonsari, M. M., “A new derivation for journal bearing stiffness and damping coefficients in polar coordinates”. Journal of Sound and Vibration, 290, pp. 500-507 (2006).CrossRefGoogle Scholar
Wada, S. and Hayashi, H., “Hydrodynamic lubrication of journal bearings by pseudo-plastic lubricants: part 1, theoretical studies”. Bulletin of the JSME, 14, pp. 268-278 (1971).CrossRefGoogle Scholar
Wada, S. and Hayashi, H., “Hydrodynamic lubrication of journal bearings by pseudo-plastic lubricants: part 2, experimental studies”. Bulletin of the JSME, 14, pp. 279-286 (1971).CrossRefGoogle Scholar
Sheela-Francisca, J., Tso, C. P. and Hung, Y. M., “Heat transfer on asymmetric thermal viscous dissipative Couette–Poiseuille flow of pseudo-plastic fluids”. Journal of Non-Newtonian Fluid Mechanics, 169, pp. 42-53 (2012).CrossRefGoogle Scholar
Mitsoulis, E., “Fountain flow of pseudo-plastic and viscoplastic fluids”. Journal of Non-Newtonian Fluid Mechanics, 165, pp. 45-55 (2012).CrossRefGoogle Scholar
Mitsoulis, E., “Annular extrudate swell of pseudo-plastic and viscoplastic fluids”. Journal of Non-Newtonian Fluid Mechanics, 141, pp. 138-147 (2007).CrossRefGoogle Scholar
Rajalingam, C., Rao, B. V. A. and Prabhu, B. S., “The effect of a non-Newtonian lubricant on piston ring lubrication”. Wear, 50, pp. 47-57 (1978).10.1016/0043-1648(78)90244-2CrossRefGoogle Scholar
Malik, M., Dass, B. and Sinhasan, R., “Performance characteristics of a centrally loaded 120 partial journal bearings using pseudoplastic lubricants”. Tribology International, 16, pp. 9-16 (1983).CrossRefGoogle Scholar
Sharma, S. C. and Saurabh, K. Y., “Performance of hydrostatic circular thrust pad bearing operating with Rabinowitsch fluid model”. Journal of Engineering Tribology, 227, pp. 1272-1284 (2013).Google Scholar
Huang, Y. and Tian, Z., “A new derivation to study the steady performance of hydrostatic thrust bearing: Rabinowitch fluid model”. Journal of Non-Newtonian Fluid Mechanics, 246, pp. 31-35 (2017).CrossRefGoogle Scholar
Singh, U. P., Ram, S. G. and Vijay, K. K., “On the squeeze film characteristics between a long cylinder and a flat plate: Rabinowitsch model”. Journal of Engineering Tribology, 227, pp. 34-42 (2013).Google Scholar
Hashimoto, H. and Wada, S., “The effects of fluid inertia forces in parallel circular squeeze film bearings lubricated with pseudo-plastic fluids”. Journal of Tribology, 108, pp. 282-287 (1986).CrossRefGoogle Scholar
Lin, J. R., Hung, T. C. and Lin, C. H., “Linear Stability Analysis of Journal Bearings Lubricated with a Non-Newtonian Rabinowitsch Fluid”. Journal of Mechanics, 35, pp. 107-112 (2019).CrossRefGoogle Scholar
Swamy, S. T. N., “The influence of non-Newtonian oil film short journal bearings on the stability of a rigid rotor”. Wear, 43, pp. 155-164 (1977).CrossRefGoogle Scholar
Nessil, A., Larbi, S., Belhaneche, H. and Malki, M., “Journal bearings lubrication aspect analysis using non-Newtonian fluids”. Advances in Tribology, 1, pp. (2013).Google Scholar
Boubendir, S., Larbi, S., Malki, M. and Bennacer, R., “Hydrodynamic self-lubricating journal bearings analysis using Rabinowitsch fluid lubricant”. Tribology International, 140, 105856 (2019).CrossRefGoogle Scholar
Sharma, S. C., Jain, S. C., Sinhasan, R. and Sah, P. L., “Static and dynamic performance characteristics of orifice compensated hydrostatic flexible journal bearings with non-Newtonian lubricants”. Tribology transactions, 44, pp. 242-248 (2001).CrossRefGoogle Scholar
Rao, P. S., Rahul, A. K. and Agarwal, S., “Effect of non-Newtonian lubrication of squeeze film conical bearing with the porous wall operating with Rabinowitsch fluid model”. Journal of Engineering Tribology, 232, pp. 1293-1303 (2018).Google Scholar
Swamy, S. T. N., Prabhu, B. S. and Rao, B. V. A., “Stiffness and damping characteristics of finite width journal bearings with a non-Newtonian film and their application to instability prediction”. Wear, 32, pp. 379-390 (1975).CrossRefGoogle Scholar
Neumark, S., Solution of cubic and quartic equations. Elsevier, Amsterdam (2014).Google Scholar
Lin, J. R., “Linear stability analysis of rotor-bearing system: couple stress fluid model”. Computers & Structures 79, pp. 801-809 (2001).CrossRefGoogle Scholar
Tian, Z. and Huang, Y., “Transformation between polar and rectangular coordinates of stiffness and dampness parameters in hydrodynamic journal bearings”. Friction, 1, pp. 1-6 (2020).Google Scholar