Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-10T14:06:53.718Z Has data issue: false hasContentIssue false
  • English
  • Français

Local positioning system as a classic alternative to atomic navigation

Published online by Cambridge University Press:  22 March 2022

B. Dubetsky
B. Dubetsky*
Affiliation:
Independent Researcher, 1849 S Ocean Dr, Apt 207, Hallandale, FL33009, USA
*
*Corresponding author. E-mail: bdubetsky@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

A local positional system (LPS) is proposed, in which particles are launched at given velocities, and a sensor system measures the trajectory of the particles in the platform frame. These measurements allow us to restore the position and orientation of the platform in the frame of the rotating Earth, without solving navigation equations. When the platform velocity is known and if the platform orientation stays the same, the LPS technique allows a navigational accuracy of 100 $\mu$m per one hour to be achieved. In this case, the LPS technique is insensitive to the type of platform trajectory. If there are also velocimeters installed on the platform, then one can restore the platform velocity and angular rate of the platform rotation with respect to the Earth. Instead of navigational equations, it is necessary to obtain the classical trajectory of a particle in the field of a rotating gravity source. Taking into account the gravity-gradient, Coriolis, and centrifugal forces, the exact expression for this trajectory is derived, which can be widely used in atomic interferometry. A new iterative method for restoring the orientation of the platform without using gyroscopes is developed. 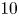The simulation allows us to determine the conditions under which the LPS navigation error per hour is approximately $10$ m.

Keywords

GPSDoppler velocity log (DVL)dynamic positioning (DP)navigationnumerical simulation03.75.Dg37.25.+k04.80.-y
Type
Research Article
Information
The Journal of Navigation , Volume 75 , Issue 2 , March 2022 , pp. 273 - 298
Check for updates
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press on behalf of The Royal Institute of Navigation

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abe, M., Adamson, P., Borcean, M., Bortoletto, D., Bridges, K., Carman, S. P., Chattopadhyay, S., Coleman, J., Curfman, N. M., DeRose, K., Deshpande, T., Dimopoulos, S., Foot, C. J., Frisch, J. C., Garber, B. E., Geer, S., Gibson, V., Glick, J., Graham, P. W., Hahn, S. R., Harnik, R., Hawkins, L., Hindley, S., Hogan, J. M., Jiang, Y., Kasevich, M. A., Kellett, R. J., Kiburg, M., Kovachy, T., Lykken, J. D., March-Russell, J., Mitchell, J., Murphy, M., Nantel, M., Nobrega, L. E., Plunkett, R. K., Rajendran, S., Rudolph, J., Sachdeva, N., Safdari, M., Santucci, J. .K, Schwartzman, A. G., Shipsey, I., Swan, H., Valerio, L. R., Vasonis, A., Wang, Y. and Wilkason, T. (2021). Matter-wave Atomic Gradiometer Interferometric Sensor (MAGIS-100), arXiv:2104.02835 [physics.atom-ph]Google Scholar
Ahmed, M. S. and Cuk, D. V. (2005). Comparison of different computation methods for strapdown inertial navigation systems. Scientific and Technical Review, LV, 22.Google Scholar
Asenbaum, P., Overstreet, C., Kim, M., Curti, J. and Kasevich, M. A. (2020). Atom-interferometric test of the equivalence principle at the $10^{-12}$ level. Physical Review Letters, 125, 191101.CrossRefGoogle ScholarPubMed
Badurina, L., Bentine, E., Blas, D., Bongs, K., Bortoletto, D., Bowcock, T., Bridges, K., Bowden, W., Buchmueller, O., Burrage, C., Coleman, J., Elertas, G., Ellis, J., Foot, C., Gibson, V., Haehnelt, M. G., Harte, T., Hedges, S., Hobson, R., Holynski, M., Jones, T., Langlois, M., Lellouch, S., Lewicki, M., Maiolino, R., Majewski, P., Malik, S., March-Russell, J., McCabe, C., Newbold, D., Sauer, B., Schneider, U., Shipsey, I., Singh, Y., Uchida, M. A., Valenzuela, T., van der Grinten, M., Vaskonen, V., Vossebeld, J., Weatherill, D. and Wilmut, I. (2020). AION: an atom interferometer observatory and network. Journal of Cosmology and Astroparticle Physics, 2020, JCAP05(2020)011. https://iopscience.iop.org/article/10.1088/1475-7516/2020/05/011CrossRefGoogle Scholar
Battelier, B., Bergé, J., Bertoldi, A., Blanchet, L., Bongs, K., Bouyer, P., Braxmaier, C., Calonico, D., Fayet, P., Gaaloul, N., Guerlin, C., Hees, A., Jetzer, P., Lämmerzahl, C., Lecomte, S., Le Poncin-Lafitte, C., Loriani, S., Métris, G., Nofrarias, M., Rasel, E., Reynaud, S., Rodrigues, M., Rothacher, M., Roura, A., Salomon, C., Schiller, S., Schleich, W. P., Schubert, C., Sopuerta, C. F., Sorrentino, F., Sumner, T. J., Tino, G. M., Tuckey, P., von Klitzing, W., Wörner, L., Wolf, P. and Zelan, M. (2019). Exploring the Foundations of the Universe with Space Tests of the Equivalence Principle. arXiv:1908.11785v3 [physics.space-ph]Google Scholar
Bongs, K., Launay, R. and Kasevich, M. A. (2006). High-order inertial phase shifts for time-domain atom interferometers. Applied Physics B, 84, 599.CrossRefGoogle Scholar
Box, G. E. P. and Muller, M. E. (1958). A note on the generation of random normal deviates. The Annals of Mathematical Statistics, 29, 610.10.1214/aoms/1177706645CrossRefGoogle Scholar
Canciani, A. (2012). Integration of cold atom interferometry ins with other sensors. Master's thesis, Second Lieutenant, Air Force Institute of Technology (USAF).Google Scholar
Canuel, B., Abend, S., Amaro-Seoane, P., Badaracco, F., Beaufils, Q., Bertoldi, A., Bongs, K., Bouyer, P., Braxmaier, C., Chaibi, W., Christensen, N., Fitzek, F., Flouris, G., Gaaloul, N., Gaffet, S., Garrido Alzar, C. L., Geiger, R., Guellati-Khelifa, S., Hammerer, K., Harms, J., Hinderer, J., Holynski, M., Junca, J., Katsanevas, S., Klempt, C., Kozanitis, C., Krutzik, M., Landragin, A., Roche, I., Leykauf, B., Lien, Y.-H., Loriani, S., Merlet, S., Merzougui, M., Nofrarias, M., Papadakos, P., Pereira Dos Santos, F., Peters, A., Plexousakis, D., Prevedelli, M., Rasel, E. M., Rogister, Y., Rosat, S., Roura, A., Sabulsky, D. O., Schkolnik, V., Schlippert, D., Schubert, C., Sidorenkov, L., Siemß, J.-N., Sopuerta, C. F., Sorrentino, F., Struckmann, C. and Tino, G. M. (2020). Technologies for the ELGAR Large Scale Atom Interferometer Array. arXiv:2007.04014v1 [physics.atom-ph]Google Scholar
Canuel, B., Leduc, F., Holleville, D., Gauguet, A., Fils, J., Virdis, A., Clairon, A., Dimarcq, N., Borde, Ch. J. and Landragin, A. (2006). 6-axis inertial sensor using cold-atom interferometry. Physical Review Letters, 97, 010402.CrossRefGoogle Scholar
Cheiney, P., Fouché, L., Templier, S., Napolitano, F., Battelier, B., Bouyer, P. and Barrett, B. (2018). Navigation-compatible hybrid quantum accelerometer using a Kalman filter. Physical Review Applied, 10, 034030CrossRefGoogle Scholar
Chui, C. K. and Chen, G. (1999). Kalman filtering with real-time applications. Berlin, Heidelberg: Springer, Sec. 1.1.CrossRefGoogle Scholar
Committee on Earth Gravity from Space (1997). In: Satellite Gravity and the Geosphere: Contributions to the Study of the Solid Earth and Its Fluid Envelopes. Washington, DC: National Academies Press, 13.Google Scholar
Dubetskii, B. Ya., Kazantsev, A. P., Chebotayev, V. P. and Yakovlev, V. P. (1984). Interference of atoms in separated optical fields. Pis'ma v Zhurnal Éksperimental'noi i Teoreticheskoi Fiziki, 39, 531 [JETP Lett. 39, 649 (1984)].Google Scholar
Dubetsky, B. and Kasevich, M. A. (2006). Atom interferometer as a selective sensor of rotation or gravity. Physical Review A, 74, 023615.CrossRefGoogle Scholar
El-Neaj, Y. A., Alpigiani, C., Amairi-Pyka, S., Araújo, H., Balaž, A., Bassi, A., Bathe-Peters, L., Battelier, B., Belić, A., Bentine, E., Bernabeu, J., Bertoldi, A., Bingham, R., Blas, D., Bolpasi, V., Bongs, K., Bose, S., Bouyer, P., Bowcock, T., Bowden, W., Buchmueller, O., Burrage, C., Calmet, X., Canuel, B., Caramete, L., Carroll, A., Cella, G., Charmandaris, V., Chattopadhyay, S., Chen, X., Chiofalo, M. L., Coleman, J., Cotter, J., Cui, Y., Derevianko, A., De Roeck, A., Djordjevic, G. S., Dornan, P., Doser, M., Drougkakis, I., Dunningham, J., Dutan, I., Easo, S., Elertas, G., Ellis, J., El Sawy, M., Fassi, F., Felea, D., Feng, C.-H., Flack, R., Foot, C., Fuentes, I., Gaaloul, N., Gauguet, A., Geiger, R., Gibson, V., Giudice, G., Goldwin, J., Grachov, O., Graham, P. W., Grasso, D., van der Grinten, M., Gündogan, M., Haehnelt, M. G., Harte, T., Hees, A., Hobson, R., Hogan, J., Holst, B., Holynski, M., Kasevich, M., Kavanagh, B. J., von Klitzing, W., Kovachy, T., Krikler, B., Krutzik, M., Lewicki, M., Lien, Y.-H., Liu, M., Luciano, G. G., Magnon, A., Mahmoud, M. A., Malik, S., McCabe, C., Mitchell, J., Pahl, J., Pal, D., Pandey, S., Papazoglou, D., Paternostro, M., Penning, B., Peters, A., Prevedelli, M., Puthiya-Veettil, V., Quenby, J., Rasel, E., Ravenhall, S., Ringwood, J., Roura, A., Sabulsky, D., Sameed, M., Sauer, B., Schäffer, S. A., Schiller, S., Schkolnik, V., Schlippert, D., Schubert, C., Sfar, H. R., Shayeghi, A., Shipsey, I., Signorini, C., Singh, Y., Soares-Santos, M., Sorrentino, F., Sumner, T., Tassis, K., Tentindo, S., Tino G, M., Tinsley, J. N., Unwin, J., Valenzuela, T., Vasilakis, G., Vaskonen, V., Vogt, C., Webber-Date, A., Wenzlawski, A., Windpassinger, P., Woltmann, M., Yazgan, E., Zhan, M.-S., Zou, X. and Zupan, J. (2020). AEDGE: atomic experiment for dark matter and gravity exploration in space. EPJ Quantum Technology, 7, 6.CrossRefGoogle Scholar
Groten, E. (2000). Parameters of common relevance of astronomy, geodesy, and geodynamics, pp. 134–140 in H. Moritz, Geodetic reference system 1980. Journal of Geodesy, 74, 128.Google Scholar
Heiskanen, W. A. and Moritz, H. (1967). Physical Geodesy. San Francisco: W. H. Freeman and Co., Sec. 2-9.Google Scholar
Hogan, J. M., Johnson, D. M. S. and Kasevich, M. A. (2008). Light-pulse Atom Interferometry. arXiv:0806.3261 [physics.atom-ph], appear in the Proceedings of the International Summer School of Physics ‘Enrico Fermi’ on Atom Optics and Space Physics (Varenna, July 2007).Google Scholar
Jekeli, C. (2001). Inertial Navigation Systems with Geodetic Applications. Berlin, New York: de Gruyter.CrossRefGoogle Scholar
Jekeli, C., Lee, J. K. and Kwon, J. H. (2007). Modeling errors in upward continuation for INS gravity compensation. Journal of Geodesy, 81, 297.CrossRefGoogle Scholar
Kasevich, M. and Chu, S. (1991). Atomic interferometry using stimulated Raman transitions. Physical Review Letters, 67, 181.CrossRefGoogle ScholarPubMed
Kasevich, M. A. and Dubetsky, B. (2005). Kinematic Sensors Employing Atom Interferometer Phases. US Patent 7, 317, 184.Google Scholar
Kasevich, M. A. and Dubetsky, B. (2008) The phase of an atom interferometer as a direct source for precise navigation. Private communication.Google Scholar
Kleinerta, S., Kajaria, E., Roura, A. and Schleich, W. P. (2015). Representation-free description of light-pulse atom interferometry including non-inertial effects. Physics Reports, 605, 1.CrossRefGoogle Scholar
Kotkin, G. L. and Serbo, V. G. (1971). Collection of Problems in Classical Mechanics. Oxford, New York: Pergamon Press, problem 6.23.Google Scholar
Lautier, J., Volodimer, L., Hardin, T., Merlet, S., Lours, M., Pereira Dos Santos, F. and Landragin, A. (2014). Hybridizing matter-wave and classical accelerometers. Applied Physics Letters, 105, 144102.CrossRefGoogle Scholar
Ramsey, N. F. (1949). A new molecular beam resonance method. The Physical Review, 76, 996.10.1103/PhysRev.76.996CrossRefGoogle Scholar
Rodrigues, O. (1840). Des lois géométriques qui ré gissent les déplacements d'un système solide dans l'espace, et de la variation des coordonnées provenant de ces déplacements considér és indépendants des causes qui peuvent les produire. Journal de Math ématiques Pures et Appliquées, 5, 380.Google Scholar
Shebshaevich, V. S., Dmitriev, P. P., Ivancevich, N. V., Kalugin, A. V., Kovalevsky, E. G., Kudryavtsev, I. V., Kutikov, V. Yu., Molchanov, Yu. B. and Maksyutenko, Yu. A. (1993). Setevye sputnikovye radionavigatsionnye sistemy. Moscow: RADIO I SVYAZ’, 220 (in Russian).Google Scholar
Tino, G. M, Bassi, A., Bianco, G., Bongs, K., Bouyer, P., Cacciapuoti, L., Capozziello, S., Chen, X., Chiofalo, M. L., Derevianko, A., Ertmer, W., Gaaloul, N., Gill, P., Graham, P. W., Hogan, J. M., Iess, L., Kasevich, M. A., Katori, H., Klempt, C., Lu, X., Ma, L.-S., Müller, H., Newbury, N. R., Oates, C. W., Peters, A., Poli, N., Rasel, E. M., Rosi, G., Roura, A., Salomon, C., Schiller, S., Schleich, W., Schlippert, D., Schreck, F., Schubert, C., Sorrentino, F., Sterr, U., Thomsen, J. W., Vallone, G., Vetrano, F., Villoresi, P., von Klitzing, W., Wilkowski, D., Wolf, P., Ye, J., Yu, N. and Zhan, M. (2019). SAGE: A proposal for a space atomic gravity explorer. The European Physical Journal D, 73, 228.CrossRefGoogle Scholar
Tino, G. M. and Kasevich(ed), M. A. (2014). Atom interferometry. Proceedings of the International School of Physics ‘Enrico Fermi’. Vol. 188. IOS Press.Google Scholar
Wang, Y. M. (2001). GSFCO0 mean sea surface, gravity anomaly, and vertical gravity gradient from satellite altimeter data. Journal of Geophysical Research, 106, 31167.CrossRefGoogle Scholar
Wang, Y. M. (2016). Geodetic Boundary Value Problems. In: Grafarend E. W. (ed.). Encyclopedia of Geodesy. Switzerland: Springer International Publishing (Outside the USA).Google Scholar
Wang, X., Kealy, A., Gilliam, C., Haine, S., Close, J., Moran, B., Talbot, K., Williams, S., Hardman, K., Freier, C., Wigley, P., White, A., Szigeti, S. and Legge, S. (2021). Enhancing Inertial Navigation Performance via Fusion of Classical and Quantum Accelerometers. arXiv:2103.09378v1 [quant-ph]Google Scholar
Wu, Y., Guo, J., Feng, X., Chen, L. Q., Yuan, C.-H. and Zhang, W. (2020). Atom-light hybrid quantum gyroscope. Physical Review Applied, 14, 064023.CrossRefGoogle Scholar
Yu, J., Jekeli, C. and Zhu, M. (2003). Analytical solutions of the Dirichlet and Neumann boundary-value problems with an ellipsoidal boundary. Journal of Geodesy, 76, 653–667.CrossRefGoogle Scholar
Zhan, M.-S., Wang, J., Ni, W.-T., Gao, D.-F., Wang, G., He, L.-X., Li, R.-B., Zhou, L., Chen, X., Zhong, J.-Q., Tang, B., Yao, Z.-W., Zhu, L., Xiong, Z.-Y., Lu, S.-B., Yu, G.-H., Cheng, Q.-F., Liu, M., Liang, Y.-R., Xu, P., He, X.-D., Ke, M., Tan, Z. and Luo, J. (2020). ZAIGA: Zhaoshan long-baseline atom interferometer gravitation antenna. International Journal of Modern Physics D, 29, 194005CrossRefGoogle Scholar