1. INTRODUCTION
The use of network Real Time Kinematic (RTK) Global Positioning System (GPS) positioning has become an important solution for many high precision applications. For the best positioning services using current techniques, the average baseline length between reference stations has to be limited to between 30 km and 80 km. However, setting up dense reference station networks in developing countries, or regions where there are access constraints, can pose difficulties. For instance, a selected reference station site must have a good observation environment, be stable, have access to power and have cabled or wireless internet or intranet. This means that it is normally very expensive to construct and manage a network of reference stations. At the same time, the demand for network RTK positioning services has been growing among the GPS user community which requires accurate and seamless kinematic position over longer distances. So it is necessary and useful to develop relevant techniques for sparse network RTK positioning and assess the resulting performance.
There are three essential technologies for achieving real-time positioning of centimetre accuracy using a sparse network. The first is the data processing for a long-range reference network to produce reliable RTK corrections, the second is the interpolation method of error models for the computation of the rover corrections according to the RTK corrections and finally the methods to be used for long-range real-time kinematic ambiguity resolution (AR) for the rover receivers.
Many researchers have proposed useful methods and developed relevant algorithms for long-range reference network ambiguity resolution. Sun et al. (1999) introduced a sequential least-square estimation algorithm for real-time network ambiguity resolution over a network of reference stations spaced 100 km to 200 km apart. Dai et al. (Reference Dai, Wang, Rizos and Han2003) and Chen et al. (Reference Chen, Rizos and Han2004) introduced the techniques for real-time integer ambiguity resolution using atmospheric delay derived from the system initialization process and the atmospheric biases estimated from previous epochs. Hu et al. (2005) proposed an ionosphere-weighted measurement model for instantaneous network ambiguity resolution with medium- to long-range receiver separations (30 km ∼ 130 km).
Network-derived ionospheric and geometric corrections were employed in precise relative positioning (Cannon et al., Reference Cannon, Lachapelle, Fortes, Alves and Townsend2001; Rizos, Reference Rizos2002; Wielgosz et al., Reference Wielgosz, Grejner-Brzezinska and Kashani2004; Kashani I, 2004). Dai et al. (Reference Dai, Han, Wang and Rizos2004) summarized the available error interpolation methods for network RTK positioning. Kashani (2004) proposed that the double-differenced (DD) ionospheric delays estimated from the previous epoch with a successful integer fix can be used as the prediction for the current epoch, but a latency of 90 seconds seemed to be a limit for reliable instantaneous AR. Grgic et al. (Reference Grgic, Kealy, Gordini, Hale and Retscher2006) presented a method using a Low-Order Surface Model (LSC) that can significantly increase the interpolated correction accuracy. Mohino et al. (Reference Mohino, Gende and Brunini2007) developed a technique to estimate the vertical total electron content (VTEC) from the La Plata ionospheric model and so computed the slant total electron content (STEC) for receivers of unknown coordinates.
Long range RTK ambiguity resolution for rover receivers has been the important work in RTK GPS positioning. Kim et al. (2000) presented that there were 325 papers on ambiguity resolution and validation before 2000 for static, rapid static, kinematic and navigation applications. Edwards et al. (1999) presented a number of tests which, together, might form the basis of a methodology for assessing the performance of a RTK GPS system. Dai et al. (2000) proposed an integrated three-step procedure for the ambiguity resolution of medium-range baselines. Colombo et al. (Reference Colombo, Hernandez-Pajares, Juan and Sanz2000) and Kashani et al. (2004) presented case studies for baselines over 100 km. Dai et al. (Reference Dai, Eslinger and Sharpe2007) used partial search-and-fix strategies during the parameter estimation of a Kalman filter. Grejner-Brzezinska et al. (Reference Grejner-Brzezinska, Kashani and Wielgosz2005) developed a multiple reference station approach for regional differential kinematic GPS positioning. The primary processing algorithms used in this study include a weighted free-net (WFN) approach with the distance-dependent weighting scheme to derive optimal estimates of the user coordinates and realistic accuracy measures. The WFN approach is combined with a single epoch (instantaneous) ambiguity resolution algorithm for baselines exceeding 100 km.
Previous research mainly focused on data processing and instantaneous ambiguity resolution of reference stations with inter-station distances of 100 km to 200 km. For a sparse network RTK system with the inter-station distance up to 300 km, novel methods and algorithms for network data processing and integer ambiguity resolution needed further study. This paper proposes a set of technologies that includes a Delaunay triangulation method to form the optimal network triangles, a three-step approach for double-differenced ambiguity resolution between reference stations and generation of network corrections, correction interpolation for the rover receivers and a long range kinematic ambiguity resolution algorithm. Using these techniques, a test network of ten reference stations and nine simulated rover stations was formed to assess the performance of proposed methodologies. The stations were all taken from Ordnance Survey's Network (OS NetTM) in the UK; hence very accurate positions of all stations were readily available. Two datasets of one hour long were collected on 12 July 2008 and processed for presentation in this paper. The precision of interpolated ionospheric corrections for the rover sites, and the positioning precision and the initialization time are estimated and the affecting factors are also analysed.
2. SPARSE NRTK POSITIONING TECHNOLOGY
With respect to the standard network RTK, realization of the sparse network RTK requires several technical advances. These advances include carrier phase ambiguity resolution over long inter-station distances, bias interpolation method and user-end long distance kinematic ambiguity resolution method. The whole procedure for gathering the raw data from a network of reference stations and producing precise positioning results is a rather complicated process.
Figure 1 shows the overall processing procedure of sparse network RTK positioning technology.
Figure 1. The procedure for sparse NRTK positioning.
In this paper, the following methods are applied to realize sparse network RTK positioning:
• The Delaunay triangulation method to form network cells (triangles);
• A three-step method for double-differenced (DD) ambiguity resolution of network RTK reference stations;
• A novel algorithm for the generation of high quality RTK corrections using a combined bias interpolation technique;
• A novel long distance kinematic ambiguity resolution method for the rover receivers.
Of these four strategies, the last one is the key. This method can overcome the inherent defects through three procedures: application of the interpolated corrections from the sparse network only to wide-lane combination; searching the ambiguities of wide-lane combination; and searching L1 ambiguities with wide-lane combination and ionosphere-free observables.
2.1. The Delaunay Triangulation for the Formation of Network Triangles
The central processing software of a Network RTK system provides the network corrections according to the biases estimated from the measurements gathered from reference stations. It is necessary to form baselines from scattered reference stations for computing the DD biases. There are many algorithms to form baselines and triangles. However, in order to solve ambiguities easily and obtain reliable and highly accurate interpolation corrections, the criteria used in forming baselines is the shortest baseline length and the criteria for triangulation is the formation of an equilateral triangle. Delaunay triangulation can meet these requirements very well and the detailed procedure can be found from Cignoni (1998).
2.2. Long Distance Ambiguity Resolution Algorithm for Network Reference Stations
The resolution of ambiguities between reference stations includes wide-lane ambiguity resolution, initial narrow-lane ambiguity resolution and ambiguity resolution of L1 and L2 carrier phase measurements. This method has several attractive characteristics. For example, there is no need to solve observational equations, and ambiguity resolution is carried out on a satellite by satellite basis. The whole process of AR is as follows:
2.2.1. DD wide-lane ambiguity resolution
Firstly, the initial ambiguity of wide-lane combination is resolved using Melbourne-Wübbena combination (Hatch, Reference Hatch1982; Wübbena, Reference Wübbena1985). The searching space is determined according to the relationship of Melbourne-Wübbena and pseudo-range ionosphere-free combinations. The integer wide-lane ambiguity is then validated by the accurate geometric range.
2.2.2. Compute the initial ambiguity of DD narrow-lane combination and create the searching space
In the previous step, the ambiguity of wide-lane combination has been fixed to an integer. The coarse ionospheric delay of narrow-lane combination can be computed from the wide-lane combination and the accurate geometric range. Then the initial ambiguity of narrow-lane combination is computed. The searching space is formed according to the precision of the wide-lane combination and the characteristic that the ambiguities, both of wide- and narrow-lanes, are either odd or even numbers.
2.2.3. Ambiguity resolution of DD L1, L2 carrier phase measurements
After the searching space is created, the relationship between the two carrier phases is used as the criterion to validate the best ambiguity (Gao, 2002).
2.3. The method of computing systemic corrections for the rovers
The method adopted in this paper is called Modified Combined Bias Interpolation (MCBI) (Tang, 2006), which is based on the method of Combined Bias Interpolation (CBI) (Gao, 2002). The method of CBI does not separate tropospheric delay, ionospheric delay and other error sources. It cannot be applied to L1, L2 and wide-lane measurements simultaneously. MCBI separates the combined bias into three individual components: the first order ionospheric delay, the tropospheric delay estimated with the tropospheric model, and the residual error. The combined bias Δ∇R can be expressed as:
$${\rm \Delta} \nabla R = {\rm \Delta} \nabla d_{ion} + {\rm \Delta} \nabla d_{trop} + \delta $$where Δ∇d trop denotes the correction computed with the tropospheric model, Δ∇d ion is the first order ionospheric delay, and δ is the sum of other residual errors including the higher order ionosphere delays, the residual error of the tropospheric model and the orbit error. By rearranging Eq. 1, the following equation can be obtained:
$${\rm \Delta} \nabla R - {\rm \Delta} \nabla d_{trop} = {\rm \Delta} \nabla d_{ion} + \delta $$Let Δ∇R′=Δ∇R−Δ∇d trop, then the new combined bias can be written as:
$${\rm \Delta} \nabla R^' = {\rm \Delta} \nabla d_{ion} + \delta $$The ionospheric delay and the residual errors can then be determined separately and applied to all measurements. The Linear Combination Model (LCM) (Dai et al., 2002) is applied to interpolate the ionospheric delay and the residual errors for the rover.
2.4. The Ambiguity Resolution Method for Long Range Baseline
This method consists of two parts: a two–step AR, where the first step is wide-lane AR and the second step is L1, L2 carrier phase AR; and, after eliminating the parameters of the coordinates, only the parameters of ambiguities are left. First the float ambiguities of wide-lane are computed using Melbourne-Wübbena combinations and then the integer ambiguities are searched out by the Least-squares AMBiguity De-correlation Adjustment (LAMBDA) method (Teunissen, et al., 1994, 1995a, 1995b). Secondly, wide-lane combinations are used to solve L1, L2 carrier phase ambiguities. In this process, in order to reduce the influence of ionospheric error, L1 ambiguities are expressed by the known wide-lane ambiguities and the ambiguities of ionosphere-free combinations. This method has two advantages: the first is that the ambiguities are integer and the second is that the influence of ionospheric error is largely reduced.
2.4.1. Wide-lane ambiguities resolution
When the parameters of coordinates are eliminated, the equations of wide-lane ambiguities Y can be expressed as follows:
$$\left[ {\matrix{ {{\bi I} \cdot \lambda _{WL}} \cr {{\bi \tilde B}} \cr}} \right]Y = \left[ {\matrix{ {{\bi L}_{MW}} \cr {{\bi L}_{WL} + Cor_{WL}} \cr}} \right]$$where 
${\bi \tilde B}$ is the solution matrix, λ WL is the wavelength of wide-lane combination, Y is ambiguity vector, Cor WL is referred to as the interpolated wide-lane combination correction, I is the unit matrix, LMW is the Melbourne-Wübbena combination observation matrix, and LWL is wide-lane observation matrix. The float ambiguities can be resolved with Equation 4. According to wide-lane float ambiguities and their covariance, multiple (usually 3 to 5) wide-lane integer ambiguities and their ratio values can be determined. Then the Sum of Squared Residuals (SOSR) can be computed and used to check the reliability of the best ambiguities. The criteria used to validate the wide-lane AR are:
$$\left\{ \matrix{Ratio \gt M \hfill \cr V_{WL}^T PV_{WL} = \min \hfill} \right.$$where M is a definitive positive number and usually is 3·0, V WL is the remaining error vector.
2.4.2. L1, L2 ambiguities resolution
After fixing the wide-lane ambiguities, the ambiguity of ionosphere-free combination can be expressed by the ambiguity of L1 carrier phase and the ambiguity of wide-lane. The equations for resolving L1 ambiguities Y are:
$$\left[ {\matrix{ {{\bi I} \cdot \lambda _{L1}} \cr {{\bi \tilde B}} \cr}} \right]{\bi Y} = \left[ {\matrix{ {{\bi L}_{WL} + Cor_{WL}} \cr {{\bi L}_{LC}} \cr}} \right]$$where 
${\bi \tilde B}$ is the solution matrix, λ L1 is the wavelength of L1, Y is the ambiguity vector, I is the unit matrix, LWL is the virtual observation vector which is computed by wide-lane combinations, and LLC is the ionosphere-free observables.
The float ambiguities of L1 and the covariance are obtained through solving Eq. 6. Multiple (usually 3 to 5) integer ambiguities and their Ratios can be determined by the LAMBDA method. Then the SOSR can be used to check the successful rate of ambiguity resolution. For a long range baseline, in order to reduce the influence of ionosphere delay, the SOSR of ionosphere-free can be computed and compared. The criteria used to validate the ionosphere-free AR are:
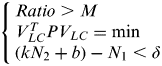$$\left\{ \matrix{Ratio \gt M \hfill \cr V_{LC}^T PV_{LC} = \min \hfill \cr (kN_2 + b) - N_1 \lt \delta \hfill} \right.$$where M is a definitive positive number and usually is 3·0, V LC is the remaining error vector, δ is a definitive positive number, (kN 2+b)−N 1 is the difference of N 2 and N 1, k and b are constant values (Gao, 2002) which are computed by the relationship of N 2 and N 1 with the known station coordinates.
3. EXPERIMENTAL DATA AND RESULT ANALYSIS
3.1. OS Net™ of the UK
The Ordnance Survey of the UK operates a network of more than 150 continuously operating GPS receivers – OS Net™ as shown in Figure 2. The Ordnance Survey is working with its partner organizations to utilise the GPS data from this network for the development and provision of a basket of real-time and post-process GPS correction services, with a choice of accuracy levels available to customers in a wide variety of application markets.
Figure 2. Ordnance Survey Active GPS Network (http://www.bigf.ac.uk/).
3.2. Use of OS Net™ to form a Sparse Network
In order to assess the performance of a sparse network RTK system covering the United Kingdom, ten reference stations were selected from the reference stations of OS Net™. The average inter-station distance was around 300 km. One Hz GPS measurements collected from these stations on July 12, 2008 were used in the test. The data were collected in two sessions: 00:00–01:00 UT (1–2 am local time), when the TEC is the lowest, and 14:00–15:00 UT (3–4 pm local time), when the TEC is at its highest in the day. Another nine stations were also selected from the OS Net™ as the rovers. Of these nine stations, six sites were located within the network and three were outside. The rover stations did not contribute to the estimation of the atmospheric corrections. The map of the reference network and the locations of the stations simulating rovers are presented in Figure 3. The receivers used at all reference stations were LEICA SR530 units. The sampling rate of the data was 1 Hz. The antenna of station LERW was ASH700936D_M and the antenna of station OSHQ was ASH700936E. The antennae of the remaining stations were LEIAT504.
Figure 3. A Sparse Testing Network of the UK.
The analysis was performed in a post-processing mode; however, the algorithm is suitable for real-time application. Naturally, for a real RTK implementation, the issue of communication links and the computing power at the rover stations must be addressed properly.
The strategy used in the sparse network data processing is the same as that introduced in Figure 1. The triangle network is formed by the Delaunay Triangulation method discussed earlier. There are a total of 17 baselines in the network. The average baseline length is 300 km. The longest length is 378·3 km and the shortest is 226·6 km. The service area covers England and Scotland. These 17 baselines were solved separately using the long-range ambiguity resolution method introduced earlier. All the ambiguities in a triangle were checked for whether the sum of a satellite's ambiguities is zero. If it was not zero, the ambiguities would be reprocessed. The corrections between reference stations were computed and stored into a file.
The algorithm used for the data processing of the rover measurements consists of several steps. The first step is that the rover's coarse position is computed in a single positioning mode. According to this position, the nearest reference station is selected as the master station and the relative corrections between the rover and the master station are interpolated.
3.3. The AR Performance of the Network
The average of times for first fix (Over 6 or all satellites are available) is 7 s. None of the ambiguities fixed is wrong by comparing with the post-processing results of software Bernese 5.0. The values of most DD ionospheric biases are between than +0·4 m and −0·4 m. The values of most DD tropospheric errors are less than 0·05 m. Generally, the satellites with the lower elevation angles have bigger DD ionospheric biases and DD tropospheric errors.
3.4. The Precision of DD Ionosphere Delay
The precision of DD ionosphere corrections affects kinematic ambiguity resolution on the rover receivers and the performance of sparse network RTK positioning. In order to analyse the precision of interpolated ionosphere corrections, we firstly computed the corrections for the nine rovers with the known coordinates. Because the rovers are also reference stations, the coordinates of these rovers are precisely known. Then, the interpolated ionosphere corrections were computed using the methods introduced in the previous sections. The difference between the known corrections and the interpolated ones can be computed on an epoch-by-epoch and satellite-by-satellite basis. The average difference of each data session is given in Table 1 and Figure 4. In Table 1 the column entitled “In” denotes whether the rover is inside the network (Y) or outside (N).
Figure 4. The one session average differences of all satellites.
Table 1. The precision of interpolated ionosphere corrections.
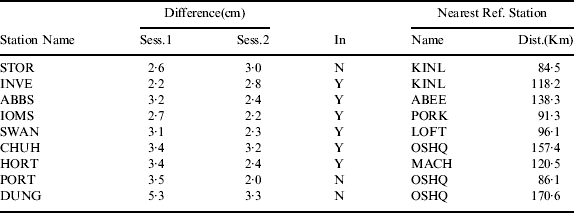
In Table 1 the average precision of these interpolated corrections is about 3·0 cm. The precision of the rovers closer to a reference station or inside the network is more stable. The worst precision is 5·3 cm attained from rover DUNG. DUNG is outside the network and the distance to the nearest reference station is 170·6 km. The average precision of interpolated corrections of the six rovers inside the network is 2·8 cm.
In order to analyse the relationship between satellite elevation angle and interpolation precision, the average correction difference of each satellite is computed and shown in Figure 4.
In Figure 4, the correction difference is increasing with the lower satellite elevation angle. When the satellite elevation angle is less than 20 degrees, half of the differences are more than 5 cm.
3.5. Simulated Real-time Positioning Results
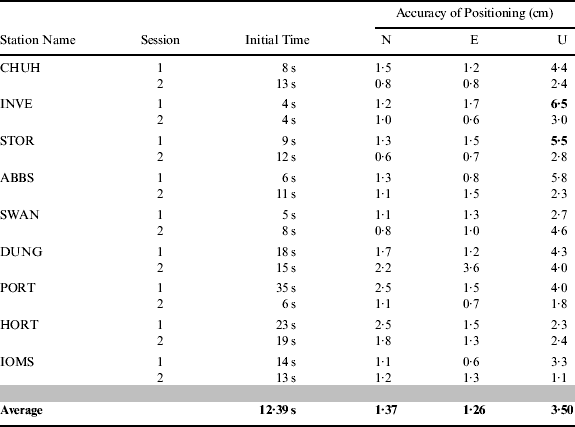
In order to test the performance of positioning, the positioning fixes of the nine rovers have been compared with their known coordinates. The initialisation time and the Three-Dimensional (3D) precision are listed at Table 3. Session 1 in this table refers to the data collected during 00:00∼01:00 UT and Session 2 the data set between 14:00∼15:00 UT. The rover locations are shown in Figure 2.
From Table 2, the average initialisation time is about 12·4 s and the maximum initialization time is 35 s. The average precision of all rovers is 1·4 cm in the north direction, 1·3 cm in the east direction and 3·5 cm in the vertical direction respectively. The maximum error of all rovers in the vertical direction is 6·5 cm at rover INVE during Session 1. The second largest vertical error estimated from rover STOR in Session 1 is 5·54 cm. The time series of 3 Dimensional (3D) errors of rover INVE are shown in Figure 5 and those of STOR in Figure 6.
Figure 5. 3D positioning errors of rover INVE.
Figure 6. 3D positioning errors of rover STOR.
Table 2. Statistics of the rover positioning results.
In Figure 5 and Figure 6, there are obvious systemic offsets in the time series of height component. If these offsets are removed (−0·064 m in Figure 6 and −0·053 m in Figure 7), the positioning RMS of INVE is 0·017 m and that of STOR is 0·010 m. The main cause for this is the effect of residual tropospheric error since the distance between the rover and reference stations is over 100 km and the model used cannot effectively remove tropospheric delay. The average of all the rovers' positioning RMS from both sessions was plotted against the distances to the nearest reference stations in Fig. 7.
Figure 7. Positioning RMS against distances to the nearest reference stations.
In Figure 7, however, we have not taken account of the work by Zheng et al. (2005) which has shown a certain correlation between base-rover distances and tropospheric interpolation errors based on the analysis of a network of 129 stations. It is possible that the sample number is statistically too small to reliably demonstrate correlation.
4. CONCLUSIONS
A complete set of positioning technologies for sparse network-based RTK is proposed in this paper. To test these methods, a sparse network consisting of ten reference stations was created from OSNet™. The precision of both interpolated corrections and positioning results were calculated. From these results and analysis, the following conclusions can be drawn:
• The precision of interpolated corrections in this sparse network is about 3 cm and has a high correlation with the satellite elevation angle. The horizontal positioning precision is 1 cm to 2 cm and the vertical 3 cm to 5 cm. This precision is equivalent to that of a traditional network RTK system. So, it is feasible to establish a sparse network RTK system with inter-station distances up to 300 km to cover the whole territory of the UK.
• In this sparse network, the precision of interpolated corrections for satellites with low elevation angles is poor, and the precision for some satellites exceeds 10 cm as shown in Figure 4. To overcome this problem, a novel method is proposed. Firstly, the interpolated corrections are used to correct wide-lane combinations and the error of 10 cm does not influence the wide-lane ambiguity resolution. After fixing wide-lane ambiguities, both wide-lane and ionosphere free observations are used in the L1 ambiguity resolution. Finally, the positioning results are computed using ionosphere free observations. The results of the testing network have proved the method is practical and efficient.
• The algorithms proposed are suitable for network-based real-time applications. Although the data used were previously recorded, all the computations were carried out in a simulated real-time processing mode.
• The precision of some interpolated corrections is close to 10 cm and some positioning results in the vertical direction have a systemic offset. How to further improve the precision of the interpolated corrections and eliminate or estimate these systemic errors will be addressed in future work.
• Although the systems of this paper are designed to perform adequately under “worst-case” conditions, the test data was from the OSNet™ of July 12, 2008 and the year 2008 was a relatively quiet solar year. The authors will test the method to perform under severe ionosphere storm conditions in their future work.
ACKNOWLEDGEMENTS
Ordnance Survey of the UK is acknowledged for providing the testing data sets of OSNet™. This research is funded by National Natural Science Foundation of China (No: 41004014), the national ‘863 High Technology Project’ of China (No. 2012AA12A202) and Supported by the 111 Project (No: B07037). Air Commodore Norman Bonnor is acknowledged for proofreading this article.
