1. INTRODUCTION
Location-based Services (LBS) have gradually expanded from military and government departments into our everyday life. From emergency responders to social networks, LBS users inevitably demand far more accurate and reliable positioning information in a wider range of areas. Although Global Navigation Satellite Systems (GNSS) can provide accurate positioning outdoors, they lack the same accuracy and robustness in more complicated environments due to signal disruption and blockage, e.g. inside buildings and urban canyons (von Watzdorf and Michahelles, Reference von Watzdorf and Michahelles2010).
Inertial navigation is a common approach in GNSS-denied environments, as it does not rely on any infrastructure other than an Inertial Measurement Unit (IMU) that works in almost any environment. However these are notorious for gyro heading drifts, which could accumulate to up to tens of metres after just a few seconds. Therefore either corrections or external measurements must be applied to inertial measurements to provide more reliable results (Abdulrahim et al., Reference Abdulrahim, Hide, Moore and Hill2011). Various Inertial Navigation System (INS) integration methods, such as INS/Global Positioning System (GPS) and INS/Wi-Fi integration, have been proposed where each sensor compliments the other if one fails during a short period (Evennou and Marx, Reference Evennou and Marx2006; Weyn and Schrooyen, Reference Weyn and Schrooyen2008). Wireless signals are available indoors and naturally become a good alternative indoors, even though they suffer signal instability (Narzullaev et al., Reference Narzullaev, Yongwan and Hoyoul2008; Kaemarungsi and Krishnamurthy, Reference Kaemarungsi and Krishnamurthy2012).
Collaborative positioning integrates multiple systems into a single network, which was first introduced in intelligent transport systems. Roadside beacons and vehicle clusters helped to maintain reliable positioning by correcting GNSS observations and reducing errors through vehicle-to-vehicle ranging when the vehicle could not receive sufficient satellite signals (Yao et al., Reference Yao, Balaei, Hassan, Alam and Dempster2011; Tang et al., Reference Tang, Kubo and Ohashi2012). For a more general idea of collaborative positioning, signal of opportunity was introduced in Yang et al. (Reference Yang, Nguyen, Venable, White and Siegel2009) where positioning is achieved by integrating a number of different types of signals in the surrounding environment. However, the overall performance can be affected by the reliability of each particular signal, the amount of data and the relative position.
This paper proposes a collaborative positioning solution for an indoor pedestrian navigation scenario, which integrates measurements from multi-users through Peer-To-Peer (P2P) ranging. Based on the signal properties in the indoor environment, this paper provides a detailed analysis on the collaborative network structure and its effects on the positioning result. A particle filter-based Adaptive Ranging constraint Collaborative Positioning (ARCP) algorithm is proposed which integrates inertial measurements, map information and relative ranging. It improves the positioning accuracy and robustness in complicated indoor environments by applying a selecting and weighting scheme to the ranging constraint on each user based on the obtained ranging measurements and network geometry. Simulations are carried out to analyse the network characteristics and the anticipated positioning outcome. Finally, trials are carried out to validate the positioning algorithm performance.
2. SELECTING THE NETWORK
Multi-users can share local environment information and constrain errors directly through P2P ranging between users (Jing et al., Reference Jing, Pinchin, Hill and Moore2013). P2P ranging is relative ranging measurements between nearby units, which can update and correct the user state model by restricting valid measurements to the measured distance and pushing the final solution towards the true position. Therefore the ranging constraint plays a crucial role in the positioning performance. To integrate only the most effective ranges, a decision-making scheme is introduced here to enhance positioning accuracy and system efficiency.
The decision is made each epoch based on the current situation, hence is adaptable to different measurement error models and network geometry. Three different aspects are considered. First of all, the ranging measurement accuracy level is estimated from signal characteristics. Secondly, the network geometry of the collaborative network is formed by selected nodes. Finally, the network size should also be considered for efficiency.
The collaborative network discussed here consists of two types of units, fixed transmitters with known positions, known as anchors (denoted as Tx), and mobile users whose positions need to be determined, known as rovers (denoted as Rx). The optimal network should consist of the minimum number of units that produces the required positioning accuracy. The Cramer-Rao Lower Bound (CRLB) of different networks is presented below to examine the relationship between network size, geometry and positioning accuracy.
2.1. Network Cramer-Rao Lower Bound
CRLB provides a lower boundary on the achievable variance of any unbiased location estimator for unknown parameters, which is useful for justifying how well an estimator can perform (Patwari et al., Reference Patwari, Ash, Kyperountas, Hero, Moses and Correal2005; Wymeersch et al., Reference Wymeersch, Lien and Win2009; Penna et al., Reference Penna, Caceres and Wymeersch2010). CRLB states that the variance of an unbiased estimator ![]() $\hat \theta $ should at least be as high as the inverse of a function of the expectation taken with respect to the probability density function (pdf) p(x; θ),
$\hat \theta $ should at least be as high as the inverse of a function of the expectation taken with respect to the probability density function (pdf) p(x; θ),
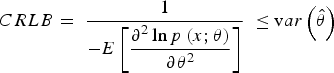 $$CRLB = {\rm \;} \displaystyle{1 \over { - E\left[ {\displaystyle{{{\partial ^2}\ln p\left( {x;\theta} \right)} \over {\partial {\theta ^2}}}} \right]}}{\rm \;} \le {\rm v}ar\left( {\hat \theta} \right)$$
$$CRLB = {\rm \;} \displaystyle{1 \over { - E\left[ {\displaystyle{{{\partial ^2}\ln p\left( {x;\theta} \right)} \over {\partial {\theta ^2}}}} \right]}}{\rm \;} \le {\rm v}ar\left( {\hat \theta} \right)$$where the derivate is evaluated at the true value of θ. Assume that we are interested in ranging measurement stated as,
where ![]() $({\hat x_u},{\hat y_u})$ is the user location, (x i, yi) is the ith reference node, r i is the ranging measurement centred at
$({\hat x_u},{\hat y_u})$ is the user location, (x i, yi) is the ith reference node, r i is the ranging measurement centred at ![]() $h({\hat \theta})$ with a noise ε of Gaussian zero mean with covariance R. If there were m nodes in the network and
$h({\hat \theta})$ with a noise ε of Gaussian zero mean with covariance R. If there were m nodes in the network and ![]() $H = \displaystyle{\partial \over {\partial \theta}} h\left( \theta \right)$. CRLB at location (x, y) is given by
$H = \displaystyle{\partial \over {\partial \theta}} h\left( \theta \right)$. CRLB at location (x, y) is given by
where ![]() $R = diag(\sigma _1^2, \sigma _2^2, \ldots, \sigma _m^2 )$,
$R = diag(\sigma _1^2, \sigma _2^2, \ldots, \sigma _m^2 )$, ![]() $\sigma _i^2 $ is the variance of ith measurement. The resulting CRLB indicates the positioning accuracy level at each location. The performance of different networks is discussed below in detail.
$\sigma _i^2 $ is the variance of ith measurement. The resulting CRLB indicates the positioning accuracy level at each location. The performance of different networks is discussed below in detail.
2.2. Ranging accuracy
Generally, ranging measurement noise ε consists of white noise w and bias b. Thus Equation (2) can be rewritten as,
The white noise is a zero mean variable with a variance of σ 2, which can be modelled based on prior observation data. To testify the error bound for range-based positioning of different measurement levels, four different anchor locations are set on each corner of a 100 m × 100 m square area. The CRLB of the entire simulated area is calculated for different noise levels with variances of σ 2 = 1, σ 2 = 3 and σ 2 = 5 while bias b = 1 m and b = 5 m respectively (Figure 1). Blue indicates low CRLB and red indicates high values.

Figure 1. CRLB with different noise variance and bias.
While CRLB increases when the variance or bias increases, meaning a lower positioning accuracy, the effect of the variance is larger than that of the bias.
2.3. Network dilution of precision
The accuracy of GNSS positioning at a point on Earth is related to the geometry of observable satellite constellation, which is reflected by the Dilution Of Precision (DOP) (Langley, Reference Langley1999). Thus good signal geometry plays a significant role in positioning which restricts the measurement uncertainty into a smaller boundary.
The geometry of the collaborative network can be assumed as the satellite constellation projected onto a 2-D scenario. If ranging measurements between a user located at ![]() $({\hat x_u},{\hat y_u})$ and surrounding units located at (x i, yi) is expressed as Equation (4), the coordinate differences form the geometry matrix,
$({\hat x_u},{\hat y_u})$ and surrounding units located at (x i, yi) is expressed as Equation (4), the coordinate differences form the geometry matrix,
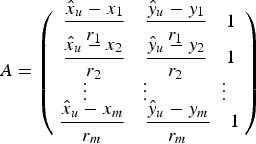 $$A = \left( {\matrix{ {\matrix{ {\displaystyle{{{{\hat x}_u} - {x_1}} \over {{r_1}}}} & {\displaystyle{{{{\hat y}_u} - {y_1}} \over {{r_1}}}} & 1 \cr}} \cr {\matrix{ {\displaystyle{{{{\hat x}_u} - {x_2}} \over {{r_2}}}} & {\displaystyle{{{{\hat y}_u} - {y_2}} \over {{r_2}}}} & 1 \cr}} \cr {\matrix{ {\; \; \vdots} & {\; \; \; \; \; \; \; \vdots} && {\; \; \; \; \; \; \; \vdots} \cr}} \cr {\matrix{ {\displaystyle{{{{\hat x}_u} - {x_m}} \over {{r_m}}}} & {\displaystyle{{{{\hat y}_u} - {y_m}} \over {{r_m}}}} & 1 \cr}} \cr}} \right)$$
$$A = \left( {\matrix{ {\matrix{ {\displaystyle{{{{\hat x}_u} - {x_1}} \over {{r_1}}}} & {\displaystyle{{{{\hat y}_u} - {y_1}} \over {{r_1}}}} & 1 \cr}} \cr {\matrix{ {\displaystyle{{{{\hat x}_u} - {x_2}} \over {{r_2}}}} & {\displaystyle{{{{\hat y}_u} - {y_2}} \over {{r_2}}}} & 1 \cr}} \cr {\matrix{ {\; \; \vdots} & {\; \; \; \; \; \; \; \vdots} && {\; \; \; \; \; \; \; \vdots} \cr}} \cr {\matrix{ {\displaystyle{{{{\hat x}_u} - {x_m}} \over {{r_m}}}} & {\displaystyle{{{{\hat y}_u} - {y_m}} \over {{r_m}}}} & 1 \cr}} \cr}} \right)$$where ̂ denotes estimated results. In 2-D positioning, the Horizontal DOP (HDOP) is defined as
DOP can be applied to analyse the collaborative network from two aspects. First of all, lower DOP indicates better positioning geometry. Secondly, increasing units could also potentially reduce the DOP. Figure 2 reflects that the positioning uncertainty boundary is markedly affected by the relative position of the units. When the two anchors are close together, DOP increases as well as the positioning uncertainty.

Figure 2. Network geometry and error boundary.
2.3.1. Network Geometry Quality
In recent works, DOP has been applied to the analysis of geometric and signal strength for GPS/Wi-Fi and cellular communications positioning system (Zirari et al., Reference Zirari, Canalda and Spies2009; Chen et al., Reference Chen, Chiu, Lee and Lin2013). In this paper, DOP is used as an indicator of the anticipated network performance. The corresponding CRLB and DOP is compared for the designated area described in Section 2.2 where two anchors placed at different locations along the side of the area, marked as red diamonds in Figures 3 and 4. Dark blue indicates low values and red indicates high values. Results indicate that low DOP areas correspond to the low CRLB areas.

Figure 3. CRLB for different geometry settings.

Figure 4. DOP for different geometry settings.
2.3.2. Network Capacity
Increasing the network size is also a solution to improve accuracy. As Yang (Reference Yang2014) suggests, increasing the number of units will give better positioning performance in collaborative positioning scenarios. As the network size increases, the relative location of the anchors becomes a less dominating factor. However, the number of anchors should be controlled so that computation cost is kept as low as possible without affecting the positioning performance. Therefore the number of anchors should be carefully selected to maintain the balance. In this case, a threshold should be identified where increasing the unit number begins to have less of an obvious impact on improving positioning performance.
The CRLB of the designated area corresponding to network sizes increasing from two to eight are computed, of which four scenarios are shown below. The anchors are located along the side of the designated area marked as red diamonds in Figure 5, while noise level remains σ 2 = 1. Results indicate an obvious decrease in CRLB when the network size increases, however the deduction rate is reduced when the number of anchors reaches four.

Figure 5. CRLB for different network sizes.
3. ADAPTIVE COLLABORATIVE POSITIONING
3.1. Gathering measurements
The proposed collaborative positioning aims to constrain inertial measurement errors by integrating external information to a Pedestrian Dead Reckoning (PDR) model. A popular method of constraining heading bias in indoor positioning is through map matching. P2P ranging is also integrated to provide further constraint. The principles of PDR are given below, as well as the characteristics of the other measurements.
3.1.1. Pedestrian Dead Reckoning
PDR obtains the current position from a relative measurement between the current state and the previous state, e.g. the distance and direction travelled. These measurements may be obtained from any inertial device that provides a step count and heading, e.g. low-cost IMUs or smartphone. The step length is usually estimated by a step recognition model or set to a constant value, e.g. 0·7 m, and later corrected through filtering. The basic PDR model is as below,
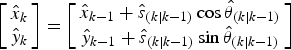 $$\left[ {\matrix{ {{{\hat x}_k}} \cr {{{\hat y}_k}} \cr}} \right] = \left[ {\matrix{ {{{\hat x}_{k - 1}} + {{\hat s}_{(k \vert k - 1)}}\cos {{\hat \theta} _{(k \vert k - 1)}}} \cr {{{\hat y}_{k - 1}} + {{\hat s}_{(k \vert k - 1)}}\sin {{\hat \theta} _{(k \vert k - 1)}}} \cr}} \right]$$
$$\left[ {\matrix{ {{{\hat x}_k}} \cr {{{\hat y}_k}} \cr}} \right] = \left[ {\matrix{ {{{\hat x}_{k - 1}} + {{\hat s}_{(k \vert k - 1)}}\cos {{\hat \theta} _{(k \vert k - 1)}}} \cr {{{\hat y}_{k - 1}} + {{\hat s}_{(k \vert k - 1)}}\sin {{\hat \theta} _{(k \vert k - 1)}}} \cr}} \right]$$
where ![]() $\left[ {{{\hat x}_k},{{\hat y}_k}} \right]$ is the estimated position at time k,
$\left[ {{{\hat x}_k},{{\hat y}_k}} \right]$ is the estimated position at time k, ![]() ${\hat s_{(k\vert k - 1)}}$ is the estimated step length from time k-1 to time k,
${\hat s_{(k\vert k - 1)}}$ is the estimated step length from time k-1 to time k, ![]() ${\hat \theta _{(k\vert k - 1)}}$ is the measured heading. Due to gyro drifts, the heading measurement
${\hat \theta _{(k\vert k - 1)}}$ is the measured heading. Due to gyro drifts, the heading measurement ![]() $\hat \theta $ tends to be biased which increases continuously if no correction is implemented.
$\hat \theta $ tends to be biased which increases continuously if no correction is implemented.
3.1.2. Peer-to-peer Ranging
Recent studies have shown that Ultra-Wideband (UWB) systems can achieve decimetre, or centimetre level ranging and positioning accuracy in an open environment (Gentile and Kik, Reference Gentile and Kik2007; Xu and Law, Reference Xu and Law2009). Hence multi-user collaborative networks can be established through P2P measurements from UWB units. Although not currently widely applied due to cost and many other reasons, the implementations of UWB in mobile devices can potentially boost its application popularity (Seo and Lee, Reference Seo and Lee2010). Furthermore, the recent advances in wireless technology brings forth Bluetooth 4.0 and 5 G Wi-Fi, both of which has greater potential in providing much higher accuracy ranging estimations than current wireless signals (Cinefra, Reference Cinefra2012).
UWB systems work on a bandwidth of more than 1 GHz and spread the signal pulses along the whole bandwidth so that they are able to transmit signals at a very high time resolution, which enables high accuracy ranging (Lee and Scholtz, Reference Lee and Scholtz2002; Koppanyi et al., Reference Koppanyi, Toth, Grejner-Brzezinska and Jozkow2014). Yet UWB measurements are also influenced by obstructions that cause Non-Line-Of-Sight (NLOS) signals, which disturb signal properties and reduce accuracy.
Many methods have been proposed to identify UWB NLOS signals and characterise its accuracy level based on signal characteristics (Ismail et al., Reference Ismail, Chong, Watanabe and Inamura2008; Marano et al., Reference Marano, Gifford, Wymeersch and Win2010; Wymeersch et al., Reference Wymeersch, Marano, Gifford and Win2012). The collaborative constraint is set adaptively according to the ranging measurement and the detected accuracy level, which is converted to the anticipated standard deviation of the ranging measurement.
3.1.3. Interior Map Information
Map matching is commonly applied to constrain measurement errors in indoor navigation by forcing the user to stay within the reasonable path, i.e. pedestrians can only walk along corridors and travel through doors (Pinchin et al., Reference Pinchin, Hide and Moore2012). As shown in Figure 6, the user could only enter Room 2 by going out of the door into the corridor (c1) and then go through the door linking c1 and Room 2. The trouble with interior maps is that they must be available prior to use.

Figure 6. Implementation of room polygons.
3.2. Particle filtering-based collaborative positioning
Particle filtering (PF) is a recursive Bayesian filtering method that handles non-linear and non-Gaussian systems. It has been widely applied to positioning and navigation problems due to its ability to integrate different measurements (Gustafsson et al., Reference Gustafsson, Gunnarsson, Bergman, Forssell, Jansson, Karlsson and Nordlund2002). PF predicts the system states through sequential Monte Carlo estimation from a large set of particles with associated weights that represent the state probability density function (pdf). The system state vector x k is a discrete time stochastic model:
where k is the time index, f k is the non-linear function of the state x k−1 and process noise v k−1. The state vector x k is recursively updated from observation z k:
where h k is usually a non-linear function with measurement noise w k. PF looks into estimating the state x k at time k, given observations z 1:k up to time k. At each epoch, the predicted pdf is updated through measurements to represent the posterior pdf of the current state. However it is usually impossible to obtain the true posterior pdf. Therefore N particles are generated to represent a discrete approximation p(x),
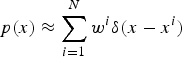 $$p(x) \approx \mathop \sum \limits_{i = 1}^N {w^i}\delta (x - {x^i})$$
$$p(x) \approx \mathop \sum \limits_{i = 1}^N {w^i}\delta (x - {x^i})$$where w i is the weight of the ith particle. As N → ∞, the approximation should approach the true posterior pdf (Arulampalam et al., Reference Arulampalam, Maskell, Gordon and Clapp2002).
A basic PF-based Collaborative Positioning (CP) is outlined below:
i. Initialisation: generate N p particles around the initial position of each Rx [x 0,y 0], all particles are assigned an equal weight
 $w_k^i = 1 / N_p$.
$w_k^i = 1 / N_p$.ii. Prediction: particles propagate forward based on the PDR prediction model Equation (6). The step length is a constant value sl with a uniformly distributed random noise
 ${\rm {\cal U}}\sim ( - {n_s},{n_s})$, the heading
${\rm {\cal U}}\sim ( - {n_s},{n_s})$, the heading  ${\hat \theta _{(t\vert t - 1)}}$ consists of a constant heading bias b h and a uniformly distributed random noise
${\hat \theta _{(t\vert t - 1)}}$ consists of a constant heading bias b h and a uniformly distributed random noise  ${\rm {\cal U}}\sim( - {n_h},{n_h})$.
${\rm {\cal U}}\sim( - {n_h},{n_h})$.iii. Update and weighting: particles that cross walls are “killed”, i.e.
 $w_k^i = 0$. The collaborative constraint is then implemented by obtaining the ranging measurements
$w_k^i = 0$. The collaborative constraint is then implemented by obtaining the ranging measurements  ${\hat r_m}$ between the current rover to each other unit, as well as the distance
${\hat r_m}$ between the current rover to each other unit, as well as the distance  $\hat d_m^i $ calculated from each particle of the rover to the other N m units. For a particular particle i, if the difference between the two is over a collaborative constraint threshold thres r(10)the particle is “killed”. thres r is given based on the anticipated accuracy level of ranging measurements.
$\hat d_m^i $ calculated from each particle of the rover to the other N m units. For a particular particle i, if the difference between the two is over a collaborative constraint threshold thres r(10)the particle is “killed”. thres r is given based on the anticipated accuracy level of ranging measurements. $$dif\,f_i = {\left\vert{\hat d}_m^i - {\hat r}_m\right\vert}_{m = 1,2, \ldots, {N_m}} \ge thres_{r}$$
$$dif\,f_i = {\left\vert{\hat d}_m^i - {\hat r}_m\right\vert}_{m = 1,2, \ldots, {N_m}} \ge thres_{r}$$iv. Resampling: if the number of “live” particles falls below a threshold, i.e.
 $N_p / 2$, new particles are generated to maintain a total number of N particles.
$N_p / 2$, new particles are generated to maintain a total number of N particles.v. Return to ii or end iteration.
This algorithm is applied to the simulated network as shown in Figure 7. Eight potential locations are indicated along the sides of a square area of 100 m × 100 m where anchors could be placed. North direction points upwards along the y-axis, East points rightwards along the x-axis. A single trajectory is defined and plotted in the green line while the magenta line indicates the PDR result. Five different location pairs for two anchors are simulated at five different locations, producing different geometries. Figure 8(a) indicates the positioning error of the networks with different DOPs, Figure 8(b) shows the DOP for each network while the rover is moving.

Figure 7. Simulated positioning network.

Figure 8. (a) Positioning errors for different networks. (b) DOP of each network.
To examine the positioning accuracy for different network sizes, the performance of networks consisting of between 2-10 anchors (shown in Figure 7) is examined. The mean positioning errors for different ranging accuracy levels, i.e. ranging error standard deviation σ err of 3, 5 and 15 respectively, are plotted in Figure 9. We see a distinct improvement in positioning when the number of anchors increases from three to four for networks when σ err = 3 and σ err = 5 m, and four to five when σ err = 15. The improvement in positioning becomes less evident after this size is reached. An increase in positioning error can actually be spotted when the number of anchors increases from 7 to 8 when σ err = 3 m and σ err = 15 m, and from 8 to 9 when σ err = 5 m. This is due to the inaccuracy in the ranging measurement; when the number of ranging constraints increases, so does the inaccuracy in the constraint. Hence such increases are more likely when the ranging measurement itself is uncertain, e.g. the increase happens twice when σ err = 15 m. Therefore, it is not a good idea to use more than the necessary number of units in a collaborative network, especially when the measurements themselves contain error or bias. Yet the optimal accuracy cannot be achieved if not enough units are used. Thus keeping a balance of the network size is important.

Figure 9. Positioning errors for different network sizes.
3.3. Modified DOP
Although DOP demonstrates the relationship between the geometry and positioning performance, it cannot reflect all details inside a collaborative network. The first factor that is not reflected in DOP is the ranging accuracy, which directly influences the effectiveness of the constraint in collaborative positioning. The constraint threshold thres r is defined as the anticipated accuracy level of the ranging measurements plus an “error boundary”. However, if this threshold is smaller than the measurement error itself, i.e. the constraint is too “tight”, the positioning estimation would be pushed towards a wrong location. On the other hand, if the bound is much larger than the error, i.e. constraint too “weak”, then the observation noise and error may not be sufficiently eliminated.
Therefore, a Modified DOP (MDOP) that integrates the ranging quality is proposed here and the geometry matrix A mod is computed as below,
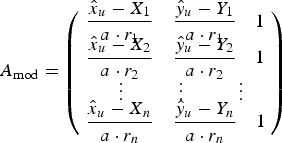 $${A_{{\rm mod}}} = \left( {\matrix{ {\matrix{ {\displaystyle{{{{\hat x}_u} - {X_1}} \over {a \cdot {r_1}}}} & {\displaystyle{{{{\hat y}_u} - {Y_1}} \over {a \cdot {r_1}}}} & 1 \cr}} \cr {\matrix{ {\displaystyle{{{{\hat x}_u} - {X_2}} \over {a \cdot {r_2}}}} & {\displaystyle{{{{\hat y}_u} - {Y_2}} \over {a \cdot {r_2}}}} & 1 \cr}} \cr {\matrix{ {\; \; \vdots} & {\; \; \; \; \; \; \; \vdots} & {\; \; \; \; \; \; \; \vdots} \cr}} \cr {\matrix{ {\displaystyle{{{{\hat x}_u} - {X_n}} \over {a \cdot {r_n}}}} & {\displaystyle{{{{\hat y}_u} - {Y_n}} \over {a \cdot {r_n}}}} & 1 \cr}} \cr}} \right)$$
$${A_{{\rm mod}}} = \left( {\matrix{ {\matrix{ {\displaystyle{{{{\hat x}_u} - {X_1}} \over {a \cdot {r_1}}}} & {\displaystyle{{{{\hat y}_u} - {Y_1}} \over {a \cdot {r_1}}}} & 1 \cr}} \cr {\matrix{ {\displaystyle{{{{\hat x}_u} - {X_2}} \over {a \cdot {r_2}}}} & {\displaystyle{{{{\hat y}_u} - {Y_2}} \over {a \cdot {r_2}}}} & 1 \cr}} \cr {\matrix{ {\; \; \vdots} & {\; \; \; \; \; \; \; \vdots} & {\; \; \; \; \; \; \; \vdots} \cr}} \cr {\matrix{ {\displaystyle{{{{\hat x}_u} - {X_n}} \over {a \cdot {r_n}}}} & {\displaystyle{{{{\hat y}_u} - {Y_n}} \over {a \cdot {r_n}}}} & 1 \cr}} \cr}} \right)$$where a is a measurement accuracy coefficient derived from accuracy detection. The detection method provides the user with how likely the measurement is to be reflecting the true distance, which is given by a, a value between 0 and 1. Hence reliable measurements produce a closer to 1 and A mod would be close to A. MDOP is computed from A mod as in Equation (12), thus the produced MDOP is usually larger than the original DOP.
While the rover is always moving during navigation, it is hard for the DOP to reflect the dynamic directional information, e.g. the direction of the bias of the current rover relative to the anchors. Figure 10 shows the error in both the East and North directions when CP is applied to the rover simulated in Figure 7. As Tx5 and Tx6 are located on either side of the rover, the network constrains the error in the North direction better than the East direction. Tx7 and Tx8 are both located to the north of the rover, thus they constrain the error in the East direction better than the North direction. Measurements coming from different directions will constrain error along different directions. The selected units should consider the dynamic situation of the rover as directions change.

Figure 10. CP Positioning error of different networks.
MDOP is not just a value that reflects the geometry with the ranging accuracy, but rather a concept of considering all the relevant information of a dynamic collaborative network, i.e. the ranging accuracy, the network geometry and the relative positions of the units.
3.4. ARCP
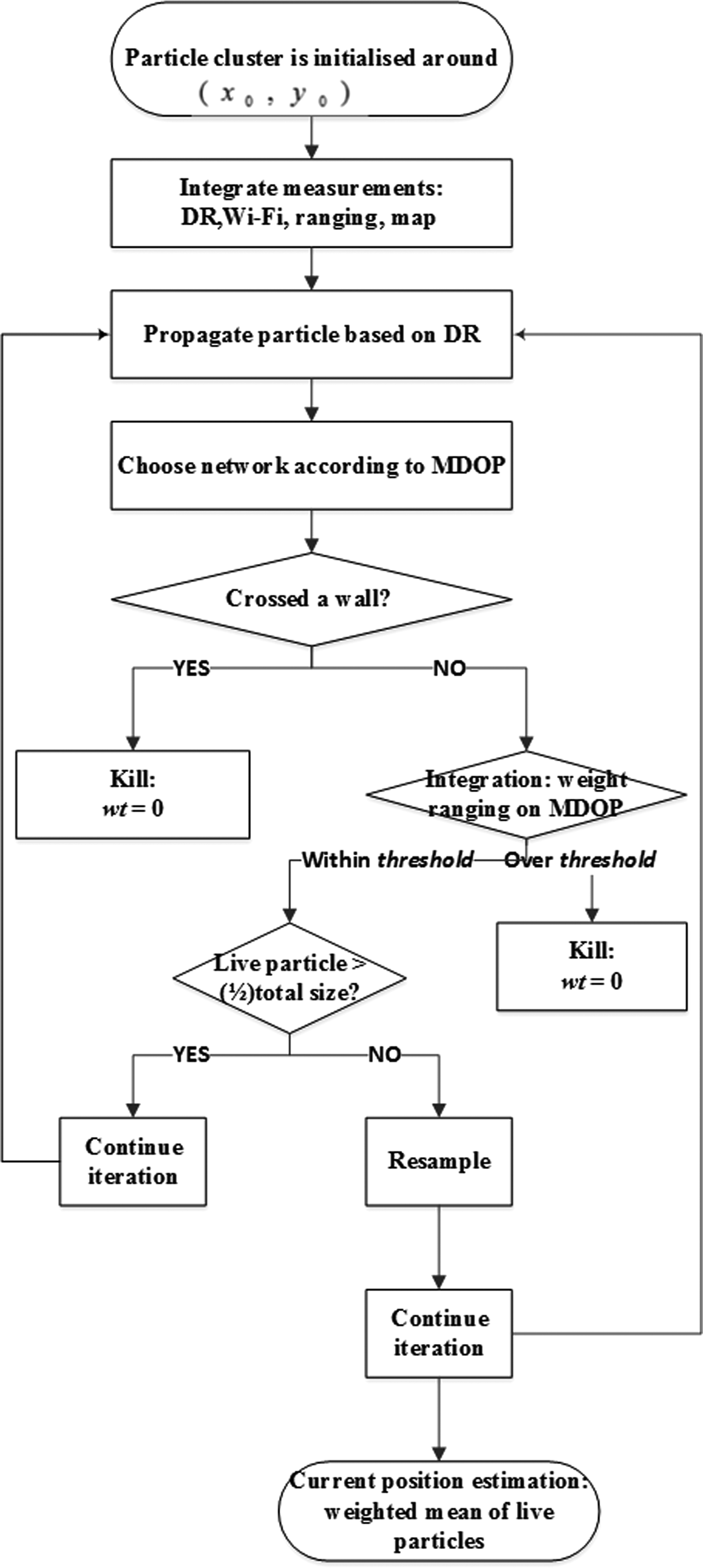
When collaborative units are available, the appropriate units should be selected to form a network with the optimal MDOP to produce the best positioning results. The Adaptive Ranging Constraint collaborative Positioning (ARCP) method is developed here and its procedure outlined in Figure 11. Compared to CP, the adaptivity of the ARCP is defined from three aspects: adaptability to varying measurement accuracies, the flexibility to select different network size and unit locations. More specifically, the adaptivity is reflected in the selection of the appropriate units.

Figure 11. Flowchart of ARCP.
Once the rover takes a step based on PDR, it will look for local units to form the collaborative network. The optimal size of the network is considered to be four according to the simulation results presented in Section 3.2. Integrating too many or not enough units will both result in reduced positioning performance. If more than four units (including rovers and anchors) are available, the estimated accuracy level of the ranging measurement from each unit is obtained. Those units with an associated a larger than 0·5 are considered as potential units. They are then combined with the current rover to form a network of four units and the MDOP of each possible network is computed. The relative positions of the units are also considered by sharing the position of the anchors and the estimated position of the other rovers. The network with the smallest MDOP value is selected as the optimal network. The constraint thres r for each ranging measurement is set according to MDOP, which reflects both a and DOP. If less than four units are available, the units would simply be included in the collaborative network and thres r set according to MDOP.
a can be converted to the estimated standard deviation of the measurement σ r, which is then applied as the constraint threshold. a is mapped onto three categories of thres r,
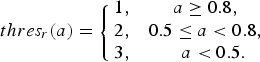 $$thre{s_r}(a) = \left\{ {\matrix{ {1,} & {a \ge 0.8,} \cr {2,} & {0.5 \le a \lt 0.8,} \cr {3,} & {{\rm \; \; \;} a \lt 0.5.} \cr}} \right.$$
$$thre{s_r}(a) = \left\{ {\matrix{ {1,} & {a \ge 0.8,} \cr {2,} & {0.5 \le a \lt 0.8,} \cr {3,} & {{\rm \; \; \;} a \lt 0.5.} \cr}} \right.$$The values are selected based on real indoor measurement error levels and indicate the expected error in metres. Most measurements should fall within category 1 or 2. A threshold of 3 indicates a very loose constraint, where the rover mostly depends on PDR propagation. The thres r is further derived from DOP based on Equation (14) which multiplies a coefficient to thres r(a). Simulations have shown that if the threshold were set to the same value as the real measurement standard deviation, the constraint would be too tight. Hence the final threshold is always larger than the expected error standard deviation. The threshold categories can be adjusted but the values applied here are selected from the combination that gives the best constraint performance for the simulations in this paper.
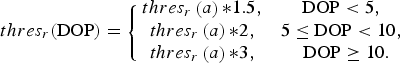 $$thre{s_r}({\rm DOP}) = \left\{ {\matrix{ {thre{s_r}\left( a \right){\ast}1.5,} & {{\rm DOP} \lt 5,} \cr {thre{s_r}\left( a \right){\ast}2,} & {5 \le {\rm DOP} \lt 10,} \cr {thre{s_r}\left( a \right){\ast}3,} & {{\rm \; \; DOP} \ge 10.} \cr}} \right.$$
$$thre{s_r}({\rm DOP}) = \left\{ {\matrix{ {thre{s_r}\left( a \right){\ast}1.5,} & {{\rm DOP} \lt 5,} \cr {thre{s_r}\left( a \right){\ast}2,} & {5 \le {\rm DOP} \lt 10,} \cr {thre{s_r}\left( a \right){\ast}3,} & {{\rm \; \; DOP} \ge 10.} \cr}} \right.$$By applying the ARCP, the possibility of selecting units with a low ranging accuracy is reduced. The constraint threshold is then also set according to the estimated measurement accuracy. Hence a collaborative network consisting of the optimal units will more likely output positions with higher accuracy and reliability. Less optimal network positioning mostly depends on inertial measurements.
ARCP is applied to the same networks as those in Figure 8 and the positioning error of ARCP and CP is compared in Figure 12. An obvious improvement can be seen when the adaptive selection is applied.

Figure 12. Positioning error comparisons for ARCP and non-adaptive CP.
4. ALGORITHM EVALUATION
4.1. Simulations
The proposed ARCP algorithm is applied to two sets of trials, denoted as Trial A and Trial B, to validate its application within real environments. Data are collected and post-processed in real-time mode on Matlab 2013 and different algorithms are implemented for comparison. For both trials, the inertial data are collected using MicroStrain 3DM-GX3®-25 IMU, which is connected to a Raspberry Pi for data logging. The step and heading information are then extracted and applied to the PDR model. The interior building map was surveyed by Leica TS30 total station and loaded into Matlab as polygons (rooms and corridors) and points (doors).
In Trial A1, all real inertial data was collected in the Nottingham Geospatial Building (NGB), University of Nottingham. Three anchors (Tx1, Tx2 and Tx3) were simulated at different locations inside the building to provide extra ranging constraints. The ranging data between the rovers and anchors were simulated based on indoor ranging performance of wireless signals, where the error variance is larger when the two rovers are in NLOS and smaller when there is no obstruction. The basic CP algorithm is applied in Trial A1 by integrating one of the anchors into the network. The measurement error of the rover is constrained by integrating the ranging measurement from the other rover and one anchor at every epoch by applying a constant threshold. The non-adaptive result of the network consisting Rx1, Rx2 and Tx1 is shown in Figure 13. The green line indicates the ground truth for both rovers, the cross dot line indicates the position estimation of Rover 1 and the circle dash line indicates the position estimation of Rover 2.

Figure 13. CP Positioning result with wall constraint (Trial A1-Tx1).
The ARCP algorithm is applied in Trial A2 where each rover selects one anchor to form a collaborative network with the other rover that produces the optimal MDOP at every epoch. thres r is adjusted according to MDOP. Results are shown in Figure 14. The plot indications are the same as Figure 13.

Figure 14. ARCP Positioning result (Trial A2).
In Trial A3, the ARCP is applied while eliminating the building map information with results as shown in Figure 15. Here, the particles are no longer restricted from crossing walls and the measurement error is bounded only by the ranging constraint.

Figure 15. ARCP Positioning result without map matching (Trial A3).
4.2. Real data
Trial B was carried out in the Business School Building, University of Nottingham. PDR data was collected using the same equipment worn on two pedestrians, Rover 1 and Rover 2. A UWB network was set up in the building as indicated with a red star in Figure 16 to act as anchors and provide ranging measurement. Each rover also carried a mobile UWB unit to receive ranging measurements from other units.

Figure 16. Trial B Ground truth for Rover 1 and Rover 2.
Data was collected for ten minutes. In every epoch, each rover selected a number of the anchors to form a collaborative network with the other rover. The network size and the ranging constraint threshold were adjusted according to the actual network quality.
The ground truth is plotted in Figure 16. Due to lack of equipment, the ground truth of Rover 2 was provided by the UWB system, whose outdoor performance was disrupted (light blue part of the trajectory in Figure 16(b)), as all units are set up indoors. The positioning results for Rover 1 and Rover 2 are shown in Figure 17 (a) and (b) respectively. The green solid line indicates the ground truth, the cyan dashed line shows the PDR output from raw inertial data. The blue line represents the ARCP output with wall constraint, and the magenta line represents the ARCP result without wall constraint.

Figure 17. ARCP Positioning result for Rover 1 and Rover 2 (Trial B).
4.3. Results
Collaborative positioning is able to constrain measurement errors by integrating relative ranging constraints into the system. However in reality, this does not always give the best performance due to the complexity of real data, which could be caused by environmental disturbance, hardware failure and human impact etc. Figure 13 shows the performance of CP when none of this is taken into consideration. Positions can be constrained mistakenly into the wrong location.
ARCP is applied to provide the system with more adaptivity to varying situations. The positioning system has more freedom to adjust the “strength” of the required constraint as well as choose the optimal collaborative network. When a network with good geometry, sufficient signals and good accuracy measurement is selected, the relative constraint is “tighter” so that only particles lying within the threshold will remain and those outside will be killed, bringing the rover state estimation closer to the truth. A less ideal network will produce a “loose” constraint so that fewer particles will be killed to avoid pushing particles towards the wrong location.
Tables 1 and 2 list the mean and maximum positioning error throughout Trial A and Trial B. Table 2 only lists the error for Rover 1, as the ground truth for Rover 2 is provided by the UWB system which is not accurate enough to justify the positioning accuracy of ARCP. PDR indicates the result of DR from inertial measurements with wall constraint. CP indicates the result of non-adaptive CP with wall constraint. The CP result in Table 1 is an average of integrating one of the three anchors each time and the CP result in Table 2 is an average of integrating all available measurements.
Table 1. Positioning errors for Trial A (NGB) (m).

Table 2. Positioning errors for Trial B (BSS) (m).

In Trial B, as two rovers and four anchors are available, only the appropriate units are selected. As anchors are not represented by particles, therefore increasing the number of anchors does not affect the computation cost too much. However, the processing time is reduced by at least 5% when a rover is integrated. Hence the network size is kept within four, which was indicated as the effective size.
As not enough factors are considered in CP, ARCP improves positioning accuracy by 25% in Trial A and 60% in Trial B compared to CP. In Trial A, the improvement is more obvious for Rover 1 as the trajectory for Rover 2 is much simpler and the wall constraint is quite sufficient to constrain the inertial bias. The improvement is also much more obvious in Trial B where real ranging data is implemented, which are noisier and more unstable. ARCP can cope with different noise levels of real data with its threshold adjustment.
In both trials, the same threshold categories are applied as specified in Equation (14). ARCP results demonstrate the ability to cope with situations without map information. Wall constraint is most effective in a straight long corridor without doors. However, such conditions are not always met and when the state predication model is noisy, wall constraints can misplace particles in the wrong room and restrict its chances of regenerating in the right location. Collaborative positioning can provide sufficient constraint even in places when wall constraint cannot. Therefore, the building map information can be eliminated in the ARCP algorithm. This means that users can start navigating in an environment where no prior information is available.
5. CONCLUSIONS
Collaborative positioning enhances positioning performance by forming a collaborative network that integrates available positioning information including P2P ranging measurements between nearby rovers and anchors to constrain the measurement errors. Ranging measurements vary in different environments and conditions. If the wrong information is integrated, position estimation may be pushed further into the wrong location while reducing positioning efficiency unnecessarily. To avoid this, only the useful measurements are selected and integrated into the positioning system.
This paper proposes an adaptive ranging constraint collaborative positioning strategy that enables the user to decide on the most effective network at each epoch. This selection is based on the network geometry, network size and ranging accuracy of the units and their measurements. All three elements are combined to produce a decisive factor, MDOP, which helps the system to select the appropriate units as well as set the proper constraint threshold. Only those units that form a good geometry while providing high ranging accuracy will be used for positioning and others will be neglected. ARCP improves the positioning accuracy by more than 60% for real data, while reducing the maximum error by 45%. The contribution of ranging constraints also enables the system to navigate when no interior building map is available.
By applying ARCP, the system produces results with higher accuracy and enhanced robustness. It allows the system to start up without prior information on the surrounding environment as long as collaborative units are found. This could be applied with Wi-Fi fingerprinting to introduce more adaptivity into the positioning system enabling it to cope with various difficult situations in the real world.