1. INTRODUCTION
Multipath propagation poses significant challenges to Global Navigation Satellite System (GNSS) receivers. Although there are many available algorithms that attempt to mitigate code multipath effect, they are of limited effectiveness in complex multipath environments such as dense urban areas with tall buildings and narrow streets. Multipath mitigation has been investigated in the time, frequency and spatial domains. There has been a tremendous amount of research on time/frequency domain techniques ranging from low-complexity correlator-based multipath mitigation methods to maximum likelihood-based techniques with massive searches on unknown signal parameters. The most common code multipath mitigation techniques include variants of the traditional Delay-Lock Loop (DLL) method, such as the double-delta correlator, strobe correlator and high resolution correlator techniques. Although these techniques are effective when the receiver is subjected to a few weak multipath reflections, performance in severe multipath scenarios, such as urban areas where reflections are numerous and often stronger than Line of Sight (LOS) signals, is still limited.
Another class of multipath mitigation techniques includes advanced methods such as the Multipath Estimating Delay Locked Loop (MEDLL) (Townsend et al., Reference Townsend, Van Nee, Fenton and Van Dierendonck1995), the Multipath Mitigation Technique (Weill, Reference Weill2002), the Fast-Iterative Maximum Likelihood Algorithm (FIMLA) (Silver et al., Reference Silver, Bagnell and Stentz2010), Sequential Maximum Likelihood (Sahmoudi and Amin, Reference Sahmoudi and Amin2008), the Reduced Search Space Multipath Likelihood (RSSML) algorithm (Zahidul et al., Reference Zahidul, Bhuiyan, Lohan and Jin2012) and deconvolution approaches (Skournetou et al., Reference Skournetou, Sayed and Lohan2011). This class of techniques is based on Maximum Likelihood (ML) estimation. ML-based multipath estimation techniques approach theoretical performance upper limits (i.e. Cramer-Rao Lower Bound). However, they introduce large computational complexities in the receiver as a result of exploring large search spaces or performing matrix inversion procedures. At the cost of a complex multi-correlator structure, advanced estimation algorithms introduce multipath mitigation performance superior to that of conventional correlation-based techniques. However, in some applications, this level of computational complexity may be too high or impossible to implement. Spatial processing using an antenna array is another signal processing method to deal with interference signals in GNSS applications (Fernandez-Prades et al., Reference Fernandez-Prades, Arribas and Closas2016). The effectiveness of antenna arrays to mitigate multipath interference has been studied using different robust beamforming techniques in GNSS applications (Broumandan et al., Reference Broumandan, Jafarnia-Jahromi, Daneshmand and Lachapelle2016). These methods are effective in mitigating narrowband and wideband interference, while increasing software and hardware complexity. There have been several research projects on improvement of positioning accuracy in areas where Non Line-of-Sight (NLOS) reception is a major problem (Kumar and Petovello, Reference Kumar and Petovello2015; Groves, Reference Groves2011). A 3D-mapping-aided GNSS approach can significantly improve navigation solutions in locations where satellite signals are blocked. Spangenberg et al. (Reference Spangenberg, Tourneret, Calmettes and Duchateau2010) have implemented a hybrid navigation system using the Global Positioning System (GPS) and dead-reckoning sensors. Two main models were used in the investigation to detect presence or absence of direct signals considering variations in mean and variance of the signal. Groves and Jiang (Reference Groves and Jiang2013) have investigated three methods, namely height aiding, C/N0 weighting and consistency checking to mitigate the effect of NLOS reception and multipath on navigation solutions.
One important issue in mitigating the effect of multipath signals based on advanced methods is that different types of multipath environments require different mitigation and tracking strategies, or at least different tuning parameters. Machine learning techniques have been used extensively to develop context-aware applications in computing and autonomous navigation. Context-aware computing (Ranganathan and Campbell, Reference Ranganathan, Campbell and Endler2003; Krause et al., Reference Krause, Smailagic and Siewiorek2006; Danylenko et al., Reference Danylenko, Kessler, Löwe, Apel and Jackson2011; Perera et al., Reference Perera, Zaslavsky, Christen and Georgakopoulos2014) aims at sensing the context of the operating environment to optimise the interaction between different applications or between applications and users. Autonomous navigation is a major issue in mobile robotics applications (Thrun, Reference Thrun1998; Thrun et al., Reference Thrun, Fox, Burgard and Dellaert2001; Bagnell et al., Reference Bagnell, Bradley, Silver, Sofman and Stentz2010; Silver et al., Reference Silver, Bagnell and Stentz2010; Choi et al., Reference Choi, Lee and Won2011; Giusti et al., Reference Giusti, Guzzi, Cirean, He, Rodríguez, Fontana, Faessler, Forster, Schmidhuber, Di Caro, Scaramuzza and Gambardella2016). The challenge for mobile robots is to learn the context of their deployed environments and to efficiently navigate through rough and unstructured terrains.
Context classification has been used in several GNSS applications (Shafiee et al., Reference Shafiee, O'Keefe and Lachapelle2011; Shivaramaiah and Dempster, Reference Shivaramaiah and Dempster2011; Groves et al., Reference Groves, Martin, Voutsis, Walter and Wang2013). Furthermore, there has been limited research on determining the context of a GNSS channel using signal amplitude. Lin et al. (Reference Lin, Ma, Broumandan and Lachapelle2013) used the Rician K-factor and C/N0 to measure the fading level of a channel and adjust the receiver operation state accordingly. C/N0 monitoring has also been used to distinguish between LOS and NLOS signals. In this paper, a pattern recognition algorithm is used to detect the type of multipath environment (urban, suburban, indoor, or open sky) and the type of receiver motion (vehicular or pedestrian). This is to provide additional capability for a GNSS receiver to adjust its tracking strategy and tune its parameters accordingly. A pattern recognition algorithm based on neural network architecture has been developed by Ziedan (Reference Ziedan2012) where the features used for recognition were directly extracted from the channel parameters. However, exact channel parameters (e.g. amplitudes and code delays of multipath or NLOS signals) are usually not available in a GNSS receiver and estimating them requires very high sampling rates. In this paper, a set of temporal and spectral classification features is extracted from the correlation sequence of the received signals. This makes the algorithm much more feasible in practice. The classification approach used in this paper is based on a Support Vector Machine (SVM) (Burges, Reference Burges1998) algorithm that takes advantage of a modified Gaussian kernel. SVMs are a group of machine learning algorithms that can classify non-linearly separable data instances by projecting the data features into a higher dimensional space and maximising the geometric distance between the decision boundary and the nearest data on each side of the decision boundary. These algorithms are well known for showing good empirical performance in classification and pattern recognition for non-linear problems. Specifically, SVM classifiers offer the advantages of being effective in high dimensional spaces (even when the number of dimensions is greater than the number of data instances), and being memory efficient and versatile (different kernel functions can be specified for the decision function).
The classification results are further used in a GNSS multipath compensation and tracking algorithm. It is assumed that an acquisition process has been performed beforehand and the focus is therefore on tracking the acquired signals. The proposed algorithm selects the type of adaptive tracking strategy and the corresponding tuning parameters based on the context of the multipath environment and the state of the receiver motion. It is assumed that the line-of-sight signal is present, even though it may be much weaker than corresponding reflected signals.
Simulations and real data measurements using Galileo E1B/C signals are performed to evaluate the effect of the above context-based tracking strategy on the delay estimation performance of a stochastic gradient-based adaptive multipath compensation system. Galileo E1 signals are modulated using a Composite Binary Offset Carrier (CBOC), which is generated by multiplexing BOC(6,1) and BOC(1,1) signals. The Auto-Correlation Function (ACF) of CBOC signals is characterised by a narrow main lobe, two side lobes and several secondary peaks. The CBOC modulation results in better multipath performance compared to the BPSK modulation used by the GPS L1 signals due to its narrower lobe.
2. MULTIPATH MODEL
The received baseband signal in a multipath channel can be modelled as an M-path signal composed of a direct path and (M − 1) reflected rays plus an Additive White Gaussian Noise (AWGN) term, n(t). The model can be represented as
 $$r(t)=s(t)^\ast h(t)=\sum^M_{k=1}A_ks(t-\tau_k)e^{j(\phi_k)}+n(t)$$
$$r(t)=s(t)^\ast h(t)=\sum^M_{k=1}A_ks(t-\tau_k)e^{j(\phi_k)}+n(t)$$
where s(t) is the transmitted spread spectrum signal, h(t) is the channel impulse response, and A k , ϕ k and τ k are the time-variant amplitude, instantaneous phase and delay parameters corresponding to the k th path (k = 1 corresponds to the LOS signal). The received signal after being down converted, filtered and sampled is correlated with a replica of the Pseudo-Noise (PN) code. The output of the correlator can be expressed as
 $$y(\tau)=\sum^M_{k=1}a_kg (\tau-\tau_k)+w_n(\tau),\quad \tau=0,T_s,\ldots,(N-1)T_s$$
$$y(\tau)=\sum^M_{k=1}a_kg (\tau-\tau_k)+w_n(\tau),\quad \tau=0,T_s,\ldots,(N-1)T_s$$
where
![]() $a_{k}=A_{k}e^{j\phi_{k}}$
is the complex path coefficient corresponding to the k
th
path, g(τ) is the ideal autocorrelation function of the PN code and w
n
(τ) is the noise term at the output of the correlator. Equation (2) can be represented in a matrix form as
$a_{k}=A_{k}e^{j\phi_{k}}$
is the complex path coefficient corresponding to the k
th
path, g(τ) is the ideal autocorrelation function of the PN code and w
n
(τ) is the noise term at the output of the correlator. Equation (2) can be represented in a matrix form as
where y is a vector of the samples of y(τ) with a length of
![]() $N=\left\lfloor\displaystyle{{T_{p}}\over{T_{s}}}\right\rfloor$
, T
p
and T
s
being the search and sampling periods, and
$N=\left\lfloor\displaystyle{{T_{p}}\over{T_{s}}}\right\rfloor$
, T
p
and T
s
being the search and sampling periods, and
The vector
![]() ${\bf w}_{n}$
with a length of N is the vector of noise samples with a covariance matrix of Q, and G is an N × M matrix that can be represented as
${\bf w}_{n}$
with a length of N is the vector of noise samples with a covariance matrix of Q, and G is an N × M matrix that can be represented as
where
![]() ${{\bf g}}_{\tau_{M}}=\lsqb g\lpar 0-\tau_{m}\rpar g\lpar T-\tau_{m}\rpar \cdots g\lpar \lpar N-1\rpar T_{s}-\tau_{m}\rpar \rsqb ^{\rm T}$
.
${{\bf g}}_{\tau_{M}}=\lsqb g\lpar 0-\tau_{m}\rpar g\lpar T-\tau_{m}\rpar \cdots g\lpar \lpar N-1\rpar T_{s}-\tau_{m}\rpar \rsqb ^{\rm T}$
.
The statistical distribution of the LOS and multipath parameters, including the complex attenuation coefficients, the number of paths, the delay parameters of different components and the temporal variations of these parameters are greatly affected by the type of multipath environment (e.g. size and shape of the reflectors as well as their spatial distribution) and the motion characteristics of the receiver (pedestrian or vehicular). Moreover, the statistical behaviour of multipath components determines the pattern of the correlation function of the received GNSS signal and its temporal variations. In addition, different operation conditions require different tracking strategies to achieve an optimised tracking performance and, consequently, highly accurate position accuracy. Therefore, identifying the type of multipath environment and the state of the receiver motion from the correlation pattern provide insightful knowledge of the channel statistics. This knowledge can be used for adjusting the tracking strategy or the tracking parameters to obtain the best attainable tracking performance under various signal conditions.
In this paper, the channel simulation software developed by Lehner et al. (German Aerospace Center), which is based on the channel models measured and presented by Lehner and Steingass (Reference Lehner and Steingass2005; Reference Lehner and Steingass2008); Lehner et al. (Reference Lehner, Steingass and Schubert2009) and Schubert et al. (Reference Schubert, Lehner, Steingass, Robertson, Fleury and Prieto-Cerdeira2009), is used to generate received signal patterns that typically appear in different multipath environments. Figure 1 and Figure 2 show channel power delay profiles as functions of time for two examples of multipath environments, namely suburban and urban environments, and for two different types of receiver motion, namely pedestrian and vehicular.

Figure 1. Simulated power delay profile of suburban channel for two different motion states: (a)-vehicular, (b)-pedestrian.

Figure 2. Simulated power delay profile of urban channel for two different motion states: (a)-vehicular, (b)-pedestrian.
For both simulation cases, in the pedestrian motion state, the maximum speed of the receiver was 7 km/h, and in the vehicular state, 50 km/h. The simulated satellite was located at azimuth and elevation angles of −45° and 30°. It can be observed by comparing these figures that in general, for the urban case, the delay spread parameter of the channel has larger values when compared to the suburban case. Moreover, the urban and suburban channels can be better distinguished under the pedestrian motion state rather than the vehicular state.
3. MULTIPATH PATTERN RECOGNITION USING SVM CLASSIFICATION
There are several different machine learning algorithms that are used to automatically learn some structure from data for many different applications (e.g. computer vision, speech recognition). Supervised classifiers are a subcategory of machine learning algorithms that are used to classify data into a number of a priori known classes using a set of labelled training data. Support vector machines are among the best off-the-shelf supervised learning algorithms developed from statistical learning theory (Vapnik, Reference Vapnik1998), and they are well-known for their good performance in handling non-linear problems (Neural-networks-based classifiers are also strong solutions in dealing with nonlinear problems and they have been analysed by Ziedan (Reference Ziedan2012). Therefore, in this paper, the SVM-based classifiers are studied).
Similar to all the other classification approaches, SVM learns a mapping from an input features vector x to an output class label
![]() $y\lpar {\bf x}\mapsto y\rpar $
where x is defined in a l-dimensional space (R
l
), which means that each instance of data is represented by l features. In the simplest binary classification case, the class labels are defined as either positive or negative one (
$y\lpar {\bf x}\mapsto y\rpar $
where x is defined in a l-dimensional space (R
l
), which means that each instance of data is represented by l features. In the simplest binary classification case, the class labels are defined as either positive or negative one (
![]() $y\in \lcub \pm1\rcub $
). The theory behind SVM is based on the idea of separating the positive and negative examples of the training set by maximising the minimum geometric distance between examples of each class, namely the geometric margin, to the decision boundary, which is a hyper-plane. This is equivalent to optimising the prediction confidence on the training data (Burges, Reference Burges1998). Since the input data may be linearly non-separable in the original feature space, it is projected into a much higher dimensional space R
n
(n may be infinite) using a non-linear mapping function
$y\in \lcub \pm1\rcub $
). The theory behind SVM is based on the idea of separating the positive and negative examples of the training set by maximising the minimum geometric distance between examples of each class, namely the geometric margin, to the decision boundary, which is a hyper-plane. This is equivalent to optimising the prediction confidence on the training data (Burges, Reference Burges1998). Since the input data may be linearly non-separable in the original feature space, it is projected into a much higher dimensional space R
n
(n may be infinite) using a non-linear mapping function
![]() ${\bi \varphi}\lpar {\bf x}\rpar $
. In other words,
${\bi \varphi}\lpar {\bf x}\rpar $
. In other words,
![]() ${\bi \varphi}\lpar {\bf x}\rpar $
is a vector in R
n
where l is much less than n.
${\bi \varphi}\lpar {\bf x}\rpar $
is a vector in R
n
where l is much less than n.
After projecting the training data into the new space, the SVM trainer searches for a linear discriminant function
![]() $f\lpar {\bf x}\rpar ={\bf w}^{T}{\bi \varphi}\lpar {\bf x}\rpar +b$
in the projected feature space (since training examples will be linearly separable after projection), and patterns are classified by the sign of
$f\lpar {\bf x}\rpar ={\bf w}^{T}{\bi \varphi}\lpar {\bf x}\rpar +b$
in the projected feature space (since training examples will be linearly separable after projection), and patterns are classified by the sign of
![]() $f\lpar {\bf x}\rpar $
. In this standard linear formulation, w is a vector of length n whose kth element is the weight value corresponding to the kth feature in
$f\lpar {\bf x}\rpar $
. In this standard linear formulation, w is a vector of length n whose kth element is the weight value corresponding to the kth feature in
![]() ${\bi \varphi}\lpar {\bf x}\rpar $
and b is a constant scalar (from a geometric point of view, w is a vector orthogonal to the decision boundary). Considering this formulation, the geometric margin of the hyper-plane, which is parametrised by (w, b) with respect to the ith training example
${\bi \varphi}\lpar {\bf x}\rpar $
and b is a constant scalar (from a geometric point of view, w is a vector orthogonal to the decision boundary). Considering this formulation, the geometric margin of the hyper-plane, which is parametrised by (w, b) with respect to the ith training example
![]() $\lpar {\bf x}^{\lpar i\rpar }\comma \; x^{\lpar i\rpar }\rpar $
, is defined as
$\lpar {\bf x}^{\lpar i\rpar }\comma \; x^{\lpar i\rpar }\rpar $
, is defined as
 $$\gamma^{(i)}=y^{(i)}\left(\left(\displaystyle{{{\bf w}}\over{\parallel{\bf w}\parallel}}\right)^T{\bf \phi}({\bf x}^{(i)})+\displaystyle{{b}\over{\parallel{\bf w}\parallel}}\right)$$
$$\gamma^{(i)}=y^{(i)}\left(\left(\displaystyle{{{\bf w}}\over{\parallel{\bf w}\parallel}}\right)^T{\bf \phi}({\bf x}^{(i)})+\displaystyle{{b}\over{\parallel{\bf w}\parallel}}\right)$$
Given a training set
![]() $S=\lcub \lpar {\bf x}_{\lpar i\rpar }\comma \; y^{\lpar i\rpar }\rpar \semicolon \; \ i=1\comma \; \ldots\comma \; m\rcub $
, the geometric margin over the entire set is defined as the smallest of the geometric margins on the individual training examples, i.e.:
$S=\lcub \lpar {\bf x}_{\lpar i\rpar }\comma \; y^{\lpar i\rpar }\rpar \semicolon \; \ i=1\comma \; \ldots\comma \; m\rcub $
, the geometric margin over the entire set is defined as the smallest of the geometric margins on the individual training examples, i.e.:
Considering the above, in its attempt to maximise γ, SVM solves the following optimisation problem (Cristianini and Shawe-Taylor, Reference Cristianini and Shawe-Taylor2000) to find w and b:
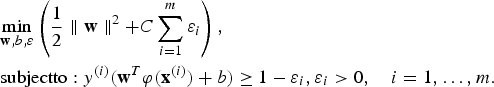 $$\eqalign{&{{\mathop {\min }\limits_{{\bf w},b,\varepsilon}}\left( {\displaystyle{1 \over 2}\parallel {\bf w}\parallel ^{2} + {C}\sum\limits_{{i} = {1}}^{m} {{\varepsilon }_{i}} } \right),} \cr &{{\rm subject to}:y^{(i)}({\bf w}^{T}{\bi \varphi }({\bf x}^{({i})}) + {b}) \ge 1 - \varepsilon _i,\varepsilon _i > 0,\quad i = 1, \ldots ,m.}}$$
$$\eqalign{&{{\mathop {\min }\limits_{{\bf w},b,\varepsilon}}\left( {\displaystyle{1 \over 2}\parallel {\bf w}\parallel ^{2} + {C}\sum\limits_{{i} = {1}}^{m} {{\varepsilon }_{i}} } \right),} \cr &{{\rm subject to}:y^{(i)}({\bf w}^{T}{\bi \varphi }({\bf x}^{({i})}) + {b}) \ge 1 - \varepsilon _i,\varepsilon _i > 0,\quad i = 1, \ldots ,m.}}$$
where
![]() $\varepsilon_{i}$
accounts for the misclassification error in the ith instance of training data. The optimisation in Equation (8) is equivalent to the following non-constraint optimisation problem:
$\varepsilon_{i}$
accounts for the misclassification error in the ith instance of training data. The optimisation in Equation (8) is equivalent to the following non-constraint optimisation problem:
 $$\min_{{\bf w},b}\left(\displaystyle{{1}\over{2}}\parallel{\bf w}\}^2+C\sum^m_{i=1}[y^{(i)}H_1 ({\bf w}^T{\bi \varphi}({\bf x}^{(i)})+b)+(1-y^{(i)})H_0 ({\bf w}^T{\bi \varphi}({\bf x}^{(i)})+b)]\right)$$
$$\min_{{\bf w},b}\left(\displaystyle{{1}\over{2}}\parallel{\bf w}\}^2+C\sum^m_{i=1}[y^{(i)}H_1 ({\bf w}^T{\bi \varphi}({\bf x}^{(i)})+b)+(1-y^{(i)})H_0 ({\bf w}^T{\bi \varphi}({\bf x}^{(i)})+b)]\right)$$
In both Equations (8) and (9), C is the regularisation parameter introduced later in this section and the H 0 and H 1 functions in Equation (9) can be represented as
The first term in Equation (9) is related to maximising the geometric margin, and the second term is related to minimising the training error.
Using the Lagrange method (Burges, Reference Burges1998) for solving the constrained optimisation in Equation (8) will result in the following optimisation form wherein “α i ”s are the Lagrange multipliers:
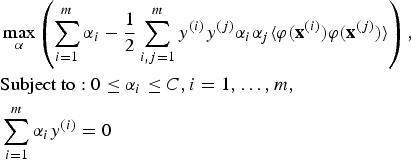 $$\eqalign{&\max_\alpha\left(\sum^m_{i=1}\alpha_i-\displaystyle{{1}\over{2}}\sum^m_{i,j=1}y^{(i)}y^{(j)} \alpha_i\alpha_j\langle{\bf \varphi}({\bf x}^{(i)}){\bf \varphi}({\bf x}^{(j)})\rangle\right), \cr &\hbox{Subject to}:0\le \alpha_i\le C, i=1,\ldots,m, \cr &\sum^m_{i=1}\alpha_iy^{(i)}=0}$$
$$\eqalign{&\max_\alpha\left(\sum^m_{i=1}\alpha_i-\displaystyle{{1}\over{2}}\sum^m_{i,j=1}y^{(i)}y^{(j)} \alpha_i\alpha_j\langle{\bf \varphi}({\bf x}^{(i)}){\bf \varphi}({\bf x}^{(j)})\rangle\right), \cr &\hbox{Subject to}:0\le \alpha_i\le C, i=1,\ldots,m, \cr &\sum^m_{i=1}\alpha_iy^{(i)}=0}$$
where
![]() $\langle{\bi \phi}\lpar {\bf x}^{\lpar i\rpar }\rpar {\bi \phi}\lpar {\bf x}^{\lpar j\rpar }\rpar \rangle$
is the dot product between
$\langle{\bi \phi}\lpar {\bf x}^{\lpar i\rpar }\rpar {\bi \phi}\lpar {\bf x}^{\lpar j\rpar }\rpar \rangle$
is the dot product between
![]() ${\bi \phi}\lpar {\bf x}^{\lpar i\rpar }\rpar $
and
${\bi \phi}\lpar {\bf x}^{\lpar i\rpar }\rpar $
and
![]() ${\bi \phi}\lpar {\bf x}^{\lpar j\rpar }\rpar $
, which is referred to as the kernel
${\bi \phi}\lpar {\bf x}^{\lpar j\rpar }\rpar $
, which is referred to as the kernel
![]() $K\lpar {\bf x}^{\lpar i\rpar }\comma \; {\bf x}^{\lpar j\rpar }\rpar $
so that
$K\lpar {\bf x}^{\lpar i\rpar }\comma \; {\bf x}^{\lpar j\rpar }\rpar $
so that
Since the optimisation cost function in Equation (11) can be entirely written in terms of the inner products of
![]() ${\bi \phi}\lpar {\bf x}^{\lpar i\rpar }\rpar $
, one does not need to know the high dimensional mapping function
${\bi \phi}\lpar {\bf x}^{\lpar i\rpar }\rpar $
, one does not need to know the high dimensional mapping function
![]() ${\bi \phi}\lpar {\bf x}\rpar $
to solve the optimisation problem. Instead, the cost function can be represented and optimised only as a function of the kernel. Specifically, computing
${\bi \phi}\lpar {\bf x}\rpar $
to solve the optimisation problem. Instead, the cost function can be represented and optimised only as a function of the kernel. Specifically, computing
![]() $K\lpar {\bf x}^{\lpar i\rpar }\comma \; {\bf x}^{\lpar j\rpar }\rpar $
is much less expensive than computing
$K\lpar {\bf x}^{\lpar i\rpar }\comma \; {\bf x}^{\lpar j\rpar }\rpar $
is much less expensive than computing
![]() ${\bi \phi}\lpar {\bf x}^{\lpar i\rpar }$
and
${\bi \phi}\lpar {\bf x}^{\lpar i\rpar }$
and
![]() ${\bi \phi}\lpar {\bf x}^{\lpar j\rpar }$
. The kernel function is a measure of similarity between the two examples. Taking advantage of the concept of kernel function allows the definition of a new set of features that are used instead of the primary feature set for training and classification. This new feature vector can be defined as
${\bi \phi}\lpar {\bf x}^{\lpar j\rpar }$
. The kernel function is a measure of similarity between the two examples. Taking advantage of the concept of kernel function allows the definition of a new set of features that are used instead of the primary feature set for training and classification. This new feature vector can be defined as
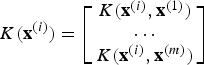 $$K({\bf x}^{({i})}) = \left[ {\matrix{ {K({\bf x}^{({i})},{\bf x}^{({1})})} \cr \cdots \cr {K({\bf x}^{({i})},{\bf x}^{({m})})} \cr } } \right]$$
$$K({\bf x}^{({i})}) = \left[ {\matrix{ {K({\bf x}^{({i})},{\bf x}^{({1})})} \cr \cdots \cr {K({\bf x}^{({i})},{\bf x}^{({m})})} \cr } } \right]$$
Therefore
![]() ${\bf x}^{\lpar i\rpar }$
is replaced by
${\bf x}^{\lpar i\rpar }$
is replaced by
![]() ${\bf k}\lpar {\bf x}^{\lpar i\rpar }\rpar $
. In the above equation, m is the total number of instances in the training set. Since the new feature vector has a length of m, the new weight vector should be also of length m. Therefore, the optimisation problem is now solved with respect to the new weight vector and constant parameter, namely
${\bf k}\lpar {\bf x}^{\lpar i\rpar }\rpar $
. In the above equation, m is the total number of instances in the training set. Since the new feature vector has a length of m, the new weight vector should be also of length m. Therefore, the optimisation problem is now solved with respect to the new weight vector and constant parameter, namely
![]() ${\bf w}'$
and b′. Considering these new definitions, the optimisation in Equation (11) is solved for α
i
using the Sequential Minimal Optimisation (SMO) algorithm (Platt et al., Reference Platt, Cristanini and Shawe-Taylor2000) and optimal
${\bf w}'$
and b′. Considering these new definitions, the optimisation in Equation (11) is solved for α
i
using the Sequential Minimal Optimisation (SMO) algorithm (Platt et al., Reference Platt, Cristanini and Shawe-Taylor2000) and optimal
![]() ${\bf w}'$
and b′ are then obtained as a function of α
i
as (Kimeldorf and Wahba, Reference Kimeldorf and Wahba1971)
${\bf w}'$
and b′ are then obtained as a function of α
i
as (Kimeldorf and Wahba, Reference Kimeldorf and Wahba1971)
 $$\eqalign{ {\bf w}&=\sum^m_{i=1}\alpha_iy^{(i)}{\bf k}({\bf x}^{(i)}), \cr b&=\displaystyle{{\max_{i:y^{(i)}=-1}({\bf w}^T{\bf k}({\bf x}^{(i)}))+\min_{i:y^{(i)}=1}({\bf w}^T{\bf k}({\bf x}^{(i)}))}\over{2}}}$$
$$\eqalign{ {\bf w}&=\sum^m_{i=1}\alpha_iy^{(i)}{\bf k}({\bf x}^{(i)}), \cr b&=\displaystyle{{\max_{i:y^{(i)}=-1}({\bf w}^T{\bf k}({\bf x}^{(i)}))+\min_{i:y^{(i)}=1}({\bf w}^T{\bf k}({\bf x}^{(i)}))}\over{2}}}$$
where m is the number of instances in the training data. Using this notation, the output label of a new example in the test set can be estimated as
Among “x (i)”s, the ones closest to the decision boundary are referred to as support vectors.
3.1. Radial Basis Function (RBF) Kernel
The question that has not been answered up to this point is how the kernel function is selected. Not every similarity function makes a valid kernel unless it satisfies the Mercer's theorem (Burges, Reference Burges1998). Based on this theorem, a similarity function is a valid kernel if and only if the kernel matrix formed from this function, the matrix whose (i,j)th element is
![]() $K\lpar x^{\lpar i\rpar }\comma \; x^{\lpar j\rpar }\rpar $
, is symmetric and positive definite. Several different non-linear kernels have been introduced and tested in the literature, including polynomial kernel, Radial Basis Function (RBF), sigmoid kernel, string kernel and chi-square kernel.
$K\lpar x^{\lpar i\rpar }\comma \; x^{\lpar j\rpar }\rpar $
, is symmetric and positive definite. Several different non-linear kernels have been introduced and tested in the literature, including polynomial kernel, Radial Basis Function (RBF), sigmoid kernel, string kernel and chi-square kernel.
The choice of the kernel and kernel/regularisation parameters can be automated by optimising a cross-validation-based model selection as will be explained in the next section. The cross-validation test performed herein led in the selection of the RBF kernel for our dataset.
The RBF kernel, also known as the Gaussian kernel is defined as
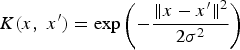 $K\lpar x\comma \; x'\rpar =\exp\left(-\displaystyle{{\Vert x-x'\Vert^{2}}\over{2\sigma^{2}}}\right)$
(Hsu et al., Reference Hsu, Chang and Lin2003) wherein the value of σ, the Gaussian radius, is also set using the cross-validation test. This function is a reasonable measure of similarity. It is close to 1 when x and x′ are close and near zero when they are far apart.
$K\lpar x\comma \; x'\rpar =\exp\left(-\displaystyle{{\Vert x-x'\Vert^{2}}\over{2\sigma^{2}}}\right)$
(Hsu et al., Reference Hsu, Chang and Lin2003) wherein the value of σ, the Gaussian radius, is also set using the cross-validation test. This function is a reasonable measure of similarity. It is close to 1 when x and x′ are close and near zero when they are far apart.
3.2. Improving the kernel properties
The performance of a support vector machine classifier greatly depends on the kernel function. It is possible to further improve the performance of SVM by modifying the selected kernel. The idea is to enlarge the spatial resolution locally in neighbourhoods of support vectors, which are located closely to the boundary surface, such that the separability between classes in the feature space is increased without changing the volume of the entire space. This is realised approximately by a conformal transformation of a kernel as follows ((Amari and Wu, Reference Amari and Wu1999):
where
![]() $\tilde{K}\lpar x\comma \; x'\rpar $
is the modified version of K(x, x′). c(x), namely the conformal transformation factor, is a positive scalar function of data that has large values at the Support Vector positions (SV) and is represented as
$\tilde{K}\lpar x\comma \; x'\rpar $
is the modified version of K(x, x′). c(x), namely the conformal transformation factor, is a positive scalar function of data that has large values at the Support Vector positions (SV) and is represented as
Moreover, in Equation (16), τ is a design parameter whose optimal value is around
![]() $\sigma/\sqrt{L}$
(Amari and Wu, Reference Amari and Wu1999), and w
i
is the element of w that corresponds to the i
th support vector.
$\sigma/\sqrt{L}$
(Amari and Wu, Reference Amari and Wu1999), and w
i
is the element of w that corresponds to the i
th support vector.
When this approach is applied to an SVM classifier, the training process is performed in two steps. In the first step, a primary kernel is used to obtain support vectors. The kernel is then modified by using the support vector information. In the second step, the modified kernel is used to obtain the final classifier.
3.3. Cross Validation and grid search
An SVM model contains a set of unknown parameters and factors such as the type of kernel, the regularisation parameter C and the kernel parameters (such as σ2 in RBF kernel) whose appropriate values must be estimated using the available data. Therefore, a parameter search must be performed to identify an approximately optimal selection of these parameters so that the classifier can accurately predict unknown data (i.e. testing data). A common strategy is to separate the available labelled data set into three parts (Hsu et al., Reference Hsu, Chang and Lin2003). The first part (which includes around 80%) of the labelled data is used as the training data. The second part (around 10%) is used as a “cross-validation” data set, and it is also used for selecting the optimum values of the unknown model parameters. Finally, the third part of the labelled data is used as the test data set to evaluate the trained classifier. The prediction accuracy obtained from the test set reflects the classification performance.
In the cross-validation test, a search grid in the model parameters space is first formed. Then, for each search point in the considered space, the classifier is trained using the training data set and is tested using the cross validation set. Finally, the search point that corresponds to the smallest prediction error on the cross-validation data set determines the optimum values of the model parameters.
The cross-validation procedure can prevent the over-fitting problem that is the case when the trained classifier perfectly fits the training data set while the prediction performance of the test data set is poor.
3.4. Multi-Class SVM Classification
The support vector machine methodology explained so far is a binary (two-class) classifier. In many cases in practice, the data must be classified into more than two classes. Multiclass SVMs are normally implemented by combining several binary SVMs (Dietterich and Bakiri, Reference Dietterich and Bakiri1995). Two well-known methods for doing this are the one-versus-all method using a winner-takes-all strategy and one-versus-one method implemented by max-wins voting (Platt et al., Reference Platt, Cristanini and Shawe-Taylor2000).
The one-versus-all multi-class classifier constructs M binary classifiers. The k
th binary classifier output function
![]() $f_{k}\lpar {\bf x}\rpar =\lpar {\bf w}^{T}{\bf k}\lpar {\bf x}\rpar +b\rpar $
is trained taking the examples from the k
th class as positive and the examples from all other classes as negative. For a new example
$f_{k}\lpar {\bf x}\rpar =\lpar {\bf w}^{T}{\bf k}\lpar {\bf x}\rpar +b\rpar $
is trained taking the examples from the k
th class as positive and the examples from all other classes as negative. For a new example
![]() ${\bf x}_{t}$
, the one-versus-all SVM strategy assigns it to the class with the largest value of f
k
(x
t
). The one-versus-one method associates one binary classifier for every pair in the set of M classes. Therefore, a total of M(M − 1)/2 binary classifiers are constructed. The (k, j)th binary classifier is trained taking the examples from the k
th class as positive and the examples from the j
th as negative. For a new example x
t
, the vote for the k
th class is incremented by one if the (k, j)
th
binary classifier such as x
t
belongs to the k
th class. Otherwise, the vote for the j
th class is added by one. After all M(M − 1)/2 classifiers vote, the one-versus-one strategy assigns x
t
to the class with the largest number of votes. The empirical results presented by Duan and Keerthi (Reference Duan and Keerthi2005) show that the performance values of the two methods are very similar. Therefore, since the one-versus-all method is faster (it consists of M classifiers instead of M(M − 1)/2 classifiers), it is used in this paper.
${\bf x}_{t}$
, the one-versus-all SVM strategy assigns it to the class with the largest value of f
k
(x
t
). The one-versus-one method associates one binary classifier for every pair in the set of M classes. Therefore, a total of M(M − 1)/2 binary classifiers are constructed. The (k, j)th binary classifier is trained taking the examples from the k
th class as positive and the examples from the j
th as negative. For a new example x
t
, the vote for the k
th class is incremented by one if the (k, j)
th
binary classifier such as x
t
belongs to the k
th class. Otherwise, the vote for the j
th class is added by one. After all M(M − 1)/2 classifiers vote, the one-versus-one strategy assigns x
t
to the class with the largest number of votes. The empirical results presented by Duan and Keerthi (Reference Duan and Keerthi2005) show that the performance values of the two methods are very similar. Therefore, since the one-versus-all method is faster (it consists of M classifiers instead of M(M − 1)/2 classifiers), it is used in this paper.
3.5. Feature Extraction for Multipath classification case
In this paper, the features for multipath classification are extracted from the correlation sequences of the received GNSS signal rather than the channel parameters (the set of complex gains and delay of multipath components) themselves. This method of feature extraction is much more feasible since accurate estimation of all channel parameters requires very high sampling rates (hundreds of MHz). Two different sets of features, namely temporal and spectral, are extracted to represent each channel example. The temporal features are more useful for classifying the type of environment. The spectral features better represent the type of receiver motion. The correlation delay axis is divided into 16 bins. The first 15 bins are equi-spaced and cover the range of delays from 0 to 0·5 chips. The last bin represents delays from 0·5 to 1 chip. Therefore, there are 32 temporal features consisting of the magnitudes and relative phases of the correlation function at the centre of each bin.
To extract the spectral features, a Fourier transform is performed on every 20 successive correlation vectors (each correlation vector is 4 ms). Therefore, for each correlation delay bin, 20 time-successive samples contribute to computing a Fourier-transformed sequence from which frequency-domain features are extracted. The index of the dominant spectral peak and its bandwidth are the two spectral features extracted for each bin. Therefore, there are a total of 32 frequency features for each channel sample. After extracting the features matrix X, each column of the matrix is normalised as
Therefore, after normalisation, all the features will be between 1 and −1. Normalisation helps to avoid features with larger absolute values dominating the ones with lower absolute values.
4. TEST RESULTS FOR THE TRAINED CLASSIFIER
The same channel models used to generate the training set and the cross-validation set examples are used in an independent simulation to generate the test set. The simulation combines the delayed and attenuated versions of a single path Galileo signal using the simulated channel parameters to generate correlation function patterns of the received signal based on Equation (1). From each generated pattern, a total of 64 features are extracted based on the strategy explained in the previous section. For this test, the training set contains 10,000 instances per class, and each of the cross-validation sets and the test set contains 2,000 instances per class. After the cross-validation test, the values of C and σ were set to 100 and 0·05, respectively. Six different classes of patterns are considered: Urban-Vehicular, Urban-Pedestrian, Suburban-Vehicular, Suburban-Pedestrian, Indoor and Open Sky. Table 1 shows the accuracy of classification for each class after evaluating the classifier on the test data set. The results in the first column are based on SVM classification using the basic RBF kernel while the results in the second column correspond to the case where the kernel is modified based on Equations (15) and (16).
Table 1. Classification accuracy.

The results in the table show that modifying the kernel can improve the classification performance, specifically in distinguishing between urban and suburban vehicular classes. As it is also observed by comparing Figure 1 and Figure 2, urban and suburban patterns are more separable under the pedestrian motion state than the car motion state. Open sky and indoor patterns are effectively distinguished from urban and suburban cases.
5. ADAPTIVE MULTIPATH COMPENSATION AND TRACKING STRATEGY
In the previous section, it was explained how the effect of multipath channel on the pattern of the correlation sequence of the received signal can be used to recognise the multipath channel and receiver motion types. To be able to effectively utilise this important information in the structure of the receiver to minimise multipath effects from the estimated tracking parameters such as code phase, the receiver should employ some highly adaptive multipath compensation mechanism. A set of adaptive algorithms derived based on the stochastic gradient equalisation methodology (Sayed, Reference Sayed2008) is used here to compensate for the effect of multipath and track its temporal variations. Each of these closed-loop algorithms relies on some tuning parameters, which can be set based on the channel type classification results extracted from the SVM classifier output. Therefore the receiver can select the appropriate tracking method and properly tune it based on the classification results. For instance, when the channel is subject to fast variations, the receiver should decrease confidence in previous data and rely more on recently captured data which is equivalent to changing a design parameter that plays this role. Moreover, some adaptive algorithms can more reliably deal with dense multipath environments. However, these algorithms are normally more complex and slower than others. Having knowledge of the channel type, the receiver can maintain a trade-off between tracking complexity and reliability by selecting an appropriate tracking method.
Gradient descent and Newton's method are two well-known optimisation recursive algorithms. The algorithms work iteratively to find a local minimum of a function. The convergence rate of these algorithms depends on a parameter known as the step size. The step size can be kept fixed or changed with time. A small and fixed step size can lead to slow convergence. The step size can be found using a line search process at every iteration. However, this can cause a high processing overhead. Alternatively, the step size can be found analytically. In situations where solving the gradient descent and Newton's method recursions are not possible, they are approximated by Least Mean Squares (LMS) and exponentially-weighted Recursive Least Squares (RLS) approaches, respectively. In an exponentially weighted RLS approach, a weight factor in the range of [0,1] is used. Setting the weight factor to less than 1 gives more weight to most recent data (Clarkson, Reference Clarkson1993). This is especially beneficial when older data are less relevant. The optimal weight factor can be found using maximum likelihood approaches.
The adaptive algorithms applied for multipath compensation and tracking in this paper are selected from the class of stochastic-gradient-based adaptive filters in both time and wavelet domains (Sokhandan et al., Reference Sokhandan, Broumandan, Curran and Lachapelle2015). Here, two stochastic gradient approaches, namely the LMS and RLS and their wavelet-domain duals, referred to as WLMS and WRLS, are used to compensate for the effect of multipath channel from the correlation samples and estimate the parameters of the LOS signal. The mathematical and computational details of these algorithms are described in the reference mentioned above.
In the next section, the trained classifier explained in the previous section is used to adaptively trigger the design parameters of the introduced tracking methods based on the type of environment. The block diagram of an adaptive stochastic-gradient-based multipath compensation technique in the wavelet domain is shown in Figure 3. In this Figure,
![]() ${\bf y}_{k}$
is the vector of raw correlation samples,
${\bf y}_{k}$
is the vector of raw correlation samples,
![]() $\hat{{\bf y}}_{k\comma l}$
is the vector of compensated correlation samples,
$\hat{{\bf y}}_{k\comma l}$
is the vector of compensated correlation samples,
![]() $\tilde{{\bf y}}_{k\comma l}$
is the vector of estimated correlation samples for LOS signal after a hard decision, G is a matrix formed from ideal correlation samples and finally τ
LOS, k
is the estimated LOS delay. Furthermore, OSC refers to an Oscillator, MSR refers to the Measurement, DWT stands for Discrete Wavelet Transform and NCO refers to Numerical Controlled Oscillator.
$\tilde{{\bf y}}_{k\comma l}$
is the vector of estimated correlation samples for LOS signal after a hard decision, G is a matrix formed from ideal correlation samples and finally τ
LOS, k
is the estimated LOS delay. Furthermore, OSC refers to an Oscillator, MSR refers to the Measurement, DWT stands for Discrete Wavelet Transform and NCO refers to Numerical Controlled Oscillator.

Figure 3. Block diagram of the adaptive system in the wavelet domain.
6. TEST RESULTS FOR ADAPTIVE TRACKING
In this section, the effect of the context-aware multipath compensation strategy selection on delay estimation performance is evaluated through a mixed multipath scenario simulation. The simulated data consists of four different multipath conditions with the same duration: vehicular urban, pedestrian urban, vehicular suburban and pedestrian suburban cases. The simulated channel samples for this section are generated using the same software used in the classification section (Lehner and Steingass, Reference Lehner and Steingass2005; Lehner and Steingass, Reference Lehner and Steingass2008; Lehner et al., Reference Lehner, Steingass and Schubert2009). In these simulations, Intermediate Frequency (IF) Galileo E1 signals (PRN 19) with a sampling rate of 50 MHz are used. The coherent integration time is 4 ms. Since the maximum excessive delay for strong echoes (near echoes) is less than a chip, the focus is to search for the components with sub-chip delays. Note that for CBOC signals, the zero-crossings of the main lobe are located around +/ − 0·35 chips and the peaks of the two side lobes are located around +/ − 0·5 chips. Each of the adaptive multipath compensation algorithms introduced in the previous section has a tuning parameter whose optimal value depends on the multipath scenario. Therefore, before performing the adaptive selection and tuning strategy, optimal values of the tuning parameters for each algorithm under each multipath scenario are estimated using a separate simulation. Figure 4 shows one simulation example of these evaluations. In this case, the optimal values of the exponential weight parameter for RLS and WRLS algorithms are investigated under a vehicular urban simulation scenario. Similar simulations are performed for the other algorithms and other simulation scenarios. The estimated optimal values are shown in Table 2. In this table, 0 < μ≤ 1 is the step size parameter used in the LMS and the WLMS algorithms and
![]() $0 < \lambda \le 1$
is the forgetting factor used the RLS and WRLS algorithms that down weights the impact of the previous signal vectors with respect to the newly received ones in computing the covariance matrix.
$0 < \lambda \le 1$
is the forgetting factor used the RLS and WRLS algorithms that down weights the impact of the previous signal vectors with respect to the newly received ones in computing the covariance matrix.

Figure 4. RMS error performance of LOS delay estimation for RLS and WRLS algorithms as a function of exponential weight parameter (λ).
Table 2. Estimated optimum values of tuning parameters of adaptive algorithms under different multipath scenarios.

Figure 5 compares the delay estimation RMS error values of different adaptive multipath compensation algorithms. The mixed strategy in this figure detects the type of multipath environment for each time snapshot using the SVM classifier, and then selects the proper tracking strategy correspondingly. The mixed strategy uses the WRLS algorithm (because it has the best performance) for three of the scenarios, which are the vehicular, pedestrian urban, and vehicular suburban cases. For each of these cases, the value of λ is selected based on Table 2. For the suburban pedestrian scenario, it uses WLMS with the corresponding value of μ based on Table 2 (because WLMS is less complex than WRLS (Sokhandan et al., Reference Sokhandan, Broumandan, Curran and Lachapelle2015)). Monte-Carlo simulations results are averaged over 8000 ms of data for each value of carrier-to-noise ratio (C/N0).

Figure 5. RMS error of LOS delay estimation of different algorithms for a mixed multipath scenario.
It can be observed in Figure 5 that adjusting the tracking strategy based on the type of environment and the state of motion of the receiver result in a 15% improvement in delay estimation performance. For pure WRLS and RLS algorithms, the value of λ is set to 0·85. For pure WLM and LMS algorithms, the value of μ is set to 0·01. Comparing the performance of the algorithms other than the mixed algorithm shows that the WRLS and WLMS techniques considerably outperform the other techniques in the sense of LOS delay estimation Root Mean Square (RMS) error. Moreover, the RMS error variations as a function of the C/N0 are much smoother for these two algorithms as compared to the other four. For example, the RMS error corresponding to WRLS algorithm starts at 15 m for a C/N0 of 20 dB-Hz and drops to 6 m for C/N0 values larger than 50 dB-Hz. For the WLMS algorithm, the RMS error starts at 22 m for a C/N0 of 20 dB-Hz and decreases to 5–6 m for C/N0 values larger than 50 dB-Hz. The implementation of the RLS and LMS algorithms in the wavelet domain results in a remarkable improvement in estimation performance compared to their implementation in the time domain. This improvement is due to the noise resistant structure of the former implementation. This is why the computational cost of implementing the algorithms in the wavelet domain is also smaller than the time-domain implementation. This is because a smaller number of correlation points is used, which results in a smaller number of matrix calculations. A very interesting point that can be inferred from Figure 5 is that the performance results of the LMS and RLS algorithms in the wavelet domain are much closer to each other than in the time domain. In fact, the WLMS algorithm with a very small computational complexity can be used instead of the WRLS algorithm, while the performance loss is insignificant. However, it can be observed that the difference in the performance of the two algorithms in the time domain (RLS and LMS) is significant.
7. REAL DATA PROCESSING RESULTS
In this section, a set of GPS L1 C/A and Galileo E1b/c signal processing results are now used to further compare the performance of the proposed adaptive filter selection and tuning algorithm with those of the fixed strategy trackers under field conditions. The GPS signals are used for positioning along with the Galileo signals because the number of visible Galileo satellites was not sufficient during the test. However, the classification results are extracted using only Galileo signals. Moreover, the performance of the proposed algorithms is compared to the MEDLL technique. The test data set was collected on a trajectory travelled by a vehicle in downtown Calgary. The trajectory was selected to include all the four multipath scenarios described earlier. The data collection equipment included a Radio Frequency (RF) front-end located inside the vehicle, a NovAtel antenna and a SPAN system mounted on the roof of the vehicle. The tightly-coupled integrated GPS-INS (GPS-Inertial Navigation System) was used to obtain continuous reference position solutions with a 1 m accuracy for performance assessment. The sampling frequency of the front-end's digitiser was 20 MHz. The sky plot of the satellites and the data collection trajectory are shown in Figure 6. The proposed delay estimation techniques were implemented in a software receiver. The tracking loop update interval was 20 ms and the PLL and DLL bandwidths were 15 and 2 Hz. In the implementation of narrow correlators, a correlator spacing of 0·1 chip was utilised. The parameters μ (for LMS and WLMS) was set to 0·07 and λ (for RLS and WRLS) was set to 0·87. For wavelet transformation, Haar's wavelet filters with one level of decomposition were used. This choice of wavelet was selected based on the deconvolution-based estimation results presented in Vaz and Daut (Reference Vaz and Daut2012). The data collection setup is shown in Figure 7.

Figure 6. Sky plot of satellites and data collection test trajectory.

Figure 7. Data collection setup.
The adaptive filter selection and tuning algorithm (referred to as Mixed) detects the type of the multipath environment for each time snapshot using the trained SVM classifier and then selects the proper tracking strategy correspondingly. It uses the WRLS algorithm for three of the scenarios (due to its superior performance), which are vehicular, pedestrian urban and vehicular suburban cases. For each of these cases, the value of λ is selected based on Table 2. For the suburban pedestrian scenario, it uses WLMS with the corresponding value of μ also based on Table 2. The time series of position estimation errors and their RMS values are plotted in Figure 8 and Figure 9. The most important observation is that the context-based algorithm outperforms the best of the fixed-strategy algorithms (WRLS technique) although the improvement is small for some cases such as the east component. For example, the SVM-based strategy results in an improvement of about 35% in the north component RMS error. Comparing the fixed strategy techniques together shows that in general, the largest RMS error values correspond to the LMS algorithm. However, RLS shows an improvement of 14% to 33% compared to the LMS and the performance of MEDLL is closely comparable to the RLS. The WLMS and WRLS algorithms demonstrate major improvements compared to their time domain duals. For example, for the vertical component, the RMS error value is 27 m for WRLS and 51 m for the RLS algorithm, which is equivalent to a 47% improvement. The corresponding improvements for the east and north components are smaller. WLMS shows similar improvements compared to the time domain LMS. Another important observation is that the performance difference between LMS and RLS is smaller when they are implemented in the wavelet domain rather than the time domain.

Figure 8. Position estimation error time series.

Figure 9. Comparison of position estimation RMS errors.
8. CONCLUSIONS
A channel pattern recognition algorithm based on a support vector machine classifier with a modified Gaussian kernel was used to extract context information about the type of multipath environment and the state of motion of a GNSS receiver. The information extracted was used to trigger the design parameters of different adaptive multipath compensation methods based on the statistics of the multipath channel. Adaptive multipath compensation methods were used based on stochastic gradient tracking algorithms, which were implemented in the time and wavelet domains. The classification test results showed that the modified classifier separates four different environment types with an accuracy of 86%. Moreover, the type of receiver motion (for urban and suburban environments) was detected with an accuracy of 92%. The simulation results showed that the delay estimation performance of the adaptive multipath tracking algorithms was improved by about 15% when the context information was used to trigger the tracking parameters of these techniques.












