Development of a Digital Accident Hotspot Map for ADAS Applications Using Geospatial Methods in GIS

Abstract

Digital maps have a large potential to support safety-related Advanced Driver Assistance Systems (ADAS) by providing detailed road and environment information. However, one critical attribute – road accident hotspot – is not available from existing digital maps, and is also difficult to derive from practical surveying. This paper provides a Geographical Information Systems (GIS)-based approach for the production of digital hotspot maps, based on a historical accident dataset and geospatial methods in a GIS. In this approach, firstly the Kernel Density Estimation (KDE) method was used to identify hotspot distribution; secondly the Percent Volume Contour (PVC) method was coupled with KDE to extract hotspot patterns; and finally the map layers of hotspot patterns were integrated with classical navigation maps. Following a description for geospatial hotspot production, the derivation of hotspot property data is also discussed. In order to prove this approach, a small-area case study was carried out in the City Centre of Nottingham. The presented results demonstrate that this approach is useful and effective for solving the hotspot creation problem for ADAS, but other future works will be required to improve data effectiveness.

1. INTRODUCTION

In recent years, Advanced Driver Assistance Systems (ADAS) have been studied widely to improve driver safety. Many electronically aided ADAS systems have been applied, such as Lane Departure Warning systems, Adaptive Cruise Control, Traffic Signal Assistant, etc. The rapid development of ADAS systems has implied higher data requirements from the driving environment for the various applications. However, in-vehicle electronic sensors (e.g. radar, infrared, camera, etc.) are either too expensive, or are limited by relatively short-range data capture capacity. Apparently, this is far less than the current requirements of ADAS applications (Safety Support, 2005; Ammoun, 2010). In order to solve this problem, attention has been given to developing enhanced digital map databases to support applications in ADAS (Li et al., 2008).

Digital maps have large potential in supporting safety-related ADAS by providing rich road and environment information. With rich map information, vehicles can be enabled with an “electronic horizon” that is superior to human sight distance as digital maps can provide numerous realistically unreachable data types beyond the horizon of the drivers. This horizon enables a “look-ahead” capability for vehicles, which is effective in avoiding potential dangers and possible hazards (Jimenez et al., 2009). In fact, if a look-ahead capacity can be enabled, a large range of ADAS applications can be created based on such a capability, including a Curve Warning System, Intelligent Speed Adaptation and Run-off Road Detection and Warning.

To take advantage of the ADAS concept, additional details/data need to be incorporated into the digital maps. Some of the data are related to safety attributes, such as legal speed limits, traffic signs, road gradient, lane information, unknown hazardous area, enhanced road geometry, etc. These types of data can be used to support a variety of value-added safety services. For instance, road curvature attributes can be used to reduce curve over-speeding by coupling with a real-time Global Navigation Satellite System (GNSS) (Li et al., 2008). Unfortunately, not all required attributes are available from existing data sources. A portion of data exists but lacks adequate specification (e.g. road curve radius). In addition, some other data, such as accident hotspots, are unavailable from existing map databases.

Accident hotspots are an important and typical safety attribute for a digital map. Road hotspots are symbolised as a type of hypothesis concept, which indicates road segments or areas with an extraordinary number of historical accidents. Hotspot-based warning can help drivers be aware of potential danger areas when closing accident hotspots, and the reminders can effectively reduce potentially dangerous behaviour such as speeding (Hecht and Heinig, 2007). However, as stated above, the challenging issue is the hotspot data sourcing because accident hotspot data cannot be directly surveyed or digitised from paper maps or aerial photographs. Therefore, researchers have been motivated to seek alternative methods to derive reliable accident hotspot maps. From available literature one available option to derive the hotspots is extracting the hotspots from historical datasets and then analysing and integrating them into traditional navigation maps. This type of approach was firstly mentioned by the European project MAP&ADAS but not deeply discussed or implemented (Hecht and Heinig, 2007). Since in-vehicle map databases are used to support real-time ADAS systems, digitisation of accident hotspots is complicated in traditional navigation maps. Examples include: 1) Hotspot accuracy requirement is suggested as less than 10 metres for future ADAS systems, but it is relatively difficult to establish the hotspot location on the correct road within this accuracy; 2) Practical considerations on using digital maps for ADAS systems, such as the quality of hotspot, data storage limitation, map updating, accommodation of complex or dynamic hotspot attributes (Safety Support, 2005).

The major contribution of this paper focuses on the development of a novel approach for hotspot map production. Hotspot maps were generated based on historical accident datasets and geospatial methods provided in a GIS. The structure of the paper is as follows: Section 2 provides a background literature review of relevant studies including a summary of developments of digital maps for ADAS applications. Section 3 details the data sources, methodology and relevant results. Section 4 provides a discussion of methodology constraints and limitations. Section 5 discusses potential application of developing such digital maps, and finally, Section 6 concludes this paper.

2. RELATED WORK

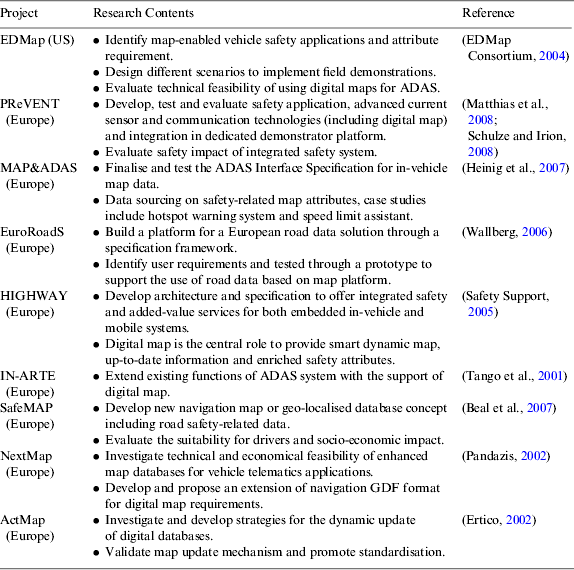
Nowadays the development of digital road maps is not only focused on the applications of navigation, but also on ADAS applications. Digital maps have been increasingly studied in conjunction with vehicle positioning and other sensors to enable a large range of active or passive safety functionalities. The extension of the digital map function as a virtual sensor in ADAS systems has been explored by many projects around Europe and the United States (see Table 1 for more information and references). Digital safety maps for ADAS applications require a greater degree of accuracy and detail when compared to classic digital road maps used for navigation and route guidance purposes (Jimenez et al., 2009). By identifying different ADAS requirements, the aforementioned projects have worked towards two aspects:

• • Enhance map precision based on existing road geometry to support ADAS accuracy requirements.

• • Include more map details from additional data sources to support various ADAS applications.

Table 1. Project summary for the development of digital maps for ADAS applications.

In the US, the EDMap project has discussed the accuracy and map information requirement of various ADAS applications. The results have shown that digital map databases appear to be very promising in safety applications but more improvements for map details and contents are required for high-level ADAS applications (EDMap Consortium, 2004). The findings from the NextMap project show that enhanced maps are both technically and economically feasible and almost all ADAS applications can benefit from enhanced safety maps (Pandazis, 2002). In addition, the ADAS forum working group was intended to organise the map attributes required for ADAS applications (Safety Support, 2005). A few pilot studies have also been made into a digital map-based curve warning system (Li et al., 2008).

A study of an accident hotspot warning system was piloted in the MAP&ADAS project where the digital hotspot map was designed to provide necessary hotspot attributes to support hotspot warning (Hecht and Heinig, 2007; Map&ADAS, 2006). The development of accident hotspots was one of the main tasks of exploring digital maps for ADAS (Ress et al., 2004). From a map point of view, the challenge for this work is to identify “real” hotspot data that are likely to lead to accidents under similar circumstances and integrate data to the classic navigation map. Two methods to produce accident hotspots mentioned in the MAP&ADAS project were accident hotspot statistics and risk index evaluation. The former method utilises the available accident data from state statistical offices and analyses different levels of detail leading to accidents. The advantage of this method is that it is simple enough to meet the experimental requirement. However, for map providers, different levels of detail of accident hotspot data are difficult to obtain and maintain. The statistical analysis method is time-consuming and not commercially feasible to process data for accident hotspots. The risk evaluation method provides a generic risk vectors assessment for different road types based on a historical dataset and attaches these risk vectors to a digital map database that is used for hotspot warning. This method is more feasible than the accident hotspot statistics method, but a few disadvantages still exist, such as the specification of road links might vary in the road map from several metres to hundreds of metres and it is thus difficult to position the accurate hotspot in a longer road segment. In addition, road intersection hotspots which are referred to hotspot area management are difficult to deal with by such a linear road segment-based method.

Using geospatial methods in a GIS for digital hotspot maps has not been mentioned in the past literature although geospatial analysts have widely studied the various hotspots issues for other subjects, such as road accident (Erdogan et al., 2008; Anderson, 2009), crime (Harada and Shimada, 2006) and animal home range (Seaman and Powell, 1996). The results here have demonstrated that geospatial methods are valuable in hotspot mapping and decision-making analysis. Based on these researches, various commercial, free or open-sourced tools or functionalities have been developed, such as the spatial analyst toolbox in ESRI ArcGIS extension, CrimeState, STAC, Hotspot Detective, etc. McCullagh (2006) has made an in-depth investigation of these methods. To date, the potential benefits of using geospatial methods in GIS for digital road maps have not been explored. Many existing geospatial analysis tools in GIS can be used for hotspot map production and will be described in this paper.

3. MATERIAL, METHODOLOGY AND RESULTS

3.1. Data sources, software platform and study area

The case study area was in the City of Nottingham. The study area contains a part of urban, metropolitan area where road accidents frequently happen. Figure 1 shows the area, accident distribution and the area roadway network. Integrated Transport Network (ITN) maps from the United Kingdom (UK) Ordnance Survey were used as the referenced road network, which provides a vector-based digital road dataset. Various road classes were included, such as A-road, B-road and C-road, and A-Roads were specifically highlighted in blue as the major trunk road in this area.

Figure 1. Metropolitan area of Nottingham, accidents on the road network.

STATS19 accident data was used as the historical accident dataset, which was collected from the UK Data Archive. The road accident data were imported to the ArcMap 10 GIS platform based on accident ID identifiers and coordinates. The locations of accidents were mapped with Ordnance Survey Great Britain 1936 (OSGB36) projection, a similar projection to road data.

The statistical method was used to identify and analyse important accident characteristics in the study area. Three-year accident records (2005–2007) were analysed on different road types (see Table 2). A high percentage, 51·2% of road accidents occurred on A-roads, compared with a relatively smaller amount of accident on B-roads (11·7%), C-roads (9·2%) and Unknown-roads (27·8%). It was found from historical data that intersection data comprised a high percentage of accidents (53%). Therefore, A-road and intersection hotspots are of interest in this research.

Table 2. Summary of historical accident characteristics at study area.

3.2. Determining accident hotspot distribution

The Kernel Density Estimation (KDE) method was used to identify road hotspots in the GIS. The KDE is one type of density statistical technique that constructs an estimate of density distribution from the structure of observed data. It has been developed as a type of spatial method in GIS (Silverman, 1986). Using KDE, it is possible to estimate the distribution of accident density based on the coordinate point of accident without other data. The description of KDE and its application to identify road hotspot patterns is described as follows.

The equation of KDE is stated as follows:

(1)$$f\,(x) = \; \displaystyle{1 \over {nh}}\mathop \sum \limits_{i = 1}^n K\left( {\displaystyle{{x - X_i} \over h}} \right)$$

In this formula the f(x) represents the estimated accident density at an Evaluation Reference Point (ERP) location x. The value n is the number of accident samples used in the study. The value h is bandwidth, also variously termed as search radius or window width. This controls the search radius of ERP point. Traffic accidents in KDE are understood as independent bivariate data. The locations of all accidents are represented as vector values in a two-dimensional geographical space as X ₁=[x ₁, y₁], X ₂=[x ₂, y₂] to X _n=[x _n, y_n] (including ERP). The value x-X _i represents the distance between the ERP and other accident points. K is the kernel function, which is a symmetrical bivariate probability function that was used to determine the shape of probability distribution over each accident point.

To calculate density f(x), the parameters such as kernel function K, search radius h, sample parameters (point coordinates and the number of sample) are required. Sample parameters are established by GIS software once the sample is imported. The probability function K is selected by the user as choices of kernel from Triangle, Normal, Biweight, Gaussian, Epanechnikov, etc. A typical example of kernel function, such as Biweight Kernel K ₁, is defined as:

(2)$$K_1 (x) = 3\pi ^{ - 1} (1 - x\prime x)^2 $$

The value x′x is the distance from the elevation point to any other point in the set divided by the bandwidth h. If x′x <1, the searched points are within the search radius and the function K ₂ is used to evaluate the density of the evaluation point. If x′x >1, then these points are too far away, it would have little density estimation influence and the points would not be selected. Therefore, if accident points are included in the density estimation, its contribution for density is weighted by a distance-based weighting function. The points near to the evaluation point have more contribution than those that are far away from the evaluation point. Kernel function and search radius are two key factors for density estimation. However, from the past literature, it is commonly accepted that different kernel functions have little influence on the final results. In this research the selection of kernel inherited this conclusion and only one fixed kernel function is selected and the influences due to different kernel functions will not be discussed in this paper.

In a GIS the KDE method is built upon raster computation. Firstly, the raster map space is sub-divided into grids of rows and columns, the intersections of each row and column create a square-based pixel or cell, as shown by Figure 2(d). In a raster map the geometry of an object is expressed by a set of neighbouring pixels and each pixel could accommodate discrete or continuous values. Different values in the pixels enable representation of different physical phenomena, such as the magnitude of temperature, the degree of soil pollution, etc. Secondly, the KDE calculates the cell values for density representation and transforms values to different colours or the shade of same colour to colourise density distribution.

Figure 2. Raster-based KDE algorithm (modified from Laver, 2005).

While implementing a KDE in a GIS, kernel function K and bandwidth h and cell size S are required to be set up beforehand, which are respectively referred to as KDE, search radius and raster quality. The computational implementation of the KDE is divided into two steps, which are referred to as point-to-point evaluation and pixel-to-point evaluation, as shown in Figure 2.

As can be seen from Figure 2, in the first stage the KDE algorithm selects one of the accident points as an ERP, as shown by example P₁ in Figure 2(a). Based on the search radius h, the other example points R₁, R₂ and R₃ in the vicinity (within radius h) are included and a density value is calculated for the selected points, in parallel based on the selected kernel function K and their distances to P₁, as shown by Figure 2(b). This procedure is repeated until all points in the distribution have been evaluated. The density values of each point were calculated, shown by Figure 2(c) as D₁, D₂, and D₃.

In the pixel-to-point evaluation stage, the raster data with specific cell size S are generated and superimposed to the random distributed accident sample (Figure 2(d)). Like the first step, the raster cells within the search radius are assigned with density values in order, (see Figure 2(e)). The subsequent points are also evaluated and the density values are calculated cumulatively within raster cells. With a computation loop for all points, a density surface is generated and colour density pattern is applied based on these cell values (see Figures 2(f) and 3).

The size of the cells is referred to as raster resolution, which represents the level of map detail and also affects the hotspot quality. Figure 3 shows the performances of two different cell sizes (i.e. 150 metres and 300 metres) based on the same kernel function and search radius. This shows that the smaller sizes of cells are referred to as higher resolution, and larger size of cell results in a lower resolution. In this research, geospatial methods are always controlled under the same cell size in order to keep effective comparison with the same parameters.

Figure 3. Raster sizes (a) 150 m and (b) 300 m, and generated map hotspot quality at a same point.

Determination of the bandwidth is an important issue because it significantly affects the results of the KDE. In general, two main methods, a statistical method and a non-statistical method were used to determine the bandwidth (Laver, 2005). The statistical method is often used for standard multivariate normal distribution samples and chooses a bandwidth mathematically. In the literature the frequent method named is the process of least squares cross validation (LSCV) and this method has been introduced in detail by Silverman (1986). However, accident occurrences are seldom close to the standard normal distribution. An accident occurrence is often affected by a set of complex accident contribution factors (e.g. road geometry, weather, lighting, etc.). The use of the statistical method to select bandwidth might violate the assumed distribution, and therefore result in data over-smoothing. Thus, the non-statistical method is often utilised, although it is more subjective and not always reproducible. The non-statistical method is preferred to choose parameters based on factors that may provide a guide to reasonable selection of bandwidth. The appropriate bandwidth is based on the “best fit” of the objective's results. For example, if the hotspot accuracy was required at a ten-metre level, the bandwidths are chosen to generate an approximate circle area with a radius of five metres to satisfy this requirement.

Four different bandwidths ranging from small bandwidth (Figure 4 Graph A: 200 metres) to large bandwidth (Figure 4 Graph D: 500 metres) were selected to test the influence of bandwidth for accident hotspot mapping. The width of cell size for all tests is optionally set as 40 metres as this generates a reasonable circle area. The risk indices 10 to 90 represent a display of accident risk. The higher index represents the higher risk of an accident. The high-density area represents frequent accident occurrences and could be understood as accident hotspots. It can be seen that when under the same cell size and kernel function, if the bandwidth is set to a small value (200 metres), the hotspot distribution display will be quite dispersed although it is reasonable to say accident hotspot distribution will not change based on the bandwidth setting. The small density areas are clearly presented as independent hotspots at road intersections. However, the number of accident hotspots appears to be too numerous and too dispersed. However, if the radius is set larger, these hotspot areas are clustered and connected. The variations of the features are overlooked in high density areas, such as the core area of the city centre with a high-value risk index. Therefore, during the selection of bandwidth it is a tough task to balance hotspot identification and bandwidth selection.

Figure 4. Different bandwidth influence on accident hotspot distribution.

In order to select an appropriate bandwidth, reasons are required to justify the selection. In the research an appropriate reason is discussed which is called “causation similarity”. This is based on the cluster theory stated by Anderson (2009). The cluster theory classifies road accident hotspots into a hierarchical structure. The theory found that traffic accidents were often clustered due to similar accident causation in spatial distribution. Small area road black-spots were clustered by a set of crashes with similar causes, and more such areas could be clustered to generate a larger hotspot area. Based on this theory, small areas are better to cluster similar accident reasons providing better accident hotspot differentiation. For example, in Figure 4 a 200 metre bandwidth provides a better pattern for understanding accident causation of many small-area hotspots. However, if the hotspot is clustered with a larger bandwidth of 500 metres, almost all hotspot characteristics are overlooked and different hotspots' causations cannot be identified from the patterns clearly because they have been merged together.

3.3. Determining accident hotspot boundaries

As stated earlier, accident density distribution is able to be presented via an isodensity raster surface by using KDE. However, it is not possible for the density surface to be applied directly on the digital map system. This is because hotspot distribution is presented by a raster-based map and hotspot zones need to be separated and differentiated by threshold values so that the system can ensure the boundary values of the hotspot. If there are no boundaries for the hotspot, ADAS systems cannot determine the actual location of hotspot warning. This motivates the creation of specific “border checkpoints” for hotspots. The borders are visual perimeters to represent a real-world accident hotspot area. A question is raised on how to reasonably extract the boundaries from the hotspot density map and integrate them to the vector-based classic road network map.

The Percent Volume Contour (PVC) method was introduced for boundary extraction for home range analysis by Seaman and Powell (1996). The traditional contour method in raster computation is to extract the boundary of a specific value from the raster data. The PVC is different to this because it is more related to probability accumulation. This could be very useful for identifying and extracting the actual hotspot because accident occurrence is based on random probability. The boundary of the PVC line represents a certain percentage of probability volume.

The basic principle of PVC is explained as follows. Firstly, as stated earlier, in hotspot raster format each cell was assigned a value of accident density on the area of that cell. Mathematically, we assumed the study area was a two-dimensional (x and y) Cartesian coordinate system and it was divided into a set of grids with side length of h. The density value of the cell at any location (x,y) is f(x,y). The microscopic probability volume v can be expressed as:

(3)$$v(x,y) = h^2 f\,(x,y)$$

For any collection of cells in the area of S, the density volume can be expressed as:

(4)$$V = h^2 \int_S {\,f\,(x,y)\,dxdy} $$

For any cell in the domain, the grid density probability d(x, y) at location (x, y) can be expressed as:

(5)$$p(x,y) = \displaystyle{{d(x,y)} \over V} = \displaystyle{{h^2 f\,(x,y)\,dxdy} \over {\int_S {\,f\,(x,y)\,dxdy} }}$$

The probability of sample data in domain SP can be expressed as:

(6)$$P[(x,y)\in SP]= \displaystyle{{\int_{SP}\, f\,(x,y)\,dxdy} \over {\int_S {\,f\,(x,y)\,dxdy} }}$$

To localise high density accident hotspots in raster data, raster computation for PVC is utilised. While KDE calculated a density surface based on the total number of accidents, the users can optionally define a volume contour representing a user-defined percentage of high-risk accident area using PVC. Figure 5 shows the raster computation process. In this case a small raster area was considered as an example density surface. Each of the cells has been assigned with density values by KDE. The densities are represented in the figure by the shade of the colour. A percentage threshold value is defined as the required probability hotspot area and the value is P _H, such as 0·7 or 70%. This means the accumulation of 70% probability volume is required. The algorithm loops all cells and finds out the cells with largest density value, such as grid P₁. The probability of P₁ calculated is accumulated to a temperate probability variable P _X. The P _X will compare with the user-defined value P _H. If P _X⩾P _H, the loop stop and the boundary was established, as seen in Figure 5(a). But if P _X<P _H, the second loop starts and the next highest density probability cells are accumulated, such as two P₂ grids, as shown in Figure 5. The value of P _X is now the accumulation of P₁+2P_2. The iteration will continue until the condition P _X⩾P _H is satisfied and all grid boundaries are established. In general, a 10% interval is often the default value for the PVC and it can be configurable in some PVC tools. This means that the 10% percentile area is the core area with the highest density of accidents and 90% is the lowest density area that almost contains all accident points. The advantage of these methods is that they are reproducible, have a predictable outcome, and more accurately reflect the key areas of accident hotspot distribution.

Figure 5. PVC approach based on probability accumulation.

The determination of contour percentage determines the border of the hotspots. In this research 50%, 70% and 90% contour percentage areas are set for extracting hotspots in the Geospatial Modelling Environment (GME), an extensive tool of ArcMap. The contour lines are computed and the results are shown by Figure 6. Firstly, from Figure 6(a), the accident density surface in 2005 is estimated based on a bandwidth of 300 m and cell size 40 m and the accident risk was distributed by the iso-surface map. In Figure 6(b) the contour lines are extracted from the existing density surface with red contours using the PVC method, including 50% (inner part), 70% (middle part) and 90% (outside boundary) as shown by Figure 6(c). This method is implemented using the self-attached script language in GME. All hotspot contours are extracted as polyline formats which are difficult to use as a hotspot map. Polylines need to be transformed to store area-based information, which is shown in Figure 6(d). It can be seen that important intersection hotspots and road segment hotspots of 50% density probability are mostly extracted. However, in the core area of road network, the hotspots are clustered and the areas of hotspot are covered with a connected area. It is difficult to use such a large area as hotspots for warning. More detailed hotspots are required in this area. A potential solution is to reduce the bandwidth in this area but keep the same bandwidth in other areas. Adaptive KDE is a potential solution to provide selectable bandwidth, but this method is beyond the scope of this paper and is planned as the next stage of research.

Figure 6. PVC presentation and polygon extraction.

3.4. Determining hotspot attributes

The attributes are related to descriptions of traffic objects on the road, such as traffic signs, lane information and road geometry. Various safety-related attributes are particularly important for digital maps. Accident hotspots can be treated as an important attribute which display geometrical road hotspots on existing road networks but are clearly not visible in reality. The hotspot attribute data (such as hotspot location, risk index, etc) are important as warning data pushed to the driver and the hotspot warning systems have to reference the data to determine the hotspot warning. As discussed in earlier sections, the hotspot patterns (expressed as polylines) can be extracted and transformed to polygon hotspots. Different hotspot geometry boundaries are generated based on a user's definition and can be extracted using contour value filtering. However, attributes of hotspots are required to be attached to the geometry layer. In this section the relevant attribute of accident hotspots for ADAS systems are discussed and the derivation of hotspot coordinates are used as an example.

For all accident hotspots, the similarity is that a number of historical accidents have happened at the location. However, accident hotspots vary due to the nature of accidents, also their vertices' coordinates (determine the hotspot location and coverage), risk degree, etc. Table 3 summarises the useful hotspot attributes for digital hotspot maps and their function definitions.

Table 3. Essential hotspot attributes and their functions.

These attributes can be computed based on the relationship between hotspot patterns and accidents using geospatial methods. For instance, the coordinates of hotspot checkpoints are key inputs to ADAS to determine if the vehicle passes through (entry and exit) the hotspots. This can be obtained by extracting point coordinates of vertices of a hotspot polygon. Similar attributes that can be extracted directly from road data contain hotspot ID, shape, hotspot accident history, etc. The other type of attributes that need to be analysed using the statistical method includes time validity, causation and safe speed, etc. For example, in order to evaluate the danger degree of an accident hotspot on a road network, the risk index is used to evaluate the risk level of hotspot danger. The accumulated accident number is often used to compute the risk level in each hotspot. If considering the severity of accidents, the weight can be assigned to each an accident with a different severity level. For example, the hotspot index risk is computed using Risk Index defined by the formula:

(7)$$RI = \sum\limits_1^N {W_i *Count\,(S_i )} $$

S _i is the severity level. Count (S _i) is the function to obtain the total number of accidents at that severity level. W _i is the weight assigned to the severity level. Other indices such as property damage can also be considered similarly.

The hotspots were extracted in a GME tool using PVC and the hotspot boundaries are expressed as polylines. However, polylines cannot be adopted directly to describe hotspots because the polygon with relevant data attributes is the best expression of hotspot objects in a digital map. This raises a requirement of transformation between different geospatial objects. Here, some of existing GIS tools can provide the transformation between polygon and polyline, such as ET Geo wizards. Some integrated GIS platforms can provide data integration based on table attributes and GIS layer. An example is shown in Figure 7 where the coordinates of vertices from hotspot polygons are obtained.

Figure 7. The attribute integration based on spatial joint method.

4. CONSTRAINTS AND LIMITATIONS

Although the geospatial methods described above are useful in producing a hotspot map, there are some constraints and limitations related to the method.

4.1. Accuracy Constraints

This method is useful but still has space to improve in terms of hotspot accuracy. The main problem with the current method is that it concerns area-based accident hotspot with various complex accident contribution factors. The results show risk density surfaces cover relatively large areas, and therefore, it is difficult to adopt for implementing real-time hotspot warning systems because hotspot details are merged together. A potential solution is to use more accurate network-based KDE to constrain the expansion of hotspot areas onto road networks (Okabe et al., 2009). This is an extensive research direction for the future.

4.2. Uncertainty in data

The other issues are caused by the uncertainty of data processing or social impact. From a technical perspective, for example, data collection and processing might introduce errors to the dataset, including human surveying errors, equipment quality, even map projection, and this uncertainty of errors is often difficult to measure. From a social impact perspective, the historical accident distribution might become inaccurate, or even incorrect, if the external traffic environment changed, e.g. opening a new supermarket might attract more traffic and increase accidents around a specific area. If road hotspots are constructed on old maps or data, it can easily lead to misunderstanding of road hotspots. Particularly, cities with fast development need to maintain the updated accident data and the change to the road networks in order to keep an accurate expression of road hotspots. This research constrains such technical and social impacts to a situation where there is no major change to the traffic environment, and the errors of data processing are small enough to be trusted.

4.3. Parameter selection

The other problem is the specification of the selected parameters, e.g. bandwidth and contour threshold values. In this research, different contours were selected and computed. It can be seen that a small-value contour line can better reflect the high-risk hotspots. However, an optimal value for generating hotspots is difficult to determine. Research into the specification of selecting contour threshold value is required to calibrate the hotspots on the road; this might need an experienced method/formula to assist the selection of parameters.

5. POTENTIAL APPLICATIONS OF HOTSPOT MAPS

The road hotspot databases are a very useful component to various ADAS applications, particularly for safety-critical applications. In this study, the main application of hotspot maps is for road hotspot warning. Hotspot maps can also be extended to other application fields as well as described in the following case studies.

The first application is based on Pay-As-You-Drive (PAYD) Insurance introduced by some companies (InsureTheBox, 2013). PAYD insurance is a new automotive insurance concept that charges based on driven miles and driving behaviour. The driving record of miles and behaviour are measured by an installed “blackbox” (including GPS, gyros, other sensors etc.) in the vehicle. The prices of insurance are established based on the assessment of historical driving data (e.g. miles, speed, accelerations). Hotspot maps can potentially contribute to this application to show the risky or safe miles that drivers have travelled or are travelling. It provides more reasonable insurance payment criteria for drivers. In addition, another potential adoption of road hotspot maps is for traffic monitoring and data collection. The hotspot maps could be embedded onto a mobile platform, e.g. smartphones, vehicle telematics systems, etc., to collect data when pedestrians or vehicles enter/exit hotspots. The real-time data can be analysed to develop new traffic theory at road hotspots.

6. CONCLUSIONS

In this paper a GIS-based approach has been developed to produce road hotspots for ADAS applications. This approach adopted a set of geospatial methods (KDE and PVC) in GIS to identify and extract road hotspots, following identification of hotspot properties. Detailed algorithms have been introduced, and a case study has been carried out to prove this approach. The constraints of this approach include the problems of hotspot accuracy, accident data uncertainty and the selection of relevant algorithm parameters. Although this approach has limitations, it is valuable in contributing to the research of generating hotspot maps for ADAS applications. Furthermore, the discussion states two potential applications of hotspot maps which could lead to developing new commercial opportunities and academic research.