1. INTRODUCTION
Considering the distance-dependent system error in a certain area that has a strong spatial correlation, the main purpose of Network Real Time Kinematic (NRTK) is to apply a certain interpolation algorithm to interpolate or extrapolate the system error at the rover station, so as to achieve a precise positioning. Therefore it is of great importance to estimate the system error precisely at the rover station, because this not only affects the reliability and success rate of the ambiguity solving, but also affects the positioning accuracy (Ge et al., Reference Ge, Zou and Dick2010; Zou, Reference Zou, Feng, Tang and Liu2013). Among different kinds of errors influencing RTK positioning, ionospheric error plays an important role in the positioning accuracy and reliability (Tang et al., Reference Tang, Liu and Liu2007; Cao et al., Reference Cao, Guo, Xie and Zhou2013). A good interpolation method could estimate the system error correction accurately for the rover, thereby reducing the ambiguity resolution time. Scholars have carried out a wide range of studies on this subject and proposed a variety of interpolation algorithms (Zhang, Reference Zhang2010), such as the Linear Interpolation Model (LIM) (Wanninger, Reference Wanninger1995), the Low order Surface fitting Model (LSM) (Dai et al., Reference Dai, Han, Wang and Rizos2001) and Distance Interpolation Method (DIM) (Gao et al., Reference Gao, Li and McLellan1997). This paper will introduce a new interpolation algorithm, the Grid correction method (GRID). The introduction is followed by the comparison with the DIM, the LIM and the KRG, in the aspect of the interpolation performance. Analysis and discussion on their performance are then given.
2. DOUBLE DIFFERENCED IONOSPHERIC DELAY BETWEEN REFERENCE STATIONS
The double differenced observation equations can be written as:
where ![]() ${k_i} = f_i^2 /(f_1^2 - f_2^2 )$;
${k_i} = f_i^2 /(f_1^2 - f_2^2 )$; ![]() $\Delta \nabla {\varphi _{\rm i}}$ is the measured double differenced carrier phase;
$\Delta \nabla {\varphi _{\rm i}}$ is the measured double differenced carrier phase; ![]() $\Delta \nabla \rho $ is the true double differenced geometric range;
$\Delta \nabla \rho $ is the true double differenced geometric range; ![]() $\Delta \nabla {N_{\rm i}}$ is the double differenced carrier phase ambiguity;
$\Delta \nabla {N_{\rm i}}$ is the double differenced carrier phase ambiguity; ![]() $\Delta \nabla {\zeta _{trop}}$ is the double differenced troposphere delay;
$\Delta \nabla {\zeta _{trop}}$ is the double differenced troposphere delay; ![]() $\Delta \nabla I$ is the double differenced ionosphere delay. After the integer ambiguities between reference stations are fixed, the noise of double differenced carrier phase measurement is so small that it can be ignored. Once the ambiguities are correctly resolved, the centimetre-level accuracy of the double differenced ionospheric measurement can be derived through a combination of the dual-frequency carrier phase measurements as follows,
$\Delta \nabla I$ is the double differenced ionosphere delay. After the integer ambiguities between reference stations are fixed, the noise of double differenced carrier phase measurement is so small that it can be ignored. Once the ambiguities are correctly resolved, the centimetre-level accuracy of the double differenced ionospheric measurement can be derived through a combination of the dual-frequency carrier phase measurements as follows,
3. NETWORK RTK INTERPOLATION ALGORITHM
Since the correlation of the atmospheric errors gets weaker as the baseline distance increases, these errors cannot be eliminated cleanly in the double differencing, so long-range NRTK positioning requires the support of the atmospheric correction, where the correction for the ionospheric error is of the most important influence. This work conducted an analysis on the commonly used DIM, LIM and KRG methods. Then the method introduced by Liao (Reference Liao2000), which uses the double differenced observations to establish a regional level ionospheric grid model, was applied to the network RTK ionospheric interpolation, and named as the Grid correction method (GRID).
3.1. Distance Interpolation Method (DIM)
This method uses the information generated by the reference stations and computes a set of interpolation coefficients to obtain the double differenced delay at the rover station (Gao et al., Reference Gao, Li and McLellan1997). The interpolation coefficient is a function of the distances between the reference stations and the rover station. The double differenced ionospheric delay at the rover station can be obtained as,
 $$\Delta \nabla I = \sum\limits_{i = 1}^{n - 1} {\displaystyle{{{c_i}} \over c}} \Delta \nabla {I_i}$$
$$\Delta \nabla I = \sum\limits_{i = 1}^{n - 1} {\displaystyle{{{c_i}} \over c}} \Delta \nabla {I_i}$$
where n − 1 is the total number of auxiliary reference stations; c i is the distance between the auxiliary reference station i and the rover station and 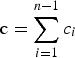 ${\rm c} = \sum\limits_{i = 1}^{n - 1} {{c_i}} $;
${\rm c} = \sum\limits_{i = 1}^{n - 1} {{c_i}} $; ![]() $\Delta \nabla {I_i}$ is the double differenced ionospheric delay between the auxiliary reference station i and master reference station.
$\Delta \nabla {I_i}$ is the double differenced ionospheric delay between the auxiliary reference station i and master reference station.
3.2. Linear Interpolation Model (LIM)
This method was first proposed by Wanninger (Reference Wanninger1995). Since the double differenced ionospheric delay ![]() $\Delta \nabla I$ is a linear function of the plane coordinate differences, it can be expressed as follows,
$\Delta \nabla I$ is a linear function of the plane coordinate differences, it can be expressed as follows,
 $$\eqalign{ \Delta \nabla I & = \displaystyle{{\partial \Delta \nabla I({X_K} - {X_M})} \over {\partial X}} + \displaystyle{{\partial \Delta \nabla I({Y_K} - {Y_M})} \over {\partial Y}} \cr & = a({X_K} - {X_M}) + b({Y_K} - {Y_M})} $$
$$\eqalign{ \Delta \nabla I & = \displaystyle{{\partial \Delta \nabla I({X_K} - {X_M})} \over {\partial X}} + \displaystyle{{\partial \Delta \nabla I({Y_K} - {Y_M})} \over {\partial Y}} \cr & = a({X_K} - {X_M}) + b({Y_K} - {Y_M})} $$The coefficients a and b in Equation (4) can be obtained by the least squares method when there are three reference stations in a certain area. With the known coefficients a and b, the double differenced ionospheric delay at the rover can be computed.
3.3. Kriging Interpolation Method (KRG)
A method which fully takes the spatial correlation between given points into account to predict the value for a point in between is the Kriging Interpolation Method. According to this method, the interpolated value at the rover can mathematically be given as (Odijk, Reference Odijk2000; Zhang, Reference Zhang2010):
In Equation (5) u represents the rover station, i is the base station and n is the total number of reference stations; ${\;C_{iu}} = \left[ \matrix{{c_{u1}} \hfill \cr {c_{u2}} \hfill \cr {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \vdots \hfill \cr {c_{un}} \hfill} \right],{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {C_i} = \left[ \matrix{{c_{11}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {c_{12}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \cdots {\kern 1pt} {\kern 1pt} {\kern 1pt} {c_{1n}} \hfill \cr {c_{21}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {c_{22}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \cdots {\kern 1pt} {\kern 1pt} {\kern 1pt} {c_{2n}} \hfill \cr {\kern 1pt} {\kern 1pt} {\kern 1pt} \vdots {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \vdots {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \ddots {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \vdots \hfill \cr {c_{n1}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {c_{n2}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \cdots {\kern 1pt} {\kern 1pt} {\kern 1pt} {c_{nn}} \hfill} \right]{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt}\!\!, {\kern 1pt} {\kern 1pt} {\kern 1pt} \Delta \nabla {I_i} = \left[ \matrix{\Delta \nabla {I_{1n}} \hfill \cr \Delta \nabla {I_{2n}} \hfill \cr {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \vdots \hfill \cr \Delta \nabla {I_{nn}} \hfill} \right]$,
${\;C_{iu}} = \left[ \matrix{{c_{u1}} \hfill \cr {c_{u2}} \hfill \cr {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \vdots \hfill \cr {c_{un}} \hfill} \right],{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {C_i} = \left[ \matrix{{c_{11}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {c_{12}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \cdots {\kern 1pt} {\kern 1pt} {\kern 1pt} {c_{1n}} \hfill \cr {c_{21}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {c_{22}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \cdots {\kern 1pt} {\kern 1pt} {\kern 1pt} {c_{2n}} \hfill \cr {\kern 1pt} {\kern 1pt} {\kern 1pt} \vdots {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \vdots {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \ddots {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \vdots \hfill \cr {c_{n1}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {c_{n2}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \cdots {\kern 1pt} {\kern 1pt} {\kern 1pt} {c_{nn}} \hfill} \right]{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt}\!\!, {\kern 1pt} {\kern 1pt} {\kern 1pt} \Delta \nabla {I_i} = \left[ \matrix{\Delta \nabla {I_{1n}} \hfill \cr \Delta \nabla {I_{2n}} \hfill \cr {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \vdots \hfill \cr \Delta \nabla {I_{nn}} \hfill} \right]$, ![]() $\Delta \nabla {I_i}$ is the double differenced ionospheric delay between the base station i and master reference station and
$\Delta \nabla {I_i}$ is the double differenced ionospheric delay between the base station i and master reference station and ![]() $\Delta \nabla {I_{nn}} = 0$. The scalar c r1r2 denotes the covariance function between locations r1 and r2, and needs to be specified to perform the interpolation. In this article, the covariance function is chosen as a simple linear function of the distance:
$\Delta \nabla {I_{nn}} = 0$. The scalar c r1r2 denotes the covariance function between locations r1 and r2, and needs to be specified to perform the interpolation. In this article, the covariance function is chosen as a simple linear function of the distance:
where l r1r2 [km] denotes the distance between locations r1and r2; l max is a certain maximum distance [km]. With respect to the choice of l max, in order to guarantee that the matrix c i is positive-definite, it should be larger than the longest distance between the base stations.
3.4. Grid correction method (GRID)
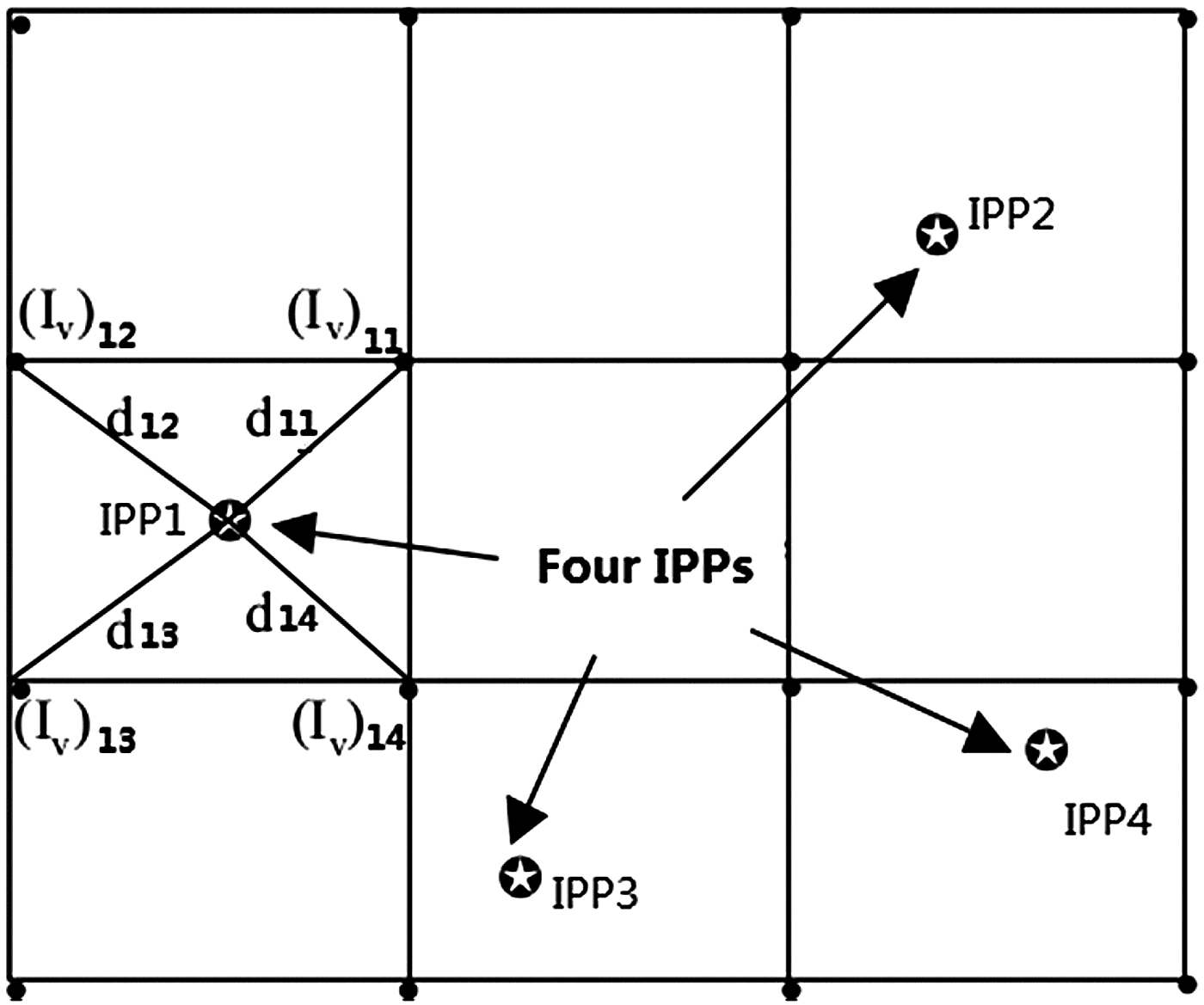
This interpolation algorithm follows the method proposed by Liao (Reference Liao2000), which uses the double differenced ionospheric delays of the reference stations to establish a regional level ionospheric grid model. This method was only previously used for the recovery of the total electron content. In this paper, the GRID method was proposed for the first time as an interpolation method of the double differenced ionospheric delay for GNSS Network RTK. The double differenced ionospheric delay for the rover can be interpolated from this grid model. Each double differenced ionospheric delay obtained by Equation (2) can be converted to the Slant Total Electron Content (STEC) at four Ionosphere Piercing Points (IPP). In order to recover the vertical TEC at the grid points, the mapped vertical TEC measurement at each IPP needs to be linked with the vertical TEC at the surrounding four grid points, as shown in Figure 1.

Figure 1. Diagram of the grid model.
In this work, the following model has been adopted to establish the functional relationship between the double differenced ionospheric measurements and the vertical TEC over the surrounding grid points (Liao, Reference Liao2000; Zhao, Reference Zhao2003):
 $$\eqalign{&\Delta \nabla I = \displaystyle{{40.28(\,f_1^2 - f_2^2 )} \over {\,f_1^2 f_2^2}} STEC_{ij}^{\,pq} = I_j^q - I_i^q - I_j^p + I_i^p \cr &\qquad= f\,({e_1})\sum\limits_{n = 1}^4 {{{({I_v})}_{1n}}\cdot {w_{1n}}} - f\,({e_2})\sum\limits_{n = 1}^4 {{{({I_v})}_{2n}}\cdot {w_{2n}}} \cr&\qquad - f\,({e_3})\sum\limits_{n = 1}^4 {{{({I_v})}_{3n}}\cdot {w_{3n}}} + f\,({e_4})\sum\limits_{n = 1}^4 {{{({I_v})}_{4n}}\cdot {w_{4n}}}} $$
$$\eqalign{&\Delta \nabla I = \displaystyle{{40.28(\,f_1^2 - f_2^2 )} \over {\,f_1^2 f_2^2}} STEC_{ij}^{\,pq} = I_j^q - I_i^q - I_j^p + I_i^p \cr &\qquad= f\,({e_1})\sum\limits_{n = 1}^4 {{{({I_v})}_{1n}}\cdot {w_{1n}}} - f\,({e_2})\sum\limits_{n = 1}^4 {{{({I_v})}_{2n}}\cdot {w_{2n}}} \cr&\qquad - f\,({e_3})\sum\limits_{n = 1}^4 {{{({I_v})}_{3n}}\cdot {w_{3n}}} + f\,({e_4})\sum\limits_{n = 1}^4 {{{({I_v})}_{4n}}\cdot {w_{4n}}}} $$where i stands for the master reference station; j stands for another auxiliary reference station; p is the reference satellite, q is the observed satellite; f(e) is the slant factor which maps the STEC to the Vertical Total Electron Content (VTEC); (I v)ij is the VTEC at the associate grid points; w mn is the weighting function. There are several weighting functions available, but the analysis from El-Arini et al. (Reference El-Arini, Hegarty, Fernow and Klobuchar1994) indicated that there is little difference in accuracy between these weighting functions. The inverse distance weighting function was chosen here and it is expressed as Equation (8), where m represents the corresponding IPP, n for the corresponding grid point:
 $${w_{mn}} = \displaystyle{1 \over {{d_{mn}}}}/\sum\limits_{k = 1}^4 {\displaystyle{1 \over {{d_{mk}}}}} $$
$${w_{mn}} = \displaystyle{1 \over {{d_{mn}}}}/\sum\limits_{k = 1}^4 {\displaystyle{1 \over {{d_{mk}}}}} $$Using Equations (7) and (8) and the least squares adjustment, the VTEC value at each grid point can be obtained, which could lead to the establishment of the regional ionospheric grid model. Also in accordance with Equation (7), the double differenced ionospheric delay for the rover can be calculated using this GRID model. This interpolation method is invariant to the choice of the master reference station because the parameters in this method are the absolute instead of the relative value of total electron content.
This method fully uses the information of each IPP. When IPPs of different satellites fall in the same grid, they could complement each other, rather than simply interpolating between the same satellites. Meanwhile, the tracking of the observable satellites could assist in computing the double differenced ionospheric delay of the newly rising satellites. In addition, when there are enough reference stations, a high spatial resolution for a regional network could follow the rapid ionosphere variation over the area. This could guarantee the high accuracy of the double differenced ionospheric delay correction.
4. TEST VALIDATION AND ANALYSIS
To analyse the performance of the above four methods, tests were conducted using Global Positioning System (GPS) datasets in three networks in China. After the integer ambiguities between reference stations are fixed, the centimetre-level accuracy of the double differenced ionospheric delays between the auxiliary reference stations station and the master reference station can be obtained, which were treated as real measurements. The Root Mean Square (RMS) is calculated by omitting one reference station from the network and comparing the interpolation results for all satellites at that station with the real measurements at each epoch.
4.1. Case Study 1
A case study was carried out with the stations illustrated in Figure 2. These stations are located in Anshan, China and their mean latitude is 40·80°. The data was collected on the Day of Year (DoY) 8/2013. A satellite elevation cut-off angle of 10° was used for analyses and the observation interval is one second. AS01 is the master reference station. The double differenced ionospheric delays (from the master reference station to the auxiliary station) for AS02, AS04 and AS07 are presented in Figure 3, the horizontal axis is the GPS time and the vertical axis is the double differenced ionospheric delay, in units of metres. Each colour denotes a specific satellite and the same colour in different plots denotes the same Satellite Vehicle (SV). It can be seen from Figure 3 that the values of the double differenced ionospheric delay are in the range of −0·4~0·4 metres. The longer the baseline length, the greater the absolute value of delay is. This is because with the baseline increasing, the spatial correlation will be getting weaker. This case study compared the above-mentioned four methods in two cases; the rover station is located inside and outside the network separately. The height of the single-layer ionosphere is set to be 450 km. According to the distribution of IPPs in this case, the grid size is configured as 2° × 4° latitude by longitude.

Figure 2. Distribution of stations in Anshan, China.

Figure 3. Double differenced ionospheric delay.
4.1.1. The rover station is inside the network
AS04 is selected as the rover in this case. The interpolation results were evaluated with the truth values, and the RMS of each epoch was used to illustrate the accuracy of each method, as shown in Figure 4. The RMSs of each epoch were averaged and listed in Table 1. It can be seen that when the rover station is inside the network, the accuracy of the GRID method is superior to the other three methods; the accuracies of LIM and KRG are close to each other while the performance of DIM is the worst.

Figure 4. Comparison among four algorithms for ionospheric corrections within the network.
Table 1. The mean RMS of three algorithms (unit: m).

4.1.2. The rover station is outside the network
AS02 is selected as the rover station, which is located outside the network. A similar statistical analysis was carried out for AS02 as well, as shown in Figure 5. The mean RMS value was listed in Table 1. It can be seen that when the rover station is outside the network, the accuracy of the GRID method is better than the other three methods.

Figure 5. Comparison among four algorithms for ionospheric corrections beyond the network.
4.1.3. Analysis
In the above test results, the GRID algorithm performs best. This method can achieve good results no matter whether the rover is inside the network or not. The GRID algorithm is less affected by the position of the rover station because it makes full use of the information of each IPP. It is also reflected in Figures 4 and 5 that KRG and LIM outperform DIM because these two methods take the directionality of the double differenced ionospheric delay into consideration. To further explain the difference in performances, the relationship between the interpolation results and elevation angles is also shown in the following. PRN 11 and PRN 16 observed by AS02 are selected for illustration. Considering that the DIM showed the poorest interpolation results and the accuracies of LIM and KRG are close to each other, LIM and GRID are chosen as examples. The results presented in Figures 6 and 7 (left: GRID; right: LIM). In the comparison for PRN16, it could be found that at around 19:00 the LIM method cannot estimate the double differenced ionospheric delay because the surrounding reference stations failed to observe this satellite. However the GRID method is still able to estimate the double differenced ionospheric delay by using the IPP information from other satellites. It also can be seen from both figures that the GRID interpolation can maintain good performance even when the satellite elevation angle is low. This further illustrates that the GRID interpolation method is more robust and it can provide a higher interpolation precision.

Figure 6. Comparison of a single satellite interpolation results (PRN11).

Figure 7. Comparison of a single satellite interpolation results (PRN16).
4.2. Case Study 2
The activity level of free electrons in the ionosphere is closely related to the latitude. With the latitude decreasing, the ionosphere becomes more active. In order to analyse the performance of the four methods in low latitudes, this paper chose the data collected from a Continuously Operating Reference Station (CORS) network in Guangdong (southern China), as the second example. The mean latitude of the stations is 22·98°. Distribution of these stations with baseline length is shown in Figure 8. GPS data of Day of Year (DoY) 146/2014 for a 24 hour span was processed by the methods described above. The height of the single-layer ionosphere is set to be 450 km. A satellite elevation cut-off angle of 10° was used for analyses and the observation interval is one second.

Figure 8. Distribution of the stations.
This example chose station ZQGT as the master reference station. Due to the dramatic effect of the free electrons, the values of the double differenced ionospheric delay are in the range of −1·0~2·0 metres while the baseline length is about 40 km. The double differenced ionospheric delay of three stations is shown in Figure 9. The horizontal axis denotes the GPS time and the vertical axis denotes the double-differenced ionospheric delay in the unit of metres. Each colour denotes a specific satellite and the same colour in different plots denotes the same SV.

Figure 9. Double differenced ionospheric delay.
4.2.1. The rover station is inside the network
In this case, the SSGT station was selected as the rover station and the interpolation results from each method were compared with the truth values. The RMSs at each epoch were used to illustrate the interpolation accuracy of each method. Regarding the distribution of the IPPs, the latitude is in the range of 9 to 33° and the longitude is in the range of 100 to 130° while the grid resolution is 1° × 2° latitude by longitude in the GRID algorithm. The RMSs of each epoch were averaged, as shown in Table 2. Figure 10 shows the RMS against time. It can be seen that the maximum RMS of GRID is less than 0·05 m, and this is superior to the other three methods. Figure 11 showed the percentage of correction using GRID method and also reflected that the GRID could achieve more than 70% accuracy interpolation. The IRIM (Ionospheric Residual Integrity Monitoring, IRIM) indicator (Chen et al., Reference Chen, Landau and Vollath2003) using GRID was also shown in Figure 11 and this indicator described the residual remaining in the baseline from ZQGT to SSGT of whole day.

Figure 10. Comparison among four algorithms for ionospheric corrections within the network.

Figure 11. Correction percentage of GRID method (top) and IRIM for ZQGT—SSGT (below).
Table 2. The mean RMS of three algorithms (unit: m).

4.2.2. The rover station is outside the network
SDGT is selected as the rover station located outside the network. A similar statistical analysis was carried out, as shown in Figure 12. The mean RMS value is listed in Table 2. It can be observed that when the rover station is outside the network, the accuracy of the GRID method is still superior to that of the other three methods.

Figure 12. Comparison among four algorithms for ionospheric corrections beyond the network.
4.3. Case Study 3
In this case, all the five stations, which are part of Zhongshan CORS, are located in the south of China and the mean latitude is 22·50°. The distribution of these stations is shown in Figure 13. The distances between the reference stations are also shown in this figure. DACH was selected as the master reference station and SHIJ as the rover. GPS data of Day of Year (DoY) 158/2014 for a 24 hours span was processed. The height of the single-layer ionosphere is set to be 450 km. A satellite elevation cut-off angle of 10° was used for analyses and the observation interval is one second.

Figure 13. Distribution of stations in Zhongshan, China
The double differenced ionospheric delays of GPS for each station are shown in Figure 14, with the horizontal axis is the GPS time and the vertical axis is in the units of metres. Each colour denotes a specific satellite and the same colour in different plots denotes the same SV. The values of the double differenced ionospheric delay can be observed in the range of −0·8~0·8 metres. Figure 15 shows the RMS against time. The mean RMS value is 0·0443 m for DIM, 0·0213 m for LIM, 0·0200 m for KRG and 0·0186 m for GRID. The PRN5 observed by the rover (SHIJ) was selected for illustrated the relationship between the interpolation results and elevation angles. Considering that the DIM showed poorest in interpolation results and the accuracies of LIM and KRG are close to each other, so LIM and GRID are chosen as examples. The results are presented in Figure 16 (left: GRID; right: LIM).

Figure 14. Double differenced ionospheric delay.

Figure 15. Comparison among four algorithms for ionospheric corrections.

Figure 16. Comparison of a single satellite interpolation results (PRN05).
5. CONCLUSIONS
In this paper, the Distance Interpolation Method (DIM), linear interpolation (LIM), the Kriging interpolation method (KRG) and the GRID correction method (GRID) were described and compared with each other on their interpolation performance. The results showed that the GRID algorithm performs better than the other three, for the reason that it fully uses the information of each IPP. When IPPs of different satellites fall in the same grid, they can complement each other, rather than being interpolated separately. In addition, when the satellite elevation angle is low, the results of GRID could still achieve a high accuracy. LIM and KRG outperform DIM because these two methods take the directionality of the double differenced ionospheric delay into consideration. DIM interpolation can obtain good results when the rover is located inside the network, but its accuracy becomes poorer when the rover station is outside the network.
ACKNOWLEDGEMENTS
This work is partially sponsored by China 863 program (Grant No. 2014AA123101/01 and 2012AA12A202), the Natural Science Foundation of China (Grant No. 41004014) and partially supported by the National Science Fund for Distinguished Young Scholars (Grant No. 41325015) as well as the Fundamental Research Funds for the Central Universities (No. 2012214020208).