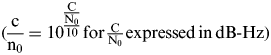1. INTRODUCTION
In recent years, various strategies have been developed for increasing the levels of integrity of Global Navigation Satellite System (GNSS)-based navigation and landing systems. In addition to Space-Based Augmentation Systems (SBAS) and Ground-Based Augmentation Systems (GBAS), GNSS augmentation may also take the form of additional information being provided by other avionics systems. As the additional avionics systems operate on separate principles to GNSS, they are not subject to the same sources of error or interference. A system such as this is referred to as an Aircraft-Based Augmentation System (ABAS). Unlike SBAS and GBAS technology, previous research on ABAS mainly concentrated on additional information being blended into the position calculation to increase accuracy and/or continuity of the integrated navigation solutions. To date, no significant attempts have been made to develop ABAS architectures capable of generating integrity signals suitable for mission- and safety-critical GNSS applications (e.g., aircraft precision approach and landing). Indeed, there are no commercial ABAS products available at present. In our research, we developed an Avionics-Based Integrity Augmentation (ABIA) architecture, specifically targeting GNSS integrity augmentation for manned and Unmanned Aerial Vehicle (UAV) applications. Although current and likely future SBAS/GBAS augmentation systems can provide significant improvement in GNSS navigation performance, an ABIA could also play a key role in GNSS Augmentation. A properly designed and flight certified ABIA would contribute significantly to mission- and safety-critical applications such as: aircraft precision approach and automatic landing, and UAV Sense-And-Avoid (SAA). Furthermore, using suitable data-link and data processing technologies, a certified ABIA capability could be a core element of the future GNSS Space-Ground-Avionics Augmentation Network (SGAAN). The arrangement of the remainder of the paper is as follows: Section 2 explains integrity flag generator simulation, Section 3 deals with integrity flag criteria, Section 4 provides simulation results and Section 5 presents conclusions and future work.
2. INTEGRITY FLAG GENERATOR SIMULATION
The ABIA Integrity Flag Generator (IFG) is designed to provide Caution and Warning Integrity Flag (CIF and WIF) alerts (i.e., in accordance with the specified Time-to-Caution [TTC] and Time-to-Warning [TTW] requirements) in all relevant flight phases. In order to evaluate the performance of the Masking, Multipath, Carrier-to-Noise (C/N0), Jamming-to-Signal (J/S) and Doppler analysis algorithms presented in Part 1 of this paper (Sabatini et al., Reference Sabatini, Moore and Hill2012), the IFG software was developed and tested in MATLAB®, together with a detailed aircraft Three Dimensional (3D) Model in the Computer Aided Three-dimensional Interactive Application (CATIA), a 3D Terrain and Objects Database (TOD), a GNSS Constellation Simulator and a Navigation/Flight Dynamics Simulator. Figure 1 shows the architecture adopted for the IFG module simulation. Another key feature of the IFG module presented in this second paper is a pre-defined set of CIF and WIF thresholds applicable to the specific aircraft dynamic conditions and satellite constellations observed during the flight.

Figure 1. ABIA IFG module simulation.
A GNSS Constellation Simulator (GCS) was implemented to support GNSS satellite visibility, signal and geometry analysis. It calculated GNSS satellite position and velocity in the Earth-Centred Earth-Fixed (ECEF) reference frame and obtained satellite visibility data from any point along the aircraft's flight trajectory. The GCS was developed in MATLAB® to simulate Global Positioning System (GPS) and Galileo constellations. However, the GCS was conceived as a flexible tool capable to incorporate other current and likely future GNSS constellations (GLONASS, COMPASS, etc.), including space-based regional and global augmentation systems. The satellites' position and velocity were calculated from Kepler's laws of orbital motion and, in the case of GPS satellites, using either the ‘YUMA’ or ‘SEM’ almanac data (Celestrak, 2012a; 2012b). An Aircraft Navigation/Dynamics Simulator (ADS) was also implemented to generate the nominal flight path trajectory and attitude (Euler) angles. The ADS employed a classical Three Degrees of Freedom (3-DOF) point-and-variable mass model. The assumptions were:
• The Earth shape is approximated as an ellipsoid using World Geodetic System 1984 (WGS-84) parameters.
• The atmosphere is considered at rest relative to the Earth.
• The International Standard Atmosphere (ISA) model is adopted to describe temperature, pressure and density variations as a function of altitude.
• The aircraft is modelled as a rigid body with a vertical plane of symmetry.
• The aircraft mass reduction in flight is due to fuel consumption only.
• Thrust, aerodynamic forces and weight act on the aircraft Centre of Gravity (CoG).
• The flight is symmetric (i.e., no sideslip).
The 3-DOF scalar equations are the following:
where:
- m=
Aircraft mass
- V=
Aerodynamic speed
- T=
Thrust magnitude
- α=
Angle of attack
- h=
Altitude
- L=
Lift magnitude
- D=
Drag, defined as a function of V, h and L
- g=
Gravity acceleration
- γ=
Flight path angle
- φ=
Bank or roll angle
- ψ=
Heading angle
- c=
Specific fuel consumption, defined as a function of V and h
- Φ=
Geodetic latitude
- θ=
Geodetic longitude
- r M=
Meridional radius of curvature
- r T=
Transverse radius of curvature
This model presents seven state variables (V, ψ, γ, m, Φ, θ, h) and three control variables (T, L, φ) (Hence, for it to be solved, at least three flight constraints must be specified for each flight manoeuvre. As described in Part 1 (Sabatini et al., Reference Sabatini, Moore and Hill2012), the ABIA IFG uses a set of predefined threshold parameters to trigger the generation of both caution and warning flags associated with; antenna obscuration, Doppler shift, multipath, direct carrier/interference and satellite geometry degradations. More details about the simulation process are provided in the following paragraphs; with a special focus on the CIF and WIF threshold setting criteria incorporated into the ABIA IFG module design.
3. INTEGRITY FLAG CRITERIA
The philosophy adopted for set-up thresholds for the ABIA CIF and WIF integrity flags is depicted in Figure 2. Integrity flags are generated based on a dedicated error analysis addressing the following aspects of GNSS performance:
• Satellite/Aircraft (receiver) (relative geometry and position errors).
• Radio Frequency (RF) signal errors (i.e., Doppler shift, jamming and multipath).
• Receiver Tracking Errors (RTE).

Figure 2. Integrity flag thresholds criteria.
In particular, the RTE models are used to support the development of robust criteria for the RF signal thresholds in addition to the criteria based on experimental results (e.g., ground and flight test activities with GNSS). In the following, we present the detailed criteria adopted for setting the various CIF and WIF thresholds.
3.1. Satellite/Aircraft Relative Geometry and Position Errors
As described in Part 1 of this paper (Sabatini et al., Reference Sabatini, Moore and Hill2012), in order to generate CIF/WIF associated to critical antenna masking conditions, a dedicated analysis is required which takes into account the variation of the attitude angles. Therefore, using the CATIA 3D model of the aircraft, a series of Antenna Obscuration Matrices (AOMs) are collected with pitch angles varying between −90° and 90° and with roll angles varying between −90° and 90°. An example of the resulting Global Masking Profile (GMP) obtained for the TORNADO Interdiction and Strike (IDS) is shown in Figure 3. The obscuration integrity flag criteria are the following:
• When the current aircraft manoeuvre will lead to less than four satellites being in view, the CIF shall be generated.
• When less than four satellites are in view, the WIF shall be generated.
Additionally, if only four satellites are in view:
• When one (or more) satellite(s) elevation angle(s) (antenna frame) is (are) less than 10 degrees, the Caution Integrity Flag shall be generated.
• When one (or more) satellite(s) elevation angle(s) is (are) less than 5 degrees, the Warning Integrity Flag shall be generated.

Figure 3. TORNADO-IDS global masking profile (B = bank and P = pitch – in degrees).
Using the definition of Dilution of Precision (DOP) factors, GNSS accuracy can be expressed as (Kaplan and Hegarty, Reference Kaplan and Hegarty2006):
where:
- σ P
is the standard deviation of the positioning accuracy.
- σ UERE
is the standard deviation of the satellite pseudorange measurement error.
For the C/A-code σ UERE is in the order of 33·3 m. Therefore, the 1-σ Estimated Position Error (EPE), Estimated Horizontal Error (EHE) and Estimated Vertical Errors (EVE) of a GNSS receiver are calculated using the Positional DOP (PDOP), the Horizontal DOP (HDOP) or the Vertical DOP (VDOP) respectively. In order to generate CIFs and WIFs that are consistent with current GNSS Required Navigation Performance (RNP), we need to introduce the Horizontal and Vertical Accuracy (HA/VA) requirements applicable to the different flight phases. Table 1 shows the GNSS signal-in-space alert requirements in terms of HA/VA for En-route, Non-Precision Approach (NPA) and for the three categories of Precision Approach. Table 2 shows the GNSS signal-in-space protection requirements. The Horizontal Alert Limit (HAL) is the radius of a circle in the horizontal plane, with its centre being at the true position, which describes the region within which the indicated horizontal position must be contained with the required probability for a particular navigation mode. Similarly, the Vertical Alert Limit (VAL) is half the length of a segment on the vertical axis, with its centre being at the true position, which describes the region within which the indicated vertical position must be contained with the required probability for a particular navigation mode.
Table 1. GNSS signal-in-space alert requirements (ICAO, 2006).

Table 2. GNSS signal-in-space protection requirements (CAA, 2003).

As a result of our discussion, the DOP integrity flags criteria are the following:
• When the EHE exceeds the HA 95% or the VA 95% alert requirements, the CIF shall be generated.
• When the EHE exceeds the HAL or the EVE exceeds the VAL, the WIF shall be generated.
During the landing phase, a GNSS Landing System (GLS) has to be augmented by GBAS in order to achieve the RNP, as well as Lateral and Vertical Protection Levels (LPL and VPL). LPL/VPL are defined as the statistical error values that bound the Lateral/Vertical Navigation System Error (NSE) with a specified level of confidence. In particular, for the case of a Local Area Augmentation System (LAAS), which allows for multiple Differential GPS (DGPS) reference receivers (up to four) to be implemented, two different hypotheses are made regarding the presence of errors in the measurements. These hypotheses are (RTCA, 2004):
• H0 Hypothesis – No faults are present in the range measurements (includes both the signal and the receiver measurements) used in the ground station to compute the differential corrections.
• H1 Hypothesis – A fault is present in one or more range measurements and is caused by one of the reference receivers used in the ground station.
Consequently, LPL and VPL are computed as follows:
The lateral and vertical accuracy (NSE 95%) and alert limits required by a GLS in the presence of a LAAS, considering the continuously varying position of the aircraft with respect to the Landing Threshold Point (LTP), are also given in (RTCA, 2004). Additionally, this RTCA standard provides the so-called Continuity of Protection Levels in terms of Predicted Lateral and Vertical Protection Levels (PLPL and PVPL). Although the definition in (RTCA, 2004) is quite comprehensive, a generic statement is made that the PVPL and PLPL computations shall be based on the ranging sources expected to be available for the duration of the approach. In other terms, it is implied that the airborne subsystem shall determine which ranging sources are expected to be available, including the ground subsystem's declaration of satellite differential correction availability (satellite setting information). Unfortunately, this generic definition does not address the various conditions for satellite signal losses associated to specific aircraft manoeuvres (including curved GLS precision approaches). Therefore, it is suggested that an extended definition of PLPL and PVPL be developed which takes into account the continuously varying satellite/aircraft relative geometry. In particular, when the current aircraft manoeuvre will lead to less than four satellites in view or unacceptable accuracy degradations, the CIF shall be generated. Following our discussion, the additional integrity flags criteria adopted for GLS in the presence of a LAAS are the following:
• When the PLPL exceeds LAL or PVPL exceeds the VAL, the CIF shall be generated.
• When the LPL exceeds the LAL or the VPL exceeds the VAL, the WIF shall be generated.
3.2. Radio Frequency Link Errors
Multipath integrity flags were defined using the Early-Late Phase (ELP) observable and the range error. In a GPS receiver having three correlators (early, prompt and late), the phase of a correlator is given by (Mubarak and Dempster, Reference Mubarak and Dempster2009):
where the subscript C can refer to early (E), prompt (P) and late (L) respectively.
The prompt phase is always kept close to zero by the carrier tracking loop. Early and late correlators are then placed on each side of the prompt, which means one of the phases of the correlator is positive and the other is negative. So, the phase difference between the two is increased in the presence of multipath. ELP is simply the phase difference between the early and late correlator outputs, where the phase of a correlator output is equal to the inverse tangent of the Q channel output divided by the I channel output. Mathematically, the ELP is calculated by (Mubarak and Dempster, Reference Mubarak and Dempster2009):
The probability of multipath detection is approximately 80% by setting the ELP threshold at 0·1 radians (Fig. 4).

Figure 4. Probability of detecting multipath for varying ELP thresholds. The symbol α indicates the ratio of multipath to direct signal amplitude (i.e., α = Am/Ad). Adapted from Mubarak and Dempster (Reference Mubarak and Dempster2010).
Additionally, as shown in Figure 5, with an ELP threshold of 0·1 radians, the Probability of False Alarm (PFA) is 0·3 when ![]() ${\textstyle{{\rm C} \over {{\rm N}_0}}} $ is 42 dB-Hz. This is an acceptable compromise for the ABIA caution flag implementation.
${\textstyle{{\rm C} \over {{\rm N}_0}}} $ is 42 dB-Hz. This is an acceptable compromise for the ABIA caution flag implementation.

Figure 5. PFA for varying ELP thresholds. Adapted from Mubarak and Dempster (Reference Mubarak and Dempster2010).
Multipath range error experimental results are also used to trigger the warning integrity flag associated to multipath. As discussed in Part 1 (Sabatini et al., Reference Sabatini, Moore and Hill2012), the effect of ground-echo signals translates into a sudden increase of the multipath ranging error of up to two orders of magnitude with respect to the airframe multipath errors alone. However, the region of potential ground-echo multipath for the L1 frequency only extends up to 448·5 metres Above Ground Level (AGL) (theoretical value applicable to all aircraft types). As a result of our analysis, the multipath integrity flags criteria are the following:
• When the ELP exceeds 0·1 radians, the CIF shall be generated.
• When the multipath ranging error shows a sudden increase with the aircraft flying in proximity of the ground (below 448·5 metres), the WIF shall be generated.
Based on results of the GPS-based Time and Space Position Information (TSPI) flight test activities (Sabatini and Palmerini, Reference Sabatini and Palmerini2008), an additional (practical) criteria was developed for the TORNADO-IDS aircraft. During TORNADO-IDS flight trials it was observed that flying above 500 ft AGL (even with pitch/bank angles exceeding 45°), the ground-echo multipath was not a factor and the multipath range error (due to the airframe only) never exceeded 2 metres. Consequently, the additional criteria applicable to the TORNADO-IDS aircraft is:
• When the multipath ranging error exceeds 2 metres and the aircraft flies in proximity of the ground (below 500 ft AGL), the WIF shall be generated.
As introduced in Part 1 (Sabatini et al., Reference Sabatini, Moore and Hill2012), avionics GNSS receivers are resistant to dynamic stress errors. A robust avionics GNSS receiver design typically employs a Frequency Lock Loop (FLL) as a backup to the Phase Lock Loop (PLL) during initial loop closure and during high-dynamic stress with loss of phase lock; it will revert to pure PLL for the steady-state low to moderate dynamics in order to produce the highest carrier Doppler phase measurements. However, flight test activities performed with avionics GPS receivers showed that the reacquisition time after loss of one or more satellite signals could be up to 40 seconds, depending on flight conditions and satellite constellations (Sabatini and Palmerini, Reference Sabatini and Palmerini2008). Additionally, the analysis of receiver data, recorded during several flights and at speeds up to 500 kn, highlighted that the Doppler effect causes a frequency shift with respect to the L1 carrier frequency, reaching a maximum value of about 15 KHz (Sabatini and Palmerini, Reference Sabatini and Palmerini2008). This value is relatively low if compared with the GPS frequency bandwidth (i.e., about 30 MHz) and the high dynamic characteristics of the carrier tracking loops internal to the avionics receiver guarantee that neither the data accuracy is degraded nor the carrier phase is lost because of Doppler shift. Nevertheless, the coupling between such a frequency shift and the signal reacquisition strategy of the receiver can significantly affect the time necessary to get data after a signal loss.
Figure 6 shows the fitting functions and associated curves relative to the acquisition time experimental data presented in (Sabatini et al., Reference Sabatini, Moore and Hill2012). These functions were conveniently used to estimate GNSS acquisition time based on satellite/aircraft relative velocity Line Of Sight (LOS). With reference to Figure 6, it is evident that for C/N0 below 28 dB-Hz the acquisition time exceeds 1 second even in low dynamics conditions. Therefore, in these conditions, the required acquisition times might become unacceptable in case of satellite signal losses during certain mission- and safety-critical GNSS applications (military weapon aiming, missile guidance, precision approach, etc.).

Figure 6. Doppler shift and signal acquisition in avionics GPS receivers.
Consequently, the following criteria were defined for the Doppler integrity flags thresholds:
• When the C/N0 is below 28 dB-Hz and the signal is lost, the CIF shall be generated if the estimated acquisition time is less than the application-specific TTA requirements.
• When the C/N0 is below 28 dB-Hz and the signal is lost, the WIF shall be generated if the estimated acquisition time exceeds the application-specific TTA requirements.
3.3. Receiver Tracking Errors
As discussed before, in order to define additional robust criteria for the ABIA integrity thresholds associated with dynamic stress errors, signal fading (C/N0 reduction) and interferences (J/S increase), a dedicated analysis of the GNSS receiver tracking performance was required. When the GNSS code and/or carrier tracking errors exceed certain thresholds, the receiver loses lock to the satellites. Since both the code and carrier tracking loops are nonlinear, especially near the threshold regions, only Monte Carlo simulations of the GNSS receiver in different dynamics and Signal to Noise Ratio (SNR) conditions can determine the receiver tracking performance (Ward, Reference Ward1997). Nevertheless, some conservative ‘rules-of-thumb’ approximating the measurement errors of the GNSS tracking loops were used for the ABIA initial design. Numerous sources of measurement errors affect the Carrier Tracking Loops and Code Tracking Loops. However, for our purposes, it was sufficient to analyze the dominant error sources in each type of tracking loop. Consider a typical avionics GNSS receiver employing a two-quadrant arctangent discriminator; the PLL threshold is given by (Kaplan and Hegarty, Reference Kaplan and Hegarty2006):
where:
- σ j=
1-sigma phase jitter from all sources except dynamic stress error.
- θ e=
dynamic stress error in the PLL tracking loop.
Expanding Equation (13), the 1-sigma threshold for the PLL tracking loop becomes (Kaplan and Hegarty, Reference Kaplan and Hegarty2006):
where:
- σ tPLL=
1-sigma thermal noise.
- σ υ=
vibration-induced oscillator phase noise.
- θ A=
Allan variance–induced oscillator jitter.
The PLL thermal noise is often thought to be the only carrier tracking error, since the other sources of PLL jitter may be either transient or negligible. The PLL thermal noise jitter is computed as follows:
 $$\sigma _{{\rm tPLL}} = \displaystyle{{360} \over {2\pi}} \sqrt {\displaystyle{{{\rm B}_{\rm n}} \over {\left( {\displaystyle{{\rm c} \over {{\rm n}_0}}} \right)\left( {1 + \displaystyle{1 \over {2{\rm T}{\displaystyle{{\rm c} \over {{\rm n}_0}}}}}} \right)}}} \quad ({\rm degrees})$$
$$\sigma _{{\rm tPLL}} = \displaystyle{{360} \over {2\pi}} \sqrt {\displaystyle{{{\rm B}_{\rm n}} \over {\left( {\displaystyle{{\rm c} \over {{\rm n}_0}}} \right)\left( {1 + \displaystyle{1 \over {2{\rm T}{\displaystyle{{\rm c} \over {{\rm n}_0}}}}}} \right)}}} \quad ({\rm degrees})$$where:
- Bn=
carrier loop noise bandwidth (Hz).
 ${\displaystyle{{\rm c} \over {{\rm n}_0}}} $$=
${\displaystyle{{\rm c} \over {{\rm n}_0}}} $$=carrier to noise power ratio
 $({\displaystyle{{\rm c} \over {{\rm n}_0}}} = 10^{\textstyle{{{\textstyle{{\rm C} \over {{\rm N}_0}}}} \over {10}}}\,{\rm for}\,{\textstyle{{\rm C} \over {{\rm N}_0}}}\, {\rm expressed\,in\,dB} {\mbox{\hbox -}} {\rm Hz)}$.
$({\displaystyle{{\rm c} \over {{\rm n}_0}}} = 10^{\textstyle{{{\textstyle{{\rm C} \over {{\rm N}_0}}}} \over {10}}}\,{\rm for}\,{\textstyle{{\rm C} \over {{\rm N}_0}}}\, {\rm expressed\,in\,dB} {\mbox{\hbox -}} {\rm Hz)}$.- T=
pre-detection integration time (seconds).
Bn and ![]() ${\textstyle{{\rm C} \over {{\rm N}_0}}} $ can be derived from the SNR model as described before. Determination of the vibration-induced oscillator phase noise is a complex analysis problem. In some cases, the expected vibration environment is so severe that the reference oscillator must be mounted using vibration isolators in order that the GPS receiver can successfully operate in PLL. The equation for vibration induced oscillator jitter is:
${\textstyle{{\rm C} \over {{\rm N}_0}}} $ can be derived from the SNR model as described before. Determination of the vibration-induced oscillator phase noise is a complex analysis problem. In some cases, the expected vibration environment is so severe that the reference oscillator must be mounted using vibration isolators in order that the GPS receiver can successfully operate in PLL. The equation for vibration induced oscillator jitter is:
 $$\sigma _\upsilon = \displaystyle{{360{\rm f}_{\rm L}} \over {2\pi}} \sqrt {\int_{{\rm f}_{\min}} ^{{\rm f}_{\max}} {\displaystyle{{{\rm S}_\upsilon ^2 ({\rm f}_{\rm m} )({\rm P}({\rm f}_{\rm m} ))} \over {{\rm f}_{\rm m}^2}} {\rm df}_{\rm m} \quad ({\rm degrees})}} \; \; \; $$
$$\sigma _\upsilon = \displaystyle{{360{\rm f}_{\rm L}} \over {2\pi}} \sqrt {\int_{{\rm f}_{\min}} ^{{\rm f}_{\max}} {\displaystyle{{{\rm S}_\upsilon ^2 ({\rm f}_{\rm m} )({\rm P}({\rm f}_{\rm m} ))} \over {{\rm f}_{\rm m}^2}} {\rm df}_{\rm m} \quad ({\rm degrees})}} \; \; \; $$where:
- fL=
L-band frequency (Hz).
- Sυ(fm)=
oscillator vibration sensitivity of
 $\Delta {\rm f}/{\rm f}_{\rm L}}}} $ per g as a function of fm.
$\Delta {\rm f}/{\rm f}_{\rm L}}}} $ per g as a function of fm.- fm=
random vibration modulation frequency (Hz).
- P(fm)=
power curve of the random vibration as a function of fm
 ${\displaystyle\left({{{\rm g2}} \over {{\rm Hz}}}\right)}$
${\displaystyle\left({{{\rm g2}} \over {{\rm Hz}}}\right)}$- g=
gravity acceleration.
Usually the oscillator vibration sensitivity Sυ(fm), is not variable over the range of the random vibration modulation frequency, then Equation (16) can be simplified to:
 $${\rm \sigma} _{\rm \upsilon} = \displaystyle{{360{\rm f}_{\rm L} {\rm S}_{\rm \upsilon}} \over {2{\rm \pi}}} \sqrt {\int_{{\rm f}_{\min}} ^{{\rm f}_{\max}} {\displaystyle{{{\rm P}({\rm f}_{\rm m} )} \over {{\rm f}_{\rm m}^2}} {\rm df}_{\rm m}}} \ ({\rm degrees})$$
$${\rm \sigma} _{\rm \upsilon} = \displaystyle{{360{\rm f}_{\rm L} {\rm S}_{\rm \upsilon}} \over {2{\rm \pi}}} \sqrt {\int_{{\rm f}_{\min}} ^{{\rm f}_{\max}} {\displaystyle{{{\rm P}({\rm f}_{\rm m} )} \over {{\rm f}_{\rm m}^2}} {\rm df}_{\rm m}}} \ ({\rm degrees})$$The equations used to determine Allan deviation phase noise are empirical. They are stated in terms of what the requirements are for the short-term stability of the reference oscillator as determined by the Allan variance method of stability measurement. The equation for second-order loop, short-term Allan deviation is:
The equation for third-order loop, short-term Allan deviation for PLL is:
where:
- σ A(τ)=
Allan deviation-induced jitter (degrees).
- fL =
L-band input frequency (Hz).
- τ=
short-term stability gate time for Allan variance measurement (seconds).
- Bn=
noise bandwidth.
Usually σ A(τ) can be determined for the oscillator and it changes very little with gate time τ. In our research, the loop filter is assumed as a third-order with a noise bandwidth Bn = 18 Hz and the gate time ![]() ${\rm \tau} = {\textstyle{1 \over {{\rm B}_{\rm n}}}} = 56\;{\rm ms}$. The Allan deviation is specified to be σ A(τ) = 10−10. The dynamic stress error depends on the loop bandwidth and order. In a third-order loop, the dynamic stress error is (Kaplan and Hegarty, Reference Kaplan and Hegarty2006):
${\rm \tau} = {\textstyle{1 \over {{\rm B}_{\rm n}}}} = 56\;{\rm ms}$. The Allan deviation is specified to be σ A(τ) = 10−10. The dynamic stress error depends on the loop bandwidth and order. In a third-order loop, the dynamic stress error is (Kaplan and Hegarty, Reference Kaplan and Hegarty2006):
 $$\theta _{{\rm e}3} = \displaystyle{{{\textstyle{{{\rm d}^3 {\rm R}} \over {{\rm dt}^3}}}} \over {\omega _0^3}} = \displaystyle{{{\textstyle{{{\rm d}^3 {\rm R}} \over {{\rm dt}^3}}}} \over {\left( {{\textstyle{{{\rm B}_{\rm n}} \over 0 \cdot 7845}}} \right)^3}} = 0 \!\cdot\! 4828\displaystyle{{{\textstyle{{{\rm d}^3 {\rm R}} \over {{\rm dt}^3}}}} \over {{\rm B}_{\rm n}^3}} \,({\rm degrees})$$
$$\theta _{{\rm e}3} = \displaystyle{{{\textstyle{{{\rm d}^3 {\rm R}} \over {{\rm dt}^3}}}} \over {\omega _0^3}} = \displaystyle{{{\textstyle{{{\rm d}^3 {\rm R}} \over {{\rm dt}^3}}}} \over {\left( {{\textstyle{{{\rm B}_{\rm n}} \over 0 \cdot 7845}}} \right)^3}} = 0 \!\cdot\! 4828\displaystyle{{{\textstyle{{{\rm d}^3 {\rm R}} \over {{\rm dt}^3}}}} \over {{\rm B}_{\rm n}^3}} \,({\rm degrees})$$where:
- R=
LOS range to the satellite.
 ${\textstyle{{{\rm d}^2 {\rm R}} \over {{\rm dt}^2}}} $$=
${\textstyle{{{\rm d}^2 {\rm R}} \over {{\rm dt}^2}}} $$=maximum LOS acceleration dynamics
 $ (^{{\scale70%\circ}}/{{\rm s}^2}}} )$.
$ (^{{\scale70%\circ}}/{{\rm s}^2}}} )$.- ω0=
loop filter natural radian frequency.
- Bn=
noise bandwidth.
For the L1 frequency we have: ![]() ${{\rm d}^3 {\rm R}} / {\rm dt}^3 = ({98} / {\rm s}^3}) \times \left(360{\rm ^{\circ}}/{\rm cycle}\right)\times{({{{1575 \cdot 42 \times 10^6\, {{{{\rm cycles}}/ {\rm s})/ {\rm c}}} = 185398^{\circ} /{\rm s}^3} $. Frequency jitter due to thermal noise and dynamic stress error are the main errors in a GNSS receiver FLL. The receiver tracking threshold is such that the 3-sigma jitter must not exceed one-fourth of the frequency pull-in range of the FLL discriminator. Therefore, the FLL tracking threshold is (Kaplan and Hegarty, Reference Kaplan and Hegarty2006):
${{\rm d}^3 {\rm R}} / {\rm dt}^3 = ({98} / {\rm s}^3}) \times \left(360{\rm ^{\circ}}/{\rm cycle}\right)\times{({{{1575 \cdot 42 \times 10^6\, {{{{\rm cycles}}/ {\rm s})/ {\rm c}}} = 185398^{\circ} /{\rm s}^3} $. Frequency jitter due to thermal noise and dynamic stress error are the main errors in a GNSS receiver FLL. The receiver tracking threshold is such that the 3-sigma jitter must not exceed one-fourth of the frequency pull-in range of the FLL discriminator. Therefore, the FLL tracking threshold is (Kaplan and Hegarty, Reference Kaplan and Hegarty2006):
where:
- 3σ tFLL=
3-sigma thermal noise frequency jitter.
- fe=
dynamic stress error in the FLL tracking loop.
Equation (21) shows that the dynamic stress frequency error is a 3-sigma effect and is additive to the thermal noise frequency jitter. The reference oscillator vibration and Allan deviation–induced frequency jitter are small-order effects on the FLL and are considered negligible. The 1-sigma frequency jitter threshold is 1/(12 T) = 0·0833/T Hz. The FLL tracking loop jitter due to thermal noise is:
 $$\sigma _{{\rm tFLL}} = \displaystyle{1 \over {2\pi {\rm T}}}\sqrt {\displaystyle{{4{\rm FB}_{\rm n}} \over {{\textstyle{{\rm C} \over {{\rm n}_0}}}}} \left[ {1 + \displaystyle{1 \over {{\textstyle{{{\rm T}_{\rm C}} \over {{\rm n}_0}}}}}} \right]} \,(\rm Hz)$$
$$\sigma _{{\rm tFLL}} = \displaystyle{1 \over {2\pi {\rm T}}}\sqrt {\displaystyle{{4{\rm FB}_{\rm n}} \over {{\textstyle{{\rm C} \over {{\rm n}_0}}}}} \left[ {1 + \displaystyle{1 \over {{\textstyle{{{\rm T}_{\rm C}} \over {{\rm n}_0}}}}}} \right]} \,(\rm Hz)$$where F is 1 at high ![]() ${\textstyle{{\rm C} \over {{\rm N}_0}}} $ and 2 near the threshold.
${\textstyle{{\rm C} \over {{\rm N}_0}}} $ and 2 near the threshold.
σ tFLL is independent of C/A or P(Y) code modulation and loop order. Since the FLL tracking loop involves one more integrator that the PLL tracking loop of the same order (4, 12), the dynamic stress error is:
 $${\rm f}_{\rm e} = \displaystyle{{\rm d} \over {{\rm dt}}}\left( {\displaystyle{1 \over {360{\rm \omega} _0^{\rm n}}} \displaystyle{{{\rm d}^{\rm n} {\rm R}} \over {{\rm dt}^{\rm n}}}} \right) = \displaystyle{1 \over {360{\rm \omega} _0^{\rm n}}} \displaystyle{{{\rm d}^{{\rm n} + 1} {\rm R}} \over {{\rm dt}^{{\rm n} + 1}}} {\rm \;} \,({\rm Hz})$$
$${\rm f}_{\rm e} = \displaystyle{{\rm d} \over {{\rm dt}}}\left( {\displaystyle{1 \over {360{\rm \omega} _0^{\rm n}}} \displaystyle{{{\rm d}^{\rm n} {\rm R}} \over {{\rm dt}^{\rm n}}}} \right) = \displaystyle{1 \over {360{\rm \omega} _0^{\rm n}}} \displaystyle{{{\rm d}^{{\rm n} + 1} {\rm R}} \over {{\rm dt}^{{\rm n} + 1}}} {\rm \;} \,({\rm Hz})$$Regarding the code tracking loop, a conservative rule-of-thumb for the Delay Lock Loop (DLL) tracking threshold is that the 3-sigma value of the jitter due to all sources of loop stress must not exceed the correlator spacing (d), expressed in chips. Therefore (4, 13):
where:
- σ DFLL=
1-sigma thermal noise code tracking jitter.
- Re=
dynamic stress error in the DLL tracking loop.
The DLL thermal noise code tracking jitter is given by:
 $$\sigma _{{\rm tDLL}} = \sqrt {\displaystyle{{4{\rm F}_1 {\rm d}^2 {\rm B}_{\rm n}} \over {{\textstyle{{\rm c} \over {{\rm n}_0}}}}} [ {2(1 - {\rm d}) + \displaystyle{{4{\rm F}_2 {\rm d}} \over {{\textstyle{{{\rm {\bf T}c}} \over {{\rm n}_0}}}}}}]} \; \,(\rm Hz)$$
$$\sigma _{{\rm tDLL}} = \sqrt {\displaystyle{{4{\rm F}_1 {\rm d}^2 {\rm B}_{\rm n}} \over {{\textstyle{{\rm c} \over {{\rm n}_0}}}}} [ {2(1 - {\rm d}) + \displaystyle{{4{\rm F}_2 {\rm d}} \over {{\textstyle{{{\rm {\bf T}c}} \over {{\rm n}_0}}}}}}]} \; \,(\rm Hz)$$where:
- F1=
DLL discriminator correlator factor (1 for time shared tau-dithered early/late correlator and 0·5 for dedicated early and late correlators).
- d=
Correlator spacing between early, prompt and late.
- Bn=
Code loop noise bandwidth.
- F2=
DLL dicriminator type factor (1 for early/late type discriminator and 0·5 for dot product type discriminator).
The DLL tracking loop dynamic stress error is given by:
 $${\rm R}_{\rm e} = \displaystyle{{{\textstyle{{{\rm dR}^{\rm n}} \over {{\rm dt}^{\rm n}}}}} \over {\omega _0^{\rm n}}} \,\; ({\rm chips})$$
$${\rm R}_{\rm e} = \displaystyle{{{\textstyle{{{\rm dR}^{\rm n}} \over {{\rm dt}^{\rm n}}}}} \over {\omega _0^{\rm n}}} \,\; ({\rm chips})$$where dRn/dtn is expressed in chips/secn.
The PLL, FLL and DLL error equations described above allow to determine the (C/N0) corresponding to the tracking threshold of the receiver. A generic criteria applicable to the ABIA system is:
where:
 $\left({\displaystyle{{\rm C} \over {\rm N}}}_0\right)_{{\rm PLL}} $$=
$\left({\displaystyle{{\rm C} \over {\rm N}}}_0\right)_{{\rm PLL}} $$=Minimum carrier-to-noise ratio for PLL carrier tracking.
 $\left({\displaystyle{{\rm C} \over {\rm N}}}_0\right)_{{\rm FLL}} $$=
$\left({\displaystyle{{\rm C} \over {\rm N}}}_0\right)_{{\rm FLL}} $$=Minimum carrier-to-noise ratio for FLL carrier tracking.
 $\left({\displaystyle{{\rm C} \over {\rm N}}}_0\right)_{{\rm DLL}} $$=
$\left({\displaystyle{{\rm C} \over {\rm N}}}_0\right)_{{\rm DLL}} $$=Minimum carrier-to-noise ratio for DLL code tracking.
Numerical solutions of Equations (13), (21) and (24) show that the weak link in unaided avionics GNSS receivers is the PLL due to its greater sensitivity to dynamics stress. Therefore, the ![]() $\left[\left({\textstyle{{\rm C} \over {\rm N}}}\right]_0\right)_{{\rm PLL}} $ threshold can be adopted in these cases. In general, when the PLL loop order is made higher, there is an improvement in dynamic stress performance. This is why third order PLL are widely adopted in avionics GNSS receivers (e.g., TORNADO-IDS). Assuming 15 to 18 Hz noise bandwidth and 5 to 20 msec pre-detection integration time (typical values for avionics receivers), the ‘rule-of-thumb’ tracking threshold for the PLL gives 25 to 28 dB-Hz. Additionally, in aided avionics receiver applications, the PLL tracking threshold can be significantly reduced by using external velocity aiding in the carrier tracking loop. With this provision, a tracking threshold of approximately 15 to 18 dB-Hz can be achieved. Using these theoretical and experimental threshold values, we can also calculate the receiver J/S performance for the various cases of practical interest, as described in (Sabatini et al., Reference Sabatini, Moore and Hill2012). When available, flight test data collected in representative portions of the aircraft operational flight envelope (or the results of Monte Carlo simulation) will be used. Taking an additional 5% margin on the 3-sigma tracking thresholds for the CIF, the following additional criteria are introduced for the ABIA integrity thresholds:
$\left[\left({\textstyle{{\rm C} \over {\rm N}}}\right]_0\right)_{{\rm PLL}} $ threshold can be adopted in these cases. In general, when the PLL loop order is made higher, there is an improvement in dynamic stress performance. This is why third order PLL are widely adopted in avionics GNSS receivers (e.g., TORNADO-IDS). Assuming 15 to 18 Hz noise bandwidth and 5 to 20 msec pre-detection integration time (typical values for avionics receivers), the ‘rule-of-thumb’ tracking threshold for the PLL gives 25 to 28 dB-Hz. Additionally, in aided avionics receiver applications, the PLL tracking threshold can be significantly reduced by using external velocity aiding in the carrier tracking loop. With this provision, a tracking threshold of approximately 15 to 18 dB-Hz can be achieved. Using these theoretical and experimental threshold values, we can also calculate the receiver J/S performance for the various cases of practical interest, as described in (Sabatini et al., Reference Sabatini, Moore and Hill2012). When available, flight test data collected in representative portions of the aircraft operational flight envelope (or the results of Monte Carlo simulation) will be used. Taking an additional 5% margin on the 3-sigma tracking thresholds for the CIF, the following additional criteria are introduced for the ABIA integrity thresholds:
• When 42·25°≤3σ PLL≤45° or 0·2375 T≤3σ FLL≤0·25 T or 0·05d≤3σ DLL≤3σ DLL d the CIF shall be generated.
• When 3σ PLL>45° or 3σ FLL>
 ${\textstyle{1 \over {4T}}}$ or 3σ PLL>d the WIF shall be generated.
${\textstyle{1 \over {4T}}}$ or 3σ PLL>d the WIF shall be generated.
Additionally, taking a 1 dB margin on the maximum J/S performance of the receiver to generate the CIF, the following criteria were adopted for the CIF and WIF flags associated to interference:
• When the difference between the received (incident) jammer power (dBw) and the received (incident) signal power (dBw) is 1 dB below the J/S performance of the receiver at its tracking threshold, the CIF shall be generated.
• When the difference between the received (incident) jammer power (dBw) and the received (incident) signal power (dBw) is above the J/S performance of the receiver at its tracking threshold, the WIF shall be generated.
During the GPS-TSPI flight test activities performed on TORNADO-IDS with unaided L1 C/A code avionics receivers (Sabatini and Palmerini, Reference Sabatini and Palmerini2008), it was also found that, in all dynamics conditions explored, a ![]() ${\textstyle{{\rm C} \over {{\rm N}_0}}} $ of 25 dB-Hz was sufficient to continue tracking of the satellites (Sabatini and Palmerini, Reference Sabatini and Palmerini2008). Consequently, taking the usual 1 dB margin for the CIF, the following additional criteria were adopted for the TORNADO-IDS C/N0 integrity flags:
${\textstyle{{\rm C} \over {{\rm N}_0}}} $ of 25 dB-Hz was sufficient to continue tracking of the satellites (Sabatini and Palmerini, Reference Sabatini and Palmerini2008). Consequently, taking the usual 1 dB margin for the CIF, the following additional criteria were adopted for the TORNADO-IDS C/N0 integrity flags:
• When the
 ${\textstyle{{\rm C} \over {{\rm N}_0}}} $ is less than 26 dB-Hz the CIF shall be generated.
${\textstyle{{\rm C} \over {{\rm N}_0}}} $ is less than 26 dB-Hz the CIF shall be generated.• When the
 ${\textstyle{{\rm C} \over {{\rm N}_0}}} $ is less than 25 dB-Hz the WIF shall be generated.
${\textstyle{{\rm C} \over {{\rm N}_0}}} $ is less than 25 dB-Hz the WIF shall be generated.
4. SIMULATION
In order to validate the design of the ABIA IFG module, a detailed simulation case study was performed on the TORNADO-IDS aircraft, whose flight dynamics and GPS receiver performance characteristics were available from previous research (Sabatini and Palmerini, Reference Sabatini and Palmerini2008). Various geometric parameters were required to draw a detailed CATIA model of the aircraft. Some of the main parameters are listed in Table 3 (Aircraft Drawings, 2012).
Table 3. TORNADO-IDS dimensions.

The TORNADO-IDS 3-D CATIA model obtained is shown in Fig. 7.

Figure 7. TORNADO-IDS 3-D CATIA model.
When calculating the antenna masking matrix and the corresponding satellite visibility, the antenna location must be included in the model. Military aircraft typically have an Upper Antenna (UA) at the top of the fuselage and a Lower Antenna (LA) at the base of the fuselage. In our case, the upper antenna is assumed to be located 1·5 m behind the cockpit along the aircraft centreline projection and 5 cm high on the aircraft skin surface (Sabatini and Palmerini, Reference Sabatini and Palmerini2008). The lower antenna is right below the upper antenna on the opposite side of the fuselage (Figure 8). When calculating the satellite visibility, the LOS is measured in the antenna frame (i.e., origin at the antenna focal point). The transformation from body-frame to antenna frame is obtained from:
The transformation matrices for the upper and lower antennae are:
 $${\rm T}_{{\rm body}}^{{\rm upper}} = \left[ {\matrix{ { - 0\! \cdot\! 88} \cr 0 \cr { - 0\! \cdot\! 74} \cr}} \right]{\rm \;} ({\rm m})$$
$${\rm T}_{{\rm body}}^{{\rm upper}} = \left[ {\matrix{ { - 0\! \cdot\! 88} \cr 0 \cr { - 0\! \cdot\! 74} \cr}} \right]{\rm \;} ({\rm m})$$ $${\rm T}_{{\rm body}}^{{\rm lower}} = \left[ {\matrix{ { - 0\! \cdot\! 88} \cr 0 \cr {2 \!\cdot\!\! 13} \cr}} \right]{\rm \;} ({\rm m})$$
$${\rm T}_{{\rm body}}^{{\rm lower}} = \left[ {\matrix{ { - 0\! \cdot\! 88} \cr 0 \cr {2 \!\cdot\!\! 13} \cr}} \right]{\rm \;} ({\rm m})$$
Figure 8. TORNADO-IDS antennae locations.
The simplified TORNADO-IDS antenna gain pattern used in the simulation is shown in Figure 9 and it is mathematically described as follows:
The simulated TORNADO-IDS aircraft trajectory included the following phases:
• Climb flight phase (0–5 min).
• Cruise flight phase (5–10 min).
• Turn and descend flight phase (10–15 min).
• Cruise flight phase (15–20 min).
• Approach flight phase (20–25 min).
In this simulation, the cruise phases correspond to straight-and-level flight segments and the approach phase is simulated as a straight descent employing GLS in the presence of a LAAS. The terrain profile was assumed to be flat and free from man-made features. No jamming sources were considered in this simulation. The initial point of the aircraft trajectory was located at London Heathrow airport (WGS 84 coordinates: 51° 28′ 39″ N, 0° 27′ 41″ W) and the GPS constellation available on 24th December 2011 (12:00 a.m.) was simulated using the YUMA almanac data (Celestrak, 2012a). Additionally, for the TORNADO-IDS GPS receiver characteristics, we considered the random vibration power curve to be flat from 20 Hz to 2000 Hz with an amplitude of 0·005 ![]() ${\textstyle{{{\rm g2}} \over {{\rm H}_{\rm z}}}} $ and the oscillator vibration sensitivity Sυ(fm) = 1×10−9 parts/g. Finally, the third-order loop noise bandwidth is 18 Hz and the maximum LOS jerk dynamic stress is 10 g/s = 98
${\textstyle{{{\rm g2}} \over {{\rm H}_{\rm z}}}} $ and the oscillator vibration sensitivity Sυ(fm) = 1×10−9 parts/g. Finally, the third-order loop noise bandwidth is 18 Hz and the maximum LOS jerk dynamic stress is 10 g/s = 98 ![]() ${\textstyle{{\rm m} \over {{\rm s}^{\rm 3}}}} $ The CIFs and WIFs relative to antenna masking, geometric accuracy degradations, S/N, multipath and Doppler shift were generated. The overall results are shown in Table 4.
${\textstyle{{\rm m} \over {{\rm s}^{\rm 3}}}} $ The CIFs and WIFs relative to antenna masking, geometric accuracy degradations, S/N, multipath and Doppler shift were generated. The overall results are shown in Table 4.

Figure 9. Simplified TORNADO-IDS antenna gain pattern.
Table 4. GPS Integrity Flags for TORNADO-IDS.

Table 5 shows the details of the specific CIFs and WIFs generated during the various TORNADO-IDS flight phases. There was only one case (flight slice 600–608 s) where the CIF was generated and not followed by the WIF (this was due to a temporary adverse relative geometry during the TDP manoeuvres). In all other cases, the CIF was followed by the WIF. It was also observed that the CIF was always triggered at least 2 seconds before the successive WIF onset (up to 6 seconds during the straight descent phase). These results contribute to corroborate the validity of the models developed for the CIF/WIF thresholds. This evidence is particularly important for the ABIA system design. In fact, it is evident that the availability of a usable CIF represents significant progress in this research with the potential for both manned aircraft and UAVs to recover from mission- and safety-critical flight conditions potentially leading to GNSS data losses. Therefore, it is envisaged that a properly designed ABIA Flight Path Guidance Module (FPM) could take full advantage of this predictive behaviour, allowing an aircraft or UAV to correct its flight trajectory/attitude in order to avoid the occurrence of the critical GNSS data losses. Additionally, it is possible that this predictive behaviour could be exploited in the pursuit of a GNSS-based auto-land capability.
Table 5. GPS Integrity Flags for TORNADO-IDS (CIF/WIF details).

5. CONCLUSIONS AND FUTURE WORK
In this research the architecture of an Avionics-Based Integrity Augmentation (ABIA) system for Global Navigation Satellite System (GNSS) applications was defined. The detailed design of the ABIA Integrity Flag Generator (IFG) module was also accomplished. This module can generate both Caution and Warning Integrity Flags (CIF and WIF) associated with antenna obscuration, geometric accuracy degradations, Signal-to-Noise Ratio (SNR), multipath and Doppler shift. A detailed simulation case study was performed on the TORNADO Interdiction and Strike (IDS) aircraft. Relevant flight manoeuvres/phases were considered in this simulation, including climb, cruise, turning descent and straight descent. From the results of this simulation activity, the following conclusions were drawn:
• The ABIA IFG is capable of generating integrity flags to provide both caution and warning signals to the pilot when GNSS signals are degraded or lost.
• After the integrity caution flag is generated, the time available for the pilot/autopilot to react (before the integrity warning flag is generated) is sufficient for safety-critical tasks including a GNSS Landing System (GLS), curved/segmented precision approach and automatic landing applications.
• In the limited range of dynamic conditions explored, data analysis showed that the ABIA system can provide useful integrity signals for Category Three (CAT-III) precision approach and automatic landing.
Our current research is focussing on the following areas:
• The examination of other types of manned aircraft (e.g., civil airliners) and Unmanned Aerial Vehicles (UAVs).
• Multipath detection and isolation in various kinds of receivers for avionics applications.
• Development and testing of ABIA Flight Path Guidance (FPG) modules for manned aircraft and UAVs.
Additional long-term objectives of our research include:
• Evaluation of the potential of Aircraft-Based Augmentation System (ABAS) techniques to improve integrity levels in a wide spectrum of civil/military mission-critical and safety-critical GNSS applications.
• Evaluation of the potential of ABAS techniques to supplement current and likely future Space-Based Augmentation Systems (SBAS) and Ground-Based Augmentation Systems (GBAS) technology for en-route, terminal, approach and surface operations.
• Investigation and comparison of different types of avionics sensor technologies and their potential to support the design of a robust ABAS architecture.
• Investigation into the potential of ABAS techniques to support UAV Sense-And-Avoid (SAA) capability.
• Investigation into the potential of ABAS techniques to enhance the performance of next generation Flight Management Systems (FMS) for Four-Dimensional Trajectory (4DT) Operations in the future Air Traffic Management (ATM) environment.