1. INTRODUCTION
An autonomous navigation system for vehicles, which employs the measurements from on board devices, is of increasing concern, as it can reduce manual efforts and enhance survivability of vehicles encountering hostile environments. Autonomous navigation applications for low-orbit Earth vehicles have been well accomplished by Global Navigation Satellite Systems (GNSS). However, GNSS cannot be readily applied to high-orbit vehicles, the orbital altitudes of which are higher than those of GNSS satellites because of the weak signal as well as the insufficient number of observable satellites. Consequently, designing an autonomous navigation system for this type of vehicle is of great interest.
X-ray pulsars are a type of neutron star that are located far from the solar system and emit electromagnetic radiation in the X-ray band (Sheikh et al., Reference Sheikh, Pines and Ray2006). The high-precision spinning period and distant location make X-ray pulsars to be promising candidates for determining the position of vehicles within the solar system. Although the idea of X-ray pulsar-based navigation was first proposed in 1981, the concept grew rapidly (Chester and Butman, Reference Chester and Butman1981; Becker et al., Reference Becker, Werner and Jessner2013). In 2004, the European Space Agency (ESA) studied the feasibility of X-ray pulsar-based Navigation system (XNAV) (Sala et al., Reference Sala, Urruela, Villares, Estalella and Paredes2004). The United States also undertook a series of projects focusing on XNAV (Keith, Reference Keith2013). Some heuristic work on XNAV have been published in recent years (Wang et al., Reference Wang, Zheng, An, Sun and Li2013; Wang et al., Reference Wang, Zheng, Sun and Li2014; Zheng et al., Reference Zheng, Wang, Jiang and Liu2015).
Although the signal of X-ray pulsars is claimed to be a pulse, a vehicle could merely record a series of photon Times Of Arrival (TOA) when observing a pulsar, because the signal of an X-ray pulsar is extremely weak. Also, the received signal is not a determined signal, but a stochastic one. Extracting the pulse TOA, the fundamental measurement in XNAV, from the recorded photon TOA series is a key technique. The technique can be resolved by means of epoch folding or a Maximum Likelihood Estimator (MLE) derived from the Non-Homogeneous Poisson Process (NHPP) to the case that the pulsar signal is assumed to be of a constant frequency (Emadzadeh and Speyer, Reference Emadzadeh and Speyer2010). However, in practical aerospace applications, vehicles always perform an orbital motion around a celestial body, resulting in the time-varying nature of the frequency of the signal. Finally, it is likely that the above-mentioned methods would fail. To attempt to solve this, Golshan and Sheikh (Reference Golshan and Sheikh2007) proposed a pulse phase tracking algorithm. The algorithm approximates the continuous-time frequency by a piece-wise constant model by dividing the whole observation period into several sufficiently short intervals during which the frequency is assumed to be constant, estimates the initial pulse phase at each interval via a MLE, and employs a Digital Phase-Locked Loop (DPLL) to track the varying frequency between neighbour intervals. Huang et al. (Reference Huang, Liang and Zhang2013) modified the DPLL to be a two-order Kalman filter and improved its performance.
A necessary condition contributing to the success of pulse phase tracking algorithms is that a reliable result of MLE can be obtained by limited photons collected within each divided interval. In order to precisely approximate the time-continue frequency by a piece-wise constant one, the divided interval should be sufficiently short. However, if the divided interval reduces to be less than a certain threshold, the resulting MLE would diverge from the Cramér-Rao Bound (CRB) and become unreliable (Tran et al., Reference Tran, Renaux, Boyer, Marcos and Larzabal2014). For some pulsars with high flux, such as the Crab pulsar, the corresponding threshold could be less than 1 s, and phenomena where the divided interval is shorter than the threshold seldom occurs. Unfortunately, those pulsars with high flux are usually young pulsars that frequently have unpredictable glitches, i.e., the spinning frequency of the pulsar abruptly changes (Lyne and Craham-Smith, Reference Lyne and Craham-Smith2012). With the current status of research, these young pulsars might not be suitable for XNAV. On the other hand, millisecond X-ray pulsars with low flux usually have spinning period stability comparable to an atomic clock and the presence of glitches are seldom detected (Lyne and Craham-Smith, Reference Lyne and Craham-Smith2012). As shown in Section 5, in an assumed situation where a typical high-orbit vehicle is observing a millisecond X-ray pulsar (such as PSR B1821-24) the threshold is about 100 s. If the divided interval is chosen to be 100 s, the phase approximated error arising from approximating the varying frequency to be a constant is above the corresponding the CRB, and cannot be neglected. The approximated error could introduce an uncompensated bias into the calculation of DPLL or of the Kalman filter and finally worsen the performance of the tracking algorithm.
In this paper, we propose a vehicle-orbital-dynamics-aided pulse-phase estimation of X-ray pulsar for XNAV. We first modify the continuous-time X-ray pulsar signal model to be a term of vehicle state varying with time and redefine the expression of pulse time of arrival, taking the vehicle motion law into account. Given the vehicle state at later epochs can be predicted by propagating the initial one, we extend the aforementioned signal model around the predicted state to the second order, analysing the impact of the corresponding truncation error. A maximum likelihood estimator is adopted to estimate the initial phase as well as the coefficients of the extended model. Some simulations are performed to verify the method and show the method has robustness to the initial error within the initial state of the vehicle and is capable of handling the phase-estimation problem for pulsars with low fluxes.
The paper is organised as follows. Section 2 reviews the conventional X-ray pulsar signal model as well as the expression of pulse TOA. In Section 3, we derive the X-ray pulsar signal model with consideration of vehicle motion laws and modify the expression of pulse TOA. In Section 4, the extended signal model is derived and a MLE is employed to estimate the initial phase. Some simulations are performed in Section 5.
2. REVIEW OF X-RAY PULSAR SIGNAL MODEL
The photon TOAs detected by a vehicle are modelled as a Non-Homogeneous Poisson Process (NHPP) with a periodic rate function λ(t) ≥ 0. And then, the probability of k photons arriving between the observation period 
$\left( {\matrix{ {t_0} \quad{t_f} \cr}} \right)$ is (Emadzadeh and Speyer, Reference Emadzadeh and Speyer2010)
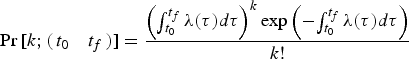$$\Pr \left[ {k;\left( {\matrix{ {t_0} & {t_f} \cr}} \right)} \right] = \displaystyle{{\left( {\int_{t_0} ^{t_f} {\lambda (\tau )d\tau}} \right)^k \exp \left( -{\int_{t_0} ^{t_f} {\lambda (\tau )d\tau}} \right)} \over {k!}}$$The rate function λ(t) denotes the aggregate rate of photons from pulsar and background, and can be expressed as
$$\lambda (t) = \alpha h\left( {\phi _{\det} \left( t \right)} \right) + \beta $$
where 
$h\left( \bullet \right)$ is the periodic pulsar profile, 
$\phi _{\det} \left( t \right)$ is the detected phase, and α and β are detected rate constants of the form
$$\alpha = F_p \eta A$$
$$\beta = F_p \eta A$$where F p and F b are the fluxes of X-ray source and background respectively, η is the efficiency of detector, and A is the area of detector.
For a vehicle, 
$\phi _{\det} \left( t \right)$ can be described by
$$\phi _{\det} \left( t \right) = \phi _0 + f_s (t - t_0 ) + \displaystyle{{\,f_s} \over c}\int_{t_0} ^t {v\left( \tau \right)d\tau} $$where ϕ 0 is the initial phase at epoch t 0, f s is the frequency of pulsar, c is the speed of light, and v is the projected velocity of vehicle on the direction of pulsar.
Assuming the vehicle is performing a uniform linear motion towards a pulsar, Equation (5) is simplified as
$$\phi _{\det} \left( t \right) = \phi _0 + \left( {1 + \displaystyle{v \over c}} \right)f_s \left( {t - t_0} \right)$$Based on Equations (2) and (6), ϕ 0 and f o = (1 + v/c)f s can be estimated via a MLE.
When ϕ 0 and f o are obtained, the pulse TOA at epoch t 0 can be represented as
$$T_0 = \displaystyle{{\phi _0} \over {\,f_o}} $$3. MODIFIED X-RAY X-RAY PULSAR SIGNAL MODEL
3.1. Modified phase propagation model
3.1.1. General form
In the Sun-centred inertial coordinate system, the configuration of vehicle and pulsar is shown in Figure 1. For the sake of simplicity, only the geometry effect is taken into account. However, the derivation can be easily extended to a case where the general relativity effect is also taken into account.
Figure 1. Configuration of vehicle and pulsar.
When the pulsar is far from the Sun, the distance between the vehicle and pulsar can be described by
$$d = \vert {\bi r} - {\bi D} \vert \approx {\bi n} \bullet \left( {{\bi r} - {\bi D}} \right)$$where r is the position of the vehicle relative to the Sun, D is the position of the pulsar relative to the Sun, and n is the direction vector of pulsar.
It follows from Equation (8) that the projected velocity of the vehicle along the direction of the pulsar is
$$v = {\bi n} \bullet \left( {{\dot {\bi r}} - {\dot{\bi D}}} \right)$$Substituting Equation (9) into Equation (5) we have
$$\phi _{\det} (t) = \phi _0 + f_s (t - t_0 ) + \displaystyle{{\,f_s} \over c}\int_{t_0} ^t {{\bi n} \bullet \left( {{\dot {\bi r}}(\tau ) - {\dot {\bi D}}(\tau )} \right)d\tau} $$which can be rewritten as
$$\phi _{\det} (t) = \phi _0 + f_s (t - t_0 ) + \displaystyle{{\,f_s} \over c}\int_{t_0} ^t {{\bi n} \bullet {\dot {\bi r}}(\tau )d\tau - \displaystyle{{\,f_s} \over c}\int^t_{t_0}{\bi n} \bullet {\dot{\bi D}}(\tau )d\tau} $$The solution of Equation (11) is
$$\phi _{\det} (t) = \phi _0 + f_s (t - t_0 ) + \displaystyle{{\,f_s} \over c}{\bi n} \bullet \left( {{\bi r}(t) - {\bi r}\left( {t_0} \right)} \right) - \displaystyle{{\,f_s} \over c}{\bi n} \bullet \left( {{\bi D}(t) - {\bi D}(t_0 )} \right)$$Assuming the pulsar is performing a uniform proper motion, the change of position of the position of pulsar can be represented as
$${\bi D}(t) - {\bi D}(t_0 ) \approx {\bi V}_p (t - t_0 )$$where Vp is the velocity of proper motion that has been calculated by astronomers (Lyne and Craham-Smith, Reference Lyne and Craham-Smith2012).
Substituting Equation (13) into Equation (12) we have
$$\phi _{\det} (t) = \phi _0 + f_s (t - t_0 ) + \displaystyle{{\,f_s} \over c}{\bi n} \bullet \left( {{\bi r}(t) - {\bi r}\left( {t_0} \right)} \right) + G_0 \left( {t,t_0} \right)$$ where 
$G_0 (t,t_0 ) = - (f_s /c){\bi n} \bullet {\bi V}_p \left( {t - t_0} \right)$ and can also be calculated in advance.
Equation (14) is the general form of the modified phase propagation model. Compared with Equation (6), Equation (14) puts little assumption on the motion of the vehicle and is more practical.
3.1.2. Modified phase propagation model for a high Earth orbit vehicle
For Earth-orbiting vehicles, r can be expressed as
$${\bi r} = {\bi r}_E + {\bi r}_{SC/E} $$where rE is the position of Earth relative to the Sun and rSC/E is the position of the vehicle relative to Earth.
Then Equation (14) can be rewritten as
$$\phi _{\det} (t) = \phi _0 + f_s (t - t_0 ) + \displaystyle{{\,f_s} \over c}{\bi n} \bullet \left( {{\bi r}_{SC/E} (t) - {\bi r}_{SC/E} \left( {t_0} \right)} \right) + \displaystyle{{\,f_s} \over c}{\bi n} \bullet \left( {{\bi r}_E (t) - {\bi r}_E \left( {t_0} \right)} \right) + G_0 \left( {t,t_0} \right)$$The position of Earth can be predicted by the planetary ephemeris such as DE405 or DE421.
We can rewrite Equation (16) as
$$\phi _{\det} (t) = \phi _0 + f_s (t - t_0 ) + \displaystyle{{\,f_s} \over c}{\bi n} \bullet \left( {{\bi r}_{SC/E} (t) - {\bi r}_{SC/E} \left( {t_0} \right)} \right) + C_0 (t,t_0 )$$
where 
$C_0 (t,t_0 ) = \left( {f_s /c} \right){\bi n} \bullet \left( {{\bi r}_E (t) - {\bi r}_E \left( {t_0} \right)} \right) + G_0 (t,t_0 )$ can be calculated in advance.
3.2. Modified definition of pulse TOA at t0
As shown in Equation (14) and (17), the frequency of the received signal is time-varying, and the pulse TOA at epoch t 0 should be
$$T_0 = \displaystyle{{\phi _0} \over {\,f_{t_0}}} $$
where 
$f_{t_0} $ is defined as the instant frequency of signal at epoch t 0 and can be calculated by
$$f_{t_0} = \left. {\displaystyle{{d\phi _{\det} \left( t \right)} \over {dt}}} \right \vert _{t = t_0} $$Substituting Equation (17) into Equation (19) yields the instant frequency for high Earth orbit vehicle in the form
$$f_{t_0} = \left[ {1 + \displaystyle{1 \over c}{\bi n} \bullet \left( {{\bi v}_{SC/E} \left( {t_0} \right) + {\bi v}_E \left( {t_0} \right) - {\bi V}_p} \right)} \right]f_s $$And then, the pulse TOA at t 0 is
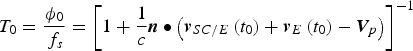$$T_0 = \displaystyle{{\phi _0} \over {\,f_s}} = \left[ {1 + \displaystyle{1 \over c}{\bi n} \bullet \left( {{\bi v}_{SC/E} \left( {t_0} \right) + {\bi v}_E \left( {t_0} \right) - {\bi V}_p} \right)} \right]^{ - 1} $$4. EXTENDED SIGNAL MODEL AND ESTIMATION METHOD
ϕ 0 in Equation (17) can be accurately estimated by employing MLE if the true position of vehicle at an arbitrary epoch has been perfectly given.
Even if the true position of the vehicle cannot be accurately obtained, we can still predict a rough position of the vehicle at latter epoch by propagating the initial vehicle state contaminated with initial error.
4.1. Extended signal model
At an arbitrary epoch t, the true position of the vehicle can be expressed as the term of predicted position and propagation error, with the expression of
$${\bi r}_{SC/E} (t) = {\tilde {\bi r}}_{SC/E} (t) + \delta {\bi r}_{SC/E} (t)$$
$${\bi r}_{SC/E} (t_0 ) = {\tilde {\bi r}}_{SC/E} (t_0 ) + \delta {\bi r}_{SC/E} (t_0 )$$
where 
${\tilde {\bi r}}_{SC/E} \left( \bullet \right)$ denotes the predicted position and 
$\delta {\bi r}_{SC/E} \left( \bullet \right)$ is the corresponding propagation error.
Substituting Equations (22) and (23) into Equation (17) yields
$$\phi _{\det} (t) = \phi _0 + f_s (t - t_0 ) + \displaystyle{{\,f_s} \over c}{\bi n} \bullet \left( {{\tilde {\bi r}}_{SC/E} (t) - {\tilde {\bi r}}_{SC/E} \left( {t_0} \right)} \right) + \displaystyle{{\,f_s} \over c}{\bi n} \bullet \left( {\delta {\bi r}_{SC/E} (t) - \delta {\bi r}_{SC/E} \left( {t_0} \right)} \right) + C_0 (t,t_0 )$$Using the orbital transition matrix, δ rSC/E (t) can be expressed as a term of δ rSC/E (t 0) and δ vSC/E (t 0), i.e., (Liu, Reference Liu1992)
$$\delta {\bi r}_{SC/E} \left( t \right) = {\bi \Phi} _{rr} (t,t_0 )\delta {\bi r}_{SC/E} \left( {t_0} \right) + {\bi \Phi} _{rv} (t,t_0 )\delta {\bi v}_{SC/E} \left( {t_0} \right)$$where Φrr (t, t 0) and Φrv (t, t 0) are the partition matrices of orbital transition matrix.
It follows from Equation (25) that Equation (24) can be rewritten as
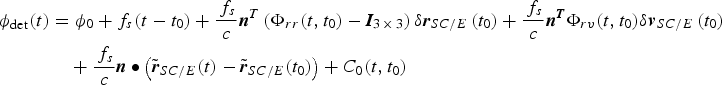$$\eqalign{ \phi _{\det} (t) &= \phi _0 + f_s (t - t_0 ) + \displaystyle{{\,f_s} \over c}{\bi n}^T \left( {{\bi \Phi} _{rr} (t\comma t_0 ) - {\bi I}_{3\, \times\, 3}} \right)\delta {\bi r}_{SC/E} \left( {t_0} \right) + \displaystyle{{\,f_s} \over c}{\bi n}^{\bi T} {\bi \Phi} _{rv} (t\comma t_0 )\delta {\bi v}_{SC/E} \left( {t_0} \right) \cr & \quad + \displaystyle{{\,f_s} \over c}{\bi n} \bullet \left( {{\tilde {\bi r}}_{SC/E} (t) - {\tilde {\bi r}}_{SC/E} (t_0 )} \right) + C_0 (t,t_0 )} $$Substituting Equations (A9) and (A10) into Equation (26) yields
$$\eqalign{ \phi _{\det} (t) &= \phi _0 + f_s (t - t_0 ) + \displaystyle{{\,f_s} \over c}\sum\limits_{k = 1}^\infty {\displaystyle{{\left( {t - t_0} \right)^k} \over {k!}}} \left[ {{\bi n}^T {\bi A}_k \delta {\bi r}_{SC/E} \left( {t_0} \right) + {\bi n}^T {\bi B}_k \delta {\bi v}_{SC/E} \left( {t_0} \right)} \right] \cr & \quad + \displaystyle{{\,f_s} \over c}{\bi n} \bullet \left( {{\tilde {\bi r}}_{SC/E} (t) - {\tilde {\bi r}}_{SC/E} (t_0 )} \right) + C_0 (t,t_0 )} $$ Denoting 
$f_{dy}^{(k)} = \displaystyle{1 \over {\left( k \right)!}}\displaystyle{{f_s} \over c}\left[ {{\bi n}^T {\bi A}_k \delta {\bi r}_{SC/E} \left( {t_0} \right) + {\bi n}^T {\bi B}_k \delta {\bi v}_{SC/E} \left( {t_0} \right)} \right]$, Equation (27) can be rewritten as
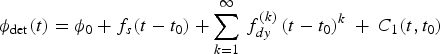$$\phi _{\det} (t) = \phi _0 + f_s (t - t_0 ) + \sum\limits_{k = 1}^\infty {\,f_{dy}^{(k)} \left( {t - t_0} \right)^k \ + \ C_1 (t,t_0 )} $$Where
$$C_1 (t,t_0 ) = \displaystyle{{\,f_s} \over c}{\bi n} \bullet \left( {{\tilde {\bi r}}_{SC/E} (t) - {\tilde {\bi r}}_{SC/E} (t_0 )} \right) + C_0 (t,t_0 )$$ Emadzadeh and Speyer (Reference Emadzadeh and Speyer2011) derived the log-likelihood function for X-ray pulsar signal to the case of constant frequency. Assuming M photons have been recorded in the observation period of 
$\left(\! {\matrix{ {t_0} \quad {t_f} \cr}} \!\right)$ and substituting Equation (30) into the derived log-likelihood function in (Emadzadeh and Speyer, Reference Emadzadeh and Speyer2011), we have
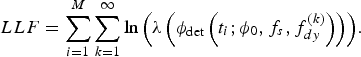$$LLF = \sum\limits_{i = 1}^M {\sum\limits_{k = 1}^\infty {\ln \left( {\lambda \left( {\phi _{\det} \left( {t_i ;\phi _0, f_s, f_{dy}^{(k)}} \right)} \right)} \right)}}. $$Based on Equation (30), ϕ 0 can be estimated by solving a high-dimension optimisation problem, the computation complexity of which heavily relies on the maximum of k, K.
We next analyse the method of setting K, simplifying Equation (30).
4.2. Estimation of initial phase
4.2.1. Method of fixing K
An appropriate K should be capable of minimising the impact of truncation error arising from the Taylor extension and of balancing the computation complexity of Equation (30).
Given that the solution of Equation (A5) can be taken as an accurate solution of the transition matrix, we define the following performance index to assess the truncation error
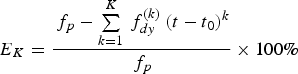$$E_K = \displaystyle{{\,f_p - \sum\limits_{k = 1}^K {\,f_{dy}^{(k)} \left( {t - t_0} \right)^k}} \over {\,f_p}} \times 100\% $$Where
$$f_p = \displaystyle{{\,f_s} \over c}\left[ {{\bi n}^T \left( {{\bar {\bi \Phi}} _{rr} (t,t_0 ) - {\bi I}_{3\, \times \,3}} \right)\delta {\bi r}_{SC/E} \left( {t_0} \right) + {\bi n}^{\bi T} {\bar {\bi \Phi}} _{rv} (t,t_0 )\delta {\bi v}_{SC/E} \left( {t_0} \right)} \right]$$ and 
${\bar {\bi \Phi}} _{rr} (t,t_0 )$ and 
${\bar {\bi \Phi}} _{rv} (t,t_0 )$ are the accurate solutions of 
${\bar {\bi \Phi}} _{rr} (t,t_0 )$ and 
${\bar {\bi \Phi}} _{rv} (t,t_0 )$.
For calculation precision, those parameters involved in the computation of Equation (31) should be normalised in advance.
4.2.2. K for high Earth orbital vehicle
Given it is difficult to understand the index in Equation (31) in an analytical way, we investigate it via simulations. We assume this scenario: a vehicle orbiting on an Earth-centred orbit observes a pulsar for 3000 s, under the assumption that there are no shadows produced by celestial bodies.
By employing the rotation-powered X-ray pulsars selected by Microcosm Inc., we change the orbital plane of the vehicle to test how the index varies. The positions of adopted pulsars are listed in Table 1, and initial orbital elements of the vehicle are listed in Table 2. In Table 2, we list the variation ranges of semi-major axis, inclination, and right ascension of the ascending node. The initial position and velocity errors along each inertial coordinate axis are chosen to be 100 m and 0·1 m/s respectively. The non-spherical perturbation and three-body perturbation are taken into account, when the orbital propagation of the vehicle is performed.
Table 1. Positions of rotation-powered X-ray pulsars. (Graven et al., Reference Graven, Collins, Sheikh, Hanson, Ray and Wood2008).
Table 2. Initial orbital elements of simulated vehicle.
For cases of K = 1 and K = 2, Figures 2 and 3 show varying indices with different semi-major axes. Data in Figures 2 and 3 represent the max performance indices out of different couples of inclination and right ascension of the ascending node. As shown in Figures 2 and 3, for the six selected pulsars, the performance index reduces as the semi-major axis increases, and could reach a value of around 1%, if K = 2 and semi-major axis is greater than 40000 km. Thus, for the balance of calculation precision and computation, K = 2 is a better option.
Figure 2. In the case of K = 1, indices varying with an increasing semi-major axis.
Figure 3. In the case of K = 2, indices varying with an increasing semi-major axis.
Denoting 
$f_{sdy} = f_s + f_{dy}^{(1)} $, Equations (28) and (30) become
$$\phi _{\det} (t) = \phi _0 + f_{sdy} \left( {t - t_0} \right) + f_{dy}^{(2)} \left( {t - t_0} \right)^2 + C_1 \left( {t,t_0} \right)$$And
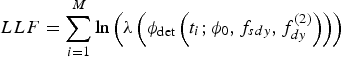$$LLF = \sum\limits_{i = 1}^M {\ln \left( {\lambda \left( {\phi _{\det} \left( {t_i ;\phi _0, f_{sdy}, f_{dy}^{(2)}} \right)} \right)} \right)} $$The solution of Equation (34) involves solving a 3-dimension optimisation problem that can be effectively performed by global optimisation algorithms (Kolda et al., Reference Kolda, Lewis and Torczon2003).
4.3. Estimation of pulse TOA
Substituting Equation (32) into Equation (19) yields 
$f_{t_0} $ in the form of
$$f_{t_0} = f_{sdy} + \displaystyle{{\,f_s} \over c}{\bi n} \bullet \left( {{\tilde {\bi v}}_E \left( {t_0} \right) + {\tilde {\bi v}}_{SC/E} \left( {t_0} \right) - {\bi V}_p} \right)$$Based on Equation (35), the pulse TOA is
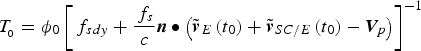$$T_{_0} = \phi _0 \left[ {\,f_{sdy} + \displaystyle{{\,f_s} \over c}{\bi n} \bullet \left( {{\tilde {\bi v}}_E \left( {t_0} \right) + {\tilde {\bi v}}_{SC/E} \left( {t_0} \right) - {\bi V}_p} \right)} \right]^{ - 1} $$5. SIMULATIONS
Millisecond X-ray pulsar PSR B1821-24 is selected as the observed pulsar with the profile shown in Figure 4 (Rutledge et al., Reference Rutledge, Fox, Kullkarni, Jacoby, Cognard, Backer and Murray2004). For simplicity, the pulsar is assumed to be stationary during the observation period. The parameters of the simulated pulsar are listed in Table 3. The position of the simulated pulsar is taken from Ren (Reference Ren2012).
Figure 4. PSR B1821-24 profile.
Table 3. Parameters of Simulated PSR B1821-24.
1. MJD is abbreviation for Modified Julian Day
2. 1 kpc = 1 × 1019m
In Table 3, the position of the pulsar is described in the J2000·0 Sun-centred Inertial Coordinate System, and the term “Distance” is used to describe the distance between the Sun and the pulsar. The Jet Propulsion Laboratory (JPL) ephemeris DE405 is employed to predict the position and velocity of Earth at the given MJD.
In the Earth-centred inertial coordinate system, the initial orbital elements of the investigated vehicle are listed in Table 4. The initial position and velocity error along each coordinate axis are chosen to be 100 m and 0·1 m/s respectively. When the orbital dynamic propagation is performed, the non-spherical perturbation and two-body perturbation are taken into account.
Table 4. Initial Orbital Elements of High-orbit Satellite.
5.1 Analysis of the proposed method
We use the Root Mean Square error (RMS error) to assess the performance of the proposed method. All the results in the remaining paper are obtained after 1000 Monte Carlo estimations. We assume the integer part of phase has been well determined, and focus on estimation performance of the fractional part of phase.
Figure 5 shows the RMS error of the estimated initial phase with an increasing observation period. The RMS error first experiences an unreliable region, becomes consistent with the CRB when the observation period is greater than 100 s, and finally reaches an accuracy of around 0·001 when the observation period is 3000 s.
Figure 5. RMS error of estimated initial phase with different observation periods.
Figure 6 shows the RMS error of pulse TOA versus an increasing observation period. Being similar to the result of the initial phase, the result of pulse TOA also converges to the corresponding CRB when the observation period is greater than 100 s. The performance of the proposed method improves as the observation period increases.
Figure 6. RMS error of pulse TOA with different observation periods.
Figure 7 shows the computational cost of the proposed method. The computational cost is assessed via the CPU time cost by the proposed method. The simulation environment contains Intel I7-4710MQ@2.5 GHz and Visual studio 6·0. The CPU time increases as the observation period increases. This is because the computational complexity of MLE heavily depends on the number of X-ray photons. It is worth noting that the parallel computation technique is adopted to reduce the computation complexity.
Figure 7. CPU time cost by proposed method with different observation periods.
Next, we analyse the factors that might affect the proposed method. The observation periods in the following investigations are all set to be 1000 s.
Figures 8 and 9 display the RMS error of the initial phase in the presence of different initial position and vehicle velocity errors. Although the performance of the proposed method would degrade if the initial position and velocity error increased, the corresponding RMS error arising from the increasing initial state error is less than 1 × 10−4 cycles, even initial position and velocity errors grow to 1000 m and 5 m/s respectively. It means the proposed method is not overly sensitive to the initial state error of the vehicle.
Figure 8. RMS error of initial phase with different initial position errors.
Figure 9. RMS error of initial phase with different initial velocity errors.
Figure 10 shows the RMS error initial phase versus semi-major axis. The RMS error decreases as the semi-major axis of the vehicle increases, and the decrease would slow down when the semi-major axis is greater than 34000 km. This means the performance of the proposed method would be little affected by the semi-major axis of a vehicle that is greater than 34000 km.
Figure 10. RMS error of estimated initial phase with different semi-major axis.
5.2. Analysis on the phase tracking algorithm
Besides the design of DPLL for tracking the time-varying frequency, the performance of the phase tracking algorithm depends on the result of MLE at each divided interval. Figure 11 shows the result of MLE under the assumption that the simulated pulsar signal has a constant frequency. The result of MLE first experiences an unreliable region lasting for 100 s and becomes consistent with CRB after then. This means the divided interval for MLE should be at least 100 s, if a reliable MLE result is needed.
Figure 11. Result of MLE versus divided interval.
Figure 12 depicts the phase-approximated errors arising from a constant frequency assumption when the divided interval lasts for 100 s. For reference, the corresponding CRB is 1·359 × 10−3. Thus, the phase approximation error is greater than CRB and cannot be ignored, making the solution of MLE biased. Given that the result of MLE is the input of DPLL which lacks the capability to handle the impact of input bias, the final performance of DPLL would worsen.
Figure 12. Approximation error versus time.
6. CONCLUSION
This paper introduces a pulse-phase estimation method for X-ray pulsar adopted in XNAV. A practical X-ray pulsar signal model, which puts little assumption on the motion of the vehicle, is derived and is simplified with the aid of vehicle orbital dynamics. The method is capable of handling the impact of continuous-time frequency without assuming the frequency is piece-wise constant.
ACKNOWLEDGEMENT
The first author is sponsored by the Chinese Scholarship Council.
APPENDIX
A1. FUNDAMENTALS OF TRANSITION MATRIX IN VEHICLE ORBITAL DYNAMICS
In a central-body-centred inertial coordinate system, such as the Earth-centred inertial coordinate system and Sun-centred inertial coordinate system, the orbital dynamics model of the vehicle is
$$\left[ {\matrix{ {\dot {\bi r}} \cr {{\dot {\bi v}}} \cr}} \right] = {\bi f}({\bi r},{\bi v},{\bi a}),$$where r, v, a are the position, velocity and acceleration of the vehicle.
Linearizing the above nonlinear system around the predicted position and velocity, 
${\tilde {\bi r}}$ and 
${\tilde {\bi v}}$, yields
$$\left[ {\matrix{ {\delta {\dot {\bi r}}} \cr {\delta {\dot {\bi v}}} \cr}} \right] = {\bi F}\left[ {\matrix{ {\delta {\bi r}} \cr {\delta {\bi v}} \cr}} \right],$$
where 
$\delta {\bi r}( \bullet )$ and 
$\delta {\bi v}( \bullet )$ denote the error within the predicted position and velocity and F is the Jacobian matrix.
We have a corresponding discrete linearization system,
$$\left[ {\matrix{ {\delta {\bi r}(t)} \cr {\delta {\bi v}(t)} \cr}} \right] = {\bi \Phi} (t,t_0 )\left[ {\matrix{ {\delta {\bi r}(t_0 )} \cr {\delta {\bi v}(t_0 )} \cr}} \right],$$where Φ(t, t 0) is the transition matrix that can be expressed as a form of partition matrix,
$${\bi \Phi} (t,t_0 ) = \left[ {\matrix{ {{\bi \Phi} _{rr} (t,t_0 )} & {{\bi \Phi} _{rv} (t,t_0 )} \cr {{\bi \Phi} _{vr} (t,t_0 )} & {{\bi \Phi} _{vv} (t,t_0 )} \cr}} \right],$$and Φrr(t,t 0), Φrv(t,t 0), Φvr(t,t 0) and Φvv(t,t 0) are all 3 × 3 matrices.
An accurate solution of Φ(t, t 0) can be obtained by solving the following differential equation (Liu, Reference Liu1992)
$${\dot {\bi \Phi}} (t,t_0 ) = {\bi F\Phi} (t,t_0 )$$with an initial condition of
$${\bi \Phi} (t_0, t_0 ) = {\bi I}_{6 \,\times\, 6}, $$where I6×6 is a 6 × 6 united matrix.
Another way to obtain Φ(t, t 0) is to employ Taylor extensions, i.e.,
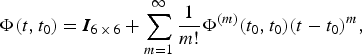$${\bi \Phi} (t,t_0 ) = {\bi I}_{6 \,\times\, 6} + \sum\limits_{m = 1}^\infty {\displaystyle{1 \over {m!}}{\bi \Phi} ^{(m)} (t_0, t_0 )} (t - t_0 )^m, $$in which Φ(m) (t 0, t 0) is the mth derivative of Φ(t 0, t 0).
Although the detailed expressions of Equation (A7) are complicated, they can be summarised as a general form of
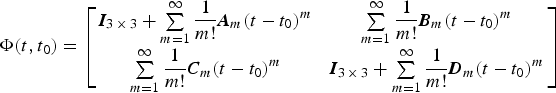$${\bi \Phi} (t,t_0 ) = \left[ {\matrix{ {{\bi I}_{3 \,\times\, 3} + \sum\limits_{m = 1}^\infty {\displaystyle{1 \over {m!}}{\bi A}_m (t - t_0 )^m}} & {\sum\limits_{m = 1}^\infty {\displaystyle{1 \over {m!}}{\bi B}_m (t - t_0 )^m}} \cr {\sum\limits_{m = 1}^\infty {\displaystyle{1 \over {m!}}{\bi C}_m (t - t_0 )^m}} & {{\bi I}_{3 \,\times\, 3} + \sum\limits_{m = 1}^\infty {\displaystyle{1 \over {m!}}{\bi D}_m (t - t_0 )^m}} \cr}} \right]$$in which Am, Bm, Cm, and Dm are 3 × 3 constant matrices and are the mth coefficient matrix of partition matrix in Φ(t, t 0).
Thus, we have
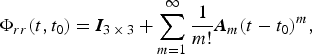$${\bi \Phi} _{rr} (t,t_0 ) = {\bi I}_{3 \,\times\, 3} + \sum\limits_{m = 1}^\infty {\displaystyle{1 \over {m!}}{\bi A}_m (t - t_0 )^m,} $$
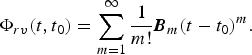$${\bi \Phi} _{rv} (t,t_0 ) = \sum\limits_{m = 1}^\infty {\displaystyle{1 \over {m!}}{\bi B}_m (t - t_0 )^m.} $$A2. CRB OF THE PROPOSED METHOD
From Equation (33), we consider the following pulsar rate function,
$$\lambda (t) = \alpha h\left( {\phi _0 + f_{sdy} \left( {t - t_0} \right) + f_{dy}^{(2)} \left( {t - t_0} \right)^2 + C_1 \left( {t,t_0} \right)} \right) + \beta. $$ The CRB for the estimation of unknown parameters, ϕ 0, f sdy, 
$f_{dy}^{(2)} $, is presented in the following lemma.
Lemma 1. Let
$${\bi \theta} \triangleq \left[ {\matrix{ {\phi _0} & {\,f_{sdy}} & {\,f_{dy}^{(2)}} \cr}} \right]^T $$be the unknown parameter vector. The CRB for estimation of θ in Equation (A12) is given by
$$CRB({\bi \theta} ) = {\bi IM}^{ - 1/2} ({\bi \theta} )$$Where
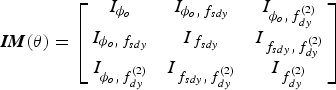$${\bi IM}({\bi \theta} ) = \left[ {\matrix{ {I_{\phi _o}} & {I_{\phi _o\comma\, f_{sdy}}} & {I_{\phi _o\comma\, f_{dy}^{(2)}}} \cr {I_{\phi _o\comma\, f_{sdy}}} & {I_{\,f_{sdy}}} & {I_{\,f_{sdy}\comma\, f_{dy}^{(2)}}} \cr {I_{\phi _o\comma\, f_{dy}^{(2)}}} & {I_{\,f_{sdy}\comma\, f_{dy}^{(2)}}} & {I_{\,f_{dy}^{(2)}}} \cr}} \right]$$in which
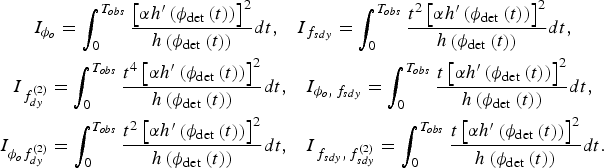$$\displaylines{I_{\phi _o} = \int_0^{T_{obs}} {\displaystyle{{\left[ {\alpha h^{\prime}\left( {\phi _{\det} \left( t \right)} \right)} \right]^2} \over {h\left( {\phi _{\det} \left( t \right)} \right)}}dt,\quad} I_{\,f_{sdy}} = \int_0^{T_{obs}} {\displaystyle{{t^2 \left[ {\alpha h^{\prime}\left( {\phi _{\det} \left( t \right)} \right)} \right]^2} \over {h\left( {\phi _{\det} \left( t \right)} \right)}}dt,} \cr I_{\,f_{dy}^{(2)}} = \int_0^{T_{obs}} {\displaystyle{{t^4 \left[ {\alpha h^{\prime}\left( {\phi _{\det} \left( t \right)} \right)} \right]^2} \over {h\left( {\phi _{\det} \left( t \right)} \right)}}dt,} \quad I_{\phi _o\comma\, f_{sdy}} = \int_0^{T_{obs}} {\displaystyle{{t\left[ {\alpha h^{\prime}\left( {\phi _{\det} \left( t \right)} \right)} \right]^2} \over {h\left( {\phi _{\det} \left( t \right)} \right)}}dt,} \cr I_{\phi _o f_{dy}^{(2)}} = \int_0^{T_{obs}} {\displaystyle{{t^2 \left[ {\alpha h^{\prime}\left( {\phi _{\det} \left( t \right)} \right)} \right]^2} \over {h\left( {\phi _{\det} \left( t \right)} \right)}}dt,} \quad I_{\,f_{sdy}\comma\, f_{sdy}^{(2)}} = \int_0^{T_{obs}} {\displaystyle{{t\left[ {\alpha h^{\prime}\left( {\phi _{\det} \left( t \right)} \right)} \right]^2} \over {h\left( {\phi _{\det} \left( t \right)} \right)}}dt.}} $$Lemma 1 is merely an improvement of Theorem 4·2 in (Emadzadeh and Speyer, Reference Emadzadeh and Speyer2011), so the proof is omitted.
The CRB for pulse TOA can be further derived, if θ in Equation (A13) is redefined as
$${\bi \theta} \triangleq \left[ {\matrix{ {T_0} & {\,f_{sdy}} & {\,f_{dy}^{(2)}} \cr}} \right]^T $$And Equation (A12) is rewritten as
$$\lambda (t) = \alpha h\left( {\,f_{t_0} T_0 + f_{sdy} \left( {t - t_0} \right) + f_{dy}^{(2)} \left( {t - t_0} \right)^2 + C_1 \left( {t,t_0} \right)} \right) + \beta. $$
