No CrossRef data available.
Article contents
A Quantitative Analysis of Avoiding Action
Published online by Cambridge University Press: 18 January 2010
Abstract
There have recently been various investigations of avoiding action when a ship is navigating by radar. The present paper attempts a numerical analysis of the changes in the apparent motion of the echo of the other vessel on the radarscope when both vessels alter course and speed simultaneously.
First we consider the case where the echo of the other vessel is approaching the centre of the radarscope—that is the vessels are on a collision course.
In Fig. I AOB represents a velocity triangle:
OA = own vessel's course and speed
OB = other vessel's course and speed
AB = other vessel's relative course and speed
When both vessels alter course, by Δα1 and Δα2 respectively, the velocity triangle becomes A′OB′ and A′B′ represents the new relative motion of the other vessel. If the triangle A′OB′ is rotated through Δα2 about O, and OB′ coincides with OB, the triangle is represented by BOC and < CDA′ = Δα2. The change θ in the other vessel's relative course caused by both vessels altering course by Δα1 and Δα2 respectively is therefore:

Now φ can be shown to satisfy the equation:
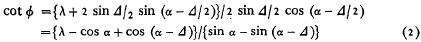
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © The Royal Institute of Navigation 1973

