INTRODUCTION
The poor performance of Global Navigation Satellite Systems (GNSS) positioning in dense urban areas is a well-known problem (Wang et al., Reference Wang, Groves and Ziebart2012). Where there are tall buildings or narrow streets, direct Line-Of-Sight (LOS) signals from many, sometimes most, of the satellites are blocked. Without direct signals from four or more satellites, an accurate position solution cannot be determined. Sometimes, a degraded position solution may be obtained using signal reflection via surrounding buildings or vehicles; these are known as Non-Line-Of-Sight (NLOS) signals (Ercek et al., Reference Ercek, Doncker and Grenez2005; Viandier et al., Reference Viandier, Nahimana, Marais and Duflos2008).
An urban canyon also affects the GNSS signal geometry. As shown in Figure 1, signals with lines of sight going across the street (perpendicular to the street direction) are much more likely to be blocked or reflected by buildings than signals with lines of sight going along the street. Consequently, the signal geometry, and hence the positioning accuracy, is much better along the direction of the street than across the street (Groves, Reference Groves2011). However, positioning accuracy in the cross-street direction is of great importance to many applications. Examples include vehicle lane detection for Intelligent Transportation Systems (ITS), location-based advertising, augmented-reality, and step-by-step guidance for the visually impaired and for tourists. Augmenting GNSS with other sensors can improve the position solution availability and robustness, but does not particularly improve the cross-street accuracy.

Figure 1. Satellite signals with Lines Of Sight (LOS) going across the street are much more likely to be blocked by buildings than signals with LOS going along the street.
3D building models constitute an additional data source that can be used to improve positioning performance in urban canyons. Initially, 3D city models were used to predict GNSS performance in urban areas (Bradbury et al., Reference Bradbury, Ziebart, Cross, Boulton and Read2007; Suh and Shibasaki, Reference Suh and Shibasaki2007; Ji et al., Reference Ji, Chen, Ding, Chhen, Zhao and Hu2010; Kleijer et al., Reference Kleijer, Odijk, Verbree and REHRL2009; Costa, Reference Costa2011). More recently, they have been used to detect and eliminate NLOS GNSS signals, improving the positioning accuracy (Peyret et al., Reference Peyret, Betaille and Mougel2011; Obst et al., Reference Obst, Bauer and Wanielik2012; Peyraud et al., Reference Peyraud, Betaille, Renault, Ortiz, Mougel, Meizel and Peyret2013). By modelling the path delay as a function of user position, NLOS signals can also be used for position determination (Bourdeau and Sahmoudi, Reference Bourdeau and Sahmoudi2012; Suzuki and Kubo, Reference Suzuki and Kubo2013; Betaille et al, Reference Betaille, Peyret, Ortiz, Miquel and Fontenay2013).
Shadow matching is a new positioning technique using GNSS, assisted by knowledge derived from 3D city models, that has the potential to provide metres-level cross-street accuracy in urban canyons (Groves, Reference Groves2011; Tiberius and Verbree, Reference Tiberius and Verbree2004). Due to obstruction by buildings, signal reception from GNSS satellites in urban canyons is highly dependent on the position within a street. The signal availability can be predicted using a 3D city model. Consequently, by determining whether a direct signal is being received from a given satellite, users can localize their position to within one of two areas of the street. Figure 2 illustrates this. With a number of satellites contributing to this process, a position solution can be determined. Unlike conventional GNSS positioning, which uses ranging, shadow matching uses the pattern-matching positioning method (Groves, Reference Groves2013).

Figure 2. The shadow-matching concept: using direct signal reception to localise position (Groves, Reference Groves2011).
A number of shadow-matching implementations have now been developed and tested. A preliminary demonstration showed that the shadow-matching technique can distinguish the pavement from a vehicle lane and identify the correct side of the street using GPS and GLONASS measurements from geodetic receivers (Wang et al., Reference Wang, Groves and Ziebart2011). Next, a full shadow-matching algorithm was developed and was shown to improve the navigation solution of geodetic GPS and GLONASS receivers (Wang et al., Reference Wang, Groves and Ziebart2013a). In these tests, the cross-street positioning error was within 5 m for 89·3% of the time and within 2 m for 63·6% of the time. Other authors have investigated the shadow-matching approach for precise positioning with long observation times (Suzuki and Kubo, Reference Suzuki and Kubo2012) and for road lane identification using telephone pole shadowing (Yozevitch et al., Reference Yozevitch, Ben-moshe and Dvir2014).
Most potential applications of shadow matching use consumer-grade GNSS user equipment, not geodetic receivers. Consumer-grade GNSS antennas have lower gain and less polarization discrimination. This makes it more difficult to distinguish the right-hand circularly polarized (RHCP) direct-LOS signals from the generally left-hand circularly polarized (LHCP) NLOS signals using the Signal to Noise Ratio (SNR). Due to space and cost constraints, smartphone antennas have the lowest gain of all and are linearly polarized, so do not distinguish between LHCP and RHCP signals. The gain also varies according to the relationship between the direction of the LOS and the orientation of the phone. Smartphone receivers are also typically more sensitive than geodetic receivers, so they will track weaker signals, most of which will be NLOS. These characteristics can potentially degrade shadow-matching performance. Therefore, a practical assessment of shadow-matching performance and the identification of the technique's main limitations requires testing on a smartphone platform.
Preliminary shadow-matching results using GPS and GLONASS measurements recorded on a smartphone were presented in Wang et al. (Reference Wang, Groves and Ziebart2013b), while Wang et al. (Reference Wang, Groves and Ziebart2013c) describes a real-time demonstration of shadow matching on an Android smartphone, which can compute a position solution within two seconds. Figure 3 presents a screenshot from the shadow-matching demonstration ‘App’. This paper presents a full performance characterisation of GNSS shadow matching on a smartphone and then discusses the steps needed to take shadow matching from a research demonstrator to a large-scale practical implementation.

Figure 3. Screenshot of the shadow-matching demonstration ‘App’. The blue dots show the conventional solution and the red dots show the shadow-matching solution, which is on the correct side of the street.
Section 2 describes the main features of the shadow-matching algorithms. Section 3 then describes the 3D city model used for this research and the experimental data collection using an Android Smartphone in central London. Section 4 compares the characteristics of the received LOS and NLOS GNSS signals, using a 3D city model and the true positions to determine which signals are which. This signal characterisation is then used to optimize the tuning of the shadow-matching algorithms, as described in Section 5. A performance assessment of the improved shadow-matching algorithm using the smartphone data is presented in Section 6, where it is compared with the smartphone's conventional GNSS navigation solution. The performance of a four-constellation shadow-matching system is then predicted by combining GPS and GLONASS data collected at different times at the same locations. Section 7 then discusses the feasibility of a large-scale implementation of shadow matching, focussing on the data requirements. Finally, Section 8 summarises the conclusions and discusses further work.
2. THE SHADOW-MATCHING ALGORITHM
There are several different ways of implementing shadow matching. The algorithm used here has two phases, an offline phase and an online phase, both of which are shown in Figure 4. The offline phase determines building boundary data from the 3D model and stores it. The online phase then determines the position solution in four steps from the building boundaries and GNSS measurements.

Figure 4. Workflow of the shadow-matching algorithm.
The building boundaries show where the building edges are located from a GNSS user's perspective within an azimuth-elevation sky plot. Satellites are visible above this edge and blocked below it. Figure 5 shows an example. The elevation of the building boundary is computed at a range of azimuths as described in Wang et al. (Reference Wang, Groves and Ziebart2013a) and Wang et al. (Reference Wang, Groves and Ziebart2012). Building boundaries are computed over a grid of candidate user locations. The altitude of these candidate user locations can be set at a certain distance above the ground, e.g. 1·5 m might be assumed for users holding smartphones in front of them. Only outdoor locations are considered. By determining the building boundaries in advance like this, the positioning algorithm is able to run in real time on a smartphone processor.

Figure 5. An example of a building boundary as azimuth-elevation pairs in a sky plot. (The centre of the plot corresponds to a 90° elevation or normal incidence)
The online phase of shadow matching comprises four steps. It begins by defining a search grid, based on an initial approximate position from conventional GNSS or another method, such as Wi-Fi, Bluetooth Low Energy or phone signal positioning. If conventional GNSS is used, it is important to minimize the impact of NLOS reception and multipath interference (Groves and Jiang, Reference Groves and Jiang2013). In the current implementation, the search area is simply a fixed-radius circle centred at the initial position solution. However, more advanced algorithms could use knowledge of the signal geometry to optimise the search area. For example, a conventional GNSS position solution in a dense urban area is normally more accurate along the direction of the street than across the street.
In the second step of shadow matching, performed at each candidate position within the search grid, each satellite's elevation is compared with the building boundary elevation at the same azimuth. The satellite is predicted to be visible if its line of sight is above the building boundary.
The third step compares the predicted and observed satellite visibility. Candidate positions are scored in two stages. Firstly, each satellite above the receiver's elevation mask angle is given a score based on the predicted and observed visibility. Secondly, the overall score for each candidate position is determined by summing the individual satellite scores.
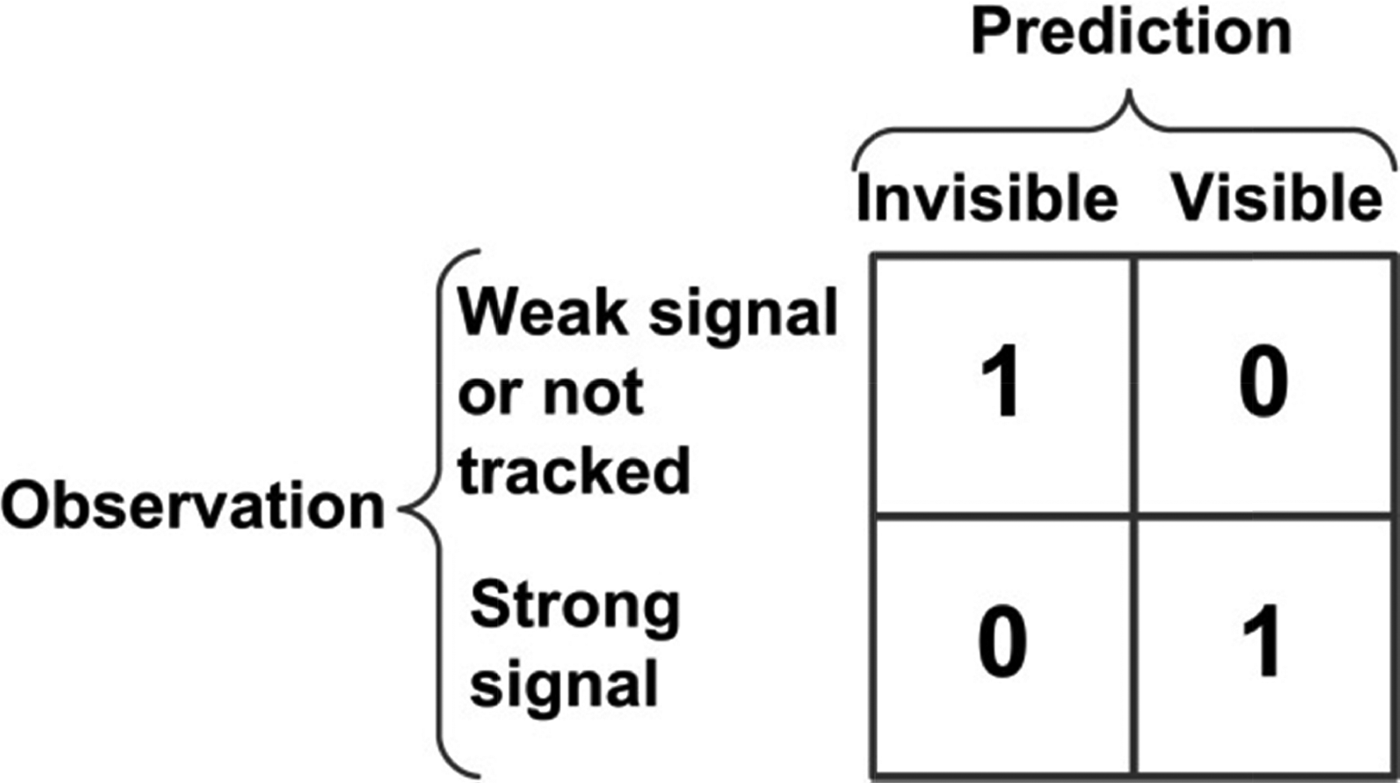
Different scoring schemes can be applied at this stage. Figure 6 shows the basic 2 by 2 scoring scheme used for the preliminary smartphone tests presented in Wang et al. (Reference Wang, Groves and Ziebart2013b). A fixed SNR threshold was used to distinguish between weak and strong signals. The determination of an optimal scoring scheme for smartphone receivers is described in Section 5.

Figure 6. Basic 2 by 2 scoring scheme applied to each satellite.
The fourth and final step of the shadow-matching algorithm is to generate a position solution using the scores of each candidate position. Like Wi-Fi fingerprinting and terrain-referenced navigation, shadow matching uses the pattern-matching positioning method (Groves, Reference Groves2013). There are many different ways of estimating a position solution from the position likelihood grid output by a pattern-matching algorithm. The current shadow-matching positioning algorithm simply averages the grid positions with the highest scores. The development of a more sophisticated position estimation algorithm is planned for future work.
A full implementation would also incorporate context detection to determine whether the user is in an indoor, urban or open environment (Groves et al., Reference Groves, Martin, Voutsis, Walter and Wang2013). The shadow-matching algorithm would then only be called in urban contexts.
3. EXPERIMENTAL DATA COLLECTION
Experimental data was collected in the Aldgate area of central London using Samsung Galaxy S3 Smartphones running a bespoke Android data logging application. The SNR measurements, satellite azimuths and elevations, and the conventional GNSS position solution are all included in the National Marine Electronics Association (NMEA) message from the phone's GNSS chip. A 3D city model of the area from ZMapping Ltd was used to generate the building boundary data used for the subsequent analysis.
The term ‘Level of Detail’ (LoD) is often used in 3D modelling to describe the level of complexity a 3D object representation has. It is a concept borrowed from computer graphics to reduce geometrical complexity of visualised objects according to the distance between objects and the user. If the CityGML convention is used to describe LoD (Hafele, Reference Häfele2011), the ZMapping model is a mixed Level of Details (LoD) 1 and LoD 2 model with decimetre-level accuracy, stored in the Virtual Reality Modelling Language (VRML) format. According to this convention, LoD 1 means the 2D shape of a building is supplied with its height information. LoD 2 means the outer boundary surfaces are described. Figure 7 visualises the 3D model used in this study.

Figure 7. The 3D model of London used in the experiments.
Twenty experimental locations with various road layouts were selected in the area covered by the city model. Figure 8 is an aerial view of the experimental area, showing each site. Pairs of sites (prefixed by R and G) are located on opposite sides of the street, facilitating the testing of shadow matching's ability to determine the correct side of the street. All sites were located on the footpath, close to a traffic lane.

Figure 8. An aerial view of the experimental area (satellite image from Google Earth).
The experimenters stood statically at each of the 20 locations for two rounds of 6 minutes each, with the smartphone held in front of the experimenter. The time between the two rounds of data collection was approximately four hours, allowing the satellite constellation to change significantly. Thus, it is considered that the two rounds of data are independent of each other. The second round of data is used for analysis in this section; whereas the first round of data is used for testing the new shadow-matching algorithm. Satellite visibility information for both GPS and GLONASS (comprising time tag, satellite azimuth, elevation and SNR) were recorded at 1 Hz for post-processing using shadow matching. Thus, a total of 24000 one-second epochs of smartphone GPS and GLONASS data were collected at the 20 locations.
Satellite visibility information for both GPS and GLONASS (comprising time tag, satellite azimuth, elevation and SNR) were recorded at 1 Hz for post-processing using shadow-matching. The conventional positioning solutions from the smartphone GNSS chip were also recorded. The truth reference was determined using a tape to measure the distance to a distinctive feature, such as a building wall or the kerb between the road and footpath and then locating that feature on the 3D city model. This process is accurate to decimetre level, which is sufficient for this study.
4. SMARTPHONE DIRECT LOS AND NLOS SIGNAL STRENGTH ANALYSIS
The standard signal-to-noise ratio measure used for GNSS is the carrier-power-to-noise-density ratio, C/N 0, which should be 40–50 dB-Hz under good reception conditions with a good antenna. The measurements presented here are approximately equal to C/N 0, but may differ slightly, depending on the measurement technique deployed by the receiver manufacturer (Betz, Reference Betz2001; Groves, Reference Groves2005). Therefore, the term SNR is used. A signal received with a higher SNR is more likely to be direct LOS than NLOS. For example, signals reflected from stone and brick buildings are weaker. However, glass and steel buildings and passing vehicles can produce strong reflected signals. Conversely, weak direct LOS signals can also be received as a result of user body masking or attenuation by trees and passing pedestrians. Thus, some NLOS signals are stronger than some direct LOS signals.
As discussed in Section 1, the characteristics of a smartphone antenna make it more difficult to distinguish direct LOS from NLOS signals using SNR measurements. The SNR measurement process itself can also be noisy (Groves, Reference Groves2005). The fluctuating nature of smartphone GNSS signals can be seen in the example SNR time series shown in Figure 9. As only direct LOS reception is currently predicted using the 3D city model, this represents a potential problem for shadow matching. In this section, the signal-to-noise ratio distributions of the direct LOS and NLOS GNSS signals received by the smartphone are separately analysed. The 3D city model is used to determine which of the received signals are direct LOS and which are NLOS using the visibility prediction method described in Section 2 and knowledge of the true user position. Signals predicted to be visible are assumed to be direct LOS. Diffracted signals are included in the NLOS category. The results of this analysis are used to improve the shadow-matching algorithm, as described in Section 5.

Figure 9. The SNR time series of each satellite at test site G09, showing the variation exhibited in measured smartphone GNSS signals.
Figure 10 presents histograms for each of the test sites showing the normalized distributions of the measured SNR of the direct LOS and NLOS signals. Figure 11 shows the LOS and NLOS SNR distributions averaged across all of the experimental sites. Both direct LOS signals, shown in red, and NLOS signals, shown in blue, were received at every test site, verifying that smartphone GNSS receivers usually capture NLOS signals in urban areas. Comparing different sites, it can be seen that, at some (e.g., R01 and G10) a higher proportion of the signals received were direct LOS whereas at others (e.g., G01 and R08), more NLOS signals than LOS were received. One reason for this is the nature of the surrounding buildings.

Figure 10. Normalized SNR distributions of LOS and NLOS reception at each site.

Figure 11. Normalized SNR distributions of LOS and NLOS signals across all test sites.
At every site, the LOS signals tend to exhibit a higher SNR than the NLOS signals. However, there is considerable overlap between them, particularly between 20 and 30 dB-Hz, confirming the expectation that both strong NLOS signals and weak LOS signals are commonly received by smartphones in dense urban environments. Consequently, an absolute SNR boundary to distinguish LOS from NLOS signals cannot be defined. Instead, the data may be used to infer the probability that a signal received with a particular SNR is LOS. For example, it can be deduced from Figure 9 that the probability of a 24 dB-Hz signal being LOS is approximately 50%, whereas a 39 dB-Hz signal has a ~90% probability of being LOS. On average, the GLONASS signals were about 1 dB-Hz stronger than the GPS signals; this was not considered significant.
For comparison with an open environment, another experiment was conducted in the middle of an open field in Regent's Park in London, where there are no obvious obstructions. Thus all signals can be assumed to be LOS. GPS and GLONASS NMEA data was recorded at a 1 Hz rate for 12 minutes. Figure 12 shows a normalized histogram of the observed SNR distribution. It shows that a peak SNR occurs between 26 to 29 dB-Hz, and fewer low-SNR satellites have been observed. The wide variation in SNR may be attributed to directional nulls in the antenna gain pattern and body masking effects.

Figure 12. Normalized SNR distributions of LOS in an open environment.
Figure 13 shows the normalized measured SNR distributions for different satellite elevations averaged across all sites. The low elevation signals are more likely to be NLOS and the higher elevation signals are more likely to be LOS as they are less likely to be blocked by buildings. It can be seen that for elevations below 40°, the SNR drops as the elevation decreases, whereas above 40°, there is little relationship between SNR and elevation.

Figure 13. Normalized SNR distributions of LOS and NLOS signals at different elevation angles.
5. A SATELLITE VISIBILITY SCORING SCHEME FOR SMARTPHONE SHADOW MATCHING
As Section 4 shows, there is considerable overlap between the SNR distributions of direct LOS and NLOS GNSS signals received by smartphones. Thus, it is not possible to set a definitive SNR threshold above which a received signal may be assumed to be direct LOS. Consequently, the simple visibility-prediction scoring scheme shown in Figure 6 cannot be expected to work well. Instead, a new probabilistic approach must be adopted in which the probability of a signal being direct LOS is estimated from the measured SNR and the satellite visibility prediction from the 3D city model scored accordingly.
Given the smartphone GNSS characteristics as analysed in Section 4, a Bayesian technique is proposed to improve the scoring scheme via sample statistics. For each value of SNR (ranging between 5 and 45 dB-Hz for a smartphone), there can be a correspondent conditional probability p(LOS|SNR=s) that a signal is LOS. These conditional probabilities form a simple Bayesian network, where all of the probabilities can be stored in a “Conditional Probability Table” (CPT) Nilsson (Reference Nilsson2009). The same principle applies to NLOS signals. Thus, given a known SNR from the smartphone GNSS receiver, the probability that a signal is direct LOS can be calculated.
From Bayes theorem, the probability of an observed signal being direct LOS given a measured SNR of s is
where p(SNR = s|LOS) is the probability of an SNR of s being measured, given that the signal is direct LOS, p(LOS) is the probability of the signal being direct LOS and p(SNR = s) is the probability of the measured SNR being s. If l i is the proportion of signals measured that are direct LOS and for which the measured SNR is i and n i is the proportion of signals measured that are NLOS and for which the measured SNR is i, then
 $$p\left( {SNR = s\ \vert\ LOS} \right) = \displaystyle{{l_s}\over {\sum\limits_i {l_i}}}$$
$$p\left( {SNR = s\ \vert\ LOS} \right) = \displaystyle{{l_s}\over {\sum\limits_i {l_i}}}$$and
where it is assumed that ![]() $\sum\limits_i {\left( {l_i + n_i} \right)} = 1$. Therefore, substituting Equations (2) to (4) into Equation (1),
$\sum\limits_i {\left( {l_i + n_i} \right)} = 1$. Therefore, substituting Equations (2) to (4) into Equation (1),
Where the data set is sufficiently large, values of l i and n i may be derived directly from the data and used to determine the CPT used in shadow matching satellite visibility scoring. The black crosses in Figure 14 (left) show the values of p(LOS | SNR = s) derived directly from the data presented in Section 4 for SNRs between 17 and 35 dB-Hz. It shows that P(LOS|SNR=s) increases when the SNR increases. This can be expected, since a higher SNR implies a higher probability that a signal is LOS. However, there is significant statistical noise. Therefore, it was decided to fit a polynomial function to this data instead of using it directly.

Figure 14. Left: Probability of LOS, i.e. p(LOS | SNR=s), when the SNR is between an upper bound and a lower bound, fitted as a linear function, a quadratic function, and a cubic function, shown in purple, green and blue, respectively. Right: The fitting error in terms of residuals for the same functions.
In the CPT model, it is assumed that when the SNR is higher than a specified upper bound, p(LOS) is regarded as a constant high probability less than 1; when the SNR is lower than a specified lower bound, p(LOS) is regarded as a constant low probability greater than 0; when the SNR is in between the upper bound and lower bound, a polynomial fitted model can be used. Extreme probabilities very close to 0 and 1 are avoided to help the shadow matching algorithm cope with very strong reflected signals and highly attenuated direct-LOS signals. Thus, robustness is favoured at the expense of sensitivity.
SNR values of 17 and 35 dB-Hz were selected for the lower and upper bounds of p(LOS | SNR = s), respectively. It can be seen from Figure 11 that there is a peak of NLOS reception when the SNR is right below 17 dB-Hz. Thus, signals with an SNR below 17 dB-Hz are assumed very likely to be NLOS. It can also be seen from the figure that when the SNR is above 35 dB-Hz the probability of NLOS reception is very low, so it is assumed that a signal is very likely to be LOS when the SNR is above 35 dB-Hz. Furthermore, because the probability of NLOS reception when the SNR is higher than 35 dB-Hz is very small, the sample size of the data is not large enough to model it reliably. To model the intermediate SNR values, a least squares method is used with three polynomial fittings, a linear fitting, a quadratic fitting, and a cubic fitting. Figure 14 (left) shows the resulting functions, while Figure 14 (right) shows the fitting error using these three methods. It can be seen that linear fitting results in a large error of up to 10%, whereas quadratic fitting offers, in most cases, errors smaller than 2%. Thus, a linear fitting is under-fitting and should not be chosen. Using a higher order of polynomial fitting, cubic fitting, provides very similar fitting errors. Thus, it is concluded that a quadratic function is sufficient and a higher-order function is thus not needed. Combining this quadratic function with the upper and lower SNR bounds gives the following CPT model for p(LOS | SNR=s):
 $$p\left( {LOS\ \vert\ SNR = s} \right) = \left\{ {\matrix{ {\,p_{o - \min}} & {s \lt s_{\min}} \cr {a_2 s^2 + a_1 s + a_0}& {s_{\min}\lt s \lt s_{\max}} \cr {\,p_{o - \max}} & {s_{\max}\lt s} }} \right.$$
$$p\left( {LOS\ \vert\ SNR = s} \right) = \left\{ {\matrix{ {\,p_{o - \min}} & {s \lt s_{\min}} \cr {a_2 s^2 + a_1 s + a_0}& {s_{\min}\lt s \lt s_{\max}} \cr {\,p_{o - \max}} & {s_{\max}\lt s} }} \right.$$where p o−min and p o-max are, respectively, the minimum and maximum probabilities of the observed signal being LOS; s min and s max are, respectively, the minimum and maximum SNRs at which the quadratic function applies; and a 0, a 1, and a 2 are the coefficients of that function. The parameters obtained from the data presented in Section 4 are: p o-min = 0·2, p o-max = 0·85, s min = 17, s max = 35, a 0 = −1·86887109, a 1 = 0·1563262666 and a 2 = −0·002245615412. It should be noted that this model is trained using a Galaxy Samsung S3 smartphone held in front of the user. Using another model of smartphone may or may not need adjustments to the parameters; this needs further research. Different values are also likely to be needed when the phone is in a pocket or bag, also a subject for further research. Context detection algorithms will be required in order to determine which parameter set to use.
The probability that the predicted and measured satellite visibility match, P m, is
where p(LOS|BB) is the probability predicted from the building boundary that a LOS signal is receivable. p(LOS|BB) is set to 0·85 if the satellite is predicted to be visible, and to 0·2 otherwise. These values allow for diffraction and 3D model errors.
The overall matching probability is obtained by multiplying the individual satellite- matching probabilities. However, it is more convenient to add the individual satellite scores. Therefore, a log-likelihood-based score between 0 and 1 is calculated from P m using
where P m-min = 0·225 and P m-max = 0·64 are the minimum and maximum possible values of the matching probability, P m.
6. PERFORMANCE ASSESSMENT OF SHADOW-MATCHING USING SMARTPHONE GPS AND GLONASS DATA
Shadow-matching performance was assessed using smartphone GPS and GLONASS data collected at 20 sites as described in Section 3. This performance assessment was conducted using the first (morning) set of data, whereas the second (afternoon) set was used for the signal strength analysis described in Section 4 and the satellite visibility scoring scheme described in Section 5. As all of the satellites were in significantly different positions, these testing and training data sets may be considered independent. The shadow-matching algorithm described in Section 2 was used with the visibility-scoring scheme described in Section 5 and a 1 m grid spacing. Previous research showed that positioning was about 5% more accurate with a 1 m grid spacing than with a 3 m spacing (Wang et al., Reference Wang, Groves and Ziebart2013c). A 40 m radius circle, centred at the conventional GNSS positioning solution from the smartphone GNSS chip, defines the boundary of the shadow-matching search area, within which candidate positions are generated.
This section first discusses a selection of satellite visibility scoring maps produced by the shadow-matching algorithm. The cross-street positioning performance is then assessed and compared with conventional GNSS positioning. Finally, the performance that might be obtained using Galileo and Beidou alongside GPS and GLONASS is predicted.
6·1. Satellite Visibility Scoring
Figure 15 shows examples of the shadow-matching scoring maps obtained at four of the experimental locations. The coloured dots represent the candidate positions, excluding indoor locations. The highest scoring candidates are shown in dark red and the lowest scoring candidates in dark blue. The true position is shown by a black cross. The highest scoring points are predominantly in the correct street and on the correct side as shown in the top left and top right subplots. However, high-scoring points can also appear on other streets, as shown in the bottom left subplot, and in the spaces behind buildings. In a few cases, the highest scores do not appear in the expected area as the bottom right subplot shows. This is typically caused by strong NLOS reception via highly reflective glass and metal buildings. A long-term solution to this problem is to predict NLOS reception using the 3D city model.

Figure 15. Example shadow-matching scoring maps at one epoch from different sites.
Figure 15 clearly demonstrates that shadow matching is much more sensitive to position changes in the cross-street direction than in the along-street direction, in line with expectations. This complements conventional GNSS positioning which is generally more precise in the along-street direction in urban areas due to the signal geometry. Thus, combining the cross-street shadow-matching solution with the along-street conventional GNSS solution will generally give the best overall position solution (Groves et al., Reference Groves, Jiang, Wang and Ziebart2012). In this paper, performance analysis focuses on the cross-street component of the position solution.
6·2. Performance comparison with conventional GNSS positioning
To assess the performance of shadow matching against a conventional GNSS positioning solution, the north and east position errors were transformed to along-street and cross-street position errors. Figure 16 shows the absolute value of the cross-street position error at each site from the first round of data. The conventional GNSS navigation solution from the smartphone GNSS chip is compared with shadow-matching using both the probability-based scoring scheme described in Section 5 and the basic scheme shown in Figure 6. Figure 17 shows the corresponding Mean Absolute Deviation (MAD) of each cross-street position error. Note that the results at each site are highly correlated because each observation period was six minutes, during which the constellation geometry changed slowly.

Figure 16. Absolute cross-street positioning error using conventional GNSS, basic shadow-matching and probability-based shadow matching.

Figure 17. Mean absolute deviation over all epochs of the cross-street position error using conventional GNSS, basic shadow matching and probability-based shadow matching.
Figures 16 and 17 show that, in most cases, shadow matching outperforms conventional GNSS positioning and the new probability-based shadow-matching algorithm outperforms the basic algorithm. At some sites, such as G09, the shadow-matching accuracy is better than 2 m at most epochs. However, there are a few cases where shadow matching is poorer than conventional GNSS positioning, e.g. G07. A common cause of poor shadow-matching performance is reception of a significant number of strong reflected signals, which can confuse the shadow-matching algorithm. For example, at site G03, a large number of NLOS signals with SNRs above 25 dB-Hz were received (see Figure 10).
Further analysis was conducted to calculate the proportion of results for which the cross-street positioning error was within certain limits. This may be thought of as the success rate for achieving certain performance specifications. For example, a typical street is around 10 m wide, so a positioning accuracy within 5 m is considered good enough to determine the correct side of the street, while 2 m is sufficient to distinguish the footpath from a traffic lane. Figure 18 shows the success rate at each site from the first round of data, while Figure 19 shows the success rate across all sites. The overall success rate for determining the correct side of a street was 54·39% using probability-based shadow matching, compared to 24·77% using conventional GNSS positioning. The success rate for distinguishing the footpath from a traffic lane was 28·55% for shadow matching and 9·52% for conventional GNSS positioning.

Figure 18. Proportion of cross-street position errors within certain ranges at each site using conventional GNSS, basic shadow matching and probability-based shadow matching.

Figure 19. Proportion of cross-street position errors within certain ranges across all sites using conventional GNSS, basic shadow matching and probability-based shadow matching.
6·3. Performance prediction of four-constellation shadow-matching
Shadow-matching uses multiple satellites to localize the user's position. Thus, using more satellites might be expected to produce a more accurate position solution. To predict how shadow matching will perform in the future when Galileo and BeiDou are fully operational, a four-constellation scenario was simulated by combining GPS and GLONASS data from two separate visits to each experimental site. The interval between visits was about four hours, allowing the satellite constellation geometry to change significantly. Figure 20 shows the MADs for each site and averaged across all sites of the cross-street positioning errors of two- and four-constellation shadow matching, together with conventional GNSS positioning (from the first observation period only). At some sites, shadow matching performed better with four constellations, while at others, it performed better with two constellations. Looking at the average across all of the sites, the two-constellation implementation performed slightly better.

Figure 20. The MAD of the cross-street positioning error of 2- and 4-constellation shadow matching and 2-constellation conventional GNSS for each site (left) and averaged across all sites (right).
Figure 21 shows the success rate for achieving cross-street positioning errors within certain bounds. Using four constellations slightly increased the probability of achieving a cross-street position solution within 1, 2 or 3 m, but reduced the likelihood of achieving a position within 4 or 5 m. A possible explanation is that in environments where the current shadow-matching algorithm works well, additional satellites provide additional information that is used to refine the position solution. However, in environments unfavourable to shadow matching, such as those with lots of highly reflective buildings, using more satellites results in more strong NLOS signals that confuse the shadow-matching algorithm.

Figure 21. The cumulative success rate of cross-street positioning error with certain metres of bound, comparing conventional GNSS and shadow matching with 2 and 4 constellations.
Overall, these results show that the number of available satellites is not the main factor limiting shadow-matching performance. Improvements to the algorithms will be needed to increase shadow matching's reliability.
7. A LARGE-SCALE IMPLEMENTATION OF SHADOW MATCHING
There are two main ways of implementing shadow-matching on a large scale: a server-based approach and a handset-based approach. In the server-based approach, the shadow-matching algorithms are implemented on a remote server using GNSS data from the user. This has the advantage that the solution is unconstrained by the user equipment's processing and data storage capacity, but the fundamental disadvantage that a communication link is necessary to determine a position solution.
In the handset-based approach, demonstrated in Wang et al. (Reference Wang, Groves and Ziebart2013c), all real-time computation is performed within the user equipment. This enables positioning without a communications link. However the available processing resources may limit the search area, grid spacing and sophistication of the shadow-matching algorithm, compromising performance. The user equipment must also be provided with building boundary data.
Without compression, building boundaries with a 1° azimuth resolution require about 300 bytes of storage per grid point. With a 3 m grid spacing, a 1 km long 20 m wide street would contain 2222 grid points, requiring 651 kB of data storage. By exploiting similarities between adjacent azimuths and grid points, substantial data compression should be possible; perhaps by a factor of ten. Thus, it should be possible to store data for 1,500 − 15,000 km of road network per gigabyte. For comparison, the Greater London metropolitan area contains about 15,000 km of road. Roads where conventional GNSS positioning works well may be excluded from the shadow-matching database. Thus, it should be practical to preload the building boundaries for several cities onto a smartphone. Real-time streaming of this data from a server is also possible and can be accommodated by a standard 3G mobile phone connection. Data dissemination is discussed further in Groves et al. (Reference Groves, Wang, Walter, Martin, Voutsis and Jiang2014).
All shadow-matching implementations require 3D city models to generate the building boundary data. The availability of the models is thus critical. Google Maps 3D, iOS 3D Maps by Apple, Bing Maps 3D by Microsoft, Nokia Maps 3D WebGL and Edushi 3D Maps are commercially available, while Open Street Maps 3D is available free of charge.
The real-time computational load with the probability-based scoring system introduced here is expected to be similar to the two seconds time scale in Wang et al. (Reference Wang, Groves and Ziebart2013c) if a 3 m search grid spacing is used. This is because both the new and old scoring steps use a SNR-to-score look-up table, which has O(n) time complexity, where n is the number of satellites.
8. CONCLUSIONS AND FURTHER WORK
Separate signal-to-noise ratio distributions of direct LOS and NLOS GNSS signals received in a dense urban area have been measured using an Android smartphone and a 3D city model. Using these distributions, a function has been derived giving the probability that a received signal is direct LOS based on the measured SNR. Using this function, a shadow-matching satellite visibility scoring scheme has been optimised for use with smartphone GNSS measurements.
Using GPS and GLONASS data recorded at 20 locations within central London, the first comprehensive performance assessment of smartphone GNSS shadow matching has been conducted. The results show that shadow matching significantly outperforms conventional GNSS positioning in the cross-street direction. The success rate for obtaining a cross-street position accuracy within 5 m, enabling the correct side of a street to be determined, was 54·39% using shadow-matching, compared to 24·77% for the conventional GNSS position.
In addition, the performance of four-constellation GNSS shadow matching was predicted using GPS and GLONASS data collected at two different times at the same sites. The additional satellites slightly improve shadow-matching performance under benign conditions, but not in more challenging environments.
Finally, the implementation of shadow matching on a larger scale has been assessed, showing that both server-based and handset-based models are feasible in terms of processing load, dissemination of building boundary information and availability of 3D mapping.
Further research is underway to improve shadow matching's reliability, particularly for smartphone applications. Satellite visibility prediction will be enhanced to predict strong NLOS signals as well as direct LOS signals. A new positioning algorithm will be developed that can handle multiple maxima in the scoring grid and combine measurements from multiple epochs.
In the longer term, shadow-matching will be implemented as part of an intelligent urban positioning system, whereby the cross-street position is determined mainly by shadow matching and the along-street position mainly by conventional ranging-based GNSS positioning (Groves et al., Reference Groves, Jiang, Wang and Ziebart2012). Such a system could also incorporate height aiding from the 3D mapping and information from other techniques, such as Wi-Fi positioning and inertial sensors, using a modular integration architecture (Groves, Reference Groves2014). To ensure that shadow-matching information is weighted correctly, a method to determine the uncertainty and reliability of the shadow-matching solution will also be developed.
ACKNOWLEDGEMENTS
The authors thank Kimon Voutsis for his assistance in the raw data collection. This work has been jointly funded by the University College London Engineering Faculty Scholarship Scheme and the Chinese Scholarship Council.