Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T04:31:46.564Z Has data issue: false hasContentIssue false
  • English
  • Français

A linear and quasi-linear investigation of the crossfield current-driven ion-acoustic instability

Published online by Cambridge University Press:  13 March 2009

R. Bharuthram  and
M. A. Hellberg
R. Bharuthram
Affiliation:
Plasma Physics Research Institute, University of Natal, Durban, 4001, South Africa
M. A. Hellberg
Affiliation:
Plasma Physics Research Institute, University of Natal, Durban, 4001, South Africa
Get access Rights & Permissions [Opens in a new window]

Abstract

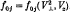The linear growth rate of the crossfield current-driven ion-acoustic instability is obtained for any equilibrium particle velocity distribution function of the type . Quasi-linear theory is then used to investigate the saturation of the instability. Several associated features, namely, particle diffusion in velocity space, anomalous resistivity, energy distribution and electron and ion heating rates are evaluated for a Maxwellian distribution. Finally, a brief comparison is made with the heating rates associated with the electron cyclotron drift instability.

Type
Research Article
Information
Journal of Plasma Physics , Volume 28 , Issue 2 , October 1982 , pp. 267 - 279
Copyright
Copyright © Cambridge University Press 1982

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Davidson, R. C. 1972 Methods in Nonlinear Plasma Theory. Academic.Google Scholar
Drummond, W. E. & Pines, D. 1962 Nucl. Fusion Suppl. Pt. 3, 1049.Google Scholar
Drummond, W. E. & Rosenbluth, M. N. 1962 Phys. Fluids, 5, 1507.Google Scholar
Dum, C. T., Chodura, R. & Biskamp, D. 1974 Phys. Rev. Lett. 32, 1231.Google Scholar
Gary, S. P. 1970 J. Plasma Phys. 4, 753.CrossRefGoogle Scholar
Gary, S. P. & Sanderson, J. J. 1970 J. Plasma Phys. 4, 739.Google Scholar
Hasegawa, A. 1975 Plasma Instabilities and Nonlinear Effects. Springer.Google Scholar
Hayzen, A. J. & Barrett, P. J. 1977 Phys. Fluids, 20, 1713.CrossRefGoogle Scholar
Hirose, A., Lonngren, K. E. & Skarsgard, H. M. 1972 Phys. Rev. Lett. 28, 270.CrossRefGoogle Scholar
Jones, R. 1979 S. Afr. J. Phys. 2, 37.Google Scholar
Lampe, M., Manheimer, W. M., McBride, J. B., Orens, J. H., Papadopoulos, K., Shanny, R. & Sudan, R. N. 1972 Phys. Fluids, 15, 662.Google Scholar
Lashmore-Davies, C. N. & Martin, T. J. 1973 Nucl. Fusion, 13, 193.Google Scholar
McBride, J. B., Ott, E., Boris, J. P. & Orens, J. H. 1972 Phys. Fluids, 15, 2367.CrossRefGoogle Scholar
Sagdeev, R. Z. & Galeev, A. A. 1969 Nonlinear Plasma Theory. Benjamin.Google Scholar
Smith, M. G. 1967 Introduction to the Theory of Partial Differential Equations. Van Nostrand.Google Scholar
Vedenov, A., Velikov, E. & Sagdeev, R. 1961 Nucl. Fusion, 1, 82.CrossRefGoogle Scholar
Virko, V. F. & Kirichenko, G. S. 1977 Soviet Phys. JETP, 46, 264.Google Scholar
Wharton, C., Korn, P., Prono, D., Robertson, S., Auer, P. & Dum, C. T. 1972 Proceedings 4th International Conference on Plasma Physics and Controlled Fusion, Madison, vol. 2, p. 25. IAEA.Google Scholar