Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-10T14:12:26.561Z Has data issue: false hasContentIssue false
  • English
  • Français

MHD turbulence: a biased review

Published online by Cambridge University Press:  12 October 2022

Alexander A. Schekochihin Open the ORCID record for Alexander A. Schekochihin [Opens in a new window]
Alexander A. Schekochihin*
Affiliation:
Rudolf Peierls Centre for Theoretical Physics, Clarendon Laboratory, University of Oxford, Parks Road, Oxford OX1 3PU, UK Merton College, Oxford OX1 4JD, UK
*
†Email address for correspondence: alex.schekochihin@physics.ox.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

This review of scaling theories of magnetohydrodynamic (MHD) turbulence aims to put the developments of the last few years in the context of the canonical time line (from Kolmogorov to Iroshnikov–Kraichnan to Goldreich–Sridhar to Boldyrev). It is argued that Beresnyak's (valid) objection that Boldyrev's alignment theory, at least in its original form, violates the Reduced-MHD rescaling symmetry can be reconciled with alignment if the latter is understood as an intermittency effect. Boldyrev's scalings, a version of which is recovered in this interpretation, and the concept of dynamic alignment (equivalently, local 3D anisotropy) are thus an example of a physical theory of intermittency in a turbulent system. The emergence of aligned structures naturally brings into play reconnection physics and thus the theory of MHD turbulence becomes intertwined with the physics of tearing, current-sheet disruption and plasmoid formation. Recent work on these subjects by Loureiro, Mallet et al. is reviewed and it is argued that we may, as a result, finally have a reasonably complete picture of the MHD turbulent cascade (forced, balanced, and in the presence of a strong mean field) all the way to the dissipation scale. This picture appears to reconcile Beresnyak's advocacy of the Kolmogorov scaling of the dissipation cutoff (as 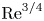$\mathrm {Re}^{3/4}$) with Boldyrev's aligned cascade. It turns out also that these ideas open the door to some progress in understanding MHD turbulence without a mean field – MHD dynamo – whose saturated state is argued to be controlled by reconnection and to contain, at small scales, a tearing-mediated cascade similar to its strong-mean-field counterpart (this is a new result). On the margins of this core narrative, standard weak-MHD-turbulence theory is argued to require some adjustment – and a new scheme for such an adjustment is proposed – to take account of the determining part that a spontaneously emergent 2D condensate plays in mediating the Alfvén-wave cascade from a weakly interacting state to a strongly turbulent (critically balanced) one. This completes the picture of the MHD cascade at large scales. A number of outstanding issues are surveyed: imbalanced turbulence (for which a new, tentative theory is proposed), residual energy, MHD turbulence at subviscous scales, and decaying MHD turbulence (where there has been dramatic progress recently, and reconnection again turned out to feature prominently). Finally, it is argued that the natural direction of research is now away from the fluid MHD theory and into kinetic territory – and then, possibly, back again. The review lays no claim to objectivity or completeness, focusing on topics and views that the author finds most appealing at the present moment.

Keywords

astrophysical plasmasplasma nonlinear phenomena
Type
Review Article
Information
Journal of Plasma Physics , Volume 88 , Issue 5 , October 2022 , 155880501
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abel, I.G., Plunk, G.G., Wang, E., Barnes, M., Cowley, S.C., Dorland, W. & Schekochihin, A.A. 2013 Multiscale gyrokinetics for rotating tokamak plasmas: fluctuations, transport and energy flows. Rep. Prog. Phys. 76, 116201.CrossRefGoogle ScholarPubMed
Adkins, T. & Schekochihin, A.A. 2018 A solvable model of Vlasov-kinetic plasma turbulence in Fourier-Hermite phase space. J. Plasma Phys. 84, 905840107.CrossRefGoogle Scholar
Adkins, T., Schekochihin, A.A., Ivanov, P.G. & Roach, C.M. 2022 Electromagnetic instabilities and plasma turbulence driven by electron-temperature gradient. J. Plasma Phys. 88, 905880410.Google Scholar
Alexakis, A. & Brachet, M.-E. 2019 On the thermal equilibrium state of large-scale flows. J. Fluid Mech. 872, 594.CrossRefGoogle Scholar
Alfvén, H. 1942 Existence of electromagnetic-hydrodynamic waves. Nature 150, 405.CrossRefGoogle Scholar
Aluie, H. & Eyink, G.L. 2010 Scale locality of magnetohydrodynamic turbulence. Phys. Rev. Lett. 104, 081101.Google ScholarPubMed
Avsarkisov, V. 2020 On the buoyancy subrange in stratified turbulence. Atmosphere 11, 659.Google Scholar
Baggaley, A.W., Shukurov, A., Barenghi, C.F. & Subramanian, K. 2010 Fluctuation dynamo based on magnetic reconnections. Astron. Nachr. 331, 46.CrossRefGoogle Scholar
Balbus, S.A. 2004 Viscous shear instability in weakly magnetized, dilute plasmas. Astrophys. J. 616, 857.CrossRefGoogle Scholar
Balkovsky, E., Fouxon, A. & Lebedev, V. 2001 Turbulence of polymer solutions. Phys. Rev. E 64, 056301.CrossRefGoogle ScholarPubMed
Bandyopadhyay, R., Matthaeus, W.H., Oughton, S. & Wan, M. 2019 Evolution of similarity lengths in anisotropic magnetohydrodynamic turbulence. J. Fluid Mech. 876, 5.Google Scholar
Banerjee, R. & Jedamzik, K. 2004 Evolution of cosmic magnetic fields: from the very early Universe, to recombination, to the present. Phys. Rev. D 70, 123003.Google Scholar
Bañón Navarro, A., Teaca, B., Told, D., Grošelj, D., Crandall, P. & Jenko, F. 2016 Structure of plasma heating in gyrokinetic Alfvénic turbulence. Phys. Rev. Lett. 117, 245101.CrossRefGoogle Scholar
Barnes, M., Parra, F.I. & Schekochihin, A.A. 2011 Critically balanced ion temperature gradient turbulence in fusion plasmas. Phys. Rev. Lett. 107, 115003.Google ScholarPubMed
Bárta, M., Büchner, J., Karlický, M. & Skála, J. 2011 Spontaneous current-layer fragmentation and cascading reconnection in solar flares. I. Model and analysis. Astrophys. J. 737, 24.CrossRefGoogle Scholar
Bárta, M., Skála, J., Karlický, M. & Büchner, J. 2012 Energy cascades in large-scale solar flare reconnection. In Multi-scale Dynamical Processes in Space and Astrophysical Plasmas (ed. M. P. Leubner & Z. Vörös), p. 43. Springer.Google Scholar
Batchelor, G.K. 1950 On the spontaneous magnetic field in a conducting liquid in turbulent motion. Proc. R. Soc. Lond. A 201, 405.Google Scholar
Batchelor, G.K. 1953 The Theory of Homogeneous Turbulence. Cambridge University Press.Google Scholar
Batchelor, G.K. 1959 Small-scale variation of convected quantities like temperature in turbulent fluid. Part 1. General discussion and the case of small conductivity. J. Fluid Mech. 5, 113.Google Scholar
Batchelor, G.K. & Proudman, I. 1956 The large-scale structure of homogeneous turbulence. Phil. Trans. R. Soc. Lond. A 248, 369.Google Scholar
Bec, J. & Khanin, K. 2007 Burgers turbulence. Phys. Rep. 447, 1.CrossRefGoogle Scholar
Berera, A. & Linkmann, M. 2014 Magnetic helicity and the evolution of decaying magnetohydrodynamic turbulence. Phys. Rev. E 90, 041003.CrossRefGoogle ScholarPubMed
Beresnyak, A. 2011 The spectral slope and Kolmogorov constant of MHD turbulence. Phys. Rev. Lett. 106, 075001.CrossRefGoogle ScholarPubMed
Beresnyak, A. 2012 a Basic properties of magnetohydrodynamic turbulence in the inertial range. Mon. Not. R. Astron. Soc. 422, 3495.Google Scholar
Beresnyak, A. 2012 b Simulations of nonlinear small-scale dynamo. Unpublished.CrossRefGoogle Scholar
Beresnyak, A. 2012 c Universal nonlinear small-scale dynamo. Phys. Rev. Lett. 108, 035002.Google ScholarPubMed
Beresnyak, A. 2013 Comment on Perez et al. [PRX 2, 041005 (2012), arXiv:1209.2011]. arXiv:1301.7425.Google Scholar
Beresnyak, A. 2014 a Reply to Comment on “Spectra of strong magnetohydrodynamic turbulence from high-resolution simulations”. arXiv:1410.0957.Google Scholar
Beresnyak, A. 2014 b Spectra of strong magnetohydrodynamic turbulence from high-resolution simulations. Astrophys. J. 784, L20.CrossRefGoogle Scholar
Beresnyak, A. 2015 On the parallel spectrum in magnetohydrodynamic turbulence. Astrophys. J. 801, L9.CrossRefGoogle Scholar
Beresnyak, A. 2017 Three-dimensional spontaneous magnetic reconnection. Astrophys. J. 834, 47.CrossRefGoogle Scholar
Beresnyak, A. 2019 MHD turbulence. Living Rev. Comput. Astrophys. 5, 2.CrossRefGoogle Scholar
Beresnyak, A. & Lazarian, A. 2006 Polarization intermittency and its influence on MHD turbulence. Astrophys. J. 640, L175.CrossRefGoogle Scholar
Beresnyak, A. & Lazarian, A. 2008 Strong imbalanced turbulence. Astrophys. J. 682, 1070.CrossRefGoogle Scholar
Beresnyak, A. & Lazarian, A. 2009 a Comparison of spectral slopes of magnetohydrodynamic and hydrodynamic turbulence and measurements of alignment effects. Astrophys. J. 702, 1190.CrossRefGoogle Scholar
Beresnyak, A. & Lazarian, A. 2009 b Structure of stationary strong imbalanced turbulence. Astrophys. J. 702, 460.CrossRefGoogle Scholar
Beresnyak, A. & Lazarian, A. 2010 Scaling laws and diffuse locality of balanced and imbalanced magnetohydrodynamic turbulence. Astrophys. J. 722, L110.CrossRefGoogle Scholar
Bershadskii, A. 2019 Cross-helicity and extended inertial range in MHD turbulence. arXiv:1909.10992.Google Scholar
Bhat, P., Zhou, M. & Loureiro, N.F. 2021 Inverse energy transfer in decaying, three dimensional, nonhelical magnetic turbulence due to magnetic reconnection. Mon. Not. R. Astron. Soc. 501, 3074.CrossRefGoogle Scholar
Bhattacharjee, A., Huang, Y.-M., Yang, H. & Rogers, B. 2009 Fast reconnection in high-Lundquist-number plasmas due to the plasmoid instability. Phys. Plasmas 16, 112102.CrossRefGoogle Scholar
Bhattacharjee, A. & Ng, C.S. 2001 Random scattering and anisotropic turbulence of shear Alfvén wave packets. Astrophys. J. 548, 318.CrossRefGoogle Scholar
Bian, X. & Aluie, H. 2019 Decoupled cascades of kinetic and magnetic energy in magnetohydrodynamic turbulence. Phys. Rev. Lett. 122, 135101.CrossRefGoogle ScholarPubMed
Biermann, L. & Schlüter, A. 1951 Cosmic radiation and cosmic magnetic fields. II. Origin of cosmic magnetic fields. Phys. Rev. 82, 863.CrossRefGoogle Scholar
Bigot, B. & Galtier, S. 2011 Two-dimensional state in driven magnetohydrodynamic turbulence. Phys. Rev. E 83, 026405.CrossRefGoogle Scholar
Biskamp, D. 1982 Effect of secondary tearing instability on the coalescence of magnetic islands. Phys. Lett. A 87, 357.CrossRefGoogle Scholar
Biskamp, D. 1986 Magnetic reconnection via current sheets. Phys. Fluids 29, 1520.CrossRefGoogle Scholar
Biskamp, D. & Bremer, U. 1994 Dynamics and statistics of inverse cascade processes in 2D magnetohydrodynamic turbulence. Phys. Rev. Lett. 72, 3819.Google ScholarPubMed
Biskamp, D. & Müller, W.-C. 1999 Decay laws for three-dimensional magnetohydrodynamic turbulence. Phys. Rev. Lett. 83, 2195.CrossRefGoogle Scholar
Biskamp, D. & Müller, W.-C. 2000 Scaling properties of three-dimensional isotropic magnetohydrodynamic turbulence. Phys. Plasmas 7, 4889.CrossRefGoogle Scholar
Biskamp, D. & Welter, H. 1989 Dynamics of decaying two-dimensional magnetohydrodynamic turbulence. Phys. Fluids B 1, 1964.CrossRefGoogle Scholar
Boldyrev, S. 2002 Kolmogorov-Burgers model for star-forming turbulence. Astrophys. J. 569, 841.Google Scholar
Boldyrev, S. 2005 On the spectrum of magnetohydrodynamic turbulence. Astrophys. J. 626, L37.Google Scholar
Boldyrev, S. 2006 Spectrum of magnetohydrodynamic turbulence. Phys. Rev. Lett. 96, 115002.CrossRefGoogle ScholarPubMed
Boldyrev, S. & Cattaneo, F. 2004 Magnetic-field generation in Kolmogorov turbulence. Phys. Rev. Lett. 92, 144501.CrossRefGoogle ScholarPubMed
Boldyrev, S., Chen, C.H.K., Xia, Q. & Zhdankin, V. 2015 Spectral breaks of Alfvénic turbulence in a collisionless plasma. Astrophys. J. 806, 238.CrossRefGoogle Scholar
Boldyrev, S., Horaites, K., Xia, Q. & Perez, J.C. 2013 Toward a theory of astrophysical plasma turbulence at subproton scales. Astrophys. J. 777, 41.CrossRefGoogle Scholar
Boldyrev, S. & Loureiro, N.F. 2017 Magnetohydrodynamic turbulence mediated by reconnection. Astrophys. J. 844, 125.Google Scholar
Boldyrev, S. & Loureiro, N.F. 2018 Calculations in the theory of tearing instability. J. Phys.: Conf. Ser. 1100, 012003.Google Scholar
Boldyrev, S. & Loureiro, N.F. 2019 Role of reconnection in inertial kinetic-Alfvén turbulence. Phys. Rev. Res. 1, 012006(R).CrossRefGoogle Scholar
Boldyrev, S. & Loureiro, N.F. 2020 Tearing instability in Alfvén and kinetic-Alfvén turbulence. J. Geophys. Res. 125, A28185.CrossRefGoogle Scholar
Boldyrev, S., Mason, J. & Cattaneo, F. 2009 Dynamic alignment and exact scaling laws in magnetohydrodynamic turbulence. Astrophys. J. 699, L39.CrossRefGoogle Scholar
Boldyrev, S., Nordlund, Å. & Padoan, P. 2002 Supersonic turbulence and structure of interstellar molecular clouds. Phys. Rev. Lett. 89, 031102.CrossRefGoogle ScholarPubMed
Boldyrev, S. & Perez, J.C. 2009 Spectrum of weak magnetohydrodynamic turbulence. Phys. Rev. Lett. 103, 225001.Google ScholarPubMed
Boldyrev, S. & Perez, J.C. 2012 Spectrum of kinetic-Alfvén turbulence. Astrophys. J. 758, L44.CrossRefGoogle Scholar
Boldyrev, S., Perez, J.C., Borovsky, J.E. & Podesta, J.J. 2011 Spectral scaling laws in magnetohydrodynamic turbulence simulations and in the solar wind. Astrophys. J. 741, L19.Google Scholar
Boldyrev, S., Perez, J.C. & Zhdankin, V. 2012 Residual energy in MHD turbulence and in the solar wind. AIP Conf. Proc. 1436, 18.CrossRefGoogle Scholar
Boozer, A.H. 2021 Magnetic reconnection and thermal equilibration. Phys. Plasmas 28, 032102.CrossRefGoogle Scholar
Boozer, A.H. & Elder, T. 2021 Example of exponentially enhanced magnetic reconnection driven by a spatially bounded and laminar ideal flow. Phys. Plasmas 28, 062303.Google Scholar
Bott, A.F.A., Arzamasskiy, L., Kunz, M.W., Quataert, E. & Squire, J. 2021 a Adaptive critical balance and firehose instability in an expanding, turbulent, collisionless plasma. Astrophys. J. 922, L35.CrossRefGoogle Scholar
Bott, A.F.A., Chen, L., Tzeferacos, P., Palmer, C.A.J., Bell, A.R., Bingham, R., Birkel, A., Froula, D.H., Katz, J., Kunz, M.W., et al. 2022 Insensitivity of a turbulent laser-plasma dynamo to initial conditions. Matter Radiat. Extrem. 7, 046901.CrossRefGoogle Scholar
Bott, A.F.A., Tzeferacos, P., Chen, L., Palmer, C.A.J., Rigby, A., Bell, A.R., Bingham, R., Birkel, A., Graziani, C., Froula, D.H., et al. 2021 b Time-resolved turbulent dynamo in a laser plasma. Proc. Natl Acad. Sci. USA 118, 2015729118.CrossRefGoogle Scholar
Bowen, T.A., Badman, S.T., Bale, S.D., Dudok de Wit, T., Horbury, T.S., Klein, K.G., Larson, D., Mallet, A., Matteini, L., McManus, M.D., et al. 2021 Nonlinear interactions in spherically polarized Alfvénic turbulence. arXiv:2110.11454.Google Scholar
Bowen, T.A., Mallet, A., Bonnell, J.W. & Bale, S.D. 2018 Impact of residual energy on solar wind turbulent spectra. Astrophys. J. 865, 45.CrossRefGoogle Scholar
Braginskii, S.I. 1965 Transport processes in a plasma. Rev. Plasma Phys. 1, 205.Google Scholar
Brandenburg, A. 2001 The inverse cascade and nonlinear alpha-effect in simulations of isotropic helical hydromagnetic turbulence. Astrophys. J. 550, 824.CrossRefGoogle Scholar
Brandenburg, A. 2011 Nonlinear small-scale dynamos at low magnetic Prandtl numbers. Astrophys. J. 741, 92.CrossRefGoogle Scholar
Brandenburg, A. 2014 Magnetic Prandtl number dependence of the kinetic-to-magnetic dissipation ratio. Astrophys. J. 791, 12.CrossRefGoogle Scholar
Brandenburg, A., Haugen, N.E.L., Li, X.-Y. & Subramanian, K. 2018 Varying the forcing scale in low Prandtl number dynamos. Mon. Not. R. Astron. Soc. 479, 2827.CrossRefGoogle Scholar
Brandenburg, A. & Kahniashvili, T. 2017 Classes of hydrodynamic and magnetohydrodynamic turbulent decay. Phys. Rev. Lett. 118, 055102.CrossRefGoogle ScholarPubMed
Brandenburg, A., Kahniashvili, T., Mandal, S., Pol, A.R., Tevzadze, A.G. & Vachaspati, T. 2019 Dynamo effect in decaying helical turbulence. Phys. Rev. Fluids 4, 024608.CrossRefGoogle Scholar
Brandenburg, A., Kahniashvili, T. & Tevzadze, A.G. 2015 Nonhelical inverse transfer of a decaying turbulent magnetic field. Phys. Rev. Lett. 114, 075001.CrossRefGoogle ScholarPubMed
Brandenburg, A. & Rempel, M. 2019 Reversed dynamo at small scales and large magnetic Prandtl number. Astrophys. J. 879, 57.CrossRefGoogle Scholar
Brandenburg, A. & Subramanian, K. 2005 Astrophysical magnetic fields and nonlinear dynamo theory. Phys. Rep. 417, 1.CrossRefGoogle Scholar
Bruno, R. & Carbone, V. 2013 The solar wind as a turbulence laboratory. Living Rev. Sol. Phys. 10, 2.CrossRefGoogle Scholar
Bulanov, S.V., Sakai, J. & Syrovatskii, S.I. 1979 Tearing-mode instability in approximately steady MHD configurations. Sov. J. Plasma Phys. 5, 280.Google Scholar
Bulanov, S.V., Syrovatskiǐ, S.I. & Sakai, J. 1978 Stabilizing influence of plasma flow on dissipative tearing instability. Sov. Phys. JETP Lett. 28, 177.Google Scholar
Busse, A., Müller, W.-C., Homann, H. & Grauer, R. 2007 Statistics of passive tracers in three-dimensional magnetohydrodynamic turbulence. Phys. Plasmas 14, 122303.CrossRefGoogle Scholar
Campanelli, L. 2004 Scaling laws in magnetohydrodynamic turbulence. Phys. Rev. D 70, 083009.CrossRefGoogle Scholar
Carbone, V., Veltri, P. & Mangeney, A. 1990 Coherent structure formation and magnetic field line reconnection in magnetohydrodynamic turbulence. Phys. Fluids A 2, 1487.CrossRefGoogle Scholar
Cassak, P.A. & Drake, J.F. 2009 The impact of microscopic magnetic reconnection on pre-flare energy storage. Astrophys. J. 707, L158.CrossRefGoogle Scholar
Cassak, P.A., Shay, M.A. & Drake, J.F. 2009 Scaling of Sweet-Parker reconnection with secondary islands. Phys. Plasmas 16, 120702.CrossRefGoogle Scholar
Cattaneo, F., Hughes, D.W. & Kim, E.-J. 1996 Suppression of chaos in a simplified nonlinear dynamo model. Phys. Rev. Lett. 76, 2057.CrossRefGoogle Scholar
Cattaneo, F. & Tobias, S.M. 2009 Dynamo properties of the turbulent velocity field of a saturated dynamo. J. Fluid Mech. 621, 205.CrossRefGoogle Scholar
Cerri, S.S. & Califano, F. 2017 Reconnection and small-scale fields in 2D-3 V hybrid-kinetic driven turbulence simulations. New J. Phys. 19, 025007.CrossRefGoogle Scholar
Cerri, S.S., Kunz, M.W. & Califano, F. 2018 Dual phase-space cascades in 3D hybrid-Vlasov- Maxwell turbulence. Astrophys. J. 856, L13.Google Scholar
Chandran, B.D.G. 1997 PhD thesis, Princeton University.Google Scholar
Chandran, B.D.G. 2008 Strong anisotropic MHD turbulence with cross helicity. Astrophys. J. 685, 646.CrossRefGoogle Scholar
Chandran, B.D.G., Li, B., Rogers, B.N., Quataert, E. & Germaschewski, K. 2010 Perpendicular ion heating by low-frequency Alfvén-wave turbulence in the solar wind. Astrophys. J. 720, 503.CrossRefGoogle Scholar
Chandran, B.D.G. & Perez, J.C. 2019 Reflection-driven magnetohydrodynamic turbulence in the solar atmosphere and solar wind. J. Plasma Phys. 85, 905850409.CrossRefGoogle Scholar
Chandran, B.D.G., Schekochihin, A.A. & Mallet, A. 2015 Intermittency and alignment in strong RMHD turbulence. Astrophys. J. 807, 39.CrossRefGoogle Scholar
Chapman, S. & Kendall, P.C. 1963 Liquid instability and energy transformation near a magnetic neutral line: a soluble non-linear hydromagnetic problem. Proc. R. Soc. Lond. A 271, 435.Google Scholar
Chavanis, P.-H. 2021 Kinetic theory of collisionless relaxation for systems with long-range interactions. arXiv:2112.13664.Google Scholar
Chen, C.H.K. 2016 Recent progress in astrophysical plasma turbulence from solar wind observations. J. Plasma Phys. 82, 535820602.Google Scholar
Chen, C.H.K., Bale, S.D., Bonnell, J.W., Borovikov, D., Bowen, T.A., Burgess, D., Case, A.W., Chandran, B.D.G., Dudok de Wit, T., Goetz, K., et al. 2020 The evolution and role of solar wind turbulence in the inner heliosphere. Astrophys. J. Suppl. 246, 53.CrossRefGoogle Scholar
Chen, C.H.K., Bale, S.D., Salem, C.S. & Maruca, B.A. 2013 Residual energy spectrum of solar wind turbulence. Astrophys. J. 770, 125.CrossRefGoogle Scholar
Chen, C.H.K. & Boldyrev, S. 2017 Nature of kinetic scale turbulence in the Earth's magnetosheath. Astrophys. J. 842, 122.Google Scholar
Chen, C.H.K., Klein, K.G. & Howes, G.G. 2019 Evidence for electron Landau damping in space plasma turbulence. Nat. Commun. 10, 740.CrossRefGoogle ScholarPubMed
Chen, C.H.K., Leung, L., Boldyrev, S., Maruca, B.A. & Bale, S.D. 2014 a Ion-scale spectral break of solar wind turbulence at high and low beta. Geophys. Res. Lett. 41, 8081.CrossRefGoogle ScholarPubMed
Chen, C.H.K., Mallet, A., Schekochihin, A.A., Horbury, T.S., Wicks, R.T. & Bale, S.D. 2012 Three-dimensional structure of solar wind turbulence. Astrophys. J. 758, 120.Google Scholar
Chen, C.H.K., Mallet, A., Yousef, T.A., Schekochihin, A.A. & Horbury, T.S. 2011 Anisotropy of Alfvénic turbulence in the solar wind and numerical simulations. Mon. Not. R. Astron. Soc. 415, 3219.CrossRefGoogle Scholar
Chen, C.H.K., Sorriso-Valvo, L., Šafránková, J. & Němeček, Z. 2014 b Intermittency of solar wind density fluctuations from ion to electron scales. Astrophys. J. 789, L8.CrossRefGoogle Scholar
Chen, X.L. & Morrison, P.J. 1990 Resistive tearing instability with equilibrium shear flow. Phys. Fluids B 2, 495.CrossRefGoogle Scholar
Chernoglazov, A., Ripperda, B. & Philippov, A. 2021 Dynamic alignment and plasmoid formation in relativistic magnetohydrodynamic turbulence. Astrophys. J. 923, L13.CrossRefGoogle Scholar
Cho, J. 2011 Magnetic helicity conservation and inverse energy cascade in electron magnetohydrodynamic wave packets. Phys. Rev. Lett. 106, 191104.CrossRefGoogle ScholarPubMed
Cho, J. & Kim, H. 2016 Spectral evolution of helical electron magnetohydrodynamic turbulence. J. Geophys. Res. A 121, 6157.CrossRefGoogle Scholar
Cho, J. & Lazarian, A. 2002 Compressible sub-Alfvénic MHD turbulence in low-$\beta$ plasmas. Phys. Rev. Lett. 88, 245001.CrossRefGoogle ScholarPubMed
Cho, J. & Lazarian, A. 2003 Compressible magnetohydrodynamic turbulence: mode coupling, scaling relations, anisotropy, viscosity-damped regime and astrophysical implications. Mon. Not. R. Astron. Soc. 345, 325.CrossRefGoogle Scholar
Cho, J. & Lazarian, A. 2004 The anisotropy of electron magnetohydrodynamic turbulence. Astrophys. J. 615, L41.CrossRefGoogle Scholar
Cho, J., Lazarian, A. & Vishniac, E.T. 2002 a New regime of magnetohydrodynamic turbulence: cascade below the viscous cutoff. Astrophys. J. 566, L49.CrossRefGoogle Scholar
Cho, J., Lazarian, A. & Vishniac, E.T. 2002 b Simulations of magnetohydrodynamic turbulence in a strongly magnetized medium. Astrophys. J. 564, 291.CrossRefGoogle Scholar
Cho, J., Lazarian, A. & Vishniac, E.T. 2003 Ordinary and viscosity-damped magnetohydrodynamic turbulence. Astrophys. J. 595, 812.CrossRefGoogle Scholar
Cho, J. & Ryu, D. 2009 Characteristic lengths of magnetic field in magnetohydrodynamic turbulence. Astrophys. J. 705, L90.CrossRefGoogle Scholar
Cho, J. & Vishniac, E.T. 2000 The anisotropy of magnetohydrodynamic Alfvénic turbulence. Astrophys. J. 539, 273.CrossRefGoogle Scholar
Cho, J., Vishniac, E.T., Beresnyak, A., Lazarian, A. & Ryu, D. 2009 Growth of magnetic fields induced by turbulent motions. Astrophys. J. 693, 1449.CrossRefGoogle Scholar
Christensson, M., Hindmarsh, M. & Brandenburg, A. 2001 Inverse cascade in decaying three-dimensional magnetohydrodynamic turbulence. Phys. Rev. E 64, 056405.CrossRefGoogle ScholarPubMed
Christensson, M., Hindmarsh, M. & Brandenburg, A. 2005 Scaling laws in decaying helical hydromagnetic turbulence. Astron. Nachr. 326, 393.CrossRefGoogle Scholar
Comisso, L. & Grasso, D. 2016 Visco-resistive plasmoid instability. Phys. Plasmas 23, 032111.CrossRefGoogle Scholar
Comisso, L., Huang, Y.-M., Lingam, M., Hirvijoki, E. & Bhattacharjee, A. 2018 Magnetohydrodynamic turbulence in the plasmoid-mediated regime. Astrophys. J. 854, 103.CrossRefGoogle Scholar
Comisso, L., Lingam, M., Huang, Y.-M. & Bhattacharjee, A. 2016 General theory of the plasmoid instability. Phys. Plasmas 23, 100702.CrossRefGoogle Scholar
Comisso, L., Lingam, M., Huang, Y.-M. & Bhattacharjee, A. 2017 Plasmoid instability in forming current sheets. Astrophys. J. 850, 142.CrossRefGoogle Scholar
Comisso, L. & Sironi, L. 2018 Particle acceleration in relativistic plasma turbulence. Phys. Rev. Lett. 121, 255101.CrossRefGoogle ScholarPubMed
Comisso, L. & Sironi, L. 2021 Pitch-angle anisotropy controls particle acceleration and cooling in radiative relativistic plasma turbulence. Phys. Rev. Lett. 127, 255102.CrossRefGoogle ScholarPubMed
Coppi, B., Galvão, R., Pellat, R., Rosenbluth, M. & Rutherford, P. 1976 Resistive internal kink modes. Sov. J. Plasma Phys. 2, 961.Google Scholar
Corrsin, S. 1963 Estimates of the relations between Eulerian and Lagrangian scales in large Reynolds number turbulence. J. Atmos. Sci. 20, 115.2.0.CO;2>CrossRefGoogle Scholar
Dahlburg, R.B., Zang, T.A. & Montgomery, D. 1986 Unstable transition properties of the driven magnetohydrodynamic sheet pinch. J. Fluid Mech. 169, 71.CrossRefGoogle Scholar
Daldorff, L.K.S., Leake, J.E. & Klimchuk, J.A. 2022 Impact of 3D structure on magnetic reconnection. Astrophys. J. 927, 196.CrossRefGoogle Scholar
Dallas, V. & Alexakis, A. 2013 a Origins of the $k^{-2}$ spectrum in decaying Taylor-Green magnetohydrodynamic turbulent flows. Phys. Rev. E 88, 053014.CrossRefGoogle ScholarPubMed
Dallas, V. & Alexakis, A. 2013 b Symmetry breaking of decaying magnetohydrodynamic Taylor-Green flows and consequences for universality. Phys. Rev. E 88, 063017.Google ScholarPubMed
Dallas, V. & Alexakis, A. 2014 The signature of initial conditions on magnetohydrodynamic turbulence. Astrophys. J. 788, L36.CrossRefGoogle Scholar
Daughton, W., Roytershteyn, V., Albright, B.J., Karimabadi, H., Yin, L. & Bowers, K.J. 2009 a Influence of Coulomb collisions on the structure of reconnection layers. Phys. Plasmas 16, 072117.CrossRefGoogle Scholar
Daughton, W., Roytershteyn, V., Albright, B.J., Karimabadi, H., Yin, L. & Bowers, K.J. 2009 b Transition from collisional to kinetic regimes in large-scale reconnection layers. Phys. Rev. Lett. 103, 065004.CrossRefGoogle ScholarPubMed
Davidson, P.A. 2013 Turbulence in Rotating, Stratified and Electrically Conducting Fluids. Cambridge University Press.CrossRefGoogle Scholar
Davidson, P.A. 2015 Turbulence: An Introduction for Scientists and Engineers. Oxford University Press.CrossRefGoogle Scholar
Del Sarto, D. & Ottaviani, M. 2017 Secondary fast reconnecting instability in the sawtooth crash. Phys. Plasmas 24, 012102.CrossRefGoogle Scholar
Del Zanna, L., Landi, S., Papini, E., Pucci, F. & Velli, M. 2016 The ideal tearing mode: theory and resistive MHD simulations. J. Phys.: Conf. Ser. 719, 012016.Google Scholar
Dobrowolny, M., Mangeney, A. & Veltri, P. 1980 Fully developed anisotropic hydromagnetic turbulence in interplanetary space. Phys. Rev. Lett. 45, 144.CrossRefGoogle Scholar
Dobrowolny, M., Veltri, P. & Mangeney, A. 1983 Dissipative instabilities of magnetic neutral layers with velocity shear. J. Plasma Phys. 29, 393.CrossRefGoogle Scholar
Dong, C., Wang, L., Comisso, L., Huang, Y.-M. & Bhattacharjee, A. 2021 MHD turbulence mediated by the plasmoid instability. In 63rd Annual Meeting of the APS Division of Plasma Physics. Bull. Amer. Phys. Soc. 66, JO09.00005.Google Scholar
Dong, C., Wang, L., Huang, Y.-M., Comisso, L. & Bhattacharjee, A. 2018 Role of the plasmoid instability in magnetohydrodynamic turbulence. Phys. Rev. Lett. 121, 165101.CrossRefGoogle ScholarPubMed
Dubrulle, B. 1994 Intermittency in fully developed turbulence: log-Poisson statistics and generalized scale covariance. Phys. Rev. Lett. 73, 959.CrossRefGoogle ScholarPubMed
Dupree, T.H. 1972 Theory of phase space density granulation in plasma. Phys. Fluids 15, 334.CrossRefGoogle Scholar
Egedal, J., Le, A. & Daughton, W. 2013 A review of pressure anisotropy caused by electron trapping in collisionless plasma, and its implications for magnetic reconnection. Phys. Plasmas 20, 061201.CrossRefGoogle Scholar
Einaudi, G. & Rubini, F. 1986 Resistive instabilities in a flowing plasma. I. Inviscid case. Phys. Fluids 29, 2563.CrossRefGoogle Scholar
Einaudi, G. & Rubini, F. 1989 Resistive instabilities in a flowing plasma. II. Effects of viscosity. Phys. Fluids B 1, 2224.Google Scholar
Elsasser, W.M. 1950 The hydromagnetic equations. Phys. Rev. 79, 183.CrossRefGoogle Scholar
Event Horizon Telescope Collaboration 2019 First M87 Event Horizon Telescope results. V. Physical origin of the asymmetric ring. Astrophys. J. 875, L5.CrossRefGoogle Scholar
Ewart, R.J., Brown, A., Adkins, T. & Schekochihin, A.A. 2022 Collisionless relaxation of a Lynden-Bell plasma. arXiv:2201.03376.CrossRefGoogle Scholar
Eyink, G., Vishniac, E., Lalescu, C., Aluie, H., Kanov, K., Bürger, K., Burns, R., Meneveau, C. & Szalay, A. 2013 Flux-freezing breakdown in high-conductivity magnetohydrodynamic turbulence. Nature 497, 466.CrossRefGoogle ScholarPubMed
Eyink, G.L. 2009 Stochastic line motion and stochastic flux conservation for nonideal hydromagnetic models. J. Math. Phys. 50, 083102.CrossRefGoogle Scholar
Eyink, G.L. 2011 Stochastic flux freezing and magnetic dynamo. Phys. Rev. E 83, 056405.CrossRefGoogle ScholarPubMed
Eyink, G.L. 2015 Turbulent general magnetic reconnection. Astrophys. J. 807, 137.CrossRefGoogle Scholar
Eyink, G.L. 2018 Cascades and dissipative anomalies in nearly collisionless plasma turbulence. Phys. Rev. X 8, 041020.Google Scholar
Eyink, G.L., Lazarian, A. & Vishniac, E.T. 2011 Fast magnetic reconnection and spontaneous stochasticity. Astrophys. J. 743, 51.CrossRefGoogle Scholar
Fan, Q.-L., Feng, X.-S. & Xiang, C.-Q. 2004 Magnetohydrodynamic simulations of turbulent magnetic reconnection. Phys. Plasmas 11, 5605.CrossRefGoogle Scholar
Fathali, M. & Khoei, S. 2019 Spectral energy transfer in a viscoelastic homogeneous isotropic turbulence. Phys. Fluids 31, 095105.CrossRefGoogle Scholar
Fouxon, A. & Lebedev, V. 2003 Spectra of turbulence in dilute polymer solutions. Phys. Fluids 15, 2060.CrossRefGoogle Scholar
Fowler, T.K. 1968 Thermodynamics of unstable plasmas. Adv. Plasma Phys. 1, 201.Google Scholar
Franci, L., Cerri, S.S., Califano, F., Landi, S., Papini, E., Verdini, A., Matteini, L., Jenko, F. & Hellinger, P. 2017 Magnetic reconnection as a driver for a sub-ion-scale cascade in plasma turbulence. Astrophys. J. 850, L16.CrossRefGoogle Scholar
Franci, L., Landi, S., Verdini, A., Matteini, L. & Hellinger, P. 2018 Solar wind turbulent cascade from MHD to sub-ion scales: large-size 3D hybrid particle-in-cell simulations. Astrophys. J. 853, 26.CrossRefGoogle Scholar
Frenkel, A. & Levich, E. 1983 “Statistical helicity invariant” and decay of inertial turbulence. Phys. Lett. A 98, 25.CrossRefGoogle Scholar
Frick, P. & Stepanov, R. 2010 Long-term free decay of MHD turbulence. Europhys. Lett. 92, 34007.CrossRefGoogle Scholar
Frisch, U. 1995 Turbulence: The Legacy of A. N. Kolmogorov. Cambridge University Press.CrossRefGoogle Scholar
Furth, H.P., Killeen, J. & Rosenbluth, M.N. 1963 Finite-resistivity instabilities of a sheet pinch. Phys. Fluids 6, 459.CrossRefGoogle Scholar
Galishnikova, A.K., Kunz, M.W. & Schekochihin, A.A. 2022 Tearing instability and current-sheet disruption in the turbulent dynamo. arXiv:2201.07757.Google Scholar
Galtier, S., Nazarenko, S.V., Newell, A.C. & Pouquet, A. 2000 A weak turbulence theory for incompressible magnetohydrodynamics. J. Plasma Phys. 63, 447.CrossRefGoogle Scholar
Gogoberidze, G., Chapman, S.C. & Hnat, B. 2012 Generation of residual energy in the turbulent solar wind. Phys. Plasmas 19, 102310.CrossRefGoogle Scholar
Goldreich, P. & Sridhar, S. 1995 Toward a theory of interstellar turbulence. 2. Strong Alfvénic turbulence. Astrophys. J. 438, 763.CrossRefGoogle Scholar
Goldreich, P. & Sridhar, S. 1997 Magnetohydrodynamic turbulence revisited. Astrophys. J. 485, 680.CrossRefGoogle Scholar
Grappin, R., Frisch, U., Pouquet, A. & Leorat, J. 1982 Alfvenic fluctuations as asymptotic states of MHD turbulence. Astron. Astrophys. 105, 6.Google Scholar
Grappin, R., Leorat, J. & Pouquet, A. 1983 Dependence of MHD turbulence spectra on the velocity field-magnetic field correlation. Astron. Astrophys. 126, 51.Google Scholar
Grappin, R., Müller, W.-C. & Verdini, A. 2016 Alfvén-dynamo balance and magnetic excess in magnetohydrodynamic turbulence. Astron. Astrophys. 589, A131.CrossRefGoogle Scholar
Grauer, R., Krug, J. & Marliani, C. 1994 Scaling of high-order structure functions in magnetohydrodynamic turbulence. Phys. Lett. A 195, 335.CrossRefGoogle Scholar
Greco, A., Perri, S., Servidio, S., Yordanova, E. & Veltri, P. 2016 The complex structure of magnetic field discontinuities in the turbulent solar wind. Astrophys. J. 823, L39.Google Scholar
Grete, P., O'Shea, B.W. & Beckwith, K. 2021 As a matter of tension: kinetic energy spectra in MHD turbulence. Astrophys. J. 909, 148.CrossRefGoogle Scholar
Grete, P., O'Shea, B.W., Beckwith, K., Schmidt, W. & Christlieb, A. 2017 Energy transfer in compressible magnetohydrodynamic turbulence. Phys. Plasmas 24, 092311.CrossRefGoogle Scholar
Grošelj, D., Chen, C.H.K., Mallet, A., Samtaney, R., Schneider, K. & Jenko, F. 2019 Kinetic turbulence in astrophysical plasmas: waves and/or structures? Phys. Rev. X 9, 031037.Google Scholar
Gruzinov, A.V. & Diamond, P.H. 1996 Nonlinear mean field electrodynamics of turbulent dynamos. Phys. Plasmas 3, 1853.Google Scholar
Hankla, A.M., Zhdankin, V., Werner, G.R., Uzdensky, D.A. & Begelman, M.C. 2022 Kinetic simulations of imbalanced turbulence in a relativistic plasma: net flow and particle acceleration. Mon. Not. R. Astron. Soc. 509, 3826.CrossRefGoogle Scholar
Hare, J.D., Lebedev, S.V., Suttle, L.G., Loureiro, N.F., Ciardi, A., Burdiak, G.C., Chittenden, J.P., Clayson, T., Eardley, S.J., Garcia, C., et al. 2017 a Formation and structure of a current sheet in pulsed-power driven magnetic reconnection experiments. Phys. Plasmas 24, 102703.CrossRefGoogle Scholar
Hare, J.D., Suttle, L., Lebedev, S.V., Loureiro, N.F., Ciardi, A., Burdiak, G.C., Chittenden, J.P., Clayson, T., Garcia, C., Niasse, N., et al. 2017 b Anomalous heating and plasmoid formation in a driven magnetic reconnection experiment. Phys. Rev. Lett. 118, 085001.CrossRefGoogle Scholar
Hare, J.D., Suttle, L.G., Lebedev, S.V., Loureiro, N.F., Ciardi, A., Chittenden, J.P., Clayson, T., Eardley, S.J., Garcia, C., Halliday, J.W.D., et al. 2018 An experimental platform for pulsed-power driven magnetic reconnection. Phys. Plasmas 25, 055703.CrossRefGoogle Scholar
Harris, E.G. 1962 On a plasma sheath separating regions of oppositely directed magnetic field. Nuovo Cimento 23, 115.CrossRefGoogle Scholar
Hatori, T. 1984 Kolmogorov-style argument for the decaying homogeneous MHD turbulence. J. Phys. Soc. Japan 53, 2539.CrossRefGoogle Scholar
Haugen, N.E., Brandenburg, A. & Dobler, W. 2004 Simulations of nonhelical hydromagnetic turbulence. Phys. Rev. E 70, 016308.CrossRefGoogle ScholarPubMed
Haugen, N.E.L., Brandenburg, A. & Dobler, W. 2003 Is nonhelical hydromagnetic turbulence peaked at small scales? Astrophys. J. 597, L141.CrossRefGoogle Scholar
Heinemann, T., McWilliams, J.C. & Schekochihin, A.A. 2011 Large-scale magnetic field generation by randomly forced shearing waves. Phys. Rev. Lett. 107, 255004.CrossRefGoogle ScholarPubMed
Higdon, J.C. 1984 Density fluctuations in the interstellar medium: evidence for anisotropic magnetogasdynamic turbulence. I — Model and astrophysical sites. Astrophys. J. 285, 109.CrossRefGoogle Scholar
Hofman, I. 1975 Resistive tearing modes in a sheet pinch with shear flow. Plasma Phys. 17, 143.CrossRefGoogle Scholar
Horbury, T.S., Forman, M. & Oughton, S. 2008 Anisotropic scaling of magnetohydrodynamic turbulence. Phys. Rev. Lett. 101, 175005.CrossRefGoogle ScholarPubMed
Hosking, D.N. & Schekochihin, A.A. 2021 Reconnection-controlled decay of magnetohydrodynamic turbulence and the role of invariants. Phys. Rev. X 11, 041005.Google Scholar
Hosking, D.N. & Schekochihin, A.A. 2022 a Cosmic-void observations reconciled with primordial magnetogenesis. arXiv:2203.03573.Google Scholar
Hosking, D.N. & Schekochihin, A.A. 2022 b Emergence of long-range correlations and thermal spectra in forced turbulence. arXiv:2202.00462.Google Scholar
Hosking, D.N., Schekochihin, A.A. & Balbus, S.A. 2020 Elasticity of tangled magnetic fields. J. Plasma Phys. 86, 905860511.Google Scholar
Hossain, M., Gray, P.C., Pontius, D. H., Jr., Matthaeus, W.H. & Oughton, S. 1995 Phenomenology for the decay of energy-containing eddies in homogeneous MHD turbulence. Phys. Fluids 7, 2886.CrossRefGoogle Scholar
Howes, G.G. 2016 The dynamical generation of current sheets in astrophysical plasma turbulence. Astrophys. J. 827, L28.CrossRefGoogle Scholar
Howes, G.G., Cowley, S.C., Dorland, W., Hammett, G.W., Quataert, E. & Schekochihin, A.A. 2006 Astrophysical gyrokinetics: basic equations and linear theory. Astrophys. J. 651, 590.CrossRefGoogle Scholar
Huang, Y.-M. & Bhattacharjee, A. 2010 Scaling laws of resistive magnetohydrodynamic reconnection in the high-Lundquist-number, plasmoid-unstable regime. Phys. Plasmas 17, 062104.Google Scholar
Huang, Y.-M. & Bhattacharjee, A. 2012 Distribution of plasmoids in high-Lundquist-number magnetic reconnection. Phys. Rev. Lett. 109, 265002.CrossRefGoogle ScholarPubMed
Huang, Y.-M. & Bhattacharjee, A. 2013 Plasmoid instability in high-Lundquist-number magnetic reconnection. Phys. Plasmas 20, 055702.CrossRefGoogle Scholar
Huang, Y.-M. & Bhattacharjee, A. 2016 Turbulent magnetohydrodynamic reconnection mediated by the plasmoid instability. Astrophys. J. 818, 20.CrossRefGoogle Scholar
Huang, Y.-M., Comisso, L. & Bhattacharjee, A. 2017 Plasmoid instability in evolving current sheets and onset of fast reconnection. Astrophys. J. 849, 75.CrossRefGoogle Scholar
Huang, Y.-M., Comisso, L. & Bhattacharjee, A. 2019 Scalings pertaining to current sheet disruption mediated by the plasmoid instability. Phys. Plasmas 26, 092112.CrossRefGoogle Scholar
Iroshnikov, R.S. 1963 Turbulence of a conducting fluid in a strong magnetic field. Astron. Zh. 40, 742.Google Scholar
Iskakov, A.B. & Schekochihin, A.A. 2008 Saturated small-scale turbulent dynamo revisited. Unpublished.Google Scholar
Iskakov, A.B., Schekochihin, A.A., Cowley, S.C., McWilliams, J.C. & Proctor, M.R.E. 2007 Numerical demonstration of fluctuation dynamo at low magnetic Prandtl numbers. Phys. Rev. Lett. 98, 208501.CrossRefGoogle ScholarPubMed
Jara-Almonte, J., Ji, H., Yamada, M., Yoo, J. & Fox, W. 2016 Laboratory observation of resistive electron tearing in a two-fluid reconnecting current sheet. Phys. Rev. Lett. 117, 095001.Google Scholar
Jemella, B.D., Drake, J.F. & Shay, M.A. 2004 Singular structure of magnetic islands resulting from reconnection. Phys. Plasmas 11, 5668.CrossRefGoogle Scholar
Jemella, B.D., Shay, M.A., Drake, J.F. & Rogers, B.N. 2003 Impact of frustrated singularities on magnetic island evolution. Phys. Rev. Lett. 91, 125002.CrossRefGoogle ScholarPubMed
Ji, H., Yamada, M., Hsu, S. & Kulsrud, R. 1998 Experimental test of the Sweet-Parker model of magnetic reconnection. Phys. Rev. Lett. 80, 3256.CrossRefGoogle Scholar
Ji, H., Yamada, M., Hsu, S., Kulsrud, R., Carter, T. & Zaharia, S. 1999 Magnetic reconnection with Sweet-Parker characteristics in two-dimensional laboratory plasmas. Phys. Plasmas 6, 1743.CrossRefGoogle Scholar
Jingade, N., Singh, N.K. & Sridhar, S. 2018 Generation of large-scale magnetic fields due to fluctuating $\alpha$ in shearing systems. J. Plasma Phys. 84, 735840601.CrossRefGoogle Scholar
Kadomtsev, B.B. & Pogutse, O.P. 1970 Collisionless relaxation in systems with Coulomb interactions. Phys. Rev. Lett. 25, 1155.CrossRefGoogle Scholar
Kadomtsev, B.B. & Pogutse, O.P. 1974 Nonlinear helical perturbations of a plasma in the tokamak. Sov. Phys. JETP 38, 283.Google Scholar
Kawazura, Y., Barnes, M. & Schekochihin, A.A. 2019 Thermal disequilibration of ions and electrons by collisionless plasma turbulence. Proc. Natl Acad. Sci. USA 116, 771.CrossRefGoogle ScholarPubMed
Kazantsev, A.P. 1968 Enhancement of a magnetic field by a conducting fluid. Sov. Phys. JETP 26, 1031.Google Scholar
Kida, S., Yanase, S. & Mizushima, J. 1991 Statistical properties of MHD turbulence and turbulent dynamo. Phys. Fluids A 3, 457.Google Scholar
Kim, E.-J. 1999 Nonlinear dynamo in a simplified statistical model. Phys. Lett. A 259, 232.CrossRefGoogle Scholar
Kim, H. & Cho, J. 2015 Inverse cascade in imbalanced electron magnetohydrodynamic turbulence. Astrophys. J. 801, 75.CrossRefGoogle Scholar
Kinney, R.M., Chandran, B., Cowley, S. & McWilliams, J.C. 2000 Magnetic field growth and saturation in plasmas with large magnetic Prandtl number. I. The two-dimensional case. Astrophys. J. 545, 907.CrossRefGoogle Scholar
Kiyani, K.H., Chapman, S.C., Khotyaintsev, Y.V., Dunlop, M.W. & Sahraoui, F. 2009 Global scale-invariant dissipation in collisionless plasma turbulence. Phys. Rev. Lett. 103, 075006.CrossRefGoogle ScholarPubMed
Kobayashi, S., Sahraoui, F., Passot, T., Laveder, D., Sulem, P.L., Huang, S.Y., Henri, P. & Smets, R. 2017 Three-dimensional simulations and spacecraft observations of sub-ion scale turbulence in the solar wind: influence of Landau damping. Astrophys. J. 839, 122.CrossRefGoogle Scholar
Kolmogorov, A.N. 1941 a Dissipation of energy in the locally isotropic turbulence. Dokl. Akad. Nauk SSSR 32, 19.Google Scholar
Kolmogorov, A.N. 1941 b Local structure of turbulence in incompressible viscous fluid at very large Reynolds numbers. Dokl. Akad. Nauk SSSR 30, 299.Google Scholar
Kolmogorov, A.N. 1941 c On the degeneration of isotropic turbulence in an incompressible viscous fluid. Dokl. Akad. Nauk SSSR 31, 538.Google Scholar
Kolmogorov, A.N. 1962 A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high Reynolds number. J. Fluid Mech. 13, 82.CrossRefGoogle Scholar
Kowal, G., Falceta-Gonçalves, D.A., Lazarian, A. & Vishniac, E.T. 2017 Statistics of reconnection-driven turbulence. Astrophys. J. 838, 91.CrossRefGoogle Scholar
Kowal, G., Falceta-Gonçalves, D.A., Lazarian, A. & Vishniac, E.T. 2020 Kelvin-Helmholtz versus tearing instability: what drives turbulence in stochastic reconnection? Astrophys. J. 892, 50.Google Scholar
Kowal, G. & Lazarian, A. 2010 Velocity field of compressible magnetohydrodynamic turbulence: wavelet decomposition and mode scalings. Astrophys. J. 720, 742.CrossRefGoogle Scholar
Kowal, G., Lazarian, A., Vishniac, E.T. & Otmianowska-Mazur, K. 2009 Numerical tests of fast reconnection in weakly stochastic magnetic fields. Astrophys. J. 700, 63.Google Scholar
Kowal, G., Lazarian, A., Vishniac, E.T. & Otmianowska-Mazur, K. 2012 Reconnection studies under different types of turbulence driving. Nonlinear Proc. Geophys. 19, 297.Google Scholar
Kraichnan, R.H. 1965 Inertial-range spectrum of hydromagnetic turbulence. Phys. Fluids 8, 1385.CrossRefGoogle Scholar
Kuhn, T.S. 1962 The Structure of Scientific Revolutions. University of Chicago Press.Google Scholar
Kulpa-Dybeł, K., Kowal, G., Otmianowska-Mazur, K., Lazarian, A. & Vishniac, E. 2010 Reconnection in weakly stochastic B-fields in 2D. Astron. Astrophys. 514, A26.CrossRefGoogle Scholar
Kulsrud, R.M. 2005 Plasma Physics for Astrophysics. Princeton University Press.CrossRefGoogle Scholar
Kulsrud, R.M. & Anderson, S.W. 1992 The spectrum of random magnetic fields in the mean field dynamo theory of the Galactic magnetic field. Astrophys. J. 396, 606.CrossRefGoogle Scholar
Kunz, M.W., Abel, I.G., Klein, K.G. & Schekochihin, A.A. 2018 Astrophysical gyrokinetics: turbulence in pressure-anisotropic plasmas at ion scales and beyond. J. Plasma Phys. 84, 715840201.CrossRefGoogle Scholar
Kunz, M.W., Schekochihin, A.A., Chen, C.H.K., Abel, I.G. & Cowley, S.C. 2015 Inertial-range kinetic turbulence in pressure-anisotropic astrophysical plasmas. J. Plasma Phys. 81, 325810501.CrossRefGoogle Scholar
Kunz, M.W., Schekochihin, A.A. & Stone, J.M. 2014 Firehose and mirror instabilities in a collisionless shearing plasma. Phys. Rev. Lett. 112, 205003.CrossRefGoogle Scholar
Kunz, M.W., Squire, J., Schekochihin, A.A. & Quataert, E. 2020 Self-sustaining sound in collisionless, high-$\beta$ plasma. J. Plasma Phys. 86, 905860603.CrossRefGoogle Scholar
Kunz, M.W., Stone, J.M. & Quataert, E. 2016 Magnetorotational turbulence and dynamo in a collisionless plasma. Phys. Rev. Lett. 117, 235101.CrossRefGoogle Scholar
Lalescu, C.C., Shi, Y. -K., Eyink, G.L., Drivas, T.D., Vishniac, E.T. & Lazarian, A. 2015 Inertial-range reconnection in magnetohydrodynamic turbulence and in the solar wind. Phys. Rev. Lett. 115, 025001.CrossRefGoogle ScholarPubMed
Landau, L. 1946 On the vibration of the electronic plasma. Zh. Eksp. Teor. Fiz. 16, 574.Google Scholar
Landau, L.D. & Lifshitz, E.M. 1987 Fluid Mechanics. Pergamon Press.Google Scholar
Landi, S., Del Zanna, L., Papini, E., Pucci, F. & Velli, M. 2015 Resistive magnetohydrodynamics simulations of the ideal tearing mode. Astrophys. J. 806, 131.CrossRefGoogle Scholar
Lapenta, G. 2008 Self-feeding turbulent magnetic reconnection on macroscopic scales. Phys. Rev. Lett. 100, 235001.CrossRefGoogle ScholarPubMed
Lazarian, A., Eyink, G., Vishniac, E. & Kowal, G. 2015 Turbulent reconnection and its implications. Phil. Trans. R. Soc. Lond. A 373, 20140144.Google ScholarPubMed
Lazarian, A., Eyink, G.L., Jafari, A., Kowal, G., Li, H., Xu, S. & Vishniac, E.T. 2020 3D turbulent reconnection: theory, tests and astrophysical implications. Phys. Plasmas 27, 012305.CrossRefGoogle Scholar
Lazarian, A. & Vishniac, E.T. 1999 Reconnection in a weakly stochastic field. Astrophys. J. 517, 700.CrossRefGoogle Scholar
Lazarian, A., Vishniac, E.T. & Cho, J. 2004 Magnetic field structure and stochastic reconnection in a partially ionized gas. Astrophys. J. 603, 180.Google Scholar
Lee, E., Brachet, M.E., Pouquet, A., Mininni, P.D. & Rosenberg, D. 2010 Lack of universality in decaying magnetohydrodynamic turbulence. Phys. Rev. E 81, 016318.CrossRefGoogle ScholarPubMed
Lee, L.C. & Fu, Z.F. 1986 Multiple X line reconnection. I. A criterion for the transition from a single X line to a multiple X line reconnection. J. Geophys. Res. 91, 6807.CrossRefGoogle Scholar
Levich, E. 2009 Coherence in turbulence: new perspective. Old New Concepts Phys. 6, 239.CrossRefGoogle Scholar
Levich, E., Shtilman, L. & Tur, A.V. 1991 The origin of coherence in hydrodynamical turbulence. Physica A 176, 241.CrossRefGoogle Scholar
Levich, E. & Tsinober, A. 1983 On the role of helical structures in three-dimensional turbulent flow. Phys. Lett. A 93, 293.CrossRefGoogle Scholar
Lithwick, Y. & Goldreich, P. 2003 Imbalanced weak magnetohydrodynamic turbulence. Astrophys. J. 582, 1220.CrossRefGoogle Scholar
Lithwick, Y., Goldreich, P. & Sridhar, S. 2007 Imbalanced strong MHD turbulence. Astrophys. J. 655, 269.CrossRefGoogle Scholar
Lomonosov, M.V. 1748 Letter to L. Euler, 5 July 1748. http://lomonosov.niv.ru/lomonosov/pisma/letter-12.htm.Google Scholar
Loureiro, N.F. 2016 Unpublished.Google Scholar
Loureiro, N.F. & Boldyrev, S. 2017 a Collisionless reconnection in magnetohydrodynamic and kinetic turbulence. Astrophys. J. 850, 182.CrossRefGoogle Scholar
Loureiro, N.F. & Boldyrev, S. 2017 b Role of magnetic reconnection in magnetohydrodynamic turbulence. Phys. Rev. Lett. 118, 245101.CrossRefGoogle ScholarPubMed
Loureiro, N.F. & Boldyrev, S. 2018 Turbulence in magnetized pair plasmas. Astrophys. J. 866, L14.CrossRefGoogle Scholar
Loureiro, N.F. & Boldyrev, S. 2020 Nonlinear reconnection in magnetized turbulence. Astrophys. J. 890, 55.CrossRefGoogle Scholar
Loureiro, N.F., Cowley, S.C., Dorland, W.D., Haines, M.G. & Schekochihin, A.A. 2005 X-point collapse and saturation in the nonlinear tearing mode reconnection. Phys. Rev. Lett. 95, 235003.CrossRefGoogle ScholarPubMed
Loureiro, N.F., Samtaney, R., Schekochihin, A.A. & Uzdensky, D.A. 2012 Magnetic reconnection and stochastic plasmoid chains in high-Lundquist-number plasmas. Phys. Plasmas 19, 042303.CrossRefGoogle Scholar
Loureiro, N.F., Schekochihin, A.A. & Cowley, S.C. 2007 Instability of current sheets and formation of plasmoid chains. Phys. Plasmas 14, 100703.CrossRefGoogle Scholar
Loureiro, N.F., Schekochihin, A.A. & Uzdensky, D.A. 2013 a Plasmoid and Kelvin-Helmholtz instabilities in Sweet-Parker current sheets. Phys. Rev. E 87, 013102.CrossRefGoogle ScholarPubMed
Loureiro, N.F., Schekochihin, A.A. & Zocco, A. 2013 b Fast collisionless reconnection and electron heating in strongly magnetized plasmas. Phys. Rev. Lett. 111, 025002.CrossRefGoogle ScholarPubMed
Loureiro, N.F., Uzdensky, D.A., Schekochihin, A.A., Cowley, S.C. & Yousef, T.A. 2009 Turbulent magnetic reconnection in 2D. Mon. Not. R. Astron. Soc. 399, L146.CrossRefGoogle Scholar
Lugones, R., Dmitruk, P., Mininni, P.D., Pouquet, A. & Matthaeus, W.H. 2019 Spatio-temporal behavior of magnetohydrodynamic fluctuations with cross-helicity and background magnetic field. Phys. Plasmas 26, 122301.CrossRefGoogle Scholar
Lugones, R., Dmitruk, P., Mininni, P.D., Wan, M. & Matthaeus, W.H. 2016 On the spatio-temporal behavior of magnetohydrodynamic turbulence in a magnetized plasma. Phys. Plasmas 23, 112304.CrossRefGoogle Scholar
Lumley, J.L. 1969 Drag reduction by additives. Annu. Rev. Fluid Mech. 1, 367.Google Scholar
Luo, Q.Y. & Wu, D.J. 2010 Observations of anisotropic scaling of solar wind turbulence. Astrophys. J. 714, L138.CrossRefGoogle Scholar
Mac Low, M.-M., Klessen, R.S., Burkert, A. & Smith, M.D. 1998 Kinetic energy decay rates of supersonic and super-Alfvénic turbulence in star-forming clouds. Phys. Rev. Lett. 80, 2754.Google Scholar
Malara, F., Veltri, P. & Carbone, V. 1992 Competition among nonlinear effects in tearing instability saturation. Phys. Fluids B 4, 3070.CrossRefGoogle Scholar
Mallet, A. 2020 The onset of electron-only reconnection. J. Plasma Phys. 86, 905860301.CrossRefGoogle Scholar
Mallet, A., Klein, K.G., Chandran, B.D.G., Grošelj, D., Hoppock, I.W., Bowen, T.A., Salem, C.S. & Bale, S.D. 2019 Interplay between intermittency and dissipation in collisionless plasma turbulence. J. Plasma Phys. 85, 175850302.CrossRefGoogle Scholar
Mallet, A. & Schekochihin, A.A. 2011 Simulations of imbalanced RMHD turbulence. Unpublished.Google Scholar
Mallet, A. & Schekochihin, A.A. 2017 A statistical model of three-dimensional anisotropy and intermittency in strong Alfvénic turbulence. Mon. Not. R. Astron. Soc. 466, 3918.CrossRefGoogle Scholar
Mallet, A., Schekochihin, A.A. & Chandran, B.D.G. 2015 Refined critical balance in strong Alfvénic turbulence. Mon. Not. R. Astron. Soc. 449, L77.CrossRefGoogle Scholar
Mallet, A., Schekochihin, A.A. & Chandran, B.D.G. 2017 a Disruption of Alfvénic turbulence by magnetic reconnection in a collisionless plasma. J. Plasma Phys. 83, 905830609.CrossRefGoogle Scholar
Mallet, A., Schekochihin, A.A. & Chandran, B.D.G. 2017 b Disruption of sheetlike structures in Alfvénic turbulence by magnetic reconnection. Mon. Not. R. Astron. Soc. 468, 4862.CrossRefGoogle Scholar
Mallet, A., Schekochihin, A.A., Chandran, B.D.G., Chen, C.H.K., Horbury, T.S., Wicks, R.T. & Greenan, C.C. 2016 Measures of three-dimensional anisotropy and intermittency in strong Alfvénic turbulence. Mon. Not. R. Astron. Soc. 459, 2130.CrossRefGoogle Scholar
Maron, J., Cowley, S. & McWilliams, J. 2004 The nonlinear magnetic cascade. Astrophys. J. 603, 569.CrossRefGoogle Scholar
Maron, J. & Goldreich, P. 2001 Simulations of incompressible magnetohydrodynamic turbulence. Astrophys. J. 554, 1175.CrossRefGoogle Scholar
Marsch, E. 2006 Kinetic physics of the solar corona and solar wind. Living Rev. Sol. Phys. 3, 1.CrossRefGoogle Scholar
Marsch, E. 2018 Solar wind and kinetic heliophysics. Ann. Geohys. 36, 1607.CrossRefGoogle Scholar
Martinović, M.M., Klein, K.G., Kasper, J.C., Case, A.W., Korreck, K.E., Larson, D., Livi, R., Stevens, M., Whittlesey, P., Chandran, B.D.G., et al. 2020 The enhancement of proton stochastic heating in the near-Sun solar wind. Astrophys. J. Suppl. 246, 30.CrossRefGoogle Scholar
Mason, J., Cattaneo, F. & Boldyrev, S. 2006 Dynamic alignment in driven magnetohydrodynamic turbulence. Phys. Rev. Lett. 97, 255002.CrossRefGoogle ScholarPubMed
Mason, J., Cattaneo, F. & Boldyrev, S. 2008 Numerical measurements of the spectrum in magnetohydrodynamic turbulence. Phys. Rev. E 77, 036403.CrossRefGoogle ScholarPubMed
Mason, J., Perez, J.C., Boldyrev, S. & Cattaneo, F. 2012 Numerical simulations of strong incompressible magnetohydrodynamic turbulence. Phys. Plasmas 19, 055902.CrossRefGoogle Scholar
Mason, J., Perez, J.C., Cattaneo, F. & Boldyrev, S. 2011 Extended scaling laws in numerical simulations of magnetohydrodynamic turbulence. Astrophys. J. 735, L26.CrossRefGoogle Scholar
Matthaeus, W.H., Ghosh, S., Oughton, S. & Roberts, D.A. 1996 Anisotropic three-dimensional MHD turbulence. J. Geophys. Res. 101, 7619.CrossRefGoogle Scholar
Matthaeus, W.H. & Goldstein, M.L. 1982 Measurement of the rugged invariants of magnetohydrodynamic turbulence in the solar wind. J. Geophys. Res. 87, 6011.CrossRefGoogle Scholar
Matthaeus, W.H. & Lamkin, S.L. 1985 Rapid magnetic reconnection caused by finite amplitude fluctuations. Phys. Fluids 28, 303.CrossRefGoogle Scholar
Matthaeus, W.H. & Lamkin, S.L. 1986 Turbulent magnetic reconnection. Phys. Fluids 29, 2513.CrossRefGoogle Scholar
Matthaeus, W.H. & Montgomery, D. 1980 Selective decay hypothesis at high mechanical and magnetic Reynolds numbers. Ann. N.Y. Acad. Sci. 357, 203.CrossRefGoogle Scholar
Matthaeus, W.H., Montgomery, D.C. & Goldstein, M.L. 1983 Turbulent generation of outward-traveling interplanetary Alfvénic fluctuations. Phys. Rev. Lett. 51, 1484.Google Scholar
Matthaeus, W.H., Pouquet, A., Mininni, P.D., Dmitruk, P. & Breech, B. 2008 Rapid alignment of velocity and magnetic field in magnetohydrodynamic turbulence. Phys. Rev. Lett. 100, 085003.CrossRefGoogle ScholarPubMed
Matthaeus, W.H., Servidio, S., Dmitruk, P., Carbone, V., Oughton, S., Wan, M. & Osman, K.T. 2012 Local anisotropy, higher order statistics, and turbulence spectra. Astrophys. J. 750, 103.Google Scholar
Matthaeus, W.H., Wan, M., Servidio, S., Greco, A., Osman, K.T., Oughton, S. & Dmitruk, P. 2015 Intermittency, nonlinear dynamics and dissipation in the solar wind and astrophysical plasmas. Phil. Trans. R. Soc. Lond. A 373, 20140154.Google ScholarPubMed
Matthaeus, W.H., Yang, Y., Wan, M., Parashar, T.N., Bandyopadhyay, R., Chasapis, A., Pezzi, O. & Valentini, F. 2020 Pathways to dissipation in weakly collisional plasmas. Astrophys. J. 891, 101.CrossRefGoogle Scholar
McKay, M.E., Berera, A. & Ho, R.D.J.G. 2019 Fully resolved array of simulations investigating the influence of the magnetic Prandtl number on magnetohydrodynamic turbulence. Phys. Rev. E 99, 013101.CrossRefGoogle ScholarPubMed
Melville, S., Schekochihin, A.A. & Kunz, M.W. 2016 Pressure-anisotropy-driven microturbulence and magnetic-field evolution in shearing, collisionless plasma. Mon. Not. R. Astron. Soc. 459, 2701.CrossRefGoogle Scholar
Meneguzzi, M., Frisch, U. & Pouquet, A. 1981 Helical and nonhelical turbulent dynamos. Phys. Rev. Lett. 47, 1060.CrossRefGoogle Scholar
Meyrand, R., Galtier, S. & Kiyani, K.H. 2016 Direct evidence of the transition from weak to strong magnetohydrodynamic turbulence. Phys. Rev. Lett. 116, 105002.CrossRefGoogle ScholarPubMed
Meyrand, R., Kanekar, A., Dorland, W. & Schekochihin, A.A. 2019 Fluidization of collisionless plasma turbulence. Proc. Natl Acad. Sci. USA 116, 1185.CrossRefGoogle ScholarPubMed
Meyrand, R., Kiyani, K.H. & Galtier, S. 2015 Weak magnetohydrodynamic turbulence and intermittency. J. Fluid Mech. 770, R1.CrossRefGoogle Scholar
Meyrand, R. & Squire, J. 2020 private communication.Google Scholar
Meyrand, R., Squire, J., Schekochihin, A.A. & Dorland, W. 2021 On the violation of the zeroth law of turbulence in space plasmas. J. Plasma Phys. 87, 535870301.CrossRefGoogle Scholar
Milanese, L.M., Loureiro, N.F., Daschner, M. & Boldyrev, S. 2020 Dynamic phase alignment in inertial Alfvén turbulence. Phys. Rev. Lett. 125, 265101.CrossRefGoogle ScholarPubMed
Milano, L.J., Matthaeus, W.H., Dmitruk, P. & Montgomery, D.C. 2001 Local anisotropy in incompressible magnetohydrodynamic turbulence. Phys. Plasmas 8, 2673.CrossRefGoogle Scholar
Militello, F., Romanelli, M., Hastie, R.J. & Loureiro, N.F. 2009 Effect of current corrugations on the stability of the tearing mode. Phys. Plasmas 16, 032101.CrossRefGoogle Scholar
Miloshevich, G., Laveder, D., Passot, T. & Sulem, P.-L. 2021 Inverse cascade and magnetic vortices in kinetic Alfvén-wave turbulence. J. Plasma Phys. 87, 905870201.CrossRefGoogle Scholar
Mininni, P.D., Pouquet, A.G. & Montgomery, D.C. 2006 Small-scale structures in three-dimensional magnetohydrodynamic turbulence. Phys. Rev. Lett. 97, 244503.CrossRefGoogle ScholarPubMed
Moffatt, H.K. 1986 Magnetostatic equilibria and analogous Euler flows of arbitrarily complex topology. Part 2. Stability considerations. J. Fluid Mech. 166, 359.CrossRefGoogle Scholar
Montgomery, D. & Turner, L. 1981 Anisotropic magnetohydrodynamic turbulence in a strong external magnetic field. Phys. Fluids 24, 825.CrossRefGoogle Scholar
Montgomery, D., Turner, L. & Vahala, G. 1978 Three-dimensional magnetohydrodynamic turbulence in cylindrical geometry. Phys. Fluids 21, 757.CrossRefGoogle Scholar
Montgomery, D., Turner, L. & Vahala, G. 1979 Most probable states in magnetohydrodynamics. J. Plasma Phys. 21, 239.CrossRefGoogle Scholar
Müller, W.-C. & Biskamp, D. 2000 Scaling properties of three-dimensional magnetohydrodynamic turbulence. Phys. Rev. Lett. 84, 475.CrossRefGoogle ScholarPubMed
Müller, W.-C., Biskamp, D. & Grappin, R. 2003 Statistical anisotropy of magnetohydrodynamic turbulence. Phys. Rev. E 67, 066302.CrossRefGoogle ScholarPubMed
Müller, W.-C. & Grappin, R. 2005 Spectral energy dynamics in magnetohydrodynamic turbulence. Phys. Rev. Lett. 95, 114502.CrossRefGoogle ScholarPubMed
Müller, W.-C., Malapaka, S.K. & Busse, A. 2012 Inverse cascade of magnetic helicity in magnetohydrodynamic turbulence. Phys. Rev. E 85, 015302.CrossRefGoogle ScholarPubMed
Nättilä, J. & Beloborodov, A.M. 2022 Heating of magnetically dominated plasma by Alfvén wave turbulence. Phys. Rev. Lett. 128, 075101.CrossRefGoogle ScholarPubMed
Nazarenko, S. 2007 2D enslaving of MHD turbulence. New J. Phys. 9, 307.CrossRefGoogle Scholar
Nazarenko, S. 2011 Wave Turbulence. Springer.CrossRefGoogle Scholar
Nazarenko, S.V. & Schekochihin, A.A. 2011 Critical balance in magnetohydrodynamic, rotating and stratified turbulence: towards a universal scaling conjecture. J. Fluid Mech. 677, 134.CrossRefGoogle Scholar
Ng, C.S. & Bhattacharjee, A. 1996 Interaction of shear-Alfven wave packets: implication for weak magnetohydrodynamic turbulence in astrophysical plasmas. Astrophys. J. 465, 845.CrossRefGoogle Scholar
Ng, C.S. & Bhattacharjee, A. 1997 Scaling of anisotropic spectra due to the weak interaction of shear-Alfvén wave packets. Phys. Plasmas 4, 605.CrossRefGoogle Scholar
Ni, L., Germaschewski, K., Huang, Y.-M., Sullivan, B.P., Yang, H. & Bhattacharjee, A. 2010 Linear plasmoid instability of thin current sheets with shear flow. Phys. Plasmas 17, 052109.CrossRefGoogle Scholar
Ogilvie, G.I. & Proctor, M.R.E. 2003 On the relation between viscoelastic and magnetohydrodynamic flows and their instabilities. J. Fluid Mech. 476, 389.CrossRefGoogle Scholar
Oishi, J.S., Mac Low, M. -M., Collins, D.C. & Tamura, M. 2015 Self-generated turbulence in magnetic reconnection. Astrophys. J. 806, L12.CrossRefGoogle Scholar
Olesen, P. 1997 Inverse cascades and primordial magnetic fields. Phys. Lett. B 398, 321.CrossRefGoogle Scholar
Olesen, P. 2015 Dimensional reduction in freely decaying turbulent non-helical magnetic fields. arXiv:1511.05007.Google Scholar
Osman, K.T., Matthaeus, W.H., Gosling, J.T., Greco, A., Servidio, S., Hnat, B., Chapman, S.C. & Phan, T.D. 2014 Magnetic reconnection and intermittent turbulence in the solar wind. Phys. Rev. Lett. 112, 215002.CrossRefGoogle Scholar
Osman, K.T., Wan, M., Matthaeus, W.H., Breech, B. & Oughton, S. 2011 Directional alignment and non-Gaussian statistics in solar wind turbulence. Astrophys. J. 741, 75.CrossRefGoogle Scholar
Ottaviani, M. & Porcelli, F. 1993 Nonlinear collisionless magnetic reconnection. Phys. Rev. Lett. 71, 3802.CrossRefGoogle ScholarPubMed
Oughton, S., Matthaeus, W.H. & Dmitruk, P. 2017 Reduced MHD in astrophysical applications: two-dimensional or three-dimensional? Astrophys. J. 839, 2.CrossRefGoogle Scholar
Oughton, S., Priest, E.R. & Matthaeus, W.H. 1994 The influence of a mean magnetic field on three-dimensional magnetohydrodynamic turbulence. J. Fluid Mech. 280, 95.CrossRefGoogle Scholar
Paris, R.B. & Sy, W.N. -C. 1983 Influence of equilibrium shear flow along the magnetic field on the resistive tearing instability. Phys. Fluids 26, 2966.CrossRefGoogle Scholar
Park, K. 2017 On the inverse transfer of (non-)helical magnetic energy in a decaying magnetohydrodynamic turbulence. Mon. Not. R. Astron. Soc. 472, 1628.CrossRefGoogle Scholar
Park, W., Monticello, D.A. & White, R.B. 1984 Reconnection rates of magnetic fields including the effects of viscosity. Phys. Fluids 27, 137.CrossRefGoogle Scholar
Parker, E.N. 1957 Sweet's mechanism for merging magnetic fields in conducting fluids. J. Geophys. Res. 62, 509.CrossRefGoogle Scholar
Parker, J.T., Highcock, E.G., Schekochihin, A.A. & Dellar, P.J. 2016 Suppression of phase mixing in drift-kinetic plasma turbulence. Phys. Plasmas 23, 070703.CrossRefGoogle Scholar
Passot, T., Sulem, P.L. & Tassi, E. 2017 Electron-scale reduced fluid models with gyroviscous effects. J. Plasma Phys. 83, 715830402.CrossRefGoogle Scholar
Perez, J.C. & Boldyrev, S. 2008 On weak and strong magnetohydrodynamic turbulence. Astrophys. J. 672, L61.CrossRefGoogle Scholar
Perez, J.C. & Boldyrev, S. 2009 Role of cross-helicity in magnetohydrodynamic turbulence. Phys. Rev. Lett. 102, 025003.CrossRefGoogle ScholarPubMed
Perez, J.C. & Boldyrev, S. 2010 a Numerical simulations of imbalanced strong magnetohydrodynamic turbulence. Astrophys. J. 710, L63.CrossRefGoogle Scholar
Perez, J.C. & Boldyrev, S. 2010 b Strong magnetohydrodynamic turbulence with cross helicity. Phys. Plasmas 17, 055903.CrossRefGoogle Scholar
Perez, J.C. & Chandran, B.D.G. 2013 Direct numerical simulations of reflection-driven, reduced magnetohydrodynamic turbulence from the Sun to the Alfvén critical point. Astrophys. J. 776, 124.CrossRefGoogle Scholar
Perez, J.C., Mason, J., Boldyrev, S. & Cattaneo, F. 2012 On the energy spectrum of strong magnetohydrodynamic turbulence. Phys. Rev. X 2, 041005.Google Scholar
Perez, J.C., Mason, J., Boldyrev, S. & Cattaneo, F. 2014 a Comment on the numerical measurements of the magnetohydrodynamic turbulence spectrum by A. Beresnyak (Phys. Rev. Lett. 106 (2011) 075001; MNRAS 422 (2012) 3495; ApJ 784 (2014) L20). arXiv:1409.8106.Google Scholar
Perez, J.C., Mason, J., Boldyrev, S. & Cattaneo, F. 2014 b Scaling properties of small-scale fluctuations in magnetohydrodynamic turbulence. Astrophys. J. 793, L13.CrossRefGoogle Scholar
Peterson, E.E., Endrizzi, D.A., Beidler, M., Bunkers, K.J., Clark, M., Egedal, J., Flanagan, K., McCollam, K.J., Milhone, J., Olson, J., et al. 2019 A laboratory model for the Parker spiral and magnetized stellar winds. Nat. Phys. 15, 1095.CrossRefGoogle Scholar
Pezzi, O., Servidio, S., Perrone, D., Valentini, F., Sorriso-Valvo, L., Greco, A., Matthaeus, W.H. & Veltri, P. 2018 Velocity-space cascade in magnetized plasmas: numerical simulations. Phys. Plasmas 25, 060704.CrossRefGoogle Scholar
Plunk, G.G., Cowley, S.C., Schekochihin, A.A. & Tatsuno, T. 2010 Two-dimensional gyrokinetic turbulence. J. Fluid Mech. 664, 407.CrossRefGoogle Scholar
Podesta, J.J. 2009 Dependence of solar-wind power spectra on the direction of the local mean magnetic field. Astrophys. J. 698, 986.CrossRefGoogle Scholar
Podesta, J.J. 2011 On the cross-helicity dependence of the energy spectrum in magnetohydrodynamic turbulence. Phys. Plasmas 18, 012907.CrossRefGoogle Scholar
Podesta, J.J. & Bhattacharjee, A. 2010 Theory of incompressible magnetohydrodynamic turbulence with scale-dependent alignment and cross-helicity. Astrophys. J. 718, 1151.CrossRefGoogle Scholar
Podesta, J.J. & Borovsky, J.E. 2010 Scale invariance of normalized cross-helicity throughout the inertial range of solar wind turbulence. Phys. Plasmas 17, 112905.CrossRefGoogle Scholar
Podesta, J.J., Chandran, B.D.G., Bhattacharjee, A., Roberts, D.A. & Goldstein, M.L. 2009 Scale-dependent angle of alignment between velocity and magnetic field fluctuations in solar wind turbulence. J. Geophys. Res. 114, A131107.CrossRefGoogle Scholar
Politano, H. & Pouquet, A. 1998 a Dynamical length scales for turbulent magnetized flows. Geophys. Res. Lett. 25, 273.CrossRefGoogle Scholar
Politano, H. & Pouquet, A. 1998 b von Kármán-Howarth equation for magnetohydrodynamics and its consequences on third-order longitudinal structure and correlation functions. Phys. Rev. E 57, R21.CrossRefGoogle Scholar
Politano, H., Pouquet, A. & Sulem, P.L. 1989 Inertial ranges and resistive instabilities in two-dimensional magnetohydrodynamic turbulence. Phys. Fluids B 1, 2330.CrossRefGoogle Scholar
Porcelli, F. 1987 Viscous resistive magnetic reconnection. Phys. Fluids 30, 1734.CrossRefGoogle Scholar
Porcelli, F., Borgogno, D., Califano, F., Grasso, D., Ottaviani, M. & Pegoraro, F. 2002 Recent advances in collisionless magnetic reconnection. Plasma Phys. Control. Fusion 44, B389.CrossRefGoogle Scholar
Porter, D.H., Jones, T.W. & Ryu, D. 2015 Vorticity, shocks, and magnetic fields in subsonic, ICM-like turbulence. Astrophys. J. 810, 93.CrossRefGoogle Scholar
Pouquet, A., Frisch, U. & Leorat, J. 1976 Strong MHD helical turbulence and the nonlinear dynamo effect. J. Fluid Mech. 77, 321.CrossRefGoogle Scholar
Pouquet, A., Frisch, U. & Meneguzzi, M. 1986 Growth of correlations in magnetohydrodynamic turbulence. Phys. Rev. A 33, 4266.CrossRefGoogle ScholarPubMed
Pouquet, A., Sulem, P.L. & Meneguzzi, M. 1988 Influence of velocity-magnetic field correlations on decaying magnetohydrodynamic turbulence with neutral X points. Phys. Fluids 31, 2635.CrossRefGoogle Scholar
Pucci, F. & Velli, M. 2014 Reconnection of quasi-singular current sheets: the “ideal” tearing mode. Astrophys. J. 780, L19.CrossRefGoogle Scholar
Pucci, F., Velli, M., Tenerani, A. & Del Sarto, D. 2018 Onset of fast “ideal” tearing in thin current sheets: dependence on the equilibrium current profile. Phys. Plasmas 25, 032113.CrossRefGoogle Scholar
Pucci, F., Viviani, M., Valentini, F., Lapenta, G., Matthaeus, W.H. & Servidio, S. 2021 Turbulent magnetogenesis in a collisionless plasma. Astrophys. J. 922, L18.CrossRefGoogle Scholar
Pusztai, I., Juno, J., Brandenburg, A., TenBarge, J.M., Hakim, A., Francisquez, M. & Sundström, A. 2020 Dynamo in weakly collisional nonmagnetized plasmas impeded by Landau damping of magnetic fields. Phys. Rev. Lett. 124, 255102.CrossRefGoogle ScholarPubMed
Quataert, E. & Gruzinov, A. 1999 Turbulence and particle heating in advection-dominated accretion flows. Astrophys. J. 520, 248.CrossRefGoogle Scholar
Rempel, E.L., Chian, A.C. -L., Brandenburg, A., Muñoz, P.R. & Shadden, S.C. 2013 Coherent structures and the saturation of a nonlinear dynamo. J. Fluid Mech. 729, 309.CrossRefGoogle Scholar
Reppin, J. & Banerjee, R. 2017 Nonhelical turbulence and the inverse transfer of energy: a parameter study. Phys. Rev. E 96, 053105.CrossRefGoogle ScholarPubMed
Retinò, A., Sundkvist, D., Vaivads, A., Mozer, F., André, M. & Owen, C.J. 2007 In situ evidence of magnetic reconnection in turbulent plasma. Nat. Phys. 3, 236.CrossRefGoogle Scholar
Richardson, L.F. 1926 Atmospheric diffusion shown on a distance-neighbour graph. Proc. R. Soc. Lond. A 110, 709.Google Scholar
Rincon, F. 2019 Dynamo theories. J. Plasma Phys. 85, 205850401.CrossRefGoogle Scholar
Rincon, F., Califano, F., Schekochihin, A.A. & Valentini, F. 2016 Turbulent dynamo in a collisionless plasma. Proc. Natl Acad. Sci. USA 113, 3950.CrossRefGoogle Scholar
Roberts, D.A., Goldstein, M.L., Klein, L.W. & Matthaeus, W.H. 1987 Origin and evolution of fluctuations in the solar wind—HELIOS observations and Helios-Voyager comparisons. J. Geophys. Res. 92, 12023.CrossRefGoogle Scholar
Robinson, D.C. & Rusbridge, M.G. 1971 Structure of turbulence in the Zeta plasma. Phys. Fluids 14, 2499.CrossRefGoogle Scholar
Roh, S., Ryu, D., Kang, H., Ha, S. & Jang, H. 2019 Turbulence dynamo in the stratified medium of galaxy clusters. Astrophys. J. 883, 138.CrossRefGoogle Scholar
Rovelli, C. 2015 Aristotle's physics: a physicist's look. J. Am. Phil. Assoc. 1, 23.CrossRefGoogle Scholar
Rutherford, P.H. 1973 Nonlinear growth of the tearing mode. Phys. Fluids 16, 1903.CrossRefGoogle Scholar
Saffman, P.G. 1967 The large-scale structure of homogeneous turbulence. J. Fluid Mech. 27, 581.CrossRefGoogle Scholar
Sahoo, G., Perlekar, P. & Pandit, R. 2011 Systematics of the magnetic-Prandtl-number dependence of homogeneous, isotropic magnetohydrodynamic turbulence. New J. Phys. 13, 013036.CrossRefGoogle Scholar
Samtaney, R., Loureiro, N.F., Uzdensky, D.A., Schekochihin, A.A. & Cowley, S.C. 2009 Formation of plasmoid chains in magnetic reconnection. Phys. Rev. Lett. 103, 105004.CrossRefGoogle ScholarPubMed
Schekochihin, A.A. 2022 Lectures on Kinetic Theory and Magnetohydrodynamics of Plasmas. Lecture Notes for the Oxford MMathPhys programme. http://www-thphys.physics.ox.ac.uk/people/AlexanderSchekochihin/KT/2015/KTLectureNotes.pdf.Google Scholar
Schekochihin, A.A. & Cowley, S.C. 2006 Turbulence, magnetic fields, and plasma physics in clusters of galaxies. Phys. Plasmas 13, 056501.CrossRefGoogle Scholar
Schekochihin, A.A. & Cowley, S.C. 2007 Turbulence and magnetic fields in astrophysical plasmas. In Magnetohydrodynamics: Historical Evolution and Trends (ed. S. Molokov, R. Moreau & H.K. Moffatt), p. 85. Springer.CrossRefGoogle Scholar
Schekochihin, A.A., Cowley, S.C., Dorland, W., Hammett, G.W., Howes, G.G., Plunk, G.G., Quataert, E. & Tatsuno, T. 2008 Gyrokinetic turbulence: a nonlinear route to dissipation through phase space. Plasma Phys. Control. Fusion 50, 124024.CrossRefGoogle Scholar
Schekochihin, A.A., Cowley, S.C., Dorland, W., Hammett, G.W., Howes, G.G., Quataert, E. & Tatsuno, T. 2009 Astrophysical gyrokinetics: kinetic and fluid turbulent cascades in magnetized weakly collisional plasmas. Astrophys. J. Suppl. 182, 310.CrossRefGoogle Scholar
Schekochihin, A.A., Cowley, S.C., Hammett, G.W., Maron, J.L. & McWilliams, J.C. 2002 A model of nonlinear evolution and saturation of the turbulent MHD dynamo. New J. Phys. 4, 84.CrossRefGoogle Scholar
Schekochihin, A.A., Cowley, S.C., Rincon, F. & Rosin, M.S. 2010 Magnetofluid dynamics of magnetized cosmic plasma: firehose and gyrothermal instabilities. Mon. Not. R. Astron. Soc. 405, 291.Google Scholar
Schekochihin, A.A., Cowley, S.C., Taylor, S.F., Hammett, G.W., Maron, J.L. & McWilliams, J.C. 2004 a Saturated state of the nonlinear small-scale dynamo. Phys. Rev. Lett. 92, 084504.CrossRefGoogle ScholarPubMed
Schekochihin, A.A., Cowley, S.C., Taylor, S.F., Maron, J.L. & McWilliams, J.C. 2004 b Simulations of the small-scale turbulent dynamo. Astrophys. J. 612, 276.CrossRefGoogle Scholar
Schekochihin, A.A., Iskakov, A.B., Cowley, S.C., McWilliams, J.C., Proctor, M.R.E. & Yousef, T.A. 2007 Fluctuation dynamo and turbulent induction at low magnetic Prandtl numbers. New J. Phys. 9, 300.CrossRefGoogle Scholar
Schekochihin, A.A., Kawazura, Y. & Barnes, M.A. 2019 Constraints on ion versus electron heating by plasma turbulence at low beta. J. Plasma Phys. 85, 905850303.CrossRefGoogle Scholar
Schekochihin, A.A., Nazarenko, S.V. & Yousef, T.A. 2012 Weak Alfvén-wave turbulence revisited. Phys. Rev. E 85, 036406.CrossRefGoogle ScholarPubMed
Schekochihin, A.A., Parker, J.T., Highcock, E.G., Dellar, P.J., Dorland, W. & Hammett, G.W. 2016 Phase mixing versus nonlinear advection in drift-kinetic plasma turbulence. J. Plasma Phys. 82, 905820212.CrossRefGoogle Scholar
Schober, J., Schleicher, D.R.G., Federrath, C., Bovino, S. & Klessen, R.S. 2015 Saturation of the turbulent dynamo. Phys. Rev. E 92, 023010.CrossRefGoogle ScholarPubMed
Seely, H. 2003 The Poetry of D. H. Rumsfeld. https://slate.com/news-and-politics/2003/04/the-poetry-of-donald-rumsfeld.html.Google Scholar
Servidio, S., Chasapis, A., Matthaeus, W.H., Perrone, D., Valentini, F., Parashar, T.N., Veltri, P., Gershman, D., Russell, C.T., Giles, B., et al. 2017 Magnetospheric Multiscale (MMS) observation of plasma velocity-space cascade: Hermite representation and theory. Phys. Rev. Lett. 119, 205101.CrossRefGoogle ScholarPubMed
Servidio, S., Dmitruk, P., Greco, A., Wan, M., Donato, S., Cassak, P.A., Shay, M.A., Carbone, V. & Matthaeus, W.H. 2011 a Magnetic reconnection as an element of turbulence. Nonlinear Proc. Geophys. 18, 675.CrossRefGoogle Scholar
Servidio, S., Greco, A., Matthaeus, W.H., Osman, K.T. & Dmitruk, P. 2011 b Statistical association of discontinuities and reconnection in magnetohydrodynamic turbulence. J. Geophys. Res. 116, A09102.CrossRefGoogle Scholar
Servidio, S., Matthaeus, W.H. & Dmitruk, P. 2008 Depression of nonlinearity in decaying isotropic MHD turbulence. Phys. Rev. Lett. 100, 095005.CrossRefGoogle ScholarPubMed
Servidio, S., Matthaeus, W.H., Shay, M.A., Cassak, P.A. & Dmitruk, P. 2009 Magnetic reconnection in two-dimensional magnetohydrodynamic turbulence. Phys. Rev. Lett. 102, 115003.CrossRefGoogle ScholarPubMed
Servidio, S., Matthaeus, W.H., Shay, M.A., Dmitruk, P., Cassak, P.A. & Wan, M. 2010 Statistics of magnetic reconnection in two-dimensional magnetohydrodynamic turbulence. Phys. Plasmas 17, 032315.CrossRefGoogle Scholar
Seta, A., Bushby, P.J., Shukurov, A. & Wood, T.S. 2020 Saturation mechanism of the fluctuation dynamo at $Pr_{M}\geq 1$. Phys. Rev. Fluids 5, 043702.CrossRefGoogle Scholar
She, Z.-S. & Leveque, E. 1994 Universal scaling laws in fully developed turbulence. Phys. Rev. Lett. 72, 336.CrossRefGoogle ScholarPubMed
She, Z.-S. & Waymire, E.C. 1995 Quantized energy cascade and log-Poisson statistics in fully developed turbulence. Phys. Rev. Lett. 74, 262.CrossRefGoogle ScholarPubMed
Shebalin, J.V., Matthaeus, W.H. & Montgomery, D. 1983 Anisotropy in MHD turbulence due to a mean magnetic field. J. Plasma Phys. 29, 525.CrossRefGoogle Scholar
Shen, C., Lin, J., Murphy, N.A. & Raymond, J.C. 2013 Statistical and spectral properties of magnetic islands in reconnecting current sheets during two-ribbon flares. Phys. Plasmas 20, 072114.CrossRefGoogle Scholar
Shi, C., Velli, M. & Tenerani, A. 2018 Marginal stability of Sweet–Parker type current sheets at low Lundquist numbers. Astrophys. J. 859, 83.Google Scholar
Shibata, K. & Tanuma, S. 2001 Plasmoid-induced-reconnection and fractal reconnection. Earth Planets Space 53, 473.CrossRefGoogle Scholar
Singh, A., Pucci, F., Tenerani, A., Shibata, K., Hillier, A. & Velli, M. 2019 Dynamic evolution of current sheets, ideal tearing, plasmoid formation and generalized fractal reconnection scaling relations. Astrophys. J. 881, 52.CrossRefGoogle Scholar
Skoutnev, V.A. 2022 Critical balance and scaling of stably stratified turbulence at low Prandtl number. arXiv:2205.01540.CrossRefGoogle Scholar
Smith, C.W., Stawarz, J.E., Vasquez, B.J., Forman, M.A. & MacBride, B.T. 2009 Turbulent cascade at 1 AU in high cross-helicity flows. Phys. Rev. Lett. 103, 201101.CrossRefGoogle ScholarPubMed
Son, D.T. 1999 Magnetohydrodynamics of the early Universe and the evolution of primordial magnetic fields. Phys. Rev. D 59, 063008.CrossRefGoogle Scholar
Southwood, D.J. & Kivelson, M.G. 1993 Mirror instability. 1. Physical mechanism of linear instability. J. Geophys. Res. A 98, 9181.CrossRefGoogle Scholar
Squire, J. & Bhattacharjee, A. 2015 Generation of large-scale magnetic fields by small-scale dynamo in shear flows. Phys. Rev. Lett. 115, 175003.CrossRefGoogle ScholarPubMed
Squire, J. & Bhattacharjee, A. 2016 The magnetic shear-current effect: generation of large-scale magnetic fields by the small-scale dynamo. J. Plasma Phys. 82, 535820201.CrossRefGoogle Scholar
Squire, J., Chandran, B.D.G. & Meyrand, R. 2020 In-situ switchback formation in the expanding solar wind. Astrophys. J. 891, L2.CrossRefGoogle Scholar
Squire, J., Kunz, M.W., Quataert, E. & Schekochihin, A.A. 2017 a Kinetic simulations of the interruption of large-amplitude shear-Alfvén waves in a high-$\beta$ plasma. Phys. Rev. Lett. 119, 155101.CrossRefGoogle Scholar
Squire, J., Meyrand, R., Kunz, M.W., Arzamasskiy, L., Schekochihin, A.A. & Quataert, E. 2022 High-frequency heating of the solar wind triggered by low-frequency turbulence. Nat. Astron. 6, 715.CrossRefGoogle Scholar
Squire, J., Quataert, E. & Schekochihin, A.A. 2016 A stringent limit on the amplitude of Alfvénic perturbations in high-beta low-collisionality plasmas. Astrophys. J. 830, L25.CrossRefGoogle Scholar
Squire, J., Schekochihin, A.A. & Quataert, E. 2017 b Amplitude limits and nonlinear damping of shear-Alfvén waves in high-beta low-collisionality plasmas. New J. Phys. 19, 055005.CrossRefGoogle Scholar
Squire, J., Schekochihin, A.A., Quataert, E. & Kunz, M.W. 2019 Magneto-immutable turbulence in weakly collisional plasmas. J. Plasma Phys. 85, 905850114.CrossRefGoogle ScholarPubMed
Sridhar, S. & Goldreich, P. 1994 Toward a theory of interstellar turbulence. 1. Weak Alfvénic turbulence. Astrophys. J. 432, 612.CrossRefGoogle Scholar
St-Onge, D.A. & Kunz, M.W. 2018 Fluctuation dynamo in a collisionless, weakly magnetized plasma. Astrophys. J. 863, L25.CrossRefGoogle Scholar
St-Onge, D.A., Kunz, M.W., Squire, J. & Schekochihin, A.A. 2020 Fluctuation dynamo in a weakly collisional plasma. J. Plasma Phys. 86, 905860503.CrossRefGoogle Scholar
Stanier, A., Daughton, W., Le, A., Li, X. & Bird, R. 2019 Influence of 3D plasmoid dynamics on the transition from collisional to kinetic reconnection. Phys. Plasmas 26, 072121.CrossRefGoogle Scholar
Steinolfson, R.S. & van Hoven, G. 1984 Nonlinear evolution of the resistive tearing mode. Phys. Fluids 27, 1207.CrossRefGoogle Scholar
Strauss, H.R. 1976 Nonlinear, three-dimensional magnetohydrodynamics of noncircular tokamaks. Phys. Fluids 19, 134.CrossRefGoogle Scholar
Stribling, T. & Matthaeus, W.H. 1991 Relaxation processes in a low-order three-dimensional magnetohydrodynamics model. Phys. Fluids B 3, 1848.CrossRefGoogle Scholar
Subramanian, K. 1999 Unified treatment of small- and large-scale dynamos in helical turbulence. Phys. Rev. Lett. 83, 2957.CrossRefGoogle Scholar
Subramanian, K. 2003 Hyperdiffusion in nonlinear large- and small-scale turbulent dynamos. Phys. Rev. Lett. 90, 245003.CrossRefGoogle ScholarPubMed
Sun, H., Yang, Y., Lu, Q., Lu, S., Wan, M. & Wang, R. 2022 Physical regimes of two-dimensional MHD turbulent reconnection in different Lundquist numbers. Astrophys. J. 926, 97.CrossRefGoogle Scholar
Sundkvist, D., Retinò, A., Vaivads, A. & Bale, S.D. 2007 Dissipation in turbulent plasma due to reconnection in thin current sheets. Phys. Rev. Lett. 99, 025004.CrossRefGoogle ScholarPubMed
Sweet, P.A. 1958 The neutral point theory of solar flares. In Electromagnetic Phenomena in Cosmical Physics (ed. B. Lehnert), IAU Symposium, vol. 6, p. 123. Cambridge University Press.CrossRefGoogle Scholar
Syrovatskiǐ, S.I. 1971 Formation of current sheets in a plasma with a frozen-in strong magnetic field. Sov. Phys. JETP 33, 933.Google Scholar
Tajima, T. & Shibata, K. 1997 Plasma Astrophysics. Addison-Wesley.Google Scholar
Tatsuno, T., Dorland, W., Schekochihin, A.A., Plunk, G.G., Barnes, M., Cowley, S.C. & Howes, G.G. 2009 Nonlinear phase mixing and phase-space cascade of entropy in gyrokinetic plasma turbulence. Phys. Rev. Lett. 103, 015003.CrossRefGoogle ScholarPubMed
Taylor, J.B. 1974 Relaxation of toroidal plasma and generation of reverse magnetic fields. Phys. Rev. Lett. 33, 1139.CrossRefGoogle Scholar
Taylor, J.B. & Newton, S.L. 2015 Special topics in plasma confinement. J. Plasma Phys. 81, 205810501.CrossRefGoogle Scholar
Teaca, B., Lalescu, C.C., Knaepen, B. & Carati, D. 2011 Controlling the level of the ideal invariant fluxes for MHD turbulence using TURBO spectral solver. arXiv:1108.2640.Google Scholar
TenBarge, J.M. & Howes, G.G. 2013 Current sheets and collisionless damping in kinetic plasma turbulence. Astrophys. J. 771, L27.CrossRefGoogle Scholar
Tenerani, A., Rappazzo, A.F., Velli, M. & Pucci, F. 2015 a The tearing mode instability of thin current sheets: the transition to fast reconnection in the presence of viscosity. Astrophys. J. 801, 145.CrossRefGoogle Scholar
Tenerani, A. & Velli, M. 2018 Nonlinear firehose relaxation and constant-B field fluctuations. Astrophys. J. 867, L26.CrossRefGoogle Scholar
Tenerani, A. & Velli, M. 2020 a Alfvénic fluctuations in the solar wind: nonlinearities and pressure anisotropy effects. Plasma Phys. Control. Fusion 62, 014001.CrossRefGoogle Scholar
Tenerani, A. & Velli, M. 2020 b Spectral signatures of recursive magnetic field reconnection. Mon. Not. R. Astron. Soc. 491, 4267.CrossRefGoogle Scholar
Tenerani, A., Velli, M. & Hellinger, P. 2017 The parametric instability of Alfvén waves: effects of temperature anisotropy. Astrophys. J. 851, 99.CrossRefGoogle Scholar
Tenerani, A., Velli, M., Pucci, F., Landi, S. & Rappazzo, A.F. 2016 “Ideally” unstable current sheets and the triggering of fast magnetic reconnection. J. Plasma Phys. 82, 535820501.CrossRefGoogle Scholar
Tenerani, A., Velli, M., Rappazzo, A.F. & Pucci, F. 2015 b Magnetic reconnection: recursive current sheet collapse triggered by ideal tearing. Astrophys. J. 813, L32.CrossRefGoogle Scholar
Ting, A.C., Montgomery, D. & Matthaeus, W.H. 1986 Turbulent relaxation processes in magnetohydrodynamics. Phys. Fluids 29, 3261.CrossRefGoogle Scholar
Tolman, E.A., Loureiro, N.F. & Uzdensky, D.A. 2018 Development of tearing instability in a current sheet forming by sheared incompressible flow. J. Plasma Phys. 84, 905840115.CrossRefGoogle Scholar
Tzeferacos, P., Rigby, A., Bott, A.F.A., Bell, A.R., Bingham, R., Casner, A., Cattaneo, F., Churazov, E.M., Emig, J., Fiuza, F., et al. 2018 Laboratory evidence of dynamo amplification of magnetic fields in a turbulent plasma. Nat. Commun. 9, 591.CrossRefGoogle Scholar
Uzdensky, D.A. 2022 Relativistic non-thermal particle acceleration in two-dimensional collisionless magnetic reconnection. J. Plasma Phys. 88, 905880114.CrossRefGoogle Scholar
Uzdensky, D.A. & Boldyrev, S.A. 2006 Unpublished.Google Scholar
Uzdensky, D.A. & Kulsrud, R.M. 2000 Two-dimensional numerical simulation of the resistive reconnection layer. Phys. Plasmas 7, 4018.CrossRefGoogle Scholar
Uzdensky, D.A., Kulsrud, R.M. & Yamada, M. 1996 Theoretical analysis of driven magnetic reconnection experiments. Phys. Plasmas 3, 1220.CrossRefGoogle Scholar
Uzdensky, D.A. & Loureiro, N.F. 2016 Magnetic reconnection onset via disruption of a forming current sheet by the tearing instability. Phys. Rev. Lett. 116, 105003.CrossRefGoogle ScholarPubMed
Uzdensky, D.A., Loureiro, N.F. & Schekochihin, A.A. 2010 Fast magnetic reconnection in the plasmoid-dominated regime. Phys. Rev. Lett. 105, 235002.CrossRefGoogle ScholarPubMed
Vacca, V., Murgia, M., Govoni, F., Enßlin, T., Oppermann, N., Feretti, L., Giovannini, G. & Loi, F. 2018 Magnetic fields in galaxy clusters and in the large-scale structure of the Universe. Galaxies 6, 142.CrossRefGoogle Scholar
Valente, P.C., da Silva, C.B. & Pinho, F.T. 2016 Energy spectra in elasto-inertial turbulence. Phys. Fluids 28, 075108.CrossRefGoogle Scholar
Varshney, A. & Steinberg, V. 2019 Elastic Alfvén waves in elastic turbulence. Nat. Comm. 10, 652.CrossRefGoogle ScholarPubMed
Vazza, F., Locatelli, N., Rajpurohit, K., Banfi, S., Domínguez-Fernández, P., Wittor, D., Angelinelli, M., Inchingolo, G., Brienza, M., Hackstein, S., et al. 2021 Magnetogenesis and the cosmic web: a joint challenge for radio observations and numerical simulations. Galaxies 9, 109.CrossRefGoogle Scholar
Vech, D. & Chen, C.H.K. 2016 Testing the effects of expansion on solar wind turbulence. Astrophys. J. 832, L16.CrossRefGoogle Scholar
Vech, D., Mallet, A., Klein, K.G. & Kasper, J.C. 2018 Magnetic reconnection may control the ion-scale spectral break of solar wind turbulence. Astrophys. J. 855, L27.CrossRefGoogle Scholar
Vega, C., Boldyrev, S. & Roytershteyn, V. 2022 a Spectra of magnetic turbulence in a relativistic plasma. Astrophys. J. 931, L10.CrossRefGoogle Scholar
Vega, C., Boldyrev, S., Roytershteyn, V. & Medvedev, M. 2022 b Turbulence and particle acceleration in a relativistic plasma. Astrophys. J. 924, L19.CrossRefGoogle Scholar
Verdini, A. & Grappin, R. 2015 Imprints of expansion on the local anisotropy of solar wind turbulence. Astrophys. J. 808, L34.CrossRefGoogle Scholar
Verdini, A., Grappin, R., Alexandrova, O., Franci, L., Landi, S., Matteini, L. & Papini, E. 2019 Three-dimensional local anisotropy of velocity fluctuations in the solar wind. Mon. Not. R. Astron. Soc. 486, 3006.CrossRefGoogle Scholar
Verdini, A., Grappin, R., Alexandrova, O. & Lion, S. 2018 3D anisotropy of solar wind turbulence: tubes or ribbons? Astrophys. J. 853, 85 [erratum: Astrophys. J. 867, 168 (2018)].CrossRefGoogle Scholar
Verma, M.K., Roberts, D.A., Goldstein, M.L., Ghosh, S. & Stribling, W.T. 1996 A numerical study of the nonlinear cascade of energy in magnetohydrodynamic turbulence. J. Geophys. Res. 101, 21619.CrossRefGoogle Scholar
Verscharen, D., Chen, C.H.K. & Wicks, R.T. 2017 On kinetic slow modes, fluid slow modes, and pressure-balanced structures in the solar wind. Astrophys. J. 840, 106.CrossRefGoogle Scholar
Waelbroeck, F.L. 1993 Onset of the sawtooth crash. Phys. Rev. Lett. 70, 3259.CrossRefGoogle ScholarPubMed
Walker, J., Boldyrev, S. & Loureiro, N. 2018 Influence of tearing instability on magnetohydrodynamic turbulence. Phys. Rev. E 98, 033209.CrossRefGoogle Scholar
Wan, M., Oughton, S., Servidio, S. & Matthaeus, W.H. 2012 von Kármán self-preservation hypothesis for magnetohydrodynamic turbulence and its consequences for universality. J. Fluid Mech. 697, 296.CrossRefGoogle Scholar
Wan, M., Rappazzo, A.F., Matthaeus, W.H., Servidio, S. & Oughton, S. 2014 Dissipation and reconnection in boundary-driven reduced magnetohydrodynamics. Astrophys. J. 797, 63.CrossRefGoogle Scholar
Wang, Y., Boldyrev, S. & Perez, J.C. 2011 Residual energy in magnetohydrodynamic turbulence. Astrophys. J. 740, L36.CrossRefGoogle Scholar
Wicks, R.T., Horbury, T.S., Chen, C.H.K. & Schekochihin, A.A. 2010 Power and spectral index anisotropy of the entire inertial range of turbulence in the fast solar wind. Mon. Not. R. Astron. Soc. 407, L31.CrossRefGoogle Scholar
Wicks, R.T., Horbury, T.S., Chen, C.H.K. & Schekochihin, A.A. 2011 Anisotropy of imbalanced Alfvénic turbulence in fast solar wind. Phys. Rev. Lett. 106, 045001.CrossRefGoogle ScholarPubMed
Wicks, R.T., Mallet, A., Horbury, T.S., Chen, C.H.K., Schekochihin, A.A. & Mitchell, J.J. 2013 a Alignment and scaling of large-scale fluctuations in the solar wind. Phys. Rev. Lett. 110, 025003.CrossRefGoogle ScholarPubMed
Wicks, R.T., Roberts, D.A., Mallet, A., Schekochihin, A.A., Horbury, T.S. & Chen, C.H.K. 2013 b Correlations at large scales and the onset of turbulence in the fast solar wind. Astrophys. J. 778, 177 [erratum: Astrophys. J. 782, 118 (2014)].CrossRefGoogle Scholar
Wong, K., Zhdankin, V., Uzdensky, D., Werner, G. & Begelman, M. 2020 First-principles demonstration of diffusive-advective particle acceleration in kinetic simulations of relativistic plasma turbulence. Astrophys. J. 893, L7.CrossRefGoogle Scholar
Xu, S. & Lazarian, A. 2016 Turbulent dynamo in a conducting fluid and a partially ionized gas. Astrophys. J. 833, 215.CrossRefGoogle Scholar
Xu, S. & Lazarian, A. 2017 Magnetohydrodynamic turbulence and turbulent dynamo in partially ionized plasma. New J. Phys. 19, 065005.CrossRefGoogle Scholar
Yaglom, A.N. 1949 Local structure of temperature field in a turbulent flow. Dokl. Akad. Nauk SSSR 69, 743.Google Scholar
Yamada, M., Ji, H., Hsu, S., Carter, T., Kulsrud, R., Bretz, N., Jobes, F., Ono, Y. & Perkins, F. 1997 Study of driven magnetic reconnection in a laboratory plasma. Phys. Plasmas 4, 1936.CrossRefGoogle Scholar
Yang, L., Li, H., Guo, F., Li, X., Li, S., He, J., Zhang, L. & Feng, X. 2020 Fast magnetic reconnection with turbulence in high Lundquist number limit. Astrophys. J. 901, L22.CrossRefGoogle Scholar
Yousef, T.A., Heinemann, T., Rincon, F., Schekochihin, A.A., Kleeorin, N., Rogachevskii, I., Cowley, S.C. & McWilliams, J.C. 2008 a Numerical experiments on dynamo action in sheared and rotating turbulence. Astron. Nachr. 329, 737.CrossRefGoogle Scholar
Yousef, T.A., Heinemann, T., Schekochihin, A.A., Kleeorin, N., Rogachevskii, I., Iskakov, A.B., Cowley, S.C. & McWilliams, J.C. 2008 b Generation of magnetic field by combined action of turbulence and shear. Phys. Rev. Lett. 100, 184501.CrossRefGoogle ScholarPubMed
Yousef, T.A., Rincon, F. & Schekochihin, A.A. 2007 Exact scaling laws and the local structure of isotropic magnetohydrodynamic turbulence. J. Fluid Mech. 575, 111.CrossRefGoogle Scholar
Yousef, T.A. & Schekochihin, A.A. 2009 Simulations of weak RMHD turbulence. Unpublished.Google Scholar
Zakharov, V.E., L'vov, V.S. & Falkovich, G. 1992 Kolmogorov Spectra of Turbulence I: Wave Turbulence. Springer.CrossRefGoogle Scholar
Zakharov, V.E. & Sagdeev, R.Z. 1970 Spectrum of acoustic turbulence. Sov. Phys. Dokl. 15, 439.Google Scholar
Zeldovich, Y.B. 1956 The magnetic field in the two-dimensional motion of a conducting turbulent liquid. Zh. Eksp. Teor. Fiz. 31, 154. English translation: Sov. Phys. JETP 4, 460 (1957).Google Scholar
Zhang, Y.-B., Bodenschatz, E., Xu, H. & Xi, H.-D. 2021 Experimental observation of the elastic range scaling in turbulent flow with polymer additives. Sci. Adv. 7, eabd3525.CrossRefGoogle ScholarPubMed
Zhdankin, V. 2022 a Generalized entropy production in collisionless plasma flows and turbulence. Phys. Rev. X 12, 031011.Google Scholar
Zhdankin, V. 2022 b Nonthermal particle acceleration from maximum entropy in collisionless plasmas. J. Plasma Phys. 88, 175880303.CrossRefGoogle Scholar
Zhdankin, V., Boldyrev, S. & Chen, C.H.K. 2016 a Intermittency of energy dissipation in Alfvénic turbulence. Mon. Not. R. Astron. Soc. 457, L69.CrossRefGoogle Scholar
Zhdankin, V., Boldyrev, S., Perez, J.C. & Tobias, S.M. 2014 Energy dissipation in magnetohydrodynamic turbulence: coherent structures or “nanoflares”? Astrophys. J. 795, 127.CrossRefGoogle Scholar
Zhdankin, V., Boldyrev, S. & Uzdensky, D.A. 2016 b Scalings of intermittent structures in magnetohydrodynamic turbulence. Phys. Plasmas 23, 055705.CrossRefGoogle Scholar
Zhdankin, V., Uzdensky, D.A. & Boldyrev, S. 2015 Temporal analysis of dissipative structures in magnetohydrodynamic turbulence. Astrophys. J. 811, 6.CrossRefGoogle Scholar
Zhdankin, V., Uzdensky, D.A. & Kunz, M.W. 2021 Production and persistence of extreme two-temperature plasmas in radiative relativistic turbulence. Astrophys. J. 908, 71.CrossRefGoogle Scholar
Zhdankin, V., Uzdensky, D.A., Perez, J.C. & Boldyrev, S. 2013 Statistical analysis of current sheets in three-dimensional magnetohydrodynamic turbulence. Astrophys. J. 771, 124.CrossRefGoogle Scholar
Zhdankin, V., Werner, G.R., Uzdensky, D.A. & Begelman, M.C. 2017 Kinetic turbulence in relativistic plasma: from thermal bath to nonthermal continuum. Phys. Rev. Lett. 118, 055103.CrossRefGoogle ScholarPubMed
Zhou, M., Bhat, P., Loureiro, N.F. & Uzdensky, D.A. 2019 Magnetic island merger as a mechanism for inverse magnetic energy transfer. Phys. Rev. Res. 1, 012004(R).CrossRefGoogle Scholar
Zhou, M., Loureiro, N.F. & Uzdensky, D.A. 2020 Multi-scale dynamics of magnetic flux tubes and inverse magnetic energy transfer. J. Plasma Phys. 86, 535860401.CrossRefGoogle Scholar
Zhou, M., Wu, D.H., Loureiro, N.F. & Uzdensky, D.A. 2021 Statistical description of coalescing magnetic islands via magnetic reconnection. J. Plasma Phys. 87, 905870620.CrossRefGoogle Scholar
Zhou, M., Zhdankin, V., Kunz, M.W., Loureiro, N.F. & Uzdensky, D.A. 2022 Spontaneous magnetization of collisionless plasma. Proc. Natl Acad. Sci. USA 119, e2119831119.CrossRefGoogle ScholarPubMed
Zienicke, E., Politano, H. & Pouquet, A. 1998 Variable intensity of Lagrangian chaos in the nonlinear dynamo problem. Phys. Rev. Lett. 81, 4640.CrossRefGoogle Scholar
Zocco, A. & Schekochihin, A.A. 2011 Reduced fluid-kinetic equations for low-frequency dynamics, magnetic reconnection, and electron heating in low-beta plasmas. Phys. Plasmas 18, 102309.CrossRefGoogle Scholar
Zrake, J. 2014 Inverse cascade of nonhelical magnetic turbulence in a relativistic fluid. Astrophys. J. 794, L26.CrossRefGoogle Scholar