Published online by Cambridge University Press: 11 October 2019
In hydrodynamic and MHD (magnetohydrodynamic) turbulence, formal expressions for the transfer rates rely on integrals over wavenumber triads 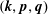 $(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})$ satisfying
$(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})$ satisfying 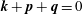 $\boldsymbol{k}+\boldsymbol{p}+\boldsymbol{q}=0$. As an example
$\boldsymbol{k}+\boldsymbol{p}+\boldsymbol{q}=0$. As an example 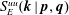 $S_{E}^{uu}(\boldsymbol{k}\mid \boldsymbol{p},\boldsymbol{q})$ denotes the kinetic energy transfer rate to the mode
$S_{E}^{uu}(\boldsymbol{k}\mid \boldsymbol{p},\boldsymbol{q})$ denotes the kinetic energy transfer rate to the mode  $\boldsymbol{k}$, from the two other modes in the triad,
$\boldsymbol{k}$, from the two other modes in the triad, 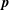 $\boldsymbol{p}$ and
$\boldsymbol{p}$ and 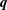 $\boldsymbol{q}$. However as noted by Kraichnan (Phys. Rev., vol. 111, 1958, pp. 1747–1747), in
$\boldsymbol{q}$. However as noted by Kraichnan (Phys. Rev., vol. 111, 1958, pp. 1747–1747), in 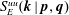 $S_{E}^{uu}(\boldsymbol{k}\mid \boldsymbol{p},\boldsymbol{q})$, what fraction of the energy transferred to the mode
$S_{E}^{uu}(\boldsymbol{k}\mid \boldsymbol{p},\boldsymbol{q})$, what fraction of the energy transferred to the mode 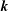 $\boldsymbol{k}$ originated from
$\boldsymbol{k}$ originated from 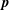 $\boldsymbol{p}$ and which from
$\boldsymbol{p}$ and which from 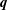 $\boldsymbol{q}$ is unknown. Such an expression is thus incongruent with the customary description of turbulence in terms of two-scale energy exchange. Notwithstanding this issue, Dar et al. (Physica D, vol. 157 (3), 2001, pp. 207–225) further decomposed these transfers into separate contributions from
$\boldsymbol{q}$ is unknown. Such an expression is thus incongruent with the customary description of turbulence in terms of two-scale energy exchange. Notwithstanding this issue, Dar et al. (Physica D, vol. 157 (3), 2001, pp. 207–225) further decomposed these transfers into separate contributions from 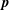 $\boldsymbol{p}$-to-
$\boldsymbol{p}$-to-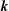 $\boldsymbol{k}$ and
$\boldsymbol{k}$ and  $\boldsymbol{q}$-to-
$\boldsymbol{q}$-to-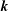 $\boldsymbol{k}$, thus introducing the concept of mode-to-mode transfers that they applied to MHD turbulence. Doing so, they had to set aside additional transfers circulating within each triad, but failed to calculate them. In the present paper we explain how to derive the complete expressions of the mode-to-mode transfers, including the circulating transfers. We do it for kinetic energy and kinetic helicity in hydrodynamic turbulence, for kinetic energy, magnetic energy and magnetic helicity in MHD turbulence. We find that the degree of non-uniqueness of the energy transfers derived from the induction equation is a priori higher than the one derived from the Navier–Stokes equations. However, separating the contribution of magnetic advection from magnetic stretching, the energy mode-to-mode transfer rates involving the magnetic field become uniquely defined, in striking contrast to the hydrodynamic case. The magnetic helicity mode-to-mode transfer rate is also found to be uniquely defined, contrary to kinetic helicity in hydrodynamics. We find that shell-to-shell transfer rates have the same properties as mode-to-mode transfer rates. Finally calculating the fluxes, we show how the circulating transfers cancel in accordance with conservation laws.
$\boldsymbol{k}$, thus introducing the concept of mode-to-mode transfers that they applied to MHD turbulence. Doing so, they had to set aside additional transfers circulating within each triad, but failed to calculate them. In the present paper we explain how to derive the complete expressions of the mode-to-mode transfers, including the circulating transfers. We do it for kinetic energy and kinetic helicity in hydrodynamic turbulence, for kinetic energy, magnetic energy and magnetic helicity in MHD turbulence. We find that the degree of non-uniqueness of the energy transfers derived from the induction equation is a priori higher than the one derived from the Navier–Stokes equations. However, separating the contribution of magnetic advection from magnetic stretching, the energy mode-to-mode transfer rates involving the magnetic field become uniquely defined, in striking contrast to the hydrodynamic case. The magnetic helicity mode-to-mode transfer rate is also found to be uniquely defined, contrary to kinetic helicity in hydrodynamics. We find that shell-to-shell transfer rates have the same properties as mode-to-mode transfer rates. Finally calculating the fluxes, we show how the circulating transfers cancel in accordance with conservation laws.