Article contents
Particle-in-cell simulations of the relaxation of electron beams in inhomogeneous solar wind plasmas
Published online by Cambridge University Press: 29 November 2016
Abstract
Previous theoretical considerations of electron beam relaxation in inhomogeneous plasmas have indicated that the effects of the irregular solar wind may account for the poor agreement of homogeneous modelling with the observations. Quasi-linear theory and Hamiltonian models based on Zakharov’s equations have indicated that when the level of density fluctuations is above a given threshold, density irregularities act to de-resonate the beam–plasma interaction, restricting Langmuir wave growth on the expense of beam energy. This work presents the first fully kinetic particle-in-cell (PIC) simulations of beam relaxation under the influence of density irregularities. We aim to independently determine the influence of background inhomogeneity on the beam–plasma system, and to test theoretical predictions and alternative models using a fully kinetic treatment. We carry out one-dimensional (1-D) PIC simulations of a bump-on-tail unstable electron beam in the presence of increasing levels of background inhomogeneity using the fully electromagnetic, relativistic EPOCH PIC code. We find that in the case of homogeneous background plasma density, Langmuir wave packets are generated at the resonant condition and then quasi-linear relaxation leads to a dynamic increase of wavenumbers generated. No electron acceleration is seen – unlike in the inhomogeneous experiments, all of which produce high-energy electrons. For the inhomogeneous experiments we also observe the generation of backwards-propagating Langmuir waves, which is shown directly to be due to the refraction of the packets off the density gradients. In the case of higher-amplitude density fluctuations, similar features to the weaker cases are found, but also packets can also deviate from the expected dispersion curve in 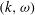 $(k,\unicode[STIX]{x1D714})$ -space due to nonlinearity. Our fully kinetic PIC simulations broadly confirm the findings of quasi-linear theory and the Hamiltonian model based on Zakharov’s equations. Strong density fluctuations modify properties of excited Langmuir waves altering their dispersion properties.
$(k,\unicode[STIX]{x1D714})$ -space due to nonlinearity. Our fully kinetic PIC simulations broadly confirm the findings of quasi-linear theory and the Hamiltonian model based on Zakharov’s equations. Strong density fluctuations modify properties of excited Langmuir waves altering their dispersion properties.
- Type
- Research Article
- Information
- Copyright
- © Cambridge University Press 2016
References
- 15
- Cited by


