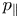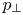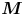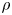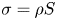1 Introduction
In magnetohydrodynamics (MHD), the ideal Chew–Goldberger–Low (CGL) equations (Chew, Goldberger & Low Reference Chew, Goldberger and Low1956) describe plasmas in which there is not enough scattering of the particles to have an isotropic pressure and only lowest-order gyro-radius effects terms are taken into account in the particle transport (i.e. finite Larmor-radius terms are neglected). These equations can be viewed as the small gyro-radius limit of the Vlasov fluid moment equations, where the pressure tensor has the anisotropic (gyrotropic) form ${\mathsf{{p}}}=p_\perp {\mathsf{{I}}} + (p_\parallel -p_\perp )\boldsymbol {\tau }\boldsymbol {\tau }$![]() . Here $\boldsymbol {\tau }=|\boldsymbol {B}|^{-1}\boldsymbol {B}$
. Here $\boldsymbol {\tau }=|\boldsymbol {B}|^{-1}\boldsymbol {B}$![]() is the unit vector along the magnetic field and ${\mathsf{{I}}}$
is the unit vector along the magnetic field and ${\mathsf{{I}}}$![]() is the identity tensor. The pressure component $p_\parallel -p_\perp$
is the identity tensor. The pressure component $p_\parallel -p_\perp$![]() controls the anisotropy, i.e. the pressure tensor is isotropic if $p_\parallel =p_\perp$
controls the anisotropy, i.e. the pressure tensor is isotropic if $p_\parallel =p_\perp$![]() .
.
Higher-order gyro-radius effects and gyro-viscosity lead to the extended anisotropic MHD equations (see, e.g., Macmahon Reference Macmahon1965; Ramos Reference Ramos2005a,Reference Ramosb; Sulem & Passot Reference Sulem and Passot2015; Hunana et al. Reference Hunana, Teneranii, Zank, Khomenko, Goldstein, Webb, Cally, Collados, Velli and Adhikari2019a). Braginskii (Reference Braginskii1965), Schnack (Reference Schnack2009) and Devlen & Pekünlü (Reference Devlen and Pekünlü2010) used an isotropic pressure decomposition, which is not an anisotropic CGL decomposition. Hunana et al. (Reference Hunana, Passot, Khomenko, Martinez-Gomez, Collados, Zank, Maneva, Goldstein and Webb2022) considered various generalisations of the Braginskii (Reference Braginskii1965) model using the Landau collisional operator for the case of multi-species plasmas. A recent Hamiltonian version of extended gyro-viscous MHD has been developed by Lingam, Morrison & Wurm (Reference Lingam, Morrison and Wurm2020).
In the present work, we develop a variational formulation of the ideal CGL plasma equations starting from the Lagrangian formulation of Newcomb (Reference Newcomb1962). Our main goals are to derive and discuss:
(1) an Euler–Poincaré (EP) action principle;
(2) a non-canonical Poisson bracket and its Casimirs;
(3) conservation laws from application of Noether's theorem to the Galilean group of Lie point symmetries;
(4) a cross-helicity conservation law from particle relabelling symmetries and its non-local nature when the entropy gradients are non-orthogonal to the magnetic field.
Previous work on the CGL equations can be found in Abraham-Shrauner (Reference Abraham-Shrauner1967), Hazeltine, Mahajan & Morrison (Reference Hazeltine, Mahajan and Morrison2013), Holm & Kupershmidt (Reference Holm and Kupershmidt1986), Ramos (Reference Ramos2005a,Reference Ramosb), Hunana et al. (Reference Hunana, Teneranii, Zank, Khomenko, Goldstein, Webb, Cally, Collados, Velli and Adhikari2019a,Reference Hunana, Teneranii, Zank, Khomenko, Goldstein, Webb, Cally, Collados, Adhikari and Vellib) and Du et al. (Reference Du, Zank, Li and Guo2020).
Cheviakov & Bogoyavlenskij (Reference Cheviakov and Bogoyavlenskij2004) and Cheviakov & Anco (Reference Cheviakov and Anco2008) derived exact, anisotropic MHD equilibria solutions of the CGL equations, with a modified equation of state for incompressible fluid flows. Cheviakov & Bogoyavlenskij (Reference Cheviakov and Bogoyavlenskij2004) obtained an infinite group of Lie symmetries of the anisotropic plasma equilibrium equations for steady flow configurations. An infinite-dimensional family of transformations between the isotropic MHD equilibrium equations and solutions of the anisotropic CGL equations were obtained. Ilgisonis (Reference Ilgisonis1996) studied the stability of steady CGL plasma equilibria in a tokamak for a generalised Grad–Shafranov equation, taking into account the fluid relabelling symmetry, and covers previous stability criteria for ideal CGL plasma and ideal MHD cases.
Our methods are adapted from MHD and ideal fluid mechanics. It is well known how to use a Lagrangian map to relate Eulerian and Lagrangian fluid quantities (Newcomb Reference Newcomb1962), and this underpins the EP action principle which is a Lagrangian counterpart of a Hamiltonian formulation (Holm, Marsden & Ratiu Reference Holm, Marsden and Ratiu1998; Webb Reference Webb2018; Webb & Anco Reference Webb and Anco2019). This action principle is based on the Lagrangian map and utilises an associated Lie algebra.
Recent work by Dewar et al. (Reference Dewar, Burby, Qu, Sato and Hole2020) and Dewar & Qu (Reference Dewar and Qu2022) developed variational principles to describe time- dependent relaxed MHD using a global cross-helicity constraint with a phase space Lagrangian action principle (PSL) as opposed to a configuration space Lagrangian (CSL) action. The theory has been used to describe multi-region, extended MHD (RxMHD) in fusion plasma devices. In ideal MHD current sheets can develop. One of the main ideas in this work is to provide a global fitting together of ideal MHD sub-regions, subject to global cross-helicity and magnetic helicity constraints by using Lagrange multipliers. This is a rather complicated theory that lies beyond the scope of the present paper.
Noether's theorem has been used to obtain conservation laws for ideal MHD (Webb & Anco Reference Webb and Anco2019); see also Padhye & Morrison (Reference Padhye and Morrison1996a,Reference Padhye and Morrisonb) and Padhye (Reference Padhye1998). A different approach to deriving conservation laws is Lie dragging of differential forms, vector fields and tensors, as developed by Moiseev et al. (Reference Moiseev, Sagdeev, Tur and Yanovsky1982), Sagdeev, Tur & Yanovskii (Reference Sagdeev, Tur and Yanovskii1990), Tur & Yanovsky (Reference Tur and Yanovsky1993), Webb et al. (Reference Webb, Dasgupta, McKenzie, Hu and Zank2014a,Reference Webb, Dasgupta, McKenzie, Hu and Zankb), Gilbert & Vanneste (Reference Gilbert and Vanneste2020), Besse & Frisch (Reference Besse and Frisch2017) and Anco & Webb (Reference Anco and Webb2020).
Section 2 summarises the ideal CGL plasma equations. The anisotropic pressure components $p_\parallel$![]() and $p_\perp$
and $p_\perp$![]() satisfy double adiabatic conservation laws. The total energy equation for the system arises from combining the internal energy equation, the kinetic energy equation and the electromagnetic energy equation (i.e. Poynting's theorem). The cross-helicity and Galilean conservation laws are obtained for barotropic and non-barotropic gas equations of state. The magnetic helicity transport equation and the conservation of magnetic helicity is described. The thermodynamics of CGL plasmas are discussed. This leads to an internal energy density of the form $e=e(\rho,S,B)$
satisfy double adiabatic conservation laws. The total energy equation for the system arises from combining the internal energy equation, the kinetic energy equation and the electromagnetic energy equation (i.e. Poynting's theorem). The cross-helicity and Galilean conservation laws are obtained for barotropic and non-barotropic gas equations of state. The magnetic helicity transport equation and the conservation of magnetic helicity is described. The thermodynamics of CGL plasmas are discussed. This leads to an internal energy density of the form $e=e(\rho,S,B)$![]() for the plasma (e.g. Holm & Kupershmidt Reference Holm and Kupershmidt1986; Hazeltine et al. Reference Hazeltine, Mahajan and Morrison2013), where $B=|\boldsymbol {B}|$
for the plasma (e.g. Holm & Kupershmidt Reference Holm and Kupershmidt1986; Hazeltine et al. Reference Hazeltine, Mahajan and Morrison2013), where $B=|\boldsymbol {B}|$![]() is the magnitude of the magnetic field. It applies to the situation when reversible energy changes occur, with the temperature of the plasma being given by $T=e_S$
is the magnitude of the magnetic field. It applies to the situation when reversible energy changes occur, with the temperature of the plasma being given by $T=e_S$![]() , and it yields an equation of state which incorporates the double adiabatic conservation laws. A comparison is given with a more restrictive different approach that applies the ideal gas law to the plasma (e.g. Du et al. Reference Du, Zank, Li and Guo2020), with an equation of state being derived as a consequence.
, and it yields an equation of state which incorporates the double adiabatic conservation laws. A comparison is given with a more restrictive different approach that applies the ideal gas law to the plasma (e.g. Du et al. Reference Du, Zank, Li and Guo2020), with an equation of state being derived as a consequence.
Section 3 describes the Lagrangian map between the Eulerian fluid particle position $\boldsymbol {x}$![]() and the Lagrangian particle position $\boldsymbol {x}_0$
and the Lagrangian particle position $\boldsymbol {x}_0$![]() . This map is obtained from integrating the system of ordinary differential equations ${\rm d}\boldsymbol {x}/{\rm d}t=\boldsymbol {u}(\boldsymbol {x},t)$
. This map is obtained from integrating the system of ordinary differential equations ${\rm d}\boldsymbol {x}/{\rm d}t=\boldsymbol {u}(\boldsymbol {x},t)$![]() with the fluid velocity $\boldsymbol {u}(\boldsymbol {x},t)$
with the fluid velocity $\boldsymbol {u}(\boldsymbol {x},t)$![]() assumed to be a known function of $\boldsymbol {x}$
assumed to be a known function of $\boldsymbol {x}$![]() and $t$
and $t$![]() and $\boldsymbol {x}=\boldsymbol {x}_0$
and $\boldsymbol {x}=\boldsymbol {x}_0$![]() at time $t=0$
at time $t=0$![]() . The Lagrangian map $\boldsymbol {x}(\boldsymbol {x}_0,t)$
. The Lagrangian map $\boldsymbol {x}(\boldsymbol {x}_0,t)$![]() is used to write the fluid equations as a variational principle (Newcomb Reference Newcomb1962; Holm et al. Reference Holm, Marsden and Ratiu1998). In this description the canonical coordinates are $\boldsymbol {q}=\boldsymbol {x}(\boldsymbol {x}_0,t)$
is used to write the fluid equations as a variational principle (Newcomb Reference Newcomb1962; Holm et al. Reference Holm, Marsden and Ratiu1998). In this description the canonical coordinates are $\boldsymbol {q}=\boldsymbol {x}(\boldsymbol {x}_0,t)$![]() , and the canonical momenta are defined by the Legendre transformation $\boldsymbol {p}=\partial L_0/\partial \dot {\boldsymbol {x}}$
, and the canonical momenta are defined by the Legendre transformation $\boldsymbol {p}=\partial L_0/\partial \dot {\boldsymbol {x}}$![]() where $L_0$
where $L_0$![]() is the Lagrangian density in a frame moving with the fluid.
is the Lagrangian density in a frame moving with the fluid.
Section 4 develops the EP action principle for the CGL plasma equations by using the general method of Holm et al. (Reference Holm, Marsden and Ratiu1998) and the results of Newcomb (Reference Newcomb1962).
In § 5, the Poisson bracket $\{F,G\}$![]() of functionals $F$
of functionals $F$![]() and $G$
and $G$![]() is described. We obtain the non-canonical Poisson bracket of Holm & Kupershmidt (Reference Holm and Kupershmidt1986) but give more details. By converting the variational derivatives for functionals from the canonical coordinates $(\boldsymbol {q},\boldsymbol {p})$
is described. We obtain the non-canonical Poisson bracket of Holm & Kupershmidt (Reference Holm and Kupershmidt1986) but give more details. By converting the variational derivatives for functionals from the canonical coordinates $(\boldsymbol {q},\boldsymbol {p})$![]() to physically motivated non-canonical coordinates, the Poisson bracket is converted to its non-canonical form in the new variables. The symplectic (i.e. Hamiltonian) form of the non-canonical Poisson bracket is determined, which is useful in proving the Jacobi identity and for writing down the Casimir determining equations. The Casimirs of the Poisson bracket commute with the Hamiltonian functional characterising the system and are obtained using the approach of Hameiri (Reference Hameiri2004) (see also Morrison Reference Morrison1982; Holm et al. Reference Holm, Marsden, Ratiu and Weinstein1985; Marsden & Ratiu Reference Marsden and Ratiu1994; Padhye & Morrison Reference Padhye and Morrison1996a,Reference Padhye and Morrisonb; Padhye Reference Padhye1998).
to physically motivated non-canonical coordinates, the Poisson bracket is converted to its non-canonical form in the new variables. The symplectic (i.e. Hamiltonian) form of the non-canonical Poisson bracket is determined, which is useful in proving the Jacobi identity and for writing down the Casimir determining equations. The Casimirs of the Poisson bracket commute with the Hamiltonian functional characterising the system and are obtained using the approach of Hameiri (Reference Hameiri2004) (see also Morrison Reference Morrison1982; Holm et al. Reference Holm, Marsden, Ratiu and Weinstein1985; Marsden & Ratiu Reference Marsden and Ratiu1994; Padhye & Morrison Reference Padhye and Morrison1996a,Reference Padhye and Morrisonb; Padhye Reference Padhye1998).
Section 6 describes Noether's theorem for the CGL variational principle using the Lagrangian variables. Noether's theorem produces conservation laws in terms of these variables from variational symmetries. The Eulerian form of the conservation laws is obtained through the Lagrangian map by use of a result of Padhye (Reference Padhye1998). The variational symmetries include the Galilean group, in particular: (i) time translation invariance yields energy conservation; (ii) space translation invariance yields momentum conservation; (iii) invariance under Galilean boosts yields centre of mass conservation; (iv) invariance of under rotations yields angular momentum conservation.
In addition, fluid relabelling symmetries are shown to be variational symmetries which yield the generalised cross-helicity conservation law for CGL plasmas. The conditions under which this conservation law is local or non-local are delineated. A local conservation law is shown to arise when the parallel and perpendicular entropies, $S_\parallel$![]() and $S_\perp$
and $S_\perp$![]() , have zero gradient along the magnetic field. Alternatively, for an internal energy density $e=e(\rho,S,B)$
, have zero gradient along the magnetic field. Alternatively, for an internal energy density $e=e(\rho,S,B)$![]() , a local conservation law occurs when $\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla } S=0$
, a local conservation law occurs when $\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla } S=0$![]() . When these conditions fail to hold in the plasma, the cross-helicity conservation law is non-local and depends on the integration of the temperatures back along the Lagrangian fluid particle paths.
. When these conditions fail to hold in the plasma, the cross-helicity conservation law is non-local and depends on the integration of the temperatures back along the Lagrangian fluid particle paths.
The present paper can be thought of as an extension of the work of Holm & Kupershmidt (Reference Holm and Kupershmidt1986). We restrict our analysis to non-relativistic flows, whereas Holm & Kupershmidt (Reference Holm and Kupershmidt1986) study both relativistic and non-relativistic flow versions of the CGL equations. Our analysis is more complete than Holm & Kupershmidt (Reference Holm and Kupershmidt1986) in the following ways. (i) Our analysis takes into account more recent developments in anisotropic moment equations for plasmas with an anisotropic pressure tensor (e.g. Hazeltine et al. Reference Hazeltine, Mahajan and Morrison2013; Hunana et al. Reference Hunana, Teneranii, Zank, Khomenko, Goldstein, Webb, Cally, Collados, Velli and Adhikari2019a). In particular, the formulations of the equation of state and the first law of thermodynamics used by Holm & Kupershmidt (Reference Holm and Kupershmidt1986) were not clear because of the brevity of the exposition. (ii) We show that a slightly more general, non-separable equation of state can be used than that of Hazeltine et al. (Reference Hazeltine, Mahajan and Morrison2013) (see (2.30) and what follows). (iii) We provide a more complete treatment of the conservation laws for the CGL system, and identify the symmetries of the Lagrangian which give rise to the conservation laws in Noether's theorem. Our analysis shows that the cross-helicity conservation law is a consequence of a fluid relabelling symmetry, which is, in general, a non-local conservation law unless $\boldsymbol {B}$![]() is normal to the entropy gradients of $S_\parallel$
is normal to the entropy gradients of $S_\parallel$![]() , $S_\perp$
, $S_\perp$![]() and $S$
and $S$![]() , in which case the conservation law is local. (iv) We describe the CGL Poisson bracket of Holm & Kupershmidt (Reference Holm and Kupershmidt1986) which uses the non-canonical variables $\rho$
, in which case the conservation law is local. (iv) We describe the CGL Poisson bracket of Holm & Kupershmidt (Reference Holm and Kupershmidt1986) which uses the non-canonical variables $\rho$![]() , $\boldsymbol {M}=\rho \boldsymbol {u}$
, $\boldsymbol {M}=\rho \boldsymbol {u}$![]() , $\sigma =\rho S$
, $\sigma =\rho S$![]() and $\boldsymbol {B}$
and $\boldsymbol {B}$![]() . The entropy variable used in the non-canonical Poisson bracket is $\sigma =\rho S$
. The entropy variable used in the non-canonical Poisson bracket is $\sigma =\rho S$![]() where $S$
where $S$![]() is the entropy. The entropy $S$
is the entropy. The entropy $S$![]() can, in turn, be decomposed into the form $S=S_\parallel +S_\perp$
can, in turn, be decomposed into the form $S=S_\parallel +S_\perp$![]() . The non-canonical Poisson bracket derivation in Appendix D is more rigorous than that used by most authors as it takes into account the variations in the basis vectors used to define vectors and tensors. However, these changes do not modify the net Poisson bracket, because they only lead at most to changes in the boundary terms in the bracket which are discarded (see, e.g., Holm, Kupershmidt & Levermore (Reference Holm, Kupershmidt and Levermore1983) for the more rigorous general derivation of the non-canonical Poisson bracket in MHD). (v) We provide a modern version of Noether's theorem which only uses the evolutionary symmetry operator. We describe the classical form of Noether's theorem obtained by Bluman & Kumei (Reference Bluman and Kumei1989), in Appendix H. In § 6.1 we derive CGL conservation laws using the more modern form of Noether's theorem. Section 6.2 gives the classical version of Noether's theorem to derive CGL plasma conservation laws.
. The non-canonical Poisson bracket derivation in Appendix D is more rigorous than that used by most authors as it takes into account the variations in the basis vectors used to define vectors and tensors. However, these changes do not modify the net Poisson bracket, because they only lead at most to changes in the boundary terms in the bracket which are discarded (see, e.g., Holm, Kupershmidt & Levermore (Reference Holm, Kupershmidt and Levermore1983) for the more rigorous general derivation of the non-canonical Poisson bracket in MHD). (v) We provide a modern version of Noether's theorem which only uses the evolutionary symmetry operator. We describe the classical form of Noether's theorem obtained by Bluman & Kumei (Reference Bluman and Kumei1989), in Appendix H. In § 6.1 we derive CGL conservation laws using the more modern form of Noether's theorem. Section 6.2 gives the classical version of Noether's theorem to derive CGL plasma conservation laws.
Section 7 concludes with a summary and discussion.
The various technical derivations used in the main results, and the Lie point symmetries of the CGL system, are summarised in Appendices A to G.
2 CGL equations and conservation laws
In this section, we first summarise the basic CGL plasma model equations, and then we discuss the thermodynamics of CGL plasmas, followed by the key conservation laws in Eulerian form: total energy; cross-helicity and non-local conserved cross-helicity; magnetic helicity. These conservation laws, in later sections, will be related to the variational symmetries of the action principle for the CGL equations and expressed in Lagrangian form. Some general remarks about Eulerian conservation law equations, which will be used in the discussions, are summarised in § 6.
2.1 CGL model
The physical variables which describe CGL plasmas are the fluid velocity $\boldsymbol {u}$![]() , fluid density $\rho$
, fluid density $\rho$![]() , magnetic field induction $\boldsymbol {B}$
, magnetic field induction $\boldsymbol {B}$![]() , the anisotropic pressure components $p_\parallel$
, the anisotropic pressure components $p_\parallel$![]() and $p_\perp$
and $p_\perp$![]() and the entropy $S$
and the entropy $S$![]() . The ideal CGL plasma equations are similar to the MHD equations and consist of: the mass continuity equation
. The ideal CGL plasma equations are similar to the MHD equations and consist of: the mass continuity equation
the momentum equation (in semi-conservative form)
in which ${\mathsf{{p}}}$![]() is the gyrotropic pressure tensor (which replaces the isotropic gas pressure $p{\mathsf{{I}}}$
is the gyrotropic pressure tensor (which replaces the isotropic gas pressure $p{\mathsf{{I}}}$![]() used in MHD) given by
used in MHD) given by
and ${\mathsf{{M}}}_B$![]() is the magnetic pressure tensor
is the magnetic pressure tensor
the entropy transport equation
Faraday's equation and Gauss's law
along with the pressure equations
where ${\mathsf{{p}}}^\parallel$![]() and ${\mathsf{{p}}}^\perp$
and ${\mathsf{{p}}}^\perp$![]() are the terms comprising the gyrotropic pressure tensor
are the terms comprising the gyrotropic pressure tensor
Through Faraday's equation (2.6) and the mass continuity equation (2.1), the pressure equations (2.8)–(2.9) can be expressed as the double adiabatic equations
which represent conservation of the particle magnetic moment and the second longitudinal adiabatic moment of the particles, where ${\rm d}/{\rm d}t=\partial /\partial t+\boldsymbol {u}\boldsymbol {\cdot }\boldsymbol {\nabla }$![]() is the Lagrangian time derivative following the flow.
is the Lagrangian time derivative following the flow.
In the momentum equation (2.2), $\varPhi$![]() is the potential of an external source of gravity (for example, in the case of the solar wind, it could represent the gravitational potential field of the Sun).
is the potential of an external source of gravity (for example, in the case of the solar wind, it could represent the gravitational potential field of the Sun).
If one counts the number of evolution equations in (2.1)–(2.11a,b) there are 10 equations for the 10 variables $\boldsymbol {u}$![]() , $\boldsymbol {B}$
, $\boldsymbol {B}$![]() , $\rho$
, $\rho$![]() , $S$
, $S$![]() , $p_\parallel$
, $p_\parallel$![]() and $p_\perp$
and $p_\perp$![]() . If one does not need to know $S$
. If one does not need to know $S$![]() , then there are nine equations for nine unknowns.
, then there are nine equations for nine unknowns.
The non-canonical Poisson bracket formulation of MHD in Morrison & Greene (Reference Morrison and Greene1982) uses Faraday's law (2.6) in the form $\partial \boldsymbol {B}/\partial t-\boldsymbol {\nabla }\times (\boldsymbol {u}\times \boldsymbol {B}) + \boldsymbol {u}\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {B}=0$![]() for the mathematical case in which $\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {B}\neq 0$
for the mathematical case in which $\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {B}\neq 0$![]() (see also Webb Reference Webb2018). In fact, the possibility of $\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {B}\neq 0$
(see also Webb Reference Webb2018). In fact, the possibility of $\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {B}\neq 0$![]() arises in numerical MHD due to numerical errors in the Gauss’ law (2.7).
arises in numerical MHD due to numerical errors in the Gauss’ law (2.7).
To determine the relationship between the entropy $S$![]() , the internal energy density $\varepsilon$
, the internal energy density $\varepsilon$![]() and the pressure components $p_\parallel$
and the pressure components $p_\parallel$![]() and $p_\perp$
and $p_\perp$![]() in (2.1)–(2.11a,b) we first note that $\varepsilon$
in (2.1)–(2.11a,b) we first note that $\varepsilon$![]() is given by
is given by
A different, related approach comes from the entropy law for ideal gases. We consider and compare both approaches.
One link between the approaches is the observation that integration of the double adiabatic equations (2.11a,b) yields
where the quantities ${\bar {S}}_\parallel$![]() and ${\bar {S}}_\perp$
and ${\bar {S}}_\perp$![]() are dimensionless forms of entropy integration constants arising from integrating the double adiabatic equations (2.11a,b). In principle, ${\bar {S}}_\parallel$
are dimensionless forms of entropy integration constants arising from integrating the double adiabatic equations (2.11a,b). In principle, ${\bar {S}}_\parallel$![]() and ${\bar {S}}_\perp$
and ${\bar {S}}_\perp$![]() must be scalars advected with the flow. In particular, these quantities could be functions of the entropy $S$
must be scalars advected with the flow. In particular, these quantities could be functions of the entropy $S$![]() satisfying (2.5). They could also be functions of other advected invariants of the flow, such as $\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla } S/\rho$
satisfying (2.5). They could also be functions of other advected invariants of the flow, such as $\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla } S/\rho$![]() (e.g. Tur & Yanovsky Reference Tur and Yanovsky1993; Webb et al. Reference Webb, Dasgupta, McKenzie, Hu and Zank2014a). For the sake of simplicity, we assume that $S_\parallel$
(e.g. Tur & Yanovsky Reference Tur and Yanovsky1993; Webb et al. Reference Webb, Dasgupta, McKenzie, Hu and Zank2014a). For the sake of simplicity, we assume that $S_\parallel$![]() and $S_\perp$
and $S_\perp$![]() depend only on $S$
depend only on $S$![]() . The overbars on ${\bar {S}}$
. The overbars on ${\bar {S}}$![]() , ${\bar {S}}_\parallel$
, ${\bar {S}}_\parallel$![]() and ${\bar {S}}_\perp$
and ${\bar {S}}_\perp$![]() denote dimensionless versions of these quantities.
denote dimensionless versions of these quantities.
If these $S_\parallel$![]() and $S_\perp$
and $S_\perp$![]() are functions solely of the entropy $S$
are functions solely of the entropy $S$![]() , then the internal energy density $\varepsilon$
, then the internal energy density $\varepsilon$![]() will have the functional form $\varepsilon (\rho,S,B)$
will have the functional form $\varepsilon (\rho,S,B)$![]() . This form also arises from the first law of thermodynamics coming from the transport equation for $\varepsilon$
. This form also arises from the first law of thermodynamics coming from the transport equation for $\varepsilon$![]() when reversible thermodynamic processes are considered. Strictly speaking, we should use normalised or dimensionless variables in (2.13a,b), i.e. we should have used the variables
when reversible thermodynamic processes are considered. Strictly speaking, we should use normalised or dimensionless variables in (2.13a,b), i.e. we should have used the variables
where the subscript zero quantities are dimensional constants. In a convenient abuse of notation, we have dropped the overbar superscripts in (2.13a,b).
2.2 Thermodynamic formulation
A physical description of $p_\parallel$![]() and $p_\perp$
and $p_\perp$![]() and their relation to the internal energy density $\varepsilon$
and their relation to the internal energy density $\varepsilon$![]() was developed first by Holm & Kupershmidt (Reference Holm and Kupershmidt1986), which in part uses the work of Volkov (Reference Volkov1966), and also later by Hazeltine et al. (Reference Hazeltine, Mahajan and Morrison2013), which discusses both reversible and irreversible thermodynamics. Here we concentrate on the ideal reversible dynamics case.
was developed first by Holm & Kupershmidt (Reference Holm and Kupershmidt1986), which in part uses the work of Volkov (Reference Volkov1966), and also later by Hazeltine et al. (Reference Hazeltine, Mahajan and Morrison2013), which discusses both reversible and irreversible thermodynamics. Here we concentrate on the ideal reversible dynamics case.
An analysis of reversible work done on the plasma reveals that the internal energy per unit mass of the CGL plasma, $e=\varepsilon /\rho$![]() , obeys the Pfaffian equation
, obeys the Pfaffian equation
where $T$![]() is the adiabatic temperature in the plasma. The expression (2.12) for the internal energy density gives the relations
is the adiabatic temperature in the plasma. The expression (2.12) for the internal energy density gives the relations
(see also Holm & Kupershmidt Reference Holm and Kupershmidt1986) and
which is the gas pressure defined by one-third of the trace of the CGL pressure tensor (2.3a–c).
The Pfaffian equation (2.15) constitutes the first law of thermodynamics for a CGL plasma. As outlined in Hazeltine et al. (Reference Hazeltine, Mahajan and Morrison2013), it can be derived from the transport equation for $\varepsilon$![]() under thermodynamic processes that involve reversible work done on the plasma described by the gyrotropic part of the Vlasov distribution function. The derivation can be generalised to include irreversible work comprising a dissipative term and a further term due to gyro-viscosity, which is a non-dissipative term obtained in the limit of no scattering. Equation (2.15) is equivalent to the non-dissipative internal energy equation (2.51) in which a source term $\rho T\,{\rm d}S/{\rm d}t$
under thermodynamic processes that involve reversible work done on the plasma described by the gyrotropic part of the Vlasov distribution function. The derivation can be generalised to include irreversible work comprising a dissipative term and a further term due to gyro-viscosity, which is a non-dissipative term obtained in the limit of no scattering. Equation (2.15) is equivalent to the non-dissipative internal energy equation (2.51) in which a source term $\rho T\,{\rm d}S/{\rm d}t$![]() has been added to the right hand-side.
has been added to the right hand-side.
The above interpretation of (2.15) implies $e=e(\rho,S,B)$![]() along with the thermodynamic relations
along with the thermodynamic relations
Thus, if $e(\rho,S,B)$![]() is known, i.e. an equation of state has been specified, then the relations (2.18a–c) give $p_\parallel$
is known, i.e. an equation of state has been specified, then the relations (2.18a–c) give $p_\parallel$![]() and $p_\perp$
and $p_\perp$![]() as functions of $\rho,S,B$
as functions of $\rho,S,B$![]() . Consistency must hold with the double adiabatic equations (2.11a,b), which constrains the possible expressions for $e(\rho,S,B)$
. Consistency must hold with the double adiabatic equations (2.11a,b), which constrains the possible expressions for $e(\rho,S,B)$![]() .
.
To derive the constraints, we first substitute the relations (2.18a–c) into the internal energy (2.17), giving
This is a first-order partial differential equation for $e(\rho,S,B)$![]() which is easily solved by using the method of characteristics (e.g. Sneddon Reference Sneddon1957):
which is easily solved by using the method of characteristics (e.g. Sneddon Reference Sneddon1957):
Integrating these differential equations yields the general solution
where $f(\xi, S)$![]() is an arbitrary function of $S$
is an arbitrary function of $S$![]() and the similarity variable $\xi$
and the similarity variable $\xi$![]() . Now, the relations (2.18a–c) imply that
. Now, the relations (2.18a–c) imply that
and
Substitution of expressions (2.23a,b) into the double adiabatic equations (2.11a,b) followed by use of the relation $B=\rho ^{2/3}\xi$![]() then yields
then yields
with ${\rm d}f/{\rm d}t = f_\xi \,{\rm d}\xi /{\rm d}t$![]() for any process in which $S$
for any process in which $S$![]() is adiabatic (cf. the entropy equation (2.5)). However, from Faraday's equation (2.6) and the mass continuity equation (2.1), we find that $\xi$
is adiabatic (cf. the entropy equation (2.5)). However, from Faraday's equation (2.6) and the mass continuity equation (2.1), we find that $\xi$![]() obeys the transport equation
obeys the transport equation
Thus, $\xi$![]() is not an advected quantity, which implies that the adiabatic equations (2.24a,b) for $f(\xi,S)$
is not an advected quantity, which implies that the adiabatic equations (2.24a,b) for $f(\xi,S)$![]() reduce to
reduce to
The general solution of this pair of equations is given by
Consequently, expressions (2.23a,b) yield the equation of state
along with the relations
from the double adiabatic integrals (2.13a,b). The corresponding internal energy (2.21a,b) and pressure (2.17) have the explicit form
and
Note that the expressions for $e$![]() and $p$
and $p$![]() in terms of the double adiabatic integrals $\bar {S}_\parallel$
in terms of the double adiabatic integrals $\bar {S}_\parallel$![]() and $\bar {S}_\perp$
and $\bar {S}_\perp$![]() hold independently of any form of equation of state. Finally, either (2.22) or (2.18a–c), both of which rely on $e=e(\rho,S,B)$
hold independently of any form of equation of state. Finally, either (2.22) or (2.18a–c), both of which rely on $e=e(\rho,S,B)$![]() , yield the plasma temperature:
, yield the plasma temperature:
Hazeltine et al. (Reference Hazeltine, Mahajan and Morrison2013) arrived at a similar but less-general result under the assumption that $f$![]() is separable in $S$
is separable in $S$![]() and $\xi$
and $\xi$![]() . This leads to $c_\parallel (S) = Q(S) d_\parallel$
. This leads to $c_\parallel (S) = Q(S) d_\parallel$![]() and $c_\perp (S) = Q(S) d_\perp$
and $c_\perp (S) = Q(S) d_\perp$![]() , where $d_\perp$
, where $d_\perp$![]() and $d_\parallel$
and $d_\parallel$![]() are constants. The assumption of separability includes, for example, the case where the gas pressure $p$
are constants. The assumption of separability includes, for example, the case where the gas pressure $p$![]() satisfies the ideal gas law:
satisfies the ideal gas law:
where $R$![]() is the gas constant. In this case, from the relation (2.17), it follows that $f$
is the gas constant. In this case, from the relation (2.17), it follows that $f$![]() must satisfy the equation $\partial f/\partial S=({2}/{3R}) f$
must satisfy the equation $\partial f/\partial S=({2}/{3R}) f$![]() . Then it further follows that $Q(S)=\exp (2S/(3R))$
. Then it further follows that $Q(S)=\exp (2S/(3R))$![]() .
.
Conditions on the derivatives of the internal energy $e$![]() for thermodynamic stability are discussed in Hazeltine et al. (Reference Hazeltine, Mahajan and Morrison2013), but these considerations lie beyond the scope of the present work.
for thermodynamic stability are discussed in Hazeltine et al. (Reference Hazeltine, Mahajan and Morrison2013), but these considerations lie beyond the scope of the present work.
2.2.1 Ideal gas law and entropy
The double adiabatic equations (2.8) for a CGL plasma can be combined in the form
which suggests the advected quantity $p_\parallel p_\perp ^2/\rho ^5$![]() may be viewed as a function of the entropy $S$
may be viewed as a function of the entropy $S$![]() . A specific functional relation can be motivated by considering the MHD limit for a non-relativistic gas, where the gas entropy is given by the standard formula
. A specific functional relation can be motivated by considering the MHD limit for a non-relativistic gas, where the gas entropy is given by the standard formula
with $C_v$![]() and $C_p$
and $C_p$![]() being the specific heats at constant volume and pressure, respectively. In a CGL plasma, the gas pressure $p$
being the specific heats at constant volume and pressure, respectively. In a CGL plasma, the gas pressure $p$![]() is given by expression (2.17) in terms of the pressure components $p_\parallel$
is given by expression (2.17) in terms of the pressure components $p_\parallel$![]() and $p_\perp$
and $p_\perp$![]() which are equal in the MHD limit, because the pressure tensor (2.3a–c) must become isotropic. This results in the relation $p_\parallel =p_\perp =p$
which are equal in the MHD limit, because the pressure tensor (2.3a–c) must become isotropic. This results in the relation $p_\parallel =p_\perp =p$![]() , and as a consequence $p_\parallel p_\perp ^2/\rho ^5 = p^3/\rho ^5 = \exp ( 3S/C_v)$
, and as a consequence $p_\parallel p_\perp ^2/\rho ^5 = p^3/\rho ^5 = \exp ( 3S/C_v)$![]() by assuming the formula (2.35a,b). Generalising this relation away from the MHD limit then suggests the formula
by assuming the formula (2.35a,b). Generalising this relation away from the MHD limit then suggests the formula

for the entropy of a CGL plasma (see, e.g., Abraham-Shrauner Reference Abraham-Shrauner1967; Du et al. Reference Du, Zank, Li and Guo2020).
Furthermore, because the double adiabatic integrals (2.13a,b) give $p_\parallel p_\perp ^2/\rho ^5=\exp (\bar {S}_\parallel +2\bar {S}_\perp )$![]() where $\bar {S}_\parallel$
where $\bar {S}_\parallel$![]() and $\bar {S}_\perp$
and $\bar {S}_\perp$![]() are each advected, the entropy formula (2.36) can be expressed as $S = (C_v/3) (\bar {S}_\parallel + 2\bar {S}_\perp )$
are each advected, the entropy formula (2.36) can be expressed as $S = (C_v/3) (\bar {S}_\parallel + 2\bar {S}_\perp )$![]() . This relation now suggests that the entropy is a sum of components
. This relation now suggests that the entropy is a sum of components
with
Correspondingly, the internal energy density (2.16a,b) of the plasma can be split into a sum of densities
with effective adiabatic indices:
Further note that
in terms of the gas pressure $p$![]() .
.
In addition, by applying the standard ideal gas law (2.33) to each of the pressure components $p_\parallel$![]() and $p_\perp$
and $p_\perp$![]() , we can define corresponding temperatures:
, we can define corresponding temperatures:
Then the internal energy density (2.39) can be expressed as
which yields the relations
from the specific heats (2.38a,b). Finally, by substituting the double adiabatic integrals (2.13a,b) into the quantities (2.42a,b) and using expressions (2.37) and (2.44a–c), we obtain
which implies the expected thermodynamic relations:
The preceding approach to the entropy of CGL plasmas has been adopted by Du et al. (Reference Du, Zank, Li and Guo2020). It is equivalent to the thermodynamic approach specialised to the case of an ideal gas in which the gas law is assumed to hold for all three pressures $p$![]() , $p_\parallel$
, $p_\parallel$![]() and $p_\perp$
and $p_\perp$![]() .
.
The net upshot of this discussion is that we take $e=e(\rho,S,B)$![]() as the equation of state for the gas in the rest of the paper. Note, however, that $S_\parallel =S_\parallel (S)$
as the equation of state for the gas in the rest of the paper. Note, however, that $S_\parallel =S_\parallel (S)$![]() and $S_\perp (S)=S-S_\parallel (S)$
and $S_\perp (S)=S-S_\parallel (S)$![]() are functions of $S$
are functions of $S$![]() . Here $e=e(\rho,S,B)$
. Here $e=e(\rho,S,B)$![]() is the form of the equation of state used by Holm & Kupershmidt (Reference Holm and Kupershmidt1986). The CGL Poisson bracket of Holm & Kupershmidt (Reference Holm and Kupershmidt1986) uses the entropy variable $\sigma =\rho S$
is the form of the equation of state used by Holm & Kupershmidt (Reference Holm and Kupershmidt1986). The CGL Poisson bracket of Holm & Kupershmidt (Reference Holm and Kupershmidt1986) uses the entropy variable $\sigma =\rho S$![]() to describe the complicated thermodynamics of the CGL plasma.
to describe the complicated thermodynamics of the CGL plasma.
2.3 Total mass and energy conservation laws
The mass continuity equation (2.1) can be expressed in the familiar co-moving form
On a volume $V(t)$![]() moving with the fluid, the corresponding mass integral is conserved:
moving with the fluid, the corresponding mass integral is conserved:
A co-moving equation for the internal energy density (2.12) is obtained by combining the parallel and perpendicular pressure equations (2.8)–(2.9), which yields
This equation can be written in terms of the gyrotropic pressure tensor ${\mathsf{{p}}}$![]() by noting from expression (2.10a–c) that
by noting from expression (2.10a–c) that
Then the co-moving equation (2.49) takes the form
which is analogous to the internal energy density equation in fluid dynamics and MHD.
The total kinetic energy equation for the plasma is obtained by taking the scalar product of the momentum equation (2.2) with $\boldsymbol {u}$![]() , which yields
, which yields
where $u = |\boldsymbol {u}|$![]() , and
, and
are the electric field $\boldsymbol {E}$![]() and the electric current $\boldsymbol {J}$
and the electric current $\boldsymbol {J}$![]() .
.
Using Maxwell's equations (2.6)–(2.7), we obtain Poynting's theorem (the electromagnetic energy equation) in the form:
The equation for the total energy in conserved form is obtained by adding the internal energy equation (2.51), the kinetic energy equation (2.52) and the electromagnetic energy equation (2.54), which gives
It is useful here to note that the Poynting electromagnetic energy flux is
The resulting energy balance equation on a volume $V(t)$![]() moving with the fluid is given by
moving with the fluid is given by
in terms of the magnetic pressure tensor (2.4). The flux terms in (2.57) represent the rate at which the total pressure tensor ${\mathsf{{p}}}+ {\mathsf{{M}}}_B$![]() does work on the fluid. Note that there is no contribution due to advection of the total energy density. Further discussion is provided in § 6.1.1 (see also Padhye Reference Padhye1998; Anco & Dar Reference Anco and Dar2009, Reference Anco and Dar2010). In addition, note that if the total pressure tensor has no perpendicular component at the moving boundary, i.e. $({\mathsf{{p}}}+{\mathsf{{M}}}_B)\boldsymbol {\cdot }\hat {\boldsymbol {n}}=0$
does work on the fluid. Note that there is no contribution due to advection of the total energy density. Further discussion is provided in § 6.1.1 (see also Padhye Reference Padhye1998; Anco & Dar Reference Anco and Dar2009, Reference Anco and Dar2010). In addition, note that if the total pressure tensor has no perpendicular component at the moving boundary, i.e. $({\mathsf{{p}}}+{\mathsf{{M}}}_B)\boldsymbol {\cdot }\hat {\boldsymbol {n}}=0$![]() , then the moving energy integral will be conserved (i.e. a constant of the motion).
, then the moving energy integral will be conserved (i.e. a constant of the motion).
2.4 Cross-helicity
The cross-helicity transport equation for a CGL plasma is obtained by taking the scalar product of $\boldsymbol {u}$![]() with Faraday's equation (2.6) plus the scalar product of $\boldsymbol {B}$
with Faraday's equation (2.6) plus the scalar product of $\boldsymbol {B}$![]() with the momentum equation (2.2), in the following form. By a standard cross-product identity, Faraday's equation can be written
with the momentum equation (2.2), in the following form. By a standard cross-product identity, Faraday's equation can be written
The momentum equation minus $\boldsymbol {u}$![]() times the mass continuity equation (2.1) yields the velocity equation:
times the mass continuity equation (2.1) yields the velocity equation:
where $-(1/\rho )\boldsymbol {\nabla }\boldsymbol {\cdot }{\mathsf{{p}}}$![]() is the acceleration due to the anisotropic pressure. Forming and adding the respective scalar products with $\boldsymbol {u}$
is the acceleration due to the anisotropic pressure. Forming and adding the respective scalar products with $\boldsymbol {u}$![]() and $\boldsymbol {B}$
and $\boldsymbol {B}$![]() then gives the equation for cross-helicity density $\boldsymbol {u}\boldsymbol {\cdot }\boldsymbol {B}$
then gives the equation for cross-helicity density $\boldsymbol {u}\boldsymbol {\cdot }\boldsymbol {B}$![]() as
as
where $u = |\boldsymbol {u}|$![]() .
.
The thermodynamic form of this transport equation (2.60) is obtained by using the equation
which relies on the Pfaffian equation (first law of thermodynamics) (2.15) for a CGL plasma with an internal energy $e(\rho,B,S)$![]() , where, from the thermodynamic relations (2.18a–c), $T=e_S$
, where, from the thermodynamic relations (2.18a–c), $T=e_S$![]() is the gas temperature and $h=\varepsilon _\rho =e+\rho e_\rho$
is the gas temperature and $h=\varepsilon _\rho =e+\rho e_\rho$![]() is the enthalpy of the fluid:
is the enthalpy of the fluid:
Here
Note that the case $\boldsymbol {\varOmega }=0$![]() corresponds to the MHD limit in which the anisotropy vanishes, $p_{\varDelta }=p_\parallel -p_\perp =0$
corresponds to the MHD limit in which the anisotropy vanishes, $p_{\varDelta }=p_\parallel -p_\perp =0$![]() . A derivation of the pressure divergence equation (2.61) is given in Appendix B. An alternative derivation is provided within the EP formulation of the CGL equations in § 4.1 and Appendix E. The scalar product of this equation with $({1}/{\rho })\boldsymbol {B}$
. A derivation of the pressure divergence equation (2.61) is given in Appendix B. An alternative derivation is provided within the EP formulation of the CGL equations in § 4.1 and Appendix E. The scalar product of this equation with $({1}/{\rho })\boldsymbol {B}$![]() reduces to
reduces to
using Gauss’ law (2.7). As a result, the cross-helicity density transport equation in thermodynamic form is simply
The term on the right-hand side of the cross-helicity transport equation (2.65) can be written in a conserved form through use of the equation
which holds for any scalar variable $\phi$![]() and follows from Faraday's equation (2.6) and the entropy equation (2.5). This leads to the non-local cross-helicity density conservation law
and follows from Faraday's equation (2.6) and the entropy equation (2.5). This leads to the non-local cross-helicity density conservation law
in terms of
where $r$![]() is a non-local variable obtained by integrating the temperature $T$
is a non-local variable obtained by integrating the temperature $T$![]() back along the path of the Lagrangian fluid element. Specifically,
back along the path of the Lagrangian fluid element. Specifically,
where ${\rm d}/{\rm d}t=\partial /\partial t+\boldsymbol {u}\boldsymbol {\cdot }\boldsymbol {\nabla }$![]() is the Lagrangian time derivative.
is the Lagrangian time derivative.
The non-local conservation law (2.67) yields a moving cross-helicity balance equation (cf. Appendix C):
on a volume $V(t)$![]() moving with the fluid. Note that if $\boldsymbol {B}$
moving with the fluid. Note that if $\boldsymbol {B}$![]() is perpendicular to the boundary, i.e. $\boldsymbol {B}\boldsymbol {\cdot }\hat {\boldsymbol {n}}=0$
is perpendicular to the boundary, i.e. $\boldsymbol {B}\boldsymbol {\cdot }\hat {\boldsymbol {n}}=0$![]() , then the cross-helicity integral $\int _{V(t)} \boldsymbol {w}\boldsymbol {\cdot }\boldsymbol {B} \,{\rm d}^3\boldsymbol {x}$
, then the cross-helicity integral $\int _{V(t)} \boldsymbol {w}\boldsymbol {\cdot }\boldsymbol {B} \,{\rm d}^3\boldsymbol {x}$![]() is conserved in the flow.
is conserved in the flow.
An alternative form of the non-local conservation law (2.67) is obtained by directly taking the divergence of the pressure tensor ${\mathsf{{p}}}$![]() using the gyrotropic expression (2.10a–c), and combining it with the gradient of the enthalpy (2.62). As shown in Appendix B, this gives
using the gyrotropic expression (2.10a–c), and combining it with the gradient of the enthalpy (2.62). As shown in Appendix B, this gives

in terms of the adiabatic integrals (2.13a,b) and (2.37). Expression (2.71) is equivalent to $-\boldsymbol {B}\boldsymbol {\cdot }(T\boldsymbol {\nabla } S)$![]() through the temperature expression (2.32). Instead, if we use the gas law temperatures (2.49) and the specific heats (2.51) associated with $p_\parallel$
through the temperature expression (2.32). Instead, if we use the gas law temperatures (2.49) and the specific heats (2.51) associated with $p_\parallel$![]() and $p_\perp$
and $p_\perp$![]() , then we can write
, then we can write
in term of the gas law entropies (2.37). Substituting expression (2.72) into the cross-helicity density transport equation (2.65) yields
This result (2.73) can be also derived using the Newcomb (Reference Newcomb1962) action principle for CGL plasmas shown in § 4.
The corresponding non-local cross-helicity density conservation law is given by
where
with $r_\parallel$![]() and $r_\perp$
and $r_\perp$![]() being non-local variables defined by the equations:
being non-local variables defined by the equations:
The non-local cross-helicity density conservation law for MHD analogous to equation (2.67) was developed in Webb et al. (Reference Webb, Dasgupta, McKenzie, Hu and Zank2014a,Reference Webb, Dasgupta, McKenzie, Hu and Zankb), Webb (Reference Webb2018), Webb & Anco (Reference Webb and Anco2019), Yahalom (Reference Yahalom2017a,Reference Yahalomb) and Yahalom & Qin (Reference Yahalom and Qin2021). A topological interpretation of the generalised cross-helicity conservation law has been found in terms of an MHD Aharonov–Bohm effect in Yahalom (Reference Yahalom2017a,Reference Yahalomb). Yahalom (Reference Yahalom2013) discussed a topological interpretation of magnetic helicity as an Aharonov Bohm effect in MHD.
If $\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla } S=0$![]() , then the non-local conservation law (2.67) reduces to a local cross- helicity density conservation law given by $r= 0$
, then the non-local conservation law (2.67) reduces to a local cross- helicity density conservation law given by $r= 0$![]() and $\boldsymbol {w}=\boldsymbol {u}$
and $\boldsymbol {w}=\boldsymbol {u}$![]() . This result is analogous to the local cross-helicity conservation law in MHD (e.g. Webb Reference Webb2018; Webb & Anco Reference Webb and Anco2019).
. This result is analogous to the local cross-helicity conservation law in MHD (e.g. Webb Reference Webb2018; Webb & Anco Reference Webb and Anco2019).
It is interesting to note that the velocity equation (2.59) can be written in the suggestive form:
where
This (2.77) turns out to arise directly from the non-canonical Hamiltonian formulation presented in § 5.1.
2.5 Magnetic helicity
In ideal MHD and in ideal CGL plasmas, Faraday's equation (2.6) written in terms of the electric field
can be uncurled to give $\boldsymbol {E}=-\boldsymbol {u}\times \boldsymbol {B}$![]() in the form
in the form
The uncurled form of Faraday's equation (2.80) implies
Combining the scalar product of Faraday's equation (2.79) with $\boldsymbol {A}$![]() plus the scalar product of the uncurled equation (2.81) with $\boldsymbol {B}$
plus the scalar product of the uncurled equation (2.81) with $\boldsymbol {B}$![]() yields the magnetic helicity transport equation
yields the magnetic helicity transport equation
which can also be written in the form
The total magnetic helicity for a volume $V(t)$![]() moving with the fluid is given by
moving with the fluid is given by
It satisfies the moving balance equation (cf. Appendix C)
where $\hat {\boldsymbol {n}}$![]() is the outward unit normal of the moving boundary $\partial V(t)$
is the outward unit normal of the moving boundary $\partial V(t)$![]() . Thus, if $\boldsymbol {B}$
. Thus, if $\boldsymbol {B}$![]() is perpendicular to the boundary, i.e. $\boldsymbol {B}\boldsymbol {\cdot }\hat {\boldsymbol {n}}=0$
is perpendicular to the boundary, i.e. $\boldsymbol {B}\boldsymbol {\cdot }\hat {\boldsymbol {n}}=0$![]() , then $H^{{M}}$
, then $H^{{M}}$![]() is conserved in the flow. This discussion applies both to ideal MHD and also to ideal CGL plasmas. (e.g. Kruskal & Kulsrud Reference Kruskal and Kulsrud1958; Woltjer Reference Woltjer1958; Moffatt Reference Moffatt1969; Berger & Field Reference Berger and Field1984; Moffatt & Ricca Reference Moffatt and Ricca1992; Arnold & Khesin Reference Arnold and Khesin1998).
is conserved in the flow. This discussion applies both to ideal MHD and also to ideal CGL plasmas. (e.g. Kruskal & Kulsrud Reference Kruskal and Kulsrud1958; Woltjer Reference Woltjer1958; Moffatt Reference Moffatt1969; Berger & Field Reference Berger and Field1984; Moffatt & Ricca Reference Moffatt and Ricca1992; Arnold & Khesin Reference Arnold and Khesin1998).
It is beyond the scope of the present exposition to discuss the issues of how to define the relative magnetic helicity for volumes $V$![]() for which $\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {n}\neq 0$
for which $\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {n}\neq 0$![]() on $\partial V$
on $\partial V$![]() (e.g. Berger & Field Reference Berger and Field1984; Finn & Antonsen Reference Finn and Antonsen1985, Reference Finn and Antonsen1988; Webb et al. Reference Webb, Hu, Dasgupta and Zank2010). Similar considerations apply to field line magnetic helicity (e.g. Prior & Yeates Reference Prior and Yeates2014) and absolute magnetic helicity (e.g. Low Reference Low2006, Reference Low2011; Berger & Hornig Reference Berger and Hornig2018).
(e.g. Berger & Field Reference Berger and Field1984; Finn & Antonsen Reference Finn and Antonsen1985, Reference Finn and Antonsen1988; Webb et al. Reference Webb, Hu, Dasgupta and Zank2010). Similar considerations apply to field line magnetic helicity (e.g. Prior & Yeates Reference Prior and Yeates2014) and absolute magnetic helicity (e.g. Low Reference Low2006, Reference Low2011; Berger & Hornig Reference Berger and Hornig2018).
It is of interest to note that, under gauge transformations (i.e. $\boldsymbol {A}\to \boldsymbol {A}+\boldsymbol {\nabla }\chi$![]() and $\phi _E\to \phi _E -\partial \chi /\partial t$
and $\phi _E\to \phi _E -\partial \chi /\partial t$![]() for an arbitrary function $\chi (t,\boldsymbol {x})$
for an arbitrary function $\chi (t,\boldsymbol {x})$![]() ), the moving balance equation is gauge invariant, but the magnetic helicity integral changes by addition of a boundary integral: $H^{{M}}\to H^{{M}} + \oint _{\partial V(t)} \chi \boldsymbol {B}\boldsymbol {\cdot }\hat {\boldsymbol {n}}\, {\rm d}A$
), the moving balance equation is gauge invariant, but the magnetic helicity integral changes by addition of a boundary integral: $H^{{M}}\to H^{{M}} + \oint _{\partial V(t)} \chi \boldsymbol {B}\boldsymbol {\cdot }\hat {\boldsymbol {n}}\, {\rm d}A$![]() . However, if the electric field potential $\phi _E$
. However, if the electric field potential $\phi _E$![]() satisfies the gauge
satisfies the gauge
then the moving flux of the magnetic helicity vanishes and the resulting (gauge-dependent) magnetic helicity $H^{{M}}$![]() is conserved in the flow. This gauge turns out to hold precisely when $\boldsymbol {A}$
is conserved in the flow. This gauge turns out to hold precisely when $\boldsymbol {A}$![]() is advected by the flow, which is shown in the following subsection.
is advected by the flow, which is shown in the following subsection.
2.6 Lie dragged (advected) quantities
A quantity, $a$![]() , is Lie dragged by the fluid flow if its advective Lie derivative vanishes:
, is Lie dragged by the fluid flow if its advective Lie derivative vanishes:
where ${\mathcal {L}}_{\boldsymbol {u}}$![]() is the ordinary Lie derivative with respect to the vector field $\boldsymbol {u}$
is the ordinary Lie derivative with respect to the vector field $\boldsymbol {u}$![]() (e.g. Tur & Yanovsky Reference Tur and Yanovsky1993; Webb et al. Reference Webb, Dasgupta, McKenzie, Hu and Zank2014a; Anco & Webb Reference Anco and Webb2020). For a scalar quantity, its advective Lie derivative reduces to its material derivative
(e.g. Tur & Yanovsky Reference Tur and Yanovsky1993; Webb et al. Reference Webb, Dasgupta, McKenzie, Hu and Zank2014a; Anco & Webb Reference Anco and Webb2020). For a scalar quantity, its advective Lie derivative reduces to its material derivative
For quantities that are vector fields or differential forms, the advective Lie derivative also contains a rotation-shear term which involves $\boldsymbol {\nabla } \boldsymbol {u}$![]() .
.
In CGL plasmas, $S$![]() is an advected scalar, as are the double adiabatic integrals (2.13a,b). There are two basic advected non-scalar quantities: the differential form ${\boldsymbol {\alpha }}=\boldsymbol {\nabla } S\boldsymbol {\cdot }{\rm d}\boldsymbol {x}\equiv \boldsymbol {\nabla }_i S \,{{\rm d} x}^i$
is an advected scalar, as are the double adiabatic integrals (2.13a,b). There are two basic advected non-scalar quantities: the differential form ${\boldsymbol {\alpha }}=\boldsymbol {\nabla } S\boldsymbol {\cdot }{\rm d}\boldsymbol {x}\equiv \boldsymbol {\nabla }_i S \,{{\rm d} x}^i$![]() and the vector field $\boldsymbol {b}=(1/\rho )\boldsymbol {B}\equiv b^i\ \boldsymbol {\nabla }_i$
and the vector field $\boldsymbol {b}=(1/\rho )\boldsymbol {B}\equiv b^i\ \boldsymbol {\nabla }_i$![]() (note the vector field $\boldsymbol {b}$
(note the vector field $\boldsymbol {b}$![]() is a directional derivative operator). The contraction of the vector field $\boldsymbol {b}$
is a directional derivative operator). The contraction of the vector field $\boldsymbol {b}$![]() with the co-vector or differential form ${\boldsymbol {\alpha }}$
with the co-vector or differential form ${\boldsymbol {\alpha }}$![]() is a scalar (note that $\boldsymbol {\nabla }_i\rfloor \,{{\rm d} x}^j=\delta ^i_j$
is a scalar (note that $\boldsymbol {\nabla }_i\rfloor \,{{\rm d} x}^j=\delta ^i_j$![]() , and $\boldsymbol {b}\rfloor {\boldsymbol {\alpha }}=b^i \alpha _i\equiv b^i\boldsymbol {\nabla }_iS$
, and $\boldsymbol {b}\rfloor {\boldsymbol {\alpha }}=b^i \alpha _i\equiv b^i\boldsymbol {\nabla }_iS$![]() ). Note that $\boldsymbol {b}$
). Note that $\boldsymbol {b}$![]() is Lie dragged with the flow, (this statement is equivalent to Faraday's equation, when one takes into account the mass continuity equation: i.e. $(\partial _t+{\mathcal {L}}_{\boldsymbol {u}})\boldsymbol {b}=0$
is Lie dragged with the flow, (this statement is equivalent to Faraday's equation, when one takes into account the mass continuity equation: i.e. $(\partial _t+{\mathcal {L}}_{\boldsymbol {u}})\boldsymbol {b}=0$![]() which implies $\partial _t \boldsymbol {b}+[\boldsymbol {u},\boldsymbol {b}]=0$
which implies $\partial _t \boldsymbol {b}+[\boldsymbol {u},\boldsymbol {b}]=0$![]() ). Here ${\boldsymbol {\alpha }}$
). Here ${\boldsymbol {\alpha }}$![]() is a one-form or co-vector, that is Lie dragged with the flow. The inner product of the vector field $\boldsymbol {b}$
is a one-form or co-vector, that is Lie dragged with the flow. The inner product of the vector field $\boldsymbol {b}$![]() with the one-form ${\boldsymbol {\alpha }}$
with the one-form ${\boldsymbol {\alpha }}$![]() is a scalar invariant which is advected with the flow (e.g. Tur & Yanovsky Reference Tur and Yanovsky1993). Thus, the quantities
is a scalar invariant which is advected with the flow (e.g. Tur & Yanovsky Reference Tur and Yanovsky1993). Thus, the quantities
are advected scalars in CGL plasmas.
The gauge (2.86) in which the magnetic helicity integral is conserved is equivalent to Lie dragging the one-form $\alpha =\boldsymbol {A}\boldsymbol {\cdot }{\rm d} \boldsymbol {x}$![]() with the fluid flow:
with the fluid flow:
which vanishes due to the uncurled form of Faraday's equation (2.80) combined with equation (2.86). Holm & Kupershmidt (Reference Holm and Kupershmidt1983a,Reference Holm and Kupershmidtb) used this advected-$\boldsymbol {A}$![]() gauge in the formulation of non-canonical Poisson brackets for MHD and for multi-fluid plasmas (see also Gordin & Petviashvili Reference Gordin and Petviashvili1987, Reference Gordin and Petviashvili1989; Padhye & Morrison Reference Padhye and Morrison1996a,Reference Padhye and Morrisonb; Padhye Reference Padhye1998).
gauge in the formulation of non-canonical Poisson brackets for MHD and for multi-fluid plasmas (see also Gordin & Petviashvili Reference Gordin and Petviashvili1987, Reference Gordin and Petviashvili1989; Padhye & Morrison Reference Padhye and Morrison1996a,Reference Padhye and Morrisonb; Padhye Reference Padhye1998).
3 The Lagrangian map
In a Lagrangian formulation of MHD and CGL plasmas, fluid elements are given labels that are constant in the fluid flow. The simplest labelling consists of initial values $\boldsymbol {x}_0=\boldsymbol {x}(0)$![]() for integrating the flow equations of a fluid element
for integrating the flow equations of a fluid element
in which the fluid velocity $\boldsymbol {u}$![]() is assumed to be a known function of $\boldsymbol {x}$
is assumed to be a known function of $\boldsymbol {x}$![]() and $t$
and $t$![]() . In general, fluid labels are given by functions $\boldsymbol {a}=\boldsymbol {a}(\boldsymbol {x}_0)$
. In general, fluid labels are given by functions $\boldsymbol {a}=\boldsymbol {a}(\boldsymbol {x}_0)$![]() .
.
A Lagrangian map is an invertible mapping from the Lagrangian fluid labels $\boldsymbol {a}$![]() to the Eulerian position coordinates $\boldsymbol {x}(t)=\boldsymbol {X}(\boldsymbol {a},t)$
to the Eulerian position coordinates $\boldsymbol {x}(t)=\boldsymbol {X}(\boldsymbol {a},t)$![]() for the motion of a fluid element. For simplicity, we take $\boldsymbol {x}$
for the motion of a fluid element. For simplicity, we take $\boldsymbol {x}$![]() and $\boldsymbol {a}=\boldsymbol {x}_0$
and $\boldsymbol {a}=\boldsymbol {x}_0$![]() to be expressed in terms of Cartesian coordinates $\boldsymbol {x}=(x,y,z)$
to be expressed in terms of Cartesian coordinates $\boldsymbol {x}=(x,y,z)$![]() and $\boldsymbol {x}_0=(x_0,y_0,z_0)$
and $\boldsymbol {x}_0=(x_0,y_0,z_0)$![]() . Then, the Lagrangian map takes the form
. Then, the Lagrangian map takes the form
with the $t$![]() dependence being suppressed in the notation. Invertibility implies that the Jacobian of this map is non-degenerate:
dependence being suppressed in the notation. Invertibility implies that the Jacobian of this map is non-degenerate:
We write $Y_{ij}$![]() to denote the inverse of the matrix $X_{ij}$
to denote the inverse of the matrix $X_{ij}$![]() , whereby
, whereby
with $\delta _{ij}$![]() denoting the components of the identity matrix. Recall the standard formulae:
denoting the components of the identity matrix. Recall the standard formulae:
where $A_{ij}={\rm cofac}(X_{ij})$![]() is the cofactor matrix of $X_{ij}$
is the cofactor matrix of $X_{ij}$![]() . In addition, note that
. In addition, note that

3.1 Map formulae
We now formulate the maps between the CGL plasma variables $\rho$![]() , $S$
, $S$![]() , $\boldsymbol {B}$
, $\boldsymbol {B}$![]() , $p_\parallel$
, $p_\parallel$![]() and $p_\perp$
and $p_\perp$![]() and their Lagrangian counterparts $\rho _0(\boldsymbol {x}_0)$
and their Lagrangian counterparts $\rho _0(\boldsymbol {x}_0)$![]() , $S_0(\boldsymbol {x}_0)$
, $S_0(\boldsymbol {x}_0)$![]() , $\boldsymbol {B}_0(\boldsymbol {x}_0)$
, $\boldsymbol {B}_0(\boldsymbol {x}_0)$![]() , $p_\parallel (\boldsymbol {x}_0)$
, $p_\parallel (\boldsymbol {x}_0)$![]() and $p_\perp (\boldsymbol {x}_0)$
and $p_\perp (\boldsymbol {x}_0)$![]() , respectively.
, respectively.
The density $\rho _0$![]() of a fluid element with label $\boldsymbol {x}_0$
of a fluid element with label $\boldsymbol {x}_0$![]() is related to the Eulerian density by the mass conservation equation
is related to the Eulerian density by the mass conservation equation
where ${\rm d}^3x = J \,{\rm d}^3x_0$![]() . This implies
. This implies
From Newcomb (Reference Newcomb1962) the Cartesian components of $B^i$![]() in the Eulerian frame are related to the Lagrangian magnetic field component $B_0^k$
in the Eulerian frame are related to the Lagrangian magnetic field component $B_0^k$![]() by the equation:
by the equation:
The derivation of (3.9) follows by noting
Equation (3.10) describes the conservation of magnetic flux, where ${\rm d}\sigma _i$![]() is the flux tube area normal to the $x^i$
is the flux tube area normal to the $x^i$![]() coordinate surface, and ${\rm d}\sigma _{0k}$
coordinate surface, and ${\rm d}\sigma _{0k}$![]() is the flux tube area normal to the $x^k_0$
is the flux tube area normal to the $x^k_0$![]() surface in the Lagrangian frame. Equation (3.11) relates the volume elements ${\rm d}^3x$
surface in the Lagrangian frame. Equation (3.11) relates the volume elements ${\rm d}^3x$![]() to ${\rm d}^3x_0$
to ${\rm d}^3x_0$![]() . From (3.11) one obtains
. From (3.11) one obtains
for the transformation between the area elements ${\rm d}\sigma _i$![]() and ${\rm d}\sigma _0^k$
and ${\rm d}\sigma _0^k$![]() . The magnetic flux conservation equation (3.10) now gives the transformation $B_0^k=A_{ik} B^i$
. The magnetic flux conservation equation (3.10) now gives the transformation $B_0^k=A_{ik} B^i$![]() which, in turn, implies the transformation (3.9).
which, in turn, implies the transformation (3.9).
An alternative form of the relation (3.9) arises from the Lie dragged or frozen-in vector field
which implies the transformation (3.9) between $B^i$![]() and $B_0^k$
and $B_0^k$![]() . In (3.13) we use the modern differential geometry notion of a vector field as a directional derivative operator (e.g. Misner, Thorne & Wheeler Reference Misner, Thorne and Wheeler1973).
. In (3.13) we use the modern differential geometry notion of a vector field as a directional derivative operator (e.g. Misner, Thorne & Wheeler Reference Misner, Thorne and Wheeler1973).
From the relation (3.9), we have
in terms of the unit vector $\tau _0=B_0^{-1}\boldsymbol {B}_0$![]() along the magnetic field $\boldsymbol {B}_0$
along the magnetic field $\boldsymbol {B}_0$![]() (cf. (2.3a–c)), with $B_0=|\boldsymbol {B}_0|$
(cf. (2.3a–c)), with $B_0=|\boldsymbol {B}_0|$![]() being the magnetic field strength at $\boldsymbol {x}_0$
being the magnetic field strength at $\boldsymbol {x}_0$![]() . Hence, we obtain
. Hence, we obtain
The latter relation can be inverted to obtain $\boldsymbol {\tau }_0$![]() in terms of $\boldsymbol {\tau }$
in terms of $\boldsymbol {\tau }$![]() through the formulae (3.5a–c):
through the formulae (3.5a–c):
Next, from the double adiabatic conservation laws (2.11a,b), we have the frozen-in quantities
By combining these equations with (3.15a,b) and (3.8), we obtain
which gives the respective relations between the pressures $p_{\parallel 0}$![]() and $p_{\perp 0}$
and $p_{\perp 0}$![]() at a fluid element with label $\boldsymbol {x}_0$
at a fluid element with label $\boldsymbol {x}_0$![]() and the Eulerian pressures $p_\parallel$
and the Eulerian pressures $p_\parallel$![]() and $p_\perp$
and $p_\perp$![]() .
.
Finally, we note that the Eulerian entropy $S$![]() is equal to the entropy $S_0$
is equal to the entropy $S_0$![]() at a fluid element with label $\boldsymbol {x}_0$
at a fluid element with label $\boldsymbol {x}_0$![]() , since $S$
, since $S$![]() is frozen-in by the transport equation (2.5).
is frozen-in by the transport equation (2.5).
3.2 Lagrangian variational principle and Euler–Lagrange equations
The Lagrangian variational principle for MHD and for CGL plasmas was obtained in Newcomb (Reference Newcomb1962):
where $L$![]() is the Lagrangian in Eulerian variables and $L_0$
is the Lagrangian in Eulerian variables and $L_0$![]() is its counterpart arising through the Lagrangian map. Here $V$
is its counterpart arising through the Lagrangian map. Here $V$![]() is a fixed spatial domain and $[t_0,t_1]$
is a fixed spatial domain and $[t_0,t_1]$![]() is a fixed time interval. In general, $L$
is a fixed time interval. In general, $L$![]() will be given by the kinetic energy density minus the potential energy density for a fluid element. The kinetic energy density for both MHD and CGL plasmas is simply $\frac {1}{2}\rho u^2$
will be given by the kinetic energy density minus the potential energy density for a fluid element. The kinetic energy density for both MHD and CGL plasmas is simply $\frac {1}{2}\rho u^2$![]() , with $u=|\boldsymbol {u}|$
, with $u=|\boldsymbol {u}|$![]() . Subtracting this expression from the total energy density for a CGL plasma (cf. the moving energy balance equation (2.57))
. Subtracting this expression from the total energy density for a CGL plasma (cf. the moving energy balance equation (2.57))
yields the potential energy density $\rho \varPhi +\varepsilon +({1}/{2\mu _0})B^2$![]() , where $\varepsilon$
, where $\varepsilon$![]() is the internal energy density (2.12). Thus, a CGL plasma has the Lagrangian
is the internal energy density (2.12). Thus, a CGL plasma has the Lagrangian
where, for the sake of completeness, we have included the energy contributed by an external gravitational potential $\varPhi (\boldsymbol {x})$![]() (e.g. which would arise from the gravitational field of the Sun in the case of solar and interplanetary physics). The corresponding Lagrangian $L_0$
(e.g. which would arise from the gravitational field of the Sun in the case of solar and interplanetary physics). The corresponding Lagrangian $L_0$![]() is obtained from the relation $L\,{\rm d}^3x=L_0\,{\rm d}^3x_0 = LJ \,{\rm d}^3x_0$
is obtained from the relation $L\,{\rm d}^3x=L_0\,{\rm d}^3x_0 = LJ \,{\rm d}^3x_0$![]() , which gives
, which gives
Substituting the Eulerian expressions (3.21), (3.18a,b), (3.14), (3.8) and (3.2) into $L_0$![]() , and then using expression (2.12) for the internal energy density in terms of the pressures $p_\parallel$
, and then using expression (2.12) for the internal energy density in terms of the pressures $p_\parallel$![]() and $p_\perp$
and $p_\perp$![]() , we obtain
, we obtain
The Euler–Lagrange equations of the resulting action principle (3.19) for a CGL plasma are obtained by variation of the Cartesian components $X^i$![]() of the Lagrangian map (3.2), modulo boundary terms: $\delta {\mathcal {A}}/\delta X^i =0$
of the Lagrangian map (3.2), modulo boundary terms: $\delta {\mathcal {A}}/\delta X^i =0$![]() . In essence, we work in a reference frame moving with the fluid flow, where the dynamics is described in terms of how the Eulerian position $\boldsymbol {x}$
. In essence, we work in a reference frame moving with the fluid flow, where the dynamics is described in terms of how the Eulerian position $\boldsymbol {x}$![]() of the frame varies with the fluid labels $\boldsymbol {x}_0$
of the frame varies with the fluid labels $\boldsymbol {x}_0$![]() and the time $t$
and the time $t$![]() through the Lagrangian map (3.2). Equivalently, the Euler–Lagrange equations are given by applying to $L_0$
through the Lagrangian map (3.2). Equivalently, the Euler–Lagrange equations are given by applying to $L_0$![]() the Euler operator (variational derivative) $E_{X^i}$
the Euler operator (variational derivative) $E_{X^i}$![]() in the calculus of variations, where $X^i(x_0^j,t)$
in the calculus of variations, where $X^i(x_0^j,t)$![]() is a function of $x^j_0$
is a function of $x^j_0$![]() and $t$
and $t$![]() . Thus,
. Thus,
where $\partial /\partial _{t}$![]() and $\partial /\partial _{x_0^j}$
and $\partial /\partial _{x_0^j}$![]() act as total derivatives. (See § 6 for more details of variational calculus.) In Appendix C, we show that when (3.24) is simplified and expressed in terms of Eulerian variables, it reduces to the Eulerian momentum equation (2.2).
act as total derivatives. (See § 6 for more details of variational calculus.) In Appendix C, we show that when (3.24) is simplified and expressed in terms of Eulerian variables, it reduces to the Eulerian momentum equation (2.2).
3.3 Hamilton's equations
We now derive the corresponding Hamilton formulation of the Euler–Lagrange equation (3.24) for a CGL plasma. Here we write $X^i=x^i$![]() for simplicity.
for simplicity.
First, the generalised momentum is defined as
Next, the Hamiltonian density is defined by the Legendre transformation:
After substitution of the CGL Lagrangian (3.23) along with $\dot {x}^i$![]() in terms of the momentum (3.25), we then obtain the expression
in terms of the momentum (3.25), we then obtain the expression
In Eulerian variables, this expression is given by
where $H$![]() is the Eulerian total energy density (3.20). The resulting Hamiltonian equations of motion consist of
is the Eulerian total energy density (3.20). The resulting Hamiltonian equations of motion consist of
which yield the momentum relation (3.25) and the Euler–Lagrange equation (3.24), where the Hamiltonian function is defined as
As in ordinary Hamiltonian mechanics, with the use of the canonical variables $q^i= x^i$![]() and $p^i={\rm \pi} ^i$
and $p^i={\rm \pi} ^i$![]() , Hamilton's equations (3.29a,b) can be written in a canonical Poisson bracket formulation:
, Hamilton's equations (3.29a,b) can be written in a canonical Poisson bracket formulation:
Here ${\mathcal {F}}$![]() is a general functional of $q^i$
is a general functional of $q^i$![]() and $p^i$
and $p^i$![]() (see Morrison Reference Morrison1982). There is an equivalent, non-canonical Poisson bracket that employs only Eulerian variables, which we present in § 5.
(see Morrison Reference Morrison1982). There is an equivalent, non-canonical Poisson bracket that employs only Eulerian variables, which we present in § 5.
4 EP action principle
In this section, we formulate the EP action principle for the CGL plasma equations. We follow the developments in Holm et al. (Reference Holm, Marsden and Ratiu1998), Webb et al. (Reference Webb, Dasgupta, McKenzie, Hu and Zank2014b), which provide the EP formulation for MHD. The main difference for a CGL plasma compared with MHD is that the internal energy density $\varepsilon =\rho e$![]() (cf. (2.16a,b)) depends on $\rho$
(cf. (2.16a,b)) depends on $\rho$![]() , $S$
, $S$![]() and $B$
and $B$![]() , whereas for MHD it depends only on $\rho$
, whereas for MHD it depends only on $\rho$![]() and $S$
and $S$![]() .
.
The Lagrangian and Hamiltonian action principles in § 3 are based on a reference frame that is attached to fluid elements, whereby the Eulerian position $\boldsymbol {x}$![]() of the frame is a function of fluid element labels $\boldsymbol {x}_0$
of the frame is a function of fluid element labels $\boldsymbol {x}_0$![]() and time $t$
and time $t$![]() , as given by the Lagrangian map (3.2). In contrast, the EP action principle is based on the use of a fixed Eulerian reference frame, in which the motion of a fluid element is given by inverting the Lagrangian map so that the fluid element label $\boldsymbol {x}_0$
, as given by the Lagrangian map (3.2). In contrast, the EP action principle is based on the use of a fixed Eulerian reference frame, in which the motion of a fluid element is given by inverting the Lagrangian map so that the fluid element label $\boldsymbol {x}_0$![]() becomes a function of $\boldsymbol {x}$
becomes a function of $\boldsymbol {x}$![]() and $t$
and $t$![]() . To set up this formulation, it is convenient to introduce the notation
. To set up this formulation, it is convenient to introduce the notation
with $g$![]() at any fixed time $t$
at any fixed time $t$![]() representing an element in the group of diffeomorphisms on Euclidean space in Cartesian coordinates $\boldsymbol {x}$
representing an element in the group of diffeomorphisms on Euclidean space in Cartesian coordinates $\boldsymbol {x}$![]() and $\boldsymbol {x}_0$
and $\boldsymbol {x}_0$![]() . Note that $g$
. Note that $g$![]() has an inverse $g^{-1}$
has an inverse $g^{-1}$![]() defined by $g^{-1}\boldsymbol {x} = \boldsymbol {x}_0$
defined by $g^{-1}\boldsymbol {x} = \boldsymbol {x}_0$![]() , whereas $g|_{t=0}$
, whereas $g|_{t=0}$![]() is just the identity map. In (4.1) and the sequel, the $t$
is just the identity map. In (4.1) and the sequel, the $t$![]() dependence of $g$
dependence of $g$![]() and $\boldsymbol {x}_0$
and $\boldsymbol {x}_0$![]() is suppressed for simplicity of notation; an overdot stands for $\dot {}=\partial /\partial t$
is suppressed for simplicity of notation; an overdot stands for $\dot {}=\partial /\partial t$![]() . The diffeomorphism group will be denoted $G\equiv {\rm Diff}({\mathbb {R}}^3)$
. The diffeomorphism group will be denoted $G\equiv {\rm Diff}({\mathbb {R}}^3)$![]() .
.
The coordinate components of a fluid element label, $x_0^i$![]() , represent advected quantities:
, represent advected quantities:
From (4.1) and (4.2), we see that
Hence, we obtain
which can be viewed as both a left-invariant vector field in the tangent space of $G$![]() and the directional derivative along the fluid flow in Euclidean space. The property of left-invariance means that, for any fixed element $h$
and the directional derivative along the fluid flow in Euclidean space. The property of left-invariance means that, for any fixed element $h$![]() in $G$
in $G$![]() , $g\to hg$
, $g\to hg$![]() implies $\eta \to (hg)^{-1}\dot {(hg)}=g^{-1}h^{-1} h\dot {g}=g^{-1}\dot {g} =\eta$
implies $\eta \to (hg)^{-1}\dot {(hg)}=g^{-1}h^{-1} h\dot {g}=g^{-1}\dot {g} =\eta$![]() , with $\dot {h}\equiv 0$
, with $\dot {h}\equiv 0$![]() .
.
Compared with the Lagrangian formulation, whose dynamical variable is $\boldsymbol {x}(\boldsymbol {x}_0,t)$![]() , the EP formulation uses the dynamical variables $\rho$
, the EP formulation uses the dynamical variables $\rho$![]() , $S$
, $S$![]() , $B$
, $B$![]() and $\boldsymbol {u}$
and $\boldsymbol {u}$![]() , which are functions of $\boldsymbol {x}$
, which are functions of $\boldsymbol {x}$![]() and $t$
and $t$![]() . Variations of the EP variables are defined through variation of the inverse Lagrangian map, $g$
. Variations of the EP variables are defined through variation of the inverse Lagrangian map, $g$![]() , in the following way.
, in the following way.
We consider a general variation $\delta g$![]() and define
and define
which represents a left-invariant vector field on the group $G$![]() . Similarly to the identification (4.4), we can write
. Similarly to the identification (4.4), we can write
viewed as the directional derivative associated with $\delta g$![]() , where $\boldsymbol {\eta }$
, where $\boldsymbol {\eta }$![]() is an Eulerian vector field. (In general, $\boldsymbol {\cdot }\partial _{\boldsymbol {x}}$
is an Eulerian vector field. (In general, $\boldsymbol {\cdot }\partial _{\boldsymbol {x}}$![]() identifies Eulerian vector fields in Euclidean space with left-invariant vector fields on the diffeomorphism group $G$
identifies Eulerian vector fields in Euclidean space with left-invariant vector fields on the diffeomorphism group $G$![]() .)
.)
Now, the variation $\delta g$![]() is intended to leave the fixed Eulerian reference frame unchanged, whereby $\delta \boldsymbol {x}\equiv 0$
is intended to leave the fixed Eulerian reference frame unchanged, whereby $\delta \boldsymbol {x}\equiv 0$![]() . Taking the corresponding variation of the inverse Lagrangian map (4.1) yields $\delta x_0^i = \delta (g^{-1} x)^i = -(g^{-1}(\delta g)g^{-1} x)^i = -\eta x_0^i$
. Taking the corresponding variation of the inverse Lagrangian map (4.1) yields $\delta x_0^i = \delta (g^{-1} x)^i = -(g^{-1}(\delta g)g^{-1} x)^i = -\eta x_0^i$![]() . Thus, because $x_0^i$
. Thus, because $x_0^i$![]() is a function of $x^j$
is a function of $x^j$![]() and $t$
and $t$![]() , we obtain
, we obtain
where ${\mathcal {L}}_{\boldsymbol {\eta }}$![]() is the Lie derivative with respect to the Eulerian vector field $\boldsymbol {\eta }$
is the Lie derivative with respect to the Eulerian vector field $\boldsymbol {\eta }$![]() .
.
More generally, the same Lie derivative operation is used to define the variation of any advected quantity (a scalar, a vector or a differential form), $a$![]() :
:
where $a$![]() satisfies the advection equation (2.87). Expressions for the induced variations of $\rho$
satisfies the advection equation (2.87). Expressions for the induced variations of $\rho$![]() , $S$
, $S$![]() , $\boldsymbol {B}$
, $\boldsymbol {B}$![]() can then be deduced by considering advected quantities in terms of those variables (cf. §§ 2.6 and 3.1). The basic advected quantities in a CGL plasma are
can then be deduced by considering advected quantities in terms of those variables (cf. §§ 2.6 and 3.1). The basic advected quantities in a CGL plasma are
where ${\rm d}A$![]() is the area element on a surface moving with the fluid. (These quantities are also referred to as a Cauchy invariant.) As $S$
is the area element on a surface moving with the fluid. (These quantities are also referred to as a Cauchy invariant.) As $S$![]() is advected, its variation is given directly by (4.8). Advection of $\rho \, {\rm d}^3x$
is advected, its variation is given directly by (4.8). Advection of $\rho \, {\rm d}^3x$![]() combined with $\delta x^i=0$
combined with $\delta x^i=0$![]() implies that $(\delta \rho )\, {\rm d}^3x = \delta (\rho \, {\rm d}^3x) = -{\mathcal {L}}_{\boldsymbol {\eta }} (\rho \, {\rm d}^3x) = -({\mathcal {L}}_{\boldsymbol {\eta }} \rho + \rho \boldsymbol {\nabla }\boldsymbol {\cdot }{\boldsymbol {\eta }})\, {\rm d}^3x$
implies that $(\delta \rho )\, {\rm d}^3x = \delta (\rho \, {\rm d}^3x) = -{\mathcal {L}}_{\boldsymbol {\eta }} (\rho \, {\rm d}^3x) = -({\mathcal {L}}_{\boldsymbol {\eta }} \rho + \rho \boldsymbol {\nabla }\boldsymbol {\cdot }{\boldsymbol {\eta }})\, {\rm d}^3x$![]() due to the well-known expansion/contraction formula ${\mathcal {L}}_{\boldsymbol {v}}({\rm d}^3x) = \boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {v} \,{\rm d}^3x$
due to the well-known expansion/contraction formula ${\mathcal {L}}_{\boldsymbol {v}}({\rm d}^3x) = \boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {v} \,{\rm d}^3x$![]() holding for any vector field $\boldsymbol {v}$
holding for any vector field $\boldsymbol {v}$![]() . Thus, we have
. Thus, we have
Next, because $(1/\rho )\boldsymbol {B}$![]() is advected, this gives
is advected, this gives

Thus, after substituting $\delta \rho$![]() from (4.11), we obtain
from (4.11), we obtain
where ${\mathcal {L}}_{\boldsymbol {\eta }}\boldsymbol {B} = [{\boldsymbol {\eta }},\boldsymbol {B}]$![]() is the commutator of vector fields.
is the commutator of vector fields.
Finally, the induced variation of $\boldsymbol {u}$![]() is given by combining the equations
is given by combining the equations
and
This yields
where $[\cdot,\cdot ]$![]() is the commutator of vector fields which coincides with the Lie bracket. Thus, we obtain the variation:
is the commutator of vector fields which coincides with the Lie bracket. Thus, we obtain the variation:
4.1 The EP equation
For CGL plasmas, the EP action principle is given by
where $L$![]() is the Lagrangian density (3.21). Here $V$
is the Lagrangian density (3.21). Here $V$![]() is a fixed spatial domain and $[t_0,t_1]$
is a fixed spatial domain and $[t_0,t_1]$![]() is a fixed time interval. The stationary points of this action principle, $\delta {\mathcal {J}}=0$
is a fixed time interval. The stationary points of this action principle, $\delta {\mathcal {J}}=0$![]() , under the variations (4.17), (4.10), (4.11) and (4.13) of the respective variables $\boldsymbol {u}$
, under the variations (4.17), (4.10), (4.11) and (4.13) of the respective variables $\boldsymbol {u}$![]() , $S$
, $S$![]() , $\rho$
, $\rho$![]() and $\boldsymbol {B}$
and $\boldsymbol {B}$![]() , turn out to yield the Eulerian momentum equation (2.2), as we now show.
, turn out to yield the Eulerian momentum equation (2.2), as we now show.
The derivation of the stationary points is non-trivial because of the form of the variations in terms of $\eta$![]() given by (4.5) and (4.6). Specifically, the variation of ${\mathcal {J}}$
given by (4.5) and (4.6). Specifically, the variation of ${\mathcal {J}}$![]() needs to be put into the form
needs to be put into the form
modulo boundary terms, where $F=\boldsymbol {F}\boldsymbol {\cdot } \partial _{\boldsymbol {x}}$![]() is both a left-invariant vector field in the tangent space of $G$
is both a left-invariant vector field in the tangent space of $G$![]() and the directional derivative along a vector field $\boldsymbol {F}$
and the directional derivative along a vector field $\boldsymbol {F}$![]() in Euclidean space. Then, because ${\boldsymbol {\eta }}$
in Euclidean space. Then, because ${\boldsymbol {\eta }}$![]() is an arbitrary vector field (corresponding to an arbitrary variation $\delta g$
is an arbitrary vector field (corresponding to an arbitrary variation $\delta g$![]() ), the equation yielding the stationary points of ${\mathcal {J}}$
), the equation yielding the stationary points of ${\mathcal {J}}$![]() is $\boldsymbol {F}=0$
is $\boldsymbol {F}=0$![]() .
.
We now proceed to find $\delta {\mathcal {J}}$![]() and $\boldsymbol {F}$
and $\boldsymbol {F}$![]() . A general expression is available for $\boldsymbol {F}$
. A general expression is available for $\boldsymbol {F}$![]() in Holm et al. (Reference Holm, Marsden and Ratiu1998), which involves the diamond operator, $\diamond$
in Holm et al. (Reference Holm, Marsden and Ratiu1998), which involves the diamond operator, $\diamond$![]() , defined by property
, defined by property
where, as earlier, $a$![]() is an advected quantity. It will be instructive to instead show how to obtain $\boldsymbol {F}$
is an advected quantity. It will be instructive to instead show how to obtain $\boldsymbol {F}$![]() from the variation (4.17), (4.10), (4.11) and (4.13) directly using the Eulerian variables.
from the variation (4.17), (4.10), (4.11) and (4.13) directly using the Eulerian variables.
From the Lagrangian density (3.21), we obtain

using the thermodynamic relations (2.18a–c), where $T$![]() is the temperature and $h$
is the temperature and $h$![]() is the enthalpy (2.62) and $p_{\varDelta }=p_\parallel -p_\perp$
is the enthalpy (2.62) and $p_{\varDelta }=p_\parallel -p_\perp$![]() is the pressure anisotropy. Here we have also used the identity $\delta B = \boldsymbol {\tau }\boldsymbol {\cdot }\delta \boldsymbol {B}$
is the pressure anisotropy. Here we have also used the identity $\delta B = \boldsymbol {\tau }\boldsymbol {\cdot }\delta \boldsymbol {B}$![]() , with ${\boldsymbol {\tau }}=\boldsymbol {B}/B$
, with ${\boldsymbol {\tau }}=\boldsymbol {B}/B$![]() being the unit vector along $\boldsymbol {B}$
being the unit vector along $\boldsymbol {B}$![]() . Note that $\tilde {\boldsymbol {B}}$
. Note that $\tilde {\boldsymbol {B}}$![]() is related $\boldsymbol {B}$
is related $\boldsymbol {B}$![]() by (2.78a,b). The main difference in these variational derivative expressions (4.21) compared with the MHD case is the addition of the anisotropy term in $\delta L/\delta \boldsymbol {B}$
by (2.78a,b). The main difference in these variational derivative expressions (4.21) compared with the MHD case is the addition of the anisotropy term in $\delta L/\delta \boldsymbol {B}$![]() , i.e. $\boldsymbol {B}$
, i.e. $\boldsymbol {B}$![]() is replaced by $\tilde {\boldsymbol {B}}$
is replaced by $\tilde {\boldsymbol {B}}$![]() .
.
The total variation of $L$![]() is given by combining the products of the variational derivatives (4.21) and the corresponding variations (4.17), (4.10), (4.11) and (4.13). This yields
is given by combining the products of the variational derivatives (4.21) and the corresponding variations (4.17), (4.10), (4.11) and (4.13). This yields

The next step is to bring each term into the form (4.19), modulo a total time derivative and a total divergence, using integration by parts. The first term in expression (4.22) expands out to give

Similarly, the third term in (4.22) yields
The second term in (4.22) simply gives
The last term in (4.22) can be rearranged by cross-product identities:
and
Now, combining the four terms (4.27), (4.25), (4.24) and (4.23) and discarding the total derivatives, we obtain
modulo total time derivatives and total divergences. This yields the desired relation
with
The equation $\boldsymbol {F}=0$![]() resulting from the variational principle (4.19) is called the EP equation. It is equivalent to the Eulerian momentum equation (2.2), after the pressure divergence identity (2.61) is used. A direct derivation of this identity is provided in Appendix B. Alternatively, (4.30) can be viewed as showing how the pressure divergence identity arises from the variational principle (4.19). Appendix E derives the identity (2.61) and the EP equation $\boldsymbol {F}=0$
resulting from the variational principle (4.19) is called the EP equation. It is equivalent to the Eulerian momentum equation (2.2), after the pressure divergence identity (2.61) is used. A direct derivation of this identity is provided in Appendix B. Alternatively, (4.30) can be viewed as showing how the pressure divergence identity arises from the variational principle (4.19). Appendix E derives the identity (2.61) and the EP equation $\boldsymbol {F}=0$![]() using the approach of Holm et al. (Reference Holm, Marsden and Ratiu1998).
using the approach of Holm et al. (Reference Holm, Marsden and Ratiu1998).
Holm & Kupershmidt (Reference Holm and Kupershmidt1986) studied a corresponding Hamiltonian form of the CGL plasma equations for both relativistic and non-relativistic flows; however, details of the EP formulation were not covered.
5 Non-canonical Poisson bracket
Morrison & Greene (Reference Morrison and Greene1980, Reference Morrison and Greene1982) and Holm & Kupershmidt (Reference Holm and Kupershmidt1983a,Reference Holm and Kupershmidtb) obtained the non-canonical Poisson bracket for ideal MHD, which involves the basic variables $\rho$![]() , $\sigma \equiv \rho S$
, $\sigma \equiv \rho S$![]() , $\boldsymbol {M}\equiv \rho \boldsymbol {u}$
, $\boldsymbol {M}\equiv \rho \boldsymbol {u}$![]() and $\boldsymbol {B}$
and $\boldsymbol {B}$![]() :
:

where ${\mathcal {F}}$![]() and ${\mathcal {G}}$
and ${\mathcal {G}}$![]() are arbitrary functionals, and subscripts denote a variational derivative. This bracket is bilinear, antisymmetric and obeys the Jacobi identity.
are arbitrary functionals, and subscripts denote a variational derivative. This bracket is bilinear, antisymmetric and obeys the Jacobi identity.
It turns out the CGL plasma Poisson bracket obtained by Holm & Kupershmidt (Reference Holm and Kupershmidt1986), $\{{\mathcal {F}},{\mathcal {G}}\}^{\textrm {CGL}}$![]() has the same form as the MHD plasma Poisson bracket except that the thermodynamics and internal energy $e(\rho,S,B)$
has the same form as the MHD plasma Poisson bracket except that the thermodynamics and internal energy $e(\rho,S,B)$![]() are completely different in the two cases. Holm & Kupershmidt (Reference Holm and Kupershmidt1986) obtained the bracket:
are completely different in the two cases. Holm & Kupershmidt (Reference Holm and Kupershmidt1986) obtained the bracket:

An overview of Hamiltonian systems is given in Morrison (Reference Morrison1998). Banerjee & Kumar (Reference Banerjee and Kumar2016) provides a Dirac bracket approach to the MHD Poisson bracket. The property that the MHD bracket is linear in the dynamical variables $\rho$![]() , $\sigma$
, $\sigma$![]() , $\boldsymbol {M}$
, $\boldsymbol {M}$![]() and $\boldsymbol {B}$
and $\boldsymbol {B}$![]() has an important mathematical relationship to semi-direct product Lie algebras, which is explained in Holm et al. (Reference Holm, Kupershmidt and Levermore1983, Reference Holm, Marsden and Ratiu1998) for general fluid systems.
has an important mathematical relationship to semi-direct product Lie algebras, which is explained in Holm et al. (Reference Holm, Kupershmidt and Levermore1983, Reference Holm, Marsden and Ratiu1998) for general fluid systems.
The variables appearing in the CGL non-canonical Poisson bracket consist of
The analysis in Appendix D starts from the canonical bracket
involving canonical Hamiltonian variables $(\boldsymbol {q},\boldsymbol {p})\equiv (\boldsymbol {x}(\boldsymbol {x}_0,t), \boldsymbol {{\rm \pi} }(\boldsymbol {x}_0,t))$![]() where $\boldsymbol {{\rm \pi} }=\rho _0 \dot {\boldsymbol {x}}$
where $\boldsymbol {{\rm \pi} }=\rho _0 \dot {\boldsymbol {x}}$![]() is the canonical momentum (cf. § 3.3). The main steps consist of using the Lagrangian map (3.2) to obtain a transformation to the non-canonical variables (5.3a–d), followed by applying a variational version of the chain rule to the variational derivatives with respect to $(\boldsymbol {q},\boldsymbol {p})$
is the canonical momentum (cf. § 3.3). The main steps consist of using the Lagrangian map (3.2) to obtain a transformation to the non-canonical variables (5.3a–d), followed by applying a variational version of the chain rule to the variational derivatives with respect to $(\boldsymbol {q},\boldsymbol {p})$![]() (see e.g. Zakharov & Kuznetsov Reference Zakharov and Kuznetsov1997). These steps are carried out by working in a fixed Lagrangian frame, while the corresponding Eulerian frame given by the Lagrangian map undergoes a variation, which includes varying Cartesian basis vectors associated to the components of $\boldsymbol {x}$
(see e.g. Zakharov & Kuznetsov Reference Zakharov and Kuznetsov1997). These steps are carried out by working in a fixed Lagrangian frame, while the corresponding Eulerian frame given by the Lagrangian map undergoes a variation, which includes varying Cartesian basis vectors associated to the components of $\boldsymbol {x}$![]() . This general approach is described in a short communication by Holm et al. (Reference Holm, Kupershmidt and Levermore1983).
. This general approach is described in a short communication by Holm et al. (Reference Holm, Kupershmidt and Levermore1983).
In the following, we give an alternative more succinct derivation of the CGL Poisson bracket (5.2). It leads to the same Poisson bracket as that obtained in Appendix D. Note that the canonical bracket (5.4) can be written in the form
Here $\boldsymbol {q}\equiv \boldsymbol {x}$![]() . The transformation of variational derivatives between the canonical variables and the new variables (5.3a–d) is effected by noting that
. The transformation of variational derivatives between the canonical variables and the new variables (5.3a–d) is effected by noting that

where $\hat {{\mathcal {F}}}(\rho,\boldsymbol {M},\sigma, \boldsymbol {B})\equiv {\mathcal {F}}(\boldsymbol {q},\boldsymbol {p})$![]() is the functional ${\mathcal {F}}(\boldsymbol {q},\boldsymbol {p})$
is the functional ${\mathcal {F}}(\boldsymbol {q},\boldsymbol {p})$![]() expressed in terms of the new variables $(\rho,\boldsymbol {M}^T,\sigma, \boldsymbol {B}^T)^\textrm {T}$
expressed in terms of the new variables $(\rho,\boldsymbol {M}^T,\sigma, \boldsymbol {B}^T)^\textrm {T}$![]() . Here $\delta \psi$
. Here $\delta \psi$![]() denotes the Eulerian variation of $\psi$
denotes the Eulerian variation of $\psi$![]() and $\Delta \psi$
and $\Delta \psi$![]() denotes the Lagrangian variation of $\psi$
denotes the Lagrangian variation of $\psi$![]() .
.
Using the transformations

in (5.6) gives the formulae

for the transformation of variational derivatives from the old variables $(\boldsymbol {x},\boldsymbol {p})$![]() to the new variables $\boldsymbol {M}$
to the new variables $\boldsymbol {M}$![]() , $\sigma$
, $\sigma$![]() , $\rho$
, $\rho$![]() and $\boldsymbol {B}$
and $\boldsymbol {B}$![]() . Using the expressions (5.8) for ${\mathcal {F}}_{\boldsymbol {x}}$
. Using the expressions (5.8) for ${\mathcal {F}}_{\boldsymbol {x}}$![]() and ${\mathcal {F}}_{\boldsymbol {p}}$
and ${\mathcal {F}}_{\boldsymbol {p}}$![]() in (5.5) and dropping the hat accents, the Poisson bracket (5.5) reduces to
in (5.5) and dropping the hat accents, the Poisson bracket (5.5) reduces to
Dropping the last pure divergence term in (5.9) (which converts to a surface integral over the boundary by Gauss's theorem), (5.9) reduces to the CGL Poisson bracket (5.2), which applies in the general case where $\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {B}\neq 0$![]() (i.e. the Jacobi identity applies for the bracket (5.2)), which is the analogue of the Morrison & Greene (Reference Morrison and Greene1982) bracket in MHD.
(i.e. the Jacobi identity applies for the bracket (5.2)), which is the analogue of the Morrison & Greene (Reference Morrison and Greene1982) bracket in MHD.
The CGL bracket (5.2) shares the same main features as the MHD bracket: it is bilinear, antisymmetric and obeys the Jacobi identity. A verification of the Jacobi identity can be given using functional multi-vectors (Olver Reference Olver1993) in the same way as for the MHD bracket (e.g. Webb Reference Webb2018, Chapter 8). An alternative verification of the Jacobi identity for the MHD bracket is given in Morrison (Reference Morrison1982); see also Chandre (Reference Chandre2013), Chandre et al. (Reference Chandre, Guillebon, Back, Tassi and Morrison2013), as well as Holm & Kupershmidt (Reference Holm and Kupershmidt1983a,Reference Holm and Kupershmidtb) who used the magnetic vector potential $\boldsymbol {A}$![]() in the advected gauge (2.90).
in the advected gauge (2.90).
In general, any Poisson bracket can be expressed in a cosymplectic form which defines a corresponding Hamiltonian (cosymplectic) operator. Using non-canonical Eulerian variables ${\mathsf{{Z}}}$![]() , the cosymplectic form is given by
, the cosymplectic form is given by
in which $\boldsymbol {\mathcal {D}}$![]() is the Hamiltonian (matrix) operator, where ${\mathsf{{T}}}$
is the Hamiltonian (matrix) operator, where ${\mathsf{{T}}}$![]() denotes the transpose. Note that, in the case ${\mathsf{{Z}}} =(\boldsymbol {q},\boldsymbol {p})$
denotes the transpose. Note that, in the case ${\mathsf{{Z}}} =(\boldsymbol {q},\boldsymbol {p})$![]() , this operator reduces to the skew matrix $\boldsymbol {\mathcal {D}} = \left (\begin {smallmatrix} 0 & {\mathsf{{I}}} \\ -{\mathsf{{I}}} & 0 \end {smallmatrix}\right )$
, this operator reduces to the skew matrix $\boldsymbol {\mathcal {D}} = \left (\begin {smallmatrix} 0 & {\mathsf{{I}}} \\ -{\mathsf{{I}}} & 0 \end {smallmatrix}\right )$![]() . Antisymmetry of the bracket (5.10), $\{{\mathcal {F}},{\mathcal {G}}\}+\{{\mathcal {G}},{\mathcal {F}}\}=0$
. Antisymmetry of the bracket (5.10), $\{{\mathcal {F}},{\mathcal {G}}\}+\{{\mathcal {G}},{\mathcal {F}}\}=0$![]() , corresponds to $\boldsymbol {\mathcal {D}}$
, corresponds to $\boldsymbol {\mathcal {D}}$![]() being skew-adjoint; the Jacobi identity, $\{\{{\mathcal {F}},{\mathcal {G}}\},{\mathcal {H}}\}+\{\{{\mathcal {H}},{\mathcal {F}}\},{\mathcal {G}}\}+\{\{{\mathcal {G}},{\mathcal {H}}\},{\mathcal {F}}\}=0$
being skew-adjoint; the Jacobi identity, $\{\{{\mathcal {F}},{\mathcal {G}}\},{\mathcal {H}}\}+\{\{{\mathcal {H}},{\mathcal {F}}\},{\mathcal {G}}\}+\{\{{\mathcal {G}},{\mathcal {H}}\},{\mathcal {F}}\}=0$![]() , corresponds to $\boldsymbol {\mathcal {D}}$
, corresponds to $\boldsymbol {\mathcal {D}}$![]() having a vanishing Schouten bracket with itself (Olver Reference Olver1993).
having a vanishing Schouten bracket with itself (Olver Reference Olver1993).
Taking
with $M^i$![]() and $B^i$
and $B^i$![]() denoting the components of $\boldsymbol {M}$
denoting the components of $\boldsymbol {M}$![]() and $\boldsymbol {B}$
and $\boldsymbol {B}$![]() , respectively, in Cartesian coordinates $x^i$
, respectively, in Cartesian coordinates $x^i$![]() , we see that the cosymplectic form (5.10) of the CGL bracket (5.2) after integration by parts is given by the Hamiltonian operator:
, we see that the cosymplectic form (5.10) of the CGL bracket (5.2) after integration by parts is given by the Hamiltonian operator:

where $\circ$![]() denotes operator composition (i.e. $\boldsymbol {\nabla } \circ a = (\boldsymbol {\nabla } a) + a\boldsymbol {\nabla }$
denotes operator composition (i.e. $\boldsymbol {\nabla } \circ a = (\boldsymbol {\nabla } a) + a\boldsymbol {\nabla }$![]() ). Here $\boldsymbol {\nabla }^k$
). Here $\boldsymbol {\nabla }^k$![]() acts as the total derivative with respect to $x^k$
acts as the total derivative with respect to $x^k$![]() . Note that the minus sign in (5.12) is due to the overall minus sign in the CGL Poisson bracket (5.2) which follows the sign convention used in the MHD bracket (5.1) in Morrison & Greene (Reference Morrison and Greene1980, Reference Morrison and Greene1982).
. Note that the minus sign in (5.12) is due to the overall minus sign in the CGL Poisson bracket (5.2) which follows the sign convention used in the MHD bracket (5.1) in Morrison & Greene (Reference Morrison and Greene1980, Reference Morrison and Greene1982).
We can convert (5.12) into vector notation by identifying $\boldsymbol {\nabla }^i F= \textrm {grad}\,F = \boldsymbol {\nabla } F$![]() , $\boldsymbol {\nabla }^j F^j= \textrm {div} \, \boldsymbol {F} =\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {F}$
, $\boldsymbol {\nabla }^j F^j= \textrm {div} \, \boldsymbol {F} =\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {F}$![]() and $\boldsymbol {\nabla }^j F^k - \boldsymbol {\nabla }^k F^j = \textrm {{curl}} \,\boldsymbol {F}= \boldsymbol {\nabla }\times \boldsymbol {F}$
and $\boldsymbol {\nabla }^j F^k - \boldsymbol {\nabla }^k F^j = \textrm {{curl}} \,\boldsymbol {F}= \boldsymbol {\nabla }\times \boldsymbol {F}$![]() .
.
5.1 Non-canonical Hamiltonian equations
A non-canonical Poisson bracket (5.10) provides a Hamiltonian formulation once a Hamiltonian functional ${\mathcal {H}}$![]() is chosen. The formulation involves expressing the dynamical variables ${\mathsf{{Z}}}(\boldsymbol {x},t)$
is chosen. The formulation involves expressing the dynamical variables ${\mathsf{{Z}}}(\boldsymbol {x},t)$![]() formally as functionals
formally as functionals
and writing Hamilton's equations in the form
Using the explicit expression (5.10) for the bracket yields
in terms of the Hamiltonian operator $\boldsymbol {\mathcal {D}}$![]() .
.
The appropriate Hamiltonian for describing CGL plasmas is given by the conserved total energy (cf. § 2.3):
where $H$![]() is the Eulerian total energy density (3.20). Substituting this Hamiltonian into the non-canonical Hamilton's equations (5.15) can be shown to yield the CGL plasma equations (2.1)–(2.6) and (2.8)–(2.9).
is the Eulerian total energy density (3.20). Substituting this Hamiltonian into the non-canonical Hamilton's equations (5.15) can be shown to yield the CGL plasma equations (2.1)–(2.6) and (2.8)–(2.9).
5.2 Casimirs
In a non-canonical Hamiltonian system, a functional ${\mathcal {C}} = \int _{V} C\, \textrm {d}^3x$![]() satisfying the equation
satisfying the equation
is called a Casimir. Existence of a non-trivial Casimir ${\mathcal {C}}\not \equiv 0$![]() indicates that the Poisson bracket is degenerate. Correspondingly, the Hamiltonian operator $\boldsymbol {\mathcal {D}}$
indicates that the Poisson bracket is degenerate. Correspondingly, the Hamiltonian operator $\boldsymbol {\mathcal {D}}$![]() in the cosymplectic form of the bracket (5.10) will have a non-trivial kernel:
in the cosymplectic form of the bracket (5.10) will have a non-trivial kernel:
where ${\mathcal {C}}_{{\mathsf{{Z}}}} \equiv {\delta {\mathcal {C}}}/{\delta {\mathsf{{Z}}}}$![]() . Note that a Casimir is a conserved integral, because the time evolution of any functional is given by the Hamiltonian equations (5.14):
. Note that a Casimir is a conserved integral, because the time evolution of any functional is given by the Hamiltonian equations (5.14):
Casimirs are useful in stability analysis of steady flows and plasma equilibria (e.g. Holm et al. Reference Holm, Marsden, Ratiu and Weinstein1985; Hameiri Reference Hameiri2004). The conservation (5.19) holds modulo boundary integrals, and an investigation of boundary conditions is needed for a Casimir to be a strictly conserved integral (i.e. a constant of motion).
All Casimirs can be determined by solving (5.17), or alternatively (5.18) (see, e.g., Hameiri (Reference Hameiri2004) and Padhye & Morrison (Reference Padhye and Morrison1996a,Reference Padhye and Morrisonb) for the MHD case). For CGL plasmas, we obtain the Casimir determining equations:

where $\boldsymbol {\nabla }$![]() ($\boldsymbol {\nabla }^k$
($\boldsymbol {\nabla }^k$![]() ) acts as the total derivative with respect to $\boldsymbol {x}$
) acts as the total derivative with respect to $\boldsymbol {x}$![]() ($x^k$
($x^k$![]() ). This is an overdetermined system of linear partial differential equations for
). This is an overdetermined system of linear partial differential equations for
with ${\mathsf{{Z}}}$![]() denoting the dynamical variables (5.11). The system can, in principle, be integrated to find ${\mathcal {C}}$
denoting the dynamical variables (5.11). The system can, in principle, be integrated to find ${\mathcal {C}}$![]() explicitly, once a differential order $l$
explicitly, once a differential order $l$![]() for the dependence of ${\mathcal {C}}$
for the dependence of ${\mathcal {C}}$![]() on derivatives of the variables is chosen. Note that solutions of the divergence form $C=\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {F}$
on derivatives of the variables is chosen. Note that solutions of the divergence form $C=\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {F}$![]() lead to ${\mathcal {C}}$
lead to ${\mathcal {C}}$![]() being a boundary integral which can be assumed to be trivial if suitable boundary conditions are imposed. This classification problem is beyond the scope of the present work.
being a boundary integral which can be assumed to be trivial if suitable boundary conditions are imposed. This classification problem is beyond the scope of the present work.
5.3 Mass, cross-helicity and magnetic helicity Casimirs
The well-known Casimirs for ideal barotropic MHD are the mass integral, the cross-helicity integral and the magnetic helicity integral. CGL plasmas with an isentropic equation of state $e=e(\rho,B)$![]() possess these same Casimirs:
possess these same Casimirs:
In the more physically realistic case with an equation of state $e=e(\rho,S,B)$![]() , ${\mathcal {C}}_1$
, ${\mathcal {C}}_1$![]() and ${\mathcal {C}}_3$
and ${\mathcal {C}}_3$![]() still hold as Casimirs, but ${\mathcal {C}}_2$
still hold as Casimirs, but ${\mathcal {C}}_2$![]() turns out to be a Casimir only in the case $\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla } S=0$
turns out to be a Casimir only in the case $\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla } S=0$![]() , as we show shortly.
, as we show shortly.
Physically, the mass integral ${\mathcal {C}}_1$![]() is the total mass of the plasma; the cross-helicity integral ${\mathcal {C}}_2$
is the total mass of the plasma; the cross-helicity integral ${\mathcal {C}}_2$![]() describes the linking of the fluid vorticity and magnetic field flux tubes; and the magnetic helicity integral ${\mathcal {C}}_3$
describes the linking of the fluid vorticity and magnetic field flux tubes; and the magnetic helicity integral ${\mathcal {C}}_3$![]() describes the knotting, linking and twist and writhe of the magnetic flux tubes (see,e.g., Berger & Field Reference Berger and Field1984; Moffatt & Ricca Reference Moffatt and Ricca1992; Hameiri Reference Hameiri2004). (Also see, e.g., Yoshida (Reference Yoshida2016), for interesting applications). In a fixed volume $V$
describes the knotting, linking and twist and writhe of the magnetic flux tubes (see,e.g., Berger & Field Reference Berger and Field1984; Moffatt & Ricca Reference Moffatt and Ricca1992; Hameiri Reference Hameiri2004). (Also see, e.g., Yoshida (Reference Yoshida2016), for interesting applications). In a fixed volume $V$![]() with a boundary $\partial V$
with a boundary $\partial V$![]() , ${\mathcal {C}}_1$
, ${\mathcal {C}}_1$![]() is conserved, $\partial {\mathcal {C}}_1/\partial t=0$
is conserved, $\partial {\mathcal {C}}_1/\partial t=0$![]() , if $\boldsymbol {u}$
, if $\boldsymbol {u}$![]() has no normal component at the boundary (cf. § 2.3). Conservation of ${\mathcal {C}}_3$
has no normal component at the boundary (cf. § 2.3). Conservation of ${\mathcal {C}}_3$![]() , $\partial {\mathcal {C}}_3/\partial t=0$
, $\partial {\mathcal {C}}_3/\partial t=0$![]() , holds if, in addition, $\boldsymbol {B}$
, holds if, in addition, $\boldsymbol {B}$![]() has no normal component at the boundary, whereas the cross-helicity integral ${\mathcal {C}}_2$
has no normal component at the boundary, whereas the cross-helicity integral ${\mathcal {C}}_2$![]() is conserved, $\partial {\mathcal {C}}_2/\partial t=0$
is conserved, $\partial {\mathcal {C}}_2/\partial t=0$![]() , only with the further condition $\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla } S=0$
, only with the further condition $\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla } S=0$![]() (cf. §§ 2.4 and 2.5).
(cf. §§ 2.4 and 2.5).
5.4 Advected Casimirs
In general, Casimirs can be sought by looking among advected scalars, $\theta$![]() , because the corresponding scalar integral $\int _{V(t)} \rho \theta \,\textrm {d}^3x$
, because the corresponding scalar integral $\int _{V(t)} \rho \theta \,\textrm {d}^3x$![]() will be conserved on volumes $V(t)$
will be conserved on volumes $V(t)$![]() moving with the flow. This implies that, on a fixed volume $V$
moving with the flow. This implies that, on a fixed volume $V$![]() , the integral $\int _{V} \rho \theta \,\textrm {d}^3x$
, the integral $\int _{V} \rho \theta \,\textrm {d}^3x$![]() will be conserved up to a flux integral $-\oint _{\partial V} \rho \theta \boldsymbol {u}\boldsymbol {\cdot }\hat {\boldsymbol {n}}\,\textrm {d}A$
will be conserved up to a flux integral $-\oint _{\partial V} \rho \theta \boldsymbol {u}\boldsymbol {\cdot }\hat {\boldsymbol {n}}\,\textrm {d}A$![]() that vanishes if $\boldsymbol {u}$
that vanishes if $\boldsymbol {u}$![]() has no normal component at the boundary $\partial V$
has no normal component at the boundary $\partial V$![]() and, therefore, $\int _{V} \rho \theta \,\textrm {d}^3x$
and, therefore, $\int _{V} \rho \theta \,\textrm {d}^3x$![]() will satisfy the Casimir property $\partial {\mathcal {C}}/\partial t=0$
will satisfy the Casimir property $\partial {\mathcal {C}}/\partial t=0$![]() . Note that this property is necessary but not sufficient for $\int _{V} \rho \theta \,\textrm {d}^3x$
. Note that this property is necessary but not sufficient for $\int _{V} \rho \theta \,\textrm {d}^3x$![]() to be a Casimir, because there are conserved integrals such as the total energy and angular momentum that do not belong to the kernel of the Poisson bracket.
to be a Casimir, because there are conserved integrals such as the total energy and angular momentum that do not belong to the kernel of the Poisson bracket.
For CGL plasmas, the basic advected scalars are $S$![]() , $\bar {S}_\parallel$
, $\bar {S}_\parallel$![]() , $\bar {S}_\perp$
, $\bar {S}_\perp$![]() . Additional advected scalars are provided by Ertel's theorem: if $\theta$
. Additional advected scalars are provided by Ertel's theorem: if $\theta$![]() is an advected scalar, then so is ${\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla }\theta }/{\rho }$
is an advected scalar, then so is ${\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla }\theta }/{\rho }$![]() . This yields the advected quantities (2.89a–c) shown in § 2.6.
. This yields the advected quantities (2.89a–c) shown in § 2.6.
One can show that
is an advected Casimir, for any function $f(S,\theta )$![]() . We omit the proof.
. We omit the proof.
6 Noether's theorem and conservation laws
Conservation laws of the CGL plasma equations (2.1) to (2.10a–c) can be derived from Noether's theorem applied to the Lie point symmetries of the Lagrangian variational principle (3.19). A brief discussion of the MHD case was outlined in Webb & Anco (Reference Webb and Anco2019). The CGL plasma conservation laws differ in comparison with the MHD conservation laws mainly in the form of pressure tensor: in particular, the MHD isotropic gas pressure tensor ${\mathsf{{p}}}=p\, {\mathsf{{I}}}$![]() is replaced by the non-isotropic CGL plasma pressure tensor ${\mathsf{{p}}}=p_\perp {\mathsf{{I}}}+(p_\parallel -p_\perp )\boldsymbol {\tau }\boldsymbol {\tau }$
is replaced by the non-isotropic CGL plasma pressure tensor ${\mathsf{{p}}}=p_\perp {\mathsf{{I}}}+(p_\parallel -p_\perp )\boldsymbol {\tau }\boldsymbol {\tau }$![]() .
.
Appendix H gives a description of Noether's first theorem, for a differential equation system described by an action principle as developed by Bluman & Kumei (Reference Bluman and Kumei1989). The analysis uses canonical Lie symmetry operators ${X}$![]() in which both the dependent and independent variables change in the Lie transformation, and also the evolutionary form of the symmetry operator denoted by $\hat {{X}}$
in which both the dependent and independent variables change in the Lie transformation, and also the evolutionary form of the symmetry operator denoted by $\hat {{X}}$![]() in which the independent variables do not change, but the dependent variables and the derivatives of the dependent variables change. The prolongation operators $\textrm {pr}\,{X}$
in which the independent variables do not change, but the dependent variables and the derivatives of the dependent variables change. The prolongation operators $\textrm {pr}\,{X}$![]() and $\textrm {pr}\,\hat {{X}}$
and $\textrm {pr}\,\hat {{X}}$![]() are described, and used to derive Noether's first theorem similar to Bluman & Kumei (Reference Bluman and Kumei1989). More recent derivations of Noether's theorem using $\textrm {pr}\,\hat {{X}}$
are described, and used to derive Noether's first theorem similar to Bluman & Kumei (Reference Bluman and Kumei1989). More recent derivations of Noether's theorem using $\textrm {pr}\,\hat {{X}}$![]() , are given by Bluman & Anco (Reference Bluman and Anco2002) and Olver (Reference Olver1993).
, are given by Bluman & Anco (Reference Bluman and Anco2002) and Olver (Reference Olver1993).
In § 6.1 we use a recent form of Noether's theorem to derive conservation laws using the evolutionary form of the prolonged symmetry operator $\textrm {pr}\,\hat {{X}}$![]() . In § 6.2 we obtain the same results from the classical form of Noether's theorem given in Appendix H. Although the recent form of Noether's theorem, is conceptually more appealing, it is not any simpler than the classical form of Noether's theorem. The classical form of Noether's theorem is perhaps easier to understand, as it relates directly back to the invariance of the action integral under Lie and divergence transformations.
. In § 6.2 we obtain the same results from the classical form of Noether's theorem given in Appendix H. Although the recent form of Noether's theorem, is conceptually more appealing, it is not any simpler than the classical form of Noether's theorem. The classical form of Noether's theorem is perhaps easier to understand, as it relates directly back to the invariance of the action integral under Lie and divergence transformations.
6.1 Noether's theorem and evolutionary symmetries
To use Noether's theorem, we need to obtain the Lie point symmetries of the Lagrangian variational principle (3.19). As this variational principle employs the variables $x^i=X^i(x_0^j,t)$![]() given by the Cartesian components of the Lagrangian map (3.2), a Lie point symmetry acting on the coordinate space $(t,x_0^j,x^i)$
given by the Cartesian components of the Lagrangian map (3.2), a Lie point symmetry acting on the coordinate space $(t,x_0^j,x^i)$![]() has the form
has the form
with $\epsilon$![]() denoting the parameter in the point symmetry transformation, where $\xi ^i$
denoting the parameter in the point symmetry transformation, where $\xi ^i$![]() , $\xi _0^i$
, $\xi _0^i$![]() , $\xi ^t$
, $\xi ^t$![]() are functions of $t,x_0^j,x^i$
are functions of $t,x_0^j,x^i$![]() . The infinitesimal transformation corresponds to the generator
. The infinitesimal transformation corresponds to the generator
whereas the finite transformation (6.1a–c) is given by exponentiation of the generator, $(t,x^i,x_0^i)\to \exp (\epsilon {X})(t,x^i,x_0^i)$![]() .
.
To be a symmetry, a generator (6.2) must leave the variational principle invariant modulo boundary terms. This is equivalent to the condition that the change in the Lagrangian must satisfy (Ovsjannikov Reference Ovsjannikov1978; Ibragimov Reference Ibragimov1985)
where the operators $D_t=\partial /\partial _{t} + \dot {x}^i\partial /\partial _{x^i} +\cdots$![]() and $D_{x_0^i} = \partial /\partial _{x_0^i} + x^{ji}\partial /\partial _{x^j} +\cdots$
and $D_{x_0^i} = \partial /\partial _{x_0^i} + x^{ji}\partial /\partial _{x^j} +\cdots$![]() denote total derivative operators with respect to the independent variables $t$
denote total derivative operators with respect to the independent variables $t$![]() and $x_0^i$
and $x_0^i$![]() and $D_{x^i}$
and $D_{x^i}$![]() denotes the partial derivative with respect to $x^i$
denotes the partial derivative with respect to $x^i$![]() keeping $\boldsymbol {x}_0$
keeping $\boldsymbol {x}_0$![]() and $t$
and $t$![]() constant. Here $\varLambda ^t_0$
constant. Here $\varLambda ^t_0$![]() and $\varLambda ^i_0$
and $\varLambda ^i_0$![]() are arbitrary potentials, that arise in Noether's theorem, because the variational derivative of a perfect derivative term has zero variational derivative. The first two terms on the right-hand side of (6.3) represent the Lie derivative ${\mathcal {L}}_{\boldsymbol {X}} L_0$
are arbitrary potentials, that arise in Noether's theorem, because the variational derivative of a perfect derivative term has zero variational derivative. The first two terms on the right-hand side of (6.3) represent the Lie derivative ${\mathcal {L}}_{\boldsymbol {X}} L_0$![]() using the chain rule for differentiation. The terms involving total derivatives of $L_0$
using the chain rule for differentiation. The terms involving total derivatives of $L_0$![]() on the right-hand side of (6.3) can be understood to arise from the change in the spatial domain $V_0$
on the right-hand side of (6.3) can be understood to arise from the change in the spatial domain $V_0$![]() and the time interval $[t_0,t_1]$
and the time interval $[t_0,t_1]$![]() in the variational principle (3.19) under the action of an infinitesimal point transformation (6.1a–c). On the left-hand side of (6.3), $\textrm {pr}$
in the variational principle (3.19) under the action of an infinitesimal point transformation (6.1a–c). On the left-hand side of (6.3), $\textrm {pr}$![]() denotes prolongation to the extended coordinate space $(t,x_0^j,x^i,\dot {x}^i,x^{ij})$
denotes prolongation to the extended coordinate space $(t,x_0^j,x^i,\dot {x}^i,x^{ij})$![]() (i.e. jet space) in which $\dot {x}^i$
(i.e. jet space) in which $\dot {x}^i$![]() and $x^{ij}$
and $x^{ij}$![]() are coordinates that correspond to $\dot {X}^i(x_0^j,t)$
are coordinates that correspond to $\dot {X}^i(x_0^j,t)$![]() and $\partial X^i(x_0^j,t)/\partial x_0^j$
and $\partial X^i(x_0^j,t)/\partial x_0^j$![]() on solutions $x^i=X^i(x_0^j,t)$
on solutions $x^i=X^i(x_0^j,t)$![]() of the Euler–Lagrange equations (3.24) of the variational principle. An explicit formula for the components of $\textrm {pr}\,{X}$
of the Euler–Lagrange equations (3.24) of the variational principle. An explicit formula for the components of $\textrm {pr}\,{X}$![]() will not be needed if we express the invariance condition (6.3) by using the characteristic form of the generator in which only the dependent variables $x^i$
will not be needed if we express the invariance condition (6.3) by using the characteristic form of the generator in which only the dependent variables $x^i$![]() undergo a transformation
undergo a transformation
which arises from how ${X}$![]() acts on solutions $x^i=X^i(x_0^j,t)$
acts on solutions $x^i=X^i(x_0^j,t)$![]() . The relationship between the two forms (6.4a,b) and (6.2) is that $\textrm {pr}\,{X}= \textrm {pr}\,\hat {{X}} + \xi ^t D_t + \xi _0^i D_{x_0^i}$
. The relationship between the two forms (6.4a,b) and (6.2) is that $\textrm {pr}\,{X}= \textrm {pr}\,\hat {{X}} + \xi ^t D_t + \xi _0^i D_{x_0^i}$![]() . Hence, (6.3) becomes (Olver Reference Olver1993; Bluman & Anco Reference Bluman and Anco2002)
. Hence, (6.3) becomes (Olver Reference Olver1993; Bluman & Anco Reference Bluman and Anco2002)
where
is a function of $t,x_0^j,x^i,\dot {x}^i,x^{ij}$![]() . The prolongation $\textrm {pr}\,\hat {{X}}$
. The prolongation $\textrm {pr}\,\hat {{X}}$![]() is given by simply extending $\hat {{X}}$
is given by simply extending $\hat {{X}}$![]() to act on $\dot {x}^i$
to act on $\dot {x}^i$![]() and $x^{ij}$
and $x^{ij}$![]() through the total derivative relations $\textrm {pr}\,\hat {{X}}(\dot {x}^i) = D_t(\hat {{X}} x^i) = D_t \xi ^t$
through the total derivative relations $\textrm {pr}\,\hat {{X}}(\dot {x}^i) = D_t(\hat {{X}} x^i) = D_t \xi ^t$![]() and $\textrm {pr}\,\hat {{X}}(x^{ij}) = D_{x_0^j}(\hat {{X}} x^i) = D_{x_0^j}\xi ^i$
and $\textrm {pr}\,\hat {{X}}(x^{ij}) = D_{x_0^j}(\hat {{X}} x^i) = D_{x_0^j}\xi ^i$![]() .
.
In turn, this form (6.5) of the invariance condition can be expressed succinctly as
using the Euler–Lagrange operator $E_{x^i}$![]() which has the property that it annihilates a function iff the function is given by a total divergence with respect to $t$
which has the property that it annihilates a function iff the function is given by a total divergence with respect to $t$![]() and $x_0^j$
and $x_0^j$![]() . The formulation (6.7) can be used as a determining equation to find all Lie point symmetries of the variational principle (3.19). (See Olver (Reference Olver1993) and Bluman & Anco (Reference Bluman and Anco2002) for a general discussion.)
. The formulation (6.7) can be used as a determining equation to find all Lie point symmetries of the variational principle (3.19). (See Olver (Reference Olver1993) and Bluman & Anco (Reference Bluman and Anco2002) for a general discussion.)
Each Lie point symmetry (6.1a–c) gives rise to a conservation law through combining the condition (6.5) and Noether's identity
where
Thus, we obtain the following statement of Noether's theorem.
Proposition 6.1 If the Lagrangian variational principle (3.19) is invariant up to boundary terms under an infinitesimal point transformation (6.1a–c), then the Euler–Lagrange equations (3.24) of the variational principle possess a conservation law
in which the conserved density and the spatial flux are given by
Explicit expressions for $\partial \hat {L}_0/\partial \dot {x}^j = (\partial L_0/\partial \dot {X}^j)|_{\boldsymbol {X}=\boldsymbol {x}}$![]() and $\partial \hat {L}_0/\partial x^{ji} = (\partial L_0/\partial X^{ji})|_{\boldsymbol {X}=\boldsymbol {x}}$
and $\partial \hat {L}_0/\partial x^{ji} = (\partial L_0/\partial X^{ji})|_{\boldsymbol {X}=\boldsymbol {x}}$![]() are provided by (C1) in Appendix C. Note that the conservation law is a local continuity equation which holds when $x^i=X^i(x_0^j,t)$
are provided by (C1) in Appendix C. Note that the conservation law is a local continuity equation which holds when $x^i=X^i(x_0^j,t)$![]() satisfies the Euler–Lagrange equations (3.24). On solutions, $D_t|_{x=\boldsymbol {X}} = \partial /\partial t$
satisfies the Euler–Lagrange equations (3.24). On solutions, $D_t|_{x=\boldsymbol {X}} = \partial /\partial t$![]() and $D_{x_0^i}|_{x=\boldsymbol {X}} = \partial /\partial x_0^i$
and $D_{x_0^i}|_{x=\boldsymbol {X}} = \partial /\partial x_0^i$![]() (acting as total derivatives).
(acting as total derivatives).
We remark that (6.11a,b) can be derived alternatively using the canonical form of a symmetry generator (6.2), which requires computing the prolongation. See Webb & Zank (Reference Webb and Zank2007) and Webb & Anco (Reference Webb and Anco2019) for the MHD case. The canonical symmetry approach to conservation laws for the CGL system is also described in Appendix H.
6.1.1 Eulerian form of a Lagrangian conservation law
A Lagrangian conservation law (6.11a,b) can be expressed equivalently as an Eulerian conservation law (Padhye Reference Padhye1998)
whose conserved density and spatial flux are given by
on solutions $x^i=X^i(x_0^j,t)$![]() of the Euler–Lagrange equations (3.24). This form (6.12)–(6.13a,b) of a conservation law is appropriate for considering conserved integrals
of the Euler–Lagrange equations (3.24). This form (6.12)–(6.13a,b) of a conservation law is appropriate for considering conserved integrals
on a fixed spatial domain $V$![]() in the CGL plasma.
in the CGL plasma.
In general, an Eulerian conservation law is a continuity equation of the form (6.12) holding on the solution space of the CGL plasma equations (2.1)–(2.10a–c). The corresponding conserved integral (6.14) has the physical content that the rate of change of the integral quantity $\int _{V} \varPhi ^t\, \textrm {d}^3x$![]() in $V$
in $V$![]() is balanced by the net flux leaving the boundary of $V$
is balanced by the net flux leaving the boundary of $V$![]() . It is often physically useful to consider instead a spatial domain $V(t)$
. It is often physically useful to consider instead a spatial domain $V(t)$![]() that moves with the plasma. The form of the conservation law for moving domains is given by
that moves with the plasma. The form of the conservation law for moving domains is given by
in terms of the moving flux
Note that the moving integral quantity $\int _{V(t)} \varPsi ^t\,\textrm {d}^3x$![]() will be an invariant (i.e. a constant of motion) when the net moving flux vanishes on the boundary $\partial V (t)$
will be an invariant (i.e. a constant of motion) when the net moving flux vanishes on the boundary $\partial V (t)$![]() . (See Anco & Webb (Reference Anco and Webb2020) for a discussion of moving domain conservation laws and invariants in fluid mechanics.) The equivalence between the conservation laws (6.14) and (6.15) can be derived by writing the continuity equation (6.12) in terms of the material (co-moving) derivative (2.88): $\textrm {d}\varPhi ^t/\textrm {d}t = -(\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {u})\varPhi ^t - \boldsymbol {\nabla }\boldsymbol {\cdot }(\boldsymbol {\varPhi }-\varPhi ^t\boldsymbol {u})$
. (See Anco & Webb (Reference Anco and Webb2020) for a discussion of moving domain conservation laws and invariants in fluid mechanics.) The equivalence between the conservation laws (6.14) and (6.15) can be derived by writing the continuity equation (6.12) in terms of the material (co-moving) derivative (2.88): $\textrm {d}\varPhi ^t/\textrm {d}t = -(\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {u})\varPhi ^t - \boldsymbol {\nabla }\boldsymbol {\cdot }(\boldsymbol {\varPhi }-\varPhi ^t\boldsymbol {u})$![]() , where $(\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {u})$
, where $(\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {u})$![]() represents the expansion or contraction of an infinitesimal volume $\textrm {d}^3x$
represents the expansion or contraction of an infinitesimal volume $\textrm {d}^3x$![]() moving with the fluid (see, e.g., Anco & Dar Reference Anco and Dar2009, Reference Anco and Dar2010).
moving with the fluid (see, e.g., Anco & Dar Reference Anco and Dar2009, Reference Anco and Dar2010).
Now, rather than seeking to find all Lie point symmetries, we consider two main classes: kinematic and fluid relabelling. Kinematic symmetries are characterised by the generator (6.1a–c) having $\xi _0^i=0$![]() , with $\xi ^t$
, with $\xi ^t$![]() and $\xi ^i$
and $\xi ^i$![]() being functions only of $t,x^i$
being functions only of $t,x^i$![]() . Fluid relabelling symmetries have $\xi ^i=\xi ^t=0$
. Fluid relabelling symmetries have $\xi ^i=\xi ^t=0$![]() in the generator (6.1a–c), with $\xi _0^i$
in the generator (6.1a–c), with $\xi _0^i$![]() being a function only of $t,x_0^i$
being a function only of $t,x_0^i$![]() .
.
A useful general remark is that any Lie point symmetry of a variational principle corresponds to a Lie point symmetry of the Euler–Lagrange equations, because invariance of a variational principle means that its extremals are preserved. Thus, one way to find all Lie point symmetries of a variational principle is by first obtaining the Lie point symmetries of the Euler–Lagrange equations and, second, checking which of those symmetries leaves invariant the variational principle.
Before deriving conservation laws using the above analysis, it is useful to note that there are three basic steps in the analysis.
(i) First it is necessary to determine for a given Lie symmetry, whether the Lie invariance condition (6.5) for the action can be satisfied by choosing the potentials $\varLambda ^t_0$
 and $\varLambda ^i_0$
and $\varLambda ^i_0$ . Here the left-hand side of (6.5) for the action $\textrm {pr}\,\hat {X}(L_0)$
. Here the left-hand side of (6.5) for the action $\textrm {pr}\,\hat {X}(L_0)$ is evaluated for the symmetry operator $X$
is evaluated for the symmetry operator $X$ .
.(ii) Determine the surface vector components $W^t$
 and $W^i$
and $W^i$ that occur in the Noether identity (6.8), where $W^t$
that occur in the Noether identity (6.8), where $W^t$ and $W^i$
and $W^i$ are given by (6.9a,b) (recall $\dot {x}^j=\partial x^j(\boldsymbol {x}_0,t)/\partial t=u^j$
are given by (6.9a,b) (recall $\dot {x}^j=\partial x^j(\boldsymbol {x}_0,t)/\partial t=u^j$ and $x^{ji}=\partial x^j/\partial x_0^i$
and $x^{ji}=\partial x^j/\partial x_0^i$ ). Then using Proposition 6.1 one can obtain the Lagrangian conservation law (6.10) with conserved density $\mathcal {I}_0^t$
). Then using Proposition 6.1 one can obtain the Lagrangian conservation law (6.10) with conserved density $\mathcal {I}_0^t$ and flux $\mathcal {I}_0^i$
and flux $\mathcal {I}_0^i$ given in (6.11a,b).
given in (6.11a,b).(iii) Determine the Eulerian form of the conservation law using the results of Padhye (Reference Padhye1998) described by (6.12) and (6.13a,b).
6.1.2 Lie invariance condition
The Lie invariance condition for the action in (6.5) may be written in the form

Here we use the notation $\hat {\boldsymbol {\xi }}\equiv \hat {\boldsymbol {\xi }}_0$![]() in the fluid re-labelling symmetry case. The Lie invariance condition (6.17) also applies for the general Lie symmetry case, including the Lie point Galilean symmetry cases, the fluid relabelling symmetry cases and other more general cases. The derivation of (6.17) from (6.5) is outlined in Appendix G. In the general case ${\hat {\xi }}^i=\xi ^i-(\xi ^tD_t+\xi ^s_0 D_{x_0^s})x^i$
in the fluid re-labelling symmetry case. The Lie invariance condition (6.17) also applies for the general Lie symmetry case, including the Lie point Galilean symmetry cases, the fluid relabelling symmetry cases and other more general cases. The derivation of (6.17) from (6.5) is outlined in Appendix G. In the general case ${\hat {\xi }}^i=\xi ^i-(\xi ^tD_t+\xi ^s_0 D_{x_0^s})x^i$![]() . The Lie invariance condition (6.17) is similar to the Eulerian Lie invariance condition for the action used by Webb & Anco (Reference Webb and Anco2019) for the case of MHD. Here the evolutionary form of the symmetry operator $X$
. The Lie invariance condition (6.17) is similar to the Eulerian Lie invariance condition for the action used by Webb & Anco (Reference Webb and Anco2019) for the case of MHD. Here the evolutionary form of the symmetry operator $X$![]() is used rather than the canonical symmetry operator used by Webb & Anco (Reference Webb and Anco2019).
is used rather than the canonical symmetry operator used by Webb & Anco (Reference Webb and Anco2019).
6.1.3 Galilean symmetries
The Eulerian form of the CGL plasma equations (2.1)–(2.10a–c) clearly indicates that they possess the Galilean group of Lie point symmetries when $\varPhi =0$![]() , which are generated by (Rogers & Ames Reference Rogers and Ames1989; Fuchs Reference Fuchs1991)
, which are generated by (Rogers & Ames Reference Rogers and Ames1989; Fuchs Reference Fuchs1991)
These generators describe a time translation ($P_0$![]() ), space translations ($P_i$
), space translations ($P_i$![]() , $i=1,2,3$
, $i=1,2,3$![]() ), Galilean boosts ($K_i$
), Galilean boosts ($K_i$![]() , $i=1,2,3$
, $i=1,2,3$![]() ) and rotations ($J_i$
) and rotations ($J_i$![]() , $i=1,2,3$
, $i=1,2,3$![]() ), respectively, about the $x$
), respectively, about the $x$![]() , $y$
, $y$![]() and $z$
and $z$![]() axes. As shown in appendix F, the only additional Lie point symmetries admitted by (2.1) to (2.10a–c) consist of scalings. Hence, Galilean symmetries and scaling symmetries comprise all kinematic Lie point symmetries of the CGL plasma equations.
axes. As shown in appendix F, the only additional Lie point symmetries admitted by (2.1) to (2.10a–c) consist of scalings. Hence, Galilean symmetries and scaling symmetries comprise all kinematic Lie point symmetries of the CGL plasma equations.
The Galilean symmetries (6.18a–d) have a corresponding Lagrangian form
Note that the prolongation of these Lagrangian generators to $\dot {x}^i=\dot {X}^i = u^i$![]() through the Lagrangian relation (3.1) for the fluid velocity yields the corresponding Eulerian generators (6.18a–d) acting on the variables $(t,x^i,u^i)$
through the Lagrangian relation (3.1) for the fluid velocity yields the corresponding Eulerian generators (6.18a–d) acting on the variables $(t,x^i,u^i)$![]() . As $\xi _0^i=0$
. As $\xi _0^i=0$![]() for all of the generators (6.19a–d), they are of kinematic type.
for all of the generators (6.19a–d), they are of kinematic type.
In the case when the gravitational potential $\varPhi$![]() is non-zero, then the preceding generators must satisfy the condition ${X} \varPhi (x^i) =0$
is non-zero, then the preceding generators must satisfy the condition ${X} \varPhi (x^i) =0$![]() to be admitted as symmetries. For example, if $\varPhi$
to be admitted as symmetries. For example, if $\varPhi$![]() is invariant under $z$
is invariant under $z$![]() -translation, then ${X}_{P_3}$
-translation, then ${X}_{P_3}$![]() and ${X}_{K_3}$
and ${X}_{K_3}$![]() are symmetries; if $\varPhi$
are symmetries; if $\varPhi$![]() is invariant under $z$
is invariant under $z$![]() -rotation, then ${X}_{J_3}$
-rotation, then ${X}_{J_3}$![]() is a symmetry; and if $\varPhi$
is a symmetry; and if $\varPhi$![]() is spherically symmetric, then ${X}_{J_i}$
is spherically symmetric, then ${X}_{J_i}$![]() , $i=1,2,3$
, $i=1,2,3$![]() , are symmetries.
, are symmetries.
6.1.4 Galilean conservation laws
It is straightforward to show that each Galilean generator (6.19a–d) satisfies the condition (6.7) for invariance of the Lagrangian variational principle (3.19) when $\varPhi =0$![]() and thereby yields a conservation law (6.10).
and thereby yields a conservation law (6.10).
Specifically, time translation ($X_{P_0}$![]() ) has $\hat {\xi }^i=-\dot {x}^i$
) has $\hat {\xi }^i=-\dot {x}^i$![]() and, thus, $\textrm {pr}\,\hat {{X}}_{P_0} L_0 = - \ddot x^i \partial L_0/\partial _{\dot {x}^i} - \dot {x}^{ij}\partial L_0/\partial _{x^{ij}} = -D_t L_0$
and, thus, $\textrm {pr}\,\hat {{X}}_{P_0} L_0 = - \ddot x^i \partial L_0/\partial _{\dot {x}^i} - \dot {x}^{ij}\partial L_0/\partial _{x^{ij}} = -D_t L_0$![]() due to $\partial L_0/\partial _t =0$
due to $\partial L_0/\partial _t =0$![]() . This gives $\varLambda _0^t = -L_0$
. This gives $\varLambda _0^t = -L_0$![]() , $\varLambda _0^i=0$
, $\varLambda _0^i=0$![]() , which yields conservation of energy
, which yields conservation of energy
with $H_0$![]() being the Hamiltonian (3.27).
being the Hamiltonian (3.27).
Space translations ($X_{P_j}$![]() ) have $\hat {\xi }^i=\delta ^i{}_j$
) have $\hat {\xi }^i=\delta ^i{}_j$![]() and, thus, $\textrm {pr}\,\hat {{X}}_{P_j} L_0 = 0$
and, thus, $\textrm {pr}\,\hat {{X}}_{P_j} L_0 = 0$![]() due to $\partial L_0/\partial _{x^i}=0$
due to $\partial L_0/\partial _{x^i}=0$![]() (where we neglect gravity) combined with $D_t\hat {\xi }^i=0$
(where we neglect gravity) combined with $D_t\hat {\xi }^i=0$![]() and $D_{x_0^j}\hat {\xi }^i=0$
and $D_{x_0^j}\hat {\xi }^i=0$![]() . Hence, $\varLambda _0^t =0$
. Hence, $\varLambda _0^t =0$![]() , $\varLambda _0^i=0$
, $\varLambda _0^i=0$![]() , which yields conservation of momentum
, which yields conservation of momentum
Galilean boosts ($X_{K_j}$![]() ) have $\hat {\xi }^i=t\delta ^i{}_j$
) have $\hat {\xi }^i=t\delta ^i{}_j$![]() and, thus, $\textrm {pr}\,\hat {{X}}_{K_j} L_0 = \rho _0 \dot {x}^j = D_t (\rho _0 x^j)$
and, thus, $\textrm {pr}\,\hat {{X}}_{K_j} L_0 = \rho _0 \dot {x}^j = D_t (\rho _0 x^j)$![]() . This gives $\varLambda _0^t =\rho _0 x^j$
. This gives $\varLambda _0^t =\rho _0 x^j$![]() , $\varLambda _0^i=0$
, $\varLambda _0^i=0$![]() , yielding conservation of Galilean momentum (centre of mass)
, yielding conservation of Galilean momentum (centre of mass)
Rotations ($X_{J_j}$![]() ) have $\hat {\xi }^i=\epsilon ^i{}_{kj}x^k$
) have $\hat {\xi }^i=\epsilon ^i{}_{kj}x^k$![]() . This leads to $\textrm {pr}\,\hat {{X}}_{J_j} L_0 = 0$
. This leads to $\textrm {pr}\,\hat {{X}}_{J_j} L_0 = 0$![]() , because $L_0$
, because $L_0$![]() depends on $x^i$
depends on $x^i$![]() only through the scalars $|\dot {x}^i|$
only through the scalars $|\dot {x}^i|$![]() and $|X_{ij}\tau _0^j|$
and $|X_{ij}\tau _0^j|$![]() which are rotationally invariant. Thus $\varLambda _0^t =0$
which are rotationally invariant. Thus $\varLambda _0^t =0$![]() , $\varLambda _0^i=0$
, $\varLambda _0^i=0$![]() , which yields conservation of axial angular momentum
, which yields conservation of axial angular momentum
The set of Galilean conservation laws (6.20a,b) to (6.23a,b) can be written in a unified form through use of the observation that
with
where $a_0$![]() , $a_1^i$
, $a_1^i$![]() , $a_2^i$
, $a_2^i$![]() and $a_3^i$
and $a_3^i$![]() ($i=1,2,3$
($i=1,2,3$![]() ) are arbitrary constants (parameterising the respective Galilean symmetry generators (6.19a–d)). Hence, we have
) are arbitrary constants (parameterising the respective Galilean symmetry generators (6.19a–d)). Hence, we have
The resulting set of Eulerian conservation laws (6.12)–(6.13a,b) takes the form
where we have used
which follow from expressions (C1) and (C6) in Appendix C, along with the formulae (3.5a–c) and (3.8). Here $p^{ij}$![]() and $M_B^{ij}$
and $M_B^{ij}$![]() represents the components of the CGL non-isotropic pressure tensor (2.3a–c) and the magnetic pressure tensor (2.4), respectively. Note that $H =\rho |\boldsymbol {u}|^2 -L$
represents the components of the CGL non-isotropic pressure tensor (2.3a–c) and the magnetic pressure tensor (2.4), respectively. Note that $H =\rho |\boldsymbol {u}|^2 -L$![]() is the Hamiltonian (3.20).
is the Hamiltonian (3.20).
In the MHD case, $p^{ij}$![]() is replaced by the components of the isotropic MHD gas pressure tensor $p\,\delta ^{ij}$
is replaced by the components of the isotropic MHD gas pressure tensor $p\,\delta ^{ij}$![]() .
.
The preceding derivations may be summarised as follows.
(i) Time translation symmetry ($a_0$
 ) yields energy conservation, for which
(6.30)\begin{equation} \left.\begin{gathered} \varPsi^t = H = \rho \left( \frac{1}{2}|\boldsymbol{u}|^2+\varPhi(\boldsymbol{x}) \right) +\varepsilon +\frac{B^2}{2\mu_0} , \\ {\boldsymbol{\varPsi}} = \left(\frac{1}{2}\rho |\boldsymbol{u}|^2 + \varepsilon+\rho\varPhi\right)\boldsymbol{u} + {\mathsf{{p}}}\boldsymbol{\cdot}\boldsymbol{u} +\frac{1}{\mu_0}\boldsymbol{E}\times\boldsymbol{B} ,\\ {\boldsymbol{\varGamma}} = {\boldsymbol{\varPsi}} -\boldsymbol{u}H =\left({\mathsf{{p}}}+{\mathsf{{M}}}_B\right)\boldsymbol{\cdot} \boldsymbol{u} , \end{gathered}\right\} \end{equation}where $\boldsymbol {E}=-\boldsymbol {u}\times \boldsymbol {B}$
) yields energy conservation, for which
(6.30)\begin{equation} \left.\begin{gathered} \varPsi^t = H = \rho \left( \frac{1}{2}|\boldsymbol{u}|^2+\varPhi(\boldsymbol{x}) \right) +\varepsilon +\frac{B^2}{2\mu_0} , \\ {\boldsymbol{\varPsi}} = \left(\frac{1}{2}\rho |\boldsymbol{u}|^2 + \varepsilon+\rho\varPhi\right)\boldsymbol{u} + {\mathsf{{p}}}\boldsymbol{\cdot}\boldsymbol{u} +\frac{1}{\mu_0}\boldsymbol{E}\times\boldsymbol{B} ,\\ {\boldsymbol{\varGamma}} = {\boldsymbol{\varPsi}} -\boldsymbol{u}H =\left({\mathsf{{p}}}+{\mathsf{{M}}}_B\right)\boldsymbol{\cdot} \boldsymbol{u} , \end{gathered}\right\} \end{equation}where $\boldsymbol {E}=-\boldsymbol {u}\times \boldsymbol {B}$
 is the electric field strength, and $\boldsymbol {E}\times \boldsymbol {B}/\mu _0$
is the electric field strength, and $\boldsymbol {E}\times \boldsymbol {B}/\mu _0$ is the Poynting flux.
is the Poynting flux.(ii) Space translation symmetry ($a_1^i, i=1,2,3$
 ) yields momentum conservation with
(6.31)\begin{equation} \left.\begin{gathered} \varPsi^t ={-}\boldsymbol{M} ={-}\rho \boldsymbol{u}, \quad {\boldsymbol{\varPsi}} ={-}{\mathsf{{T}}} ,\\ {\boldsymbol{\varGamma}} = {\boldsymbol{\varPsi}} -\boldsymbol{u}{\boldsymbol{\varPsi}}^t ={-}\left({\mathsf{{p}}} +{\mathsf{{M}}}_B\right) , \end{gathered}\right\} \end{equation}where
) yields momentum conservation with
(6.31)\begin{equation} \left.\begin{gathered} \varPsi^t ={-}\boldsymbol{M} ={-}\rho \boldsymbol{u}, \quad {\boldsymbol{\varPsi}} ={-}{\mathsf{{T}}} ,\\ {\boldsymbol{\varGamma}} = {\boldsymbol{\varPsi}} -\boldsymbol{u}{\boldsymbol{\varPsi}}^t ={-}\left({\mathsf{{p}}} +{\mathsf{{M}}}_B\right) , \end{gathered}\right\} \end{equation}where (6.32)\begin{equation} {\mathsf{{T}}} = \rho \boldsymbol{u}\boldsymbol{u} + {\mathsf{{p}}}+ {\mathsf{{M}}}_B \end{equation}is the CGL plasma stress tensor.
(6.32)\begin{equation} {\mathsf{{T}}} = \rho \boldsymbol{u}\boldsymbol{u} + {\mathsf{{p}}}+ {\mathsf{{M}}}_B \end{equation}is the CGL plasma stress tensor.
(iii) Galilean boost symmetry yields centre of mass conservation, with
(6.33)\begin{equation} \left.\begin{gathered} \varPsi^t = \rho \boldsymbol{x} -t\boldsymbol{M} = \rho (\boldsymbol{x} -t\boldsymbol{u}) , \quad {\boldsymbol{\varPsi}} = \rho \boldsymbol{u} \boldsymbol{x} -t{\mathsf{{T}}},\\ {\boldsymbol{\varGamma}} = {\boldsymbol{\varPsi}}-\boldsymbol{u}(\rho \boldsymbol{x} -t\boldsymbol{M}) ={-}t \left({\mathsf{{p}}} +{\mathsf{{M}}}_B\right) .\end{gathered}\right\} \end{equation}
(iv) Rotational symmetry yields angular momentum conservation, with
(6.34)\begin{equation} \left.\begin{gathered} \varPsi^t = \boldsymbol{x}\times \boldsymbol{M} = \rho \boldsymbol{x}\times \boldsymbol{u}, \quad {\boldsymbol{\varPsi}} = \boldsymbol{x}\times {\mathsf{{T}}} ,\\ {\boldsymbol{\varGamma}} = {\boldsymbol{\varPsi}} -\boldsymbol{u}(\boldsymbol{x}\times \boldsymbol{M}) = \boldsymbol{x}\times \left({\mathsf{{p}}} + {\mathsf{{M}}}_B\right) , \end{gathered}\right\} \end{equation}where $\boldsymbol {M} =\rho \boldsymbol {u}$
 is the momentum density vector.
is the momentum density vector.
6.1.5 Fluid relabelling symmetries
Fluid relabelling symmetries correspond to transformations (6.1a–c) that change the Lagrangian fluid labels $\boldsymbol {x}_0$![]() , but leave the Eulerian variables and $\boldsymbol {x}$
, but leave the Eulerian variables and $\boldsymbol {x}$![]() and $t$
and $t$![]() invariant: $x_0^i \to x_0^i +\epsilon \xi _0^i +O(\epsilon ^2)$
invariant: $x_0^i \to x_0^i +\epsilon \xi _0^i +O(\epsilon ^2)$![]() , where $\xi _0^i=\xi _0^i(t,x_0^j)$
, where $\xi _0^i=\xi _0^i(t,x_0^j)$![]() . The symmetry generator has the form
. The symmetry generator has the form
For evaluating the condition for invariance of the Lagrangian variational principle (3.19), we need the characteristic form of the generator:
To proceed we use the formulation (6.5) instead of (6.7), which allows for consideration of functions $\varLambda _0^t$![]() , $\varLambda _0^i$
, $\varLambda _0^i$![]() that can involve non-localpotentials. This generality is necessary to derive the cross-helicity conservation law (2.67)–(2.68) which involves the temperature potential (2.69a,b).
that can involve non-localpotentials. This generality is necessary to derive the cross-helicity conservation law (2.67)–(2.68) which involves the temperature potential (2.69a,b).
6.1.6 Noether's theorem for fluid-relabelling conservation laws
The Lie invariance condition (6.17) in the fluid relabelling symmetry cases, may be written in the form

where
For cross-helicity conservation, $\hat {\boldsymbol {\xi }}=-\boldsymbol {B}/\rho$![]() and ${\boldsymbol {\xi }}_0=\boldsymbol {B}_0/\rho _0$
and ${\boldsymbol {\xi }}_0=\boldsymbol {B}_0/\rho _0$![]() . Setting $\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {B}=0$
. Setting $\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {B}=0$![]() (Gauss's law), the left-hand side of (6.37) vanishes. The condition that the right-hand side of (6.37) vanish is satisfied by the choices
(Gauss's law), the left-hand side of (6.37) vanishes. The condition that the right-hand side of (6.37) vanish is satisfied by the choices
where $\boldsymbol {G}$![]() is given by (6.38). Evaluating formulae (6.38) and (6.39a,b) gives the formulae
is given by (6.38). Evaluating formulae (6.38) and (6.39a,b) gives the formulae
where $h=e+p_\parallel /\rho$![]() is the enthalpy of the CGL plasma. Here $\hat {\boldsymbol {\xi }}=-\boldsymbol {B}/\rho$
is the enthalpy of the CGL plasma. Here $\hat {\boldsymbol {\xi }}=-\boldsymbol {B}/\rho$![]() and ${\boldsymbol {\xi }}_0=\boldsymbol {B}_0/\rho _0$
and ${\boldsymbol {\xi }}_0=\boldsymbol {B}_0/\rho _0$![]() , which gives rise to the cross-helicity conservation laws described by (6.45a,b) and (6.46).
, which gives rise to the cross-helicity conservation laws described by (6.45a,b) and (6.46).
Noether's theorem given by Proposition 6.1 now gives the following main result.
Proposition 6.2 The Lagrangian variational principle (3.19) is invariant up to boundary terms under the infinitesimal fluid relabelling transformation
The resulting conservation law (6.10)–(6.11a,b) of the Euler–Lagrange equations (3.24)) is obtained by using (6.41)–(6.42) for $\varLambda ^t_0$![]() and $\varLambda ^i_0$
and $\varLambda ^i_0$![]() and using the results
and using the results
Here $W^t_0$![]() and $W^i_0$
and $W^i_0$![]() are given by (6.9a,b), in which the derivatives of $L_0$
are given by (6.9a,b), in which the derivatives of $L_0$![]() are given by (G2a–c). This yields the conserved density and the flux
are given by (G2a–c). This yields the conserved density and the flux
The corresponding Eulerian conservation law (6.12)–(6.13a,b) is given by

This is the cross-helicity density conservation law (2.67)–(2.69a,b).
6.2 Classical Noether approach
In this subsection we use a classical version of Noether's theorem (see, e.g., Bluman & Kumei (Reference Bluman and Kumei1989) and Appendix H) to derive conservation laws for the CGL plasma action (3.19) that uses the canonical Lie symmetry operator ${\tilde X}=\textrm {pr}\,X$![]() rather than the evolutionary form $\textrm {pr}\,{\hat X}$
rather than the evolutionary form $\textrm {pr}\,{\hat X}$![]() . The canonical symmetry operator form of Noether's theorem was used by Webb & Zank (Reference Webb and Zank2007) and Webb & Anco (Reference Webb and Anco2019) for the MHD fluid case. In this approach one searches for Lie transformations and divergence transformations that leave the action (6.1a–c) invariant, where
. The canonical symmetry operator form of Noether's theorem was used by Webb & Zank (Reference Webb and Zank2007) and Webb & Anco (Reference Webb and Anco2019) for the MHD fluid case. In this approach one searches for Lie transformations and divergence transformations that leave the action (6.1a–c) invariant, where
is the divergence transformation. Here $D_0=\partial /\partial t$![]() and $D_i=\partial /\partial x_0^i$
and $D_i=\partial /\partial x_0^i$![]() are total partial derivatives with respect to $t$
are total partial derivatives with respect to $t$![]() and $x_0^i$
and $x_0^i$![]() . Note we use ${\bar {\varLambda }}^\alpha _0$
. Note we use ${\bar {\varLambda }}^\alpha _0$![]() and ${\bar {\varLambda }}^\alpha$
and ${\bar {\varLambda }}^\alpha$![]() to denote the potentials, in order to distinguish them from the potentials used for the evolutionary potentials in § 6.1.
to denote the potentials, in order to distinguish them from the potentials used for the evolutionary potentials in § 6.1.
The condition for the action to remain invariant under (6.1a–c) and (6.47) may be written in the form (cf. Bluman & Kumei Reference Bluman and Kumei1989):
where
is the prolonged, canonical Lie symmetry operator.
Here $\textrm {pr}\,X$![]() is related to $\textrm {pr}\,{\hat X}$
is related to $\textrm {pr}\,{\hat X}$![]() by the equations (Ovsjannikov Reference Ovsjannikov1978; Ibragimov Reference Ibragimov1985; Bluman & Kumei Reference Bluman and Kumei1989)
by the equations (Ovsjannikov Reference Ovsjannikov1978; Ibragimov Reference Ibragimov1985; Bluman & Kumei Reference Bluman and Kumei1989)

where the evolutionary symmetry generator ${\hat {\xi }}^i$![]() is given by (6.4a,b) and $\xi ^t\equiv \xi ^0_0$
is given by (6.4a,b) and $\xi ^t\equiv \xi ^0_0$![]() .
.
Noether's theorem follows from Noether's identity:
where $E_{x^i}(L_0)\equiv \delta {\mathcal {J}}/\delta x^i$![]() is the variational derivative of the action ${\mathcal {J}}$
is the variational derivative of the action ${\mathcal {J}}$![]() with respect to $x^i$
with respect to $x^i$![]() . For the case of CGL plasmas, the surface terms $W^\alpha$
. For the case of CGL plasmas, the surface terms $W^\alpha$![]() are given by
are given by
(see Bluman & Kumei (Reference Bluman and Kumei1989) and Ibragimov (Reference Ibragimov1985) for more general cases).
If the Lie invariance condition (6.48) is satisfied, then the left-hand side of (6.51) vanishes and, consequently, the right-hand side of (6.51) must vanish. If, in addition, the Euler–Lagrange equations $E_{x^i}(L_0)=0$![]() are satisfied, then (6.51) implies
are satisfied, then (6.51) implies
which is the conservation law of Noether's first theorem, which applies if the Euler–Lagrange equations $E_{x^i}(L_0)=0$![]() are independent, which is the case for a finite Lie algebra of Lie point symmetries.
are independent, which is the case for a finite Lie algebra of Lie point symmetries.
In the more general case where the symmetries depend on continuous functions $\{ \phi ^k (\boldsymbol {x}_0,t): 1\leqslant k\leqslant N\}$![]() , then the Lie pseudo-algebra of symmetries is infinite dimensional. In this case, Noether's second theorem implies that the Euler–Lagrange equations are not all independent, and that there exists differential relations between the Euler–Lagrange equations (see, e.g., Olver (Reference Olver1993) and Hydon & Mansfield (Reference Hydon and Mansfield2011) for details). Noether's second theorem, in some cases results in mathematically trivial conservation laws. Charron & Zadra (Reference Charron and Zadra2018) discuss Ertel's theorem and Noether's second theorem.
, then the Lie pseudo-algebra of symmetries is infinite dimensional. In this case, Noether's second theorem implies that the Euler–Lagrange equations are not all independent, and that there exists differential relations between the Euler–Lagrange equations (see, e.g., Olver (Reference Olver1993) and Hydon & Mansfield (Reference Hydon and Mansfield2011) for details). Noether's second theorem, in some cases results in mathematically trivial conservation laws. Charron & Zadra (Reference Charron and Zadra2018) discuss Ertel's theorem and Noether's second theorem.
For the CGL plasma model, the $W^\alpha$![]() from (6.52a,b) are given by
from (6.52a,b) are given by
Substitution of (6.54a,b) for the $W^\alpha$![]() into Noether's theorem (6.53) gives the Lagrangian conservation law
into Noether's theorem (6.53) gives the Lagrangian conservation law
where

are the conserved density and flux.
The Lagrangian conservation law (6.55) corresponds to an Eulerian conservation law of the form (6.12) (e.g. Padhye Reference Padhye1998) with conserved density $\varPsi ^t$![]() , and flux $\varPsi ^j$
, and flux $\varPsi ^j$![]() given by
given by

where

The Lagrangian and Eulerian conservation laws for the Galilean group (§§ 6.1.2–6.1.3) and the cross-helicity conservation law associated with the fluid relabelling symmetry $\hat {\boldsymbol {\xi }}=-\boldsymbol {B}/\rho$![]() (§§ 6.1.4–6.1.5) now follow from (6.56)–(6.58) for appropriate choices of the potentials ${\bar {\varLambda }}^t_0$
(§§ 6.1.4–6.1.5) now follow from (6.56)–(6.58) for appropriate choices of the potentials ${\bar {\varLambda }}^t_0$![]() and ${\bar {\varLambda }}^j_0$
and ${\bar {\varLambda }}^j_0$![]() and of the symmetry generators $\xi ^i$
and of the symmetry generators $\xi ^i$![]() , $\xi ^i_0$
, $\xi ^i_0$![]() and $\xi ^t$
and $\xi ^t$![]() . Note that the evolutionary symmetry potentials used in § 6.1 are different than those used in this subsection (§ 6.2).
. Note that the evolutionary symmetry potentials used in § 6.1 are different than those used in this subsection (§ 6.2).
Example 6.3 The time translation symmetry of the Lagrangian action (3.19), satisfies the Lie invariance condition (6.48) by choosing
where $i,s=1,2,3,$![]() and $\alpha =0,1,2,3$
and $\alpha =0,1,2,3$![]() is a variational symmetry of the action (3.19). The corresponding conservation law using Noether's theorem results (6.57) is the energy conservation law:
is a variational symmetry of the action (3.19). The corresponding conservation law using Noether's theorem results (6.57) is the energy conservation law:

where ${\mathsf{{p}}}$![]() is the CGL pressure tensor (2.3a–c), $\boldsymbol {E}=-\boldsymbol {u}\times \boldsymbol {B}$
is the CGL pressure tensor (2.3a–c), $\boldsymbol {E}=-\boldsymbol {u}\times \boldsymbol {B}$![]() is the electric field strength and $\boldsymbol {E}\times \boldsymbol {B}/\mu _0$
is the electric field strength and $\boldsymbol {E}\times \boldsymbol {B}/\mu _0$![]() is the Poynting flux.
is the Poynting flux.
Example 6.4 If the gravitational potential $\varPhi (\boldsymbol {x})$![]() is independent of $x^{j_1}$
is independent of $x^{j_1}$![]() say, then the Lie invariance condition (6.48) for a divergence symmetry of the action is satisfied, by the choice
say, then the Lie invariance condition (6.48) for a divergence symmetry of the action is satisfied, by the choice
and condition (6.48) reduces to the equation
Then using (6.47) we obtain the momentum conservation equation in the $x^{j_1}$![]() direction in the form
direction in the form

In the case where gravity can be neglected (i.e. $\varPhi =0$![]() ) the superscript $j_1$
) the superscript $j_1$![]() can be dropped in (6.63). Technically, the conservation of momentum law appears more complicated in non-Cartesian coordinates (e.g. in spherical geometry), where the metric tensor, the covariant derivative and the affine connection play an important role.
can be dropped in (6.63). Technically, the conservation of momentum law appears more complicated in non-Cartesian coordinates (e.g. in spherical geometry), where the metric tensor, the covariant derivative and the affine connection play an important role.
Example 6.5 The Galilean boost symmetry, with infinitesimal generators
($i,s=1,2,3$![]() ) and (6.57) gives rise to the centre of mass conservation law
) and (6.57) gives rise to the centre of mass conservation law
provided
Thus, one obtains the centre of mass conservation law for Galilean boosts perpendicular to the external gravitational field. Thus, for a spherically symmetric gravitational potential (e.g. for the Sun), a Galilean boost conservation law exists for a boost ${\boldsymbol {\xi }}=\boldsymbol {\varOmega }t$![]() perpendicular to the radial direction.
perpendicular to the radial direction.
Example 6.6 The Lie transformation generators
give rise to the angular momentum conservation equation
where
define the mass flux or momentum density $\boldsymbol {M}$![]() and $\boldsymbol {x}\times {\mathsf{{T}}}$
and $\boldsymbol {x}\times {\mathsf{{T}}}$![]() respectively. The invariance condition (6.48) for a divergence symmetry of the action, requires
respectively. The invariance condition (6.48) for a divergence symmetry of the action, requires

Note that the second term in the first line of (6.70) vanishes because the term in large square brackets is symmetric in $s$![]() and $k$
and $k$![]() .
.
For the case where $\boldsymbol {\varOmega }=\varOmega \boldsymbol {e}_z$![]() the condition (6.70) reduces to the equation
the condition (6.70) reduces to the equation
where $(r,\theta,\phi )$![]() are spherical polar coordinates. Condition (6.71) is satisfied for $\varPhi =\varPhi (r,\theta )$
are spherical polar coordinates. Condition (6.71) is satisfied for $\varPhi =\varPhi (r,\theta )$![]() .
.
Example 6.7 The fluid relabelling symmetry transformations
and the choices
for the gauge potentials ${\bar {\varLambda }}^\alpha$![]() ($\alpha =0,1,2,3$
($\alpha =0,1,2,3$![]() ), leave the action invariant (i.e. (6.48) is satisfied). Using (6.57) to calculate $\varPsi ^t$
), leave the action invariant (i.e. (6.48) is satisfied). Using (6.57) to calculate $\varPsi ^t$![]() and $\varPsi ^j$
and $\varPsi ^j$![]() gives the results (6.46) for the cross-helicity conservation law (2.67)–(2.69a,b).
gives the results (6.46) for the cross-helicity conservation law (2.67)–(2.69a,b).
The above examples illustrate the use of the classical version of Noether's first theorem in obtaining conservation laws of the CGL equations.
7 Summary and concluding remarks
In this paper an investigation has been carried out of the ideal CGL plasma equations, based in part on the Lagrangian variational formulation of Newcomb (Reference Newcomb1962), in which there is an anisotropic pressure tensor, with pressure components $p_\parallel$![]() and $p_\perp$
and $p_\perp$![]() parallel and perpendicular to the magnetic field $\boldsymbol {B}$
parallel and perpendicular to the magnetic field $\boldsymbol {B}$![]() , which satisfy the so-called double adiabatic equations which, in turn, can be described by using entropy components: $S_\parallel$
, which satisfy the so-called double adiabatic equations which, in turn, can be described by using entropy components: $S_\parallel$![]() and $S_\perp$
and $S_\perp$![]() parallel and perpendicular to $\boldsymbol {B}$
parallel and perpendicular to $\boldsymbol {B}$![]() (e.g. Du et al. Reference Du, Zank, Li and Guo2020).
(e.g. Du et al. Reference Du, Zank, Li and Guo2020).
The total energy conservation law, and the cross-helicity and magnetic helicity conservation laws were obtained (§ 2). The total energy equation was decomposed into the sum of three energy equations, namely the internal energy equation or co-moving energy equation, the total kinetic energy equation and Poynting's theorem (the electromagnetic energy equation). The cross-helicity transport equation involves the effective enthalpy $h=(p_\parallel +\varepsilon )/\rho$![]() of the gas associated with pressure work terms parallel to $\boldsymbol {B}$
of the gas associated with pressure work terms parallel to $\boldsymbol {B}$![]() . If the internal energy density of the plasma per unit mass has the form $e=e(\rho,S,B)\equiv \varepsilon /\rho$
. If the internal energy density of the plasma per unit mass has the form $e=e(\rho,S,B)\equiv \varepsilon /\rho$![]() (Holm & Kupershmidt Reference Holm and Kupershmidt1986; Hazeltine et al. Reference Hazeltine, Mahajan and Morrison2013) one obtains a cross-helicity transport equation of the form
(Holm & Kupershmidt Reference Holm and Kupershmidt1986; Hazeltine et al. Reference Hazeltine, Mahajan and Morrison2013) one obtains a cross-helicity transport equation of the form
where $T=e_S$![]() is the temperature of the gas. If $\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla } S=0$
is the temperature of the gas. If $\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla } S=0$![]() , then (7.1) is a local conservation law. More generally, if the source term $Q=T\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla } S\neq 0$
, then (7.1) is a local conservation law. More generally, if the source term $Q=T\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla } S\neq 0$![]() , (7.1) can be reduced to a non-local conservation law of the form
, (7.1) can be reduced to a non-local conservation law of the form
where
Here $\textrm {d}/\textrm {d}t=\partial /\partial t+\boldsymbol {u}\boldsymbol {\cdot }\boldsymbol {\nabla }$![]() is the advective time derivative following the flow. The CGL plasma conservation law (7.2) generalises the non-local, MHD cross-helicity conservation law of Webb et al. (Reference Webb, Dasgupta, McKenzie, Hu and Zank2014a,Reference Webb, Dasgupta, McKenzie, Hu and Zankb) and Yahalom (Reference Yahalom2017a,Reference Yahalomb). Here $\varPhi (\boldsymbol {x})$
is the advective time derivative following the flow. The CGL plasma conservation law (7.2) generalises the non-local, MHD cross-helicity conservation law of Webb et al. (Reference Webb, Dasgupta, McKenzie, Hu and Zank2014a,Reference Webb, Dasgupta, McKenzie, Hu and Zankb) and Yahalom (Reference Yahalom2017a,Reference Yahalomb). Here $\varPhi (\boldsymbol {x})$![]() is the potential for an external gravitational field. Similar transport equations for cross-helicity to (7.1) and (7.3a,b) were also developed in terms of the parallel and perpendicular temperatures $T_\parallel$
is the potential for an external gravitational field. Similar transport equations for cross-helicity to (7.1) and (7.3a,b) were also developed in terms of the parallel and perpendicular temperatures $T_\parallel$![]() and $T_\perp$
and $T_\perp$![]() defined as $T_\parallel =p_\parallel /(\rho R)$
defined as $T_\parallel =p_\parallel /(\rho R)$![]() and $T_\perp =p_\perp /(\rho R)$
and $T_\perp =p_\perp /(\rho R)$![]() .
.
There are two different, but equivalent forms of the momentum (or force) equation for the CGL system. The form of the momentum equation obtained by Newcomb (Reference Newcomb1962) Lagrangian action principle reduces to the form
where $\boldsymbol {J}=\boldsymbol {\nabla }\times \boldsymbol {B}/\mu _0$![]() is the current. This equation is essentially the same as the MHD momentum equation, except that the isotropic gas pressure tensor $p{\mathsf{{I}}}$
is the current. This equation is essentially the same as the MHD momentum equation, except that the isotropic gas pressure tensor $p{\mathsf{{I}}}$![]() is replaced by the anisotropic CGL pressure tensor ${\mathsf{{p}}}=p_\parallel \boldsymbol {\tau }\boldsymbol {\tau } +p_\perp ({\mathsf{{I}}}-\boldsymbol {\tau }\boldsymbol {\tau })$
is replaced by the anisotropic CGL pressure tensor ${\mathsf{{p}}}=p_\parallel \boldsymbol {\tau }\boldsymbol {\tau } +p_\perp ({\mathsf{{I}}}-\boldsymbol {\tau }\boldsymbol {\tau })$![]() . However,
. However,
(e.g. (2.61), (B6) and (E12)) where
Using $\boldsymbol {\nabla }\boldsymbol {\cdot }{\mathsf{{p}}}$![]() from (7.5) and (7.6a–c) in (7.4) results in the CGL momentum equation in the form
from (7.5) and (7.6a–c) in (7.4) results in the CGL momentum equation in the form
where
In the form (7.7) the anisotropic pressure force term $-\boldsymbol {\nabla }\boldsymbol {\cdot }{\mathsf{{p}}}/\rho$![]() has been partly transformed into the modified force ${\tilde {J}}\times \boldsymbol {B}/\rho$
has been partly transformed into the modified force ${\tilde {J}}\times \boldsymbol {B}/\rho$![]() where $\tilde {\boldsymbol {J}}=(\boldsymbol {\nabla }\times \tilde {\boldsymbol {B}})/\mu _0$
where $\tilde {\boldsymbol {J}}=(\boldsymbol {\nabla }\times \tilde {\boldsymbol {B}})/\mu _0$![]() in which $\tilde {\boldsymbol {B}}$
in which $\tilde {\boldsymbol {B}}$![]() is the modified magnetic induction $\tilde {\boldsymbol {B}}$
is the modified magnetic induction $\tilde {\boldsymbol {B}}$![]() . The form of $\tilde {\boldsymbol {J}}$
. The form of $\tilde {\boldsymbol {J}}$![]() suggests that $-\boldsymbol {\nabla }\times \boldsymbol {\varOmega }$
suggests that $-\boldsymbol {\nabla }\times \boldsymbol {\varOmega }$![]() could be interpreted as a magnetisation current.
could be interpreted as a magnetisation current.
It is interesting to note that $\tilde {B}=B(1-\mu _0 p_\varDelta /B^2)<0$![]() if $p_\varDelta =(p_\parallel -p_\perp )>B^2/\mu _0$
if $p_\varDelta =(p_\parallel -p_\perp )>B^2/\mu _0$![]() , which corresponds to the firehose instability threshold (e.g. Stix Reference Stix1992; Hunana et al. Reference Hunana, Zank, Goldstein, Webb and Adhikari2016; Hunana & Zank Reference Hunana and Zank2017). The mirror instability threshold for the CGL plasma model does not correspond to plasma kinetic theory. For the CGL plasma model with zero electron pressure (i.e. cold electrons) the mirror instability occurs if $p_\perp -p_\parallel >(5/6)p_\perp +p_\parallel p_B/ p_\perp$
, which corresponds to the firehose instability threshold (e.g. Stix Reference Stix1992; Hunana et al. Reference Hunana, Zank, Goldstein, Webb and Adhikari2016; Hunana & Zank Reference Hunana and Zank2017). The mirror instability threshold for the CGL plasma model does not correspond to plasma kinetic theory. For the CGL plasma model with zero electron pressure (i.e. cold electrons) the mirror instability occurs if $p_\perp -p_\parallel >(5/6)p_\perp +p_\parallel p_B/ p_\perp$![]() , whereas kinetic theory gives the threshold for the instability as $p_\perp -p_\parallel > p_\parallel p_B/ p_\perp$
, whereas kinetic theory gives the threshold for the instability as $p_\perp -p_\parallel > p_\parallel p_B/ p_\perp$![]() where $p_B=B^2/(2\mu )$
where $p_B=B^2/(2\mu )$![]() is the magnetic pressure. Note the firehose instability occurs if the parallel pressure dominates the perpendicular pressure. Similarly if $p_\perp$
is the magnetic pressure. Note the firehose instability occurs if the parallel pressure dominates the perpendicular pressure. Similarly if $p_\perp$![]() dominates $p_\parallel$
dominates $p_\parallel$![]() one obtains the mirror instability.
one obtains the mirror instability.
In the approaches of Hazeltine et al. (Reference Hazeltine, Mahajan and Morrison2013) and Holm & Kupershmidt (Reference Holm and Kupershmidt1986), the internal energy density per unit mass, $e$![]() satisfies the first law of thermodynamics, in the form
satisfies the first law of thermodynamics, in the form
The variational formulation of Newcomb (Reference Newcomb1962) does not explicitly require (7.10) to apply. The Lagrangian action principle ofNewcomb (Reference Newcomb1962) leads to the correct momentum equation for the CGL plasma, and to a Hamiltonian formulation of the equations in Lagrangian variables.
The Lagrangian variational principle for ideal CGL plasmas obtained by Newcomb (Reference Newcomb1962) was used in § 3 to obtain a canonical Hamiltonian formulation of the equations based on the canonical coordinates $\boldsymbol {q}=\boldsymbol {x}(\boldsymbol {x}_0,t)$![]() and the canonical momentum ${\boldsymbol {{\rm \pi} }}=\rho _0\dot {\boldsymbol {x}}(\boldsymbol {x}_0,t)$
and the canonical momentum ${\boldsymbol {{\rm \pi} }}=\rho _0\dot {\boldsymbol {x}}(\boldsymbol {x}_0,t)$![]() , and also to establish that stationary variations of the action give the CGL momentum equation in both its Lagrangian and Eulerian forms.
, and also to establish that stationary variations of the action give the CGL momentum equation in both its Lagrangian and Eulerian forms.
Section 4 provides an EP action principle derivation of the CGL momentum equation (see also Appendix E, which uses the approach of Holm et al. Reference Holm, Marsden and Ratiu1998).
By transforming the canonical Poisson bracket for the CGL system of § 3, to non-canonical physical variables leads to the non-canonical Poisson bracket for the CGL system of § 5. The detailed transformation formulae from the canonical coordinates to the physical variables $\psi =(\rho,\sigma, \boldsymbol {M}, \boldsymbol {B})^\textrm {T}$![]() is described in Appendix D. By writing the non-canonical Poisson bracket in cosymplectic form, leads to a system of equations for the Casimirs $C$
is described in Appendix D. By writing the non-canonical Poisson bracket in cosymplectic form, leads to a system of equations for the Casimirs $C$![]() , as solutions of the Poisson bracket equation: $\{C,K\}=0$
, as solutions of the Poisson bracket equation: $\{C,K\}=0$![]() where $K$
where $K$![]() is an arbitrary functional of the physical variables. The Casimirs satisfy ${\mathcal {C}}_ t=\{C,K\}=0$
is an arbitrary functional of the physical variables. The Casimirs satisfy ${\mathcal {C}}_ t=\{C,K\}=0$![]() . Hamiltonian dynamics of the system takes place on the symplectic leaves $C=\textrm {const}.$
. Hamiltonian dynamics of the system takes place on the symplectic leaves $C=\textrm {const}.$![]() of the system.
of the system.
The classical Casimirs for ideal fluids and plasmas are the mass conservation integral, the cross-helicity integral for barotropic flows and the magnetic helicity. For the CGL plasma case, there is effectively one entropy function that is Lie dragged with the flow, because $S_\parallel$![]() and $S_\perp$
and $S_\perp$![]() are assumed to be functions only of $S$
are assumed to be functions only of $S$![]() . In principle, a more complicated bracket would arise, if one used the possibility that the adiabatic integrals for $p_\perp$
. In principle, a more complicated bracket would arise, if one used the possibility that the adiabatic integrals for $p_\perp$![]() and $p_\parallel$
and $p_\parallel$![]() depended on other scalar invariants that are advected with the flow. For example, the integrals (2.13a,b) could also depend on the scalar invariant $\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla } S/\rho$
depended on other scalar invariants that are advected with the flow. For example, the integrals (2.13a,b) could also depend on the scalar invariant $\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla } S/\rho$![]() . This possibility was not explored in the present paper.
. This possibility was not explored in the present paper.
The links between Noether's theorem and conservation laws for CGL plasmas are developed (§ 6). The evolutionary symmetry form of the Lie invariance condition for the action is used. This approach differs from the canonical symmetry operator form of the invariance condition (e.g. Webb & Anco (Reference Webb and Anco2019), see also Appendix H). In the evolutionary form of the symmetry operator, the independent variables are frozen and all the Lie transformation changes are restricted to changes in the dependent variables and their derivatives (see,e.g., Ibragimov Reference Ibragimov1985; Olver Reference Olver1993; Bluman & Anco Reference Bluman and Anco2002). In the canonical symmetry approach, both the dependent and independent variables and their derivatives change.
The CGL plasma equations admit the Galilean Lie point symmetry group, and three extra scaling symmetries (Appendix F). The Galilean group leads to: (i) the energy conservation law due to time translation invariance of the action; (ii) the momentum conservation equations due to space translation invariances; (iii) the conservation of angular momentum due to rotational invariance about some given rotation axis; and (iv) the uniform centre of mass conservation law which is due to invariance under Galilean boosts. These conservation laws are derived using the evolutionary form of Noether's theorem.
The non-local cross-helicity conservation law (6.45a,b)–(6.46) (see also (2.67)) arises from a fluid relabelling symmetry with generators $\hat {\boldsymbol {\xi }}=-\boldsymbol {B}/\rho$![]() and ${\boldsymbol {\xi }}_0=\boldsymbol {B}_0/\rho _0$
and ${\boldsymbol {\xi }}_0=\boldsymbol {B}_0/\rho _0$![]() and with non-trivial potentials $\varLambda ^t_0$
and with non-trivial potentials $\varLambda ^t_0$![]() and $\varLambda ^i_0$
and $\varLambda ^i_0$![]() . It is a non-local conservation law that depends on the Lagrangian time integral of the temperature back along the fluid flow trajectory. The cross-helicity conservation law for MHD, is a local conservation law for the case of a barotropic gas (i.e. $p=p(\rho )$
. It is a non-local conservation law that depends on the Lagrangian time integral of the temperature back along the fluid flow trajectory. The cross-helicity conservation law for MHD, is a local conservation law for the case of a barotropic gas (i.e. $p=p(\rho )$![]() ), but is a non-local conservation law for the non-barotropic case where $p=p(\rho,S)$
), but is a non-local conservation law for the non-barotropic case where $p=p(\rho,S)$![]() (see also Yahalom (Reference Yahalom2017a,Reference Yahalomb); Yahalom & Qin (Reference Yahalom and Qin2021) for a topological interpretation). The CGL entropies $S_\parallel$
(see also Yahalom (Reference Yahalom2017a,Reference Yahalomb); Yahalom & Qin (Reference Yahalom and Qin2021) for a topological interpretation). The CGL entropies $S_\parallel$![]() and $S_\perp$
and $S_\perp$![]() are not constants, but are non-trivial scalars that are advected with the background flow.
are not constants, but are non-trivial scalars that are advected with the background flow.
Lingam et al. (Reference Lingam, Morrison and Wurm2020) studied extended variational principles of MHD (and CGL) type including gyro-viscous effects (i.e. higher-order finite Larmor radius effects in the collisionless limit). A single gyro-viscous term is added to the usual action. The gyro-viscous term alters the total momentum density, but it does not alter the divergence of the mass flux. The total momentum density has the form: $\boldsymbol {M}^c=\boldsymbol {M}+\boldsymbol {M}^*$![]() , where $\boldsymbol {M}=\rho \boldsymbol {u}$
, where $\boldsymbol {M}=\rho \boldsymbol {u}$![]() is the mass flux and $\boldsymbol {M}^*$
is the mass flux and $\boldsymbol {M}^*$![]() has the form $\boldsymbol {M}^*=\boldsymbol {\nabla }\times \boldsymbol {L}^*$
has the form $\boldsymbol {M}^*=\boldsymbol {\nabla }\times \boldsymbol {L}^*$![]() , where $\boldsymbol {L}^*$
, where $\boldsymbol {L}^*$![]() is the internal angular momentum of the particle ($\boldsymbol {L}^*=(2m/e){\boldsymbol {\mu }}$
is the internal angular momentum of the particle ($\boldsymbol {L}^*=(2m/e){\boldsymbol {\mu }}$![]() and ${\boldsymbol {\mu }}=\mu \boldsymbol {\tau }$
and ${\boldsymbol {\mu }}=\mu \boldsymbol {\tau }$![]() is the vector form of the particle adiabatic moment. These ideas are related to papers by Newcomb (Reference Newcomb1972, Reference Newcomb1973, Reference Newcomb1983), Morrison, Lingam & Acevedo (Reference Morrison, Lingam and Acevedo2014) and others. Our analysis can be extended in principle to include gyro-viscosity in the collisionless limit. However, to what extent the action principle approach, reproduces the kinetic plasma and fluid approaches to gyro-viscosity requires further investigation.
is the vector form of the particle adiabatic moment. These ideas are related to papers by Newcomb (Reference Newcomb1972, Reference Newcomb1973, Reference Newcomb1983), Morrison, Lingam & Acevedo (Reference Morrison, Lingam and Acevedo2014) and others. Our analysis can be extended in principle to include gyro-viscosity in the collisionless limit. However, to what extent the action principle approach, reproduces the kinetic plasma and fluid approaches to gyro-viscosity requires further investigation.
Analysis of the CGL plasma equations using Clebsch potentials (e.g. Zakharov & Kuznetsov Reference Zakharov and Kuznetsov1997; Yahalom Reference Yahalom2017a, Reference Yahalomb; Webb Reference Webb2018, Ch. 8; Yahalom & Qin Reference Yahalom and Qin2021) may yield further insights. Similarly, further study of the Lie symmetries the CGL plasma equations would be useful. Investigation of conservation laws for the CGL equations by using Lie dragging remains open for further investigation.
Acknowledgements
The work of GMW was supported in part by NASA grant 80NSSC19K0075. GMW acknowledges stimulating discussions with Darryl Holm on the CGL plasma equations. SCA is supported by an NSERC Discovery research grant. We acknowledge discussions of the CGL plasma equations, and the anisotropic plasma moment equations and their closures with Peter Hunana. We acknowledge the partial support of an NSF EPSCoR RII-Track-1 cooperative agreement OIA-1655280 and a NASA IMAP-subaward under NASA contract 80GSFC19C0027.
Editor Thierry Passot thanks the referees for their advice in evaluating this article.
Competing interests
The authors have no competing interests to declare.
Appendix A
In this appendix, we briefly discuss the derivation of the CGL plasma equations. These equations were originally derived by Chew et al. (Reference Chew, Goldberger and Low1956) and later by many authors (e.g. Kulsrud Reference Kulsrud1983; Ramos Reference Ramos2005a,Reference Ramosb). Some of the derivations use the adiabatic drift approximation, but others simply involve taking moments of the collisionless Vlasov equation or Boltzmann equation over the particle momenta. We use the latter approach.
Following Hunana et al. (Reference Hunana, Teneranii, Zank, Khomenko, Goldstein, Webb, Cally, Collados, Velli and Adhikari2019a,Reference Hunana, Teneranii, Zank, Khomenko, Goldstein, Webb, Cally, Collados, Adhikari and Vellib), we introduce the velocity phase space distribution function $f(\boldsymbol {x}, \boldsymbol {v},t)$![]() of the particles where $\textrm {d}N=f(\boldsymbol {x},\boldsymbol {v},t) \,\textrm {d}^3v\,\textrm {d}^3\boldsymbol {x}$
of the particles where $\textrm {d}N=f(\boldsymbol {x},\boldsymbol {v},t) \,\textrm {d}^3v\,\textrm {d}^3\boldsymbol {x}$![]() is the number of particles in a volume of phase space at the point $(\boldsymbol {x},\boldsymbol {v})$
is the number of particles in a volume of phase space at the point $(\boldsymbol {x},\boldsymbol {v})$![]() at time $t$
at time $t$![]() , with velocity volume element $d^3v$
, with velocity volume element $d^3v$![]() and position volume element $\textrm {d}^3\boldsymbol {x}$
and position volume element $\textrm {d}^3\boldsymbol {x}$![]() . The lower order moments of the velocity distribution function averaged over all velocities $\boldsymbol {v}$
. The lower order moments of the velocity distribution function averaged over all velocities $\boldsymbol {v}$![]() are defined as
are defined as

where $n$![]() is the particle number density, $\boldsymbol {u}$
is the particle number density, $\boldsymbol {u}$![]() is the fluid velocity, and in Cartesian coordinates, $p_{ij}$
is the fluid velocity, and in Cartesian coordinates, $p_{ij}$![]() represents the components of the pressure tensor ${\mathsf{{p}}}$
represents the components of the pressure tensor ${\mathsf{{p}}}$![]() and $q_{ijk}$
and $q_{ijk}$![]() represents the components of the heat flux tensor ${\mathsf{{q}}}$
represents the components of the heat flux tensor ${\mathsf{{q}}}$![]() . Note that both of these tensors are symmetric.
. Note that both of these tensors are symmetric.
From adiabatic motion of guiding centre theory, the pressure tensor ${\mathsf{{p}}}$![]() at lowest order can be written in the form
at lowest order can be written in the form
where $\boldsymbol {\tau }=\boldsymbol {B}/B$![]() is the unit vector along the magnetic field, $p_\parallel$
is the unit vector along the magnetic field, $p_\parallel$![]() and $p_\perp$
and $p_\perp$![]() are the gyrotropic components of ${\mathsf{{p}}}$
are the gyrotropic components of ${\mathsf{{p}}}$![]() parallel and perpendicular to the magnetic field $\boldsymbol {B}$
parallel and perpendicular to the magnetic field $\boldsymbol {B}$![]() and ${\varPi }$
and ${\varPi }$![]() represents the non-gyrotropic components of ${\mathsf{{p}}}$
represents the non-gyrotropic components of ${\mathsf{{p}}}$![]() . In the limit of a strong background magnetic field $\boldsymbol {B}$
. In the limit of a strong background magnetic field $\boldsymbol {B}$![]() in which the particle gyro-radius is $r_g\ll L$
in which the particle gyro-radius is $r_g\ll L$![]() where $L$
where $L$![]() is the scale length for variation of $\boldsymbol {B}$
is the scale length for variation of $\boldsymbol {B}$![]() , and for times $T\gg T_\varOmega$
, and for times $T\gg T_\varOmega$![]() where $T_\varOmega$
where $T_\varOmega$![]() is the gyro-period, the particle distribution is approximately gyrotropic while the non-gyrotropic pressure ${\varPi }$
is the gyro-period, the particle distribution is approximately gyrotropic while the non-gyrotropic pressure ${\varPi }$![]() can be neglected to first order in $r_g/L$
can be neglected to first order in $r_g/L$![]() and $T_\varOmega /T$
and $T_\varOmega /T$![]() .
.
Hereafter, $\mathsf{{A}}^{\mathsf{{S}}}=\mathsf{{A}}+\mathsf{{A}}^{\textrm {{T}}}$![]() denotes the symmetrised form of ${\mathsf{{A}}}$
denotes the symmetrised form of ${\mathsf{{A}}}$![]() , where $\textrm {T}$
, where $\textrm {T}$![]() denotes the transpose.
denotes the transpose.
Taking the first moment of the Vlasov equation with respect to $\boldsymbol {v}$![]() gives the pressure tensor equation
gives the pressure tensor equation
where
The equations for the parallel pressure $p_\parallel$![]() and perpendicular pressure $p_\perp$
and perpendicular pressure $p_\perp$![]() obtained from (A3) respectively reduce to
obtained from (A3) respectively reduce to
and

Neglecting the non-gyrotropic component ${\varPi }$![]() of the pressure tensor, and neglecting the heat flux tensor components ${\mathsf{{q}}}$
of the pressure tensor, and neglecting the heat flux tensor components ${\mathsf{{q}}}$![]() gives the simplified CGL plasma equations for $p_\parallel$
gives the simplified CGL plasma equations for $p_\parallel$![]() and $p_\perp$
and $p_\perp$![]() as
as
The double adiabatic equations (2.8) for $p_\parallel$![]() and $p_\perp$
and $p_\perp$![]() follow by combining these transport equations (A7) and (A8) with the mass continuity equation (2.1) in the form
follow by combining these transport equations (A7) and (A8) with the mass continuity equation (2.1) in the form
and the magnetic field strength equation
which comes from Faraday's equation (2.6).
Appendix B
In this appendix, we derive the two equivalent forms of the pressure divergence equation (2.61) and (2.71) used in the derivation of the corresponding forms of the cross-helicityconservation law (2.67) and (2.74). Throughout we take $\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {B}=0$![]() .
.
We start from the non-zero terms on the right-hand side of (2.61):
By applying a standard cross-product identity on the first term in (2.61), we expand

In this expression, the second and third terms combine into $-\boldsymbol {\tau }\boldsymbol {\cdot }\boldsymbol {\nabla }( p_\varDelta \boldsymbol {\tau })$![]() ; the fourth term vanishes $(\boldsymbol {\nabla } \boldsymbol {\tau }) \boldsymbol {\cdot }\boldsymbol {\tau } = \boldsymbol {\nabla }(\frac {1}{2}\boldsymbol {\tau }\boldsymbol {\cdot }\boldsymbol {\tau }) =0$
; the fourth term vanishes $(\boldsymbol {\nabla } \boldsymbol {\tau }) \boldsymbol {\cdot }\boldsymbol {\tau } = \boldsymbol {\nabla }(\frac {1}{2}\boldsymbol {\tau }\boldsymbol {\cdot }\boldsymbol {\tau }) =0$![]() since $\boldsymbol {\tau }$
since $\boldsymbol {\tau }$![]() is a unit vector; and with the Gauss’ law equation written as $\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {\tau } = -\boldsymbol {\tau }\boldsymbol {\cdot }\boldsymbol {\nabla }\ln B$
is a unit vector; and with the Gauss’ law equation written as $\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {\tau } = -\boldsymbol {\tau }\boldsymbol {\cdot }\boldsymbol {\nabla }\ln B$![]() , the last term can be expressed as $-p_\varDelta (\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {\tau })\boldsymbol {\tau }$
, the last term can be expressed as $-p_\varDelta (\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {\tau })\boldsymbol {\tau }$![]() . Thus, (B2) reduces to
. Thus, (B2) reduces to
Next, we expand the remaining term in (B1) by using the Pfaffian differential equation (2.15) in the gradient form:
This yields

by using expressions (2.62) for enthalpy and (2.16a,b) for internal energy. Finally, we combine the terms (B5) and (B3), which gives
because the pressure tensor (2.10a–c) can be written in terms of $p_\varDelta$![]() as
as
This yields the first form of the pressure divergence equation (2.61).
We derive the second form of the pressure divergence equation (2.71) by starting from the terms on its left-hand side
Expanding the first term in (B8) by use of the gyrotropic expression (B7), we obtain
The scalar product of this expression with $\boldsymbol {\tau }$![]() yields
yields
through the Gauss’ law equation in the form $\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {\tau } = -\boldsymbol {\tau }\boldsymbol {\cdot }\boldsymbol {\nabla }\ln B$![]() . The second term in (B8) can be expanded using the enthalpy (2.62). After taking the scalar product with $\boldsymbol {\tau }$
. The second term in (B8) can be expanded using the enthalpy (2.62). After taking the scalar product with $\boldsymbol {\tau }$![]() , this gives
, this gives
The combined terms (B10) and (B11) yield
Now, we substitute the gradient of the expressions for $p_\parallel$![]() and $p_\perp$
and $p_\perp$![]() in terms of adiabatic integrals (2.37):
in terms of adiabatic integrals (2.37):

Then (B12) reduces to the form
which gives the pressure divergence equation (2.71) after we use the relations (2.29a,b) for the adiabatic integrals in terms of ${\bar {S}}_\parallel$![]() and ${\bar {S}}_\perp$
and ${\bar {S}}_\perp$![]() .
.
Appendix C
In this appendix, we show how the Eulerian momentum equation (2.2) is obtained from the Euler–Lagrange equation (3.24) of the Lagrangian (3.23). We follow the approach in Newcomb (Reference Newcomb1962).
From expression (3.23), we have

which uses expression (3.14) for $\zeta ^2$![]() , and the derivative expression in (3.5a–c) for $J$
, and the derivative expression in (3.5a–c) for $J$![]() . Then, substituting the derivatives (C1) into the Euler–Lagrange equation (3.24), we obtain
. Then, substituting the derivatives (C1) into the Euler–Lagrange equation (3.24), we obtain

To proceed, we need the derivative identity:
holding for any function $f$![]() (see Newcomb Reference Newcomb1962). This identity arises from the middle property in (3.5a–c) as follows. Differentiating with respect to $x_0^k$
(see Newcomb Reference Newcomb1962). This identity arises from the middle property in (3.5a–c) as follows. Differentiating with respect to $x_0^k$![]() gives $\partial J/\partial x_0^j = X_{ij} \partial A_{ik}/\partial x_0^k + A_{ik} \partial X_{ij}/\partial x_0^k$
gives $\partial J/\partial x_0^j = X_{ij} \partial A_{ik}/\partial x_0^k + A_{ik} \partial X_{ij}/\partial x_0^k$![]() . By using commutativity of partial derivatives $\partial X_{ij}/\partial x_0^k =\partial X_{ik}/\partial x_0^k$
. By using commutativity of partial derivatives $\partial X_{ij}/\partial x_0^k =\partial X_{ik}/\partial x_0^k$![]() and substituting Jacobi's formula for derivative of a determinant $\partial J/\partial x_0^i = A_{jk} \partial X_{jk}/\partial x_0^i$
and substituting Jacobi's formula for derivative of a determinant $\partial J/\partial x_0^i = A_{jk} \partial X_{jk}/\partial x_0^i$![]() , we find $\partial A_{ik}/\partial x_0^k =0$
, we find $\partial A_{ik}/\partial x_0^k =0$![]() . This leads to the identity (C3), after applying the chain rule and again using the middle property in (3.5a–c).
. This leads to the identity (C3), after applying the chain rule and again using the middle property in (3.5a–c).
There are two main steps for simplifying (C2). First, through relations (3.14), (3.16) and (3.18a,b), followed by use of the identity (C3), we can express the two divergence terms in (C2) in the form:

Note these terms imply that
Second, from the density relation (3.8) and the fluid element flow equation (3.1), we see that in (C2) the first term is simply
while the second term can be expressed as

by use of relation (3.6).
Thus, the Euler–Lagrange equation (C2) becomes
The stationary points of the action principle are given by the equation $E_{X^i}(L_0) =0$![]() . From expression (C9), the resulting equation coincides with the Eulerian momentum equation (2.2).
. From expression (C9), the resulting equation coincides with the Eulerian momentum equation (2.2).
Note that, in terms of the Lagrangian variables, the Euler–Lagrange equation (C2) is a nonlinear wave system for $X^i(x_0^j,t)$![]() , where $X_{ij} = \partial X^i/\partial x_0^j$
, where $X_{ij} = \partial X^i/\partial x_0^j$![]() and $A_{ij} = J^{-1} ( \partial X^i/\partial x_0^j )^{-1}$
and $A_{ij} = J^{-1} ( \partial X^i/\partial x_0^j )^{-1}$![]() . (See also Golovin (Reference Golovin2011), Webb et al. (Reference Webb, Zank, Kaghashvili and Ratkiewicz2005b) and Webb & Anco (Reference Webb and Anco2019) for the MHD case).
. (See also Golovin (Reference Golovin2011), Webb et al. (Reference Webb, Zank, Kaghashvili and Ratkiewicz2005b) and Webb & Anco (Reference Webb and Anco2019) for the MHD case).
Appendix D
Eckart (Reference Eckart1963) used the Lagrangian map and Jacobians to describe fluids. Lundgren (Reference Lundgren1963) used Eulerian and Lagrangian variations in MHD and in plasma physics (see also Newcomb Reference Newcomb1962). In Lundgren (Reference Lundgren1963) a small parameter $\epsilon$![]() is used to describe the variations, where the physical quantity $\psi$
is used to describe the variations, where the physical quantity $\psi$![]() has the functional form: $\psi =\psi (\boldsymbol {x},\boldsymbol {x}_0,\epsilon )$
has the functional form: $\psi =\psi (\boldsymbol {x},\boldsymbol {x}_0,\epsilon )$![]() in which $\boldsymbol {x}=\boldsymbol {X}(\boldsymbol {x}_0,t)$
in which $\boldsymbol {x}=\boldsymbol {X}(\boldsymbol {x}_0,t)$![]() is the Lagrangian map. Eulerian ($\delta \psi$
is the Lagrangian map. Eulerian ($\delta \psi$![]() ) and Lagrangian ($\Delta \psi$
) and Lagrangian ($\Delta \psi$![]() ) variations of $\psi$
) variations of $\psi$![]() are defined as
are defined as
Thus, for an Eulerian variation, $\delta \psi$![]() is evaluated with $\boldsymbol {x}$
is evaluated with $\boldsymbol {x}$![]() held constant, whereas for a Lagrangian variation $\Delta \psi$
held constant, whereas for a Lagrangian variation $\Delta \psi$![]() , $\boldsymbol {x}_0$
, $\boldsymbol {x}_0$![]() is held constant. Thus, $\delta \boldsymbol {x}=0$
is held constant. Thus, $\delta \boldsymbol {x}=0$![]() and $\Delta \boldsymbol {x}_0=0$
and $\Delta \boldsymbol {x}_0=0$![]() .
.
Using the chain rule for differentiation, it follows that

Dewar (Reference Dewar1970) used a variational principle for linear Wentzel–Kramers–Brillouin (WKB) MHD waves in a non-uniform background plasma flow. Webb et al. (Reference Webb, Zank, Kaghashvili and Ratkiewicz2005a) used a variational principle to describe non-WKB waves in a non-uniform background flow. Webb et al. (Reference Webb, Zank, Kaghashvili and Ratkiewicz2005b) used similar ideas to describe nonlinear waves in a non-uniform flow by variational methods.
In this appendix, we describe the use of Eulerian and Lagrangian variations in defining the Poisson bracket for CGL plasmas.
We derive the CGL plasma non-canonical bracket (5.2) starting from the canonical Poisson bracket (5.4). This canonical bracket is properly defined in a Lagrangian frame, i.e. a physical reference frame moving with the fluid flow, where all quantities are functions of the fluid element labels $x_0^i$![]() and time $t$
and time $t$![]() . Non-scalar quantities (e.g. vectors, differential forms, tensors) are expressed in terms of their components with respect to the Cartesian basis vectors of this frame (corresponding to the coordinates $x_0^i$
. Non-scalar quantities (e.g. vectors, differential forms, tensors) are expressed in terms of their components with respect to the Cartesian basis vectors of this frame (corresponding to the coordinates $x_0^i$![]() , $i=1,2,3$
, $i=1,2,3$![]() ). These components are designated by a subscript $0$
). These components are designated by a subscript $0$![]() .
.
The canonical bracket (5.4) has the component form
where $q^i=x^i(x_0,t)$![]() and $p^i={\rm \pi} ^i(x_0,t)$
and $p^i={\rm \pi} ^i(x_0,t)$![]() comprise the canonical coordinates and momenta, with ${\rm \pi} ^i = \rho _0 \dot {x}^i$
comprise the canonical coordinates and momenta, with ${\rm \pi} ^i = \rho _0 \dot {x}^i$![]() , as used in formulating Hamilton's equations (3.29a,b). Note that the fluid element motion is expressed through the relation
, as used in formulating Hamilton's equations (3.29a,b). Note that the fluid element motion is expressed through the relation
Here ${\mathcal {F}}$![]() and ${\mathcal {G}}$
and ${\mathcal {G}}$![]() are functionals which depend on $q^i$
are functionals which depend on $q^i$![]() , $p^i$
, $p^i$![]() , as well as a set of advected quantities ${\mathsf{{a}}}(x_0^j,t)$
, as well as a set of advected quantities ${\mathsf{{a}}}(x_0^j,t)$![]() which are used in describing the dynamics.
which are used in describing the dynamics.
For a CGL plasma, the basic advected quantities are listed in (4.9a–d). We take
Note we assume $S_\parallel$![]() and $S_\perp$
and $S_\perp$![]() are functionals of $s$
are functionals of $s$![]() . Accordingly, functionals will be expressed as
. Accordingly, functionals will be expressed as
in terms of the Lagrangian variables
The non-canonical Poisson bracket (5.2) employs the Eulerian variables (5.11). The transformation from Lagrangian variables (D7) to these Eulerian variables is effected in the following four steps.
Firstly, the Eulerian form of a functional (D6) is given by
with ${\mathsf{{Z}}}=(\rho,\sigma,\boldsymbol {B},\boldsymbol {M})$![]() . The vector variables here will be expanded in components with respect to the Eulerian basis vectors corresponding to $x^i$
. The vector variables here will be expanded in components with respect to the Eulerian basis vectors corresponding to $x^i$![]() viewed as coordinates in an Eulerian frame. It will be convenient to take the basis vectors to be derivative operators (via the standard correspondence between vectors and directional derivatives, e.g. Schutz (Reference Schutz1980)):
viewed as coordinates in an Eulerian frame. It will be convenient to take the basis vectors to be derivative operators (via the standard correspondence between vectors and directional derivatives, e.g. Schutz (Reference Schutz1980)):
Second, using the notation in Newcomb (Reference Newcomb1962), we define $\Delta x^i$![]() to represent a variation of $x^i(x_0,t)$
to represent a variation of $x^i(x_0,t)$![]() in which $x_0^i$
in which $x_0^i$![]() and $t$
and $t$![]() are held fixed: $\Delta x_0^i=0$
are held fixed: $\Delta x_0^i=0$![]() and $\Delta t=0$
and $\Delta t=0$![]() . Note that $\Delta x^i$
. Note that $\Delta x^i$![]() will itself be some function of $x_0^i$
will itself be some function of $x_0^i$![]() and $t$
and $t$![]() ; we write it in the Eulerian form:
; we write it in the Eulerian form:
where, on the right-hand side, $x^i$![]() is regarded as a function of $x_0^i$
is regarded as a function of $x_0^i$![]() and $t$
and $t$![]() . Likewise, $\Delta {\rm \pi}^i = \Delta (\rho _0 \dot {x}^i) = \rho _0 \delta \dot {x}^i$
. Likewise, $\Delta {\rm \pi}^i = \Delta (\rho _0 \dot {x}^i) = \rho _0 \delta \dot {x}^i$![]() is a corresponding variation of ${\rm \pi} ^i(x_0,t)$
is a corresponding variation of ${\rm \pi} ^i(x_0,t)$![]() , where $\rho _0$
, where $\rho _0$![]() is unchanged because it is a function of only $x_0^i$
is unchanged because it is a function of only $x_0^i$![]() and $t$
and $t$![]() . In Eulerian form:
. In Eulerian form:
using the relation (D4) and the advection result (3.8), where $J$![]() is the determinant of the Jacobian matrix of partial derivatives of $x^i(x_0,t)$
is the determinant of the Jacobian matrix of partial derivatives of $x^i(x_0,t)$![]() (cf. (3.3)).
(cf. (3.3)).
The third step is to derive formulae for the variation of the Eulerian variables ${\mathsf{{Z}}}$![]() . These formulae depend on the specific tensorial nature of each variable and will be obtained through the variation of the advected variables (D5) in component form. Hereafter we suppress the $t$
. These formulae depend on the specific tensorial nature of each variable and will be obtained through the variation of the advected variables (D5) in component form. Hereafter we suppress the $t$![]() dependence in all variables and quantities whenever it is convenient.
dependence in all variables and quantities whenever it is convenient.
We start with the scalar field $S_0$![]() . Since it is advected (i.e. frozen in), this implies $S(x) = S_0(x_0)$
. Since it is advected (i.e. frozen in), this implies $S(x) = S_0(x_0)$![]() . Applying a variation (D10), we consequently see that
. Applying a variation (D10), we consequently see that
Next we consider $\rho (x)\,\textrm {d}^3x$![]() , which is properly viewed as an advected differential 3-form (see, e.g., Schutz Reference Schutz1980). Its advection property is expressed by (3.8). As $x_0$
, which is properly viewed as an advected differential 3-form (see, e.g., Schutz Reference Schutz1980). Its advection property is expressed by (3.8). As $x_0$![]() and $t$
and $t$![]() are held fixed, a variation (D10) yields
are held fixed, a variation (D10) yields
Now we use the variation of the determinant relation $\textrm {d}^3x = J(x)\,\textrm {d}^3x_0$![]() , which is given by $\Delta \textrm {d}^3x = \partial _{x^i}(\Delta x^i)\, \textrm {d}^3x = (\Delta J(x)) \,\textrm {d}^3x_0$
, which is given by $\Delta \textrm {d}^3x = \partial _{x^i}(\Delta x^i)\, \textrm {d}^3x = (\Delta J(x)) \,\textrm {d}^3x_0$![]() . This yields the result
. This yields the result
Substituting this variation into (D13), we obtain
Last we consider the vector field $\boldsymbol {b}(x)\equiv \boldsymbol {B}(x)/\rho (x)$![]() , which has the advection property (3.13). We use this property in component form: $b^i(x)\partial _{x^i} = b_0^i(x_0)\partial _{x_0^i}$
, which has the advection property (3.13). We use this property in component form: $b^i(x)\partial _{x^i} = b_0^i(x_0)\partial _{x_0^i}$![]() . Again, because all of the quantities on the right-hand side are held fixed in a variation (D10), we see that
. Again, because all of the quantities on the right-hand side are held fixed in a variation (D10), we see that
To determine $\Delta \partial _{x^i}$![]() , we use the coordinate basis relation $\partial _{x^i} \rfloor \,{\textrm {d} x}^j=\delta _i^j$
, we use the coordinate basis relation $\partial _{x^i} \rfloor \,{\textrm {d} x}^j=\delta _i^j$![]() where $\delta _i^j$
where $\delta _i^j$![]() is the Kronecker symbol. Taking the variation gives $\Delta \partial _{x^i} \rfloor \,{\textrm {d} x}^j= - \partial _{x^i} \rfloor \Delta {\textrm {d} x}^j$
is the Kronecker symbol. Taking the variation gives $\Delta \partial _{x^i} \rfloor \,{\textrm {d} x}^j= - \partial _{x^i} \rfloor \Delta {\textrm {d} x}^j$![]() , where
, where
As $\Delta \partial _{x^i}$![]() must have the form of a linear transformation, say $\phi _i{}^k$
must have the form of a linear transformation, say $\phi _i{}^k$![]() , applied to $\partial _{x^k}$
, applied to $\partial _{x^k}$![]() , we find $\phi _i{}^k \partial _{x^k} \rfloor \,{\textrm {d} x}^j = \phi _i{}^j = - \partial _{x^i} \rfloor \,{\textrm {d} x}^k \partial _{x^k}\epsilon ^j(x)= -\partial _{x^i}\epsilon ^j(x)$
, we find $\phi _i{}^k \partial _{x^k} \rfloor \,{\textrm {d} x}^j = \phi _i{}^j = - \partial _{x^i} \rfloor \,{\textrm {d} x}^k \partial _{x^k}\epsilon ^j(x)= -\partial _{x^i}\epsilon ^j(x)$![]() . Thus, we have
. Thus, we have
Substituting this formula into (D16) yields
By applying the variations (D12), (D15) and (D19) to the quantities $\sigma (x) = \rho (x) S(x)$![]() and $B^i(x)=\rho (x) b^i(x)$
and $B^i(x)=\rho (x) b^i(x)$![]() , we readily obtain
, we readily obtain
and
To complete the derivation of $\delta {\mathsf{{Z}}}$![]() , we also need to find the variation of $M^i(x) = \rho (x) u^i(x)$
, we also need to find the variation of $M^i(x) = \rho (x) u^i(x)$![]() , which can be obtained directly from the relation (D4). Taking the variation of this relation yields
, which can be obtained directly from the relation (D4). Taking the variation of this relation yields
This result implies that $\Delta M^i(x) = (\Delta \rho (x)) u^i(x) + \rho (x)(\Delta u^i(x)) = \rho (x) [ \textrm {d}\epsilon ^i(x)/\textrm {d}t -(\partial _{x^j} \epsilon ^j(x))u^i(x) ]$![]() , and thus we obtain
, and thus we obtain
Now, the fourth step consists of transforming the variational derivatives ${\mathcal {F}}_{q^i}\equiv \delta {\mathcal {F}}/\delta x^i$![]() and ${\mathcal {F}}_{p^i}\equiv \delta {\mathcal {F}}/\delta {\rm \pi}^i$
and ${\mathcal {F}}_{p^i}\equiv \delta {\mathcal {F}}/\delta {\rm \pi}^i$![]() into an equivalent form with respect to the Eulerian variables that comprise ${\mathsf{{Z}}}$
into an equivalent form with respect to the Eulerian variables that comprise ${\mathsf{{Z}}}$![]() . Consider a variation of a functional ${\mathcal {F}}$
. Consider a variation of a functional ${\mathcal {F}}$![]() . From (D6), we obtain
. From (D6), we obtain
where we have used (D10)–(D11) and (D22), along with $\Delta {\mathsf{{a}}}=0$![]() which holds because the quantities (D5) comprising ${\mathsf{{a}}}$
which holds because the quantities (D5) comprising ${\mathsf{{a}}}$![]() are advected. Similarly, from (D8), we obtain
are advected. Similarly, from (D8), we obtain

where we have substituted (D15), (D20), (D21) and (D23), integrated by parts, and then used the cancellation
which holds by the chain rule. Finally, from the two expressions (D24) and (D25), we equate the coefficients of $\epsilon ^i$![]() , and likewise the coefficients of $\textrm {d}\epsilon ^i/\textrm {d}t$
, and likewise the coefficients of $\textrm {d}\epsilon ^i/\textrm {d}t$![]() , because $\epsilon ^i$
, because $\epsilon ^i$![]() and $\textrm {d}\epsilon ^i/\textrm {d}t$
and $\textrm {d}\epsilon ^i/\textrm {d}t$![]() are arbitrary functions of $x$
are arbitrary functions of $x$![]() . This yields the key result
. This yields the key result

which are the transformation formulae for the variational derivatives.
Substitution of these formulae (D27) into the canonical bracket (D3) gives

after integration by parts to remove derivatives off of $B^i$![]() . This completes the derivation of the CGL Poisson bracket, which is the counterpart of the MHD bracket Morrison & Greene (Reference Morrison and Greene1982). Note that, for using the bracket (D28), we can convert all terms into vector notation as shown in (5.2).
. This completes the derivation of the CGL Poisson bracket, which is the counterpart of the MHD bracket Morrison & Greene (Reference Morrison and Greene1982). Note that, for using the bracket (D28), we can convert all terms into vector notation as shown in (5.2).
Equations (D4) for $\dot {x}^i(x_0,t)$![]() and (D10) for the variation $\delta x^i(x_0,t)$
and (D10) for the variation $\delta x^i(x_0,t)$![]() can be set up in an alternative way by means of the Lagrangian map (4.1), using diffeomorphisms $g(t)$
can be set up in an alternative way by means of the Lagrangian map (4.1), using diffeomorphisms $g(t)$![]() on Euclidean space similarly to the set up for the EP action principle in § 4. However, here the variations are not the same as those used for the EP action principle, because those variations took place in the Eulerian frame and involved fixing $x^i$
on Euclidean space similarly to the set up for the EP action principle in § 4. However, here the variations are not the same as those used for the EP action principle, because those variations took place in the Eulerian frame and involved fixing $x^i$![]() , with $x_0^i$
, with $x_0^i$![]() being a function of $x$
being a function of $x$![]() and $t$
and $t$![]() . To proceed, we view $g(t)$
. To proceed, we view $g(t)$![]() , at any fixed time $t$
, at any fixed time $t$![]() , as an element in the group of diffeomorphisms $G\equiv \textrm {Diff}({\mathbb {R}}^3)$
, as an element in the group of diffeomorphisms $G\equiv \textrm {Diff}({\mathbb {R}}^3)$![]() acting on Euclidean space in terms of the Cartesian coordinates $x_0^i$
acting on Euclidean space in terms of the Cartesian coordinates $x_0^i$![]() . The Lagrangian map (4.1) then can be expressed in component form:
. The Lagrangian map (4.1) then can be expressed in component form:
(Concretely, $g$![]() can be thought of as a matrix in the fundamental representation of the group $G$
can be thought of as a matrix in the fundamental representation of the group $G$![]() .) Thus, we can write
.) Thus, we can write
where
represent right-invariant vector fields on the group $G$![]() , which are identified with Eulerian vector fields (directional derivatives) at the point $x^i$
, which are identified with Eulerian vector fields (directional derivatives) at the point $x^i$![]() in Euclidean space. Note the property of right-invariance means that, for any fixed element $h$
in Euclidean space. Note the property of right-invariance means that, for any fixed element $h$![]() in $G$
in $G$![]() , $g\to gh$
, $g\to gh$![]() implies $\delta g g^{-1}\to \delta (gh) (gh)^{-1} = \delta g h h^{-1}g^{-1} = \delta g g^{-1}$
implies $\delta g g^{-1}\to \delta (gh) (gh)^{-1} = \delta g h h^{-1}g^{-1} = \delta g g^{-1}$![]() and $g_t g^{-1}\to (gh)_t (gh)^{-1} = g_t h h^{-1}g^{-1} = g_t g^{-1}$
and $g_t g^{-1}\to (gh)_t (gh)^{-1} = g_t h h^{-1}g^{-1} = g_t g^{-1}$![]() , due to $\partial _t h= \delta h\equiv 0$
, due to $\partial _t h= \delta h\equiv 0$![]() . The variation of the Eulerian variables ${\mathsf{{Z}}}$
. The variation of the Eulerian variables ${\mathsf{{Z}}}$![]() can be shown to arise from using the push-forward action of $g(t)$
can be shown to arise from using the push-forward action of $g(t)$![]() , and the pull-back action of $g(t)^{-1}$
, and the pull-back action of $g(t)^{-1}$![]() , on scalar fields, vector fields, differential forms and tensor fields in the Lagrangian frame.
, on scalar fields, vector fields, differential forms and tensor fields in the Lagrangian frame.
A closer connection to the variations used for the EP action principle arises if the variations derived in (D12), (D15), (D20), (D21) and (D23), are reformulated in the following way. A variation of any one of these quantities, $\delta {\mathsf{{Z}}}(x)$![]() , can be expressed as the sum of a contribution from varying only its dependence on $x^i$
, can be expressed as the sum of a contribution from varying only its dependence on $x^i$![]() , in addition to a contribution from varying ${\mathsf{{Z}}}$
, in addition to a contribution from varying ${\mathsf{{Z}}}$![]() with $x^i$
with $x^i$![]() being unchanged. For example, consider $\delta S(x)= (\delta S)(x) + (\delta x^i)\partial _{x^i} S(x)$
being unchanged. For example, consider $\delta S(x)= (\delta S)(x) + (\delta x^i)\partial _{x^i} S(x)$![]() . The pointwise contribution is given by
. The pointwise contribution is given by
from the total variation (D12). Likewise, $\delta \rho (x) = (\delta \rho )(x) + (\delta x^i)\partial _{x^i}\rho (x)$![]() leads to
leads to
from the total variation (D15). As another example, $\delta B^i(x)= \delta (B^i)(x) + (\delta x^j)\partial _{x^j} B^i(x)$![]() gives
gives
using the total variation (D21). When the analogous pointwise variations are considered for the components of the advected quantities (D5), we see that they take the form of a Lie derivative:
Note that here we have expressed the volume element as a 3-form: $\textrm {d}^3x = e_{ijk} {\textrm {d} x}^i\!\wedge {\textrm {d} x}^j\!\wedge {\textrm {d} x}^k$![]() , where $e_{ijk}$
, where $e_{ijk}$![]() is the Levi–Civita symbol. The Lie derivative in the variations (D36a–c) denotes the standard Lie derivative formula in component form. These formulae can be written more properly by including the basis vectors: e.g. $(\delta b^i(x))\partial _{x^i} = -{\mathcal {L}}_{\boldsymbol {\epsilon }} (b^i(x)\partial _{x^i})$
is the Levi–Civita symbol. The Lie derivative in the variations (D36a–c) denotes the standard Lie derivative formula in component form. These formulae can be written more properly by including the basis vectors: e.g. $(\delta b^i(x))\partial _{x^i} = -{\mathcal {L}}_{\boldsymbol {\epsilon }} (b^i(x)\partial _{x^i})$![]() , where the Lie derivative then acts in the standard geometrical way. This result coincides with the general formulation in Holm et al. (Reference Holm, Kupershmidt and Levermore1983). In addition, it shows that the variations of the non-advected Eulerian variables given by (D34) and (D35) can be expressed in terms of Lie derivatives:
, where the Lie derivative then acts in the standard geometrical way. This result coincides with the general formulation in Holm et al. (Reference Holm, Kupershmidt and Levermore1983). In addition, it shows that the variations of the non-advected Eulerian variables given by (D34) and (D35) can be expressed in terms of Lie derivatives:
These formulae are used in the classical work of Newcomb (Reference Newcomb1962). They can be used to derive the transformation formula (D27) for the variational derivatives by taking a pointwise variation of a functional:
which differs from (D27) by lacking a contribution from varying the volume element. Nevertheless, this leads to the same expression (D28) for the bracket (cf. the cancellation of terms (D26)).
Appendix E
In this appendix, we outline the general approach of Holm et al. (Reference Holm, Marsden and Ratiu1998) on the EP variational principles, with application to CGL plasmas. The action is of the form:
The stationary points of ${\mathcal {A}}$![]() are given by $\delta {\mathcal {J}}=0$
are given by $\delta {\mathcal {J}}=0$![]() , where the variables $a$
, where the variables $a$![]() are advected quantities (2.87) subject to the variations
are advected quantities (2.87) subject to the variations
Here ${\boldsymbol {\eta }}$![]() is an arbitrary, sufficiently differentiable vector field. Alternatively, ${\boldsymbol {\eta }}$
is an arbitrary, sufficiently differentiable vector field. Alternatively, ${\boldsymbol {\eta }}$![]() arises from a Lagrangian map as discussed in § 4.
arises from a Lagrangian map as discussed in § 4.
For the CGL plasma case, the Lagrangian density $L[u,a]$![]() is given by (3.21), where the $a$
is given by (3.21), where the $a$![]() are the advected quantities $S$
are the advected quantities $S$![]() , $\rho \,\textrm {d}^3x$
, $\rho \,\textrm {d}^3x$![]() , $\boldsymbol {B}/\rho \equiv \boldsymbol {b}$
, $\boldsymbol {B}/\rho \equiv \boldsymbol {b}$![]() (cf. (4.9a–d)). The magnetic flux 2-form $B_x \,{\textrm {d} y}\wedge \,\textrm {d}z+B_y \,\textrm {d}z\wedge \,{\textrm {d}\kern 0.05em x}+B_z \,{\textrm {d} x}\wedge \,{\textrm {d} y}$
(cf. (4.9a–d)). The magnetic flux 2-form $B_x \,{\textrm {d} y}\wedge \,\textrm {d}z+B_y \,\textrm {d}z\wedge \,{\textrm {d}\kern 0.05em x}+B_z \,{\textrm {d} x}\wedge \,{\textrm {d} y}$![]() is a Lie dragged invariant of the flow (Webb et al. Reference Webb, Dasgupta, McKenzie, Hu and Zank2014a). (Note $p_\parallel$
is a Lie dragged invariant of the flow (Webb et al. Reference Webb, Dasgupta, McKenzie, Hu and Zank2014a). (Note $p_\parallel$![]() , $p_\perp$
, $p_\perp$![]() and $e$
and $e$![]() are defined in terms of $\rho$
are defined in terms of $\rho$![]() , $S$
, $S$![]() and $B$
and $B$![]() via the equation of state for $e(\rho,S, B)$
via the equation of state for $e(\rho,S, B)$![]() ). The expression for the action $\mathcal {J}$
). The expression for the action $\mathcal {J}$![]() is the same as in (4.18). From (E2) and (4.9a–d), the variation $\delta a$
is the same as in (4.18). From (E2) and (4.9a–d), the variation $\delta a$![]() is obtained:
is obtained:

The variational equation $\delta {\mathcal {J}}=0$![]() is expressed as:
is expressed as:
which can be shown to imply for arbitrary ${\boldsymbol {\eta }}$![]() that
that
(see Holm et al. (Reference Holm, Marsden and Ratiu1998) for details). This is the general form of the EP equation. The diamond operator $\diamond$![]() is defined by the property (4.20).
is defined by the property (4.20).
For the CGL plasma action principle, the EP equation (E5) has the form
The term in (E6) involving the diamond operator can be determined from the variation

where boundary integral terms have been discarded. From (E7) and (E4), we identify the diamond operator term $(\delta L/\delta a)\diamond a$![]() as being the term in the square brackets. Substituting the variational derivatives of $L$
as being the term in the square brackets. Substituting the variational derivatives of $L$![]() , which are given by (4.21), we obtain
, which are given by (4.21), we obtain

where
The auxiliary calculations

and the thermodynamic relation
can be combined to give the identity
This equation was derived in (B6).
Substituting the identity (E12) into (E8) gives:
which, when used in the EP equation (E6) yields the Eulerian momentum equation (2.2).
Appendix F
In this appendix, we summarise the complete Lie point symmetry group for the CGL system (2.1)–(2.9). We restrict attention to the case where there is no gravity (i.e. $\varPhi =0$![]() in (2.2)). (For the general theory of Lie point symmetries, see Ovsjannikov Reference Ovsjannikov1978; Ibragimov Reference Ibragimov1985; Olver Reference Olver1993; Ovsjannikov Reference Ovsjannikov1994; Bluman & Anco Reference Bluman and Anco2002; Golovin Reference Golovin2009; Bluman, Cheviakov & Anco Reference Bluman, Cheviakov and Anco2010.)
in (2.2)). (For the general theory of Lie point symmetries, see Ovsjannikov Reference Ovsjannikov1978; Ibragimov Reference Ibragimov1985; Olver Reference Olver1993; Ovsjannikov Reference Ovsjannikov1994; Bluman & Anco Reference Bluman and Anco2002; Golovin Reference Golovin2009; Bluman, Cheviakov & Anco Reference Bluman, Cheviakov and Anco2010.)
The independent and dependent variables in (2.1)–(2.9) consist of $t$![]() , $x^i$
, $x^i$![]() , $\rho$
, $\rho$![]() , $u^i$
, $u^i$![]() , $B^i$
, $B^i$![]() , $S$
, $S$![]() , $p_\parallel$
, $p_\parallel$![]() and $p_\perp$
and $p_\perp$![]() . Thus, every Lie point symmetry arises from a generator of the form
. Thus, every Lie point symmetry arises from a generator of the form
under which (2.1)–(2.9) are invariant on the space of solutions. Here
are functions of the independent and dependent variables. For computational purposes, it is easiest to work with the characteristic form of the generator in which only the dependent variables undergo a transformation:
where
for each dependent variable $v=(\rho,u^i,B^i,S,p_\parallel,p_\perp )$![]() . The generator $\hat {{X}}$
. The generator $\hat {{X}}$![]() has the convenient property that it commutes with total derivatives with respect to $t,x^i$
has the convenient property that it commutes with total derivatives with respect to $t,x^i$![]() , and so the prolongation of $\hat {{X}}$
, and so the prolongation of $\hat {{X}}$![]() acting on derivatives of $v$
acting on derivatives of $v$![]() is easy to compute.
is easy to compute.
The determining equations for Lie point symmetries are given by applying $\textrm {pr}\hat {{X}}$![]() to each equation (2.1)–(2.9) and evaluating the resulting system on the solution space of (2.1)–(2.9) which is carried out by putting (2.1)–(2.9) into a solved form with respect to a set of leading derivatives. (See Olver (Reference Olver1993) for a general discussion.) The resulting system of determining equations then splits with respect to all derivative variables that appear in the system. This yields an overdetermined linear system of equations for the functions (F2). The system can be solved straightforwardly by use of computer algebra (e.g. Maple or Mathematica).
to each equation (2.1)–(2.9) and evaluating the resulting system on the solution space of (2.1)–(2.9) which is carried out by putting (2.1)–(2.9) into a solved form with respect to a set of leading derivatives. (See Olver (Reference Olver1993) for a general discussion.) The resulting system of determining equations then splits with respect to all derivative variables that appear in the system. This yields an overdetermined linear system of equations for the functions (F2). The system can be solved straightforwardly by use of computer algebra (e.g. Maple or Mathematica).
The Lie point symmetry generators are found to be given by the 10 Galilean transformation generators (6.18a–d) and the following 3 scaling generators

In terms of the quantities $p=(p_\parallel +2 p_\perp )/3$![]() and $p_{\varDelta }=p_\parallel -p_\perp$
and $p_{\varDelta }=p_\parallel -p_\perp$![]() , the third scaling symmetry has the equivalent form:
, the third scaling symmetry has the equivalent form:
For comparison, the Lie point symmetries for MHD (Rogers & Ames Reference Rogers and Ames1989; Fuchs Reference Fuchs1991) are given by the 10 Galilean transformation generators (6.18a–d) and the 2 scaling generators $S_1$![]() and $S_2$
and $S_2$![]() plus a scaling generator $S_{3'} =2\rho \partial _\rho +2p\partial _{p} +B^i\partial _{B^i}$
plus a scaling generator $S_{3'} =2\rho \partial _\rho +2p\partial _{p} +B^i\partial _{B^i}$![]() which differs from $S_3$
which differs from $S_3$![]() by omitting the term involving $p_\varDelta$
by omitting the term involving $p_\varDelta$![]() .
.
A full study of subalgebras of the Galilean Lie algebra was given in Ovsjannikov (Reference Ovsjannikov1978, Reference Ovsjannikov1994, Reference Ovsjannikov1999) and Grundland & Lalague (Reference Grundland and Lalague1995).
Appendix G
Here we derive the Lie invariance condition (6.17) for the action, which follows from (6.5). We start from the appropriate expansion for $\textrm {pr}\,\hat {{X}}L_0$![]() :
:
The derivatives of $L_0$![]() in (G1) are given in Appendix C, namely
in (G1) are given in Appendix C, namely

where

By noting that
and
We obtain

Noting
we obtain the equations

In the derivation of (G9) we used the identity
with $\boldsymbol {A}=\hat {\boldsymbol {\xi }}\times \boldsymbol {B}$![]() and $\boldsymbol {C}=\tilde {\boldsymbol {B}}$
and $\boldsymbol {C}=\tilde {\boldsymbol {B}}$![]() .
.

Using (G11) in (G4) gives a simplification of $R_1$![]() , which can in turn be used to obtain $\textrm {pr}\,\hat {{X}}(L_0)$
, which can in turn be used to obtain $\textrm {pr}\,\hat {{X}}(L_0)$![]() in (G1). Substitution of the resultant $\textrm {pr}\,\hat {{X}}(L_0)$
in (G1). Substitution of the resultant $\textrm {pr}\,\hat {{X}}(L_0)$![]() in (6.5) gives (6.17) as the condition for Lie invariance of the action.
in (6.5) gives (6.17) as the condition for Lie invariance of the action.
Appendix H
In this appendix, we provide a derivation of Noether's first theorem, using the approach of Bluman & Kumei (Reference Bluman and Kumei1989). This analysis should be useful for readers not acquainted with the classical approach to Noether's first theorem. These ideas are used in § 6.2 to describe Noether's theorem.
Consider a system of differential equations in the dependent variables $u^\alpha$![]() ($1\leqslant \alpha \leqslant m$
($1\leqslant \alpha \leqslant m$![]() ) and independent variables $x^i$
) and independent variables $x^i$![]() ($1\leqslant i\leqslant n$
($1\leqslant i\leqslant n$![]() ) of the form
) of the form
the subscripts in $u^\alpha _i$![]() , $u^\alpha _{ij},\ldots$
, $u^\alpha _{ij},\ldots$![]() , denote partial derivatives with the respect to the independent variables $x^i$
, denote partial derivatives with the respect to the independent variables $x^i$![]() $(1\leqslant i\leqslant n)$
$(1\leqslant i\leqslant n)$![]() , which arise from extremal variations of the action
, which arise from extremal variations of the action
which remain invariant under infinitesimal Lie transformations of the form
The variation of $J[\boldsymbol {u}]$![]() is defined as
is defined as
where $\varOmega$![]() is the region of integration. The variation $\delta J$
is the region of integration. The variation $\delta J$![]() to $O(\epsilon )$
to $O(\epsilon )$![]() in (H4) reduces to
in (H4) reduces to
The term $LD_i\xi ^i$![]() in (H5) represents changes in the volume element:
in (H5) represents changes in the volume element:
The Lie derivative term:

describes the changes in $L(\boldsymbol {x},u^\alpha,u^\alpha _i,u^\alpha _{ij},\ldots )$![]() due to the Lie transformations of $x^i$
due to the Lie transformations of $x^i$![]() and $u^\alpha$
and $u^\alpha$![]() in (H3a–c), in which the form of $L$
in (H3a–c), in which the form of $L$![]() does not change. The term $D_i\varLambda ^i$
does not change. The term $D_i\varLambda ^i$![]() describes changes of $J$
describes changes of $J$![]() due to changes in the form of $L$
due to changes in the form of $L$![]() due to a divergence transformation (under such a transformation the action remains invariant). From (H5) the action $J[\boldsymbol {u}]$
due to a divergence transformation (under such a transformation the action remains invariant). From (H5) the action $J[\boldsymbol {u}]$![]() remains invariant under the Lie transformations (H3a–c) to $O(\epsilon )$
remains invariant under the Lie transformations (H3a–c) to $O(\epsilon )$![]() if
if
It turns out that there is an equivalent extended Lie symmetry operator, $\textrm {pr} (\hat {X})$![]() , of the form
, of the form
called the evolutionary operator (e.g. Olver Reference Olver1993) which describes Lie transformations:
where
The operator $\textrm {pr}(\hat {{X}})$![]() is related to $\textrm {pr}({X})$
is related to $\textrm {pr}({X})$![]() by the formula
by the formula
where $D_j=\textrm {d}/{\textrm {d} x}^j$![]() is the total, partial derivative with respect to $x^j$
is the total, partial derivative with respect to $x^j$![]() . From (H9), we obtain the formulae
. From (H9), we obtain the formulae
for the transformation of partial derivatives under $\textrm {pr}(\hat {X})$![]() . These transformations are different from the transformations of derivatives formulae under the canonical prolonged symmetry operator $\textrm {pr}\,{X}$
. These transformations are different from the transformations of derivatives formulae under the canonical prolonged symmetry operator $\textrm {pr}\,{X}$![]() , namely
, namely
and similarly for transformations of the higher-order derivatives of $u^\alpha$![]() .
.
Evaluation of $\delta J[\boldsymbol {u}]$![]() using $\textrm {pr}(\hat {{X}})$
using $\textrm {pr}(\hat {{X}})$![]() gives the variational equation:
gives the variational equation:
from which it follows that
where the $W^i[\boldsymbol {u},\hat {\boldsymbol {\eta }}]$![]() are surface terms given by
are surface terms given by
and $\delta L/\delta \psi$![]() is given by
is given by
Here $E_\psi$![]() denotes the Euler operator or variational derivative with respect to $\psi$
denotes the Euler operator or variational derivative with respect to $\psi$![]() used in the Calculus of variations. In particular, the equations
used in the Calculus of variations. In particular, the equations

are the Euler–Lagrange equations for the variational principle $\delta J=0$![]() .
.
Using $\textrm {pr}({X})L$![]() from (H12), the Lie invariance condition (H8) for the action reduces to
from (H12), the Lie invariance condition (H8) for the action reduces to
Using (H16) for $\textrm {pr}(\hat {{X}})L$![]() in (H20) we obtain the Noether theorem identity:
in (H20) we obtain the Noether theorem identity:
For the case of a finite point Lie group of symmetries (i.e. for a finite number of point symmetries $\hat {\eta }^{\gamma }$![]() ), for which the Euler–Lagrange equations $E_\gamma (L)=0$
), for which the Euler–Lagrange equations $E_\gamma (L)=0$![]() are satisfied, and (H21) reduces to the conservation law
are satisfied, and (H21) reduces to the conservation law
associated with Noether's first theorem.
If the symmetries $\hat {\eta }^\gamma$![]() depend on continuous functions $\{\phi ^k(\boldsymbol {x}: 1\leqslant k\leqslant N\}$
depend on continuous functions $\{\phi ^k(\boldsymbol {x}: 1\leqslant k\leqslant N\}$![]() , then the Lie pseudo-algebra of symmetries is infinite dimensional. In this case Noether's second theorem implies that the Euler–Lagrange equations are not all independent and that there exists differential relations between the Euler–Lagrange equations (see, e.g., Olver (Reference Olver1993) and Hydon & Mansfield (Reference Hydon and Mansfield2011) for details).
, then the Lie pseudo-algebra of symmetries is infinite dimensional. In this case Noether's second theorem implies that the Euler–Lagrange equations are not all independent and that there exists differential relations between the Euler–Lagrange equations (see, e.g., Olver (Reference Olver1993) and Hydon & Mansfield (Reference Hydon and Mansfield2011) for details).