Collisional broadening of nonlinear resonant wave–particle interactions

Abstract

A general procedure for understanding plasma behaviour when resonant wave–particle interactions are the sole destabilizing and transport mechanism or only heating and/or current drive source is highlighted without recourse to involved numerical or analytical treatments. These phenomena are characterized by transport that appears to be collisionless even though collisions play a central role in narrow collisional boundary layers. The order of magnitude estimates, which include nonlinear effects, are shown to provide expressions in agreement with the principal results of recent toroidal Alfvén eigenmode (TAE), toroidal magnetic field ripple, and heating and current drive treatments. More importantly, the retention of nonlinearities leads to new estimates of the alpha particle energy diffusivity at saturation for TAE modes, and the ripple threshold at which superbanana plateau evaluations of alpha particle transport are modified by nonlinear radial drift effects. In addition, the estimates indicate when quasilinear descriptions for heating and current drive will begin to fail. The phenomenological procedure demonstrates that in magnetic fusion relevant plasmas, narrow collisional boundary layers must be retained for resonant wave–particle interactions as they enhance the role of collisions, and make stochastic particle motion unlikely to be more important than other nonlinear processes.

1. Introduction

Resonant interactions of charged particles with waves in plasmas are a concern when they drive deleterious instabilities, and are a tool when they are used for heating, and to drive currents. For example, alpha particles (or energetic particles produced by heating) act as a destabilizing drive for toroidal Alfvén eigenmodes (TAEs) (Cheng & Chance 1986; Fu & Van Dam 1989) that are a concern in fusion relevant plasmas, and ripple (Goldston & Towner 1981; White 2013; Catto 2019a) due to the toroidal field coils causes alpha particle loss, while radio frequency (rf) heating and current drive (Fisch 1987; Brambilla 1999; Jaeger et al. 2003; Wright et al. 2004; Bonoli 2014) schemes impart energy and/or momentum by resonant particle interactions using applied waves to achieve high performance plasmas. While these processes are often difficult to evaluate in detail, some of the general features of these complex behaviours can be obtained by rather simple estimates, leading to new insights and improved understanding of the crucial role collisional boundary layers play in establishing nonlinear TAE saturation or altering rf heating and current drive. These estimates are possible when the resonant particles are the only drive for instability and transport or the only source of heating and/or current drive, because the plasmas of interest are weakly collisional with long mean free paths. The existence of the velocity dependence of the wave–particle interactions and the diffusive nature of collisions means there are resonant paths in velocity space enclosed by very narrow collisional boundary layers (Su & Oberman 1968; Johnston 1971; Auerbach 1977) that are sensitive to nonlinearities.

Recent investigations (Zhou & White 2016; Duarte et al. 2019, 2020; Duarte & Gorelenkov 2019; White et al. 2019; Catto 2020; Catto & Tolman 2021; Tolman & Catto 2021) suggest that collisions in these narrow boundary layers cannot be ignored when stochastic particle trajectories are retained (for clarity, stochasticity always refers herein only to collisionless particle motion and not diffusive collisions). These studies find that collisional boundary layer effects must be retained even when nonlinearities enter to saturate mode growth driven by resonant wave–particle interactions, or when nonlinear behaviour limits the validity of a quasilinear (QL) treatment of rf heating and current drive. Moreover, they imply that nonlinear behaviour enters at perturbation amplitudes well below the collisionless threshold for full stochasticity (Chirikov 1979). In what follows, rather general forms of the kinetic equation are used to demonstrate the important role of the narrow collisional boundary layers and how they ensure that the nonlinear terms enter at quite small perturbation amplitudes. Very little algebra is required to recover and understand these straightforward estimates and obtain new results and insights.

For these demonstrations both low frequency $(\omega \ll \varOmega )$ drift kinetic and gyrokinetic and high frequency $(\omega \sim \varOmega )$ gyrokinetic equations for the non-adiabatic resonant particle response are considered. Here, $\omega$ is the wave frequency and $\varOmega = ZeB/Mc$ the species cyclotron frequency with B the magnetic field, e the charge on a proton, Z and M the relevant species charge number and mass, and c the speed of light. To obtain the equation for the non-adiabatic response, the portion of the response that leads to adiabatic behaviour (such as the adiabatic Maxwell–Boltzmann response) is removed until only TAE and ripple drives due to departures from axisymmetry and time variation remain (Tolman & Catto 2021), or until only the irreversible resonant response is left to evaluate for rf (Catto, Lee & Ram 2017; Catto 2020; Catto & Tolman 2021). To focus on the key physics elements only the essential terms in the kinetic equations are retained and simplifications (such as approximate pitch angle scattering collision operators) are used whenever possible. In all cases it is necessary that the wave–particle resonance contain velocity dependence and the collision operator be diffusive so that a narrow collisional boundary layer is formed. The use of simplified pitch angle scattering collision operators is not a limitation if only the linearized kinetic equation is considered as the estimates are then made in what is referred to as the resonant plateau regime whereby the key results do not depend on collision frequency even though collisions are crucial to the physics (recall that the plateau regime of neoclassical theory is independent of collision frequency even though it is between the weakly collisional banana regime and the collisional Pfirsch–Schlüter regime – see for example Helander & Sigmar 2005). Of course, the details of the collision operator will matter once the perturbation amplitude is large enough for the nonlinear terms in the kinetic equation to enter. However, as only nonlinear estimates are made here these details are unimportant.

To understand resonant plateau regime behaviour in the low frequency cases of TAE modes and field ripple, the spatial diffusivity D is estimated from

(1.1)\begin{equation}D = \varUpsilon {\varDelta ^2}/\tau .\end{equation}

It is shown to be independent of the collision frequency because of cancelation in the combination of the correlation time $\tau$, the radial spatial decorrelation or step size $\varDelta$ squared, and the fraction $\varUpsilon$ of the particles in resonance with the wave. In the high frequency case of § 4 the velocity space diffusivity is estimated in a similar manner using a velocity space step.

To verify most of the distinctive features of resonant plateau behaviour and to make simple nonlinear estimates, the low frequency limit is considered next for TAEs and then in § 3 for ripple.

2. TAE transport due to alphas

Alfvén eigenmodes (AEs) are spatially localized modes existing in the gaps of the Alfvén wave continuum (Cheng & Chance 1986; Fu & Van Dam 1989; Heidbrink 2008) with TAE modes residing in the lowest frequency gap. They are driven unstable by energetic particles in general and in particular by the alpha particles generated in fusion reactions. TAEs driven by alphas are a concern if they are able to transport energy to the wall before it can be deposited in the electrons. The steady state level of the alpha energy diffusivity, which is about to be estimated, is the key to determining whether this is a serious concern. A TAE mode has an approximate wave frequency $\omega = |{k_{||}}|{v_A}$ defined by a toroidal mode number n and two adjacent poloidal mode numbers m and m + 1 according to $(qn - m)/qR \simeq \omega /{v_A} \simeq (m + 1 - qn)/qR$, where ${v_A} = B/\sqrt {4{\rm \pi}{M_i}{n_i}}$ is the Alfvén speed and ${k_{||}} = (qn - m)/qR$, with ${n_i}$ and ${M_i}$ the background ion density and mass, q the safety factor, and R the major radius. Consequently, $qn - m = 1/2$ and $\omega \simeq {v_A}/2qR$ for a TAE mode.

TAE modes are particularly interesting and complex because the wave frequency must be ordered as comparable to the bounce or transit frequency, ${v_0}/qR$, for the alphas that are born isotropically in velocity space with a speed of ${v_0}$. Consequently, bounce or transit average descriptions are not appropriate and the use of the longitudinal invariant is invalid. Additionally, the trapped birth alphas resonate with the magnetic drift ${\omega _\alpha }$ tangential to the flux surface, while the sign of the tangential drift for the passing birth alphas is in the opposite direction so they instead experience a drift modified Landau resonance with ${k_{||}}{v_{||}}\sim {v_0}/2qR$ (Tolman & Catto 2021). The TAEs considered here are driven unstable solely by the radial gradient of the alpha density or, more precisely, the radial gradient of the unperturbed alpha distribution function. Without the resonant alphas there is no instability or transport. The unperturbed alpha distribution function ${f_0}$ is referred to as a slowing down tail distribution function as there are no alphas with speeds above the velocity space step at the birth speed ${v_0}$. As the alphas are born isotropically in velocity space and there are no collisional boundary layers, the unperturbed distribution function is completely determined by electron and ion drag. The perturbed radial motion off of a flux surface due to a TAE mode is primarily due to its departure from axisymmetry caused by its toroidal angle dependence $\zeta$ and is given by the radial velocity (Tolman & Catto 2021)

(2.1)\begin{equation}{V_r} \equiv {{\left( {c\frac{{\partial \phi }}{{\partial \zeta }} - {v_{||}}\frac{{\partial {A_{||}}}}{{\partial \zeta }} + \frac{{\mu B}}{\varOmega }\frac{{\partial {B_{||}}}}{{\partial \zeta }}} \right)} \bigg/ {(R{B_p})}}\sim in{{\left( {c\phi - {v_{||}}{A_{||}} + \frac{{\mu B}}{\varOmega }{B_{||}}} \right)} / {(R{B_p})}},\end{equation}

with $\phi$ and ${A_{||}}$ the perturbed electrostatic and parallel vector potentials, ${B_{||}}$ the perturbed parallel magnetic field, $\mu = v_ \bot ^2/2B$ the magnetic moment, $\varOmega$ the alpha cyclotron frequency, and ${B_p}$ the poloidal magnetic field. The $\zeta$derivatives arise because the presence of TAE modes means that the canonical angular momentum is no longer a constant of the motion. The wave frequency terms (due to temporal variation) that multiply the radial drift (due to energy no longer being a constant of the motion) are stabilizing and are ignored to keep the argument as simple as possible.

To express ${V_r}$ in terms of the perturbed magnetic field ${\boldsymbol{B}_1}$ for a TAE mode, ${B_{||}}$ is neglected, and the near vanishing of the perturbed parallel electric field, ${k_{||}}c\phi \simeq \omega {A_{||}}$, is employed along with ${v_{||}}\sim {v_0}$ and ${B_1} \simeq |\boldsymbol{\nabla }{A_{||}}|\sim n{A_{||}}B/{\kern 1pt} R{B_p}$ to obtain

(2.2)\begin{equation}\frac{{{V_r}}}{{{v_0}}}\sim \frac{{{v_A} + {v_0}}}{{{v_0}}}\frac{{{B_1}}}{B}\sim \frac{{{B_1}}}{B}.\end{equation}

Upon removing the adiabatic alpha response by taking the perturbed alpha distribution function ${f_1}$ to be ${f_1} = h + (Ze\phi /Mv)\partial {f_0}/\partial v$, the alpha kinetic equation for the non-adiabatic response h is of the form (Tolman & Catto 2021)

(2.3)\begin{equation}{\left. {\frac{{\textrm{d}h}}{{\textrm{d}t}}} \right|_{\textrm{res}}} + {V_r}\left( {\frac{{\partial {f_0}}}{{\partial r}} + \frac{{\partial h}}{{\partial r}}} \right) \simeq C\{ h\} ,\end{equation}

where the nonlinear term $\partial h/\partial r$ is retained, $C\{ h\}$ denotes the collision operator for alphas, and the resonance between the alphas and the TAE mode means there is a resonant path with

(2.4)\begin{equation}{\left. {\frac{{\textrm{d}h}}{{\textrm{d}t}}} \right|_{\textrm{res}}}\sim (\omega - n{\omega _\alpha } - \sigma |{k_{||}}{v_{||}}|)h \simeq 0,\end{equation}

where $\sigma = 0$ for the trapped alphas and $\sigma ={\pm} 1$ for the passing alphas. Collisional boundary layers occur because of the resonances indicated in (2.4) and the diffusive nature of pitch angle scattering by the ions. In the absence of radial drift, the resonant alphas drift tangentially while de-trapping and re-trapping in the perturbed wells. Irreversible behaviour and loss requires radial drift and collisions as well as wave–particle resonance. In (2.3) the linear term ${V_r}\partial {f_0}/\partial r$ destabilizes the TAE mode and the nonlinear term ${V_r}\partial h/\partial r$ provides saturation. We assume there are many modes across the radial region of interest and they possess a collisionally broadened overlap so that they are within a collisional step size of one another with poloidally coupling allowed and many toroidal mode numbers present. The collisional radial steps lead to the radial heat transport of the alphas (Tolman & Catto 2021). The procedure used here to make estimates is not expected to be completely appropriate for neoclassical tearing modes (NTMs) as a finite amplitude seed perturbation is required for instability.

The alpha resonance can be broadened in two ways: velocity space collisions, and spatially by nonlinear behaviour due de-trapping and re-trapping caused by the radial drift departure from axisymmetry, mode coupling, any stochasticity of the particle trajectories (as in a Poincaré puncture plot of three-dimensional configuration space), and/or by some other microscale turbulent mechanism (Pace et al. 2013; Gorelenkov & Duarte 2021). Moreover, the estimates to follow are not made near marginal stability as is sometimes assumed (Duarte et al. 2019, 2020; Duarte & Gorelenkov 2019; Gorelenkov & Duarte 2021). Hence, expanding in pitch angle $\lambda = 2\mu {B_0}/{v^2}$ and radius r about the resonance at $\lambda = {\lambda _{\textrm{res}}}$ and $r - {r_{\textrm{res}}}\sim \delta$ leads to

(2.5)\begin{equation}n{\omega _\alpha } \simeq \omega + n\frac{{\partial {\omega _\alpha }}}{{\partial \lambda }}(\lambda - {\lambda _{\textrm{res}}}) + n\frac{{\partial {\omega _\alpha }}}{{\partial r}}(r - {r_{\textrm{res}}}) + \cdots ,\end{equation}

with ${\omega _\alpha }$ slowly varying in pitch angle and radius and $v_{||}^2 = {v^2}(1 - \lambda B/{B_0})$. The details of the nonlinear detuning are unimportant for the purpose of making estimates as long as they introduce small spatial scales that cause the resonance to smear radially, while collisions result in a velocity space boundary layer. The new radial scales remain small, but increase in extent and size with increasing wave amplitude until nonlinear saturation occurs. For the moment only trapped alphas are considered so that $\omega \simeq n{\omega _\alpha }$, but the passing will be considered shortly by very similar arguments. Estimating the velocity space collisional boundary layer width by $\lambda - {\lambda _{\textrm{res}}} = w$ and the radial decorrelation width or step size by $r - {r_{\textrm{res}}} = \delta$, and taking $\partial {\omega _\alpha }/\partial \lambda \sim {\omega _\alpha }$ and $\partial {\omega _\alpha }/\partial r\sim {\omega _\alpha }/a$ with a the minor radius leads to the additive form

(2.6)\begin{equation}{\left. {\frac{{\textrm{d}h}}{{\textrm{d}t}}} \right|_{\textrm{res}}}\sim n{\omega _\alpha }\left( {w + \frac{\delta }{a}} \right).\end{equation}

For a pitch angle scattering collision operator in a narrow boundary layer

(2.7)\begin{equation}C\{ h\} \simeq \nu {\partial ^2}h/{\kern 1pt} \partial {\lambda ^2}\sim \nu h/{w^2},\end{equation}

with $\nu$ the pitch angle scattering collision frequency of alphas with the background ions, $\lambda = 2\mu {B_0}/{v^2}$, and ${B_0}$ the on axis magnetic field (electron drag does not enter because it is not diffusive and cannot form a narrow collisional boundary layer). In addition,

(2.8)\begin{equation}\partial {f_0}/\partial r\sim {f_0}/a,\end{equation}

with a the minor radius, but for a narrow radial layer

(2.9)\begin{equation}\partial h/{\kern 1pt} \partial r\sim h/\delta .\end{equation}

The preceding leads to the conjecture that the kinetic equation contains five different terms that must balance after a collisional correlation time and when the nonlinear term becomes large enough to saturate the TAE mode

(2.10)\begin{equation}n{\omega _\alpha }\left( {w + \frac{\delta }{a}} \right)h\sim {V_r}\left( {\frac{{{f_0}}}{a} + \frac{h}{\delta }} \right)\sim \frac{\nu }{{{w^2}}}h.\end{equation}

At this resonant version of ‘critical balance’ (Barnes, Parra & Schekochihin 2011) all five terms compete at saturation to give four conditions that follow. The first two set the velocity space boundary layer width $w\sim {(\nu /n{\omega _\alpha })^{1/3}}$ and its relation to the radial decorrelation width or step size $\delta \sim wa$, while a third relates the radial step size $\delta$ to the amplitude of the perturbed TAE mode amplitude ${V_r}$ at saturation $\delta \sim {(a{V_r}/n{\omega _\alpha })^{1/2}}$. The final condition must be satisfied to keep the ratio of the perturbed over unperturbed distribution functions $h/{\kern 1pt} {f_0}\sim \delta /{\kern 1pt} a$ small, to give a weak non-adiabatic or irreversible response once collisions suppress phase mixing. The four conditions lead to

(2.11)\begin{equation}w\sim \delta /a\sim h/{\kern 1pt} {f_0}\sim {({V_r}/an{\omega _\alpha })^{1/2}}\sim {(\nu /n{\omega _\alpha })^{1/3}} \ll 1,\end{equation}

and the observation that the weaker the collisions, the lower the saturation level, in agreement with the results and saturation estimate in Tolman & Catto (2021).

As expected, the radial distance $\delta$ from an isolated linear resonance at which stochasticity no longer acts is proportional to the square root of the TAE perturbation amplitude. It is approximately the radial width observed in the presence of diffusive collisions for the perturbed distribution function when blurred Poincaré plots are no longer a useful diagnostic (see figure 8 of White et al. 2019). Importantly, and perhaps unsurprisingly, it is small so the saturation amplitude is well below the Chirikov (1979) threshold for fully stochastic particle trajectories of roughly $\delta /a\sim {({V_r}/an{\omega _\alpha })^{1/2}}\sim 1$.

The condition for a narrow collisional boundary layer $w \ll 1$ about each resonance path $\omega \simeq |nq - m|{v_A}/qR \simeq n{\omega _\alpha }$ ensures consistency of all these estimates. A more rigorous treatment of the boundary layer is possible in the linear limit by solving

(2.12)\begin{equation}in\frac{{\partial {\omega _\alpha }}}{{\partial \lambda }}(\lambda - {\lambda _{\textrm{res}}})h - \nu \frac{{{\partial ^2}h}}{{\partial {\lambda ^2}}} ={-} {V_r}\frac{{\partial {f_0}}}{{\partial r}}.\end{equation}

Letting $u = {(n\partial {\omega _\alpha }/\partial \lambda )^{1/3}}(\lambda - {\lambda _{\textrm{res}}})/{\nu ^{1/3}} \equiv (\lambda - {\lambda _{\textrm{res}}})/{\kern 1pt} w$, leads to the Su & Oberman (1968) form

(2.13)\begin{equation}\frac{{{\partial ^2}h}}{{\partial {u^2}}} - iuh = \frac{{{V_r}\partial {f_0}/\partial r}}{{{\nu ^{1/3}}{{(n\partial {\omega _\alpha }/\partial \lambda )}^{2/3}}}},\end{equation}

with solution

(2.14)\begin{equation}h ={-} \frac{{{V_r}}}{\nu }\frac{{\partial {f_0}}}{{\partial r}}{w^2}\int_0^\infty {\textrm{d}\kern0.06em x\,{\textrm{e}^{ - \textrm{i}ux - {x^3}/3}}} \mathop \to \limits_{|u|\gg 1} \frac{{i{V_r}\partial {f_0}/\partial r}}{{(\lambda - {\lambda _{\textrm{res}}})n\partial {\omega _\alpha }/\partial \lambda }}.\end{equation}

The real part of this solution contains the delta function behaviour via

(2.15)\begin{equation}P \equiv \frac{1}{{{\rm \pi} w}}\int_0^\infty {\textrm{d}\kern0.06em x\,{\textrm{e}^{ - {x^3}/3}}\cos (ux)} ,\end{equation}

where upon integrating over pitch angle for $\varsigma \gg 1$ gives

(2.16)\begin{equation}\int_{{\lambda _{res}} - \varsigma w}^{{\lambda _{res}} + \varsigma w} {\textrm{d}\lambda } P = \frac{1}{\rm \pi}\int_0^\infty {\textrm{d}\kern0.06em x\,{\textrm{e}^{ - {x^3}/3}}\int_{ - \varsigma }^\varsigma {\textrm{d}u} \cos (ux)} = \frac{2}{\rm \pi}\int_0^\infty {\textrm{d}\kern0.06em x\,{\textrm{e}^{ - {x^3}/3}}\frac{{\sin (\varsigma x)}}{x}} \simeq 1.\end{equation}

The function $P(\lambda )$ vs. $\lambda - {\lambda _{\textrm{res}}}$ is plotted in figure 1 and has a width w as shown, which is the width of the delta function limit $P \to \delta (\lambda - {\lambda _{\textrm{res}}})\sim 1/w$. Functions proportional to P are found when collisions are retained for Langmuir waves (Auerbach 1977), near marginality for QL treatments of resonant particle effects (Duarte et al. 2019), and for rf (Catto 2020). Once the steady state collisionally modified resonant response (2.15) is integrated over velocity space, as in (2.16), the lowest order resonant contribution is independent of collisions and thereby leads to the resonant plateau terminology employed herein. While (2.12)–(2.16) provide important insight, they no longer hold in the fully developed nonlinear state of the estimates of (2.10). Within a QL framework the QL step ${V_r}/{\nu _{\textrm{eff}}}$ is assumed small compared with $\delta$.

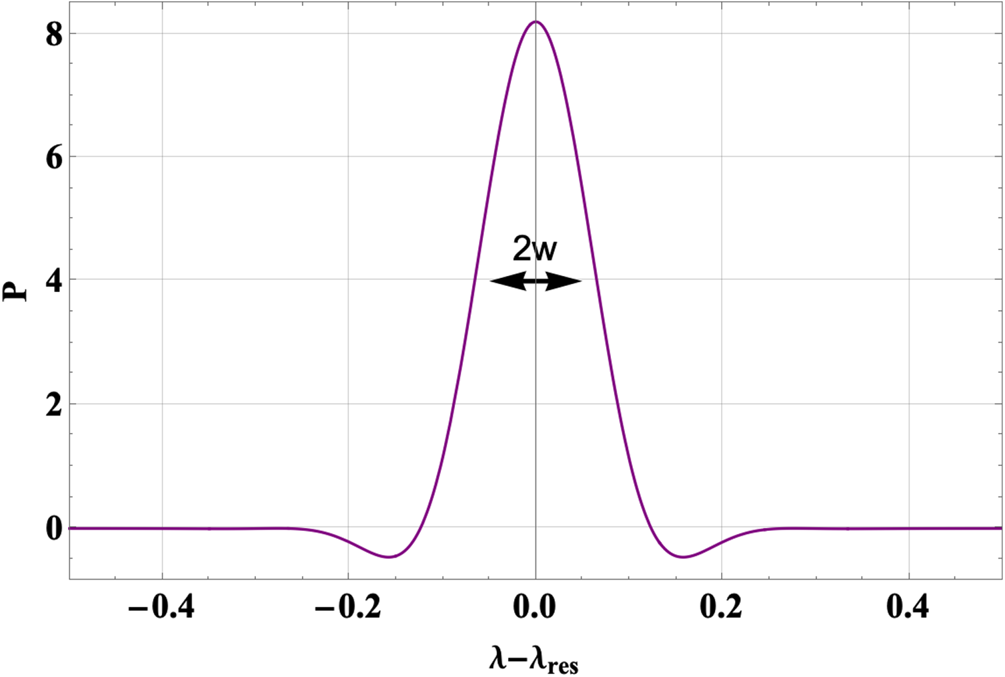
Figure 1. The approximate delta function $P(\lambda )$ vs. $(\lambda - {\lambda _{\textrm{res}}})$ with the width w = 0.05 indicated.

Collisions act to replenish the narrow boundary layers about all the resonant paths in velocity space that are depleted by radial transport acting to flatten the total distribution function on the radial scale $\delta$. A schematic of the flattening associated with an isolated resonance is shown in figure 2 with the height of the plateau of order $h/{\kern 1pt} {f_0}$. TAE instability growth persists until the nonlinear terms enter to provide a detuning saturation mechanism that allows the estimates of (2.10) to be made without relying on a QL approach. In the absence of collisions or dissipation there is nothing to limit the resonant alpha particle driven TAE growth until nonlinearity enters to disrupt the wave–particle resonance drive term. With collisions, the radial gradient drive is continuously being nonlinearly restored since $h/\delta \sim {f_0}/a$ and ${V_r}/\delta \sim {\nu _{\textrm{eff}}}$. As the TAE mode growth continues it becomes nonlinear, and saturation becomes possible by one or more turbulent processes such as mode coupling, trapping, the stochasticity of the particle trajectories, and/or the nonlinear frequency shift bifurcating the initial mode and then generating further nonlinear sideband splitting (Fasoli et al. 1998).

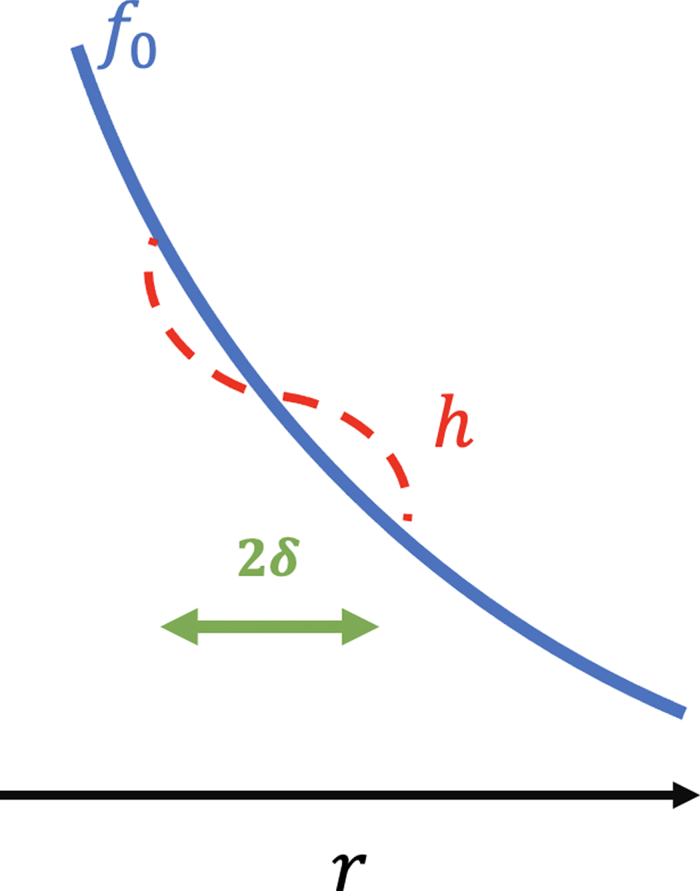
Figure 2. Schematic showing the radial scale $\delta$ of flattening associated with an isolated resonance.

The narrow collisional boundary layer means the effective collision frequency is ${\nu _{\textrm{eff}}}\sim \nu /{w^2}$ with an associated correlation time $\tau$ given by

(2.17)\begin{equation}\tau \equiv \nu _{\textrm{eff}}^{ - 1}\sim {\nu ^{ - 1/3}}{(n{\omega _\alpha })^{ - 2/3}}\sim {(a/n{\omega _\alpha }{V_r})^{1/2}}.\end{equation}

The estimates of (2.10) are made for times longer than $\tau = \nu _{\textrm{eff}}^{ - 1}$.

The resonant plateau amplitude scaling with collisionality of ${V_r}\sim a{\nu ^{2/3}}{(n{\omega _\alpha })^{1/3}} \propto {\nu ^{2/3}}$ is observed by Zhou & White (2016) and White et al. (2019), and is approximately consistent with the larger TAE amplitude scaling found numerically by Slaby et al. (2018). Moreover, following Meng et al. (2018), White et al. (2019), and Duarte et al. (2019) by defining a nonlinear trapping frequency ${\omega _{\textrm{trapping}}} \equiv{-} {V_r}{h^{ - 1}}\partial h/\partial r\sim {V_r}/\delta$, leads to rewriting the critical balance estimate as ${\omega _{\textrm{trapping}}}\sim {\nu _{\textrm{eff}}}$, consistent with their numerical findings from the ORBIT code with a pitch angle scattering collision operator for a single mode at saturation. In addition, defining a linear drive rate ${\gamma _{\textrm{drive}}}$ by ${\gamma _{\textrm{drive}}}h \equiv{-} {V_r}\partial {f_0}/\partial r$, gives ${\gamma _{\textrm{drive}}}\sim {V_r}/\delta \sim {\omega _{\textrm{trapping}}}$.

The ${\nu _{\textrm{eff}}}$ in (2.17) is the same order as ${\nu _{\textrm{scatt}}}$ in Duarte et al. (2019). Consequently, using ${\omega _{\textrm{trapping}}}\sim {\nu _{\textrm{eff}}}$ and replacing their $\varOmega$ by $n{\omega _\alpha }$ and ${\omega _b}$ by ${\omega _{\textrm{trapping}}}$ in their QL result (13), leads to $h/{\kern 1pt} {f_0}\sim {(\nu /n{\omega _\alpha })^{1/3}}$ in agreement with (2.11), as shown schematically in figure 2. Interestingly, the Duarte et al. (2019) results employ the kinetic equation of Berk, Breizman & Petviashvili (1997) that does not allow a radial spatial drive as their $\varOmega$ is the velocity space variable of their model Fokker–Planck operator. In spite of this difference their result is in broad agreement with estimates (2.11) as $\delta \sim wa$ (although collisions refresh radial spatial gradients but do not restore velocity space inversions).

The trapped portion of the alpha particle diffusivity is estimated next, where the trapped fraction is ${\varepsilon ^{1/2}}$ with $\varepsilon$ the inverse aspect ratio. Only the resonant fraction w of the trapped alphas contributes to the transport, giving the fraction of the trapped particles in resonance with the wave to be $\varUpsilon \sim {\varepsilon ^{1/2}}w$. Using $\varDelta \sim \delta$ the trapped diffusivity ${D_t}$ can be written in different ways

(2.18)\begin{equation}{D_t}\sim {\varepsilon ^{1/2}}w\frac{{{\delta ^2}}}{\tau }\sim \frac{{{\varepsilon ^{1/2}}V_r^2}}{{n{\omega _\alpha }}}\sim \frac{{{\varepsilon ^{1/2}}{a^2}{\nu ^{4/3}}}}{{{{(n{\omega _\alpha })}^{1/3}}}}.\end{equation}

Notice that the form proportional to $V_r^2 \propto {({B_1}/{B_0})^2}$ is in agreement with Nagaoka et al. (2008). The detailed behaviour of the penultimate form is consistent with the QL evaluation by Tolman & Catto (2021), and the final form $(D \propto {\nu ^{4/3}})$ is particularly interesting and consistent with their estimate of the diffusivity when the TAEs reach a nonlinear saturated state.

To keep the birth alphas well confined, the number diffusing across the minor radius in a slowing down time ${\tau _s}$ must be small,

(2.19)\begin{equation}{D_t}{\tau _s}/{a^2}\sim {\varepsilon ^{1/2}}{\nu ^{4/3}}{\tau _s}/{(n{\omega _\alpha })^{1/3}} \ll 1,\end{equation}

where for birth alphas ${\omega _\alpha }\sim v_0^2/{\varOmega _p}{R^2}$ with ${\varOmega _p} = Ze{B_p}/Mc$ the poloidal alpha gyrofrequency. As $\nu {\tau _s}$, ${(\nu /n{\omega _\alpha })^{1/3}}$, and ${\varepsilon ^{1/2}}$ are each small, the trapped alphas are expected to be well confined in the presence of saturated TAE modes.

Tolman & Catto (2021) find that the passing transport due to an unstable mode is typically larger than that for the trapped alphas. The preceding estimates can be repeated for the passing alphas by letting $n{\omega _\alpha } \to {k_{||}}{v_{||}}\sim {v_0}/qR$ and ${\varepsilon ^{1/2}} \to 1$, with a related Su & Oberman (1968) form in the linear regime of

(2.20)\begin{equation}P \equiv \frac{1}{{{\rm \pi} w}}Re\int_0^\infty {\textrm{d}\kern0.06em x\,{\textrm{e}^{ - \textrm{i}ux - {x^3}/3}} = \frac{{{k_{||}}{v_ \bot }}}{{\rm \pi} }Re\int_0^\infty {\textrm{d}t} \,{\textrm{e}^{ - \textrm{i}({k_{||}}{v_{||}} - \omega )t - \nu k_{||}^2v_ \bot ^2{t^3}/3}}} ,\end{equation}

with $u = {({k_{||}}/v_ \bot ^2\nu )^{1/3}}({v_{||}} - \omega /{k_{||}})$ and $w = {(\nu /{k_{||}}{v_ \bot })^{1/3}}$. Collisions will cause any transient passing alpha behaviour to become unimportant within a few $\tau = \nu _{\textrm{eff}}^{ - 1} = {(\nu {\kern 1pt} k_{||}^2v_ \bot ^2)^{ - 1/3}}\sim {({q^2}{R^2}/\nu v_0^2)^{1/3}}$, while collisionless linear growth at the rate ${\gamma _L}$ at earlier times requires ${\gamma _L} \gg {\nu _{\textrm{eff}}}$. Recall that time scales longer than $\tau = \nu _{\textrm{eff}}^{ - 1}$ are of interest here, with full nonlinearity attained once the amplitude grows to ${\omega _{\textrm{trapping}}}\sim {\nu _{\textrm{eff}}}$.

As ${(\nu qR/{\kern 1pt} {v_0})^{1/3}} \ll 1$, a narrow collisional boundary layer is assured for the passing alphas, and the dimensionless diffusivity becomes

(2.21)\begin{equation}{D_p}{\tau _s}/{a^2}\sim {(\nu qR/{\kern 1pt} {v_0})^{1/3}}\nu {\tau _s}\sim {10^{ - 4}},\end{equation}

while

(2.22)\begin{equation}{B_1}/B\sim {(\nu qR/{v_0})^{2/3}}(a/{\kern 1pt} qR)\sim {10^{ - 5}},\end{equation}

in agreement with the Tolman & Catto (2021) results and again too small to be a concern. Therefore, in the presence of saturated TAE modes, the passing alphas are also expected to be well confined. For these estimates R = 10 m, B = 5 T, n = 20, and $\nu^{-1} \simeq 30\;s$ are used, with ${v_0} = 1.3 \times {10^9}\;\textrm{cm}\;{s ^{ - 1}}$ at birth.

The preceding estimates imply that when the nonlinear terms in the alpha kinetic equation enter to provide saturation of the TAE mode, the saturated amplitude will be so small that the associated radial transport will be negligible as suggested by the careful evaluations of Tolman & Catto (2021). Moreover, the amplitude at saturation is well below any level at which stochastic particle motion dominates so it can only enter at the same order as any other nonlinear mechanisms and can never be more important than collisions.

If ${D_p}$ and/or ${D_t}$ were to approach ${a^2}/{\tau _s}$, QL losses would modify ${f_0}$ for the birth alphas. However, doing so violates the narrow boundary layer treatment by requiring such strong collisions that ${(\nu qR/{\kern 1pt} {v_0})^{1/3}} \gg 1$ and/or ${(\nu /n{\omega _\alpha })^{1/3}} \gg 1$. Consequently, QL modifications to ${f_0}$ may be of limited utility (Gorelenkov et al. 2019).

The estimates for alpha particles may need to be refined substantially to address the more complex problem of neutral beam injected energetic particles driving TAEs, and perhaps for reverse shear AEs, as strong velocity space anisotropy can provide an additional destabilization mechanism. To date two different explanations have been put forth (Ghantous et al. 2012; Heidbrink et al. 2013; Collins et al. 2016, 2017). However, none of these treatments retain collisional boundary layer effects, which should be playing a role (Zhou & White 2016; White et al. 2019). In addition, the more recent interpretation (Collins et al. 2016, 2017) invokes stochastic particle orbits (at ${B_1}/B\sim {10^{ - 4}}$) based on using measurements to fit the neutral beam source and the fast ion thermalization sink in the continuity equation. The remaining radial flux term (which is found to diverge near the magnetic axis) is inferred using ideal magnetohyrodynamics (MHD) fields in a collisionless version of ORBIT to find radial transport losses that increase with neutral beam power and AE amplitude rather than the catastrophic loss expected at the onset of stochasticity (when there should be little or no thermalization sink).

3. Ripple transport of alphas

Very similar arguments to those in the preceding section are next used to make estimates for ripple transport in the superbanana plateau regime (Galeev et al. 1969; Shaing 2015; Catto 2019b). They allow a bound on the ripple amplitude to be estimated. Ripple transport of alphas is driven by the ${B_{||}}$ term in the radial drift (2.1) of the bounce or transit averaged kinetic equation (2.3) with $\omega = 0$. It is only an issue for trapped particles, as for them there is a zero when the tangential drift ${\omega _\alpha }$ reverses. Expanding about the pitch angle ${\lambda _0}$ and radius ${r_0}$ for which ${\omega _\alpha }({\lambda _0},{r_0}) = 0$ and assuming weak ripple, leads to

(3.1)\begin{equation}{\omega _\alpha } \simeq (\lambda - {\lambda _0})\partial {\omega _\alpha }/\partial {\lambda _0} + (r - {r_0})\partial {\omega _\alpha }/\partial {r_0}\sim w\partial {\omega _\alpha }/\partial {\lambda _0} + \delta \partial {\omega _\alpha }/\partial {r_0},\end{equation}

and the earlier Su & Oberman form (2.13) with the substitution ${\lambda _{\textrm{res}}} \to {\lambda _0}$ implying $P \to \delta (\lambda - {\lambda _0})\sim 1/w$. Then the replacement $n{\omega _\alpha } \to n\partial {\omega _\alpha }/\partial {\lambda _0}\sim nv_0^2/{\varOmega _p}{R^2}$ can be made in the trapped estimates of section 2. In this case only ${B_{||}}$ is retained as $\phi$ and ${A_{||}}$ vanish, leading to ${V_r}\sim (nv_0^2/{\varOmega _p}R){B_{||}}/B$. As a result, the saturation estimate ${V_r}\sim a{\nu ^{2/3}}{(n{\omega _\alpha })^{1/3}}$ must be modified and reinterpreted as the ripple amplitude at which a superbanana plateau treatment fails. Making these changes yields the new result that

(3.2)\begin{equation}{B_{||}}/B\sim (a/{\kern 1pt} R){(\nu R/{\kern 1pt} {v_0})^{2/3}}{(R{\varOmega _p}/n{v_0})^{2/3}}\sim {10^{ - 4}},\end{equation}

as the ripple threshold at which superbanana plateau evaluations will begin to fail because nonlinear radial drift departures from the flux surface will begin to enter, possibly causing the transport to enter a regime linear in collisionality similar to what was considered in Hazeltine & Catto (1981). The numerical estimate is again based on R = 10 m, B = 5 T, n = 20, and $\nu^{-1} \simeq 30\;\textrm{s}$, where the alpha birth speed is ${v_0} = 1.3 \times {10^9}\;\textrm{cm}\;{\textrm{s}^{ - 1}}$. For ripple the diffusivity is

(3.3)\begin{equation}{D_{\textrm{rip}}}\sim {\varepsilon ^{1/2}}wV_r^2/{\nu _{\textrm{eff}}}\sim {\varepsilon ^{1/2}}V_r^2/(n{\kern 1pt} \partial {\omega _\alpha }/\partial {\lambda _0})\sim {\varepsilon ^{1/2}}(nv_0^2/{\varOmega _p}){({B_{||}}/B)^2},\end{equation}

in agreement with the tokamak limit of scaling evaluated by Catto (2019b). However, for finite magnetic shear $s = r{q^{ - 1}}\partial q/\partial r\sim 1$, Tolman & Catto (2021) have shown that the sign reversal of the drift occurs very close to the trapped–passing boundary so that the resonant plateau and $\sqrt \nu$ (Calvo et al. 2017) transport regimes merge and this estimate becomes sensitive to shear.

Once again using $\partial {\omega _\alpha }/\partial {\lambda _0}\sim v_0^2/{\varOmega _p}{R^2}$ and then inserting ${({B_{||}}{\kern 1pt} /B)^2}$ suggests that superbanana plateau evaluations of ripple transport will fail only when the alpha diffusivity reaches very high levels

(3.4)\begin{equation}{D_{\textrm{rip}}}{\tau _s}/{a^2}\sim {\varepsilon ^{1/2}}\nu {\tau _s}{(\nu R/{v_0})^{1/3}}{({\varOmega _p}R/n{v_0})^{1/3}}\sim 1.\end{equation}

Such high levels of ripple transport of alphas will not occur in the core of any sensibly designed tokamak as ${B_{||}}/B\mathrm{\ \mathbin{\lower.3ex\hbox{$\buildrel< \over {\smash{\scriptstyle\sim}\vphantom{_x}}$}}\ }{10^{ - 4}}$, but may be possible in the lower collisionality regimes of optimized stellarators where larger departures from quasi-symmetry remain a challenge to completely remove (Landreman & Sengupta 2019).

4. Radio frequency heating and current drive

All rf heating and current drive is due to resonant wave-particle interactions which nonlinear affects may alter for strong applied fields. However, the estimates for rf are somewhat different as any spatial broadening of the resonance is negligible because QL spatial diffusion is weak (Catto & Tolman 2021). In this case, keeping the nonlinear term leads to considering a high frequency kinetic equation of the form

(4.1)\begin{equation}\frac{{\textrm{d}{f_1}}}{{\textrm{d}t}} + \boldsymbol{a}\boldsymbol{\cdot }{\nabla _v}({f_0} + {f_1}) = \nu v_{\textrm{th}}^2\frac{{{\partial ^2}{f_1}}}{{\partial v_{||}^2}},\end{equation}

where $v_{\rm th}$ is the species thermal speed, $\boldsymbol{a} = (Ze/M)(\boldsymbol{e} + {c^{ - 1}}\boldsymbol{v} \times \boldsymbol{b})$ is the acceleration due to the applied rf electric and magnetic fields $\boldsymbol{e}$ and $\boldsymbol{b}$, and $\textrm{d}{f_1}/\textrm{d}t = \partial {f_1}/\partial t + \boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{\nabla }{f_1}$.

Ignoring drifts and removing the adiabatic response using ${f_1} = h + (Ze\,{e_{||}}/ i\omega MB)\partial {f_0}/\partial \mu$, with ${e_{||}}$ the parallel component of $\boldsymbol{e}$, leads to the kinetic equation for the non-adiabatic irreversible response h (Catto et al. 2017; Catto 2020; Catto & Tolman 2021),

(4.2)\begin{equation}{\left. {\frac{{\textrm{d}h}}{{\textrm{d}t}}} \right|_{\textrm{res}}} + \boldsymbol{a}\boldsymbol{\cdot }\boldsymbol{v}\left[ {\frac{1}{v}\frac{{\partial {f_0}}}{{\partial v}} + \frac{{(\omega - {k_{||}}{v_{||}})}}{{\omega B}}\frac{{\partial {f_0}}}{{\partial \mu }}} \right] + \boldsymbol{a}\boldsymbol{\cdot }{\nabla _v}h \simeq \nu v_{\textrm{th}}^2\frac{{{\partial ^2}h}}{{\partial v_{||}^2}}.\end{equation}

In this case

(4.3)\begin{equation}{\left. {\frac{{\textrm{d}h}}{{\textrm{d}t}}} \right|_{\textrm{res}}}\sim (\omega - p\varOmega - {k_{||}}{v_{||}})h\sim {k_{||}}{v_{\textrm{th}}}wh,\end{equation}

with w the collisional boundary layer width, as the resonance is only broadened in velocity space by collisions. In addition,

(4.4)\begin{gather}\nu v_{\textrm{th}}^2{\partial ^2}h/\partial v_{||}^2\sim \nu h/{w^2},\end{gather}

(4.5)\begin{gather}\frac{{\partial {f_0}}}{{\partial v}} + \frac{{v(\omega - {k_{||}}{v_{||}})}}{{\omega B}}\frac{{\partial {f_0}}}{{\partial \mu }}\sim \frac{{{f_0}}}{{{v_{\textrm{th}}}}},\end{gather}

and

(4.6)\begin{equation}{\nabla _v}h\sim h/w{v_{\textrm{th}}}.\end{equation}

The nonlinear term $\boldsymbol{a}\boldsymbol{\cdot }{\kern 1pt} {\nabla _v}h$ causes a breakdown of QL theory for rf waves once the amplitude of the rf waves is large enough affect the balance in (4.2).

The preceding discussion implies the kinetic equation has four different terms when the applied rf amplitude is large enough for the nonlinear terms to enter. Therefore, a ‘resonant critical balance’ estimate yields

(4.7)\begin{equation}{k_{||}}{v_{\textrm{th}}}wh\sim |\boldsymbol{a}|({f_0} + {w^{ - 1}}h)/{v_{\textrm{th}}}\sim \nu h/{w^2}.\end{equation}

As usual, critical balance means that all terms compete and this time gives three conditions. One condition sets the boundary layer width w in velocity space and another sets the requirement for the non-adiabatic response h to remain small, leading to

(4.8)\begin{equation}w\sim h/{\kern 1pt} {f_0}\sim {(\nu /{k_{||}}{v_{\textrm{th}}})^{1/3}} \ll 1.\end{equation}

When the perturbed distribution function h is of the order indicated by (4.8) the nonlinear effects ignored by standard QL treatments may no longer be negligible.

The final condition is the rf acceleration amplitude $|\boldsymbol{a}|$ at which the applied rf becomes strong enough that nonlinear effects must be retained and a QL treatment starts to fail

(4.9)\begin{equation}|\boldsymbol{a}|/{k_{||}}v_{\textrm{th}}^2\sim {(\nu /{k_{||}}{v_{\textrm{th}}})^{2/3}} \ll 1.\end{equation}

Applied rf field amplitudes approaching or exceeding (4.9) may lead to substantial nonlinear modifications to the linear kinetic equation used to derive the QL operator.

To estimate the QL diffusivity observe that $|\boldsymbol{a}|\propto {\nu ^{2/3}}$ and $w\sim {(|\boldsymbol{a}|/{k_{||}}v_{\textrm{th}}^2)^{1/2}} \propto \sqrt {|\boldsymbol{a}|}$. Using ${\nu _{\textrm{eff}}}\sim \nu /{w^2}$ the velocity space QL diffusivity is

(4.10)\begin{equation}{D_{\textrm{ql}}}\sim |\boldsymbol{a}{|^2}/{\nu _{\textrm{eff}}}\sim |\boldsymbol{a}{|^2}/{\nu ^{1/3}}{({k_{||}}{v_{\textrm{th}}})^{2/3}}\sim \nu v_{\textrm{th}}^2.\end{equation}

When integrated over the boundary layer width w, the penultimate form of (4.10) is independent of $\nu$. The last estimate in (4.10) is obtained using (4.9).

To better understand the role of collisions in the linear response, notice that in the familiar constant magnetic field linear limit the kinetic equation

(4.11)\begin{equation}i(\omega - p\varOmega - {k_{||}}{v_{||}})h + \nu v_{\textrm{th}}^2\frac{{{\partial ^2}h}}{{\partial v_{||}^2}} = \boldsymbol{a}\boldsymbol{\cdot }\boldsymbol{v}\left[ {\frac{1}{v}\frac{{\partial {f_0}}}{{\partial v}} + \frac{{(\omega - {k_{||}}{v_{||}})}}{{\omega B}}\frac{{\partial {f_0}}}{{\partial \mu }}} \right] \equiv W,\end{equation}

is a Su & Oberman (1968) form with $u = {({k_{||}}/v_{\textrm{th}}^2\nu )^{1/3}}[{v_{||}} - (\omega - p\varOmega )/{k_{||}}] \equiv [{v_{||}} - (\omega - p\varOmega )/{k_{||}}]/{v_{\textrm{th}}}w$. Therefore, the solution is

(4.12)\begin{equation}h ={-} \frac{{W{w^2}}}{\nu }\int_0^\infty {\textrm{d}\kern0.06em x\,{\textrm{e}^{ - \textrm{i}ux - {x^3}/3}}} ,\end{equation}

and delta function behaviour $v_{\textrm{th}}\delta [{v_{||}}{\kern 1pt} - (\omega - p\varOmega )/{k_{||}}]\sim 1/{\kern 1pt} w$ again arises upon integration over velocity space, leading to a resonant plateau behaviour, where $w = {(\nu /{k_{||}}{v_{\textrm{th}}})^{1/3}}$. The detailed spatial variation of the linear fields for the resonant particles is modified by the collisional dependence of (4.12) even though the velocity space moments of h and QL diffusivity appear unchanged to lowest order.

All these estimates are consistent with the results in Catto (2020, 2021) and Catto & Tolman (2021). Moreover, the critical balance nature of the estimates here is consistent with the findings there that QL treatments will start to fail once the distribution function departs significantly from Maxwellian. This assertion is verified by allowing the QL operator $Q\{ {f_0}\} \sim {D_{\textrm{ql}}}{f_0}/v_{\textrm{th}}^2$ to compete with the collision operator,

(4.13)\begin{equation}{D_{\textrm{ql}}}{f_0}/v_{\textrm{th}}^2\sim \nu {f_0},\end{equation}

where $C\{ {f_0}\} \sim \nu {f_0}$ as no resonance occurs for the unperturbed distribution function. Condition (4.13) is the same as (4.10), which is when stochasticity and other nonlinear effects enter because the rf amplitude is large enough to satisfy (4.9). Consequently, (4.9) is an estimate of the applied rf field amplitude at which QL treatments of rf are expected to begin failing, as evidenced by a significant departure from Maxwellian.

5. Discussion

The preceding sections outline a simple resonant critical balance procedure for nonlinear kinetic equations that reproduces recent results within numerical coefficients and unimportant logarithmic factors for TAE and ripple transport, and rf heating and current drive. The procedure requires that the resonant particles be essential to the physical process of interest, that is, no instability or transport or heating and/or current drive occurs without them. In particular, the nonlinear bound on the saturated level of TAE transport leads to estimates of the passing and trapped alpha particle energy diffusivity at saturation that are consistent with and slightly extend the results of Tolman & Catto (2021). The need to retain collisions in narrow boundary layers about the resonant paths in velocity space enhances the role of collisions. There is no need to appeal to phenomenological velocity space diffusion caused by rf waves as in Fasoli et al. (1998), which, of course, will play no role in alpha particle driven TAE modes. Moreover, for the first time estimates are made of the ripple threshold at which superbanana plateau evaluations fail and the associated transport descriptions are unreliable due nonlinear radial drift effects. And finally, even though QL descriptions justifiably enjoy great success in modelling rf heating and current drive, the critical balance estimates here add to recent concerns (Catto 2020, 2021; Catto & Tolman 2021) as to possible limitations of QL treatments.

The procedure outlined here for making estimates is expected to be widely applicable when resonant wave–particle interactions are of essential importance. However, its usefulness is limited to situations in which the nonlinear terms enter to provide saturation rather than further destabilization. For example, NTMs are linearly stable, but driven unstable by nonlinear effects (La Haye 2006). Consequently, resonant plateau behaviour will play a different role for NTMs as the nonlinear estimation procedure here is only an indication of the onset of when nonlinear alpha effects enter and not when mode saturation occurs, as it does not include a mechanism to generate a finite amplitude seed field. In addition, the procedure does not hold when a separate external energy source maintains or creates a destabilizing phase space profile at saturation.

The wide applicability of resonant plateau behaviour outlined in the preceding sections implies that narrow collisional boundary layers act to allow the interplay of various nonlinear mechanisms to provide saturation and prevent stochastic particle motion from dominating. Simply stated, magnetic field line stochasticity is unlikely to dominate resonant wave-particle interactions in the weakly collisional plasmas of interest to magnetic fusion.