Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-14T06:37:48.375Z Has data issue: false hasContentIssue false
  • English
  • Français

Collisional effects on resonant particles in quasilinear theory

Published online by Cambridge University Press:  11 May 2020

Peter J. Catto Open the ORCID record for Peter J. Catto [Opens in a new window]
Peter J. Catto*
Affiliation:
Plasma Science and Fusion Center, Massachusetts Institute of Technology, Cambridge, MA02139, USA
*
†Email address for correspondence: catto@psfc.mit.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

A careful examination of the effects of collisions on resonant wave–particle interactions leads to an alternate interpretation and deeper understanding of the quasilinear operator originally formulated by Kennel & Engelmann (Phys. Fluids, vol. 9, 1966, pp. 2377–2388) for collisionless, magnetized plasmas, and widely used to model radio frequency heating and current drive. The resonant and nearly resonant particles are particularly sensitive to collisions that scatter them out of and into resonance, as for Landau damping as shown by Johnston (Phys. Fluids, vol. 14, 1971, pp. 2719–2726) and Auerbach (Phys. Fluids, vol. 20, 1977, pp. 1836–1844). As a result, the resonant particle–wave interactions occur in the centre of a narrow collisional boundary when the collision frequency $\unicode[STIX]{x1D708}$ is very small compared to the wave frequency $\unicode[STIX]{x1D714}$. The diffusive nature of the pitch angle scattering combined with the wave–particle resonance condition enhances the collision frequency by 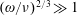$(\unicode[STIX]{x1D714}/\unicode[STIX]{x1D708})^{2/3}\gg 1$, resulting in an effective resonant particle collisional interaction time of 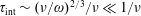$\unicode[STIX]{x1D70F}_{\text{int}}\sim (\unicode[STIX]{x1D708}/\unicode[STIX]{x1D714})^{2/3}/\unicode[STIX]{x1D708}\ll 1/\unicode[STIX]{x1D708}$. A collisional boundary layer analysis generalizes the standard quasilinear operator to a form that is fully consistent with Kennel–Englemann, but allows replacing the delta function appearing in the diffusivity with a simple integral (having the appropriate delta function limit) retaining the new physics associated with the narrow boundary layer, while preserving the entropy production principle. The limitations of the collisional boundary layer treatment are also estimated, and indicate that substantial departures from Maxwellian are not permitted.

Keywords

plasma heatingplasma nonlinear phenomenaplasma waves
Type
Research Article
Information
Journal of Plasma Physics , Volume 86 , Issue 3 , June 2020 , 815860302
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Auerbach, S. P. 1977 Collisional damping of Langmuir waves in the collisionless limit. Phys. Fluids 20, 1836–1844.CrossRefGoogle Scholar
Becoulet, A., Gambier, D. J. & Samain, A. 1991 Hamiltonian theory of the ion cyclotron minority heating dynamics in tokamak plasmas. Phys. Fluids B 3, 137–150.CrossRefGoogle Scholar
Catto, P. J. 1978 Linearized gyrokinetics. Plasma Phys. 20, 719–722.CrossRefGoogle Scholar
Catto, P. J. 2019 Collisional alpha transport in a weakly non-quasisymmetric stellarator magnetic field. J. Plasma Phys. 85, 905850213; corrigendum 85, 945850501.Google Scholar
Catto, P. J., Lee, J. P. & Ram, A. K. 2017 A quasilinear operator retaining magnetic drift effects in tokamak geometry. J. Plasma Phys. 83, 905830611 (29 pp).CrossRefGoogle Scholar
Catto, P. J. & Myra, J. R. 1992 A quasilinear description for fast wave minority heating permitting off magnetic axis heating in a tokamak. Phys. Fluids B 4, 187–199.CrossRefGoogle Scholar
Eriksson, L.-G., Mantsinen, M. J., Hellsten, T. & Carlsson, J. 1999 On the orbit-averaged Monte Carlo operator describing ion cyclotron resonance frequency wave–particle interaction in a tokamak. Phys. Plasmas 8, 513–518.CrossRefGoogle Scholar
Hinton, F. L. & Hazeltine, R. D. 1976 Theory of plasma transport in toroidal confinement systems. Rev. Mod. Phys. 48, 239–308.CrossRefGoogle Scholar
Jaeger, E. F., Harvey, R. W., Berry, L. A., Myra, J. R., Dumont, R. J., Phillips, C. K., Smithe, D. N., Barrett, R. F., Batchelor, D. B., Bonoli, P. T. et al. 2006 Global-wave solutions with self-consistent velocity distributions in ion cyclotron heated plasma. Nucl. Fusion 46, S397–S408.CrossRefGoogle Scholar
Johnson, T., Hellsten, T. & Eriksson, L.-G. 2006 Analysis of a quasilinear model for ion cyclotron interactions in tokamaks. Nucl. Fusion 46, S433–S441.CrossRefGoogle Scholar
Johnston, G. L. 1971 Dominant effects of Coulomb collisions on maintenance of Landau damping. Phys. Fluids 14, 2719–2726.CrossRefGoogle Scholar
Kennel, C. F. & Engelmann, F. 1966 Velocity space diffusion from weak plasma turbulence in a magnetic field. Phys. Fluids 9, 2377–2388.CrossRefGoogle Scholar
Lamalle, P. U. 1997 On the radiofrequency response of tokamak plasmas. Plasma Phys. Control. Fusion 39, 1409–1460.CrossRefGoogle Scholar
Lee, J. P., Wright, J., Bertelli, N., Jaeger, E. F., Valeo, E., Harvey, R. & Bonoli, P. 2017 Quasilinear diffusion coefficients in a finite Larmor radius expansion for ion cyclotron heated plasmas. Phys. Plasmas 24, 052502 (15 pp).CrossRefGoogle Scholar
Lee, X. S., Myra, J. R. & Catto, P. J. 1983 General frequency gyrokinetics. Phys. Fluids 26, 223–229.CrossRefGoogle Scholar
Parra, F. I. & Catto, P. J. 2008 Limitations of gyrokinetics on transport time scales. Plasma Phys. Control. Fusion 50, 065014 (23 pp).CrossRefGoogle Scholar
Su, C. H. & Oberman, C. 1968 Collisional damping of a plasma echo. Phys. Rev. Lett. 20, 427–429.CrossRefGoogle Scholar