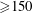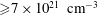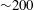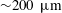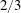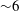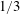Conceptual design of initial opacity experiments on the national ignition facility

Abstract

Accurate models of X-ray absorption and re-emission in partly stripped ions are necessary to calculate the structure of stars, the performance of hohlraums for inertial confinement fusion and many other systems in high-energy-density plasma physics. Despite theoretical progress, a persistent discrepancy exists with recent experiments at the Sandia Z facility studying iron in conditions characteristic of the solar radiative–convective transition region. The increased iron opacity measured at Z could help resolve a longstanding issue with the standard solar model, but requires a radical departure for opacity theory. To replicate the Z measurements, an opacity experiment has been designed for the National Facility (NIF). The design uses established techniques scaled to NIF. A laser-heated hohlraum will produce X-ray-heated uniform iron plasmas in local thermodynamic equilibrium (LTE) at temperatures ${\geqslant}150$ eV and electron densities ${\geqslant}7\times 10^{21}~\text{cm}^{-3}$. The iron will be probed using continuum X-rays emitted in a ${\sim}200$ ps, ${\sim}200~\unicode[STIX]{x03BC}\text{m}$ diameter source from a 2 mm diameter polystyrene (CH) capsule implosion. In this design, $2/3$ of the NIF beams deliver 500 kJ to the ${\sim}6$ mm diameter hohlraum, and the remaining $1/3$ directly drive the CH capsule with 200 kJ. Calculations indicate this capsule backlighter should outshine the iron sample, delivering a point-projection transmission opacity measurement to a time-integrated X-ray spectrometer viewing down the hohlraum axis. Preliminary experiments to develop the backlighter and hohlraum are underway, informing simulated measurements to guide the final design.

1 Introduction

In typical stars, radiation flow out of the fusion core is mediated by the opacity of the higher-Z impurities in the stellar plasma, since ions with more bound electrons have greater probability of absorbing and re-emitting photons, thus impeding radiative energy transfer. As radiation diverging from the stellar core flows through progressively cooler plasma, ions begin to accumulate bound electrons, and the opacity of the plasma rises. A fundamental transition region, the ‘R-C Boundary’, is formed when the opacity becomes large enough that radiative processes must give way to convective heat transfer. In the sun, the R-C Boundary occurs at approximately 70 % of the solar radius, at plasma temperatures around 190 eV (Bahcall & Pinsonneault 1995; Turck-Chiéze & Couvidat 2011).

In the 1980s and 1990s, improvements in many-body atomic physics led to significant refinement of opacity calculations (Rogers & Iglesias 1994), which were validated at relatively low temperatures ( ${<}100$  eV) by several experiments, (e.g. Davidson et al. 1988; Springer et al. 1992; Perry et al. 1996) and one might have considered opacity to be ‘solved’. However, experiments have only recently been able to access the higher temperatures needed to validate solar opacity models (Bailey et al. 2007).

Recent measurements using the Z facility at Sandia National Laboratories in the United States have found anomalously low transmission (high opacity) through X-ray-heated iron samples at near-local-thermodynamic-equilibrium (LTE) conditions over a broad portion of the iron L-shell spectrum (Bailey et al. 2015). Earlier measurements at less extreme conditions ( $T=156$  eV, $n_{e}=7\times 10^{21}~\text{cm}^{-3}$ ) showed good agreement with theory (Bailey et al. 2007), but the recent measurements at higher density (up to $4\times 10^{22}~\text{cm}^{-3}$ ) and temperature (up to 195 eV) diverge from theory by up to a factor of two, despite extensive efforts to root out potential systematic errors. Iron (and nearby abundant metals) are of particular interest for the R-C Boundary of the sun, because they have significant numbers of bound electrons in L-shell charge states, e.g. the Ne-like, F-like and O-like ions, and the transition energies of these charge states enhance the opacity significantly in a portion of the spectrum significant for radiative transfer at temperatures around 150–200 eV. Oxygen’s K-shell charge states are thought to contribute the most to the Rosseland mean opacity of the sun at the R-C Boundary itself, but iron is a close second, and plays a strong role inward from the R-C Boundary (Turck-Chiéze et al. 2010).

When a careful experiment disagrees with an established theory, an independent replication of the experiment becomes necessary. The National Ignition Facility (NIF) (Miller, Moses & Wuest 2004a , b ; Haynam et al. 2007) currently appears to be the most capable alternative to Z for producing mm-scale iron samples at these conditions, and for measuring the opacity of these samples with precision comparable to that achieved at Z. This motivates the current experimental design. But it should be noted that this is only one approach to using an energetic laser to measure opacities. Given the significance of the problem and the need to probe conditions down to the solar core, it is worth exploring and eventually developing multiple techniques for generating hot, dense LTE plasmas, using multiple facilities. Recent possibilities include supersonic radiation fronts (Keiter, Mussack & Klein 2013), double ablation fronts, (Le Pennec et al. 2015) or, less recently but in a more extreme departure from past techniques, axisymmetric cylindrical implosions (Rose 2005).

2 Experimental approach

Although there are a large number of ways to use a large multi-beam laser to heat a sample and produce a transmission spectrum, this design has focused on reducing development time and risk by adapting existing, successful techniques from prior opacity measurements, and attempting to avoid issues uncovered on less-successful prior measurements. Figure 1 illustrates the approach chosen here.

Figure 1. NIF Opacity Platform. A capsule backlighter transmits X-rays axially through a hohlraum-heated sample to a spectrometer in the upper pole.

NIF’s design is well suited to heat gold or uranium-walled hohlraums ${>}4$  mm in diameter using 500 kJ or more of laser energy, making it relatively straightforward to scale up prior hohlraum-based opacity measurements. The prior experiments used 10–40 kJ from the HELEN, Nova or Omega lasers to heat 1.0–2.5 mm diameter hohlraums up to ${\sim}100$  eV (e.g. Davidson et al. 1988; Perry et al. 1996). The choice of axial rather than orthogonal backlighting is motivated by a desire to retain two-dimensional (2-D) cylindrical geometry to simplify integrated target calculations, and also the fact that axial backlighting on NIF can be accomplished with a much simpler laser–target configuration.

The NIF design uses the point-projection approach to opacity measurements, in which a very small, very brief, broadband X-ray source projects an absorption spectrum onto a time-integrated detector (Perry et al. 1996). In this technique, the X-ray transmission, $T$ , of a uniform sample follows the relation

(2.1) $$\begin{eqnarray}T(h\unicode[STIX]{x1D708})=\exp [-\unicode[STIX]{x1D70C}L\unicode[STIX]{x1D705}(h\unicode[STIX]{x1D708})],\end{eqnarray}$$

where $h\unicode[STIX]{x1D708}$ is the photon energy, $\unicode[STIX]{x1D70C}$ is the plasma density in $\text{g}~\text{cm}^{-3}$ , $L$ is the path length through the sample in cm and $\unicode[STIX]{x1D705}(h\unicode[STIX]{x1D708})$ is the opacity (mass absorption coefficient of X-rays) as a function of photon energy in $\text{cm}^{2}~\text{g}^{-1}$ . From this relationship the opacity $\unicode[STIX]{x1D705}$ can be extracted as $\unicode[STIX]{x1D705}=-\ln (T)/\unicode[STIX]{x1D70C}L$ , and compared to that calculated theoretically, provided the sample plasma is in or very near LTE. Typical experimental values for the present design (see below for details) are $h\unicode[STIX]{x1D708}$ from 500–2000 eV, $\unicode[STIX]{x1D70C}$ of 0.04– $0.2~\text{g}~\text{cm}^{-3}$ and $L$ of 10–100  $\unicode[STIX]{x03BC}\text{m}$ .

The logarithmic dependence of $\unicode[STIX]{x1D705}$ on $T$ implies that the opacity can be measured most accurately when $T$ is neither too small ( ${<}0.2$ ) or too large ( ${>}0.6$ ). At small values of $T$ , the experimental uncertainty $\unicode[STIX]{x0394}T$ becomes comparable to $T$ and results in a large uncertainty in $\unicode[STIX]{x1D705}$ due to the rapid divergence in $\ln (T)$ . For $T$ near unity, $\ln (T)$ approaches zero, $\text{d}(\ln (T))/\text{d}T$ approaches unity and the uncertainty $\unicode[STIX]{x0394}T$ again translates into $\unicode[STIX]{x0394}\unicode[STIX]{x1D705}$ that is large relative to $\unicode[STIX]{x1D705}$ . As a useful rule of thumb, for $0.2<T<0.6$ , a transmission uncertainty $\unicode[STIX]{x0394}T<0.02$ (absolute) translates into an uncertainty in $\ln (T)$ of 7 % (relative). Including a relative uncertainty of 7 % for the sample’s areal density $\unicode[STIX]{x1D70C}L$ , this implies that a transmission uncertainty $\unicode[STIX]{x0394}T<0.02$ is adequate to measure the opacity $\unicode[STIX]{x1D705}$ to 10 % precision at each point in the spectrum.

To measure the L-shell opacity of iron relevant to the solar opacity problem, the experiment must work at relatively low photon energies, where hohlraum emission and sample self-emission can both contribute significant background signals (Springer et al. 1994). This is particularly important in the NIF design, which at least initially will use a time-integrated detector (X-ray film or imaging plate). These detectors have wider dynamic range, better spatial resolution and greater ease of calibration relative to time-resolved detectors (microchannel plate framing cameras), but where the self-emission of the target is significant relative to the backlighter, care must be taken to correct for all the sources of background emission. The NIF design is able to accomplish this as shown in figure 2 and detailed below.

As shown in figure 2, the point-like backlighter source at bottom projects X-rays through an aperture plate (collimator), into the laser-heated hohlraum oven and through or around the opacity sample inside the hohlraum. The backlighter X-rays, along with self-emission from the sample and hohlraum, then diffract off a Bragg crystal (at ${\sim}570$  mm), onto the detector (at ${\sim}630$  mm). On the detector, the region marked ‘U’ shows the umbra of the shadow made by the opacity sample, ‘P $_{\text{1}}$ ’ is the associated penumbra, ‘V’ is the region which directly views the backlighter, ‘P2’ is its associated penumbra, ‘E’ sees the emission from the hohlraum and sample but is blocked by the collimator from seeing the backlighter and ‘G’ records instrumental backgrounds. The detector may be either X-ray film or imaging plate and is time integrated. The backlighter X-rays passing around the sample on both sides provide information on the unattenuated backlighter spectrum, but since the backlighter’s X-ray pulse is much shorter than the hohlraum’s emission, the self-emission contributes a significant amount of signal on the detector and requires a correction.

Figure 2. NIF point-projection geometry raytrace. Plotted above is a planar cross-section of the NIF opacity target-diagnostic geometry, showing how a point-projection approach may deliver the key quantities for a transmission measurement. This cross-section features the space-resolving dimension of the spectrometer and the vertical symmetry axis of the target; the spectrally resolving dimension lies in and out of the page. Since the geometry is symmetric about the vertical axis, only half of the system is shown. The inset enlarges the target region to show the backlighter, collimator, hohlraum exterior and sample in more detail. In both plots the horizontal scale has been greatly enlarged ( ${\sim}10\times$ ) for clarity.

This time-integrated point-projection approach delivers the X-ray transmission, and thus the opacity, from the following relationship:

(2.2) $$\begin{eqnarray}T=(U-E)/(V-E).\end{eqnarray}$$

The analysis of the point-projection data starts with the umbral region $U$ , and subtracts off the hohlraum and sample emission from region $E$ , to extract the absorption spectrum which passed through the sample. Assuming that the backgrounds $G$ are spatially uniform across the entire detector, this correction also eliminates the backgrounds common to regions $G$ , $U$ and $E$ . Similarly the backlighter-viewing region $V$ is corrected by subtracting $E$ (and backgrounds) to obtain the original backlighter spectrum.

Instrument backgrounds may include contributions arising from non-Bragg scattering, hard X-ray fluorescence, film fog and so on. Minimizing these contributions will improve the accuracy of the transmission analysis by reducing statistical noise arising from the background subtractions. The above equation assumes that the background contributions contaminate both the umbral and backlighter-viewing spectra equally; if not, a more complex analysis of the data would be required.

Minimizing $\unicode[STIX]{x0394}T$ to below 0.02 places requirements on the photometrics of the backlighter, emission and absorption measurements, which are discussed in § 7. Of potential interest, the hohlraum and sample emission may be separable, and the time-integrated sample self-emission may itself provide an additional constraint on the opacity models, provided the time history of the plasma conditions can be accurately determined.

3 Hohlraum and sample design

The initial design for this experiment adapts the classic ‘Nova Opacity’ design (Perry et al. 1996), which has two laser entrance chambers on either side of a central sample chamber. The opacity sample itself sits in the centre of the sample chamber, and is expected to be similar to that used at Z, namely an iron–magnesium or iron–aluminium mixture embedded in a low-Z ‘tamper’ made of plastic or beryllium, which slows the expansion of the X-ray-heated iron and ensures a uniform plasma density. In the ‘Nova-style’ design, two annular rings separate each end of the sample chamber from the laser entrance cavities, and protect the sample from seeing the non-LTE gold M-band X-ray emission from the laser-heated hohlraum walls. The annular shield rings come at a significant price in terms of central cavity temperature, but ensure that the X-ray-heated sample is truly in LTE conditions. Figure 3 illustrates this hohlraum, in a design tailored for initial scoping experiments.

Figure 3. NIF-scale ‘Nova style’ opacity hohlraum. This hohlraum is 5.75 mm in diameter, 10 mm in length, with 3.1 mm laser entrance holes and 2.3 mm diameter interior shield holes. This particular design uses conical exterior shields to block a radiation temperature diagnostic from seeing into the laser entrance holes, allowing the central cavity temperature to be measured through the small black viewing hole just above the lower (red) shield ring.

Pre-shot simulations of the 5.75 mm diameter ‘Nova-style’ NIF hohlraum have been performed by two of the authors (Dodd and DeVolder) using the 2-D radiation hydrodynamics code LASNEX and assuming 500 kJ of laser heating for 3 ns (250 kJ into each laser entrance hole, or ‘LEH’). The simulation also assumes planar foil sample placed across the midplane of the hohlraum. The simulation obtains a radiation temperature at the sample ranging from 150–175 eV from 2–3 ns. While it is hoped that innovative future designs will achieve even better performance, this initial design already appears adequate to replicate the conditions of the earlier Z experiments, and to begin probing the regime in which the Z data disagree with theory. The detailed design of the samples for NIF is underway but it is expected that the samples will be similar to those on Z: a thin layer of iron:magnesium mixture coated onto a ${\sim}10~\unicode[STIX]{x03BC}\text{m}$ thick plastic substrate and overcoated with an additional 10  $\unicode[STIX]{x03BC}\text{m}$ of plastic.

Figure 4. Initial concept of the LampShade hohlraum for opacity measurements. The hohlraum’s outer wall is shown as mesh to illustrate the interior conical shields. The hohlraum is 5.75 mm in diameter, 10 mm long, with 4.6 mm diameter laser entrance holes. External shields serve the same purpose as those shown in figure 3.

It should be noted that one trade-off in the axial transmission approach is that gold plasma from the laser-heated spots near the ends of the hohlraum will flow towards and stagnate on the axis of the hohlraum, possibly becoming dense enough after 2–3 ns to block the axial transmission measurement. This ‘gold stagnation’ problem has been addressed already in the context of inertial confinement fusion research, and can be mitigated through a combination of larger entrance chambers, shorter laser pulses, filling of the hohlraum with low-Z gas that holds back the laser-heated plumes from the walls, and/or filling of the hohlraum with low-Z material (e.g. plastic) from a lining on either the laser entrance holes or the walls of the hohlraum. It is presently expected that lining the LEH and tailoring the shape of the hohlraums will be sufficient for the opacity experiments.

An additional, novel hohlraum design, expected to reduce the axial stagnation and potentially achieve higher sample temperature, is shown in figure 4. This ‘LampShade’ hohlraum has the same exterior dimensions as the ‘Nova-style’ design, but replaces the annular interior shield rings with conical sections resembling household lamp shades. As in the ‘Nova-style’ design, these shields prevent the central sample from seeing laser-heated hot spots, but in addition they deflect plasma filling to slow down the gold stagnation. The design shown in figure 4 also achieves sample temperatures of 170 eV in LASNEX simulations with 500 kJ of laser heating in 3 ns, despite losing significantly more energy out the larger laser entrance cavities. (The laser entrance holes on this initial design were 4.6 mm in diameter, versus 3.1 mm on the Nova-style hohlraum.) Areas for future work include the refinement and optimization of this design along with the Nova-style design, and also detailed design of the tamped iron samples.

4 Backlighter design

In a point-projection absorption spectroscopy experiment, the backlighter is required to deliver a pulse of X-rays significantly shorter than the sample lifetime ( ${\sim}1$  ns), from a source significantly smaller than the sample ( ${\sim}1~\text{mm}^{2}$ ). To obtain a high-quality absorption spectrum, the backlighter must nonetheless deliver more total X-ray flux than the sample self-emission, at least in the spectral range of interest. As an upper limit for the self-emission from a mm-scale sample in a NIF opacity hohlraum, one can assume a blackbody at the sample temperature (e.g. $T\sim 150$  eV) with a duration matching the hohlraum drive (2–3 ns). It follows that the sample self-emission can be nearly $0.5~\text{J}/\text{eV}/\text{sr}$ , or 1–2 kJ total over the spectral band of interest from ${\sim}500$ –2000 eV as described below. The backlighter must be at least this bright. Considering laser-to-X-ray conversion efficiencies, this implies that a significant fraction of NIF’s laser energy must drive the backlighter.

Prior experiments at the laser systems HELEN and Nova used quasi-continuum emission from a high-Z coated fibre backlighter source, illuminated by a tightly focused laser beam (Davidson et al. 1988; Perry et al. 1996). However, on NIF it is advantageous to avoid removing the standard laser phase plates, which is very time consuming. This limits the laser beams to spots ${>}1$  mm in diameter for nearly all beams. Obtaining a tight focus is possible for a small number of beams, but then the backlighter would not be bright enough. Furthermore, because of the stringent photometric requirements of a precise opacity measurement, a premium is placed on having a spectrally uniform ‘true continuum’ X-ray source, rather than a quasi-continuum with potentially unresolved spectral structure. Fortunately it is possible to use a NIF-scale version of the direct-drive plastic capsule backlighters developed for transmission spectroscopy measurements at the Omega laser (Yaakobi et al. 2003; Hansen et al. 2008; Ping et al. 2013).

Capsule implosions have three attractive properties as opacity backlighters: (i) sufficiently small size, ${\sim}100$ –200  $\unicode[STIX]{x03BC}\text{m}$ full-width at half-max, to support point-projection measurements on mm-scale samples; (ii) sufficiently brief duration, ${\sim}200$  ps, to ‘gate’ the transmission measurement even using a time-integrated detector; and (iii) the ability to tailor the output spectrum by careful selection of backlighter material. In the X-ray band of interest here (approximately 500–2000 eV), high-purity plastics are especially attractive because they contain no higher-Z materials that would create line structures conflicting with the material to be measured. Diamond and beryllium are also attractive materials for this application, but plastic shells can be produced at much lower cost and in a range of diameters and thicknesses. Use of an oxygen-free pure-CH plastic (such as polystyrene) is preferred to oxygen-bearing plastics such as polyester (Mylar) or polyimide (Kapton), because a backlighter spectrum free of oxygen lines potentially enables the oxygen contamination of the opacity sample itself to be assessed spectroscopically, in situ on the laser shot. There is a trade-off in this approach, which is that polystyrene shells do not hold gas fills, so the spectral output must derive entirely from the plastic shell itself.

Figure 5. (main) One-dimensional HYDRA pre-shot simulation of capsule implosion X-ray emission (backlighter source) versus time from start of laser pulse, showing source duration of ${\sim}200$  ps. Solid trace is emission at X-ray energies ${>}700$  eV, relevant to iron opacity measurement; dashed curve shows total emission including lower-energy emission. (inset) Laser intensity ( $\text{TW}~\text{cm}^{-2}$ ) versus position on a 2.0 mm diameter capsule, as viewed from a point above the equator, showing polar-hot drive (‘pancake’ implosion) using 64 NIF beams.

Figure 5 summaries the NIF capsule backlighter design. Laser light ablating a plastic shell 2 mm in diameter and ${\sim}20~\unicode[STIX]{x03BC}\text{m}$ thick drives an implosion which produces a hot, compressed core that in turn emits a bright X-ray flash. Geometrically, the NIF beams are classified as either ‘inner cone’ (64 beams) or ‘outer cone’ (128 beams) based on their angle of propagation with respect to the hohlraum axis. The inner cone beams, 23– $30^{\circ }$  off-axis, are difficult to couple to the hohlraum walls, so they are used to drive the backlighter with $1/3$ of NIF’s energy. Four of the authors (Craxton, McKenty, Zhang and Garcia) have done 2-D laser-pointing optimization and coupling calculations to support this design, and a fifth (Liedahl) has done 1-D radiation hydrodynamics simulations to estimate the X-ray yield and duration to assist in laser pulse shaping. The simulations reveal a significant amount of emission from 0.5 to 2.5 ns, as the laser ablates the plastic shell, prior to the core flash at ${\sim}2.7$  ns. The simulated core flash, ${\sim}200$  ps in duration and ${\sim}100~\unicode[STIX]{x03BC}\text{m}$ in diameter, is dominated by the opacity-relevant ‘harder’ x-rays (energies ${>}700$  eV), while the earlier ‘run-in’ is a mixture of ‘harder’ and ‘softer’ X-rays (below 700 eV) including carbon K-shell emission from the plastic shell material. Since the capsule is accelerated by ablation (inverse rocket effect), the run-in emission occurs mainly at high radius ( ${>}0.8$  mm). The collimator’s 0.5 mm aperture (see figure 2) also blocks the axial spectrometer from seeing nearly all the run-in emission, so the transmission spectrum is almost entirely obtained during the brief period of the core flash. The $20~\unicode[STIX]{x03BC}\text{m}$ thickness is nearly optimal for this laser set-up: significantly thicker shells (e.g. 30–40  $\unicode[STIX]{x03BC}\text{m}$ thick) will not accelerate as much, resulting in weaker output; thinner shells will be fully ablated (‘burn through’) before imploding, also resulting in weaker output.

Given the 2-D nature of the laser drive, actual capsule performance is expected to differ somewhat from the 1-D simulation. The non-uniform illumination shown in the inset to figure 5 leads to a ‘pancake’ implosion whose core is elongated normal to the transmission axis. This is expected to increase the backlighter source diameter and duration, reduce the core temperature and total X-ray yield, but should have the beneficial effects of (i) beaming more X-rays along the axis of the experiment since more of the emitting surface is visible from the axis, and (ii) spoiling very-hard X-ray output which would cause undesirable background in the spectrometer. Results of experiments to establish the actual capsule performance are being prepared for publication (Opachich et al. 2017).

5 Instrumentation and diagnosis of plasma conditions

The iron L-shell transitions of interest in replicating the Z opacity measurement span a broad spectral range from ${\sim}700$ to ${>}1300$  eV in photon energy. To infer the temperature and density of the sample, the NIF experiment will follow the Z experiment and include either Mg or Al co-mixed into in the sample, to use the well-understood characteristics of the K-shell line absorption as diagnostics. In particular, temperature is inferred from the ionization balance, and density from Stark broadening of the line profiles (Bailey et al. 2009). These transitions extend up to around 2000 eV and have only minimal interference with the iron spectral features.

In addition to iron, L-shell spectra of nearby elements such as chromium and nickel are also of interest, both in their own right and to assess potential systematic issues with the iron data. For a given density and temperature, chromium ions will have somewhat fewer bound electrons and nickel somewhat more compared to iron, so changes in the spectra when switching from one material to the next can be a sensitive test of the opacity models.

Figure 6. Conceptual design of NIF Opacity Spectrometer, showing X-ray paths (red) from a source at the origin, diffracted off either of two cylindrical Bragg crystals (mounted onto green circle; active region black), and recorded onto either of two $180\times 35$  mm pieces of X-ray film (dashed horizontal line). The instrument housing is not shown but is constrained by the DIM boundary and laser stay-out zone shown in blue.

To encompass these options and provide an absolute wavelength calibration using the K-edge of oxygen, the NIF Opacity Spectrometer (OpSpec) is being designed to view X-rays from 540 to 2100 eV. The OpSpec’s conceptual layout is shown in figure 6, featuring the spectrally resolved direction (vertical at crystal, horizontal at film) with the source to the left. OpSpec is designed to fit into NIF’s polar (axial) diagnostic instrument manipulator (Polar DIM). A convex, cylindrically curved crystal is used, similar to the Sandia TIXTL opacity spectrometers used on Z (Bailey et al. 2008) and in the tradition of the Henway design fielded on Nova and Omega (Koppel & Eckels 1977).

A key feature of this broadband spectrometer design is that it allows both the iron opacity and the K-shell diagnostic lines to be measured simultaneously, on every shot, in absorption and thus time gated by the backlighter, using only a single instrument on a single line of sight. OpSpec’s expected resolving power, $E/\unicode[STIX]{x0394}E\sim 1000$ , is comparable to that of the instruments used on Z, and on NIF the short duration of the capsule backlighter flash also minimizes any averaging over time-varying plasma conditions. OpSpec on NIF should therefore be capable of inferring the plasma conditions with comparable accuracy to the Z measurements, using the K-shell lines of the co-mixed Mg or Al in the sample.

Details of the instrument design and engineering have been published separately (Ross et al. 2015, 2016) but a few aspects of the design are worth mentioning since they extend the capability of NIF to perform opacity experiments. The axial orientation of the spectrometer is driven by the axially symmetric laser–target geometry on NIF. Obtaining the full spectrum from 540 to 2100 eV requires a wide range of Bragg angles, which implies placing the detector to the side. For this geometry, crystals made of potassium acid phthalate (KAP) provide the required spectral coverage. To increase the imaging area to 70 mm as in figure 2, and to take advantage of the experiment’s axial symmetry, two separate crystals and two pieces of film (or imaging plate) are positioned side by side (in-and-out of the page in this view). This creates the possibility of measuring simultaneously the transmission through two separate samples, possibly with two different compositions or thicknesses, to assess systematic effects that might compromise the measurement. In particular, equation (2.1) above implies that measurements of otherwise-identical samples with two different thicknesses, $L_{1}$ and $L_{2}$ , should yield different transmissions, $T_{1}$ and $T_{2}$ , in the ratio $T_{2}=T_{1}^{(L_{2}/L_{1})}$ (Bailey et al. 2009). The NIF experiment should be able to record two transmission spectra on a single shot, and if they follow this relationship as on prior experiments (Perry et al. 1996) this provides greater confidence in the accuracy of the measurements.

To assess possible systematic errors in the Z approach, additional measurements are possible on NIF, in addition to the OpSpec absorption spectra. In particular, to verify the Stark broadening technique for inferring density from absorption spectra, the sample density on NIF can also be extracted from time-resolved images of the sample (both edge on and face on), using the measured expansion over time relative to the known initial size and density. To reach the conditions of the lower-temperature Z experiments (Bailey et al. 2007), samples on NIF must expand ${\sim}50~\unicode[STIX]{x03BC}\text{m}$ , so a 20 % uncertainty in density is possible assuming expansion measurements with 5–10  $\unicode[STIX]{x03BC}\text{m}$ spatial resolution. The expansion measurement also verifies the uniformity of the sample, since the integrated X-ray emission along each ray through the sample depends strongly on the uniformity of the plasma conditions. This measurement can potentially be made with either a time-gated, bandpass-filtered X-ray imager, or a time-gated X-ray spectrometer with 1-D imaging along the axis of sample expansion, such as MSPEC (Heeter et al. 2004; May, Heeter & Emig 2004; Marrs et al. 2014). The latter option would allow time-resolved emission spectra to be used to verify the temperatures inferred from the axially backlit K-shell absorption spectra from OpSpec, and design work is underway to develop this option. This data will be complemented by the axial time-integrated self-emission spectra from OpSpec.

6 Initial simulated measurements

An opacity ‘experiment simulator’ is under development to estimate the expected measurements and guide design refinements in the backlighter, hohlraum and spectrometer. The simulator takes as inputs a backlighter spectrum; parameters describing the sample density, temperature, size and emission duration; and calculated opacity values. It propagates the backlighter source through the sample and computes the expected absorption and emission spectra, then adds noise to the data. Figure 7 shows an example of such a calculation, for a sample temperature of 150 eV, density of $0.04~\text{g}~\text{cm}^{-3}$ , thickness (after heating and expansion) of 50  $\unicode[STIX]{x03BC}\text{m}$ , and emission duration of 3 ns. The latter is a conservative estimate given current hohlraum designs. At present the experiment simulator uses the X-ray spectrum calculated from the 1-D HYDRA backlighter simulation whose X-ray flux output is shown in figure 5. For the expected iron opacities the simulator uses data supplied by one of the authors (Wilson) from the VISTA opacity model, but the results will be very similar for other models.

Figure 7. Simulated measurement of iron opacity on NIF at $T=150$  eV,  $\unicode[STIX]{x1D70C}=0.04~\text{g}~\text{cm}^{-3}$ . The expected signal in the backlighter zone (region $V$ in figure 2) is shown in black and includes both the backlighter spectrum and the time-integrated sample self-emission. The expected signal in the transmission zone (region $U$ in figure 2) includes the backlighter spectrum attenuated by the sample absorption and the time-integrated sample self-emission. The expected signal in the self-emission zone (region $E$ in figure 2) is shown in red.

Figure 7 shows interesting features not normally present in most opacity experiments. Figure 7 shows that the red trace (self-emission integrated for 3 ns) is likely to be a significant correction in some parts of the spectrum (where opacity is high). If this self-emission correction is measured poorly, it will introduce a significant error into the inferred opacity. However, if it can be measured well, it provides potentially valuable consistency checks on the data. When the optical depth is high, the transmission drops to zero and the absorption (blue) and self-emission (red) traces should converge, much like stalactites and stalagmites in a cave. In figure 7 this effect is most visible for the line features between 1000 and 1200 eV and the quasi-continuum around 900 eV. Where transmission is near zero, one can only infer a lower bound for the opacity. But one should be able to measure the level of experimental error in the measured absorption and emission spectra from their level of disagreement in portions of the spectrum where they should match. Furthermore, by conducting a series of experiments with varying sample thickness, it is possible to increase the transmission even in high-opacity regions, to infer the opacity across the whole spectrum.

From the expected experimental spectra, the simulator follows the relation $T=(U-E)/(V-E)$ to compute the simulated experimental transmission, as shown in figure 8. This transmission can be directly compared with the theoretical transmission of the same sample. For the noise levels assumed in figure 7, the expected experimental error in transmission, $\unicode[STIX]{x0394}T$ , is just below 0.02. As explained in § 2, the uncertainty $|\unicode[STIX]{x0394}T|\leqslant 0.02$ is consistent with an inferred opacity uncertainty of 10 % for the portions of the spectrum with $0.2<T<0.6$ . The simulation provides a tool to quantify the maximum noise and self-emission background levels consistent with achieving $|\unicode[STIX]{x0394}T|\leqslant 0.02$ .

Figure 8. Simulated transmission, transmission expected from calculated opacity and error between the two. The root-mean-square error, which is also the expected measurement uncertainty $\unicode[STIX]{x0394}T$ , is just below 0.02 for this set of assumptions.

Regarding the photometric noise acceptable in the spectrometer, because readouts of individual pixels on the recording medium (e.g. X-ray film or imaging plate) have more noise than acceptable, the simulation reinforces our understanding that multiple data points must be obtained and averaged together. In the Z platform, this data averaging is accomplished by fielding multiple space-imaging spectrometers and averaging data from multiple shots (Bailey et al. 2015). With the relatively high-magnification point-projection approach on NIF, the desired data are dispersed over a wide area on the detector, so measurements of individual pixels can be averaged together in a single shot. This motivates the large width (70 mm) of the detector.

As an example, in the current NIF design, a 0.5 mm sample positioned 30 mm from the backlighter and 600 mm from the detector yields an absorption image that is 10 mm wide in the space-resolving direction. This is split in half by symmetry (5 mm on each half of the OpSpec) and reduced by the ${\sim}2$  mm gap between the crystals and between the two pieces of film, but between the two detectors one can expect at least 5 mm of high-quality image. Meanwhile, individual pixels from the film scanner are 0.01 mm in size, so for each photon energy up to 5000 individual spectral measurements can be extracted and averaged together, reducing statistical noise by a factor of ${\sim}70$ . Assuming spectral data whose noise is dominated by, say, 10 % pixel-to-pixel digitizer noise, averaging over 5000 pixels reduces the noise to ${<}0.2\,\%$ . Considering the ‘spectral algebra’ to obtain transmission, $T=(U-E)/(V-E)$ , one expects an uncertainty $\unicode[STIX]{x0394}T\sim 0.006$ , comfortably below the 0.02 requirement. This approach requires strong photometrics ( ${\sim}10^{6}~\text{photons}~\text{pixel}^{-1}$ ) to ensure that photon statistical noise is not dominant over digitizer noise, but this assumption is consistent with current expectations for the opacity spectrometer throughput and backlighter yield. This approach also assumes that the crystal reflectivity at each position is either uniform or well known, which must be dealt with through calibrations. Obtaining high overall accuracy of the measurement will also require eliminating or compensating for any systematic errors.

It is expected that these simulated measurements will be updated as improved simulations and eventually experimental data become available for the capsule backlighter, opacity spectrometer and hohlraum and sample emission. In particular, as the characteristics of the spectrometer become known, the resolving power and photometric efficiency versus photon energy can also be added, yielding a close approximation of the actual measurements to guide future improvements to spectrometer, detector, laser and target designs. But these initial calculations already indicate that high-quality transmission opacity measurements should be achievable with NIF.

7 Summary and future work

The X-ray opacity of mid- and high-Z plasmas governs the transport of radiation in stars, hohlraums and other high-energy-density systems. Despite substantial progress theoretically, it is not yet clear from validating experiments that opacity has been ‘solved’. The National Ignition Facility is well positioned to replicate a set of Z facility opacity experiments which show substantial disagreement with opacity theory for conditions important to understanding the solar radiation–convection transition layer. Radiation hydrodynamics calculations in 2-D indicate that the parameters of the Z experiment ( $T\geqslant 150$  eV, $n_{e}\geqslant 7\times 10^{21}~\text{cm}^{-3}$ ) are achievable inside a NIF-heated hohlraum, using either of two designs. The sample will be backlit using a capsule implosion as a continuum radiation source, which is calculated to deliver an adequate X-ray yield. The resulting transmission spectrum will be measured using a time-integrated convex crystal spectrometer similar in design to that used at Z, but with a point-projection geometry. Experiments to develop both the capsule backlighter and the hohlraum are underway, the spectrometer design is complete and in fabrication, and detailed results will be published when available. Initial simulations of this type of measurement, using preliminary backlighter and sample parameters, indicate that spectroscopically resolved opacities might be measured to a precision of 10 % provided the sample areal density is known to 7 % and the transmission can be measured to $\pm 0.02$ within the range $0.2<T<0.6$ . This requires minimizing the noise in the spectra, and will be a key performance metric for the NIF experiment.