1 Introduction
Pulsar wind nebulae (PWNe) have long been recognized as outstanding laboratories of astro-plasma physics in extreme conditions, see e.g. Kirk, Lyubarsky & Petri (Reference Kirk, Lyubarsky, Petri and Becker2009) and Arons (Reference Arons2012), and the Crab nebula, as a result of its proximity, plays a very special role among those objects.
At the price of non-trivial assumptions regarding the physical conditions behind the termination shock of the pulsar wind, which separates the free streaming wind from the hot shocked wind in the nebula, phenomenological models have been very successful in explaining the general spectral energy distribution and morphological features of the Crab nebula, using analytical calculations (e.g. Kennel & Coroniti Reference Kennel and Coroniti1984a ,Reference Kennel and Coroniti b ; Atoyan & Aharonian Reference Atoyan and Aharonian1996) or increasingly sophisticated numerical simulations (e.g. Komissarov & Lyubarsky Reference Komissarov and Lyubarsky2003, Reference Komissarov and Lyubarsky2004; Bucciantini et al. Reference Bucciantini, Blondin, Del Zanna and Amato2003; Del Zanna, Amato & Bucciantini Reference Del Zanna, Amato and Bucciantini2004; Porth, Komissarov & Keppens Reference Porth, Komissarov and Keppens2014), see also Amato (Reference Amato2015) and Kargaltsev et al. (Reference Kargaltsev, Cerutti, Lyubarsky and Striani2015) for reviews.
Nonetheless, various puzzles plague the current understanding of the microphysics of PWNe; among them, two are particularly noteworthy: how the wind converts its Poynting flux – which supposedly greatly dominates the particle kinetic energy at the base of the wind – into particle thermal energy behind the termination shock, reaching rough equipartition between these components; and how particle acceleration takes place behind the termination shock.
The present paper examines a speculative scenario, which could potentially solve part of the above puzzles; it specifically assumes that the termination shock of the pulsar wind is nonlinearly corrugated, the precise meaning of this being given in § 2.1. It then shows that such corrugation efficiently converts an incoming ordered magnetic energy into turbulence, thereby slowing down appreciably the flow velocity behind the termination shock. A significant part of the turbulence can be further dissipated through collisionless effects on short length-scales, leading to pre-acceleration of the pairs, up to close equipartition with the incoming magnetic energy. The corrugation of the shock may thus achieve efficient dissipation of the incoming Poynting flux, in a way that is reminiscent of the dissipation through reconnection of a striped wind in the equatorial plane (Lyubarsky Reference Lyubarsky2003). Finally, it is speculated (and argued) that the turbulence seeded by corrugation may also sustain an efficient Fermi process, leading to a particle spectrum close to what is observed.
This paper is organized as follows: § 2 discusses the physics of a corrugated shock wave in the magneto-hydrodynamics (MHD) limit; § 3 recalls some results on the collisionless damping of relativistic MHD waves in a relativistic plasma, then discusses the physics of particle pre-acceleration in the resulting turbulence and the development of a relativistic Fermi process at high energies. Section 4 discusses various possible sources of corrugation and examines how the present results can be applied to PWNe. Finally, § 5 provides a summary of the discussion and some conclusions.
2 A relativistic corrugated termination shock
2.1 Definitions
Assume that the termination of the pulsar wind, which separates the cold magnetized incoming wind from the hot shocked wind, is corrugated. Potential sources of corrugation will be addressed in § 4. For simplicity, we neglect effects of spherical symmetry, which are not important to the present discussion, and therefore consider a planar shock, moving at velocity
![]() $\overline{{\it\beta}_{\text{f}}}$
along the
$\overline{{\it\beta}_{\text{f}}}$
along the
![]() $x$
-direction relative to the downstream plasma, i.e. relative to the nebula. The (uncorrugated) shock surface is defined by
$x$
-direction relative to the downstream plasma, i.e. relative to the nebula. The (uncorrugated) shock surface is defined by
with corresponding shock normal four-vector:
where
![]() $\overline{{\it\gamma}_{\text{f}}}\equiv (1-\overline{{\it\beta}_{\text{f}}}^{2})^{-1/2}$
denotes the bulk Lorentz factor of the shock front relative to downstream.
$\overline{{\it\gamma}_{\text{f}}}\equiv (1-\overline{{\it\beta}_{\text{f}}}^{2})^{-1/2}$
denotes the bulk Lorentz factor of the shock front relative to downstream.
Corrugation can be described by a perturbation of the shock surface:
where
![]() $\boldsymbol{x}_{\bot }\equiv (y,z)$
represents the coordinates in the (uncorrugated) shock front plane. For simplicity, consider for the purpose of this subsection a corrugation on a single length-scale characterized by a wavenumber
$\boldsymbol{x}_{\bot }\equiv (y,z)$
represents the coordinates in the (uncorrugated) shock front plane. For simplicity, consider for the purpose of this subsection a corrugation on a single length-scale characterized by a wavenumber
![]() $\boldsymbol{k}_{\bot }=(k_{y},k_{z})$
defined in the uncorrugated shock front plane, with harmonic behaviour at frequency
$\boldsymbol{k}_{\bot }=(k_{y},k_{z})$
defined in the uncorrugated shock front plane, with harmonic behaviour at frequency
![]() ${\it\omega}_{\boldsymbol{k}}$
:
${\it\omega}_{\boldsymbol{k}}$
:
The frequency
![]() ${\it\omega}_{\boldsymbol{k}}$
is directly related to
${\it\omega}_{\boldsymbol{k}}$
is directly related to
![]() $\boldsymbol{k}=(k_{x},\boldsymbol{k}_{\bot })$
and to the nature of the wave inducing the corrugation of the shock front (Lemoine, Ramos & Gremillet Reference Lemoine, Ramos and Gremillet2016);
$\boldsymbol{k}=(k_{x},\boldsymbol{k}_{\bot })$
and to the nature of the wave inducing the corrugation of the shock front (Lemoine, Ramos & Gremillet Reference Lemoine, Ramos and Gremillet2016);
![]() $k_{x}$
represents here the
$k_{x}$
represents here the
![]() $x$
-wavenumber of that mode. At a relativistic shock, one typically has
$x$
-wavenumber of that mode. At a relativistic shock, one typically has
![]() ${\it\omega}_{\boldsymbol{k}}\sim |\boldsymbol{k}|$
, hence this scaling is retained in the following.
${\it\omega}_{\boldsymbol{k}}\sim |\boldsymbol{k}|$
, hence this scaling is retained in the following.
In the linear approximation, the first-order perturbation of the shock normal is written:
or, for the above single-wave corrugation pattern,
A strongly corrugated shock is such that the above linear approximation breaks down, i.e.
![]() $|{\it\delta}\ell |\gtrsim 1$
, which translates into
$|{\it\delta}\ell |\gtrsim 1$
, which translates into
Both conditions express the fact that the departure from the unperturbed shock surface becomes larger than the perpendicular wavelength in the shock front rest frame. For a moderately magnetized shock wave, with
![]() ${\it\sigma}_{1}\lesssim 3$
, one has
${\it\sigma}_{1}\lesssim 3$
, one has
![]() $\overline{{\it\gamma}_{\text{f}}}\sim 1$
, hence a shock front at the onset of nonlinear corrugation is such that
$\overline{{\it\gamma}_{\text{f}}}\sim 1$
, hence a shock front at the onset of nonlinear corrugation is such that
![]() $|k{\it\delta}X|\sim 1$
(with
$|k{\it\delta}X|\sim 1$
(with
![]() ${\it\delta}X$
expressed in the downstream rest frame as previously).
${\it\delta}X$
expressed in the downstream rest frame as previously).
If the incoming upstream flow is strongly magnetized, i.e.
![]() ${\it\sigma}_{1}\gtrsim 3$
,
${\it\sigma}_{1}\gtrsim 3$
,
![]() $\overline{{\it\gamma}_{\text{f}}}$
becomes larger than unity. However, the mean shock velocity
$\overline{{\it\gamma}_{\text{f}}}$
becomes larger than unity. However, the mean shock velocity
![]() ${\it\beta}_{\text{f}}$
along the shock normal can be strongly modified by corrugation; as discussed in the following, in particular, the generation of turbulence in the nonlinearly corrugated shock transition can reduce the actual
${\it\beta}_{\text{f}}$
along the shock normal can be strongly modified by corrugation; as discussed in the following, in particular, the generation of turbulence in the nonlinearly corrugated shock transition can reduce the actual
![]() ${\it\beta}_{\text{f}}$
to sub-relativistic values, implying
${\it\beta}_{\text{f}}$
to sub-relativistic values, implying
![]() ${\it\gamma}_{\text{f}}\sim 1$
. It is therefore speculated that
${\it\gamma}_{\text{f}}\sim 1$
. It is therefore speculated that
![]() $|k{\it\delta}X|\sim 1$
remains a valid threshold for nonlinear corrugation in the large magnetization regime
$|k{\it\delta}X|\sim 1$
remains a valid threshold for nonlinear corrugation in the large magnetization regime
![]() ${\it\sigma}_{1}\gtrsim 3$
.
${\it\sigma}_{1}\gtrsim 3$
.
Actually, one could potentially envisage even larger values of
![]() ${\it\delta}X$
; however, nonlinear back-reaction would likely limit
${\it\delta}X$
; however, nonlinear back-reaction would likely limit
![]() ${\it\delta}X$
to the above threshold of nonlinearity, hence this value is retained in the following.
${\it\delta}X$
to the above threshold of nonlinearity, hence this value is retained in the following.
Interestingly, the condition
![]() $|k{\it\delta}X_{\boldsymbol{k}}|\gtrsim 1$
is compatible with a very small amplitude
$|k{\it\delta}X_{\boldsymbol{k}}|\gtrsim 1$
is compatible with a very small amplitude
![]() $|{\it\delta}X|$
, as measured relative to the scale of the termination shock (noted
$|{\it\delta}X|$
, as measured relative to the scale of the termination shock (noted
![]() $R$
), provided
$R$
), provided
![]() $|kR|\gg 1$
. In other words, the shock may be strongly corrugated on short spatial scales which are not observable at large distances, but which remain macroscopic compared to the thickness of the actual shock transition. The latter requirement is not essential for the present scenario, but the MHD description that this model uses can only be applied on scales much larger than the shock thickness, which is set by kinetic physics. To provide quantitative estimates, consider the case of the Crab nebula: if electrons are inflowing through the shock with a Lorentz factor
$|kR|\gg 1$
. In other words, the shock may be strongly corrugated on short spatial scales which are not observable at large distances, but which remain macroscopic compared to the thickness of the actual shock transition. The latter requirement is not essential for the present scenario, but the MHD description that this model uses can only be applied on scales much larger than the shock thickness, which is set by kinetic physics. To provide quantitative estimates, consider the case of the Crab nebula: if electrons are inflowing through the shock with a Lorentz factor
![]() ${\it\gamma}_{\text{w}}=10^{4}{\it\gamma}_{\text{w},4}$
(relative to the downstream-nebula rest frame), the typical gyroradius of these particles in the downstream magnetic field (strength
${\it\gamma}_{\text{w}}=10^{4}{\it\gamma}_{\text{w},4}$
(relative to the downstream-nebula rest frame), the typical gyroradius of these particles in the downstream magnetic field (strength
![]() $B_{d}\sim 0.1~\text{mG}$
),
$B_{d}\sim 0.1~\text{mG}$
),
![]() $r_{\text{g}}\sim 10^{11}{\it\gamma}_{\text{w},4}~\text{cm}$
sets the typical thickness of the shock transition layer. Therefore, corrugation is envisaged here on all scales
$r_{\text{g}}\sim 10^{11}{\it\gamma}_{\text{w},4}~\text{cm}$
sets the typical thickness of the shock transition layer. Therefore, corrugation is envisaged here on all scales
![]() $k^{-1}$
larger than the above and smaller than
$k^{-1}$
larger than the above and smaller than
![]() $R\sim 3\times 10^{17}~\text{cm}$
. As discussed in § 4, this range of scales encompasses the gyroradii of all accelerated particles, even the highest-energy ones, indicating that corrugation may exert a strong influence on their kinematics.
$R\sim 3\times 10^{17}~\text{cm}$
. As discussed in § 4, this range of scales encompasses the gyroradii of all accelerated particles, even the highest-energy ones, indicating that corrugation may exert a strong influence on their kinematics.

Figure 1. Various quantities plotted at
![]() $t=0$
as a function of
$t=0$
as a function of
![]() $y$
, the coordinate along the direction
$y$
, the coordinate along the direction
![]() $\boldsymbol{y}$
, which is both perpendicular to the shock normal (
$\boldsymbol{y}$
, which is both perpendicular to the shock normal (
![]() $\boldsymbol{x}$
) and to the direction of the background magnetic field (
$\boldsymbol{x}$
) and to the direction of the background magnetic field (
![]() $\boldsymbol{z}$
), in a case of nonlinear corrugation described by (2.8), assuming no rippling along
$\boldsymbol{z}$
), in a case of nonlinear corrugation described by (2.8), assuming no rippling along
![]() $\boldsymbol{z}$
. Upper sinusoidal dotted line:
$\boldsymbol{z}$
. Upper sinusoidal dotted line:
![]() $-\boldsymbol{\ell }_{0}/\boldsymbol{\ell }_{1}$
describing the spatial behaviour of the temporal component of the shock normal; the average value over
$-\boldsymbol{\ell }_{0}/\boldsymbol{\ell }_{1}$
describing the spatial behaviour of the temporal component of the shock normal; the average value over
![]() $y$
, i.e. 0.7, represents the average velocity of the shock front relative to downstream. Lower sinusoidal dotted line:
$y$
, i.e. 0.7, represents the average velocity of the shock front relative to downstream. Lower sinusoidal dotted line:
![]() $-\boldsymbol{\ell }_{2}/\boldsymbol{\ell }_{1}$
, describing the rippling of the shock front in the
$-\boldsymbol{\ell }_{2}/\boldsymbol{\ell }_{1}$
, describing the rippling of the shock front in the
![]() $\boldsymbol{y}$
direction. Horizontal dashed curve: (relativistic) Alfvén three-velocity of waves in the downstream plasma, whose modulations are at too small an amplitude to emerge on this figure. Solid (blue) line:
$\boldsymbol{y}$
direction. Horizontal dashed curve: (relativistic) Alfvén three-velocity of waves in the downstream plasma, whose modulations are at too small an amplitude to emerge on this figure. Solid (blue) line:
![]() $y$
-component of the downstream flow three-velocity (on the shock front). Dashed (blue) thick line:
$y$
-component of the downstream flow three-velocity (on the shock front). Dashed (blue) thick line:
![]() $x$
-component of the downstream flow three-velocity. Finally, the arrows indicate the direction of the downstream three-velocity in the
$x$
-component of the downstream flow three-velocity. Finally, the arrows indicate the direction of the downstream three-velocity in the
![]() $(y,x)$
plane (for this arrow representation, the ordinate axis should be understood as indicating the
$(y,x)$
plane (for this arrow representation, the ordinate axis should be understood as indicating the
![]() $x$
-direction, while the abscissa points into the
$x$
-direction, while the abscissa points into the
![]() $y$
-direction).
$y$
-direction).
2.2 A particular nonlinear solution
In the nonlinear regime where the above perturbative description breaks down, it is possible to extract an analytical solution of the shock crossing equations in a 2D limit, in which all quantities remain unperturbed along the direction of the background magnetic field (taken to be
![]() $\boldsymbol{z}$
here), see Lemoine et al. (Reference Lemoine, Ramos and Gremillet2016). The downstream quantities characterizing the state of the plasma can then be expressed at any time, on the corrugated shock front, in terms of the shock normal. The magnitude of the shock corrugation amplitude, which depends on the past history of the accumulated flow, is related through a non-trivial differential relation to the shock normal, see (2.2) and (2.3) in particular. The present description does not attempt to describe this corrugation amplitude but to describe the state of the downstream plasma on the shock front.
$\boldsymbol{z}$
here), see Lemoine et al. (Reference Lemoine, Ramos and Gremillet2016). The downstream quantities characterizing the state of the plasma can then be expressed at any time, on the corrugated shock front, in terms of the shock normal. The magnitude of the shock corrugation amplitude, which depends on the past history of the accumulated flow, is related through a non-trivial differential relation to the shock normal, see (2.2) and (2.3) in particular. The present description does not attempt to describe this corrugation amplitude but to describe the state of the downstream plasma on the shock front.
An example is shown in figure 1, which assumes an upstream magnetization parameter
![]() ${\it\sigma}_{1}=1$
, a relative Lorentz factor between up- and down-stream
${\it\sigma}_{1}=1$
, a relative Lorentz factor between up- and down-stream
![]() ${\it\gamma}_{1}=100$
, and a shock normal four-vector arbitrarily set to:
${\it\gamma}_{1}=100$
, and a shock normal four-vector arbitrarily set to:
In the downstream rest frame, this four-normal describes a mean shock velocity of
![]() ${\it\beta}_{\text{f}}\simeq 0.7$
(corresponding to the unperturbed shock crossing conditions for the above values of the magnetization and flow velocity), with harmonic corrugation slightly below the onset of the nonlinear limit.
${\it\beta}_{\text{f}}\simeq 0.7$
(corresponding to the unperturbed shock crossing conditions for the above values of the magnetization and flow velocity), with harmonic corrugation slightly below the onset of the nonlinear limit.
For the particular case of perturbations confined to the
![]() $y$
-direction, the equations of shock crossing lead to
$y$
-direction, the equations of shock crossing lead to
![]() $B_{x|2}=B_{y|2}=0$
: the magnetic field retains only a
$B_{x|2}=B_{y|2}=0$
: the magnetic field retains only a
![]() $z$
-component, modulated along
$z$
-component, modulated along
![]() $\boldsymbol{y}$
. Note that
$\boldsymbol{y}$
. Note that
![]() $B_{x|2}$
and
$B_{x|2}$
and
![]() $B_{y|2}$
vanish on the corrugated shock surface, but not necessarily further downstream. One would need to follow the characteristics of the system to study the evolution of these two quantities downstream of the shock; in the linear limit at least, one can show that the outgoing wave modes develop a net
$B_{y|2}$
vanish on the corrugated shock surface, but not necessarily further downstream. One would need to follow the characteristics of the system to study the evolution of these two quantities downstream of the shock; in the linear limit at least, one can show that the outgoing wave modes develop a net
![]() ${\it\delta}B_{x|2}$
and
${\it\delta}B_{x|2}$
and
![]() ${\it\delta}B_{y|2}$
further downstream of the shock. Moreover, in a more general case with
${\it\delta}B_{y|2}$
further downstream of the shock. Moreover, in a more general case with
![]() $k_{z}\neq 0$
, both components
$k_{z}\neq 0$
, both components
![]() ${\it\delta}B_{x|2}$
and
${\it\delta}B_{x|2}$
and
![]() ${\it\delta}B_{y|2}$
would not vanish on the shock surface.
${\it\delta}B_{y|2}$
would not vanish on the shock surface.
As illustrated by figure 1, the shock crossing equations imply the existence of significant velocity fluctuations along
![]() $x$
and
$x$
and
![]() $y$
, with different modulations. In turn, these generate sheared flows with non-vanishing
$y$
, with different modulations. In turn, these generate sheared flows with non-vanishing
![]() ${\bf\beta}\times \boldsymbol{B}$
in the downstream, leading to the stretching and compression of magnetic field lines. These flow motions also generate convective electric fields,
${\bf\beta}\times \boldsymbol{B}$
in the downstream, leading to the stretching and compression of magnetic field lines. These flow motions also generate convective electric fields,
![]() $\boldsymbol{E}=-{\bf\beta}\times \boldsymbol{B}$
, with
$\boldsymbol{E}=-{\bf\beta}\times \boldsymbol{B}$
, with
![]() $|\boldsymbol{E}|\sim |\boldsymbol{B}|$
because
$|\boldsymbol{E}|\sim |\boldsymbol{B}|$
because
![]() $|{\it\beta}|$
is close to unity. The resulting turbulence should thus be prone to dissipation and particle acceleration on short time scales.
$|{\it\beta}|$
is close to unity. The resulting turbulence should thus be prone to dissipation and particle acceleration on short time scales.
2.3 Jump conditions at a corrugated shock front
As the upstream plasma inflows through the corrugated shock, the ordered magnetic energy is thus converted in part into turbulence modes. Assume that the MHD fluid immediately behind the shock can be described by an enthalpy density
![]() $w_{2}$
and pressure
$w_{2}$
and pressure
![]() $p_{2}$
with equation of state
$p_{2}$
with equation of state
![]() $w_{2}\simeq 4p_{2}$
(relativistically hot fluid), and by a magnetic field
$w_{2}\simeq 4p_{2}$
(relativistically hot fluid), and by a magnetic field
![]() $\boldsymbol{B}=\boldsymbol{B}_{2}+{\bf\delta}\boldsymbol{B}_{2}$
, with
$\boldsymbol{B}=\boldsymbol{B}_{2}+{\bf\delta}\boldsymbol{B}_{2}$
, with
![]() $\langle {\bf\delta}\boldsymbol{B}_{2}\rangle =0$
. The index
$\langle {\bf\delta}\boldsymbol{B}_{2}\rangle =0$
. The index
![]() $_{2}$
applies to downstream quantities; upstream quantities will be indexed with
$_{2}$
applies to downstream quantities; upstream quantities will be indexed with
![]() $_{1}$
. The average can be taken in the ensemble of realizations of the corrugation, or as usual, in the ergodic hypothesis, along the shock front plane.
$_{1}$
. The average can be taken in the ensemble of realizations of the corrugation, or as usual, in the ergodic hypothesis, along the shock front plane.
On spatial scales much larger than the thickness of the shock, but much smaller than the corrugation amplitude
![]() $|{\it\delta}X|$
, the jump conditions at the shock are expressed through the integration of the conservation laws along the perturbed normal direction. However, the present discussion is rather concerned with computing the asymptotic behaviour of the downstream plasma, on a distance scale
$|{\it\delta}X|$
, the jump conditions at the shock are expressed through the integration of the conservation laws along the perturbed normal direction. However, the present discussion is rather concerned with computing the asymptotic behaviour of the downstream plasma, on a distance scale
![]() $\gg |{\it\delta}X|$
away from the shock. On such scales, the shock can be seen as a planar discontinuity, although the jump conditions should reflect the fact that turbulence has been generated in the transition layer. These jump conditions should thus be written in the downstream plasma rest frame as
$\gg |{\it\delta}X|$
away from the shock. On such scales, the shock can be seen as a planar discontinuity, although the jump conditions should reflect the fact that turbulence has been generated in the transition layer. These jump conditions should thus be written in the downstream plasma rest frame as
where the shock normal
![]() $\boldsymbol{\ell }_{{\it\mu}}=(-{\it\gamma}_{\text{f}}{\it\beta}_{\text{f}},{\it\gamma}_{\text{f}},0,0)$
as in (2.2) above. A distinction has to be made however in the notations: in (2.2), the overline symbols indicate that the solution applies in the absence of corrugation, while in the present case, corrugation is assumed to be present on small spatial scales, leading to the production of downstream MHD turbulence, so that the value of
$\boldsymbol{\ell }_{{\it\mu}}=(-{\it\gamma}_{\text{f}}{\it\beta}_{\text{f}},{\it\gamma}_{\text{f}},0,0)$
as in (2.2) above. A distinction has to be made however in the notations: in (2.2), the overline symbols indicate that the solution applies in the absence of corrugation, while in the present case, corrugation is assumed to be present on small spatial scales, leading to the production of downstream MHD turbulence, so that the value of
![]() ${\it\beta}_{\text{f}}$
which is determined further below differs from
${\it\beta}_{\text{f}}$
which is determined further below differs from
![]() $\overline{{\it\beta}_{\text{f}}}$
above.
$\overline{{\it\beta}_{\text{f}}}$
above.
The energy-momentum tensor in the ideal MHD approximation is written
in terms of the magnetic four-vector
![]() $\boldsymbol{b}^{{\it\mu}}$
:
$\boldsymbol{b}^{{\it\mu}}$
:
where
![]() $\boldsymbol{u}^{{\it\mu}}$
represents the turbulent fluid four-velocity behind the shock, and latin indices represent spatial indices.
$\boldsymbol{u}^{{\it\mu}}$
represents the turbulent fluid four-velocity behind the shock, and latin indices represent spatial indices.
The average energy-momentum tensor of the turbulent downstream fluid is given by the correlators
![]() $\langle b^{{\it\alpha}}b^{{\it\beta}}\rangle$
, which can be calculated in full generality. In order to derive simple estimates however, the velocity field and the magnetic perturbations are assumed uncorrelated, i.e.
$\langle b^{{\it\alpha}}b^{{\it\beta}}\rangle$
, which can be calculated in full generality. In order to derive simple estimates however, the velocity field and the magnetic perturbations are assumed uncorrelated, i.e.
and correlators involving odd powers of the turbulent fluid three-velocity are assumed to vanish; in particular,
![]() $\langle u^{i}\rangle =0$
by definition of the downstream rest frame. Finally, one may assume isotropic turbulence, meaning
$\langle u^{i}\rangle =0$
by definition of the downstream rest frame. Finally, one may assume isotropic turbulence, meaning
This assumption makes it possible to simplify the calculations, but it is not crucial to the present analysis, as discussed further on.
Then one writes
where
![]() $b_{(0)}^{{\it\alpha}}$
does not contain any
$b_{(0)}^{{\it\alpha}}$
does not contain any
![]() ${\it\delta}B_{i}$
component, while
${\it\delta}B_{i}$
component, while
![]() $b_{(1)}^{{\it\alpha}}$
does not contain any
$b_{(1)}^{{\it\alpha}}$
does not contain any
![]() $B_{i}$
term. Assuming that the average background field lies along
$B_{i}$
term. Assuming that the average background field lies along
![]() $\boldsymbol{z}$
, one readily obtains
$\boldsymbol{z}$
, one readily obtains
and
A key observation here is that these correlators do not share the same dependence. To proceed further and obtain a more tractable expression leading to a simple estimate of the modified jump conditions, assume that the turbulence in the downstream rest frame is moderately relativistic; this is actually ensured if the corrugation is mildly nonlinear and
![]() ${\it\sigma}_{1}$
not large compared to unity, as discussed in Lemoine et al. (Reference Lemoine, Ramos and Gremillet2016). The following expressions thus retain only the leading-order terms in powers of
${\it\sigma}_{1}$
not large compared to unity, as discussed in Lemoine et al. (Reference Lemoine, Ramos and Gremillet2016). The following expressions thus retain only the leading-order terms in powers of
![]() $u$
in the above correlators, which then reduce to standard non-relativistic expressions for magnetized turbulence:
$u$
in the above correlators, which then reduce to standard non-relativistic expressions for magnetized turbulence:
It should be understood that this set of approximations is intended to show in a quantitative way how corrugation affects the jump conditions at the MHD shock. Qualitatively speaking however, the key point is that the correlators of the turbulence modes contained in
![]() $\langle b^{{\it\alpha}}b^{{\it\beta}}\rangle$
differ from those of the average background field.
$\langle b^{{\it\alpha}}b^{{\it\beta}}\rangle$
differ from those of the average background field.
With the above approximations, the non-zero downstream energy-momentum tensor components can be written:
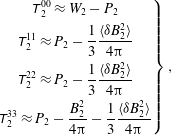 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \unicode[STIX]{x1D61B}_{2}^{00}\approx W_{2}-P_{2}\\ \displaystyle \unicode[STIX]{x1D61B}_{2}^{11}\approx P_{2}-\frac{1}{3}\frac{\langle {\it\delta}B_{2}^{2}\rangle }{4{\rm\pi}}\\ \displaystyle \unicode[STIX]{x1D61B}_{2}^{22}\approx P_{2}-\frac{1}{3}\frac{\langle {\it\delta}B_{2}^{2}\rangle }{4{\rm\pi}}\\ \displaystyle \unicode[STIX]{x1D61B}_{2}^{33}\approx P_{2}-\frac{B_{2}^{2}}{4{\rm\pi}}-\frac{1}{3}\frac{\langle {\it\delta}B_{2}^{2}\rangle }{4{\rm\pi}}\end{array}\right\}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \unicode[STIX]{x1D61B}_{2}^{00}\approx W_{2}-P_{2}\\ \displaystyle \unicode[STIX]{x1D61B}_{2}^{11}\approx P_{2}-\frac{1}{3}\frac{\langle {\it\delta}B_{2}^{2}\rangle }{4{\rm\pi}}\\ \displaystyle \unicode[STIX]{x1D61B}_{2}^{22}\approx P_{2}-\frac{1}{3}\frac{\langle {\it\delta}B_{2}^{2}\rangle }{4{\rm\pi}}\\ \displaystyle \unicode[STIX]{x1D61B}_{2}^{33}\approx P_{2}-\frac{B_{2}^{2}}{4{\rm\pi}}-\frac{1}{3}\frac{\langle {\it\delta}B_{2}^{2}\rangle }{4{\rm\pi}}\end{array}\right\}, & & \displaystyle\end{eqnarray}$$
with
![]() $W_{2}\equiv w_{2}+B_{2}^{2}/(4{\rm\pi})+\langle {\it\delta}B_{2}^{2}\rangle /(4{\rm\pi})$
a generalized enthalpy density and
$W_{2}\equiv w_{2}+B_{2}^{2}/(4{\rm\pi})+\langle {\it\delta}B_{2}^{2}\rangle /(4{\rm\pi})$
a generalized enthalpy density and
![]() $P_{2}\equiv p_{2}+B_{2}^{2}/(8{\rm\pi})+\langle {\it\delta}B_{2}^{2}\rangle /(8{\rm\pi})$
a generalized pressure.
$P_{2}\equiv p_{2}+B_{2}^{2}/(8{\rm\pi})+\langle {\it\delta}B_{2}^{2}\rangle /(8{\rm\pi})$
a generalized pressure.
The shock jump conditions for energy and momentum fluxes are then expressed as
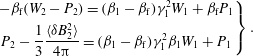 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle -{\it\beta}_{\text{f}}(W_{2}-P_{2})=({\it\beta}_{1}-{\it\beta}_{\text{f}}){\it\gamma}_{1}^{2}W_{1}+{\it\beta}_{\text{f}}P_{1}\\ \displaystyle P_{2}-\frac{1}{3}\frac{\langle {\it\delta}B_{2}^{2}\rangle }{4{\rm\pi}}=({\it\beta}_{1}-{\it\beta}_{\text{f}}){\it\gamma}_{1}^{2}{\it\beta}_{1}W_{1}+P_{1}\end{array}\right\}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle -{\it\beta}_{\text{f}}(W_{2}-P_{2})=({\it\beta}_{1}-{\it\beta}_{\text{f}}){\it\gamma}_{1}^{2}W_{1}+{\it\beta}_{\text{f}}P_{1}\\ \displaystyle P_{2}-\frac{1}{3}\frac{\langle {\it\delta}B_{2}^{2}\rangle }{4{\rm\pi}}=({\it\beta}_{1}-{\it\beta}_{\text{f}}){\it\gamma}_{1}^{2}{\it\beta}_{1}W_{1}+P_{1}\end{array}\right\}. & & \displaystyle\end{eqnarray}$$
The above equations are written in the downstream rest frame, so that
![]() ${\it\beta}_{1}$
corresponds to the velocity of upstream relative to downstream. Neglecting
${\it\beta}_{1}$
corresponds to the velocity of upstream relative to downstream. Neglecting
![]() $P_{1}$
in front of
$P_{1}$
in front of
![]() $P_{2}$
(or, alternatively
$P_{2}$
(or, alternatively
![]() ${\it\gamma}_{1}^{2}W_{1}$
) and assuming a hot relativistic plasma downstream,
${\it\gamma}_{1}^{2}W_{1}$
) and assuming a hot relativistic plasma downstream,
![]() $p_{2}=w_{2}/4$
, one obtains easily
$p_{2}=w_{2}/4$
, one obtains easily
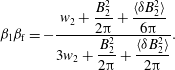 $$\begin{eqnarray}\displaystyle {\it\beta}_{1}{\it\beta}_{\text{f}}=-\frac{\displaystyle w_{2}+\frac{B_{2}^{2}}{2{\rm\pi}}+\frac{\langle {\it\delta}B_{2}^{2}\rangle }{6{\rm\pi}}}{\displaystyle 3w_{2}+\frac{B_{2}^{2}}{2{\rm\pi}}+\frac{\langle {\it\delta}B_{2}^{2}\rangle }{2{\rm\pi}}}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\beta}_{1}{\it\beta}_{\text{f}}=-\frac{\displaystyle w_{2}+\frac{B_{2}^{2}}{2{\rm\pi}}+\frac{\langle {\it\delta}B_{2}^{2}\rangle }{6{\rm\pi}}}{\displaystyle 3w_{2}+\frac{B_{2}^{2}}{2{\rm\pi}}+\frac{\langle {\it\delta}B_{2}^{2}\rangle }{2{\rm\pi}}}. & & \displaystyle\end{eqnarray}$$
This equation reduces to the standard result
![]() ${\it\beta}_{\text{f}}\rightarrow 1/3$
in the limits
${\it\beta}_{\text{f}}\rightarrow 1/3$
in the limits
![]() ${\it\beta}_{1}\rightarrow -1$
(ultra-relativistic limit),
${\it\beta}_{1}\rightarrow -1$
(ultra-relativistic limit),
![]() $B_{2}\rightarrow 0$
and
$B_{2}\rightarrow 0$
and
![]() $\langle {\it\delta}B_{2}^{2}\rangle ^{1/2}\rightarrow 0$
(hydrodynamic shock), e.g. Kirk & Duffy (Reference Kirk and Duffy1999). In the highly magnetized and uncorrugated case, meaning
$\langle {\it\delta}B_{2}^{2}\rangle ^{1/2}\rightarrow 0$
(hydrodynamic shock), e.g. Kirk & Duffy (Reference Kirk and Duffy1999). In the highly magnetized and uncorrugated case, meaning
![]() $w_{2}\ll B_{2}^{2}/(4{\rm\pi})$
and
$w_{2}\ll B_{2}^{2}/(4{\rm\pi})$
and
![]() $\langle {\it\delta}B_{2}^{2}\rangle ^{1/2}\rightarrow 0$
, one also recovers
$\langle {\it\delta}B_{2}^{2}\rangle ^{1/2}\rightarrow 0$
, one also recovers
![]() ${\it\beta}_{1}{\it\beta}_{\text{f}}\simeq -1$
, indicating that the shock moves away from downstream at a relativistic velocity. As discussed by Kennel & Coroniti (Reference Kennel and Coroniti1984a
), the mismatch between this solution and the general morphology of the Crab nebula points towards a smaller than unity magnetization parameter behind the termination shock.
${\it\beta}_{1}{\it\beta}_{\text{f}}\simeq -1$
, indicating that the shock moves away from downstream at a relativistic velocity. As discussed by Kennel & Coroniti (Reference Kennel and Coroniti1984a
), the mismatch between this solution and the general morphology of the Crab nebula points towards a smaller than unity magnetization parameter behind the termination shock.
More interestingly, if
![]() $\langle {\it\delta}B_{2}^{2}\rangle ^{1/2}$
is not negligible compared to
$\langle {\it\delta}B_{2}^{2}\rangle ^{1/2}$
is not negligible compared to
![]() $B_{2}$
, one finds a solution with a shock moving away from downstream at sub-relativistic velocities, independently of how strongly magnetized the flow initially was. Consider for instance the case of equipartition
$B_{2}$
, one finds a solution with a shock moving away from downstream at sub-relativistic velocities, independently of how strongly magnetized the flow initially was. Consider for instance the case of equipartition
![]() $\langle {\it\delta}B_{2}^{2}\rangle ^{1/2}\sim B_{2}$
and
$\langle {\it\delta}B_{2}^{2}\rangle ^{1/2}\sim B_{2}$
and
![]() $w_{2}\ll B_{2}^{2}/(4{\rm\pi})$
, which is effectively what one expects if corrugation is mildly nonlinear. Then
$w_{2}\ll B_{2}^{2}/(4{\rm\pi})$
, which is effectively what one expects if corrugation is mildly nonlinear. Then
![]() ${\it\beta}_{\text{f}}\simeq 2/3$
for
${\it\beta}_{\text{f}}\simeq 2/3$
for
![]() ${\it\beta}_{1}\simeq -1$
. Other interesting limits are
${\it\beta}_{1}\simeq -1$
. Other interesting limits are
![]() $\langle {\it\delta}B_{2}^{2}\rangle \gg B_{2}^{2}$
(strong corrugation), leading to
$\langle {\it\delta}B_{2}^{2}\rangle \gg B_{2}^{2}$
(strong corrugation), leading to
![]() ${\it\beta}_{\text{f}}\simeq 1/3$
as in a pure hydrodynamical shock; or
${\it\beta}_{\text{f}}\simeq 1/3$
as in a pure hydrodynamical shock; or
![]() $\langle {\it\delta}B_{2}^{2}\rangle \sim B_{2}^{2}\sim 4{\rm\pi}w_{2}$
, leading to
$\langle {\it\delta}B_{2}^{2}\rangle \sim B_{2}^{2}\sim 4{\rm\pi}w_{2}$
, leading to
![]() ${\it\beta}_{\text{f}}\simeq 0.5$
.
${\it\beta}_{\text{f}}\simeq 0.5$
.
These particular solutions emerge whenever the field line tension of the turbulence can contribute to the
![]() $xx$
component of
$xx$
component of
![]() $\unicode[STIX]{x1D61B}^{{\it\mu}{\it\nu}}$
, i.e. whenever the correlators
$\unicode[STIX]{x1D61B}^{{\it\mu}{\it\nu}}$
, i.e. whenever the correlators
![]() $\langle b^{{\it\mu}}b^{{\it\nu}}\rangle$
possess a non-trivial
$\langle b^{{\it\mu}}b^{{\it\nu}}\rangle$
possess a non-trivial
![]() $xx$
component. As discussed here and in the previous section, such a component could arise from the shock corrugation directly or from the nonlinear processing of the magnetic modulations induced by shock corrugation. The following subsections also argue that the partial dissipation of such turbulence would preheat the pairs and thus lead to a solution with a moderate shock velocity relative to downstream (corresponding to the last case of equipartition discussed above).
$xx$
component. As discussed here and in the previous section, such a component could arise from the shock corrugation directly or from the nonlinear processing of the magnetic modulations induced by shock corrugation. The following subsections also argue that the partial dissipation of such turbulence would preheat the pairs and thus lead to a solution with a moderate shock velocity relative to downstream (corresponding to the last case of equipartition discussed above).
3 Particle pre-acceleration and acceleration
3.1 Collisionless damping of hydromagnetic waves
Even if
![]() $w_{2}\ll B_{2}^{2}/(4{\rm\pi}),\langle {\it\delta}B_{2}^{2}\rangle /(4{\rm\pi})$
immediately downstream of the shock, various dissipative effects will transfer energy from the magnetized turbulence to the particles, thereby decreasing the magnetization of the plasma to values of order unity (see below). This section discusses the collisionless damping of magnetosonic modes at the Landau resonance; stochastic particle acceleration will be discussed in § 3.2; other processes, such as turbulent reconnection, are of course plausible sources of dissipation.
$w_{2}\ll B_{2}^{2}/(4{\rm\pi}),\langle {\it\delta}B_{2}^{2}\rangle /(4{\rm\pi})$
immediately downstream of the shock, various dissipative effects will transfer energy from the magnetized turbulence to the particles, thereby decreasing the magnetization of the plasma to values of order unity (see below). This section discusses the collisionless damping of magnetosonic modes at the Landau resonance; stochastic particle acceleration will be discussed in § 3.2; other processes, such as turbulent reconnection, are of course plausible sources of dissipation.
The collisionless damping of hydromagnetic waves in a relativistic plasma has been discussed by Barnes & Scargle (Reference Barnes and Scargle1973). At the Landau resonance, they find
where
![]() ${\it\omega}$
corresponds to the wave frequency,
${\it\omega}$
corresponds to the wave frequency,
![]() $W_{{\it\delta}B_{k}}\sim {\it\delta}B_{k}^{2}/(4{\rm\pi})$
to the wave energy density,
$W_{{\it\delta}B_{k}}\sim {\it\delta}B_{k}^{2}/(4{\rm\pi})$
to the wave energy density,
![]() ${\it\theta}$
to the angle between
${\it\theta}$
to the angle between
![]() $\boldsymbol{k}$
and
$\boldsymbol{k}$
and
![]() $\boldsymbol{B}_{2}$
,
$\boldsymbol{B}_{2}$
,
![]() ${\it\Theta}$
to the Heaviside function, and
${\it\Theta}$
to the Heaviside function, and
![]() ${\it\sigma}$
to the magnetization, i.e. the ratio between the magnetic energy density and the electron energy density. Finally,
${\it\sigma}$
to the magnetization, i.e. the ratio between the magnetic energy density and the electron energy density. Finally,
is the resonance parameter.
As discussed in Barnes & Scargle (Reference Barnes and Scargle1973), the presence of the Heaviside function limits the damping coefficient of waves by defining a critical angle beyond which Landau damping vanishes. The real frequency of magnetosonic waves propagating at an angle
![]() ${\it\theta}$
to the magnetic field is given by
${\it\theta}$
to the magnetic field is given by
with the plus sign pertaining to fast magnetosonic waves, and the minus sign to slow magnetosonic waves;
![]() ${\it\beta}_{+}^{2}\equiv {\it\beta}_{A}^{2}+c_{s}^{2}-{\it\beta}_{A}^{2}c_{s}^{2}$
in terms of the (relativistic) Alfvén velocity
${\it\beta}_{+}^{2}\equiv {\it\beta}_{A}^{2}+c_{s}^{2}-{\it\beta}_{A}^{2}c_{s}^{2}$
in terms of the (relativistic) Alfvén velocity
![]() ${\it\beta}_{A}$
and sound velocity
${\it\beta}_{A}$
and sound velocity
![]() $c_{s}$
. Assuming an isotropic bath of waves, one can calculate the average damping coefficient, relatively to the mode wavenumber, as
$c_{s}$
. Assuming an isotropic bath of waves, one can calculate the average damping coefficient, relatively to the mode wavenumber, as
For fast magnetosonic waves in a strongly magnetized plasma (
![]() ${\it\sigma}\gg 1$
), the fast magnetosonic wave phase velocity approaches unity, so that the critical angle
${\it\sigma}\gg 1$
), the fast magnetosonic wave phase velocity approaches unity, so that the critical angle
![]() ${\it\theta}_{c}\sim 0$
, implying
${\it\theta}_{c}\sim 0$
, implying
![]() $\langle \text{Im}\,{\it\omega}/kc\rangle \approx 0$
; those waves are effectively undamped in the highly magnetized regime. At more moderate magnetization, damping may become appreciable however: at
$\langle \text{Im}\,{\it\omega}/kc\rangle \approx 0$
; those waves are effectively undamped in the highly magnetized regime. At more moderate magnetization, damping may become appreciable however: at
![]() ${\it\sigma}=1$
for instance,
${\it\sigma}=1$
for instance,
![]() $\langle \text{Im}\,{\it\omega}/kc\rangle \approx 10^{-4}$
.
$\langle \text{Im}\,{\it\omega}/kc\rangle \approx 10^{-4}$
.
For slow magnetosonic waves, however, one finds typically
at
![]() ${\it\sigma}\gtrsim 1$
.
${\it\sigma}\gtrsim 1$
.
The above should be considered as a lower limit to
![]() $\text{Im}\,{\it\omega}$
since the above neglects Landau-synchrotron damping effects, as well as other dissipative effects. It nevertheless makes it possible to set an upper limit on the damping length associated with the shock corrugation:
$\text{Im}\,{\it\omega}$
since the above neglects Landau-synchrotron damping effects, as well as other dissipative effects. It nevertheless makes it possible to set an upper limit on the damping length associated with the shock corrugation:
![]() ${\it\lambda}_{\text{diss.}}\simeq {\it\beta}_{\text{f}}c\langle \text{Im}\,{\it\omega}\rangle ^{-1}$
.
${\it\lambda}_{\text{diss.}}\simeq {\it\beta}_{\text{f}}c\langle \text{Im}\,{\it\omega}\rangle ^{-1}$
.
In the more realistic case of corrugation spread over a broad range of
![]() $k$
-modes, the above indicates that the short-scale modes (large
$k$
-modes, the above indicates that the short-scale modes (large
![]() $k$
) will dissipate on short length-scales
$k$
) will dissipate on short length-scales
![]() $\propto k^{-1}$
. Turbulence on the large scales may dissipate through cascading to shorter scales, followed by damping; given that fluctuations are mildly relativistic behind the shock front if corrugation is mildly non-relativistic, as discussed above, the typical time scale of eddy cascading may not be much larger than
$\propto k^{-1}$
. Turbulence on the large scales may dissipate through cascading to shorter scales, followed by damping; given that fluctuations are mildly relativistic behind the shock front if corrugation is mildly non-relativistic, as discussed above, the typical time scale of eddy cascading may not be much larger than
![]() $(kc)^{-1}$
, implying an efficient damping of slow magnetosonic turbulence. The general picture that characterizes nonlinear shock corrugation is thus the generation of a turbulent layer behind the shock front, a part of which dissipates on a small length-scale
$(kc)^{-1}$
, implying an efficient damping of slow magnetosonic turbulence. The general picture that characterizes nonlinear shock corrugation is thus the generation of a turbulent layer behind the shock front, a part of which dissipates on a small length-scale
![]() ${\it\lambda}_{\text{diss.}}\sim O(k_{\text{peak}}^{-1})$
,
${\it\lambda}_{\text{diss.}}\sim O(k_{\text{peak}}^{-1})$
,
![]() $k_{\text{peak}}$
denoting the mode on which the maximum turbulent power is concentrated.
$k_{\text{peak}}$
denoting the mode on which the maximum turbulent power is concentrated.
At such a corrugated shock front,
![]() $\langle {\it\delta}B_{2}^{2}\rangle \sim B_{2}^{2}$
and slow magnetosonic waves carry a significant fraction of the turbulence magnetic energy density. Therefore, on a distance scale
$\langle {\it\delta}B_{2}^{2}\rangle \sim B_{2}^{2}$
and slow magnetosonic waves carry a significant fraction of the turbulence magnetic energy density. Therefore, on a distance scale
![]() ${\it\lambda}_{\text{diss.}}$
, a fraction
${\it\lambda}_{\text{diss.}}$
, a fraction
![]() ${\it\eta}_{s}$
, with
${\it\eta}_{s}$
, with
![]() ${\it\eta}_{s}$
not far below unity, of the magnetic energy density has been dissipated into particles, reducing the magnetization from
${\it\eta}_{s}$
not far below unity, of the magnetic energy density has been dissipated into particles, reducing the magnetization from
immediately downstream of the shock, to
beyond the dissipation layer. Consequently, if
![]() ${\it\sigma}_{2<}\gtrsim 1$
and
${\it\sigma}_{2<}\gtrsim 1$
and
![]() ${\it\eta}_{s}\gtrsim 1/{\it\sigma}_{2<}$
, the magnetization is reduced to values
${\it\eta}_{s}\gtrsim 1/{\it\sigma}_{2<}$
, the magnetization is reduced to values
![]() ${\it\sigma}_{2>}\simeq (1-{\it\eta}_{s})/{\it\eta}_{s}$
, of order unity, independently of how high the magnetization initially was.
${\it\sigma}_{2>}\simeq (1-{\it\eta}_{s})/{\it\eta}_{s}$
, of order unity, independently of how high the magnetization initially was.
In this way, a magnetized relativistic corrugated shock wave can efficiently dissipate the incoming magnetic energy into the shock, leading to a near hydrodynamical shock with a magnetization of order unity beyond
![]() ${\it\lambda}_{\text{diss.}}$
.
${\it\lambda}_{\text{diss.}}$
.
3.2 Phenomenological model of particle pre-acceleration
The acceleration of particles in a bath of magnetized turbulence can be described in a phenomenological way through a Fokker–Planck equation for the distribution function
![]() $f(\boldsymbol{p},t)$
of particlesFootnote
1
:
$f(\boldsymbol{p},t)$
of particlesFootnote
1
:
where
![]() $q$
models the injection of particles into the dissipation region,
$q$
models the injection of particles into the dissipation region,
![]() ${\it\tau}_{\text{esc}}$
the escape time scale out of the dissipation region and
${\it\tau}_{\text{esc}}$
the escape time scale out of the dissipation region and
![]() ${\dot{p}}$
characterizes systematic energy gains/losses. Dissipation is characterized by the diffusion coefficient in momentum space
${\dot{p}}$
characterizes systematic energy gains/losses. Dissipation is characterized by the diffusion coefficient in momentum space
The injection function takes the form
![]() $q(p)={\dot{n}}/(4{\rm\pi}p_{0}^{2}){\it\delta}(p-p_{0})$
, with
$q(p)={\dot{n}}/(4{\rm\pi}p_{0}^{2}){\it\delta}(p-p_{0})$
, with
![]() ${\dot{n}}$
the density of particles per unit time inflowing into the shock, as measured in the downstream rest frame; the injection momentum
${\dot{n}}$
the density of particles per unit time inflowing into the shock, as measured in the downstream rest frame; the injection momentum
![]() $p_{0}$
is related to the shock Lorentz factor through
$p_{0}$
is related to the shock Lorentz factor through
![]() $p_{0}\simeq {\it\gamma}_{1}mc$
.
$p_{0}\simeq {\it\gamma}_{1}mc$
.
Ignoring systematic energy gains/losses and considering a stationary state, standard techniques (e.g. Schlickeiser Reference Schlickeiser1984) make it possible to solve the above equation for various momentum dependences of
![]() $D_{pp}$
and
$D_{pp}$
and
![]() ${\it\tau}_{\text{esc}}$
. In the problem at hand, escape presumably takes place through advection at velocity
${\it\tau}_{\text{esc}}$
. In the problem at hand, escape presumably takes place through advection at velocity
![]() ${\it\beta}_{\text{f}}$
, as the dissipation region is confined to a distance
${\it\beta}_{\text{f}}$
, as the dissipation region is confined to a distance
![]() ${\it\lambda}_{\text{diss.}}$
from the shock front, which itself moves away at velocity
${\it\lambda}_{\text{diss.}}$
from the shock front, which itself moves away at velocity
![]() ${\it\beta}_{\text{f}}$
. Thus
${\it\beta}_{\text{f}}$
. Thus
![]() ${\it\tau}_{\text{esc}}\propto p^{0}$
; as for the momentum diffusion coefficient, it is written
${\it\tau}_{\text{esc}}\propto p^{0}$
; as for the momentum diffusion coefficient, it is written
where
![]() ${\it\tau}_{s,0}$
characterizes the typical acceleration time scale at momentum
${\it\tau}_{s,0}$
characterizes the typical acceleration time scale at momentum
![]() $p_{0}$
. For
$p_{0}$
. For
![]() ${\it\alpha}=0$
, corresponding to the simplest scaling with an interaction time in the turbulence that does not depend on momentum, one finds
${\it\alpha}=0$
, corresponding to the simplest scaling with an interaction time in the turbulence that does not depend on momentum, one finds
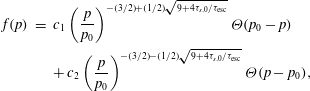 $$\begin{eqnarray}\displaystyle f(p) & = & \displaystyle c_{1}\left(\frac{p}{p_{0}}\right)^{-(3/2)+(1/2)\sqrt{9+4{\it\tau}_{s,0}/{\it\tau}_{\text{e sc }}}}{\it\Theta}(p_{0}-p)\nonumber\\ \displaystyle & & \displaystyle +\,c_{2}\left(\frac{p}{p_{0}}\right)^{-(3/2)-(1/2)\sqrt{9+4{\it\tau}_{s,0}/{\it\tau}_{\text{e sc }}}}{\it\Theta}(p-p_{0}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f(p) & = & \displaystyle c_{1}\left(\frac{p}{p_{0}}\right)^{-(3/2)+(1/2)\sqrt{9+4{\it\tau}_{s,0}/{\it\tau}_{\text{e sc }}}}{\it\Theta}(p_{0}-p)\nonumber\\ \displaystyle & & \displaystyle +\,c_{2}\left(\frac{p}{p_{0}}\right)^{-(3/2)-(1/2)\sqrt{9+4{\it\tau}_{s,0}/{\it\tau}_{\text{e sc }}}}{\it\Theta}(p-p_{0}),\end{eqnarray}$$
where
![]() $c_{1}$
and
$c_{1}$
and
![]() $c_{2}$
are two integration constants related to
$c_{2}$
are two integration constants related to
![]() ${\dot{n}}$
,
${\dot{n}}$
,
![]() $p_{0}$
,
$p_{0}$
,
![]() ${\it\tau}_{s,0}$
and
${\it\tau}_{s,0}$
and
![]() ${\it\tau}_{\text{esc}}$
. The asymptotic behaviour at large momenta is thus a power-law
${\it\tau}_{\text{esc}}$
. The asymptotic behaviour at large momenta is thus a power-law
![]() $f(p)\propto p^{-s_{f}}$
with index
$f(p)\propto p^{-s_{f}}$
with index
which depends on how fast escape balances acceleration. One should keep in mind that this index is that of the distribution function in the acceleration zone, so that the index of the distribution function per momentum interval
![]() $\text{d}N/\text{d}p\propto p^{-s}$
in this acceleration zone is
$\text{d}N/\text{d}p\propto p^{-s}$
in this acceleration zone is
![]() $s=s_{f}-2$
. As to the distribution of escaping particles, i.e. those that eventually populate the nebula, its index is in principle modified by the escape rate, i.e.
$s=s_{f}-2$
. As to the distribution of escaping particles, i.e. those that eventually populate the nebula, its index is in principle modified by the escape rate, i.e.
but since
![]() ${\it\tau}_{\text{esc}}\propto p^{0}$
here, the index remains unchanged.
${\it\tau}_{\text{esc}}\propto p^{0}$
here, the index remains unchanged.
The above phenomenological model indicates that the dissipation of the turbulence produced by corrugation leads to a power-law with index
![]() $s$
comprised between
$s$
comprised between
![]() $1$
and
$1$
and
![]() $2$
if
$2$
if
![]() ${\it\tau}_{s,0}\sim {\it\tau}_{\text{esc}}$
. The development of this power-law does not remain unbounded, because most of the energy is then carried by particles of maximum momentum, if
${\it\tau}_{s,0}\sim {\it\tau}_{\text{esc}}$
. The development of this power-law does not remain unbounded, because most of the energy is then carried by particles of maximum momentum, if
![]() $s<2$
. Thus, in the absence of significant energy losses, one expects that the dissipation process saturates at a momentum such that a significant fraction of the turbulence energy density has been dissipated into the particles, i.e. such that the backreaction of the dissipation process on the turbulence energy density cannot be ignored. This takes place on a length scale
$s<2$
. Thus, in the absence of significant energy losses, one expects that the dissipation process saturates at a momentum such that a significant fraction of the turbulence energy density has been dissipated into the particles, i.e. such that the backreaction of the dissipation process on the turbulence energy density cannot be ignored. This takes place on a length scale
![]() ${\it\lambda}_{\text{diss.}}$
which, accounting for all dissipative processes, characterizes the width of the layer beyond which a fraction of order unity of the magnetized turbulence energy has been dumped into the particles.
${\it\lambda}_{\text{diss.}}$
which, accounting for all dissipative processes, characterizes the width of the layer beyond which a fraction of order unity of the magnetized turbulence energy has been dumped into the particles.
3.3 Fermi acceleration
One may also expect the development of a relativistic Fermi process in the above conditions. As a note of caution, however, the following discussion remains qualitative and further work would be needed to establish this statement on solid grounds.
At a relativistic shock of moderate to large magnetization, the Fermi process is inhibited because of the superluminal nature of the magnetic configuration. Lemoine, Pelletier & Revenu (Reference Lemoine, Pelletier and Revenu2006) and Pelletier, Lemoine & Marcowith (Reference Pelletier, Lemoine and Marcowith2009) have discussed in some detail what prevents Fermi cycles in such a configuration but it may be useful for the present discussion to recall the salient points. Consider a planar relativistic magnetized shock, with some turbulence upstream of the shock, laid on a scale
![]() ${\it\lambda}$
assumed much larger than the typical gyroradius
${\it\lambda}$
assumed much larger than the typical gyroradius
![]() $r_{\text{g}}$
of accelerated particles in the downstream rest frame. A key point is that the accelerated particles only probe a region of size
$r_{\text{g}}$
of accelerated particles in the downstream rest frame. A key point is that the accelerated particles only probe a region of size
![]() $r_{\text{g}}$
during their Fermi cycles in such turbulence: those that probe a deeper region downstream of the shock are actually unable to return to the shock because of the superluminal nature of the shock wave: in order to do so, particles would need to diffuse across the magnetic field at an effective velocity larger than
$r_{\text{g}}$
during their Fermi cycles in such turbulence: those that probe a deeper region downstream of the shock are actually unable to return to the shock because of the superluminal nature of the shock wave: in order to do so, particles would need to diffuse across the magnetic field at an effective velocity larger than
![]() ${\it\beta}_{\text{f}}$
. Thus, on the length scale
${\it\beta}_{\text{f}}$
. Thus, on the length scale
![]() $r_{\text{g}}\ll {\it\lambda}$
probed by the particles, the turbulence appears as an essentially coherent magnetic field. One may then show that incoming particles can execute at most 1.5 Fermi cycles up
$r_{\text{g}}\ll {\it\lambda}$
probed by the particles, the turbulence appears as an essentially coherent magnetic field. One may then show that incoming particles can execute at most 1.5 Fermi cycles up
![]() $\rightarrow$
down
$\rightarrow$
down
![]() $\rightarrow$
up
$\rightarrow$
up
![]() $\rightarrow$
down in this configuration before being advected downstream, away from the shock. Those particles that are able to return once to the shock are those whose momentum is oriented relative to the magnetic field in such a way as to authorize a bounce on the downstream magnetic field, pushing them back across the shock; but, for a near coherent upstream magnetic field, this can happen only once for any particle.
$\rightarrow$
down in this configuration before being advected downstream, away from the shock. Those particles that are able to return once to the shock are those whose momentum is oriented relative to the magnetic field in such a way as to authorize a bounce on the downstream magnetic field, pushing them back across the shock; but, for a near coherent upstream magnetic field, this can happen only once for any particle.
For this reason, at a steady planar shock front, it has been proposed that particle acceleration was associated with the development of intense micro-turbulence on a scale
![]() $\ll r_{\text{g}}$
, in the shock precursor (Lemoine et al.
Reference Lemoine, Pelletier and Revenu2006; Pelletier et al.
Reference Pelletier, Lemoine and Marcowith2009). This point of view has been validated by particle-in-cell numerical simulations which observe the concomitant development of micro-turbulence and of particle acceleration (e.g. Spitkovsky Reference Spitkovsky2008; Martins et al.
Reference Martins, Fonseca, Silva and Mori2009; Sironi, Spitkovsky & Arons Reference Sironi, Spitkovsky and Arons2013).
$\ll r_{\text{g}}$
, in the shock precursor (Lemoine et al.
Reference Lemoine, Pelletier and Revenu2006; Pelletier et al.
Reference Pelletier, Lemoine and Marcowith2009). This point of view has been validated by particle-in-cell numerical simulations which observe the concomitant development of micro-turbulence and of particle acceleration (e.g. Spitkovsky Reference Spitkovsky2008; Martins et al.
Reference Martins, Fonseca, Silva and Mori2009; Sironi, Spitkovsky & Arons Reference Sironi, Spitkovsky and Arons2013).
However, a crucial point of the previous argument is that the direction of the coherent magnetic field line in the shock front plane is conserved through the crossing of the shock. If this direction were randomized through some process, then particles could bounce on the downstream magnetic field with a non-zero probability at any Fermi cycle and return to the shock. This bounce would be similar to an isotropization of the particle directions downstream, i.e. similar to a fast isotropic scattering process. Therefore, it would lead to the development of a Fermi process as modelled by early test-particle Monte Carlo simulations (which implicitly assumed the non-conservation of the direction of the magnetic field in the shock front plane) (e.g. Bednarz & Ostrowski Reference Bednarz and Ostrowski1998; Kirk et al.
Reference Kirk, Guthmann, Gallant and Achterberg2000; Achterberg et al.
Reference Achterberg, Gallant, Kirk and Guthmann2001; Lemoine & Pelletier Reference Lemoine and Pelletier2003), with an index
![]() $s\simeq 2.2$
for
$s\simeq 2.2$
for
![]() $\text{d}N/\text{d}p\propto p^{-s}$
.
$\text{d}N/\text{d}p\propto p^{-s}$
.
Returning to the corrugated shock front, if
![]() $\langle {\it\delta}B_{2}^{2}\rangle ^{1/2}\sim B_{2}$
on a scale
$\langle {\it\delta}B_{2}^{2}\rangle ^{1/2}\sim B_{2}$
on a scale
![]() $k^{-1}$
, corrugation precisely does the above: even in the absence of upstream turbulence, the in-plane direction of the downstream magnetic field is randomized on a scale
$k^{-1}$
, corrugation precisely does the above: even in the absence of upstream turbulence, the in-plane direction of the downstream magnetic field is randomized on a scale
![]() $k^{-1}$
by the generation of turbulence at the corrugated shock. This should therefore lead to an efficient Fermi process for particles of gyroradius
$k^{-1}$
by the generation of turbulence at the corrugated shock. This should therefore lead to an efficient Fermi process for particles of gyroradius
![]() $r_{\text{g}}\sim k^{-1}$
, although this should admittedly be explicitly demonstrated by dedicated numerical simulations. Interestingly, if corrugation sustains acceleration in the above way, the typical acceleration time scale is then expected of order
$r_{\text{g}}\sim k^{-1}$
, although this should admittedly be explicitly demonstrated by dedicated numerical simulations. Interestingly, if corrugation sustains acceleration in the above way, the typical acceleration time scale is then expected of order
![]() $r_{\text{g}}/c$
in the shock frame, as in the above test-particle simulations of the relativistic Fermi process.
$r_{\text{g}}/c$
in the shock frame, as in the above test-particle simulations of the relativistic Fermi process.
How this process affects particles of gyroradius
![]() $r_{\text{g}}\ll k^{-1}$
is not obvious. In a first approximation, one could expect Fermi acceleration to be inoperant in that range of gyroradii because those particles ‘see’ the turbulent field as an essentially coherent field. However, the scale
$r_{\text{g}}\ll k^{-1}$
is not obvious. In a first approximation, one could expect Fermi acceleration to be inoperant in that range of gyroradii because those particles ‘see’ the turbulent field as an essentially coherent field. However, the scale
![]() $r_{\text{g}}$
is then also much smaller than the corrugation amplitude
$r_{\text{g}}$
is then also much smaller than the corrugation amplitude
![]() $|{\it\delta}X|$
, hence the time dependence of the corrugation, the rippled shock structure and the relativistic turbulence existing in this layer could help sustain acceleration. At the opposite extreme,
$|{\it\delta}X|$
, hence the time dependence of the corrugation, the rippled shock structure and the relativistic turbulence existing in this layer could help sustain acceleration. At the opposite extreme,
![]() $r_{\text{g}}\gg k^{-1}$
, the turbulence may sustain acceleration, as long as the scattering frequency
$r_{\text{g}}\gg k^{-1}$
, the turbulence may sustain acceleration, as long as the scattering frequency
![]() $k^{-1}/r_{\text{g}}^{2}$
remains larger than the advection frequency
$k^{-1}/r_{\text{g}}^{2}$
remains larger than the advection frequency
![]() $r_{\text{g},0}^{-1}$
in the background magnetic field (the index 0 meaning that
$r_{\text{g},0}^{-1}$
in the background magnetic field (the index 0 meaning that
![]() $r_{\text{g},0}$
is to be calculated relatively to the background field).
$r_{\text{g},0}$
is to be calculated relatively to the background field).
In any case, one does not expect corrugation to occur on a single scale
![]() $k$
, but on a broad range of scales; in this case, the above argument suggests that acceleration should at least take place for all
$k$
, but on a broad range of scales; in this case, the above argument suggests that acceleration should at least take place for all
![]() $r_{\text{g}}$
in gyroresonance with the inertial range provided
$r_{\text{g}}$
in gyroresonance with the inertial range provided
![]() $\langle {\it\delta}B_{2}^{2}\rangle ^{1/2}\sim B_{2}$
can be realized on those scales, i.e. provided corrugation is mildly nonlinear on all scales.
$\langle {\it\delta}B_{2}^{2}\rangle ^{1/2}\sim B_{2}$
can be realized on those scales, i.e. provided corrugation is mildly nonlinear on all scales.
The overall picture becomes somewhat more complicated in the presence of dissipation downstream of the shock, in particular how stochastic energy gains interplay with systematic energy gains due to the Fermi process. However, given that the Fermi process only transfers a small fraction of the available energy to a small fraction of particles, one may expect that dissipation would build up the hard power-law until near equipartition with the magnetic field and that the Fermi power-law would develop at higher momenta, until it saturates due to energy losses.
4 Discussion
The previous sections have argued that the corrugation of a magnetized relativistic shock front, at the onset of the nonlinear regime of corrugation, could lead to interesting phenomenology. In particular, it could provide an efficient source of dissipation of the magnetic energy of the upstream flow, by converting the ordered magnetic field into turbulence modes via its advection through the rippled shock, with subsequent dissipation of the turbulent modes into suprathermal particle energy, reducing the initial magnetization to values of order unity on a length scale
![]() ${\it\lambda}_{\text{diss.}}$
. It has also been shown that this conversion into turbulence appreciably slows down the flow velocity behind the shock (as now seen in the shock rest frame). This section discusses possible sources of the corrugation and how the above picture fits in a general model of PWNe.
${\it\lambda}_{\text{diss.}}$
. It has also been shown that this conversion into turbulence appreciably slows down the flow velocity behind the shock (as now seen in the shock rest frame). This section discusses possible sources of the corrugation and how the above picture fits in a general model of PWNe.
4.1 Sources of corrugation
The stability of a shock front responding to small perturbations forms a topic of research with a long history, going back to the pioneering studies of D’Iakov (Reference D’Iakov1958) and Kontorovich (Reference Kontorovich1958). Theorems guarantee the stability of relativistic shock waves with a polytropic equation of state (Anile & Russo Reference Anile and Russo1986, Reference Anile and Russo1987), although a corrugation instability may emerge in specific cases, such as in a relativistic radiative shock (Tsintsadze et al. Reference Tsintsadze, Chilashvili, Shukla and Tsintsadze1997). In this limit of instability to corrugation, small perturbations would induce a deformation which would grow exponentially in time; this possibility is, however, not considered in the present work.
Even if stable with respect to the corrugation instability, a shock front may respond strongly to incoming perturbations, as discussed in the above references, or in Landau & Lifshitz (Reference Landau and Lifshitz1987). A recent discussion of the response, possibly resonant, of a relativistic magnetized shock to small amplitude disturbances can be found in Lemoine et al. (Reference Lemoine, Ramos and Gremillet2016); its consequences are discussed further below.
Corrugation can be seeded by at least three sources: turbulence waves originating from downstream and impacting the shock, turbulence modes originating from upstream being advected through the shock, and through instabilities seeded upstream of the shock by the accelerated particles themselves.
As far as downstream waves are concerned, only fast magnetosonic modes propagating at a group velocity larger than the shock velocity
![]() ${\it\beta}_{\text{f}}$
are able to induce corrugation. If
${\it\beta}_{\text{f}}$
are able to induce corrugation. If
![]() ${\it\delta}{\it\psi}_{\boldsymbol{k}}$
denotes the amplitude of the wave (with
${\it\delta}{\it\psi}_{\boldsymbol{k}}$
denotes the amplitude of the wave (with
![]() ${\it\delta}{\it\psi}_{\boldsymbol{k}}\equiv {\it\delta}B_{\boldsymbol{k}}/B$
), the corrugation amplitude can be written to a reasonable accuracy as
${\it\delta}{\it\psi}_{\boldsymbol{k}}\equiv {\it\delta}B_{\boldsymbol{k}}/B$
), the corrugation amplitude can be written to a reasonable accuracy as
The presence of
![]() $k^{-1}$
is directly related to the dimension of the quantity of the left-hand side, of course. This result implies that nonlinear corrugation of the shock front requires nonlinear fast magnetosonic waves, meaning
$k^{-1}$
is directly related to the dimension of the quantity of the left-hand side, of course. This result implies that nonlinear corrugation of the shock front requires nonlinear fast magnetosonic waves, meaning
![]() ${\it\delta}B/B\sim 1$
for the incoming waves or, in other words, that the turbulence carries an energy density comparable to that of the average magnetic field advected through the shock. This is certainly not a trivial requirement, but it seems to be fulfilled at least in the numerical simulations of Camus et al. (Reference Camus, Komissarov, Bucciantini and Hughes2009) which observed a strong backreaction of the nebular turbulence on the shock. One should also keep in mind that the above implicitly assumes a stationary configuration; time-dependent turbulence might have a stronger effect, as suggested by the discussion of Lyutikov, Balsara & Matthews (Reference Lyutikov, Balsara and Matthews2012). Those simulations have not addressed the dynamical range of scales over which the corrugation could be present; presumably however, all scales up to the shock termination radius
${\it\delta}B/B\sim 1$
for the incoming waves or, in other words, that the turbulence carries an energy density comparable to that of the average magnetic field advected through the shock. This is certainly not a trivial requirement, but it seems to be fulfilled at least in the numerical simulations of Camus et al. (Reference Camus, Komissarov, Bucciantini and Hughes2009) which observed a strong backreaction of the nebular turbulence on the shock. One should also keep in mind that the above implicitly assumes a stationary configuration; time-dependent turbulence might have a stronger effect, as suggested by the discussion of Lyutikov, Balsara & Matthews (Reference Lyutikov, Balsara and Matthews2012). Those simulations have not addressed the dynamical range of scales over which the corrugation could be present; presumably however, all scales up to the shock termination radius
![]() $R$
could be excited.
$R$
could be excited.
If turbulence is present upstream of the shock front to substantial levels, as proposed recently (Zrake Reference Zrake2015), nonlinear corrugation should follow owing to the existence of a resonance of the response of the shock to the incoming turbulence (Lemoine et al.
Reference Lemoine, Ramos and Gremillet2016). This latter work has shown that the resonance occurs when the fast magnetosonic mode, which is sourced downstream of the shock by the shock corrugation, has a group velocity corresponding to
![]() ${\it\beta}_{\text{f}}$
, i.e. when this fast mode surfs along with the shock front. The large response of the shock corrugation was then interpreted as the build-up of fast magnetosonic energy on the shock front. Since the group velocity is determined by the wavenumber
${\it\beta}_{\text{f}}$
, i.e. when this fast mode surfs along with the shock front. The large response of the shock corrugation was then interpreted as the build-up of fast magnetosonic energy on the shock front. Since the group velocity is determined by the wavenumber
![]() $k_{x}$
at a given
$k_{x}$
at a given
![]() $\boldsymbol{k}_{\bot }$
, this resonance selects one value of the incoming
$\boldsymbol{k}_{\bot }$
, this resonance selects one value of the incoming
![]() $k_{x}$
, with typically
$k_{x}$
, with typically
![]() $k_{x}\sim |\boldsymbol{k}_{\bot }|$
at a magnetized relativistic shock where
$k_{x}\sim |\boldsymbol{k}_{\bot }|$
at a magnetized relativistic shock where
![]() ${\it\beta}_{\text{f}}$
does not lie far below unity.
${\it\beta}_{\text{f}}$
does not lie far below unity.
Depending on
![]() $\boldsymbol{k}_{\bot }$
, one may observe a formally infinite response of the shock, or a large amplification of the incoming waves at the resonance. This thus opens the possibility of reaching the threshold of nonlinear corrugation with a source whose energy content is less than that of the incoming ordered magnetic field. The study of Lemoine et al. (Reference Lemoine, Ramos and Gremillet2016) has been conducted in linearized MHD, therefore it cannot probe the deep nonlinear regime of corrugation; it seems reasonable to assume that, on those resonant scales, the shock is corrugated with amplitude
$\boldsymbol{k}_{\bot }$
, one may observe a formally infinite response of the shock, or a large amplification of the incoming waves at the resonance. This thus opens the possibility of reaching the threshold of nonlinear corrugation with a source whose energy content is less than that of the incoming ordered magnetic field. The study of Lemoine et al. (Reference Lemoine, Ramos and Gremillet2016) has been conducted in linearized MHD, therefore it cannot probe the deep nonlinear regime of corrugation; it seems reasonable to assume that, on those resonant scales, the shock is corrugated with amplitude
![]() $|k_{\bot }{\it\delta}X_{\boldsymbol{k}}|\sim 1$
, as envisaged here. Furthermore, since there exists one resonant wavenumber
$|k_{\bot }{\it\delta}X_{\boldsymbol{k}}|\sim 1$
, as envisaged here. Furthermore, since there exists one resonant wavenumber
![]() $k_{x}$
for each
$k_{x}$
for each
![]() $\boldsymbol{k}_{\bot }$
, one should expect that nonlinear corrugation takes place on all inertial scales present in the incoming turbulence spectrum. Note that these wavenumbers are specified in the downstream rest frame; in the upstream rest frame, which moves relative to the former with Lorentz factor
$\boldsymbol{k}_{\bot }$
, one should expect that nonlinear corrugation takes place on all inertial scales present in the incoming turbulence spectrum. Note that these wavenumbers are specified in the downstream rest frame; in the upstream rest frame, which moves relative to the former with Lorentz factor
![]() ${\it\gamma}_{1}$
and velocity
${\it\gamma}_{1}$
and velocity
![]() ${\it\beta}_{1}$
,
${\it\beta}_{1}$
,
![]() $k_{x|1}=k_{x}/{\it\gamma}_{1}-{\it\beta}_{1}{\it\omega}_{A|1}/c$
, i.e.
$k_{x|1}=k_{x}/{\it\gamma}_{1}-{\it\beta}_{1}{\it\omega}_{A|1}/c$
, i.e.
![]() $k_{x|1}\simeq -{\it\beta}_{1}{\it\beta}_{A|1}k_{z}$
for
$k_{x|1}\simeq -{\it\beta}_{1}{\it\beta}_{A|1}k_{z}$
for
![]() ${\it\gamma}_{1}\gg 1$
and an Alfvén wave of frequency
${\it\gamma}_{1}\gg 1$
and an Alfvén wave of frequency
![]() ${\it\omega}_{A|1}={\it\beta}_{A|1}k_{z}c$
.
${\it\omega}_{A|1}={\it\beta}_{A|1}k_{z}c$
.
The sourcing of corrugation through MHD instabilities seeded in the upstream plasma by the accelerated particles themselves represents an interesting alternative. Such instabilities have been discussed in Pelletier et al. (Reference Pelletier, Lemoine and Marcowith2009) and studied through dedicated numerical simulations in Casse, Marcowith & Keppens (Reference Casse, Marcowith and Keppens2013). They can be seen as a generalization of the Bell instability (Bell Reference Bell2004) to the relativistic regime and for perpendicular shocks: the existence of a net charge or current of suprathermal particles executing Fermi orbits in the shock precursor then destabilizes magnetosonic modes of the upstream plasma. If magnetosonic waves are amplified, one may then expect them to induce a resonant response of the shock. Of course, the sourcing of corrugation by the accelerated particles brings in an amusing chicken-and-egg problem if corrugation is a necessary condition for the development of the relativistic Fermi process, as advocated in the previous section.
4.2 Application to the Crab nebula
Let us finally discuss how the above discussion might apply to the termination shock of the Crab pulsar wind. One should first point out, however, that the existence of dissipation has been demonstrated by Komissarov (Reference Komissarov2013), through the comparison between the present content in magnetic energy in the Crab nebula and that input over its lifetime.
In terms of spectral energy distribution, it is well known that one can reproduce the main observational features by assuming the existence of a broken power-law of the pair population (Atoyan & Aharonian Reference Atoyan and Aharonian1996), with index
![]() $s\simeq 1.6$
for
$s\simeq 1.6$
for
![]() $\text{d}N/\,\text{d}{\it\gamma}$
for
$\text{d}N/\,\text{d}{\it\gamma}$
for
![]() ${\it\gamma}\lesssim {\it\gamma}_{\text{b}}$
, and
${\it\gamma}\lesssim {\it\gamma}_{\text{b}}$
, and
![]() $s\simeq 2.3$
above; the break Lorentz factor inferred is of order
$s\simeq 2.3$
above; the break Lorentz factor inferred is of order
![]() ${\it\gamma}_{\text{b}}\simeq 2\times 10^{6}$
. The maximum synchrotron photon energy is approximately
${\it\gamma}_{\text{b}}\simeq 2\times 10^{6}$
. The maximum synchrotron photon energy is approximately
![]() $100$
MeV, corresponding to the radiation reaction limit energy
$100$
MeV, corresponding to the radiation reaction limit energy
![]() ${\sim}m_{e}c^{2}/{\it\alpha}_{\text{e.m.}}$
(
${\sim}m_{e}c^{2}/{\it\alpha}_{\text{e.m.}}$
(
![]() ${\it\alpha}_{\text{e.m.}}\simeq 1/137$
the electromagnetic fine structure constant). Finally, the magnetic field inferred from a modelling of the nebula,
${\it\alpha}_{\text{e.m.}}\simeq 1/137$
the electromagnetic fine structure constant). Finally, the magnetic field inferred from a modelling of the nebula,
![]() $B\sim 200~{\rm\mu}\text{G}$
, corresponds to rough equipartition with the pair population.
$B\sim 200~{\rm\mu}\text{G}$
, corresponds to rough equipartition with the pair population.
In the present model, this rough equipartition is a natural consequence of magnetic dissipation of turbulence into the pair population. Furthermore, as argued in § 3.2, the pre-acceleration of particles in the turbulence seeded by corrugation may also produce a power-law with an index
![]() $s$
comprised between
$s$
comprised between
![]() $1$
and
$1$
and
![]() $2$
, as observed. If
$2$
, as observed. If
![]() $\text{d}N/\,\text{d}{\it\gamma}\propto {\it\gamma}^{-s}$
with
$\text{d}N/\,\text{d}{\it\gamma}\propto {\it\gamma}^{-s}$
with
![]() $1<s<2$
below
$1<s<2$
below
![]() ${\it\gamma}_{\text{b}}$
, then the break Lorentz factor
${\it\gamma}_{\text{b}}$
, then the break Lorentz factor
where
is the mean Lorentz factor per particle, after a fraction
![]() ${\it\epsilon}_{e}$
of the wind luminosity
${\it\epsilon}_{e}$
of the wind luminosity
![]() $L_{\text{w}}$
has been transferred in the
$L_{\text{w}}$
has been transferred in the
![]() ${\dot{N}}$
pairs advected through the shock per unit time. Assuming a multiplicity
${\dot{N}}$
pairs advected through the shock per unit time. Assuming a multiplicity
![]() ${\it\kappa}=10^{6}{\it\kappa}_{6}$
beyond the standard Goldreich–Julian injection rate
${\it\kappa}=10^{6}{\it\kappa}_{6}$
beyond the standard Goldreich–Julian injection rate
![]() ${\dot{N}}_{\text{GJ}}\simeq e^{-1}\sqrt{L_{\text{w }}c}$
(Goldreich & Julian Reference Goldreich and Julian1969), as seems required for the Crab, one finds
${\dot{N}}_{\text{GJ}}\simeq e^{-1}\sqrt{L_{\text{w }}c}$
(Goldreich & Julian Reference Goldreich and Julian1969), as seems required for the Crab, one finds
![]() ${\it\gamma}_{\text{d}}\simeq 5\times 10^{4}{\it\kappa}_{6}^{-1}$
for
${\it\gamma}_{\text{d}}\simeq 5\times 10^{4}{\it\kappa}_{6}^{-1}$
for
![]() ${\it\epsilon}_{e}\sim 1$
. Setting
${\it\epsilon}_{e}\sim 1$
. Setting
![]() ${\it\gamma}_{\text{b}}\simeq 2\times 10^{6}$
for
${\it\gamma}_{\text{b}}\simeq 2\times 10^{6}$
for
![]() $s=1.6$
then requires a wind Lorentz factor
$s=1.6$
then requires a wind Lorentz factor
From a theoretical point of view, this value seems appealing, because it somewhat alleviates the requirements regarding the acceleration of the wind, which represents a nagging issue in this field (e.g. Kirk et al. Reference Kirk, Lyubarsky, Petri and Becker2009).
Detailed numerical simulations of the Crab nebula have shown that it is possible to explain the main morphological features of this nebula provided the shock accelerates pairs efficiently (e.g. for a review see Kargaltsev et al.
Reference Kargaltsev, Cerutti, Lyubarsky and Striani2015). Interestingly, the nebula reveals slow-moving structures called ‘wisps’, originating from the termination shock; those features have a typical angular size of
![]() $1^{\prime \prime }$
, corresponding to roughly
$1^{\prime \prime }$
, corresponding to roughly
![]() $0.01\text{pc}\sim 0.1R$
(e.g. Schweizer et al.
Reference Schweizer, Bucciantini, Idec, Nilsson, Tennant, Weisskopf and Zanin2013). If those wisps are interpreted as long-lived modes produced by the corrugated shock, then it argues in favour of corrugation up to scales close to
$0.01\text{pc}\sim 0.1R$
(e.g. Schweizer et al.
Reference Schweizer, Bucciantini, Idec, Nilsson, Tennant, Weisskopf and Zanin2013). If those wisps are interpreted as long-lived modes produced by the corrugated shock, then it argues in favour of corrugation up to scales close to
![]() $0.1R$
. Since the highest-energy pairs in the nebula have an energy of
$0.1R$
. Since the highest-energy pairs in the nebula have an energy of
![]() ${\sim}1$
PeV, the maximum gyroradius of accelerated particles is
${\sim}1$
PeV, the maximum gyroradius of accelerated particles is
![]() $r_{\text{g},\text{max}}\sim 0.01$
pc for a nebular field of
$r_{\text{g},\text{max}}\sim 0.01$
pc for a nebular field of
![]() $100~{\rm\mu}\text{G}$
, i.e. of the same order of magnitude as the size of the wisps. In the context of the above discussion, which has suggested that the accelerated particles could seed corrugation on scales
$100~{\rm\mu}\text{G}$
, i.e. of the same order of magnitude as the size of the wisps. In the context of the above discussion, which has suggested that the accelerated particles could seed corrugation on scales
![]() $r_{\text{g}}$
through instabilities in the shock precursor, this connection is rather intriguing. Moreover, the possibility of corrugation up to scales
$r_{\text{g}}$
through instabilities in the shock precursor, this connection is rather intriguing. Moreover, the possibility of corrugation up to scales
![]() $k^{-1}\sim r_{\text{g},\text{max}}$
indicates that Fermi acceleration should be operative up to those scales. As discussed in § 3.3, acceleration should further proceed with an acceleration time scale
$k^{-1}\sim r_{\text{g},\text{max}}$
indicates that Fermi acceleration should be operative up to those scales. As discussed in § 3.3, acceleration should further proceed with an acceleration time scale
![]() ${\sim}r_{\text{g}}/c$
, leading to Bohm-type acceleration up to the radiation reaction limit.
${\sim}r_{\text{g}}/c$
, leading to Bohm-type acceleration up to the radiation reaction limit.
In this regard, one may note that other models trying to explain the pre-acceleration of pairs in the nebula and the dissipation through magnetic reconnection generally fail to account for Bohm acceleration to high energies, because the annihilation of the magnetic field in the striped part of the wind leaves behind a short-scale turbulence, with a slow scattering time scale, hence leading to a maximal energy well below that observed in the Crab nebula, see e.g. Sironi et al. (Reference Sironi, Spitkovsky and Arons2013).
5 Conclusions
This paper has speculated that the termination shock of pulsar winds might be strongly corrugated. It has discussed possible sources of corrugation and exhibited various interesting phenomenological consequences.
Corrugation could in principle be excited by the interaction of downstream fast magnetosonic modes catching up the shock front, through the advection of upstream turbulence modes, or through the generation in the shock precursor of turbulence by particle acceleration. As discussed here and in Lemoine et al. (Reference Lemoine, Ramos and Gremillet2016), the latter two possibilities are more interesting in the present context because of the existence of a resonance in the response of the shock to upstream perturbations, leading to possible large amplification of turbulent modes.
Once corrugation is excited on a range of scales, a fraction of order unity of the incoming ordered magnetic energy is converted into turbulence, immediately downstream of the shock. This conversion appreciably slows down the flow velocity along the shock normal, which could help us to understand why the post-shock nebula moves so slowly in the pulsar rest frame, in accord with the seminal discussion of Kennel & Coroniti (Reference Kennel and Coroniti1984a ). Various dissipative effects could then transfer a sizable fraction of the turbulence energy density into the pair population. In particular, slow magnetosonic modes are rapidly dissipated in a relativistic plasma. A direct consequence is that, independently of the upstream magnetization of the flow, the downstream magnetization beyond this dissipative layer would decrease to values of order unity. This, of course, has significant virtues for understanding the phenomenological properties of the Crab nebula, which indeed reveals a rough equipartition between the pairs and the magnetic energy content.
The pre-acceleration of the pairs in the dissipative layer through stochastic acceleration leads to the emergence of a power-law, with an index
![]() $s$
typically between
$s$
typically between
![]() $1$
and
$1$
and
![]() $2$
, because stochastic acceleration is balanced by escape losses due to advection outside of the dissipative layer. The present paper has also speculated that the excitation of turbulence on a broad range of scales behind the shock could sustain a relativistic Fermi process with a Bohm-type acceleration time scale; this point remains to be demonstrated, however, using, for instance, dedicated test-particle simulations. It has then been shown that this combination of stochastic pre-acceleration followed by Fermi acceleration could potentially aid understanding of the spectral features of the Crab nebula, provided the Lorentz factor of the termination shock is
$2$
, because stochastic acceleration is balanced by escape losses due to advection outside of the dissipative layer. The present paper has also speculated that the excitation of turbulence on a broad range of scales behind the shock could sustain a relativistic Fermi process with a Bohm-type acceleration time scale; this point remains to be demonstrated, however, using, for instance, dedicated test-particle simulations. It has then been shown that this combination of stochastic pre-acceleration followed by Fermi acceleration could potentially aid understanding of the spectral features of the Crab nebula, provided the Lorentz factor of the termination shock is
![]() ${\it\gamma}_{1}\sim 4\times 10^{3}$
in the nebula rest frame (assuming a pair multiplicity
${\it\gamma}_{1}\sim 4\times 10^{3}$
in the nebula rest frame (assuming a pair multiplicity
![]() ${\it\kappa}\sim 10^{6}$
).
${\it\kappa}\sim 10^{6}$
).
Further work is required along several lines to test this speculative model. In particular, dedicated numerical simulations are needed to understand the physics of corrugation in the nonlinear regime through the interaction of a relativistic magnetized shock with upstream perturbations. As mentioned above, dedicated numerical simulations would also be needed to understand how such a corrugated shock can accelerate particles, and with what efficiency. It would be interesting to understand how the accelerated particles could themselves seed perturbations in the upstream plasma, and how such perturbations could influence the shock corrugation pattern. Finally, such simulations would have to be properly placed in a global context to understand the impact of the nebular turbulence on the shock itself.
Acknowledgements
It is a pleasure to thank A. Bykov, L. Gremillet, R. Keppens, G. Pelletier and O. Ramos for insightful discussions and advice. This work has been financially supported by the Programme National Hautes Énergies (PNHE) of the C.N.R.S. and by the ANR-14-CE33-0019 MACH project.



