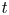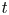1. Introduction
Disruptions pose serious challenges to the operation and design of tokamaks. Due to rapidly growing instabilities, thermal and magnetic energy is rapidly lost during a disruption, the magnetic confinement of the plasma is destroyed and energy is deposited into the confining vessel, potentially causing serious damages. Hence, to maintain a reliable fusion operation, disruption mitigation mechanisms should be triggered with sufficient warning time prior to the disruption. Recent advances on real-time disruption prediction have been made using machine learning (Berkery et al. Reference Berkery, Sabbagh, Bell, Gerhardt and LeBlanc2017; Rea & Granetz Reference Rea and Granetz2018; Kates-Harbeck, Svyatkovskiy & Tang Reference Kates-Harbeck, Svyatkovskiy and Tang2019; Pau et al. Reference Pau, Fanni, Carcangiu, Cannas, Sias, Murari and Rimini2019; Rea et al. Reference Rea, Montes, Erickson, Granetz and Tinguely2019, Reference Rea, Montes, Pau, Granetz and Sauter2020; Aymerich et al. Reference Aymerich, Sias, Pisano, Cannas, Carcangiu, Sozzi, Stuart, Carvalho and Fanni2022). Disruption prediction is a challenging task for various reasons. One of them is the imbalanced data situation; for some disruption classes, only a few measurements are available, making it difficult to obtain robust results. This is challenging, especially when working with neural networks, as they require a large training data set in order to give satisfying results and to avoid overfitting (see e.g. Aggarwal Reference Aggarwal2018). However, generating such an amount of training data from additional discharges is expensive and also potentially harmful for the reactor. Particularly with regard to future reactors such as ITER or SPARC, a sufficient data set will not be available at the time these reactors start operating.
Data augmentation is one possibility to balance the training data set by creating rare disruption events and thereby improving the prediction performance of machine learning models. The aim of data augmentation is to produce an arbitrarily large number of artificial samples that have the same statistical properties as the original small data set. Especially in the context of image classification, data augmentation is a widely used technique to improve the prediction accuracy and avoid overfitting (Shorten & Khoshgoftaar Reference Shorten and Khoshgoftaar2019). Commonly used methods are random transformation-based approaches, such as cropping or flipping. However, these methods are not expedient for the task at hand, as time dependencies and the causal structure of physical signals are destroyed by such transformations (Iwana & Uchida Reference Iwana and Uchida2021; Wen et al. Reference Wen, Sun, Yang, Song, Gao, Wang and Xu2021). More elaborate methods for multivariate time series generation using neural networks (Yoon, Jarrett & van der Schaar Reference Yoon, Jarrett and van der Schaar2019) require substantially more samples per class than usually available for disruption prediction. Other advanced data augmentation methods are based on decomposition into trend, seasonal/periodic signal and noise (Cleveland et al. Reference Cleveland, Cleveland, McRae and Terpenning1990; Wen et al. Reference Wen, Gao, Song, Sun, Xu and Zhu2019) or involve statistical modelling of the dynamics using, e.g. mixture autoregressive models (Kang, Hyndman & Li Reference Kang, Hyndman and Li2020).
Here, we tackle the above-mentioned challenges by relying on a non-parametric Bayesian approach to design the multivariate surrogate model based on Student $t$![]() process regression (Shah, Wilson & Ghahramani Reference Shah, Wilson and Ghahramani2014; Roth et al. Reference Roth, Ardeshiri, Özkan and Gustafsson2017) to generate additional data. This model is closely related to the more commonly used Gaussian process regression (Williams & Rasmussen Reference Williams and Rasmussen1996). One drawback of standard Gaussian processes regression is the assumption of Gaussian noise, which is inaccurate due to outliers in the present application case. This results in unreliable uncertainty estimates. There have been attempts to make Gaussian process regression robust against outliers by using a Student $t$
process regression (Shah, Wilson & Ghahramani Reference Shah, Wilson and Ghahramani2014; Roth et al. Reference Roth, Ardeshiri, Özkan and Gustafsson2017) to generate additional data. This model is closely related to the more commonly used Gaussian process regression (Williams & Rasmussen Reference Williams and Rasmussen1996). One drawback of standard Gaussian processes regression is the assumption of Gaussian noise, which is inaccurate due to outliers in the present application case. This results in unreliable uncertainty estimates. There have been attempts to make Gaussian process regression robust against outliers by using a Student $t$![]() distributed noise model and relying on approximate inference (Neal Reference Neal1997; Vanhatalo, Jylanki & Vehtari Reference Vanhatalo, Jylänki and Vehtari2009). However, our approach rather builds on Student $t$
distributed noise model and relying on approximate inference (Neal Reference Neal1997; Vanhatalo, Jylanki & Vehtari Reference Vanhatalo, Jylänki and Vehtari2009). However, our approach rather builds on Student $t$![]() processes with an analytic inference scheme (Shah et al. Reference Shah, Wilson and Ghahramani2014) that also allows a heavy tailed noise distribution and gives robust results even for noisy data corrupted by outliers.
processes with an analytic inference scheme (Shah et al. Reference Shah, Wilson and Ghahramani2014) that also allows a heavy tailed noise distribution and gives robust results even for noisy data corrupted by outliers.
Another challenge imposed by high-resolution time series data is the computational complexity of multivariate Gaussian or Student $t$![]() process regression of $O(N^3)$
process regression of $O(N^3)$![]() , where $N = DT$
, where $N = DT$![]() is the number of training data points given by the product of dimensions $D$
is the number of training data points given by the product of dimensions $D$![]() and time steps $T$
and time steps $T$![]() of the multivariate time series. For typical values of $N>1000$
of the multivariate time series. For typical values of $N>1000$![]() , traditional regression requires too much computing time. We instead use the state space formulation of a Student $t$
, traditional regression requires too much computing time. We instead use the state space formulation of a Student $t$![]() process as a linear time invariant stochastic differential equation, which can be solved using a corresponding filter and smoother (Solin & Särkkä Reference Solin and Särkkä2015). In the case of a Gaussian process, the analogous approach is the well-known Kalman filter and Rauch–Tung–Striebel (RTS) smoother (Särkkä Reference Särkkä2013; Särkkä & Solin Reference Särkkä and Solin2019). This ansatz reduces the computational complexity to $O(N)$
process as a linear time invariant stochastic differential equation, which can be solved using a corresponding filter and smoother (Solin & Särkkä Reference Solin and Särkkä2015). In the case of a Gaussian process, the analogous approach is the well-known Kalman filter and Rauch–Tung–Striebel (RTS) smoother (Särkkä Reference Särkkä2013; Särkkä & Solin Reference Särkkä and Solin2019). This ansatz reduces the computational complexity to $O(N)$![]() , making it also suitable for high-resolution time series.
, making it also suitable for high-resolution time series.
Here, we are working with a multi-output state space model to generate multivariate time series. We first assume that dimensions of the multivariate time series are not correlated. This is done to avoid the requirement of optimizing all hyperparameters at the same time, which is practically unfeasible due to the limited amount of available data. To still account for signal interdependencies, we then induce correlations and cross-correlations via colouring transformations in a post-processing step.
To balance the training data set, we use several local surrogate models to generate data coming from different disruption classes. From a small set – usually less than 10 discharges – of multivariate time series with $D$![]() measurement signals coming from one disruption class with similar operating conditions, we estimate the posterior distribution. We then sample from the trained model in order to generate similar data that enlarge the training database. To evaluate if the generated samples are from the same distribution as the training data, we use several methods from time series analysis, descriptive statistics and clustering algorithms to show that generated and training samples are almost indistinguishable.
measurement signals coming from one disruption class with similar operating conditions, we estimate the posterior distribution. We then sample from the trained model in order to generate similar data that enlarge the training database. To evaluate if the generated samples are from the same distribution as the training data, we use several methods from time series analysis, descriptive statistics and clustering algorithms to show that generated and training samples are almost indistinguishable.
2. Methods
2.1. Student $t$ processes
processes
Student $t$![]() processes (TPs) are a generalization of the widely used Gaussian processes (GPs) (Williams & Rasmussen Reference Williams and Rasmussen1996; Shah et al. Reference Shah, Wilson and Ghahramani2014). TPs allow for a heavy tailed noise distribution (estimated by an additional hyperparameter $\nu > 2$
processes (TPs) are a generalization of the widely used Gaussian processes (GPs) (Williams & Rasmussen Reference Williams and Rasmussen1996; Shah et al. Reference Shah, Wilson and Ghahramani2014). TPs allow for a heavy tailed noise distribution (estimated by an additional hyperparameter $\nu > 2$![]() ) and therefore put less weight on outliers compared with GPs (Shah et al. Reference Shah, Wilson and Ghahramani2014; Roth et al. Reference Roth, Ardeshiri, Özkan and Gustafsson2017). This is illustrated in figure 1 for a test case of synthetic data corrupted by outliers. As in GP regression, we consider a set of $N$
) and therefore put less weight on outliers compared with GPs (Shah et al. Reference Shah, Wilson and Ghahramani2014; Roth et al. Reference Roth, Ardeshiri, Özkan and Gustafsson2017). This is illustrated in figure 1 for a test case of synthetic data corrupted by outliers. As in GP regression, we consider a set of $N$![]() training observations $\mathcal {D} = \{ (t_i, y_i) \}_{i = 1}^T$
training observations $\mathcal {D} = \{ (t_i, y_i) \}_{i = 1}^T$![]() of scalar function values $y_i = f(t_i)$
of scalar function values $y_i = f(t_i)$![]() plus measurement noise at training points $t_i$
plus measurement noise at training points $t_i$![]() with $i = 0, 1,\ldots, T$
with $i = 0, 1,\ldots, T$![]() (in our case, time). We model these data points using a TP with zero mean and covariance function $k(t, t^\prime )$
(in our case, time). We model these data points using a TP with zero mean and covariance function $k(t, t^\prime )$![]() ,
,
Similar to the GP, a kernel function $k(t, t^\prime )$![]() quantifies the covariance between values of $f$
quantifies the covariance between values of $f$![]() at times $(t, t^\prime )$
at times $(t, t^\prime )$![]() and yields an $N \times N$
and yields an $N \times N$![]() covariance matrix $\boldsymbol{\mathsf{K}}$
covariance matrix $\boldsymbol{\mathsf{K}}$![]() with components ${\mathsf{K}}_{ij} = k(t_i, t_j)$
with components ${\mathsf{K}}_{ij} = k(t_i, t_j)$![]() for the random vector of all observed ${y_i}$
for the random vector of all observed ${y_i}$![]() . Kernel hyperparameters determine further details, e.g. a length scale $l$
. Kernel hyperparameters determine further details, e.g. a length scale $l$![]() quantifies how fast correlations vanish with increasing distance in $t$
quantifies how fast correlations vanish with increasing distance in $t$![]() . The additional hyperparameter $\nu > 2$
. The additional hyperparameter $\nu > 2$![]() corresponds to the degrees of freedom that specify the noise distribution. The predicted distribution of a scalar output $f(t_*)$
corresponds to the degrees of freedom that specify the noise distribution. The predicted distribution of a scalar output $f(t_*)$![]() at test point $t_*$
at test point $t_*$![]() is given in closed form by
is given in closed form by
where $\boldsymbol{\mathsf{K}}_y = \boldsymbol{\mathsf{K}} + \sigma ^2_n \boldsymbol{\mathsf{I}}$![]() is the measurement noise parametrized by the noise variance $\sigma _n^2$
is the measurement noise parametrized by the noise variance $\sigma _n^2$![]() . Here, $\boldsymbol {k}_*$
. Here, $\boldsymbol {k}_*$![]() is an $N$
is an $N$![]() -dimensional vector with the $i$
-dimensional vector with the $i$![]() th entry being $k(t_*, t_i)$
th entry being $k(t_*, t_i)$![]() ; $k_{**} = k(t_*, t_*)$
; $k_{**} = k(t_*, t_*)$![]() describes the covariance between training and test data and the variance at the test point $t_*$
describes the covariance between training and test data and the variance at the test point $t_*$![]() . In contrast to GP regression, the posterior variance $\mathbb {V}[f(t_*)]$
. In contrast to GP regression, the posterior variance $\mathbb {V}[f(t_*)]$![]() of the prediction explicitly depends on training observations by taking data variability into account and results in more reliable uncertainty estimates. An analogous expression to (2.3) is obtained for the covariance matrix between predictions at multiple $t_*$
of the prediction explicitly depends on training observations by taking data variability into account and results in more reliable uncertainty estimates. An analogous expression to (2.3) is obtained for the covariance matrix between predictions at multiple $t_*$![]() (Shah et al. Reference Shah, Wilson and Ghahramani2014).
(Shah et al. Reference Shah, Wilson and Ghahramani2014).

Figure 1. Predicted mean and $95\,\%$![]() confidence band with (a) GP and (b) TP trained on $N = 100$
confidence band with (a) GP and (b) TP trained on $N = 100$![]() training data points following $f(t) = \textrm {sin}(2t)\cos (0.4t)$
training data points following $f(t) = \textrm {sin}(2t)\cos (0.4t)$![]() corrupted by Gaussian noise $0.1 \mathcal {N}(0, 1)$
corrupted by Gaussian noise $0.1 \mathcal {N}(0, 1)$![]() , with several outliers.
, with several outliers.
2.2. State space formulation
As in GP regression, the computational complexity increases with $O(N^3)$![]() , as an inversion of the covariance matrix via Cholesky factorization is necessary to train TPs (Williams & Rasmussen Reference Williams and Rasmussen1996). This makes GP and also TP regression unfavourable for high-resolution time series data. However, as shown by Solin & Särkkä (Reference Solin and Särkkä2015), the TP regression problem can be reformulated as an $m$
, as an inversion of the covariance matrix via Cholesky factorization is necessary to train TPs (Williams & Rasmussen Reference Williams and Rasmussen1996). This makes GP and also TP regression unfavourable for high-resolution time series data. However, as shown by Solin & Särkkä (Reference Solin and Särkkä2015), the TP regression problem can be reformulated as an $m$![]() th-order linear time invariant stochastic differential equation (SDE)
th-order linear time invariant stochastic differential equation (SDE)
where $\hat {\boldsymbol {f}}(t) = (f(t), {{\rm d}f(t)}/{{\rm d}t},\ldots, {{\rm d}^{m-1} f(t)}/{{\rm d}t^{m-1}})^\top$![]() , the feedback matrix $\boldsymbol{\mathsf{F}}$
, the feedback matrix $\boldsymbol{\mathsf{F}}$![]() and noise effect matrix $\boldsymbol{\mathsf{L}}$
and noise effect matrix $\boldsymbol{\mathsf{L}}$![]() are derived from the underlying TP, $\boldsymbol{\mathsf{H}} = (1, 0,\ldots, 0)$
are derived from the underlying TP, $\boldsymbol{\mathsf{H}} = (1, 0,\ldots, 0)$![]() is the measurement or observation matrix and $\boldsymbol {w}(t)$
is the measurement or observation matrix and $\boldsymbol {w}(t)$![]() is a vector of white noise processes with spectral density $\gamma \boldsymbol{\mathsf{Q}}$
is a vector of white noise processes with spectral density $\gamma \boldsymbol{\mathsf{Q}}$![]() , where $\gamma$
, where $\gamma$![]() is a scaling factor (Solin & Särkkä Reference Solin and Särkkä2015).
is a scaling factor (Solin & Särkkä Reference Solin and Särkkä2015).
To solve this SDE for discrete points in time by estimating the posterior distribution $p(\hat {\boldsymbol {y}}_{0:T}|\boldsymbol {y}_{1:T})$![]() of the latent state $\hat {\boldsymbol {y}}_{0:T}$
of the latent state $\hat {\boldsymbol {y}}_{0:T}$![]() given noisy observations $\boldsymbol {y}_{1:T}$
given noisy observations $\boldsymbol {y}_{1:T}$![]() , we use the corresponding Student $t$
, we use the corresponding Student $t$![]() filter and smoother as outlined in Solin & Särkkä (Reference Solin and Särkkä2015). Here, the posterior is estimated by using marginal distributions: (i) filtering distribution $p(\hat {\boldsymbol {y}}_t|\boldsymbol {y}_{1:t})$
filter and smoother as outlined in Solin & Särkkä (Reference Solin and Särkkä2015). Here, the posterior is estimated by using marginal distributions: (i) filtering distribution $p(\hat {\boldsymbol {y}}_t|\boldsymbol {y}_{1:t})$![]() given by the update step in Algorithm , (ii) prediction distribution $p(\hat {\boldsymbol {y}}_{t+k}|\boldsymbol {y}_{1:t})$
given by the update step in Algorithm , (ii) prediction distribution $p(\hat {\boldsymbol {y}}_{t+k}|\boldsymbol {y}_{1:t})$![]() given by the prediction step in Algorithm for $k$
given by the prediction step in Algorithm for $k$![]() steps after the current time step $t$
steps after the current time step $t$![]() and (iii) smoothing distributions $p(\hat {\boldsymbol {y}}_t|\boldsymbol {y}_{1:T})$
and (iii) smoothing distributions $p(\hat {\boldsymbol {y}}_t|\boldsymbol {y}_{1:T})$![]() for $t < T$
for $t < T$![]() given by Algorithm (Särkkä Reference Särkkä2013). The initial distribution is determined by the prior state mean given by the measurements at $t = 0$
given by Algorithm (Särkkä Reference Särkkä2013). The initial distribution is determined by the prior state mean given by the measurements at $t = 0$![]() and prior state covariance $\boldsymbol{\mathsf{P}}_0$
and prior state covariance $\boldsymbol{\mathsf{P}}_0$![]() given by the stationary covariance (Solin & Särkkä Reference Solin and Särkkä2015). The augmented states ${\rm d}f/{\rm d}t$
given by the stationary covariance (Solin & Särkkä Reference Solin and Särkkä2015). The augmented states ${\rm d}f/{\rm d}t$![]() that are not measured and noise are initialized with $0$
that are not measured and noise are initialized with $0$![]() .
.
For example, the state space formulation of the Matérn 3/2 kernel is given by the following expressions for feedback, noise effect matrix and spectral density (Särkkä & Solin Reference Särkkä and Solin2019):

where $\lambda = \sqrt {3}/l$![]() . Hyperparameters $l$
. Hyperparameters $l$![]() , $\sigma ^2$
, $\sigma ^2$![]() , $\sigma _n^2$
, $\sigma _n^2$![]() and $\nu$
and $\nu$![]() needed in the Student $t$
needed in the Student $t$![]() filter algorithm are estimated by minimizing the negative log likelihood (Solin & Särkkä Reference Solin and Särkkä2015). The log likelihood is sequentially calculated using the Student $t$
filter algorithm are estimated by minimizing the negative log likelihood (Solin & Särkkä Reference Solin and Särkkä2015). The log likelihood is sequentially calculated using the Student $t$![]() filter (Algorithm ). When the hyperparameters are optimized, the predictive distribution is first calculated via Algorithm and then smoothed using Algorithm . In order to include the noise model with $\sigma _n^2$
filter (Algorithm ). When the hyperparameters are optimized, the predictive distribution is first calculated via Algorithm and then smoothed using Algorithm . In order to include the noise model with $\sigma _n^2$![]() corresponding to $\boldsymbol{\mathsf{K}}_y = \boldsymbol{\mathsf{K}} + \sigma ^2_n \boldsymbol{\mathsf{I}}$
corresponding to $\boldsymbol{\mathsf{K}}_y = \boldsymbol{\mathsf{K}} + \sigma ^2_n \boldsymbol{\mathsf{I}}$![]() in traditional TP regression, the SDE is directly augmented by the entangled noise model. As the model is not only augmented with the noise model, but also with the first derivative of the target function we want to predict, we can immediately infer ${\rm d}f(t)/{\rm d}t$
in traditional TP regression, the SDE is directly augmented by the entangled noise model. As the model is not only augmented with the noise model, but also with the first derivative of the target function we want to predict, we can immediately infer ${\rm d}f(t)/{\rm d}t$![]() from the given observations $y$
from the given observations $y$![]() .
.
Here, the task at hand concerns multivariate time series $\boldsymbol{\mathsf{Y}}$![]() with multiple measurements $n$
with multiple measurements $n$![]() with $D$
with $D$![]() dimensions where the $i$
dimensions where the $i$![]() th row is $\boldsymbol {y}_i = \boldsymbol {f}(t_i)$
th row is $\boldsymbol {y}_i = \boldsymbol {f}(t_i)$![]() at every time step $t_i$
at every time step $t_i$![]() . To facilitate the training of the model, we consider an uncorrelated model, such that the associated random processes are not correlated. In traditional GP/TP regression, this corresponds to a multi-output model with a block-diagonal covariance matrix. The multi-output state space model to estimate $p(\hat {\boldsymbol{\mathsf{Y}}}_{0:T}|\boldsymbol{\mathsf{Y}}_{1:T})$
. To facilitate the training of the model, we consider an uncorrelated model, such that the associated random processes are not correlated. In traditional GP/TP regression, this corresponds to a multi-output model with a block-diagonal covariance matrix. The multi-output state space model to estimate $p(\hat {\boldsymbol{\mathsf{Y}}}_{0:T}|\boldsymbol{\mathsf{Y}}_{1:T})$![]() is built by stacking the univariate SDE models resulting in a block-diagonal structure for feedback and covariance matrices. Then, the dynamics of $\boldsymbol {y}_i$
is built by stacking the univariate SDE models resulting in a block-diagonal structure for feedback and covariance matrices. Then, the dynamics of $\boldsymbol {y}_i$![]() is independent. We sample uncorrelated multivariate time series from this model and apply colouring transformations in a following post-processing step to account for correlations (§ 2.4). Each dimension has its own set of hyperparameters in order to grasp the dynamics that happen on different time scales. The measurement covariance matrix $\boldsymbol{\mathsf{R}}$
is independent. We sample uncorrelated multivariate time series from this model and apply colouring transformations in a following post-processing step to account for correlations (§ 2.4). Each dimension has its own set of hyperparameters in order to grasp the dynamics that happen on different time scales. The measurement covariance matrix $\boldsymbol{\mathsf{R}}$![]() (Algorithm ) is estimated using the covariance of $n$
(Algorithm ) is estimated using the covariance of $n$![]() measurements for each dimension at every time step.
measurements for each dimension at every time step.
2.3. Student $t$ sampler
sampler
To sample from the estimated posterior distribution, we employ a Student $t$![]() sampler, which is a modified version of the sampling technique presented by Durbin & Koopman (Reference Durbin and Koopman2002). First, we draw a $t$
sampler, which is a modified version of the sampling technique presented by Durbin & Koopman (Reference Durbin and Koopman2002). First, we draw a $t$![]() distributed random sequence $\hat {\boldsymbol{\mathsf{X}}}_{0:T} = \hat {\boldsymbol {x}}_{i, 0:T}$
distributed random sequence $\hat {\boldsymbol{\mathsf{X}}}_{0:T} = \hat {\boldsymbol {x}}_{i, 0:T}$![]() from the prior estimated by the trained Student $t$
from the prior estimated by the trained Student $t$![]() model. These sequences are initialized by $\mathcal {T}(0, \boldsymbol{\mathsf{P}}_0)$
model. These sequences are initialized by $\mathcal {T}(0, \boldsymbol{\mathsf{P}}_0)$![]() and then filtered using Algorithm and smoothed via Algorithm , which yields $\mathbb {E}(\hat {\boldsymbol{\mathsf{X}}}_{0:T}|\boldsymbol{\mathsf{Y}}^+_{1:T})$
and then filtered using Algorithm and smoothed via Algorithm , which yields $\mathbb {E}(\hat {\boldsymbol{\mathsf{X}}}_{0:T}|\boldsymbol{\mathsf{Y}}^+_{1:T})$![]() where $\boldsymbol{\mathsf{Y}}^+_{1:T} = \boldsymbol{\mathsf{H}} \hat {\boldsymbol{\mathsf{X}}}_{0:T}$
where $\boldsymbol{\mathsf{Y}}^+_{1:T} = \boldsymbol{\mathsf{H}} \hat {\boldsymbol{\mathsf{X}}}_{0:T}$![]() , with the stacked measurement matrix $\boldsymbol{\mathsf{H}} = (\boldsymbol{\mathsf{I}},0,0)$
, with the stacked measurement matrix $\boldsymbol{\mathsf{H}} = (\boldsymbol{\mathsf{I}},0,0)$![]() that extracts only the first component of $\hat {\boldsymbol {x}}_t$
that extracts only the first component of $\hat {\boldsymbol {x}}_t$![]() in every time step $t$
in every time step $t$![]() . Here, $\boldsymbol{\mathsf{Y}}^+_{1:T}$
. Here, $\boldsymbol{\mathsf{Y}}^+_{1:T}$![]() are data associated with the filtered and smoothed sequence $\hat {\boldsymbol{\mathsf{X}}}_{0:T}$
are data associated with the filtered and smoothed sequence $\hat {\boldsymbol{\mathsf{X}}}_{0:T}$![]() given by (). Finally, to obtain a random sequence $\bar {\boldsymbol{\mathsf{Y}}}_{0:T} = \bar {\boldsymbol {y}}_{i, 0:T} \sim p(\hat {\boldsymbol{\mathsf{Y}}}_{0:T}|\boldsymbol{\mathsf{Y}}_{1:T})$
given by (). Finally, to obtain a random sequence $\bar {\boldsymbol{\mathsf{Y}}}_{0:T} = \bar {\boldsymbol {y}}_{i, 0:T} \sim p(\hat {\boldsymbol{\mathsf{Y}}}_{0:T}|\boldsymbol{\mathsf{Y}}_{1:T})$![]() , we combine
, we combine
where $\boldsymbol{\mathsf{H}}$![]() extracts the first component of $\hat {\boldsymbol {y}}_t$
extracts the first component of $\hat {\boldsymbol {y}}_t$![]() in every time step $t$
in every time step $t$![]() . This procedure gives a $D$
. This procedure gives a $D$![]() -dimensional multivariate time series for $T$
-dimensional multivariate time series for $T$![]() time steps.
time steps.
2.4. Post-processing
Given the trained model, we sample data $\bar {\boldsymbol{\mathsf{Y}}}_{1:T}$![]() from the estimated posterior, where rows are dimensions $\bar {y}_{i}$
from the estimated posterior, where rows are dimensions $\bar {y}_{i}$![]() and columns are time steps; $\bar {\boldsymbol{\mathsf{Y}}}_{1:T}$
and columns are time steps; $\bar {\boldsymbol{\mathsf{Y}}}_{1:T}$![]() can be split into a mean given by the smoothing distribution and deviations due to the sampling. Correlations between dimensions $D$
can be split into a mean given by the smoothing distribution and deviations due to the sampling. Correlations between dimensions $D$![]() of the generated data are not reproduced correctly with the uncorrelated model. However, with three different post-processing methods of increasing complexity compared in the results, we aim to handle correlations.
of the generated data are not reproduced correctly with the uncorrelated model. However, with three different post-processing methods of increasing complexity compared in the results, we aim to handle correlations.
We thus want to inscribe the average covariance $\boldsymbol{\varSigma}$![]() over all samples empirically observed in the training data $\boldsymbol{\mathsf{Y}}_{1:T}$
over all samples empirically observed in the training data $\boldsymbol{\mathsf{Y}}_{1:T}$![]() into the generated data $\bar {\boldsymbol{\mathsf{Y}}}_{1:T}$
into the generated data $\bar {\boldsymbol{\mathsf{Y}}}_{1:T}$![]() . However, the covariance matrix $\bar {\boldsymbol{\varSigma} }$
. However, the covariance matrix $\bar {\boldsymbol{\varSigma} }$![]() of $\bar {\boldsymbol{\mathsf{Y}}}_{1:T}$
of $\bar {\boldsymbol{\mathsf{Y}}}_{1:T}$![]() has small non-zero off-diagonal elements. Therefore, we first perform a Zero Components Analysis (ZCA) whitening (also known as Mahalanobis) transformation (see e.g. Kessy, Lewin & Strimmer Reference Kessy, Lewin and Strimmer2018):
has small non-zero off-diagonal elements. Therefore, we first perform a Zero Components Analysis (ZCA) whitening (also known as Mahalanobis) transformation (see e.g. Kessy, Lewin & Strimmer Reference Kessy, Lewin and Strimmer2018):
The transformed data $\boldsymbol{\mathsf{Z}}$![]() have a diagonal covariance matrix $\boldsymbol{\varLambda}_{\boldsymbol{\mathsf{Z}}}$
have a diagonal covariance matrix $\boldsymbol{\varLambda}_{\boldsymbol{\mathsf{Z}}}$![]() , with unit variances on the diagonal. We then colour the generated data via a colouring transformation (Kessy et al. Reference Kessy, Lewin and Strimmer2018)
, with unit variances on the diagonal. We then colour the generated data via a colouring transformation (Kessy et al. Reference Kessy, Lewin and Strimmer2018)
obtaining data $\tilde {\boldsymbol{\mathsf{Y}}}$![]() , which now have the same (temporally local) covariance as the training data $\boldsymbol{\mathsf{Y}}$
, which now have the same (temporally local) covariance as the training data $\boldsymbol{\mathsf{Y}}$![]() .
.
Another possibility is to directly take the distribution of the training data covariance matrix $\boldsymbol{\varSigma}$![]() over samples into account by using samples from a corresponding multivariate Gaussian distribution as data covariance matrices. This generates variation in the covariance of the generated data, especially if there are local differences between the samples. However, on average for a large enough sample size, we recover the training data covariance matrix $\boldsymbol{\varSigma}$
over samples into account by using samples from a corresponding multivariate Gaussian distribution as data covariance matrices. This generates variation in the covariance of the generated data, especially if there are local differences between the samples. However, on average for a large enough sample size, we recover the training data covariance matrix $\boldsymbol{\varSigma}$![]() .
.
To also take time-lagged correlations into account, we must adjust not only covariances but also cross-covariances in our generated data. Therefore, we use the cross-covariance matrix given by
where the expected value $\mathbb {E}[\cdot ]$![]() is estimated by averaging over all combinations of lags $t_1 - t_2$
is estimated by averaging over all combinations of lags $t_1 - t_2$![]() in addition to the sample mean. Here, $\mu _{i, t}$
in addition to the sample mean. Here, $\mu _{i, t}$![]() is the expected value of $\bar {y}_{i, t}$
is the expected value of $\bar {y}_{i, t}$![]() . To decorrelate and colour the data in the way described above, we formally use a global covariance matrix $\boldsymbol{\varSigma} _g$
. To decorrelate and colour the data in the way described above, we formally use a global covariance matrix $\boldsymbol{\varSigma} _g$![]() of size $D T \times D T$
of size $D T \times D T$![]() involving correlations both over time and across dimensions of the multivariate time series. The global covariance matrix is a periodic block matrix given by
involving correlations both over time and across dimensions of the multivariate time series. The global covariance matrix is a periodic block matrix given by
for the cross-covariance $\boldsymbol{\varSigma} _c$![]() with lag. The generated data is coloured using the global covariance matrix:
with lag. The generated data is coloured using the global covariance matrix:
This incorporates the empirical cross-covariance for all time lags and between all dimensions $D$![]() of the generated data.
of the generated data.
3. Evaluation of generated data
As the generated data serve as augmented training data for later analyses, statistical properties of the original training data should be reflected in the generated data. Therefore, we perform statistical tests to check if training and generated share key statistical properties.
3.1. Distribution and Wasserstein distance
To measure the distance between the distribution of the training and the generated data, we use the Wasserstein-1 metric (Villani Reference Villani2008)
where $\varGamma (P,V)$![]() denotes the set of all probability distributions on $\mathbb {R} \times \mathbb {R}$
denotes the set of all probability distributions on $\mathbb {R} \times \mathbb {R}$![]() , with $P, V$
, with $P, V$![]() being its marginals. The minimizer $\gamma$
being its marginals. The minimizer $\gamma$![]() of (3.1) denotes the optimal transport plan to transport $P$
of (3.1) denotes the optimal transport plan to transport $P$![]() to $V$
to $V$![]() . We compare each signal separately and average the corresponding Wasserstein distances. Although the problem concerns time series data, we discard all time information and only consider the global distribution of the data due to the small amount of available training data samples.
. We compare each signal separately and average the corresponding Wasserstein distances. Although the problem concerns time series data, we discard all time information and only consider the global distribution of the data due to the small amount of available training data samples.
3.2. Maximum mean discrepancy two-sample test
In addition to the Wasserstein distance, we perform the kernel two-sample test (Gretton et al. Reference Gretton, Borgwardt, Rasch, Schölkopf and Smola2012) for each signal (again discarding time information). The null hypothesis we want to test is that both $n$![]() training data $\boldsymbol{y}_{i,1:T}$
training data $\boldsymbol{y}_{i,1:T}$![]() and $m$
and $m$![]() generated data samples $\tilde {\boldsymbol{y}}_{i, 1:T}$
generated data samples $\tilde {\boldsymbol{y}}_{i, 1:T}$![]() follow the same distribution $P$
follow the same distribution $P$![]() . We use the maximum mean discrepancy (MMD) test statistic via a kernel $g$
. We use the maximum mean discrepancy (MMD) test statistic via a kernel $g$![]()

where $g(x, y) = \textrm {exp}(-||x-y||^2/(2\sigma ^2))$![]() with $\sigma = \textrm {Median}(|\varUpsilon _i - \varUpsilon _j|)/2$
with $\sigma = \textrm {Median}(|\varUpsilon _i - \varUpsilon _j|)/2$![]() and $\varUpsilon$
and $\varUpsilon$![]() is the combined sample of $\boldsymbol{y}_{i, 1:T}$
is the combined sample of $\boldsymbol{y}_{i, 1:T}$![]() and $\tilde {\boldsymbol{y}}_{i, 1:T}$
and $\tilde {\boldsymbol{y}}_{i, 1:T}$![]() . To estimate a threshold for the acceptance of the null hypothesis for a given confidence level, bootstrapping is performed via mixing samples $\boldsymbol{y}_{i, 1:T}$
. To estimate a threshold for the acceptance of the null hypothesis for a given confidence level, bootstrapping is performed via mixing samples $\boldsymbol{y}_{i, 1:T}$![]() and $\tilde {\boldsymbol{y}}_{i, 1:T}$
and $\tilde {\boldsymbol{y}}_{i, 1:T}$![]() , which generates a distribution with 10 000 samples that satisfies the null hypothesis. Finally, we can estimate a $p$
, which generates a distribution with 10 000 samples that satisfies the null hypothesis. Finally, we can estimate a $p$![]() -value for the MMD of the generated data distributions.
-value for the MMD of the generated data distributions.
3.3. Auto- and cross-correlation
To evaluate if the generated data reflect the temporal dependencies of the training data, we calculate auto- and cross-correlations $\rho _{rs}$![]() for training and generated data by normalizing the cross-covariance $\boldsymbol{\varSigma} _c$
for training and generated data by normalizing the cross-covariance $\boldsymbol{\varSigma} _c$![]() in (2.10) by $1/(\sigma _{r, t_1}\sigma _{s, t_2})$
in (2.10) by $1/(\sigma _{r, t_1}\sigma _{s, t_2})$![]() . Here, $\sigma _{s, t}$
. Here, $\sigma _{s, t}$![]() is the standard deviation of $\tilde {y}_{s, t}$
is the standard deviation of $\tilde {y}_{s, t}$![]() . If $r = s$
. If $r = s$![]() , this diagnostic becomes the auto-correlation – see, e.g. Park (Reference Park2017). For $t_1=t_2$
, this diagnostic becomes the auto-correlation – see, e.g. Park (Reference Park2017). For $t_1=t_2$![]() , the local correlation matrix follows. We evaluate the mean squared error (MSE) to the auto- and cross-correlation of the training data. Evidently, the global colouring transformation (2.10) produces a perfect match in this diagnostic.
, the local correlation matrix follows. We evaluate the mean squared error (MSE) to the auto- and cross-correlation of the training data. Evidently, the global colouring transformation (2.10) produces a perfect match in this diagnostic.
3.4. Power spectral density
All frequencies that are present in the training data set should also appear in the generated data. This can be evaluated using the power spectral density (PSD), which provides an estimate of power distribution across the frequency of a signal. We evaluate the mean squared error between the PSD of the training data and generated data.
3.5. Embedding via kernel principal component analysis
We apply two-dimensional (2-D) kernel principal component analysis (PCA) on the training data with flattened temporal dimension and project the generated data onto the first two principal components of the training data to evaluate the embedding and visualize if both training and generated data lie on the same submanifold (Schölkopf, Smola & Müller Reference Schölkopf, Smola and Müller1998). In all test cases, a polynomial kernel of degree $3$![]() with optimized kernel coefficient (minimization of the reconstruction error) is used.
with optimized kernel coefficient (minimization of the reconstruction error) is used.
The distance between the embedded distributions of training and generated data is measured by using the sliced Wasserstein distance that takes advantage of the very efficient calculation of 1-D Wasserstein distances (Bonneel et al. Reference Bonneel, Rabin, Peyré and Pfister2015; Flamary et al. Reference Flamary, Courty, Gramfort, Alaya, Boisbunon, Chambon, Chapel, Corenflos, Fatras and Nemo2021). The multivariate distribution is sliced and randomly projected on a 1-D subspace, and the corresponding 1-D Wasserstein distances are averaged to obtain an estimation for the multivariate distribution. With an increasing number of projections, the sliced Wasserstein distance converges. Here, we use $10^3$![]() projections to estimate the distance $W_{\textrm {emb}}$
projections to estimate the distance $W_{\textrm {emb}}$![]() between the embedded distributions.
between the embedded distributions.
3.6. Multivariate functional PCA
For the evaluation of the correctly represented temporal evolution of the generated data, we apply multivariate functional principal component analysis (mfPCA) on the training data and project the generated data onto the eigenbasis of the training data (Happ & Greven Reference Happ and Greven2018). Then, we reconstruct both training and generated data with the same eigenbasis and evaluate the variance of the residuals.
3.7. Dynamic time warping
For time series comparison, dynamic time warping (DTW) is widely used to measure the similarity between two temporal sequences $\boldsymbol{y}_{i, 1:T}$![]() and $\tilde {\boldsymbol{y}}_{j, 1:T}$
and $\tilde {\boldsymbol{y}}_{j, 1:T}$![]() (Berndt & Clifford Reference Berndt and Clifford1994). This metric is formulated as an optimization problem
(Berndt & Clifford Reference Berndt and Clifford1994). This metric is formulated as an optimization problem

where $\gamma$![]() is the alignment path such that the Euclidean distance between $\boldsymbol{y}_{i, 1:T}$
is the alignment path such that the Euclidean distance between $\boldsymbol{y}_{i, 1:T}$![]() and $\tilde {\boldsymbol{y}}_{j, 1:T}$
and $\tilde {\boldsymbol{y}}_{j, 1:T}$![]() is minimal. Hence, $\textrm {DTW}$
is minimal. Hence, $\textrm {DTW}$![]() gives the distance between two time series with the best temporal alignment. We compare each training data sample with each generated data sample and use the mean to compare different post-processing methods.
gives the distance between two time series with the best temporal alignment. We compare each training data sample with each generated data sample and use the mean to compare different post-processing methods.
3.8. Self-organizing maps on time series
Finally, we apply time series clustering based on DTW self-organizing maps (SOMs) on both the training and generated data (Vettigli Reference Vettigli2018). If the generated data are a potentially useful extension of the training data, the clustering should show similar results. Therefore, we compute a clustering model on the training data and use the trained model to predict cluster labels of both the training and generated data. From the predicted labels, we evaluate the $F1$![]() score (harmonic mean of precision and recall) (Murphy Reference Murphy2022) with the ground truth.
score (harmonic mean of precision and recall) (Murphy Reference Murphy2022) with the ground truth.
4. Numerical experiments
We evaluate the performance of the proposed model using disruption data from several discharges from the DIII-D tokamak taken from the 2016 experimental campaign. These disruptions were already included in previously published papers on data-driven applications in fusion (Montes et al. Reference Montes, Rea, Tinguely, Sweeney, Zhu and Granetz2021).
We cluster the available data sets depending on the similarity of the conditions and on the occurring instability. Here, we use the model to augment five signals of the training data set (referred to as $\beta _n$![]() , the normalized $\beta$
, the normalized $\beta$![]() given by $\beta _n = \beta a B_T / I_p$
given by $\beta _n = \beta a B_T / I_p$![]() , where $\beta$
, where $\beta$![]() is the ratio of plasma pressure to magnetic pressure, $B_T$
is the ratio of plasma pressure to magnetic pressure, $B_T$![]() is the toroidal magnetic field, $a$
is the toroidal magnetic field, $a$![]() the minor radius and $I_p$
the minor radius and $I_p$![]() the plasma current; normalized internal inductance $li$
the plasma current; normalized internal inductance $li$![]() ; plasma elongation $\kappa$
; plasma elongation $\kappa$![]() ; safety factor $q_{95}$
; safety factor $q_{95}$![]() ; Greenwald fraction $n/n_G$
; Greenwald fraction $n/n_G$![]() ) for different disruptions: (i) disruptions due to locked modes (LMs) in high $\beta$
) for different disruptions: (i) disruptions due to locked modes (LMs) in high $\beta$![]() , low torque plasmas with $n=1$
, low torque plasmas with $n=1$![]() resonant magnetic perturbations (RMPs) applied (shots 166463, 166464, 166465, 166466, 166468, 166469), (ii) disruptions due to LMs during an RMP edge localized mode (ELM) suppression experiment applied to an ITER-like plasma shape (shots 166452, 166454, 166457, 166460) and (iii) density accumulation events during detachment studies of helium plasmas (shots 166933, 166934, 166937).
resonant magnetic perturbations (RMPs) applied (shots 166463, 166464, 166465, 166466, 166468, 166469), (ii) disruptions due to LMs during an RMP edge localized mode (ELM) suppression experiment applied to an ITER-like plasma shape (shots 166452, 166454, 166457, 166460) and (iii) density accumulation events during detachment studies of helium plasmas (shots 166933, 166934, 166937).
For each disruption class, the model is trained on these few available training samples. The choice of signals is influenced by the use case of augmenting the training database for a neural network for disruption prediction, but in general, the method is extendable to any number and any kind of signals.
Following the flow shown in figure 2, preprocessing is performed on the training data. As we are primarily interested in the behaviour close to a disruption, we align the samples according to their end time and only consider the stable flat-top phase. Additionally, all data are rescaled via min–max scaling to a range of $[-0.5, 0.5]$![]() . This stabilizes the optimization of the hyperparameters in the Student $t$
. This stabilizes the optimization of the hyperparameters in the Student $t$![]() filter algorithm, as the input to the optimizer is of order 1. Missing data points are interpolated linearly. All discharges are sampled every $25$
filter algorithm, as the input to the optimizer is of order 1. Missing data points are interpolated linearly. All discharges are sampled every $25$![]() ms. Then, we set up the state space Student $t$
ms. Then, we set up the state space Student $t$![]() surrogate model. In all experiments, a Matérn 3/2 kernel as in (2.6a–d) is used. We train the surrogate model by optimizing its hyperparameters by minimizing the negative log likelihood using the Scipy implementation of L-BFGS-B (Virtanen et al. Reference Virtanen, Gommers, Oliphant, Haberland, Reddy, Cournapeau, Burovski, Peterson, Weckesser and Bright2020), and resulting values for all experiments can be found in Appendix B, table 4. Each signal has its own set of hyperparameters in order to be able to handle the dynamics that happen on different time scales. Subsequently, we apply the Student $t$
surrogate model. In all experiments, a Matérn 3/2 kernel as in (2.6a–d) is used. We train the surrogate model by optimizing its hyperparameters by minimizing the negative log likelihood using the Scipy implementation of L-BFGS-B (Virtanen et al. Reference Virtanen, Gommers, Oliphant, Haberland, Reddy, Cournapeau, Burovski, Peterson, Weckesser and Bright2020), and resulting values for all experiments can be found in Appendix B, table 4. Each signal has its own set of hyperparameters in order to be able to handle the dynamics that happen on different time scales. Subsequently, we apply the Student $t$![]() filter and smoother (Algorithms and ) with optimized hyperparameters to our data. From the estimated distribution, we draw $1000$
filter and smoother (Algorithms and ) with optimized hyperparameters to our data. From the estimated distribution, we draw $1000$![]() samples from the posterior using the Student $t$
samples from the posterior using the Student $t$![]() sampler and perform the colouring transformations in the post-processing. Finally, after rescaling the samples to the original data range, we evaluate the generated data sets by using the defined metrics. In general, the generation of the time series samples is of $O(N)$
sampler and perform the colouring transformations in the post-processing. Finally, after rescaling the samples to the original data range, we evaluate the generated data sets by using the defined metrics. In general, the generation of the time series samples is of $O(N)$![]() , but some of the metrics used to evaluate the generate data are not. Therefore, we limited the number of samples in the given analysis to $1000$
, but some of the metrics used to evaluate the generate data are not. Therefore, we limited the number of samples in the given analysis to $1000$![]() .
.

Figure 2. Data processing flow.
5. Results and analysis
For each disruption class, we draw $1000$![]() samples from the posterior estimated by the trained model and compare four available post-processing methods: (I) uncorrelated model (here, no post-processing is performed), (II) colouring transformation with the empirical covariance matrix, (III) colouring transformation with the empirical cross-covariance matrix to account for lagged correlations and (IV) colouring transformation with the sampled covariance matrix. The results for test cases (i) and (ii) are presented in Appendix in C.1 and C.2.
samples from the posterior estimated by the trained model and compare four available post-processing methods: (I) uncorrelated model (here, no post-processing is performed), (II) colouring transformation with the empirical covariance matrix, (III) colouring transformation with the empirical cross-covariance matrix to account for lagged correlations and (IV) colouring transformation with the sampled covariance matrix. The results for test cases (i) and (ii) are presented in Appendix in C.1 and C.2.
In figure 3, a visual comparison is given between training data and generated data for the colouring transformation with empirical cross-covariance matrix, together with the estimated mean and $95\,\%$![]() confidence intervals for the disruption data from DIII-D for test case (i). The model is able to capture the general trend given by the training data and can also reproduce outliers. In general, the generated data fit the distribution of the training data.
confidence intervals for the disruption data from DIII-D for test case (i). The model is able to capture the general trend given by the training data and can also reproduce outliers. In general, the generated data fit the distribution of the training data.

Figure 3. (a) Training data and (b) 10 generated data sets from the state space Student $t$![]() surrogate model together with the estimated mean (black solid line) and $95\,\%$
surrogate model together with the estimated mean (black solid line) and $95\,\%$![]() confidence (grey shaded region) for test case (i). Different colours correspond to different shots of training data and different samples of the generated data, respectively.
confidence (grey shaded region) for test case (i). Different colours correspond to different shots of training data and different samples of the generated data, respectively.
We continue with a thorough statistical analysis, which allows a ranking of the different post-processing methods following the metrics outlined in § 3. The results are given in table 1 for test case (i). Other experiments give similar results, as indicated in Appendix in C.1 (table 5), and C.2 (table 7) for test cases (ii) and (iii), respectively.
Table 1. Post-processing method comparison for test case (i). Mean and standard deviation over five dimensions and $N = 1000$![]() samples generated from the trained model for statistical metrics described in § 3. Best values are highlighted in bold.
samples generated from the trained model for statistical metrics described in § 3. Best values are highlighted in bold.

To put the calculated metrics into context, we identify nearby non-disruptive shots coming from the same specific campaign with similar operating conditions for test case (ii). Then, we evaluate the Wasserstein distance between nearby non-disruptive and disruptive discharges to compare the obtained Wasserstein distances for the generated data for this disruption class. For test case (ii), we identify five nearby non-disruptive shots 166433, 166434, 166442, 166444, 166455 and found $W_1 = 0.31 \pm 0.12$![]() between non-disruptive and disruptive discharges. Additionally, the 2-D kernel PCA embedding of nearby non-disruptive and disruptive discharges evaluated by the estimation of the 2-D sliced Wasserstein distance is estimated. We observe $W_{\textrm {emb}} = 0.74 \pm 0.01$
between non-disruptive and disruptive discharges. Additionally, the 2-D kernel PCA embedding of nearby non-disruptive and disruptive discharges evaluated by the estimation of the 2-D sliced Wasserstein distance is estimated. We observe $W_{\textrm {emb}} = 0.74 \pm 0.01$![]() for test case (ii). The achieved Wasserstein distance between training and generated data for this disruption class is significantly smaller in all post-processing methods, as given in table 5. The same holds for the Wasserstein distance of the 2-D kernel PCA embedding. This is promising, as it implies that the augmented data are much more similar to disruptive discharges within their proper class than to non-disruptive discharges from the same campaign in these measures.
for test case (ii). The achieved Wasserstein distance between training and generated data for this disruption class is significantly smaller in all post-processing methods, as given in table 5. The same holds for the Wasserstein distance of the 2-D kernel PCA embedding. This is promising, as it implies that the augmented data are much more similar to disruptive discharges within their proper class than to non-disruptive discharges from the same campaign in these measures.
For test cases (i) and (iii), non-disruptive discharges from those specific campaigns are not available. Therefore, we investigate the distributions in stable and unstable phases of the training and generated disruptive discharges in more detail. Using the average time stamp of the manually labelled training data, this information about the stable and unstable phase was propagated to label the generated data. Then we calculate the Wasserstein distance averaged over all features between training and generated data for both phases separately. The obtained results for all test cases are given in table 2. For comparison, we also estimate the Wasserstein distances between stable and unstable phases and found $W_1 = 0.36 \pm 0.07$![]() for test case (i), $W_1 = 0.37 \pm 0.08$
for test case (i), $W_1 = 0.37 \pm 0.08$![]() for test case (ii) and $W_1 = 0.24 \pm 0.1$
for test case (ii) and $W_1 = 0.24 \pm 0.1$![]() for test case (iii). The obtained distances between training and generated data within the different phases lie sufficiently below the distances between stable and unstable parts of the discharges.
for test case (iii). The obtained distances between training and generated data within the different phases lie sufficiently below the distances between stable and unstable parts of the discharges.
Table 2. Post-processing method comparison for disruption data from DIII-D. Mean and standard deviation of the Wasserstein metric between training and generated data for stable and unstable phases of the disruptive discharges. The Wasserstein metric is averaged over five dimensions and $N = 1000$![]() samples generated from the trained model.
samples generated from the trained model.

The superiority of the post-processing with the empirical cross-covariance is apparent in figure 4, where the auto- (on the diagonal) and cross-covariance for all estimated signals are shown. As we are inscribing the empirical cross-covariance into the uncorrelated generated data from the model, the cross-covariance fits exactly, and the cross-covariances lie on top of each other. When using either the empirical covariance or the sample covariance, only the cross-covariance at lag $0$![]() matches the cross-covariance of the training data. Both post-processing methods give on average the same cross-covariance for $1000$
matches the cross-covariance of the training data. Both post-processing methods give on average the same cross-covariance for $1000$![]() generated samples. Additionally, the difference in covariance at lag $0$
generated samples. Additionally, the difference in covariance at lag $0$![]() is shown in figure 5.
is shown in figure 5.

Figure 4. Comparison of the cross-covariance in the training and generated data with cross-covariance (solid lines on top of each other, numerical error of order $10^{-16}$![]() ), covariance or sampled covariance post-processing (dashed lines) and uncorrelated model (dotted line) for test case (i).
), covariance or sampled covariance post-processing (dashed lines) and uncorrelated model (dotted line) for test case (i).

Figure 5. Comparison of the covariance of training data (a) and the difference from the generated data (b) with uncorrelated model, (c) empirical covariance, (d) cross-covariance and (e) sampled covariance post-processing for test case (i). Note the different scaling in the colour scale.
Figure 6 displays the kernel density of the 2-D kernel PCA embedding of the generated data in the eigenspace of the training data. All four methods generate data that lie on the same submanifold as the training data. However, when cross-covariances are included, the shape of the training data is better reproduced. In test case (i) shown in figure 6, one of the three extrema is not reproduced by the generated data. By evaluating the embedding for different combinations of input signals, a likely explanation is that $\beta _n$![]() causes this extremum. The reason why the generated data are not able to reproduce this extremum in the eigenspace is due to the multi-modality of the distribution around the drop in $\beta _n$
causes this extremum. The reason why the generated data are not able to reproduce this extremum in the eigenspace is due to the multi-modality of the distribution around the drop in $\beta _n$![]() in the range $2.75\unicode{x2013}3.00\ {\rm s}$
in the range $2.75\unicode{x2013}3.00\ {\rm s}$![]() . This is also one limitation of the presented model as it is not able to represent multi-modality of a cluster correctly. One possibility is to further refine the considered clusters to augment the data base (in the extreme case, down to one single discharge). In general, the number of available training data samples is very limited, as we are working with manually labelled disruptive data from DIII-D. Therefore, the results here only give an idea of whether the features apparent in the training data are also apparent in the generated data.
. This is also one limitation of the presented model as it is not able to represent multi-modality of a cluster correctly. One possibility is to further refine the considered clusters to augment the data base (in the extreme case, down to one single discharge). In general, the number of available training data samples is very limited, as we are working with manually labelled disruptive data from DIII-D. Therefore, the results here only give an idea of whether the features apparent in the training data are also apparent in the generated data.

Figure 6. Kernel density estimation of the 2-D kernel PCA embedding of the (a) training data and generated data via (b) uncorrelated model, (c) empirical covariance, (d) cross-covariance and (e) sampled covariance post-processing for test case (i). The embedded training data are shown in grey in all plots. The colour scale representing the density is the same in all plots.
Besides the Wasserstein distance, DTW is difficult to interpret without context. Again, we calculate the metric between nearby non-disruptive and disruptive discharges for test case (ii) and obtain $\textrm {DTW} = 2.9 \pm 1.6$![]() . The large error is due to averaging over all signals. Overall, the distances between the generated and training data for this disruption class lie below the distance between nearby non-disruptive and disruptive discharges for this test case. In test cases (i) and (iii), where non-disruptive data from the same campaigns are not available, DTW distances between generated and training data with included correlations are of the same order as in test case (ii).
. The large error is due to averaging over all signals. Overall, the distances between the generated and training data for this disruption class lie below the distance between nearby non-disruptive and disruptive discharges for this test case. In test cases (i) and (iii), where non-disruptive data from the same campaigns are not available, DTW distances between generated and training data with included correlations are of the same order as in test case (ii).
The training data were also reconstructed using the multivariate functional PCA with $5$![]() components. We observe the following reconstruction mean squared errors for test case (i) $0.006$
components. We observe the following reconstruction mean squared errors for test case (i) $0.006$![]() , (ii) $0.003$
, (ii) $0.003$![]() and (iii) $0.008$
and (iii) $0.008$![]() . We use the first five eigenfunctions of the training data as a basis to project the generated data of each test case. The reconstruction error of the generated data with included correlations in the post-processing is still of the same order.
. We use the first five eigenfunctions of the training data as a basis to project the generated data of each test case. The reconstruction error of the generated data with included correlations in the post-processing is still of the same order.
Finally, we use SOMs for time series clustering to evaluate if the label prediction works similarly well for the generated data. Here, we only use three classes, as the training data look quite similar for different signals. The results for three different experiments are given in table 3. Between the four post-processing methods, no significant difference is evident. The clustering algorithm performs as well on all methods as on the original training data.
Table 3. The $F1$![]() score for DTW SOM clustering of different post-processing methods for test case (i).
score for DTW SOM clustering of different post-processing methods for test case (i).

6. Conclusion and outlook
We applied Student $t$![]() process regression in a state space formulation to introduce robust data augmentation for multivariate time series. The state space formulation reduces the computational complexity and is thus suitable for high-resolution time series. We used the model to learn the distribution of time series coming from a given disruption class. From the estimated posterior, time series were generated to augment the training database. To evaluate if the original and generated data share key statistical properties, multiple statistical analyses and classic machine learning clustering algorithms have been carried out. We found that, within the scope of the used metrics, the generated time series resemble the training data to a sufficient extent. An important limitation of the method is multi-modality in the training data set which a Student $t$
process regression in a state space formulation to introduce robust data augmentation for multivariate time series. The state space formulation reduces the computational complexity and is thus suitable for high-resolution time series. We used the model to learn the distribution of time series coming from a given disruption class. From the estimated posterior, time series were generated to augment the training database. To evaluate if the original and generated data share key statistical properties, multiple statistical analyses and classic machine learning clustering algorithms have been carried out. We found that, within the scope of the used metrics, the generated time series resemble the training data to a sufficient extent. An important limitation of the method is multi-modality in the training data set which a Student $t$![]() process cannot reproduce. In this case, the training data sets can be further split.
process cannot reproduce. In this case, the training data sets can be further split.
When the method is applied to augment the training database for the neural network disruption predictor, a thorough analysis of the existing (labelled) training database is necessary to decide which disruption classes are not available in sufficient quantity. For each of those classes, we will train the surrogate model and then be able to generate data to balance the data set. Subsequently, the performance of the neural network trained with the augmented training database will be evaluated. Due to the broad range of evaluation metrics, we are optimistic that the generated data will improve and robustify the performance.
Another perspective regards disruption prediction of future devices, where little data will be available to train machine learning-based approaches. In this case, the surrogate model could be used and updated, as more data are being collected and can therefore update machine learning-driven models.
To improve the proposed method, the integration of correlations and cross-correlations on the level of a multivariate surrogate model instead of the colouring in post-processing will be investigated in future work (Boyle & Frean Reference Boyle and Frean2004; Vandenberg-Rodes & Shahbaba Reference Vandenberg-Rodes and Shahbaba2015). Another possible extension of the current method could also take spatial information of profiles into account (Wilkinson et al. Reference Wilkinson, Chang, Andersen and Solin2020).
However, the approach developed here is sufficiently generic to be used for data augmentation in a broad range of applications, e.g. time series in climate research.
Acknowledgements
Editor William Dorland thanks the referees for their advice in evaluating this article.
Funding
The present contribution is supported by the Helmholtz Association of German Research Centers under the joint research school HIDSS-0006 ‘Munich School for Data Science – MUDS’ (K.R.) and the MIT-Germany Lockheed Martin Seed Fund (K.R., C.R., A.M., R.G., U.v.T.). This work has been carried out within the framework of the EUROfusion Consortium, funded by the European Union via the Euratom Research and Training Programme (Grant Agreement No 101052200 – EUROfusion). Views and opinions expressed are, however, those of the author(s) only and do not necessarily reflect those of the European Union or the European Commission. Neither the European Union nor the European Commission can be held responsible for them (C.A.). This work was supported by the Federal Ministry of Education and Research (BMBF) of Germany by Grant No. 01IS18036A (D.R., B.B.). This material is based upon work supported by the U.S. Department of Energy, Office of Science, Office of Fusion Energy Sciences, using the DIII-D National Fusion Facility, a DOE Office of Science user facility, under Award(s) DE- SC0014264, and DE-FC02-04ER54698 (C.R., A.M., R.G.).
Disclaimer
This report was prepared as an account of work sponsored by an agency of the United States Government. Neither the United States Government nor any agency thereof, nor any of their employees, makes any warranty, express or implied, or assumes any legal liability or responsibility for the accuracy, completeness or usefulness of any information, apparatus, product or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process or service by trade name, trademark, manufacturer or otherwise does not necessarily constitute or imply its endorsement, recommendation or favouring by the United States Government or any agency thereof. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Algorithm
Algorithm 1 Multivariate Student-t filter (Solin & Särkkä 2015)

Algorithm 2 Multivariate Student-t smoother (Solin & Särkkä 2015)

Appendix B. Hyperparameters
For the different test cases, we used the hyperparameters given in table 4.
Table 4. Optimized hyperparameters for the state space Student $t$![]() surrogate model for all test cases.
surrogate model for all test cases.

Appendix C. Results for other test cases
In the following sections, the results for test cases (ii) and (iii) are presented.
C.1. Test case (ii): disruption due to MHD instability during RMP ELM control
A visual comparison of the training and the generated data for test case (ii) is shown in figure 7. Here, the disruption occurs due to magnetohydrodynamic (MHD) instability induced by RMPs applied to control ELMs (shots 166452, 166454, 166457, 166460). The results of the statistical analysis are given in table 5 and are of the same order as for test case (i). Figures 8 and 9 show the cross-covariance and the covariance of the training and generated data. Figure 10 displays the kernel density of 2-D PCA embedding of the generated data. Again, the results show that the generated data lives on the same submanifold for all four post-processing methods. In table 6, the $F1$![]() score for DTW SOM clustering is given.
score for DTW SOM clustering is given.

Figure 7. (a) Training data and (b) 10 generated data sets from the state space Student $t$![]() surrogate model together with the estimated mean (black solid line) and $95\,\%$
surrogate model together with the estimated mean (black solid line) and $95\,\%$![]() confidence (grey shaded region) for test case (ii). Different colours correspond to different shots of training data and different samples of the generated data, respectively.
confidence (grey shaded region) for test case (ii). Different colours correspond to different shots of training data and different samples of the generated data, respectively.
Table 5. Post-processing method comparison for test case (ii). Mean and standard deviation over five dimensions and $N = 1000$![]() samples generated from the trained model for statistical metrics described in § 3. Best values are highlighted in bold.
samples generated from the trained model for statistical metrics described in § 3. Best values are highlighted in bold.


Figure 8. Comparison of cross-covariance of training data and generated data with cross-covariance (solid lines on top of each other, numerical error of order $10^{-16}$![]() ), covariance or sampled covariance (dashed lines) post-processing and uncorrelated model (dotted line) for test case (ii).
), covariance or sampled covariance (dashed lines) post-processing and uncorrelated model (dotted line) for test case (ii).

Figure 9. Comparison of covariance of training data (a) and difference of generated data (b) with uncorrelated model, (c) empirical covariance, (d) cross-covariance and (e) sampled covariance post-processing for test case (ii). Note the different scaling in the colour scale.

Figure 10. Kernel density estimation of the 2-D kernel PCA embedding of the (a) training data and generated data via (b) uncorrelated model, (c) empirical covariance, (d) cross-covariance and (e) sampled covariance post-processing for test case (ii). The embedded training data are shown in grey in all plots. The colour scale representing the density is the same in all plots.
Table 6. The $F1$![]() score for DTW SOM clustering of different post-processing methods for test case (ii).
score for DTW SOM clustering of different post-processing methods for test case (ii).

C.2. Test case (iii): density accumulation
For the third test case with a disruption occurring due to density accumulation (shots 166933, 166934, 166937), the visual comparison is given in figure 11 followed by the results of the statistical analysis in table 7. The cross-covariance and covariance are displayed in figures 12 and 13, respectively. The embedding is shown in figure 14. Here, the skew of the embedding caused by the broad distribution of $\kappa$![]() is not perfectly reproduced by the generated data. However, the results should be regarded with caution as only 3 training data samples are available in this test case. This presents also a limit to this metric. However, when looking at samples of the generated data shown in figure 11, this broad range present in the training data is still well reproduced by the generated data. In this test case, the uncorrelated model performs worst as correlations are not reproduced. The results for generated data with included correlations are again of the same order of magnitude as for test cases (i) and (ii). The results obtained for the $F1$
is not perfectly reproduced by the generated data. However, the results should be regarded with caution as only 3 training data samples are available in this test case. This presents also a limit to this metric. However, when looking at samples of the generated data shown in figure 11, this broad range present in the training data is still well reproduced by the generated data. In this test case, the uncorrelated model performs worst as correlations are not reproduced. The results for generated data with included correlations are again of the same order of magnitude as for test cases (i) and (ii). The results obtained for the $F1$![]() score for DTW SOM clustering are given in table 8.
score for DTW SOM clustering are given in table 8.

Figure 11. (a) Training data and (b) 10 generated data sets from the state space Student $t$![]() surrogate model together with the estimated mean (black solid line) and $95\,\%$
surrogate model together with the estimated mean (black solid line) and $95\,\%$![]() confidence (grey shaded region) for test case (iii). Different colours correspond to different shots of training data and different samples of the generated data, respectively.
confidence (grey shaded region) for test case (iii). Different colours correspond to different shots of training data and different samples of the generated data, respectively.

Figure 12. Comparison of cross-covariance of training data and generated data with cross-covariance (solid lines on top of each other, numerical error of order $10^{-16}$![]() ), covariance or sampled covariance (dashed lines) post-processing and uncorrelated model (dotted line) for test case (iii).
), covariance or sampled covariance (dashed lines) post-processing and uncorrelated model (dotted line) for test case (iii).

Figure 13. Comparison of covariance of training data (a) and difference of generated data (b) with uncorrelated model, (c) empirical covariance, (d) cross-covariance and (e) sampled covariance post-processing for test case (iii). Note the different scaling in the colour scale.

Figure 14. Kernel density estimation of the 2-D kernel PCA embedding of the (a) training data and generated data via (b) uncorrelated model, (c) empirical covariance, (d) cross-covariance and (e) sampled covariance post-processing for test case (iii). The embedded training data are shown in grey in all plots. The colour scale representing the density is the same in all plots.
Table 7. Post-processing method comparison for test case (iii). Mean and standard deviation over five dimensions and $N = 1000$![]() samples generated from the trained model for statistical metrics described in § 3. Best values are highlighted in bold.
samples generated from the trained model for statistical metrics described in § 3. Best values are highlighted in bold.

Table 8. The $F1$![]() score for DTW SOM clustering of different post-processing methods for test case (iii).
score for DTW SOM clustering of different post-processing methods for test case (iii).