Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-13T03:50:02.439Z Has data issue: false hasContentIssue false
  • English
  • Français

Description of global EGAM in the maximum of local frequency during current ramp-up discharges in DIII-D

Published online by Cambridge University Press:  09 June 2022

F. Camilo de Souza Open the ORCID record for F. Camilo de Souza [Opens in a new window] ,
N. Gorelenkov ,
A. Elfimov ,
R. Galvão ,
C. Collins ,
M. Podesta  and
E. Fredrickson
F. Camilo de Souza*
Affiliation:
Institute of Physics, University of São Paulo, São Paulo, Brazil
N. Gorelenkov
Affiliation:
Princeton Plasma Physics Laboratory, Princeton, NJ USA
A. Elfimov
Affiliation:
Institute of Physics, University of São Paulo, São Paulo, Brazil
R. Galvão
Affiliation:
Institute of Physics, University of São Paulo, São Paulo, Brazil
C. Collins
Affiliation:
General Atomics, San Diego, CA, USA
M. Podesta
Affiliation:
Princeton Plasma Physics Laboratory, Princeton, NJ USA
E. Fredrickson
Affiliation:
Princeton Plasma Physics Laboratory, Princeton, NJ USA
*
†Email address for correspondence: fabio.camilo.souza@usp.br
Get access Rights & Permissions [Opens in a new window]

Abstract

Energetic-particle-induced geodesic acoustic modes, EGAMs (Fu, Phys. Rev. Let., vol. 101, 2008, pp. 185002), driven by neutral beam injection (NBI), have been observed in many DIII-D tokamak experiments (Nazikian et al., Phys. Rev. Lett., vol. 101, 2008, pp. 185001). This mechanism has been theoretically investigated in (Qiu et al., Plasma Phys. Control. Fusion, vol. 52, 2010, pp. 095003), using a sharp energetic particle distribution function, and in (Qu et al., Plasma Phys. Control. Fusion, vol. 59, 2017, pp. 055018), where the dispersion relation and eigenmode behaviour were obtained for the situation of early beam scenario, that is, for times smaller than the beam slowing down time. 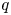In this work, we extend these studies determining the eigenmode for beyond the slowing down time, in a scenario with reverse safety factor $q$ profile, where a small concentration of energetic ions can produce an off-axis maximum in the GAM dispersion relation. The characteristics of EGAM are analytically studied with the drift kinetic equation together with the MHD code NOVA. The toroidal energetic ion transit frequency, coupled with the GAM frequency, produces the maximum in the dispersion relation where the eigenmode can be found. The quantitative correspondence of experimental results with the predictions of the proposed model is analysed.

Keywords

fusion plasmaplasma instabilitiesplasma waves
Type
Research Article
Information
Journal of Plasma Physics , Volume 88 , Issue 3 , June 2022 , 905880308
Check for updates
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

deceased.

References

REFERENCES

Askinazi, L.G., Belokurov, A.A., Bulanin, V.V., Gurchenko, A.D., Gusakov, E.Z., Kiviniemi, T.P., Lebedev, S.V., Kornev, V.A., Korpilo, T., Krikunov, S.V., et al. 2017 Physics of gam-initiated l-h transition in a tokamak. Plasma Phys. Control. Fusion 59, 014037.CrossRefGoogle Scholar
Berk, H.L., Boswell, C.J., Borba, D., Figueiredo, A.C.A., Johnson, T., Nave, M.F.F., Pinches, S.D., Sharapov, S.E. & the JET Contributors 2006 Explanation of the jet $n = 0$ chirping mode. Nucl. Fusion 46, S888.CrossRefGoogle Scholar
Cheng, C.Z. & Chance, M.S. 1986 Low’ shear alfvén spectra in axisymmetric toroidal plasmas. Phys. Fluids 29, 3695.CrossRefGoogle Scholar
Cheng, C.Z. & Chance, M.S. 1987 Nova: a nonvariational code for solving the MHD stability of axisymmetric toroidal plasmas. J. Comput. Phys. 71, 124–146.CrossRefGoogle Scholar
Cheng, C.Z., Chen, L. & Chance, M.S. 1985 High-n ideal and resistive shear alfvén waves in tokamaks. Ann. Phys. 161, 21–47.CrossRefGoogle Scholar
Chen, Y., Zhang, W., Bao, J., Lin, Z., Dong, C., Cao, J. & Li, D. 2020 Verification of energetic-particle-induced geodesic acoustic mode in gyrokinetic particle simulations. Chin. Phys. Lett. 37, 095201.CrossRefGoogle Scholar
Collins, C.S., Heidbrink, W.W., Austin, M.E., Kramer, G.J., Pace, D.C., Petty, C.C., Stagner, L., Van Zeeland, M.A., White, R.B., Zhu, Y.B., et al. 2016 Observation of critical-gradient behavior in alfvén-eigenmode-induced fast-ion transport. Phys. Rev. Lett. 116, 095001.CrossRefGoogle ScholarPubMed
Conway, G.D. 2008 Turbulence measurements in fusion plasmas. Plasma Phys. Control. Fusion 50, 124026.CrossRefGoogle Scholar
Conway, G.D., Angioni, C., Ryter, F., Sauter, P. & Vicente, J. 2011 Mean and oscillating plasma flows and turbulence interactions across the l-h confinement transition. Phys. Rev. Lett. 106, 065001.CrossRefGoogle ScholarPubMed
de Souza, F.C., Elfimov, A.G. & Galvão, R.M.O. 2018 Geodesic modes driven by plasma fluxes during oblique nb heating in tokamaks. Phys. Plasmas 25, 122507.CrossRefGoogle Scholar
de Souza, F.C., Elfimov, A.G., Galvão, R.M.O., Krbec, J., Seidl, J., Stockel, J., Hron, M., Havlicek, J. & Mitosinkova, K. 2017 Geodesic mode instability driven by electron and ion fluxes during neutral beam injection in tokamaks. Phys. Lett. A 381, 3066.CrossRefGoogle Scholar
Diamond, P.H., Itoh, S.I., Itoh, K. & Hahm, T.S. 2005 Zonal flows in plasma—a review. Plasma Phys. Control. Fusion 47, R35.CrossRefGoogle Scholar
Elfimov, A.G., Galvão, R.M.O & Gorelenkov, N.N. 2019 Geodesic modes driven by untrapped resonances of nb energetic ions in tokamaks. Phys. Plasmas 26, 102508.CrossRefGoogle Scholar
Fu, G.Y. 2008 Energetic-particle-induced geodesic acoustic mode. Phys. Rev. Let. 101, 185002.CrossRefGoogle ScholarPubMed
Gorelenkov, N.N., Berk, H.L., Fredrickson, E., Sharapov, S.E. & the JET EFDA Contributors 2007 Predictions and observations of low-shear beta-induced shear alfvén–acoustic eigenmodes in toroidal plasmas. Phys. Lett. A 370, 70–77.CrossRefGoogle Scholar
Gorelenkov, N.N., Cheng, C.Z. & Fu, G.Y. 1999 Fast particle finite orbit width and Larmor radius effects on low-n toroidicity induced Alfvén eigenmode excitation. Phys. Plasmas 6, 2802.CrossRefGoogle Scholar
Gorelenkov, N.N., Duarte, V.N., Podesta, M. & Berk, H.L. 2018 Resonance broadened quasi-linear (rbq) model for fast ion distribution relaxation due to alfvénic eigenmodes. Nucl. Fusion 58, 082016.CrossRefGoogle Scholar
Hallatschek, K. & Biskamp, D. 2001 Transport control by coherent zonal flows in the core/edge transitional regime. Phys. Rev. Lett. 86, 1223.CrossRefGoogle ScholarPubMed
Hazeltine, R.D. 1973 Recursive derivation of drift-kinetic equation. Plasma Phys. 15, 77–80.CrossRefGoogle Scholar
Heidbrink, W.W. 2008 Basic physics of alfvén instabilities driven by energetic particles in toroidally confined plasmas. Phys. Plasmas 15, 055501.CrossRefGoogle Scholar
Heidbrink, W.W., Collins, C.S., Podesta, M., Kramer, G.J., Pace, D.C., Petty, C.C., Stagner, L., Van Zeeland, M.A., White, R.B. & Zhu, Y.B. 2017 Fast-ion transport by alfvén eigenmodes above a critical gradient threshold. Phys. Plasmas 24, 056109.CrossRefGoogle Scholar
Itoh, S.I., Itoh, K., Sasaki, M., Fujisawa, A., Ido, T. & Nagashima, Y. 2007 Geodesic acoustic mode spectroscopy. Plasma Phys. Control. Fusion 49, L7–L10.CrossRefGoogle Scholar
Lakhin, V.P. & Sorokina, E.A. 2014 Geodesic acoustic eigenmode for tokamak equilibrium with maximum of local gam frequency. Phys. Lett. A 378, 535–538.CrossRefGoogle Scholar
Lebedev, V.B., Yushmanov, P.N., Diamond, P.H., Novakovskii, S.V. & Smolyakov, A.I. 1996 Plateau regime dynamics of the relaxation of poloidal rotation in tokamak plasmas. Phys. Plasmas 3, 3023.CrossRefGoogle Scholar
LeVeque, R.J. 2007 Finite difference methods for ordinary and partial differential equations: steady-state and time-dependent problems, Steady-State and Time-Dependent Problems, Society for Industrial and Applied Mathematics, p. 113–138.Google Scholar
Melnikov, A.V., Eliseev, L.G., Perfilov, S.V., Lysenko, S.E., Shurygin, R.V., Zenin, V.N., Grashin, S.A., Krupnik, L.I., Kozachek, A.S., Solomatin, R.Y., et al. 2015 The features of the global gam in oh and ecrh plasmas in the t-10 tokamak. Nucl. Fusion 55, 063001.CrossRefGoogle Scholar
Nazikian, R., Fu, G.Y., Austin, M.E., Berk, H.L., Budny, R.V., Gorelenkov, N.N., Heidbrink, W.W., Holcomb, C.T., Kramer, G.J., McKee, G.R., et al. 2008 Intense geodesic acousticlike modes driven by suprathermal ions in a tokamak plasma. Phys. Rev. Lett. 101, 185001.CrossRefGoogle Scholar
Podesta, M., Gorelenkova, M.V., Gorelenkov, N.N. & White, R.B. 2017 Computation of alfvén eigenmode stability and saturation through a reduced fast ion transport model in the transp tokamak transport code. Plasma Phys. Control. Fusion 59, 095008.CrossRefGoogle Scholar
Podesta, M., Gorelenkova, M.V. & White, R.B. 2014 A reduced fast ion transport model for the tokamak transport code transp. Plasma Phys. Control. Fusion 56, 055003.CrossRefGoogle Scholar
Qiu, Z., Zonca, F. & Chen, L. 2010 Nonlocal theory of energetic-particle-induced geodesic acoustic mode. Plasma Phys. Control. Fusion 52, 095003.CrossRefGoogle Scholar
Qu, Z.S., Hole, M.J. & Fitzgerald, M. 2017 Linear radial structure of reactive energetic geodesic acoustic modes. Plasma Phys. Control. Fusion 59, 055018.CrossRefGoogle Scholar
Sharapov, S.E., Alper, B., Berk, H.L., Borba, D.N., Breizman, B.N., Challis, C.D., Fasoli, A., Hawkes, N.C., Hender, T.C., Mailloux, J., et al. 2002 Alfvén wave cascades in a tokamak. Phys. Plasmas 9, 2027.CrossRefGoogle Scholar
Stix, T.H. 1972 Heating of toroidal plasmas by neutral injection. Plasma Phys. 14, 367.CrossRefGoogle Scholar
Winsor, N., Johnson, J. & Dawson, J.M. 1968 Geodesic acoustic waves in hydromagnetic systems. Phys. Fluids 11, 2448.CrossRefGoogle Scholar
Zarzoso, D., Garbet, X., Sarazin, Y., Dumont, R. & Grandgirard, V. 2012 Fully kinetic description of the linear excitation and nonlinear saturation of fast-ion-driven geodesic acoustic mode instability. Phys. Plasmas 19, 22102.CrossRefGoogle Scholar