Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Landreman, M.
Buller, S.
and
Drevlak, M.
2022.
Optimization of quasi-symmetric stellarators with self-consistent bootstrap current and energetic particle confinement.
Physics of Plasmas,
Vol. 29,
Issue. 8,
Landreman, Matt
2022.
Mapping the space of quasisymmetric stellarators using optimized near-axis expansion.
Journal of Plasma Physics,
Vol. 88,
Issue. 6,
Law, Frederick
Cerfon, Antoine
Peherstorfer, Benjamin
and
Wechsung, Florian
2023.
Meta variance reduction for Monte Carlo estimation of energetic particle confinement during stellarator optimization.
Journal of Computational Physics,
Vol. 495,
Issue. ,
p.
112524.
Bindel, David
Landreman, Matt
and
Padidar, Misha
2023.
Understanding trade-offs in stellarator design with multi-objective optimization.
Journal of Plasma Physics,
Vol. 89,
Issue. 5,
Jorge, R
Goodman, A
Landreman, M
Rodrigues, J
and
Wechsung, F
2023.
Single-stage stellarator optimization: combining coils with fixed boundary equilibria.
Plasma Physics and Controlled Fusion,
Vol. 65,
Issue. 7,
p.
074003.
Giuliani, Andrew
Wechsung, Florian
Cerfon, Antoine
Landreman, Matt
and
Stadler, Georg
2023.
Direct stellarator coil optimization for nested magnetic surfaces with precise quasi-symmetry.
Physics of Plasmas,
Vol. 30,
Issue. 4,
Lee, Brandon F.
Paul, Elizabeth J.
Stadler, Georg
and
Landreman, Matt
2023.
Stellarator coil optimization supporting multiple magnetic configurations.
Nuclear Fusion,
Vol. 63,
Issue. 1,
p.
014002.
Yu, Guodong
Liu, Ke
Qian, Tianyi
Xie, Yidong
Nie, Xianyi
and
Zhu, Caoxiang
2024.
Quasi-single-stage optimization for permanent magnet stellarators.
Nuclear Fusion,
Vol. 64,
Issue. 7,
p.
076055.
Kappel, John
Landreman, Matt
and
Malhotra, Dhairya
2024.
The magnetic gradient scale length explains why certain plasmas require close external magnetic coils.
Plasma Physics and Controlled Fusion,
Vol. 66,
Issue. 2,
p.
025018.
Giuliani, Andrew
2024.
Direct stellarator coil design using global optimization: application to a comprehensive exploration of quasi-axisymmetric devices.
Journal of Plasma Physics,
Vol. 90,
Issue. 3,
Jorge, R.
Giuliani, A.
and
Loizu, J.
2024.
Simplified and flexible coils for stellarators using single-stage optimization.
Physics of Plasmas,
Vol. 31,
Issue. 11,
Smiet, C. B.
Loizu, J.
Balkovic, E.
and
Baillod, A.
2025.
Efficient single-stage optimization of islands in finite-β stellarator equilibria.
Physics of Plasmas,
Vol. 32,
Issue. 1,
Hegna, C.C.
Anderson, D.T.
Andrew, E.C.
Ayilaran, A.
Bader, A.
Bohm, T.D.
Mata, K. Camacho
Canik, J.M.
Carbajal, L.
Cerfon, A.
Clark, D.W.S.
Cooper, W.A.
Davila, N.M.
Dorland, W.D.
Duff, J.M.
Goh, B.
Guttenfelder, W.
Holland, C.
Huet, D.P.
Kessing, J.
Knilans, M.
Landreman, M.
Lau, C.
Le Bars, G.
Malkus, A.
Mandell, N.R.
Medasani, B.
Moreno, C.
Morrissey, J.
Pedersen, T.S.
Pflug, E.
Ramirez, S.
Smandych, J.
Schmitt, J.C.
Sinha, P.
Singh, L.
Suzuki, Y.
Tillack, M.S.
Rodriguez, J. Varela
Willis, K.
and
Wilson, P.P.H.
2025.
The Infinity Two fusion pilot plant baseline plasma physics design.
Journal of Plasma Physics,
Vol. 91,
Issue. 3,
Tomassetti, Giordano
2025.
Direct and surrogate optimization in applied superconductivity: state of the art, perspectives and challenges.
Superconductor Science and Technology,
Vol. 38,
Issue. 7,
p.
073001.
Giuliani, Andrew
Rodríguez, Eduardo
and
Spivak, Marina
2025.
A comprehensive exploration of quasisymmetric stellarators and their coil sets.
Journal of Plasma Physics,
Vol. 91,
Issue. 5,
Baillod, A.
Paul, E.J.
Rawlinson, G.
Haque, M.
Freiberger, S.W.
and
Thapa, S.
2025.
Integrating novel stellarator single-stage optimization algorithms to design the Columbia stellarator experiment.
Nuclear Fusion,
Vol. 65,
Issue. 2,
p.
026046.
Fu, Lanke
Paul, Elizabeth J.
Kaptanoglu, Alan A.
and
Bhattacharjee, Amitava
2025.
Global stellarator coil optimization with quadratic constraints and objectives.
Nuclear Fusion,
Vol. 65,
Issue. 2,
p.
026045.
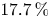 to $6.6\,\%$
to $6.6\,\%$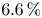 . We also demonstrate 16-coil configurations with alpha loss ${<}1\,\%$
. We also demonstrate 16-coil configurations with alpha loss ${<}1\,\%$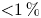 and neoclassical transport magnitude $\epsilon _{\text {eff}}^{3/2}$
and neoclassical transport magnitude $\epsilon _{\text {eff}}^{3/2}$ less than approximately $5\times 10^{-9}$
less than approximately $5\times 10^{-9}$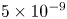 .
.

