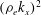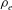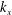1. Introduction
There are three main triggering processes for magnetic reconnection in equilibrium collisionless plasma systems: Landau resonance of tearing mode perturbations and demagnetized ions (e.g. Schindler Reference Schindler1974; Galeev & Zelenyi Reference Galeev and Zelenyi1976), inertia of magnetized electrons (e.g. Laval, Pellat & Vuillemin Reference Laval, Pellat and Vuillemin1966; Porcelli et al. Reference Porcelli, Borgogno, Califano, Grasso, Ottaviani and Pegoraro2002; Zelenyi & Artemyev Reference Zelenyi and Artemyev2013, and references therein) and effective collisions induced by particle scattering on electromagnetic turbulence (e.g. Huba, Gladd & Papadopoulos Reference Huba, Gladd and Papadopoulos1977; Coroniti Reference Coroniti1980; Büchner & Zelenyi Reference Büchner and Zelenyi1987). All these three processes can drive the instability of an equilibrium (or quasi-equilibrium) current sheet and result in magnetic field reconfiguration. The situation can be much more complicated for dynamical plasma systems where the turbulent magnetic reconnection destroys (or reforms) current sheets and magnetic discontinuities (Servidio et al. Reference Servidio, Dmitruk, Greco, Wan, Donato, Cassak, Shay, Carbone and Matthaeus2011; Greco et al. Reference Greco, Valentini, Servidio and Matthaeus2012; Rappazzo et al. Reference Rappazzo, Matthaeus, Ruffolo, Servidio and Velli2012; Karimabadi et al. Reference Karimabadi, Roytershteyn, Daughton and Liu2013). However, in this study we concentrate on consideration of small perturbations of an equilibrium current sheet. This is typical situation for magnetic reconnection in the Earth’s magnetotail where the ion Landau resonance is considered to be a main candidate for tearing mode excitation (Schindler Reference Schindler2006; Zelenyi et al. Reference Zelenyi, Artemyev, Malova and Popov2008; Sitnov & Swisdak Reference Sitnov and Swisdak2011) where the numerous spacecraft observations have revealed the manifestations of reconnection events (e.g. Petrukovich et al. Reference Petrukovich, Sergeev, Zelenyi, Mukai, Yamamoto, Kokubun, Shiokawa, Deehr, Budnick and Büchner1998; Baumjohann Reference Baumjohann2002; Angelopoulos et al. Reference Angelopoulos, McFadden, Larson, Carlson, Mende, Frey, Phan, Sibeck, Glassmeier and Auster2008; Nagai et al. Reference Nagai, Shinohara, Fujimoto, Matsuoka, Saito and Mukai2011). However, many physical problems of ion (resonant) tearing mode still remain unsolved (see discussion in Pellat, Coroniti & Pritchett Reference Pellat, Coroniti and Pritchett1991; Quest, Karimabadi & Brittnacher Reference Quest, Karimabadi and Brittnacher1996; Sitnov et al. Reference Sitnov, Sharma, Guzdar and Yoon2002). Thus, the idea of effective dissipation induced by particle scattering due to wave–particle interaction appears to be quite promising. Previous estimates (Coroniti Reference Coroniti1985) and modern spacecraft observations (e.g. Eastwood et al. Reference Eastwood, Phan, Bale and Tjulin2009) were somewhat pessimistic concerning this idea – the observed level of electromagnetic turbulence appears to be insufficient to support the required effective collision conductivity in the Earth’s magnetotail. In this paper, we consider an additional effect responsible for the enhancement of effective collisions. Although, we concentrate on magnetotail reconnection, the proposed effect can also be important for laboratory devices where a weakly collisional reconnection geometry is reproduced (Le et al. Reference Le, Egedal, Daughton, Roytershteyn, Karimabadi and Forest2015).
The kinetic investigation of current sheet stability with the effects of particle effective collisions requires the consideration of the Vlasov–Maxwell equations with a collision integral (e.g. Zelenyi & Artemyev Reference Zelenyi and Artemyev2013, and references therein). Due to the complicated form of the full collision integral (Pitaevskii & Lifshitz Reference Pitaevskii and Lifshitz1981), the practical approach is reduced to the inclusion of an approximate form of this integral into a kinetic equation. For example, one of the most popular forms of the collision operator
![]() $Y[f]$
acting on the velocity distribution
$Y[f]$
acting on the velocity distribution
![]() $f=f_{0}+{\it\delta}f$
has been proposed by Bhatnagar, Gross & Krook (Reference Bhatnagar, Gross and Krook1954):
$f=f_{0}+{\it\delta}f$
has been proposed by Bhatnagar, Gross & Krook (Reference Bhatnagar, Gross and Krook1954):
where
![]() ${\it\nu}$
is Coulomb collision frequency (later treated more generally as a frequency of effective collisions due to interaction of electrons with different wave modes),
${\it\nu}$
is Coulomb collision frequency (later treated more generally as a frequency of effective collisions due to interaction of electrons with different wave modes),
![]() $m$
and
$m$
and
![]() $T$
are the mass and temperature of the particles,
$T$
are the mass and temperature of the particles,
![]() $f_{0}$
and
$f_{0}$
and
![]() $n_{0}$
are the unperturbed velocity distribution and plasma density and
$n_{0}$
are the unperturbed velocity distribution and plasma density and
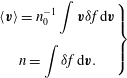 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \left\langle \boldsymbol{v}\right\rangle =n_{0}^{-1}\int \boldsymbol{v}{\it\delta}f\,\text{d}\boldsymbol{v}\\ \displaystyle n=\int {\it\delta}f\,\text{d}\boldsymbol{v}.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \left\langle \boldsymbol{v}\right\rangle =n_{0}^{-1}\int \boldsymbol{v}{\it\delta}f\,\text{d}\boldsymbol{v}\\ \displaystyle n=\int {\it\delta}f\,\text{d}\boldsymbol{v}.\end{array}\right\}\end{eqnarray}$$
We also note that
![]() $\int \!\boldsymbol{v}f_{0}\,\text{d}\boldsymbol{v}=0$
and
$\int \!\boldsymbol{v}f_{0}\,\text{d}\boldsymbol{v}=0$
and
![]() $n_{0}=\int \!f_{0}\,\text{d}\boldsymbol{v}$
.
$n_{0}=\int \!f_{0}\,\text{d}\boldsymbol{v}$
.
The integral (1.1) describes the relaxation of the velocity distributions to the initial state
![]() $f_{0}$
. This integral does not include any derivatives of the perturbation
$f_{0}$
. This integral does not include any derivatives of the perturbation
![]() ${\it\delta}f$
and thus does not take into account any information about the internal fine structure of
${\it\delta}f$
and thus does not take into account any information about the internal fine structure of
![]() ${\it\delta}f$
. In this paper, we show how the consideration of exact form of the collision integral can modify the effective frequency
${\it\delta}f$
. In this paper, we show how the consideration of exact form of the collision integral can modify the effective frequency
![]() ${\it\nu}$
with particle gyration in the background magnetic field produces significant modulations in the distribution function
${\it\nu}$
with particle gyration in the background magnetic field produces significant modulations in the distribution function
![]() ${\it\delta}f$
.
${\it\delta}f$
.
2. Collisions in a weakly magnetized plasma
To consider the effect of a finite electron gyroradius on effective collisions below we use the full expression of the Landau form of the collision integral
![]() $Y[f]=-m^{-1}(\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{s})$
where the density of particle flux
$Y[f]=-m^{-1}(\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{s})$
where the density of particle flux
![]() $\boldsymbol{s}$
has the following components (Pitaevskii & Lifshitz Reference Pitaevskii and Lifshitz1981):
$\boldsymbol{s}$
has the following components (Pitaevskii & Lifshitz Reference Pitaevskii and Lifshitz1981):
 $$\begin{eqnarray}\displaystyle s_{{\it\alpha}} & = & \displaystyle \frac{{\rm\pi}e^{2}{\it\Lambda}}{m}\mathop{\sum }_{{\it\beta}}\int \left(\frac{\partial f(\boldsymbol{v}^{\prime })}{\partial v_{{\it\beta}}^{\prime }}+\frac{mv_{{\it\beta}}^{\prime }}{T}f(\boldsymbol{v}^{\prime })\right)f_{0}(\boldsymbol{v})\frac{w^{2}{\it\delta}_{{\it\beta}{\it\alpha}}-w_{{\it\alpha}}w_{{\it\beta}}}{w^{2}}\,\text{d}\boldsymbol{v}^{\prime }\nonumber\\ \displaystyle & & \displaystyle -\,\frac{{\rm\pi}e^{2}{\it\Lambda}}{m}\mathop{\sum }_{{\it\beta}}\int \left(\frac{\partial f(\boldsymbol{v})}{\partial v_{{\it\beta}}}+\frac{mv_{{\it\beta}}}{T}f(\boldsymbol{v})\right)f_{0}(\boldsymbol{v}^{\prime })\frac{w^{2}{\it\delta}_{{\it\beta}{\it\alpha}}-w_{{\it\alpha}}w_{{\it\beta}}}{w^{2}}\,\text{d}\boldsymbol{v}^{\prime },\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle s_{{\it\alpha}} & = & \displaystyle \frac{{\rm\pi}e^{2}{\it\Lambda}}{m}\mathop{\sum }_{{\it\beta}}\int \left(\frac{\partial f(\boldsymbol{v}^{\prime })}{\partial v_{{\it\beta}}^{\prime }}+\frac{mv_{{\it\beta}}^{\prime }}{T}f(\boldsymbol{v}^{\prime })\right)f_{0}(\boldsymbol{v})\frac{w^{2}{\it\delta}_{{\it\beta}{\it\alpha}}-w_{{\it\alpha}}w_{{\it\beta}}}{w^{2}}\,\text{d}\boldsymbol{v}^{\prime }\nonumber\\ \displaystyle & & \displaystyle -\,\frac{{\rm\pi}e^{2}{\it\Lambda}}{m}\mathop{\sum }_{{\it\beta}}\int \left(\frac{\partial f(\boldsymbol{v})}{\partial v_{{\it\beta}}}+\frac{mv_{{\it\beta}}}{T}f(\boldsymbol{v})\right)f_{0}(\boldsymbol{v}^{\prime })\frac{w^{2}{\it\delta}_{{\it\beta}{\it\alpha}}-w_{{\it\alpha}}w_{{\it\beta}}}{w^{2}}\,\text{d}\boldsymbol{v}^{\prime },\end{eqnarray}$$
where
![]() $\boldsymbol{w}=\boldsymbol{v}-\boldsymbol{v}^{\prime }$
,
$\boldsymbol{w}=\boldsymbol{v}-\boldsymbol{v}^{\prime }$
,
![]() ${\it\alpha},{\it\beta}=x,y,z$
,
${\it\alpha},{\it\beta}=x,y,z$
,
![]() ${\it\Lambda}=\ln ({\it\lambda}_{D}q^{2}/T)$
and
${\it\Lambda}=\ln ({\it\lambda}_{D}q^{2}/T)$
and
![]() ${\it\lambda}_{D}$
is the Debye length.
${\it\lambda}_{D}$
is the Debye length.
Considering the perturbation
![]() ${\it\delta}f=f(\boldsymbol{v})\exp (\text{i}{\it\Phi})$
of the initial distribution function
${\it\delta}f=f(\boldsymbol{v})\exp (\text{i}{\it\Phi})$
of the initial distribution function
![]() $f_{0}(\boldsymbol{v})$
, the phase of the perturbation is
$f_{0}(\boldsymbol{v})$
, the phase of the perturbation is
![]() ${\it\Phi}=\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{r}-{\it\omega}t$
. The corresponding perturbations to the electromagnetic field are
${\it\Phi}=\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{r}-{\it\omega}t$
. The corresponding perturbations to the electromagnetic field are
![]() ${\it\delta}\boldsymbol{B}=\boldsymbol{B}\exp (\text{i}{\it\Phi})$
,
${\it\delta}\boldsymbol{B}=\boldsymbol{B}\exp (\text{i}{\it\Phi})$
,
![]() ${\it\delta}\boldsymbol{E}=\boldsymbol{E}\exp (\text{i}{\it\Phi})$
, while the background magnetic field is
${\it\delta}\boldsymbol{E}=\boldsymbol{E}\exp (\text{i}{\it\Phi})$
, while the background magnetic field is
![]() $\boldsymbol{B}_{0}=B_{0}\boldsymbol{e}_{z}$
. The wave vector of perturbations
$\boldsymbol{B}_{0}=B_{0}\boldsymbol{e}_{z}$
. The wave vector of perturbations
![]() $\boldsymbol{k}$
is assumed to lie in the
$\boldsymbol{k}$
is assumed to lie in the
![]() $(x,z)$
plane. In this case, the perturbation of the Valsov equation takes the form
$(x,z)$
plane. In this case, the perturbation of the Valsov equation takes the form
We introduce the force
![]() $\boldsymbol{F}=(q/m)(\boldsymbol{E}+c^{-1}[\boldsymbol{v}\times \boldsymbol{B}])$
, cylindrical velocity coordinates
$\boldsymbol{F}=(q/m)(\boldsymbol{E}+c^{-1}[\boldsymbol{v}\times \boldsymbol{B}])$
, cylindrical velocity coordinates
![]() $v_{x}=v_{\bot }\cos {\it\theta}$
,
$v_{x}=v_{\bot }\cos {\it\theta}$
,
![]() $v_{y}=v_{\bot }\sin {\it\theta}$
and rewrite (2.2) as
$v_{y}=v_{\bot }\sin {\it\theta}$
and rewrite (2.2) as
where
![]() $[\boldsymbol{v}\times \boldsymbol{B}_{0}](\partial /\partial \boldsymbol{v})=-B_{0}(\partial /\partial {\it\theta})$
. Then we divide (2.3) by
$[\boldsymbol{v}\times \boldsymbol{B}_{0}](\partial /\partial \boldsymbol{v})=-B_{0}(\partial /\partial {\it\theta})$
. Then we divide (2.3) by
![]() $\exp (\text{i}{\it\Phi})$
and introduce
$\exp (\text{i}{\it\Phi})$
and introduce
![]() ${\it\Omega}_{0}=qB_{0}/mc$
,
${\it\Omega}_{0}=qB_{0}/mc$
,
![]() ${\it\lambda}={\it\omega}-k_{z}v_{z}$
:
${\it\lambda}={\it\omega}-k_{z}v_{z}$
:
We introduce the function
![]() $W=({\it\lambda}{\it\theta}-k_{x}v_{\bot }\cos {\it\theta})/{\it\Omega}_{0}$
and function
$W=({\it\lambda}{\it\theta}-k_{x}v_{\bot }\cos {\it\theta})/{\it\Omega}_{0}$
and function
![]() $g(\boldsymbol{v})=f(\boldsymbol{v})\exp (\text{i}W)$
. Thus, (2.4) can be rewritten as
$g(\boldsymbol{v})=f(\boldsymbol{v})\exp (\text{i}W)$
. Thus, (2.4) can be rewritten as
To derive the dispersion relation for perturbations, one should substitute into (2.5) the Maxwell equations for electromagnetic field perturbations (
![]() ${\sim}\boldsymbol{F}$
) expressed through function
${\sim}\boldsymbol{F}$
) expressed through function
![]() $g$
(see, e.g. Zelenyi & Artemyev Reference Zelenyi and Artemyev2013). In this case, the final wave frequency/growth rate would depend on collision frequency (e.g. for the simplified collision integral (1.1) the operator
$g$
(see, e.g. Zelenyi & Artemyev Reference Zelenyi and Artemyev2013). In this case, the final wave frequency/growth rate would depend on collision frequency (e.g. for the simplified collision integral (1.1) the operator
![]() $Y$
is proportional to collision frequency
$Y$
is proportional to collision frequency
![]() ${\it\nu}$
). However, we would like to estimate the effect of a finite electron gyroradius on collision frequency
${\it\nu}$
). However, we would like to estimate the effect of a finite electron gyroradius on collision frequency
![]() ${\it\nu}$
. Thus, we compare the term
${\it\nu}$
. Thus, we compare the term
![]() ${\sim}Y$
for the two systems: when simplified (1.1) can be used and
${\sim}Y$
for the two systems: when simplified (1.1) can be used and
![]() $Y\sim {\it\nu}$
and when the full collision integral
$Y\sim {\it\nu}$
and when the full collision integral
![]() $Y[f]=-m^{-1}(\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{s})$
with (2.1) should be taken into account. For this reason, we carefully consider the second term in (2.5) and estimate the main part of this term
$Y[f]=-m^{-1}(\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{s})$
with (2.1) should be taken into account. For this reason, we carefully consider the second term in (2.5) and estimate the main part of this term
In the limit
![]() $k_{x}\sqrt{2T/m}/{\it\Omega}_{0}\gg 1$
, function
$k_{x}\sqrt{2T/m}/{\it\Omega}_{0}\gg 1$
, function
![]() $g\exp (-\text{i}W)$
contains the fast oscillating term
$g\exp (-\text{i}W)$
contains the fast oscillating term
![]() ${\sim}\exp (\text{i}k_{x}v_{\bot }\sin {\it\theta}/{\it\Omega}_{0})=\exp (\text{i}k_{x}v_{y}/{\it\Omega}_{0})$
. Thus, in (2.1) we should keep the main terms corresponding to the derivative
${\sim}\exp (\text{i}k_{x}v_{\bot }\sin {\it\theta}/{\it\Omega}_{0})=\exp (\text{i}k_{x}v_{y}/{\it\Omega}_{0})$
. Thus, in (2.1) we should keep the main terms corresponding to the derivative
![]() $\partial f/\partial v_{y}$
. The first term in (2.1) contains the integral
$\partial f/\partial v_{y}$
. The first term in (2.1) contains the integral
![]() $\int (\partial f/\partial v_{y}^{\prime })\,\text{d}v_{y}^{\prime }\sim f$
. Therefore, the second term with
$\int (\partial f/\partial v_{y}^{\prime })\,\text{d}v_{y}^{\prime }\sim f$
. Therefore, the second term with
![]() $\partial f/\partial v_{y}$
is more important and we can write:
$\partial f/\partial v_{y}$
is more important and we can write:
The main part of
![]() $s_{{\it\alpha}}$
from (2.8) is
$s_{{\it\alpha}}$
from (2.8) is
Thus, the integrand of (2.6) takes the form
In dimensionless form (2.10) can be written as
where
![]() ${\tilde{Y}}$
is the initial collision integral (2.1) without derivatives over fast oscillation terms. Equation (2.11) shows that the effect of a finite electron gyroradius provides the multiplication factor
${\tilde{Y}}$
is the initial collision integral (2.1) without derivatives over fast oscillation terms. Equation (2.11) shows that the effect of a finite electron gyroradius provides the multiplication factor
![]() $2k_{x}^{2}T/{\it\Omega}_{0}^{2}m$
. This factor is omitted in the simplified form of the collision integral (1.1). Therefore, if we operate with the collision frequency
$2k_{x}^{2}T/{\it\Omega}_{0}^{2}m$
. This factor is omitted in the simplified form of the collision integral (1.1). Therefore, if we operate with the collision frequency
![]() ${\it\nu}$
from (1.1) then this expression for collision frequency
${\it\nu}$
from (1.1) then this expression for collision frequency
![]() ${\it\nu}$
(Coulomb or effective) should be multiplied by the term
${\it\nu}$
(Coulomb or effective) should be multiplied by the term
![]() $2k_{x}^{2}T/{\it\Omega}_{0}^{2}m\gg 1$
. Of course, for a complete investigation of system stability one should consider the full collision integral (2.1), but for many applications the simplified approach with collision frequency
$2k_{x}^{2}T/{\it\Omega}_{0}^{2}m\gg 1$
. Of course, for a complete investigation of system stability one should consider the full collision integral (2.1), but for many applications the simplified approach with collision frequency
![]() ${\it\nu}$
can be applied with the corresponding correction
${\it\nu}$
can be applied with the corresponding correction
![]() ${\sim}2k_{x}^{2}T/{\it\Omega}_{0}^{2}m$
. Finally, we come to the following expression for the effective collision frequency in a system with weakly magnetized electrons:
${\sim}2k_{x}^{2}T/{\it\Omega}_{0}^{2}m$
. Finally, we come to the following expression for the effective collision frequency in a system with weakly magnetized electrons:
where
![]() ${\it\rho}_{e}=\sqrt{2T/m}/{\it\Omega}_{0}$
is the electron gyroradius. Note, that (2.12) provides only a simplified estimate of the effect of electron finite gyroradius on system stability. However, this simplified expression gives us the opportunity to estimate this effect for realistic system parameters. In the next section we use the modified collision frequency (2.12) to estimate the effect of effective conductivity in the regions with weak magnetic field, in particular in the reconnection regions in near-Earth plasma systems.
${\it\rho}_{e}=\sqrt{2T/m}/{\it\Omega}_{0}$
is the electron gyroradius. Note, that (2.12) provides only a simplified estimate of the effect of electron finite gyroradius on system stability. However, this simplified expression gives us the opportunity to estimate this effect for realistic system parameters. In the next section we use the modified collision frequency (2.12) to estimate the effect of effective conductivity in the regions with weak magnetic field, in particular in the reconnection regions in near-Earth plasma systems.
3. Estimates of
 $k_{x}{\it\rho}_{e}$
parameter for space plasma reconnection systems
$k_{x}{\it\rho}_{e}$
parameter for space plasma reconnection systems
Let us consider the classical 2-D X-line with magnetic field configuration
![]() $\boldsymbol{B}=B_{0}(z/L_{z})\boldsymbol{e}_{x}+B_{z}(x/L_{x})\boldsymbol{e}_{z}$
(see scheme in figure 1). The reversal of the
$\boldsymbol{B}=B_{0}(z/L_{z})\boldsymbol{e}_{x}+B_{z}(x/L_{x})\boldsymbol{e}_{z}$
(see scheme in figure 1). The reversal of the
![]() $B_{x}$
magnetic field component in the neutral plane
$B_{x}$
magnetic field component in the neutral plane
![]() $z=0$
generates so-called neutral region
$z=0$
generates so-called neutral region
![]() $|z|<\sqrt{{\it\rho}_{0}L_{z}}$
with
$|z|<\sqrt{{\it\rho}_{0}L_{z}}$
with
![]() ${\it\rho}_{0}=\sqrt{2Tm}c/eB_{0}$
where particles are not affected by the
${\it\rho}_{0}=\sqrt{2Tm}c/eB_{0}$
where particles are not affected by the
![]() $B_{x}$
magnetic field and can move practically freely along the
$B_{x}$
magnetic field and can move practically freely along the
![]() $y$
-axis (Dobrowolny Reference Dobrowolny1968). The same region appears around the
$y$
-axis (Dobrowolny Reference Dobrowolny1968). The same region appears around the
![]() $x=0$
plane due to
$x=0$
plane due to
![]() $B_{z}$
reversal:
$B_{z}$
reversal:
![]() $|x|<\sqrt{{\it\rho}_{z}L_{x}}$
with
$|x|<\sqrt{{\it\rho}_{z}L_{x}}$
with
![]() ${\it\rho}_{z}=\sqrt{2Tm}c/eB_{z}$
. Particles, moving within this region are affected by the effective (averaged gyroradius) magnetic field with amplitude
${\it\rho}_{z}=\sqrt{2Tm}c/eB_{z}$
. Particles, moving within this region are affected by the effective (averaged gyroradius) magnetic field with amplitude
![]() $\tilde{B}_{z}=B_{z}\sqrt{{\it\rho}_{z}L_{x}}/L_{x}=B_{z}\sqrt{{\it\rho}_{z}/L_{x}}$
, while the effective particle gyroradius is equal to the spatial scale
$\tilde{B}_{z}=B_{z}\sqrt{{\it\rho}_{z}L_{x}}/L_{x}=B_{z}\sqrt{{\it\rho}_{z}/L_{x}}$
, while the effective particle gyroradius is equal to the spatial scale
![]() ${\it\rho}_{e}=\sqrt{2Tm}c/e\tilde{B}_{z}=\sqrt{{\it\rho}_{z}L_{x}}$
. If we assume that the X-line is generated by the tearing instability with a wavelength equal to
${\it\rho}_{e}=\sqrt{2Tm}c/e\tilde{B}_{z}=\sqrt{{\it\rho}_{z}L_{x}}$
. If we assume that the X-line is generated by the tearing instability with a wavelength equal to
![]() $L_{x}=2{\rm\pi}/k_{x}$
(see the scheme in figure 1), then the factor from (2.12) can be written as
$L_{x}=2{\rm\pi}/k_{x}$
(see the scheme in figure 1), then the factor from (2.12) can be written as
Figure 2 shows values of
![]() $X$
as a function of electron temperature
$X$
as a function of electron temperature
![]() $T$
,
$T$
,
![]() $L_{x}$
and
$L_{x}$
and
![]() $B_{z}$
. For the initial stage of the tearing instability (when
$B_{z}$
. For the initial stage of the tearing instability (when
![]() $B_{z}$
is still very small) with a wavelength
$B_{z}$
is still very small) with a wavelength
![]() $L_{x}$
which is not too long the factor
$L_{x}$
which is not too long the factor
![]() $X$
is larger than one. Thus, the effect of a finite electron gyroradius can amplify energy dissipation due to effective collisions.
$X$
is larger than one. Thus, the effect of a finite electron gyroradius can amplify energy dissipation due to effective collisions.

Figure 1. Schematic view of the X-line region.

Figure 2. Factor
![]() $X$
as a function of
$X$
as a function of
![]() $L_{x}$
for two values of
$L_{x}$
for two values of
![]() $B_{z}$
and four values of electron temperature
$B_{z}$
and four values of electron temperature
![]() $T$
.
$T$
.
To estimate the effect of the factor
![]() $X$
on magnetic reconnection in real plasma systems we consider the effective collisions induced by two types of turbulence: lower-hybrid drift (LHD) turbulence (Huba et al.
Reference Huba, Gladd and Papadopoulos1977) and kinetic Alfvén wave (KAW) turbulence (Chaston et al.
Reference Chaston, Johnson, Wilber, Acuna, Goldstein and Reme2009).
$X$
on magnetic reconnection in real plasma systems we consider the effective collisions induced by two types of turbulence: lower-hybrid drift (LHD) turbulence (Huba et al.
Reference Huba, Gladd and Papadopoulos1977) and kinetic Alfvén wave (KAW) turbulence (Chaston et al.
Reference Chaston, Johnson, Wilber, Acuna, Goldstein and Reme2009).
Wavelengths of the electromagnetic LHD mode (
![]() ${\sim}{\it\rho}_{e}\sqrt{m_{i}/m_{e}}$
(Daughton Reference Daughton2003)) and KAW (
${\sim}{\it\rho}_{e}\sqrt{m_{i}/m_{e}}$
(Daughton Reference Daughton2003)) and KAW (
![]() ${<}0.3{\it\rho}_{e}(m_{i}/me)$
(Voitenko Reference Voitenko1998; Chen et al.
Reference Chen, Wu, Zhao, Tang and Huang2014)) are small enough to consider these waves to be small-scale magnetic field perturbations for the large-scale reconnection process. On the other hand, these modes effectively interact both with ions (through the Cherenkov resonance
${<}0.3{\it\rho}_{e}(m_{i}/me)$
(Voitenko Reference Voitenko1998; Chen et al.
Reference Chen, Wu, Zhao, Tang and Huang2014)) are small enough to consider these waves to be small-scale magnetic field perturbations for the large-scale reconnection process. On the other hand, these modes effectively interact both with ions (through the Cherenkov resonance
![]() $\boldsymbol{k}\boldsymbol{v}={\it\omega}$
(Karney Reference Karney1978; Karimabadi et al.
Reference Karimabadi, Akimoto, Omidi and Menyuk1990; Chaston et al.
Reference Chaston, Bonnell, Wygant, Mozer, Bale, Kersten, Breneman, Kletzing, Kurth and Hospodarsky2014)) and electrons (through the Landau resonance
$\boldsymbol{k}\boldsymbol{v}={\it\omega}$
(Karney Reference Karney1978; Karimabadi et al.
Reference Karimabadi, Akimoto, Omidi and Menyuk1990; Chaston et al.
Reference Chaston, Bonnell, Wygant, Mozer, Bale, Kersten, Breneman, Kletzing, Kurth and Hospodarsky2014)) and electrons (through the Landau resonance
![]() $k_{\Vert }v_{\Vert }={\it\omega}$
(Hasegawa Reference Hasegawa1976; Cairns & McMillan Reference Cairns and McMillan2005)). Both modes are widely observed in the vicinity of the reconnection region where their contributions to the electromagnetic field turbulence are the strongest among wave modes (Eastwood et al.
Reference Eastwood, Phan, Bale and Tjulin2009; Fujimoto, Shinohara & Kojima Reference Fujimoto, Shinohara and Kojima2011; Huang et al.
Reference Huang, Zhou, Sahraoui, Vaivads, Deng, André, He, Fu, Li and Yuan2012). Thus, LHD and KAW can the provide an exchange of energy between the ions and electrons, supporting the anomalous (effective) conductivity. The general form of the frequency of effective collisions
$k_{\Vert }v_{\Vert }={\it\omega}$
(Hasegawa Reference Hasegawa1976; Cairns & McMillan Reference Cairns and McMillan2005)). Both modes are widely observed in the vicinity of the reconnection region where their contributions to the electromagnetic field turbulence are the strongest among wave modes (Eastwood et al.
Reference Eastwood, Phan, Bale and Tjulin2009; Fujimoto, Shinohara & Kojima Reference Fujimoto, Shinohara and Kojima2011; Huang et al.
Reference Huang, Zhou, Sahraoui, Vaivads, Deng, André, He, Fu, Li and Yuan2012). Thus, LHD and KAW can the provide an exchange of energy between the ions and electrons, supporting the anomalous (effective) conductivity. The general form of the frequency of effective collisions
![]() ${\it\nu}$
is provided by the quasi-linear equation (Galeev & Sagdeev Reference Galeev, Sagdeev and Leontovich1979):
${\it\nu}$
is provided by the quasi-linear equation (Galeev & Sagdeev Reference Galeev, Sagdeev and Leontovich1979):
where
![]() $v_{D}$
is particle drift velocity (i.e.
$v_{D}$
is particle drift velocity (i.e.
![]() $en_{0}v_{D}$
is a current density),
$en_{0}v_{D}$
is a current density),
![]() ${\it\Gamma}(k)$
is a wave growth/damping rate,
${\it\Gamma}(k)$
is a wave growth/damping rate,
![]() ${\it\omega}(k)$
is a wave frequency and
${\it\omega}(k)$
is a wave frequency and
![]() $W_{k}$
is a wave energy density. For current sheet configurations the maximum value of
$W_{k}$
is a wave energy density. For current sheet configurations the maximum value of
![]() ${\it\nu}_{LHD}$
was derived by Huba, Drake & Gladd (Reference Huba, Drake and Gladd1980):
${\it\nu}_{LHD}$
was derived by Huba, Drake & Gladd (Reference Huba, Drake and Gladd1980):
where
![]() ${\it\omega}_{pe}$
is the plasma frequency,
${\it\omega}_{pe}$
is the plasma frequency,
![]() ${\it\omega}_{LH}\approx {\it\Omega}_{e}\sqrt{m_{e}/m_{i}}$
and
${\it\omega}_{LH}\approx {\it\Omega}_{e}\sqrt{m_{e}/m_{i}}$
and
![]() ${\it\Omega}_{e}=eB_{z}/m_{e}c$
is the electron gyrofrequency,
${\it\Omega}_{e}=eB_{z}/m_{e}c$
is the electron gyrofrequency,
![]() $T_{e}$
is electron temperature and
$T_{e}$
is electron temperature and
![]() $E_{y}$
corresponds to the amplitude of wave electric field oscillations.
$E_{y}$
corresponds to the amplitude of wave electric field oscillations.
For KAW the maximum growth rate corresponds to Landau excitation
![]() ${\it\Gamma}\approx {\it\omega}/kv_{D}$
(Hasegawa & Mima Reference Hasegawa and Mima1978) where the wave frequency is
${\it\Gamma}\approx {\it\omega}/kv_{D}$
(Hasegawa & Mima Reference Hasegawa and Mima1978) where the wave frequency is
![]() ${\it\omega}_{KAW}=k_{\Vert }v_{A}\sqrt{1+(k_{\bot }{\it\rho}_{i})^{2}}$
with ion gyroradius
${\it\omega}_{KAW}=k_{\Vert }v_{A}\sqrt{1+(k_{\bot }{\it\rho}_{i})^{2}}$
with ion gyroradius
![]() ${\it\rho}_{i}$
and Alfvén velocity
${\it\rho}_{i}$
and Alfvén velocity
![]() $v_{A}$
(Hasegawa Reference Hasegawa1976). The corresponding collision frequency can be estimated as
$v_{A}$
(Hasegawa Reference Hasegawa1976). The corresponding collision frequency can be estimated as
where we take into account that
![]() $k_{\bot }{\it\rho}_{i}\sim 1$
,
$k_{\bot }{\it\rho}_{i}\sim 1$
,
![]() $v_{D}\sim v_{Ti}\sim v_{A}$
.
$v_{D}\sim v_{Ti}\sim v_{A}$
.
Following Coroniti (Reference Coroniti1985), one can determine the critical amplitude of electric field energy
![]() $E_{y}^{2}$
necessary to organize the magnetic field dissipation within the domain with spatial scale
$E_{y}^{2}$
necessary to organize the magnetic field dissipation within the domain with spatial scale
![]() ${\sim}L_{z}\sim {\it\rho}_{i}$
:
${\sim}L_{z}\sim {\it\rho}_{i}$
:
where
![]() $M_{A}$
is an Alfvén–Mach number for a particle flowing to the reconnection region. Generally
$M_{A}$
is an Alfvén–Mach number for a particle flowing to the reconnection region. Generally
![]() $M_{A}\sim 0.1$
for magnetospheric physics, while
$M_{A}\sim 0.1$
for magnetospheric physics, while
![]() $(v_{A}/c)^{2}\approx 10^{-5}$
for the Earth’s magnetotail. Equation (3.6) shows that one can decrease the estimate for the critical amplitude of wave electric field proportionally to
$(v_{A}/c)^{2}\approx 10^{-5}$
for the Earth’s magnetotail. Equation (3.6) shows that one can decrease the estimate for the critical amplitude of wave electric field proportionally to
![]() ${\sim}1/\sqrt{X}\sim 1/3{-}1/10$
(see figure 2) after taking into account the Pitaevskii effect. For magnetotail current sheets the typical amplitude of LHD waves can reach
${\sim}1/\sqrt{X}\sim 1/3{-}1/10$
(see figure 2) after taking into account the Pitaevskii effect. For magnetotail current sheets the typical amplitude of LHD waves can reach
![]() $10~\text{mV}~\text{m}^{-1}$
(Eastwood et al.
Reference Eastwood, Phan, Bale and Tjulin2009; Fujimoto et al.
Reference Fujimoto, Shinohara and Kojima2011; Norgren et al.
Reference Norgren, Vaivads, Khotyaintsev and André2012), while the estimate of the amplitude from (3.6) is
$10~\text{mV}~\text{m}^{-1}$
(Eastwood et al.
Reference Eastwood, Phan, Bale and Tjulin2009; Fujimoto et al.
Reference Fujimoto, Shinohara and Kojima2011; Norgren et al.
Reference Norgren, Vaivads, Khotyaintsev and André2012), while the estimate of the amplitude from (3.6) is
![]() $\sqrt{(E_{y}^{2})_{LHD}}\sim 30/\sqrt{X}~\text{mV}~\text{m}^{-1}$
(Coroniti Reference Coroniti1985). Thus, a factor
$\sqrt{(E_{y}^{2})_{LHD}}\sim 30/\sqrt{X}~\text{mV}~\text{m}^{-1}$
(Coroniti Reference Coroniti1985). Thus, a factor
![]() $X\sim 10$
can help to produce the necessary magnetic energy dissipation due to effective collisions. Amplitudes of KAW electric field are often weaker
$X\sim 10$
can help to produce the necessary magnetic energy dissipation due to effective collisions. Amplitudes of KAW electric field are often weaker
![]() ${\sim}1~\text{mV}~\text{m}^{-1}$
(Chaston et al.
Reference Chaston, Bonnell, Clausen and Angelopoulos2012). The critical amplitude for KAW is
${\sim}1~\text{mV}~\text{m}^{-1}$
(Chaston et al.
Reference Chaston, Bonnell, Clausen and Angelopoulos2012). The critical amplitude for KAW is
![]() $\sqrt{(E_{y}^{2})_{KAW}}$
is of the order of
$\sqrt{(E_{y}^{2})_{KAW}}$
is of the order of
![]() ${\sim}1/\sqrt{X}~\text{mV}~\text{m}^{-1}$
. The Pitaevskii effect of reducing the estimate (3.6) 2–3 times demonstrates an important role of KAW in running magnetic reconnection. Therefore, we conclude that in realistic magnetotail conditions for both cases (LHDI and KAW) the effect of finite electron gyroradius can increase effective collisions and help to overturn Coroniti (Reference Coroniti1985) objections.
${\sim}1/\sqrt{X}~\text{mV}~\text{m}^{-1}$
. The Pitaevskii effect of reducing the estimate (3.6) 2–3 times demonstrates an important role of KAW in running magnetic reconnection. Therefore, we conclude that in realistic magnetotail conditions for both cases (LHDI and KAW) the effect of finite electron gyroradius can increase effective collisions and help to overturn Coroniti (Reference Coroniti1985) objections.
4. Discussion and conclusions
The additional effect of the enhancement of effective collisions for
![]() $k{\it\rho}_{e}>1$
perturbations was taken into account in the analysis of the electron resistive tearing mode (Zelenyi & Taktakishvili Reference Zelenyi and Taktakishvili1981). This mode is excited by
$k{\it\rho}_{e}>1$
perturbations was taken into account in the analysis of the electron resistive tearing mode (Zelenyi & Taktakishvili Reference Zelenyi and Taktakishvili1981). This mode is excited by
![]() ${\it\nu}\neq 0$
with the growth rate
${\it\nu}\neq 0$
with the growth rate
![]() ${\it\gamma}={\it\nu}\text{X}({\it\gamma}_{0}/k_{x}\sqrt{2T_{e}m_{e}})$
where
${\it\gamma}={\it\nu}\text{X}({\it\gamma}_{0}/k_{x}\sqrt{2T_{e}m_{e}})$
where
![]() ${\it\gamma}_{0}/k_{x}\sqrt{2T_{e}m_{e}}=2{\rm\pi}^{-1/2}({\it\rho}_{e}/L_{z})^{3/2}(1-k_{x}^{2}L_{z}^{2})/k_{x}L_{z}$
is the growth rate of the electron tearing mode (Laval et al.
Reference Laval, Pellat and Vuillemin1966; Galeev & Sudan Reference Galeev and Sudan1985). Therefore, for
${\it\gamma}_{0}/k_{x}\sqrt{2T_{e}m_{e}}=2{\rm\pi}^{-1/2}({\it\rho}_{e}/L_{z})^{3/2}(1-k_{x}^{2}L_{z}^{2})/k_{x}L_{z}$
is the growth rate of the electron tearing mode (Laval et al.
Reference Laval, Pellat and Vuillemin1966; Galeev & Sudan Reference Galeev and Sudan1985). Therefore, for
![]() $X$
factor high enough, the growth rate of the resistive tearing mode increases. This mode is produced by effective collisions and cannot be stabilized by electron magnetization (in contrast to the classical electron tearing mode (Schindler Reference Schindler1974; Galeev & Zelenyi Reference Galeev and Zelenyi1976)). Moreover, for a tearing mode with
$X$
factor high enough, the growth rate of the resistive tearing mode increases. This mode is produced by effective collisions and cannot be stabilized by electron magnetization (in contrast to the classical electron tearing mode (Schindler Reference Schindler1974; Galeev & Zelenyi Reference Galeev and Zelenyi1976)). Moreover, for a tearing mode with
![]() $k{\it\rho}_{e}>1$
the WKB approximation in the investigation of current sheet stability can be safely applied (Lembege & Pellat Reference Lembege and Pellat1982) supporting the validity of the expressions for the growth rates
$k{\it\rho}_{e}>1$
the WKB approximation in the investigation of current sheet stability can be safely applied (Lembege & Pellat Reference Lembege and Pellat1982) supporting the validity of the expressions for the growth rates
![]() ${\it\gamma}$
and
${\it\gamma}$
and
![]() ${\it\gamma}_{0}$
derived for the case where the wavelength is not too long.
${\it\gamma}_{0}$
derived for the case where the wavelength is not too long.
Effective collisions are often considered in numerical models of magnetic reconnection as a trigger for the reconnection process (Daughton, Lapenta & Ricci Reference Daughton, Lapenta and Ricci2004; Daughton et al.
Reference Daughton, Roytershteyn, Karimabadi, Yin, Albright, Bergen and Bowers2011; Karimabadi et al.
Reference Karimabadi, Roytershteyn, Daughton and Liu2013). In this case, estimates of the reconnection rate can be based on the classical theory of an effective conductivity (Galeev & Sudan Reference Galeev and Sudan1985; Yoon & Lui Reference Yoon and Lui2006) with a proper estimate for the effective collision rate. Thus, the effect of fine structured velocity distributions (when
![]() ${\it\rho}k_{x}>1$
) can be very important. The same effect can be provided by numerical resistivity which supports the slow growth of magnetic islands when the tearing instability is saturated by nonlinear effects (Lipatov & Zelenyi Reference Lipatov and Zelenyi1982).
${\it\rho}k_{x}>1$
) can be very important. The same effect can be provided by numerical resistivity which supports the slow growth of magnetic islands when the tearing instability is saturated by nonlinear effects (Lipatov & Zelenyi Reference Lipatov and Zelenyi1982).
Figure 2 shows that the most pronounced effect of a finite electron gyroradius corresponds to small-scale reconnection (i.e. small
![]() $L_{x}$
) where instead of one large-scale X-line we deal with a chain of small-scale magnetic islands. Indeed, strong anisotropy of electrons accelerated in the primary reconnection region generates high-amplitude curvature currents (Egedal, Le & Daughton Reference Egedal, Le and Daughton2013; Artemyev et al.
Reference Artemyev, Petrukovich, Nakamura and Zelenyi2015) responsible for the formation of very thin current sheets with vanishing
$L_{x}$
) where instead of one large-scale X-line we deal with a chain of small-scale magnetic islands. Indeed, strong anisotropy of electrons accelerated in the primary reconnection region generates high-amplitude curvature currents (Egedal, Le & Daughton Reference Egedal, Le and Daughton2013; Artemyev et al.
Reference Artemyev, Petrukovich, Nakamura and Zelenyi2015) responsible for the formation of very thin current sheets with vanishing
![]() $B_{z}$
magnetic field (Nakamura et al.
Reference Nakamura, Baumjohann, Runov and Asano2006; Artemyev et al.
Reference Artemyev, Petrukovich, Frank, Nakamura and Zelenyi2013; Le et al.
Reference Le, Egedal, Ng, Karimabadi, Scudder, Roytershteyn, Daughton and Liu2014). Instability of such thin current sheets results in secondary reconnection in the outflow region of the primary large-scale X-line (so-called plasmoid instability) with the corresponding birth of a multitude of small-scale X- and O-magnetic points (Daughton et al.
Reference Daughton, Roytershteyn, Karimabadi, Yin, Albright, Bergen and Bowers2011; Huang, Bhattacharjee & Forbes Reference Huang, Bhattacharjee and Forbes2013). Thus, the secondary reconnection of such thin current sheets can occur within the region of
$B_{z}$
magnetic field (Nakamura et al.
Reference Nakamura, Baumjohann, Runov and Asano2006; Artemyev et al.
Reference Artemyev, Petrukovich, Frank, Nakamura and Zelenyi2013; Le et al.
Reference Le, Egedal, Ng, Karimabadi, Scudder, Roytershteyn, Daughton and Liu2014). Instability of such thin current sheets results in secondary reconnection in the outflow region of the primary large-scale X-line (so-called plasmoid instability) with the corresponding birth of a multitude of small-scale X- and O-magnetic points (Daughton et al.
Reference Daughton, Roytershteyn, Karimabadi, Yin, Albright, Bergen and Bowers2011; Huang, Bhattacharjee & Forbes Reference Huang, Bhattacharjee and Forbes2013). Thus, the secondary reconnection of such thin current sheets can occur within the region of
![]() $k_{x}{\it\rho}_{e}>1$
. To illustrate this scenario we show two events of Cluster spacecraft observations of magnetic reconnection in the Earth’s magnetotail (see figure 3). The characteristic
$k_{x}{\it\rho}_{e}>1$
. To illustrate this scenario we show two events of Cluster spacecraft observations of magnetic reconnection in the Earth’s magnetotail (see figure 3). The characteristic
![]() $B_{z}$
reversal and plasma flows
$B_{z}$
reversal and plasma flows
![]() $v_{x}$
indicate that Cluster is in close vicinity to the X-line. We calculate the electron gyroradius
$v_{x}$
indicate that Cluster is in close vicinity to the X-line. We calculate the electron gyroradius
![]() ${\it\rho}_{e}$
using local measurements of the
${\it\rho}_{e}$
using local measurements of the
![]() $B_{z}$
and
$B_{z}$
and
![]() $B_{y}$
magnetic field (
$B_{y}$
magnetic field (
![]() $B_{x}$
is assumed to be zero). Around the X-line
$B_{x}$
is assumed to be zero). Around the X-line
![]() ${\it\rho}_{e}$
reaches
${\it\rho}_{e}$
reaches
![]() ${\sim}1000~\text{km}$
, thus
${\sim}1000~\text{km}$
, thus
![]() $X$
becomes larger than one for
$X$
becomes larger than one for
![]() $L_{x}<6R_{E}$
. For example, the secondary reconnection with a wavelength of approximately
$L_{x}<6R_{E}$
. For example, the secondary reconnection with a wavelength of approximately
![]() ${\sim}2R_{E}$
corresponds to an increase of effective collision frequency by a factor
${\sim}2R_{E}$
corresponds to an increase of effective collision frequency by a factor
![]() $X\sim 3$
. We also note that for both events shown in figure 3, current sheet thicknesses were approximately
$X\sim 3$
. We also note that for both events shown in figure 3, current sheet thicknesses were approximately
![]() ${\sim}800~\text{km}$
and
${\sim}800~\text{km}$
and
![]() ${\sim}600~\text{km}$
(see estimates of current density amplitudes in Artemyev et al.
Reference Artemyev, Petrukovich, Nakamura and Zelenyi2015). Thus, for
${\sim}600~\text{km}$
(see estimates of current density amplitudes in Artemyev et al.
Reference Artemyev, Petrukovich, Nakamura and Zelenyi2015). Thus, for
![]() $L_{x}\sim 2R_{E}$
the ratio
$L_{x}\sim 2R_{E}$
the ratio
![]() $L_{x}/L_{z}\sim 18$
and the corresponding current sheets are very prolonged and stretched.
$L_{x}/L_{z}\sim 18$
and the corresponding current sheets are very prolonged and stretched.

Figure 3. Two cases of Cluster spacecraft crossing a reconnection region (see the characteristic reversal of
![]() $B_{z}$
). Both cases are taken from Artemyev et al. (Reference Artemyev, Petrukovich, Nakamura and Zelenyi2015).
$B_{z}$
). Both cases are taken from Artemyev et al. (Reference Artemyev, Petrukovich, Nakamura and Zelenyi2015).
To conclude, we consider the effects of a finite electron gyroradius for current sheet stability in the case when effective collisions are present in the system. Following Pitaevskii (Reference Pitaevskii1963) we demonstrate that a fast electron gyrorotation results in a fine structure of the perturbations of the electron distribution function. As a result, the full expression for the collision integral gives a multiplication factor
![]() $\text{X}\sim (k_{x}{\it\rho}_{e})^{2}$
for collision frequency (where
$\text{X}\sim (k_{x}{\it\rho}_{e})^{2}$
for collision frequency (where
![]() $k_{x}$
is a transverse wavenumber). For realistic conditions in the Earth’s magnetotail this factor can often be larger than one and thus can increase the effect of particle scattering by electromagnetic turbulence. We show that effect of a finite electron gyroradius should be particularly strong for the secondary reconnection of very thin current sheets formed in the outflow region of the primary X-line.
$k_{x}$
is a transverse wavenumber). For realistic conditions in the Earth’s magnetotail this factor can often be larger than one and thus can increase the effect of particle scattering by electromagnetic turbulence. We show that effect of a finite electron gyroradius should be particularly strong for the secondary reconnection of very thin current sheets formed in the outflow region of the primary X-line.
Acknowledgement
Work of A.V.A. was supported by Russian Scientific Foundation (project no. 14-12-00824).