Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T04:52:54.150Z Has data issue: false hasContentIssue false
  • English
  • Français

Effects of intermittency via non-Gaussianity on turbulent transport in magnetized plasmas

Published online by Cambridge University Press:  10 March 2022

D.I. Palade Open the ORCID record for D.I. Palade [Opens in a new window]  and
L. Pomârjanschi
D.I. Palade*
Affiliation:
National Institute of Laser, Plasma and Radiation Physics, Atomiștilor Street 409, 077125 Măgurele, Bucharest, Romania
L. Pomârjanschi
Affiliation:
Faculty of Physics, University of Bucharest, Atomiștilor Street 405, 077125 Măgurele, Romania
*
†Email address for correspondence: dragos.palade@inflpr.ro
Get access Rights & Permissions [Opens in a new window]

Abstract

We analyse how the turbulent transport of $\boldsymbol {E}\times \boldsymbol {B}$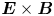 type in magnetically confined plasmas is affected by the intermittent features of turbulence. The latter are modelled via the non-Gaussian distribution $P(\phi )$ 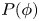of the turbulent electric potential $\phi$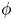. Our analysis is performed at an analytical level and confirmed numerically using two statistical approaches. We have found that the diffusion is inhibited linearly by intermittency, mainly via the kurtosis of the distribution $P(\phi )$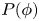. The associated susceptibility for this linear process is shown to be dependent on the poloidal velocity $V_p$ and on the correlation time $\tau _c$ (or the Kubo number $K_\star$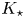, the ratio between $\tau _c$ 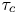and the specific time of flight $\tau _{{\rm fl}}$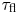) with a maximum at $\tau _c\approx \tau _{{\rm fl}}$ ($K_\star \approx 1$). Intermittency does not affect the scaling of diffusion with the Kubo number.

Keywords

fusion plasmaplasma nonlinear phenomena
Type
Research Article
Information
Journal of Plasma Physics , Volume 88 , Issue 2 , April 2022 , 905880202
Check for updates
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Anderson, J. & Botha, G.J.J. 2015 Statistical properties of Charney-Hasegawa-Mima zonal flows. Phys. Plasmas 22 (5), 052305, https://aip.scitation.org/doi/pdf/10.1063/1.4919852.CrossRefGoogle Scholar
Anderson, J. & Hnat, B. 2017 Statistical analysis of Hasegawa-Wakatani turbulence. Phys. Plasmas 24 (6), 062301.CrossRefGoogle Scholar
Angioni, C., Fable, E., Greenwald, M., Maslov, M., Peeters, A.G., Takenaga, H. & Weisen, H. 2009 Particle transport in tokamak plasmas, theory and experiment. Plasma Phys. Control. Fusion 51 (12), 124017.CrossRefGoogle Scholar
Antar, G.Y., Devynck, P., Garbet, X. & Luckhardt, S.C. 2001 a Turbulence intermittency and burst properties in tokamak scrape-off layer. Phys. Plasmas 8 (5), 1612–1624.CrossRefGoogle Scholar
Antar, G.Y., Krasheninnikov, S.I., Devynck, P., Doerner, R.P., Hollmann, E.M., Boedo, J.A., Luckhardt, S.C. & Conn, R.W. 2001 b Experimental evidence of intermittent convection in the edge of magnetic confinement devices. Phys. Rev. Lett. 87, 065001.CrossRefGoogle ScholarPubMed
Beadle, C.F. & Ricci, P. 2020 Understanding the turbulent mechanisms setting the density decay length in the tokamak scrape-off layer. J. Plasma Phys. 86 (1), 175860101.CrossRefGoogle Scholar
Boldyrev, S. 2005 On the spectrum of magnetohydrodynamic turbulence. Astrophys. J. 626 (1), L37–L40.CrossRefGoogle Scholar
Bourdelle, C., Garbet, X., Imbeaux, F., Casati, A., Dubuit, N., Guirlet, R. & Parisot, T. 2007 A new gyrokinetic quasilinear transport model applied to particle transport in tokamak plasmas. Phys. Plasmas 14 (11), 112501.CrossRefGoogle Scholar
Casati, A., Gerbaud, T., Hennequin, P., Bourdelle, C., Candy, J., Clairet, F., Garbet, X., Grandgirard, V., Gürcan, O.D., Heuraux, S., et al. 2009 Turbulence in the tore supra tokamak: measurements and validation of nonlinear simulations. Phys. Rev. Lett. 102, 165005.CrossRefGoogle ScholarPubMed
Cheng, J., Yan, L.W., Hong, W.Y., Zhao, K.J., Lan, T., Qian, J., Liu, A.D., Zhao, H.L., Liu, Y., Yang, Q.W., et al. 2010 Statistical characterization of blob turbulence across the separatrix in HL-2a tokamak. Plasma Phys. Control. Fusion 52 (5), 055003.CrossRefGoogle Scholar
Claessens, M. 2020 ITER: The Giant Fusion Reactor. Copernicus.CrossRefGoogle Scholar
Corrsin, S. 1951 On the spectrum of isotropic temperature fluctuations in an isotropic turbulence. J. Appl. Phys. 22 (4), 469–473.CrossRefGoogle Scholar
Croitoru, A., Palade, D., Vlad, M. & Spineanu, F. 2017 Turbulent transport of alpha particles in tokamak plasmas. Nucl. Fusion 57 (3), 036019.CrossRefGoogle Scholar
Filippas, A.V., Bengston, R.D., Li, G., Meier, M., Ritz, C.P. & Powers, E.J. 1995 Conditional analysis of floating potential fluctuations at the edge of the texas experimental tokamak upgrade (text-u). Phys. Plasmas 2 (3), 839–845.CrossRefGoogle Scholar
Fonck, R.J., Cosby, G., Durst, R.D., Paul, S.F., Bretz, N., Scott, S., Synakowski, E. & Taylor, G. 1993 Long-wavelength density turbulence in the TFTR tokamak. Phys. Rev. Lett. 70, 3736–3739.CrossRefGoogle ScholarPubMed
Fülöp, T. & Nordman, H. 2009 Turbulent and neoclassical impurity transport in tokamak plasmas. Phys. Plasmas 16 (3), 032306.CrossRefGoogle Scholar
Gao, X., Zhang, T., Han, X., Zhang, S., Kong, D., Qu, H., Wang, Y., Wen, F., Liu, Z. & Huang, C. 2015 Experimental study of pedestal turbulence on EAST tokamak. Nucl. Fusion 55 (8), 083015.CrossRefGoogle Scholar
Ghilea, M.C., Ruffolo, D., Chuychai, P., Sonsrettee, W., Seripienlert, A. & Matthaeus, W.H. 2011 Magnetic field line random walk for disturbed flux surfaces: trapping effects and multiple routes to Bohm diffusion. Astrophys. J. 741 (1), 16.CrossRefGoogle Scholar
Gonçalves, B., Henriques, I., Hidalgo, C., Silva, C., Figueiredo, H., Naulin, V., Nielsen, A. & Mendonça, J. 2018 Radial structure of vorticity in the plasma boundary of tokamak plasmas. In 45th EPS Conference on Plasma Physics, pp. P2–1084. European Physical Society.Google Scholar
Hauff, T. & Jenko, F. 2006 Turbulent ${\rm e}\times {\rm b}$ advection of charged test particles with large gyroradii. Phys. Plasmas 13 (10), 102309.CrossRefGoogle Scholar
Holland, C., White, A.E., McKee, G.R., Shafer, M.W., Candy, J., Waltz, R.E., Schmitz, L. & Tynan, G.R. 2009 Implementation and application of two synthetic diagnostics for validating simulations of core tokamak turbulence. Phys. Plasmas 16 (5), 052301.CrossRefGoogle Scholar
Isichenko, M.B. 1992 Percolation, statistical topography, and transport in random media. Rev. Mod. Phys. 64, 961–1043.CrossRefGoogle Scholar
Jenko, F. & Dorland, W. 2001 Nonlinear electromagnetic gyrokinetic simulations of tokamak plasmas. Plasma Phys. Control. Fusion 43 (12A), A141–A150.CrossRefGoogle Scholar
Jenko, F. & Dorland, W. 2002 Prediction of significant tokamak turbulence at electron gyroradius scales. Phys. Rev. Lett. 89, 225001.CrossRefGoogle ScholarPubMed
Kraichnan, R.H. 1968 Small-scale structure of a scalar field convected by turbulence. Phys. Fluids 11 (5), 945–953, https://aip.scitation.org/doi/pdf/10.1063/1.1692063.CrossRefGoogle Scholar
Kraichnan, R.H. & Montgomery, D. 1980 Two-dimensional turbulence. Rep. Prog. Phys. 43 (5), 547–619.CrossRefGoogle Scholar
Krasheninnikov, S. 2001 On scrape off layer plasma transport. Phys. Lett. A 283 (5), 368–370.CrossRefGoogle Scholar
Leonard, A.W. 2014 Edge-localized-modes in tokamaks. Phys. Plasmas 21 (9), 090501.CrossRefGoogle Scholar
Levinson, S., Beall, J., Powers, E. & Bengtson, R. 1984 Space/time statistics of the turbulence in a tokamak edge plasma. Nucl. Fusion 24 (5), 527–539.CrossRefGoogle Scholar
Lipschultz, B., Bonnin, X., Counsell, G., Kallenbach, A., Kukushkin, A., Krieger, K., Leonard, A., Loarte, A., Neu, R., Pitts, R., et al. 2007 Plasma–surface interaction, scrape-off layer and divertor physics: implications for ITER. Nucl. Fusion 47 (9), 1189.CrossRefGoogle Scholar
Liu, Y., Li, J., Sun, S. & Yu, B. 2019 Advances in Gaussian random field generation: a review. Comput. Geosci. 23 (5), 1011–1047.CrossRefGoogle Scholar
van Milligen, B.P., Sánchez, R., Carreras, B.A., Lynch, V.E., LaBombard, B., Pedrosa, M.A., Hidalgo, C., Gonçalves, B. & Balbín, R. 2005 Additional evidence for the universality of the probability distribution of turbulent fluctuations and fluxes in the scrape-off layer region of fusion plasmas. Phys. Plasmas 12 (5), 052507.CrossRefGoogle Scholar
Monin, A. & Yaglom, A. 1973 Statistical Fluid Mechanics: Mechanics of Turbulence. MIT Press.Google Scholar
Negrea, M. 2019 Diffusion of stochastic magnetic field lines with average poloidal magnetic component. Plasma Phys. Control. Fusion 61 (6), 065004.CrossRefGoogle Scholar
Negrea, M., Petrisor, I. & Shalchi, A. 2017 Stochastic field-line wandering in magnetic turbulence with shear. II. Decorrelation trajectory method. Phys. Plasmas 24 (11), 112303.CrossRefGoogle Scholar
Ottaviani, M. 1992 Scaling laws of test particle transport in two-dimensional turbulence. Europhys. Lett. 20 (2), 111–116.CrossRefGoogle Scholar
Palade, D.I. 2021 Turbulent transport of fast ions in tokamak plasmas in the presence of resonant magnetic perturbations. Phys. Plasmas 28 (2), 022508.CrossRefGoogle Scholar
Palade, D.I. & Vlad, M. 2021 Fast generation of gaussian random fields for direct numerical simulations of stochastic transport. Stat. Comput. 31 (5), 60.CrossRefGoogle Scholar
Palade, D.I., Vlad, M. & Spineanu, F. 2021 Turbulent transport of the w ions in tokamak plasmas: properties derived from a test particle approach. Nucl. Fusion 61 (11), 116031.CrossRefGoogle Scholar
Pereira, F.A.C., Sokolov, I.M., Toufen, D.L., Guimarães-Filho, Z.O., Caldas, I.L. & Gentle, K.W. 2019 Statistical properties of intermittent bursts in the texas helimak. Phys. Plasmas 26 (5), 052301.CrossRefGoogle Scholar
Pommois, P., Veltri, P. & Zimbardo, G. 2001 Kubo number and magnetic field line diffusion coefficient for anisotropic magnetic turbulence. Phys. Rev. E 63, 066405.CrossRefGoogle ScholarPubMed
Qi, L., Kwon, J.-M., Hahm, T., Yi, S. & Choi, M. 2019 Characteristics of trapped electron transport, zonal flow staircase, turbulence fluctuation spectra in elongated tokamak plasmas. Nucl. Fusion 59 (2), 026013.CrossRefGoogle Scholar
Reuss, J.-D. & Misguich, J.H. 1996 Low-frequency percolation scaling for particle diffusion in electrostatic turbulence. Phys. Rev. E 54, 1857–1869.CrossRefGoogle ScholarPubMed
Reuss, J.-D., Vlad, M. & Misguich, J. 1998 Percolation scaling for transport in turbulent plasmas. Phys. Lett. A 241 (1), 94–98.CrossRefGoogle Scholar
Riva, F., Militello, F., Elmore, S., Omotani, J.T., Dudson, B., Walkden, N.R. & the MAST team 2019 Three-dimensional plasma edge turbulence simulations of the mega ampere spherical tokamak and comparison with experimental measurements. Plasma Phys. Control. Fusion 61 (9), 095013.CrossRefGoogle Scholar
Shafer, M.W., Fonck, R.J., McKee, G.R., Holland, C., White, A.E. & Schlossberg, D.J. 2012 2D properties of core turbulence on DIII-D and comparison to gyrokinetic simulations. Phys. Plasmas 19 (3), 032504.CrossRefGoogle Scholar
Vio, R., Andreani, P. & Wamsteker, W. 2001 Numerical simulation of non-Gaussian random fields with prescribed correlation structure. Publ. Astron. Soc. Pacific 113 (786), 1009.CrossRefGoogle Scholar
Vlad, M., Palade, D.I. & Spineanu, F. 2021 Effects of the parallel acceleration on heavy impurity transport in turbulent tokamak plasmas. Plasma Phys. Control. Fusion 63 (3), 035007.CrossRefGoogle Scholar
Vlad, M. & Spineanu, F. 2016 Direct effects of the resonant magnetic perturbation on turbulent transport. Nucl. Fusion 56 (9), 092003.CrossRefGoogle Scholar
Vlad, M., Spineanu, F., Misguich, J.H. & Balescu, R. 1998 a Diffusion with intrinsic trapping in two-dimensional incompressible stochastic velocity fields. Phys. Rev. E 58, 7359–7368.CrossRefGoogle Scholar
Vlad, M., Spineanu, F., Misguich, J.H. & Balescu, R. 1998 b Diffusion with intrinsic trapping in two-dimensional incompressible stochastic velocity fields. Phys. Rev. E 58, 7359–7368.CrossRefGoogle Scholar
Vlad, M., Spineanu, F., Misguich, J.H. & Balescu, R. 2001 Diffusion in biased turbulence. Phys. Rev. E 63, 066304.CrossRefGoogle ScholarPubMed
Vlad, M., Spineanu, F., Misguich, J.H., Reuss, J.-D., Balescu, R., Itoh, K. & Itoh, S.-I. 2004 Lagrangian versus eulerian correlations and transport scaling. Plasma Phys. Control. Fusion 46 (7), 1051–1063.CrossRefGoogle Scholar
Wang, L., Tynan, G.R., Hong, R., Nie, L., Chen, Y., Ke, R., Wu, T., Long, T., Zheng, P. & Xu, M. 2019 Edge turbulence evolution and intermittency development near the density limit on the HL-2A tokamak. Phys. Plasmas 26 (9), 092303.CrossRefGoogle Scholar
Wang, W.X., Lin, Z., Tang, W.M., Lee, W.W., Ethier, S., Lewandowski, J.L.V., Rewoldt, G., Hahm, T.S. & Manickam, J. 2006 Gyro-kinetic simulation of global turbulent transport properties in tokamak experiments. Phys. Plasmas 13 (9), 092505.CrossRefGoogle Scholar
Zank, G.P., Dosch, A., Hunana, P., Florinski, V., Matthaeus, W.H. & Webb, G.M. 2011 The transport of low-frequency turbulence in astrophysical flows. I. Governing equations. Astrophys. J. 745 (1), 35.CrossRefGoogle Scholar
Zohm, H. 1996 Edge localized modes (ELMs). Plasma Phys. Control. Fusion 38 (2), 105–128.CrossRefGoogle Scholar
Zweben, S.J., Boedo, J.A., Grulke, O., Hidalgo, C., LaBombard, B., Maqueda, R.J., Scarin, P. & Terry, J.L. 2007 Edge turbulence measurements in toroidal fusion devices. Plasma Phys. Control. Fusion 49 (7), S1–S23.CrossRefGoogle Scholar