Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-27T21:10:54.837Z Has data issue: false hasContentIssue false
  • English
  • Français

Electromagnetic instabilities and plasma turbulence driven by electron-temperature gradient

Published online by Cambridge University Press:  23 August 2022

T. Adkins Open the ORCID record for T. Adkins [Opens in a new window] ,
A.A. Schekochihin Open the ORCID record for A.A. Schekochihin [Opens in a new window] ,
P.G. Ivanov Open the ORCID record for P.G. Ivanov [Opens in a new window]  and
C.M. Roach Open the ORCID record for C.M. Roach [Opens in a new window]
T. Adkins*
Affiliation:
Rudolf Peierls Centre for Theoretical Physics, University of Oxford, Oxford OX1 3PU, UK Merton College, Oxford OX1 4JD, UK Culham Centre for Fusion Energy, United Kingdom Atomic Energy Authority, Abingdon OX14 3DB, UK
A.A. Schekochihin
Affiliation:
Rudolf Peierls Centre for Theoretical Physics, University of Oxford, Oxford OX1 3PU, UK Merton College, Oxford OX1 4JD, UK
P.G. Ivanov
Affiliation:
Rudolf Peierls Centre for Theoretical Physics, University of Oxford, Oxford OX1 3PU, UK
C.M. Roach
Affiliation:
Culham Centre for Fusion Energy, United Kingdom Atomic Energy Authority, Abingdon OX14 3DB, UK
*
†Email address for correspondence: toby.adkins@physics.ox.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

Electromagnetic (EM) instabilities and turbulence driven by the electron-temperature gradient (ETG) are considered in a local slab model of a tokamak-like plasma. Derived in a low-beta asymptotic limit of gyrokinetics, the model describes perturbations at scales both larger and smaller than the electron inertial length $d_e$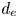, but below the ion Larmor scale $\rho _i$, capturing both electrostatic and EM regimes of turbulence. The well-known electrostatic instabilities – slab and curvature-mediated ETG – are recovered, and a new instability is found in the EM regime, called the thermo-Alfvénic instability (TAI). It exists in both a slab version (sTAI, destabilising kinetic Alfvén waves) and a curvature-mediated version (cTAI), which is a cousin of the (electron-scale) kinetic ballooning mode. The cTAI turns out to be dominant at the largest scales covered by the model (greater than $d_e$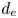 but smaller than $\rho _i$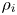), its physical mechanism hinging on the fast equalisation of the total temperature along perturbed magnetic field lines (in contrast to kinetic ballooning mode, which is pressure balanced). A turbulent cascade theory is then constructed, with two energy-injection scales: $d_e$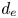, where the drivers are slab ETG and sTAI, and a larger (parallel system size dependent) scale, where the driver is cTAI. The latter dominates the turbulent transport if the temperature gradient is greater than a certain critical value, which scales inversely with the electron beta. The resulting heat flux scales more steeply with the temperature gradient than that due to electrostatic ETG turbulence, giving rise to stiffer transport. This can be viewed as a physical argument in favour of near-marginal steady-state in electron-transport-controlled plasmas (e.g. the pedestal). While the model is simplistic, the new physics that is revealed by it should be of interest to those attempting to model the effect of EM turbulence in tokamak-relevant configurations with high beta and large ETGs.

Keywords

fusion plasmaplasma instabilitiesplasma nonlinear phenomena
Type
Research Article
Information
Journal of Plasma Physics , Volume 88 , Issue 4 , August 2022 , 905880410
Check for updates
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abel, I.G., Barnes, M., Cowley, S.C., Dorland, W. & Schekochihin, A.A. 2008 Linearized model Fokker–Planck collision operators for gyrokinetic simulations. I. Theory. Phys. Plasmas 15, 122509.CrossRefGoogle Scholar
Abel, I.G. & Cowley, S.C. 2013 Multiscale gyrokinetics for rotating tokamak plasmas: II. Reduced models for electron dynamics. New J. Phys. 15, 023041.CrossRefGoogle Scholar
Abel, I.G. & Hallenbert, A. 2018 Multiscale modelling for tokamak pedestals. J. Plasma Phys. 84, 745840202.CrossRefGoogle Scholar
Abel, I.G., Plunk, G.G., Wang, E., Barnes, M., Cowley, S.C., Dorland, W. & Schekochihin, A.A. 2013 Multiscale gyrokinetics for rotating tokamak plasmas: fluctuations, transport and energy flows. Rep. Prog. Phys. 76, 116201.CrossRefGoogle ScholarPubMed
Adkins, T.G. & Schekochihin, A.A. 2018 A solvable model of Vlasov-kinetic plasma turbulence in Fourier-Hermite phase space. J. Plasma Phys. 84, 905840107.CrossRefGoogle Scholar
Alexandrova, O., Saur, J., Lacombe, C., Mangeney, A., Mitchell, J., Schwartz, S.J. & Robert, P. 2009 Universality of solar-wind turbulent spectrum from MHD to electron scales. Phys. Rev. Lett. 103, 165003.CrossRefGoogle ScholarPubMed
Aleynikova, K. & Zocco, A. 2017 Quantitative study of kinetic ballooning mode theory in simple geometry. Phys. Plasmas 24, 092106.CrossRefGoogle Scholar
Applegate, D.J., Roach, C.M., Connor, J.W., Cowley, S.C., Dorland, W., Hastie, R.J. & Joiner, N. 2007 Micro-tearing modes in the mega ampere spherical tokamak. Plasma Phys. Control. Fusion 49, 1113.CrossRefGoogle Scholar
Barnes, M., Parra, F.I. & Schekochihin, A.A. 2011 Critically balanced ion temperature gradient turbulence in fusion plasmas. Phys. Rev. Lett. 107, 115003.CrossRefGoogle ScholarPubMed
Beer, M.A. & Hammett, G.W. 1996 Toroidal gyrofluid equations for simulations of tokamak turbulence. Phys. Plasmas 3, 4046.CrossRefGoogle Scholar
Biglari, H., Diamond, P.H. & Rosenbluth, M.N. 1989 Toroidal ion-pressure-gradient-driven drift instabilities and transport revisited. Phys. Fluids B 1, 109.CrossRefGoogle Scholar
Boldyrev, S. 2005 On the spectrum of magnetohydrodynamic turbulence. Astrophys. J. 626, L37.CrossRefGoogle Scholar
Boldyrev, S., Horaites, K., Xia, Q. & Perez, J.C. 2013 Toward a theory of astrophysical plasma turbulence at subproton scales. Astrophys. J. 777, 41.CrossRefGoogle Scholar
Boldyrev, S. & Perez, J.C. 2012 Spectrum of kinetic-Alfvén turbulence. Astrophys. J. 758, L44.CrossRefGoogle Scholar
Braginskii, S.I. 1965 Transport processes in a plasma. Rev. Plasma Phys. 1, 205.Google Scholar
Callen, J.D. 1977 Drift-wave turbulence effects on magnetic structure and plasma transport in tokamaks. Phys. Rev. Lett. 39, 1540.CrossRefGoogle Scholar
Chapman-Oplopoiou, B., Hatch, D.R., Field, A.R., Frassinetti, L., Hillesheim, J., Horvath, L., Maggi, C.F., Parisi, J., Roach, C.M., Saarelma, S. et al. 2022 The role of ETG modes in JET-ILW pedestals with varying levels of power and fuelling. Nucl. Fusion 62, 086028.CrossRefGoogle Scholar
Chen, C.H.K., Boldyrev, S., Xia, Q. & Perez, J.C. 2013 Nature of subproton scale turbulence in the solar wind. Phys. Rev. Lett. 110, 225002.CrossRefGoogle ScholarPubMed
Cho, J. & Lazarian, A. 2004 The anisotropy of electron magnetohydrodynamic turbulence. Astrophys. J. 615, L41.CrossRefGoogle Scholar
Cho, J. & Lazarian, A. 2009 Simulations of electron magnetohydrodynamic turbulence. Astrophys. J. 701, 236.CrossRefGoogle Scholar
Colyer, G.J., Schekochihin, A.A., Parra, F.I., Roach, C.M., Barnes, M.A., Ghim, Y.-C. & Dorland, W. 2017 Collisionality scaling of the electron heat flux in ETG turbulence. Plasma Phys. Control. Fusion 59, 055002.CrossRefGoogle Scholar
Cowley, S.C. 1985 Some aspects of anomalous transport in tokamaks: stochastic magnetic fields, tearing modes and nonlinear ballooning instabilities. PhD thesis, Princeton Univ., NJ.Google Scholar
Cowley, S.C., Kulsrud, R.M. & Sudan, R. 1991 Considerations of ion-temperature-gradient-driven turbulence. Phys. Fluids B 3, 2767.CrossRefGoogle Scholar
Dickinson, D., Roach, C.M., Saarelma, S., Scannell, R., Kirk, A. & Wilson, H.R. 2013 Microtearing modes at the top of the pedestal. Plasma Phys. Control. Fusion 55, 074006.CrossRefGoogle Scholar
Dorland, W. & Hammett, G.W. 1993 Gyrofluid turbulence models with kinetic effects. Phys. Fluids B 5, 812.CrossRefGoogle Scholar
Dorland, W., Jenko, F., Kotschenreuther, M. & Rogers, B.N. 2000 Electron temperature gradient turbulence. Phys. Rev. Lett. 85, 5579.CrossRefGoogle ScholarPubMed
Dougherty, J.P. 1964 Model Fokker-Planck Equation for a Plasma and Its Solution. Phys. Fluids 7, 1788.CrossRefGoogle Scholar
Drake, J.F., Gladd, N.T., Liu, C.S. & Chang, C.L. 1980 Microtearing modes and anomalous transport in tokamaks. Phys. Rev. Lett. 44, 994.CrossRefGoogle Scholar
Drake, J.F. & Lee, Y.C. 1977 Kinetic theory of tearing instabilities. Phys. Fluids 20, 1341.CrossRefGoogle Scholar
Eyink, G.L. & Aluie, H. 2006 The breakdown of Alfvén's theorem in ideal plasma flows: necessary conditions and physical conjectures. Physica D 223, 82.CrossRefGoogle Scholar
Faddeeva, V.N. & Terent'ev, N.M. 1954 Tables of Values of the Function $w(z)=\exp (-z^{2})(1+2i/\sqrt {{\rm \pi} }\int _0^{z} \exp (t^{2}) \,\mathrm {d} t)$ for Complex Argument. Gostekhizdat, English translation. Pergamon Press, 1961.Google Scholar
Field, A.R., Challis, C.D., Fontdecaba, J.M., Frassinetti, L., Horvath, L., Kim, H.-T., Maggi, C., Roach, C.M., Saarelma, S., Sertoli, M. et al. 2020 The dependence of exhaust power components on edge gradients in JET-C and JET-ILW H-mode plasmas. Plasma Phys. Control. Fusion 62, 055010.CrossRefGoogle Scholar
Franci, L., Landi, S., Verdini, A., Matteini, L. & Hellinger, P. 2018 Solar wind turbulent cascade from MHD to sub-ion scales: large-size 3D hybrid particle-in-cell simulations. Astrophys. J. 853, 26.CrossRefGoogle Scholar
Fried, B.D. & Conte, S.D. 1961 The Plasma Dispersion Function. Academic Press.Google Scholar
Goldreich, P. & Sridhar, S. 1995 Toward a theory of interstellar turbulence. 2: strong Alfvénic turbulence. Astrophys. J. 438, 763.CrossRefGoogle Scholar
Goldreich, P. & Sridhar, S. 1997 Magnetohydrodynamic turbulence revisited. Astrophys. J. 485, 680.CrossRefGoogle Scholar
Goswami, P., Passot, T. & Sulem, P.L. 2005 A Landau fluid model for warm collisionless plasmas. Phys. Plasmas 12, 102109.CrossRefGoogle Scholar
Grošelj, D., Chen, C.H.K., Mallet, A., Samtaney, R., Schneider, K. & Jenko, F. 2019 Kinetic turbulence in astrophysical plasmas: waves and/or structures? Phys. Rev. X 9, 031037.Google Scholar
Grošelj, D., Mallet, A., Loureiro, N.F. & Jenko, F. 2018 Fully kinetic simulation of 3D kinetic Alfvén turbulence. Phys. Rev. Lett. 120, 105101.CrossRefGoogle ScholarPubMed
Gültekin, Ö. & Gürcan, Ö.D. 2018 Stable and unstable roots of ion temperature gradient driven mode using curvature modified plasma dispersion functions. Plasma Phys. Control. Fusion 60, 025021.CrossRefGoogle Scholar
Gültekin, Ö. & Gürcan, Ö.D. 2020 Generalized curvature modified plasma dispersion functions and Dupree renormalization of toroidal ITG. Plasma Phys. Control. Fusion 62, 025018.CrossRefGoogle Scholar
Gürcan, Ö.D. 2014 Numerical computation of the modified plasma dispersion function with curvature. J. Comput. Phys. 269, 156.CrossRefGoogle Scholar
Guttenfelder, W., Candy, J., Kaye, S.M., Nevins, W.M., Bell, R.E., Hammett, G.W., LeBlanc, B.P. & Yuh, H. 2012 Scaling of linear microtearing stability for a high collisionality National Spherical Torus Experiment discharge. Phys. Plasmas 19, 022506.CrossRefGoogle Scholar
Guttenfelder, W., Groebner, R.J., Canik, J.M., Grierson, B.A., Belli, E.A. & Candy, J. 2021 Testing predictions of electron scale turbulent pedestal transport in two DIII-D ELMy H-modes. Nucl. Fusion 61, 056005.CrossRefGoogle Scholar
Guttenfelder, W., Peterson, J.L., Candy, J., Kaye, S.M., Ren, Y., Bell, R.E., Hammett, G.W., LeBlanc, B.P., Mikkelsen, D.R., Nevins, W.M. et al. 2013 Progress in simulating turbulent electron thermal transport in NSTX. Nucl. Fusion 53, 093022.CrossRefGoogle Scholar
Ham, C.J., Bokshi, A., Brunetti, D., Ramirez, G.B., Chapman, B., Connor, J.W., Dickinson, D., Field, A.R., Frassinetti, L., Gillgren, A. et al. 2021 Towards understanding reactor relevant tokamak pedestals. Nucl. Fusion 61, 096013.CrossRefGoogle Scholar
Hammett, G.W., Beer, M.A., Dorland, W., Cowley, S.C. & Smith, S.A. 1993 Developments in the gyrofluid approach to tokamak turbulence simulations. Plasma Phys. Control. Fusion 35, 973.CrossRefGoogle Scholar
Hammett, G.W., Dorland, W. & Perkins, F.W. 1992 Fluid models of phase mixing, Landau damping, and nonlinear gyrokinetic dynamics. Phys. Fluids B 4, 2052.CrossRefGoogle Scholar
Hammett, G.W. & Perkins, F.W. 1990 Fluid moment models for Landau damping with application to the ion-temperature-gradient instability. Phys. Rev. Lett. 64, 3019.CrossRefGoogle Scholar
Hardman, M.R., Parra, F.I., Chong, C., Adkins, T., Anastopoulos-Tzanis, M.C., Barnes, M., Dickinson, D., Parisi, J.F. & Wilson, H.R. 2022 Extended electron tails in electrostatic microinstabilities and the nonadiabatic response of passing electrons. Plasma Phys. Control. Fusion 64 (5), 055004.CrossRefGoogle Scholar
Hassam, A.B. 1980 a Fluid theory of tearing instabilities. Phys. Fluids 23, 2493.CrossRefGoogle Scholar
Hassam, A.B. 1980 b Higher-order Chapman-Enskog theory for electrons. Phys. Fluids 23, 38.CrossRefGoogle Scholar
Hatch, D.R., Jenko, F., Bañón Navarro, A. & Bratanov, V. 2013 Transition between saturation regimes of gyrokinetic turbulence. Phys. Rev. Lett. 111, 175001.CrossRefGoogle ScholarPubMed
Hatch, D.R., Kotschenreuther, M., Mahajan, S.M., Merlo, G., Field, A.R., Giroud, C., Hillesheim, J.C., Maggi, C.F., Perez von Thun, C., Roach, C.M. et al. 2019 Direct gyrokinetic comparison of pedestal transport in JET with carbon and ITER-like walls. Nucl. Fusion 59, 086056.CrossRefGoogle Scholar
Hatch, D.R., Kotschenreuther, M., Mahajan, S.M., Pueschel, M.J., Michoski, C., Merlo, G., Hassan, E., Field, A.R., Frassinetti, L., Giroud, C. et al. 2021 Microtearing modes as the source of magnetic fluctuations in the JET pedestal. Nucl. Fusion 61, 036015.CrossRefGoogle Scholar
Hazeltine, R.D., Dobrott, D. & Wang, T.S. 1975 Kinetic theory of tearing instability. Phys. Fluids 18, 1778.CrossRefGoogle Scholar
Helander, P. & Sigmar, D.J. 2005 Collisional Transport in Magnetized Plasmas. Cambridge University Press.Google Scholar
Horton, W., Hong, B.G. & Tang, W.M. 1988 Toroidal electron temperature gradient driven drift modes. Phys. Fluids 31, 2971.CrossRefGoogle Scholar
Howes, G.G., Cowley, S.C., Dorland, W., Hammett, G.W., Quataert, E. & Schekochihin, A.A. 2006 Astrophysical gyrokinetics: basic equations and linear theory. Astrophys. J. 651, 590.CrossRefGoogle Scholar
Howes, G.G., Tenbarge, J.M., Dorland, W., Quataert, E., Schekochihin, A.A., Numata, R. & Tatsuno, T. 2011 Gyrokinetic simulations of solar wind turbulence from ion to electron scales. Phys. Rev. Lett. 107, 035004.CrossRefGoogle ScholarPubMed
Ishizawa, A., Maeyama, S., Watanabe, T.H., Sugama, H. & Nakajima, N. 2013 Gyrokinetic turbulence simulations of high-beta tokamak and helical plasmas with full-kinetic and hybrid models. Nucl. Fusion 53, 053007.CrossRefGoogle Scholar
Ishizawa, A., Urano, D., Nakamura, Y., Maeyama, S. & Watanabe, T.H. 2019 Persistence of ion temperature gradient turbulent transport at finite normalized pressure. Phys. Rev. Lett. 123, 025003.CrossRefGoogle ScholarPubMed
Ishizawa, A., Watanabe, T.-H., Sugama, H., Maeyama, S. & Nakajima, N. 2014 Electromagnetic gyrokinetic turbulence in finite-beta helical plasmas. Phys. Plasmas 21, 055905.CrossRefGoogle Scholar
Ivanov, P.G, Schekochihin, A.A. & Dorland, W. 2022 Dimits transition in three-dimensional ion-temperature-gradient turbulence. J. Plasma Phys. (in preparation, URL: arXiv:2203.02769).Google Scholar
Ivanov, P.G., Schekochihin, A.A., Dorland, W., Field, A.R. & Parra, F.I. 2020 Zonally dominated dynamics and Dimits threshold in curvature-driven ITG turbulence. J. Plasma Phys. 86, 855860502.CrossRefGoogle Scholar
Jenko, F., Dorland, W. & Hammett, G.W. 2001 Critical gradient formula for toroidal electron temperature gradient modes. Phys. Plasmas 8, 4096.CrossRefGoogle Scholar
Jenko, F., Dorland, W., Kotschenreuther, M. & Rogers, B.N. 2000 Electron temperature gradient driven turbulence. Phys. Plasmas 7, 1904.CrossRefGoogle Scholar
Kolmogorov, A.N. 1941 Local structure of turbulence in incompressible viscous fluid at very large Reynolds numbers. Dokl. Acad. Nauk SSSR 30, 299.Google Scholar
Kotschenreuther, M., Dorland, W., Beer, M.A. & Hammett, G.W. 1995 Quantitative predictions of tokamak energy confinement from first-principles simulations with kinetic effects. Phys. Plasmas 2, 2381.CrossRefGoogle Scholar
Kotschenreuther, M., Liu, X., Hatch, D.R., Mahajan, S., Zheng, L., Diallo, A., Groebner, R., Hillesheim, J.C., Maggi, C.F., the DIII-D TEAM et al. 2019 Gyrokinetic analysis and simulation of pedestals to identify the culprits for energy losses using ‘fingerprints’. Nucl. Fusion 59, 096001.CrossRefGoogle Scholar
Kulsrud, R.M. 1983 MHD description of plasma. In Handbook of Plasma Physics, Volume 1 (ed. A.A. Galeev & R.N. Sudan), p. 1. North-Holland.Google Scholar
Landau, L. 1946 On the vibration of the electronic plasma. Zh. Eksp. Teor. Fiz. 16, 574.Google Scholar
Larakers, J.L., Curie, M., Hatch, D.R., Hazeltine, R.D. & Mahajan, S.M. 2021 Global theory of microtearing modes in the tokamak pedestal. Phys. Rev. Lett. 126, 225001.CrossRefGoogle ScholarPubMed
Larakers, J.L., Hazeltine, R.D. & Mahajan, S.M. 2020 A comprehensive conductivity model for drift and micro-tearing modes. Phys. Plasmas 27, 062503.CrossRefGoogle Scholar
Lee, Y.C., Dong, J.Q., Guzdar, P.N. & Liu, C.S. 1987 Collisionless electron temperature gradient instability. Phys. Fluids 30 (5), 1331–1339.CrossRefGoogle Scholar
Liu, C.S. 1971 Instabilities in a magnetoplasma with skin current. Phys. Rev. Lett. 27, 1637–1640.CrossRefGoogle Scholar
Loureiro, N.F., Dorland, W., Fazendeiro, L., Kanekar, A., Mallet, A., Vilelas, M.S. & Zocco, A. 2016 Viriato: a Fourier-Hermite spectral code for strongly magnetized fluid-kinetic plasma dynamics. Comput. Phys. Commun. 206, 45–63.CrossRefGoogle Scholar
Maeyama, S., Kusaka, S. & Watanabe, T.-H. 2021 Effects of ion polarization and finite-$\beta _e$ on heat transport in slab electron-temperature-gradient driven turbulence. Phys. Plasmas 28, 052512.CrossRefGoogle Scholar
Mandell, N.R., Dorland, W. & Landreman, M. 2018 Laguerre–Hermite pseudo-spectral velocity formulation of gyrokinetics. J. Plasma Phys. 84 (1), 905840108.CrossRefGoogle Scholar
Manheimer, W.M. & Cook, I. 1978 A theory of particle and energy flux from the magnetic flutter of drift waves. US Defense Technical Information Center (URL: https://apps.dtic.mil/sti/citations/ADA053947).Google Scholar
Meyrand, R. & Galtier, S. 2013 Anomalous $k_{\perp }^{-8/3}$ spectrum in electron magnetohydrodynamic turbulence. Phys. Rev. Lett. 111, 264501.CrossRefGoogle ScholarPubMed
Mishchenko, A., Plunk, G.G. & Helander, P. 2018 Electrostatic stability of electron-positron plasmas in dipole geometry. J. Plasma Phys. 84, 905840201.CrossRefGoogle Scholar
Moradi, S., Pusztai, I., Guttenfelder, W., Fülöp, T. & Mollén, A. 2013 Microtearing modes in spherical and conventional tokamaks. Nucl. Fusion 53, 063025.CrossRefGoogle Scholar
Nazarenko, S.V. & Schekochihin, A.A. 2011 Critical balance in magnetohydrodynamic, rotating and stratified turbulence: towards a universal scaling conjecture. J. Fluid Mech. 677, 134.CrossRefGoogle Scholar
Newcomb, W.A. 1958 Motion of magnetic lines of force. Ann. Phys. 3, 347.CrossRefGoogle Scholar
Parisi, J.F., Parra, F.I., Roach, C.M., Giroud, C., Dorland, W., Hatch, D.R., Barnes, M., Hillesheim, J.C., Aiba, N., Ball, J. et al. 2020 Toroidal and slab ETG instability dominance in the linear spectrum of JET-ILW pedestals. Nucl. Fusion 60, 126045.CrossRefGoogle Scholar
Parker, J.T., Highcock, E.G., Schekochihin, A.A. & Dellar, P.J. 2016 Suppression of phase mixing in drift-kinetic plasma turbulence. Phys. Plasmas 23, 070703.CrossRefGoogle Scholar
Passot, T. & Sulem, P.L. 2004 A Landau fluid model for dispersive magnetohydrodynamics. Phys. Plasmas 11, 5173.CrossRefGoogle Scholar
Passot, T., Sulem, P.L. & Tassi, E. 2017 Electron-scale reduced fluid models with gyroviscous effects. J. Plasma Phys. 83, 715830402.CrossRefGoogle Scholar
Patel, B.S., Dickinson, D., Roach, C.M. & Wilson, H.R. 2021 Linear gyrokinetic stability of a high $\beta$ non-inductive spherical tokamak. Nucl. Fusion 62 (1), 016009.CrossRefGoogle Scholar
Predebon, I. & Sattin, F. 2013 On the linear stability of collisionless microtearing modes. Phys. Plasmas 20, 040701.CrossRefGoogle Scholar
Pueschel, M.J., Hatch, D.R., Görler, T., Nevins, W.M., Jenko, F., Terry, P.W. & Told, D. 2013 a Properties of high-$\beta$ microturbulence and the non-zonal transition. Phys. Plasmas 20, 102301.CrossRefGoogle Scholar
Pueschel, M.J. & Jenko, F. 2010 Transport properties of finite-$\beta$ microturbulence. Phys. Plasmas 17, 062307.CrossRefGoogle Scholar
Pueschel, M.J., Kammerer, M. & Jenko, F. 2008 Gyrokinetic turbulence simulations at high plasma beta. Phys. Plasmas 15, 102310.CrossRefGoogle Scholar
Pueschel, M.J., Terry, P.W. & Hatch, D.R. 2014 Aspects of the non-zonal transition. Phys. Plasmas 21, 055901.CrossRefGoogle Scholar
Pueschel, M.J., Terry, P.W., Jenko, F., Hatch, D.R., Nevins, W.M., Görler, T. & Told, D. 2013 b Extreme heat fluxes in gyrokinetic simulations: a new critical β. Phys. Rev. Lett. 110, 155005.CrossRefGoogle ScholarPubMed
Pueschel, M.J., Terry, P.W., Told, D. & Jenko, F. 2015 Enhanced magnetic reconnection in the presence of pressure gradients. Phys. Plasmas 22, 062105.CrossRefGoogle Scholar
Rafiq, T., Weiland, J., Kritz, A.H., Luo, L. & Pankin, A.Y. 2016 Microtearing modes in tokamak discharges. Phys. Plasmas 23, 062507.CrossRefGoogle Scholar
Ren, Y., Belova, E., Gorelenkov, N., Guttenfelder, W., Kaye, S.M., Mazzucato, E., Peterson, J.L., Smith, D.R., Stutman, D., Tritz, K. et al. 2017 Recent progress in understanding electron thermal transport in NSTX. Nucl. Fusion 57, 072002.CrossRefGoogle Scholar
Ricci, P., Rogers, B.N., Dorland, W. & Barnes, M. 2006 Gyrokinetic linear theory of the entropy mode in a Z pinch. Phys. Plasmas 13, 062102.CrossRefGoogle Scholar
Roach, C.M., Abel, I.G., Akers, R.J., Arter, W., Barnes, M., Camenen, Y., Casson, F.J., Colyer, G., Connor, J.W., Cowley, S.C. et al. 2009 Gyrokinetic simulations of spherical tokamaks. Plasma Phys. Control. Fusion 51, 124020.CrossRefGoogle Scholar
Roach, C.M., Applegate, D.J., Connor, J.W., Cowley, S.C., Dorland, W.D., Hastie, R.J., Joiner, N., Saarelma, S., Schekochihin, A.A., Akers, R.J. et al. 2005 Microstability physics as illuminated in the spherical tokamak. Plasma Phys. Control. Fusion 47, B323.CrossRefGoogle Scholar
Rogers, B.N., Zhu, B. & Francisquez, M. 2018 Gyrokinetic theory of slab universal modes and the non-existence of the gradient drift coupling (GDC) instability. Phys. Plasmas 25, 052115.CrossRefGoogle Scholar
Sahraoui, F., Goldstein, M.L., Belmont, G., Canu, P. & Rezeau, L. 2010 Three dimensional anisotropic k spectra of turbulence at subproton scales in the solar wind. Phys. Rev. Lett. 105, 131101.CrossRefGoogle ScholarPubMed
Schekochihin, A.A., Cowley, S.C., Dorland, W., Hammett, G.W., Howes, G.G., Plunk, G.G., Quataert, E. & Tatsuno, T. 2008 Gyrokinetic turbulence: a nonlinear route to dissipation through phase space. Plasma Phys. Control. Fusion 50, 124024.CrossRefGoogle Scholar
Schekochihin, A.A., Cowley, S.C., Dorland, W., Hammett, G.W., Howes, G.G., Quataert, E. & Tatsuno, T. 2009 Astrophysical gyrokinetics: kinetic and fluid turbulent cascades in magnetized weakly collisional plasmas. Astrophys. J. Suppl. 182, 310.CrossRefGoogle Scholar
Schekochihin, A.A., Kawazura, Y. & Barnes, M.A. 2019 Constraints on ion versus electron heating by plasma turbulence at low beta. J. Plasma Phys. 85, 905850303.CrossRefGoogle Scholar
Schekochihin, A.A., Parker, J.T., Highcock, E.G., Dellar, P.J., Dorland, W. & Hammett, G.W. 2016 Phase mixing versus nonlinear advection in drift-kinetic plasma turbulence. J. Plasma Phys. 82, 905820212.CrossRefGoogle Scholar
Shimomura, Y., Murakami, Y., Polevoi, A.R., Barabaschi, P., Mukhovatov, V. & Shimada, M. 2001 ITER: opportunity of burning plasma studies. Plasma Phys. Control. Fusion 43, 385.CrossRefGoogle Scholar
Similon, P., Sedlak, J.E., Stotler, D., Berk, H.L., Horton, W. & Choi, D. 1984 Guiding-center dispersion function. J. Comput. Phys. 54, 260.CrossRefGoogle Scholar
Sips, A.C.C. 2005 Advanced scenarios for ITER operation. Plasma Phys. Control. Fusion 47, A19.CrossRefGoogle Scholar
Smith, S.A. 1997 Dissipative closures for statistical moments, fluid moments, and subgrid scales in plasma turbulence. PhD thesis, Princeton University (URL: http://w3.pppl.gov/hammett/sasmith/thesis.html).Google Scholar
Snyder, P.B. 1999 Gyrofluid theory and simulation of electromagnetic turbulence and transport in tokamak plasmas. PhD thesis, Princeton University (URL: https://w3.pppl.gov/~hammett/gyrofluid/papers/1999/thesis.pdf).Google Scholar
Snyder, P.B. & Hammett, G.W. 2001 a A Landau fluid model for electromagnetic plasma microturbulence. Phys. Plasmas 8, 3199.CrossRefGoogle Scholar
Snyder, P.B. & Hammett, G.W. 2001 b Electromagnetic effects on plasma microturbulence and transport. Phys. Plasmas 8, 744.CrossRefGoogle Scholar
Snyder, P.B., Hammett, G.W. & Dorland, W. 1997 Landau fluid models of collisionless magnetohydrodynamics. Phys. Plasmas 4, 3974.CrossRefGoogle Scholar
Tang, W.M., Connor, J.W. & Hastie, R.J. 1980 Kinetic-ballooning-mode theory in general geometry. Nucl. Fusion 20, 1439.CrossRefGoogle Scholar
Terry, P.W., Carmody, D., Doerk, H., Guttenfelder, W., Hatch, D.R., Hegna, C.C., Ishizawa, A., Jenko, F., Nevins, W.M., Predebon, I. et al. 2015 Overview of gyrokinetic studies of finite-beta microturbulence. Nucl. Fusion 55, 104011.CrossRefGoogle Scholar
Told, D., Jenko, F., TenBarge, J.M., Howes, G.G. & Hammett, G.W. 2015 Multiscale nature of the dissipation range in gyrokinetic simulations of Alfvénic turbulence. Phys. Rev. Lett. 115, 025003.CrossRefGoogle ScholarPubMed
Waltz, R.E. 1988 Three-dimensional global numerical simulation of ion temperature gradient mode turbulence. Phys. Fluids 31, 1962.CrossRefGoogle Scholar
Waltz, R.E. 2010 Nonlinear subcritical magnetohydrodynamic beta limit. Phys. Plasmas 17, 072501.CrossRefGoogle Scholar
Wan, W., Parker, S.E., Chen, Y., Groebner, R.J., Yan, Z., Pankin, A.Y. & Kruger, S.E. 2013 Global gyrokinetic simulations of the H-mode tokamak edge pedestal. Phys. Plasmas 20, 055902.CrossRefGoogle Scholar
Wan, W., Parker, S.E., Chen, Y., Yan, Z., Groebner, R.J. & Snyder, P.B. 2012 Global gyrokinetic simulation of tokamak edge pedestal instabilities. Phys. Rev. Lett. 109, 185004.CrossRefGoogle ScholarPubMed
Wang, L., Zhu, B., Xu, X.-Q. & Li, B. 2019 A Landau-fluid closure for arbitrary frequency response. AIP Adv. 9, 015217.CrossRefGoogle Scholar
Watanabe, T.-H. & Sugama, H. 2004 Kinetic simulation of steady states of ion temperature gradient driven turbulence with weak collisionality. Phys. Plasmas 11, 1476.CrossRefGoogle Scholar
Wolf, R.C. 2003 Internal transport barriers in tokamak plasmas. Plasma Phys. Control. Fusion 45, R1.CrossRefGoogle Scholar
Xu, R. & Kunz, M.W. 2016 Linear Vlasov theory of a magnetised, thermally stratified atmosphere. J. Plasma Phys. 82, 905820507.CrossRefGoogle Scholar
Zielinski, J., Smolyakov, A.I., Beyer, P. & Benkadda, S. 2017 Electromagnetic electron temperature gradient driven instability in toroidal plasmas. Phys. Plasmas 24, 024501.CrossRefGoogle Scholar
Zocco, A., Loureiro, N.F., Dickinson, D., Numata, R. & Roach, C.M. 2015 Kinetic microtearing modes and reconnecting modes in strongly magnetised slab plasmas. Plasma Phys. Control. Fusion 57, 065008.CrossRefGoogle Scholar
Zocco, A. & Schekochihin, A.A. 2011 Reduced fluid-kinetic equations for low-frequency dynamics, magnetic reconnection, and electron heating in low-beta plasmas. Phys. Plasmas 18, 102309.CrossRefGoogle Scholar
Zocco, A., Xanthopoulos, P., Doerk, H., Connor, J.W. & Helander, P. 2018 Threshold for the destabilisation of the ion-temperature-gradient mode in magnetically confined toroidal plasmas. J. Plasma Phys. 84, 715840101.CrossRefGoogle Scholar