Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-13T02:14:47.840Z Has data issue: false hasContentIssue false
  • English
  • Français

Electromagnetic turbulence in increased β plasmas in the Large Plasma Device

Published online by Cambridge University Press:  09 July 2021

G.D. Rossi Open the ORCID record for G.D. Rossi [Opens in a new window] ,
T.A. Carter Open the ORCID record for T.A. Carter [Opens in a new window] ,
B. Seo Open the ORCID record for B. Seo [Opens in a new window] ,
J. Robertson Open the ORCID record for J. Robertson [Opens in a new window] ,
M.J. Pueschel Open the ORCID record for M.J. Pueschel [Opens in a new window]  and
P.W. Terry
G.D. Rossi*
Affiliation:
Department of Physics and Astronomy, University of California, Los Angeles, 405 Hilgard Ave, Los Angeles, CA90034, USA
T.A. Carter
Affiliation:
Department of Physics and Astronomy, University of California, Los Angeles, 405 Hilgard Ave, Los Angeles, CA90034, USA
B. Seo
Affiliation:
Physical Sciences Department, Embry-Riddle Aeronautical University, Daytona Beach, FL32114, USA
J. Robertson
Affiliation:
Department of Physics and Astronomy, University of California, Los Angeles, 405 Hilgard Ave, Los Angeles, CA90034, USA
M.J. Pueschel
Affiliation:
Dutch Institute for Fundamental Energy Research, Eindhoven, Netherlands
P.W. Terry
Affiliation:
Department of Physics, University of Wisconsin-Madison, Madison, Wisconsin53706, USA
*
†Email address for correspondence: grossi@g.ucla.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

The variation of pressure-gradient-driven turbulence with plasma $\beta$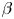 (up to $\beta \approx 15\,\%$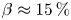) is investigated in linear, magnetized plasma. The magnitude of magnetic fluctuations is observed to increase substantially with increasing $\beta$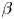. More importantly, parallel magnetic fluctuations are observed to dominate at higher $\beta$ 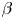values, with $\delta B_\parallel / \delta B_\perp \approx 2$ 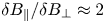and $\delta B / B_0 \approx 1\,\%$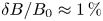. Parallel magnetic fluctuations are strongly correlated with density fluctuations and the two are observed to be out of phase. The relative magnitude of and cross-phase between density and parallel magnetic field fluctuations are consistent with the dynamic pressure balance ($P+{B_{0}^2}/{2\mu _0} = \textrm {constant}$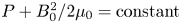). A local slab model theory for electromagnetic, modified drift Alfvén waves, including parallel magnetic fluctuations, shows partial agreement with experimental observations.

Keywords

plasma wavesplasma instabilities
Type
Research Article
Information
Journal of Plasma Physics , Volume 87 , Issue 4 , August 2021 , 905870401
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Burke, A.T., Maggs, J.E. & Morales, G.J. 2000 Experimental study of fluctuations excited by a narrow temperature filament in a magnetized plasma. Phys. Plasmas 7 (5), 1397–1407.CrossRefGoogle Scholar
Candy, J. 2005 Beta scaling of transport in microturbulence simulations. Phys. Plasmas 12 (7), 072307.CrossRefGoogle Scholar
Carreras, B.A. 1997 Progress in anomalous transport research in toroidal magnetic confinement devices. IEEE Trans. Plasma Sci. 25 (6), 1281–1321.CrossRefGoogle Scholar
Carter, T.A. 2006 Intermittent turbulence and turbulent structures in a linear magnetized plasma. Phys. Plasmas 13 (1), 010701.CrossRefGoogle Scholar
Carter, T.A. & Maggs, J.E. 2009 Modifications of turbulence and turbulent transport associated with a bias-induced confinement transition in the large plasma device. Phys. Plasmas 16 (1), 012304.CrossRefGoogle Scholar
Citrin, J., Garcia, J., Görler, T., Jenko, F., Mantica, P., Told, D., Bourdelle, C., Hatch, D.R., Hogeweij, G.M.D., Johnson, T., et al. 2015 Electromagnetic stabilization of tokamak microturbulence in a high-$\beta$ regime. Plasma Phys. Control. Fusion 57 (1), 014032.CrossRefGoogle Scholar
Doyle, E.J. 2007 Chapter 2: plasma confinement and transport. Nucl. Fusion 47 (6), S18.Google Scholar
Everson, E.T., Pribyl, P., Constantin, C.G., Zylstra, A., Schaeffer, D., Kugland, N.L. & Niemann, C. 2009 Design, construction, and calibration of a three-axis, high-frequency magnetic probe (b-dot probe) as a diagnostic for exploding plasmas. Rev. Sci. Instrum. 80 (11), 113505.CrossRefGoogle ScholarPubMed
Gekelman, W., Pribyl, P., Lucky, Z., Drandell, M., Leneman, D., Maggs, J., Vincena, S., Van Compernolle, B., Tripathi, S.K.P., Morales, G., et al. 2016 The upgraded large plasma device, a machine for studying frontier basic plasma physics. Rev. Sci. Instrum. 87 (2), 025105.CrossRefGoogle ScholarPubMed
Goldston, R.J. & Rutherford, P.H. 1995 Introduction to Plasma Physics. CRC Press.CrossRefGoogle Scholar
Horton, W., Correa, C., Chagelishvili, G.D., Avsarkisov, V.S., Lominadze, J.G., Perez, J.C., Kim, J.-H. & Carter, T.A. 2009 On generation of alfvénic-like fluctuations by drift wave–zonal flow system in large plasma device experiments. Phys. Plasmas 16 (9), 092102.CrossRefGoogle Scholar
Horton, W., Perez, J.C., Carter, T. & Bengtson, R. 2005 Vorticity probes and the characterization of vortices in the Kelvin–Helmholtz instability in the large plasma device experiment. Phys. Plasmas 12 (2), 022303.CrossRefGoogle Scholar
Jenko, F. & Scott, B.D. 1999 Numerical computation of collisionless drift alfvén turbulence. Phys. Plasmas 6 (7), 2705–2713.CrossRefGoogle Scholar
Kikuchi, M. 1993 Prospects of a stationary tokamak reactor. Plasma Phys. Control. Fusion 35 (SB), B39.CrossRefGoogle Scholar
Lee, W., Angus, J.R., Umansky, M.V. & Krasheninnikov, S.I. 2015 Electromagnetic effects on plasma blob-filament transport. J. Nucl. Mater. 463, 765–768.CrossRefGoogle Scholar
Liewer, P.C. 1985 Measurements of microturbulence in tokamaks and comparisons with theories of turbulence and anomalous transport. Nucl. Fusion 25 (5), 543.CrossRefGoogle Scholar
Maggs, J.E., Carter, T.A. & Taylor, R.J. 2007 Transition from Bohm to classical diffusion due to edge rotation of a cylindrical plasma. Phys. Plasmas 14 (5), 052507.CrossRefGoogle Scholar
Maggs, J.E. & Morales, G.J. 2012 Exponential power spectra, deterministic chaos and lorentzian pulses in plasma edge dynamics. Plasma Phys. Control. Fusion 54 (12), 124041.CrossRefGoogle Scholar
Morales, G.J., Maggs, J.E., Burke, A.T. & Pe nano, J.R. 1999 Alfvénic turbulence associated with density and temperature filaments. Plasma Phys. Control. Fusion 41 (3A), A519–A529.CrossRefGoogle Scholar
Pace, D.C., Shi, M., Maggs, J.E., Morales, G.J. & Carter, T.A. 2008 Exponential frequency spectrum in magnetized plasmas. Phys. Rev. Lett. 101, 085001.CrossRefGoogle ScholarPubMed
Pe nano, J.R., Morales, G.J. & Maggs, J.E. 2000 Drift-alfvén fluctuations associated with a narrow pressure striation. Phys. Plasmas 7 (1), 144–157.CrossRefGoogle Scholar
Pueschel, M.J., Hatch, D.R., Görler, T., Nevins, W.M., Jenko, F., Terry, P.W. & Told, D. 2013 Properties of high-$\beta$ microturbulence and the non-zonal transition. Phys. Plasmas 20 (10), 102301.CrossRefGoogle Scholar
Pueschel, M.J. & Jenko, F. 2010 Transport properties of finite-$\beta$ microturbulence. Phys. Plasmas 17 (6), 062307.CrossRefGoogle Scholar
Pueschel, M.J., Jenko, F., Told, D. & Büchner, J. 2011 Gyrokinetic simulations of magnetic reconnection. Phys. Plasmas 18 (11), 112102.CrossRefGoogle Scholar
Pueschel, M.J., Kammerer, M. & Jenko, F. 2008 Gyrokinetic turbulence simulations at high plasma beta. Phys. Plasmas 15 (10), 102310.CrossRefGoogle Scholar
Pueschel, M.J., Rossi, G., Told, D., Terry, P.W., Jenko, F. & Carter, T.A. 2017 A basic plasma test for gyrokinetics: GDC turbulence in LAPD. Plasma Phys. Control. Fusion 59 (2), 024006.CrossRefGoogle Scholar
Pueschel, M.J., Sydora, R.D., Terry, P.W., Tyburska-Pueschel, B., Francisquez, M., Jenko, F. & Zhu, B. 2020 Pair plasma instability in homogeneous magnetic guide fields. Phys. Plasmas 27 (10), 102111.CrossRefGoogle Scholar
Pueschel, M.J., Terry, P.W., Told, D. & Jenko, F. 2015 Enhanced magnetic reconnection in the presence of pressure gradients. Phys. Plasmas 22 (6), 062105.CrossRefGoogle Scholar
Rechester, A.B. & Rosenbluth, M.N. 1978 Electron heat transport in a tokamak with destroyed magnetic surfaces. Phys. Rev. Lett. 40, 38–41.CrossRefGoogle Scholar
Rogers, B.N., Zhu, B. & Francisquez, M. 2018 Gyrokinetic theory of slab universal modes and the non-existence of the gradient drift coupling (GDC) instability. Phys. Plasmas 25 (5), 052115.CrossRefGoogle Scholar
Schaffner, D.A., Carter, T.A., Rossi, G.D., Guice, D.S., Maggs, J.E., Vincena, S. & Friedman, B. 2013 Turbulence and transport suppression scaling with flow shear on the large plasma device. Phys. Plasmas 20 (5), 055907.CrossRefGoogle Scholar
Smolyakov, A., Diamond, P. & Kishimoto, Y. 2002 Secondary instabilities of large scale flow and magnetic field in the electromagnetic short wavelength drift-alfven wave turbulence. Phys. Plasmas 9 (9), 3826–3834.CrossRefGoogle Scholar
Snyder, P.B. & Hammett, G.W. 2001 Electromagnetic effects on plasma microturbulence and transport. Phys. Plasmas 8 (3), 744–749.CrossRefGoogle Scholar
Terasawa, T., Hoshino, M., Sakai, J.-I. & Hada, T. 1986 Decay instability of finite-amplitude circularly polarized alfven waves: a numerical simulation of stimulated brillouin scattering. J. Geophys. Res. 91 (A4), 4171–4187.CrossRefGoogle Scholar
Terry, P.W., Carmody, D., Doerk, H., Guttenfelder, W., Hatch, D.R., Hegna, C.C., Ishizawa, A., Jenko, F., Nevins, W.M., Predebon, I., et al. 2015 Overview of gyrokinetic studies of finite-$\beta$ microturbulence. Nucl. Fusion 55 (10), 104011.CrossRefGoogle Scholar
Terry, P.W., Li, P.-Y., Pueschel, M.J. & Whelan, G.G. 2021 Threshold heat-flux reduction by near-resonant energy transfer. Phys. Rev. Lett. 126, 025004.CrossRefGoogle ScholarPubMed
Van Compernolle, B. & Morales, G.J. 2017 Avalanches driven by pressure gradients in a magnetized plasma. Phys. Plasmas 24 (11), 112302.CrossRefGoogle Scholar
Weidl, M.S., Winske, D., Jenko, F. & Niemann, C. 2016 Hybrid simulations of a parallel collisionless shock in the large plasma device. Phys. Plasmas 23 (12), 122102.CrossRefGoogle Scholar
Weiland, J. & Hirose, A. 1992 Electromagnetic and kinetic effects on the ion temperature gradient mode. Nucl. Fusion 32 (1), 151.CrossRefGoogle Scholar
Whelan, G.G., Pueschel, M.J. & Terry, P.W. 2018 Nonlinear electromagnetic stabilization of plasma microturbulence. Phys. Rev. Lett. 120, 175002.CrossRefGoogle ScholarPubMed
Zhou, S., Heidbrink, W.W., Boehmer, H., McWilliams, R., Carter, T.A., Vincena, S., Friedman, B. & Schaffner, D. 2012 Sheared-flow induced confinement transition in a linear magnetized plasma. Phys. Plasmas 19 (1), 012116.CrossRefGoogle Scholar
Zimbardo, G., Perri, S., Pommois, P. & Veltri, P. 2012 Anomalous particle transport in the heliosphere. Adv. Space Res. 49 (11), 1633–1642, advances in theory and observation of solar system dynamics – I.CrossRefGoogle Scholar