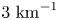Electron cyclotron resonance during plasma initiation

Abstract

Electron-cyclotron resonance heating (ECRH) is the main heating mechanism in the Wendelstein 7-X (W7-X) stellarator. Although second-harmonic ECRH (X2) has been used routinely for plasma startup, startup at third harmonic (X3) is known to be much more difficult. In this work, we investigate the energy gain of particles during nonlinear wave–particle interaction for conditions relevant to second- and third-harmonic startups in W7-X. We take into account both the beam and the ambient magnetic field inhomogeneities. The latter is shown to significantly increase the mean energy gain resulting from a single wave–particle resonant interaction. In W7-X-like conditions, the improvement in maximum gained energy is up to 4 times the analogous uniform magnetic field case. However, this improvement is not enough to ensure X3 startup. The optimal magnetic field inhomogeneity length scale for average energy gain and start up in W7-X-like conditions is found to be in the range of $1$ to $3\ {\rm km}^{-1}$. A possibility of using multiple beams with neighbouring resonances is also considered. A considerable enhancement of the energy gain is demonstrated.

1. Introduction

Electron-cyclotron resonance heating (ECRH) is one the most common mechanisms of plasma heating. It is applied in both tokamak and stellarator experiments. At high plasma temperature, linear theory describes the heating. However, during plasma initiation, nonlinear effects are very important because both the time of flight of an electron through the beam and the collision time are larger than the wave–particle interaction time (Taylor, Cairns & O'Brien 1988; Farina & Pozzoli 1991).

The importance of nonlinear wave–particle interaction during plasma initiation was previously demonstrated for a plane-wave approximation (Jaeger, Lichtenberg & Lieberman 1972; Carter et al. 1986), and in a homogeneous magnetic field for a Gaussian beam structure (Farina & Pozzoli 1991; Seol, Hegna & Callen 2009; Farina 2018). Therefore, it is instrumental to understand the nonlinear interaction when designing and optimising reactor startup scenarios, such as ECRH-assisted startup in the International Thermonuclear Experimental Reactor (ITER), and higher-harmonic startup in Wendelstein 7-X (W7-X) (Marushchenko et al. 2019). In particular, Farina (2018) highlights the difficulty of using the third harmonic (X3) for startup, demonstrating that, in a homogeneous background field, the interaction is too weak to support a startup using modern gyrotrons.

At the earliest stages before breakdown, the characteristic energy of the particles is assumed to be in the range of meV. Nonlinear wave–particle interaction in such conditions has been studied by Seol et al. (2009) and Farina (2018). The ionisation avalanche, however, is facilitated by the secondary electrons. These electrons have a typical energy of a few eVs. Successful ionisation avalanche requires that the secondary electron energy gain exceed the ionisation potential and losses. Energy gain of such electrons is the main focus of our work.

Both the ambient magnetic field inhomogeneity and relativistic effects can have a significant effect on resonance detuning, i.e. the imperfection in the resonance condition

(1.1)\begin{equation} \omega - {k}_{{\parallel}} v_{{\parallel}} - \frac{n \omega_c}{\gamma} = 0, \end{equation}

where $\omega$ and ${k}_{\parallel }$ are the wave frequency and parallel component (to the unperturbed magnetic field $\boldsymbol {B}$) of the wave vector, $v_{\parallel }$ is the particle parallel velocity, $\gamma \equiv 1/\sqrt {1 - v^2/\mathrm{c}^2}$ is the relativistic gamma factor for the electron with speed v, $n$ is the resonance number and $\omega _c \equiv \mathrm {e}|{\boldsymbol {B}}|/m$ is the non-relativistic electron-cyclotron frequency. Here e is the elementary charge, m is the electron rest mass and c is the speed of light. For instance, a 10 eV electron with parallel energy of 1 eV executes around $5 \times 10^{3}$ gyrations as it passes through a 4 cm beam in a 1.7 T magnetic field. The resulting accumulated relativistic phase shift is of order unity, since the relativistic detuning per gyration is of order $2 {\rm \pi}(\gamma - 1) \approx 10^{-4}$ for a 10 eV electron. A similar variation of the ambient magnetic field would also yield a phase shift of order unity.

In this paper, we outline the derivation of the equations of motion relevant for an inhomogeneous beam shape and ambient magnetic field using the relativistic guiding-centre motion. Apart from parameters changing on long length scales compared with the gyro-radius, there is no assumption on the beam structure (wave-vector or field-strength variations). These equations are used to numerically solve the single wave-interaction energy gain for experimentally relevant magnetic field inhomogeneity length scales. We demonstrate that, at third harmonic in W7-X-relevant conditions, it is possible for electrons to gain energies up to 100 eV starting from a few eV – a condition necessary for the ionisation avalanche. However, the phase-space region where this is the case is very narrow. The region can be extended by using multiple beams with neighbouring resonances. Combining the resonance regions of multiple beams results in a much larger energy gain.

The results are analysed using the Hamiltonian phase-space structure. We analyse the impact of power, beam field inhomogeneity and plasma temperature on the averaged energy gain.

2. Electron cyclotron resonance extension to guiding-centre theory

In W7-X, several gyrotrons, each with a power output of 1 MW, are responsible for the breakdown process. The electromagnetic wave created by a single gyrotron is approximately of Gaussian profile. At the focus, the wave is spread out over a disc with a radius of the order of 2 cm (Hailer et al. 2003). The maximum wave magnetic field strength is of order $10^{-3}$ to $10^{-2}$ T. In SI units, the maximum wave electric field is ${1.1}\ {\rm MV}\ {\rm m}^{-1}$ for a 1 MW beam focused to a 2 cm beam waist. In this case, the wave introduces a small perturbation to the otherwise large background magnetic field. This permits usage of the guiding-centre approach.

A number of ECRH extensions of the guiding-centre theory have been considered previously (Grebogi, Kaufman & Littlejohn 1979; Rognlien 1983; Taylor et al. 1988; Ye & Kaufman 1992). Here, we outline the derivation of the equations of motion and wave–particle Hamiltonian using the Lagrangian formalism, paying particular attention to the role of the ambient field inhomogeneity.

2.1. Wave correction to guiding-centre Lagrangian

Particle motion in electromagnetic fields can be described using a Lagrangian formalism, with the relativistic phase-space Lagrangian given by

(2.1)\begin{equation} L(\boldsymbol{r}, \boldsymbol{p}, {\dot{\boldsymbol{r}}}, t) ={-}m \mathrm{c}^2\sqrt{1 + \frac{{\boldsymbol{p}} ^2}{m^2 \mathrm{c}^2}} + {\dot{\boldsymbol{r}}} \boldsymbol{\cdot} (q \boldsymbol{A}+\boldsymbol{p})- q \phi, \end{equation}

where $\boldsymbol {r}$ represents the particle position, $\boldsymbol {p}$ the momentum and $\phi$ and $\boldsymbol {A}$ are the scalar and vector potentials. By splitting the field term, $\boldsymbol {A}$, into a sum of a slowly varying background field, $\boldsymbol {A} _B$, and a wave field, $\boldsymbol {A} _w$, and similarly for the scalar potential $\phi = \phi _B + \tilde {\phi }_w$, the Lagrangian in (2.1) may be represented as a sum of a part corresponding to the waveless relativistic guiding-centre motion dependent on $\boldsymbol {A}_B, \phi_B$, $L_{{\rm GC}}$ and the wave part $L_{w}=q{\dot {\boldsymbol {r}}} \boldsymbol {\cdot } \boldsymbol {A}_w - q \tilde {\phi }_w$

(2.2)\begin{equation} L = L_{{\rm GC}} + L_{w}. \end{equation}

We consider the wave field in the form

(2.3)\begin{gather} \boldsymbol{A}_w(\boldsymbol{r}, t) = \frac{\boldsymbol{E}(\boldsymbol{r})}{\omega} \sin(\varphi(\boldsymbol{r}) - \omega t), \end{gather}

(2.4)\begin{gather}\tilde{\phi}_w = \phi_w(\boldsymbol{r}) \sin(\varphi(\boldsymbol{r})-\omega t), \end{gather}

where $\omega$ is the wave frequency. We assume that the wave amplitude, $\boldsymbol {E}(\boldsymbol {r})$, potential amplitude $\phi _w$ and the wave vector

(2.5)\begin{equation} \boldsymbol{k} (\boldsymbol{r}) \equiv \boldsymbol{\nabla}\varphi(\boldsymbol{r}). \end{equation}

vary slowly. We suppose that the wave field created by ${\boldsymbol {A}} _w, \tilde {\phi }_w$ is small, in the sense that it introduces only a small correction to the fast time-scale gyro-motion. The details of the ordering scheme can be found in Appendix A.

We ultimately want to describe wave–particle resonance on a time scale of many gyrations. An appropriate transformation of (2.1) into slowly varying variables has to be found. Without the wave it is appropriate to use the guiding-centre coordinates, corresponding to a transformation to the frame moving with the velocity $-(\boldsymbol {\nabla }\phi + \partial \boldsymbol {A}_B/\partial t) \boldsymbol {\times } \boldsymbol {B} / B^2$ in which the fast time-scale equations of motion reduce to

(2.6)\begin{equation} {\dot{\boldsymbol{p}}} \approx q \frac{\boldsymbol{p}}{m \gamma} \boldsymbol{\times} \boldsymbol{B}. \end{equation}

However, the guiding-centre coordinates are perturbed by high frequency fields. In Appendix C, we find that, in the presence of a wave, the correction to the guiding-centre velocity yielding the fast time scale equation of motion (2.6) is given by (C9) (which yields (C10)). This correction scales linearly with $|{{\boldsymbol {E}}}|$ for both resonant and non-resonant particles. In this work, we consider resonant particles for which the long term deviation from the unperturbed trajectories is expected to scale as $\sqrt {|{{\boldsymbol {E}}}|}$. This implies that, for small enough fields, the deviation significantly exceeds the coordinate correction. We therefore ignore this correction and rely on the unperturbed guiding-centre coordinates in the guiding-centre formulation. Furthermore, we verify the validity of this approximation against full orbit calculations.

The waveless guiding-centre part takes the form of Wimmel (1983), Littlejohn (1983) and Cary & Brizard (2009) as

(2.7)\begin{equation} L_{{\rm GC}} = \left[q \boldsymbol{A}_B(\boldsymbol{R}, t) + p_\parallel \hat{b}(\boldsymbol{R}, t)\right] \boldsymbol{\cdot} \dot{\boldsymbol{R}} + \frac{m \mu}{-q} \dot{\zeta} - m \mathrm{c}^2 \sqrt{1 + \frac{2 \mu B(\boldsymbol{R}, t)}{m \mathrm{c}^2} + \frac{p_\parallel^2}{m^2 \mathrm{c}^2}} - q \phi(\boldsymbol{R}, t), \end{equation}

where the dynamical variables are the position of the guiding centre $\boldsymbol {R}$, the momentum parallel to the magnetic field $p_\parallel$, the gyro-phase $\zeta$ and the magnetic moment $\mu$, which is related to the perpendicular momentum, $p_\perp$, through $\mu \equiv {p_{\perp }^2}/{2\,m B}$. The vector $\hat b$ denotes the field direction, $\hat {b} \equiv \boldsymbol {B}/B$. The particle position $\boldsymbol {r}$ differs from the $\zeta$-independent guiding centre $\boldsymbol {R}$ by the gyro-radius $\boldsymbol {\rho }$, i.e. $\boldsymbol {r} = \boldsymbol {R} + \boldsymbol {\rho }$.

We introduce a local coordinate system with $\hat {x} \equiv \boldsymbol {k}_\perp (\boldsymbol {R})/|\boldsymbol {k}_\perp |$ and $\hat {y} \equiv \hat {b} \times \hat {x}$. The perpendicular wave vector is given by $\boldsymbol {k}_\perp \equiv \boldsymbol {k} - \boldsymbol {k}_\parallel$, where the parallel wave vector is $\boldsymbol {k} _\parallel \equiv \boldsymbol {k} \boldsymbol {\cdot } \hat {b}\hat {b}$. Then, the wave part of the Lagrangian is

(2.8)\begin{equation} L_{w} = q {\dot{\boldsymbol{r}}} \boldsymbol{\cdot} \boldsymbol{A} _w - q \tilde{\phi}_w. \end{equation}

The wave-vector potential part of $L_w$ can be rewritten approximately as

(2.9)\begin{equation} q {\dot{\boldsymbol{r}}} \boldsymbol{\cdot} \boldsymbol{A} _w \approx q \frac{\dot{\boldsymbol{R}} + \dot{\boldsymbol{\rho}}}{\omega} \boldsymbol{\cdot} \left\{E_x(\boldsymbol{R}) \hat{x} +E_y(\boldsymbol{R}) \hat{y} + E_z(\boldsymbol{R}) \hat{z}\right\} \sin(\boldsymbol{\rho}\boldsymbol{\cdot} \boldsymbol{\nabla} \varphi(\boldsymbol{R}) + \varphi(\boldsymbol{R}) - \omega t), \end{equation}

and similarly for the wave scalar potential

(2.10)\begin{equation} \tilde{\phi}_w \approx \phi_w(\boldsymbol{R})\sin(\boldsymbol{\rho}\boldsymbol{\cdot} \boldsymbol{\nabla}\varphi(\boldsymbol{R}) + \varphi(\boldsymbol{R}) - \omega t). \end{equation}

Field strengths and the wave vector are approximated by the value at the guiding-centre position $\boldsymbol {R}$. The gyro-radius is given by

(2.11)\begin{equation} \boldsymbol{\rho} = \frac{p_\perp(\boldsymbol{R}, \mu, t)}{- q B(\boldsymbol{R})}(\cos(\zeta) \hat{x} + \sin(\zeta) \hat{y}), \end{equation}

and to lowest order in $\rho$, the particle velocity perpendicular to $\boldsymbol {B}$

(2.12)\begin{equation} \dot{\boldsymbol{\rho}} = \dot{\zeta}\frac{p_\perp(\boldsymbol{R}, \mu, t)}{q B(\boldsymbol{R})} (\sin(\zeta) \hat{x} - \cos(\zeta) \hat{y}). \end{equation}

The ordering in Appendix A allows us to use the gyro-radius and velocity at the guiding centre, where $B(\boldsymbol {r}) \approx B(\boldsymbol {R})$, even for the wave phase.

Equation (2.9) describes different types of interaction: longitudinal $X$-mode interaction with $E_x$, and transverse $X$-mode interaction with $E_y$, interaction due to the gyro-motion

(2.13)\begin{equation} \dot{\boldsymbol{\rho}}\boldsymbol{\cdot} {\boldsymbol{A}}_{w,i} \equiv \frac{\dot{\boldsymbol{\rho}}}{\omega} \boldsymbol{\cdot} E_i \hat{i} \sin({-}b(\boldsymbol{R}, \mu, t) \cos(\zeta) + \varphi(\boldsymbol{R}) - \omega t), \end{equation}

and the interaction due to the guiding-centre motion, which mainly comes from $O$-mode interaction

(2.14)\begin{equation} \dot{\boldsymbol{R}} \boldsymbol{\cdot} {\boldsymbol{A}}_{w,i} \equiv \frac{\dot{\boldsymbol{R}}}{\omega} \boldsymbol{\cdot} E_i \hat{i} \sin({-}b(\boldsymbol{R}, \mu, t) \cos(\zeta) + \varphi(\boldsymbol{R}) - \omega t). \end{equation}

The interpretation of $E_x$ being longitudinal is true if ${k}_{\parallel }=0$, otherwise the $E_x$ term could consist of some combination of longitudinal/transverse components. The variable

(2.15)\begin{equation} b(\boldsymbol{R}, \mu, t) \equiv \frac{p_{{\perp}}(\boldsymbol{R}, \mu, t)}{q B(\boldsymbol{R}, t)} |{\boldsymbol{k}_\perp(\boldsymbol{R})|}, \end{equation}

is the product of the perpendicular wave vector and gyro-radius, possibly with a sign from $q$. With these definitions, $L_w$ can be written as

(2.16)\begin{equation} L_{w} \approx{-}q \phi_w(\boldsymbol{R})\sin(\boldsymbol{\rho}\boldsymbol{\cdot} \boldsymbol{\nabla} \varphi(\boldsymbol{R}) + \varphi(\boldsymbol{R}) - \omega t) + \sum_{i=x,y,z}( q \dot{\boldsymbol{\rho}}\boldsymbol{\cdot} {\boldsymbol{A}}_{w,i} + q\dot{\boldsymbol{R}} \boldsymbol{\cdot} {\boldsymbol{A}}_{w,i}). \end{equation}

Equation (2.16) is expanded in terms of Bessel functions (see for e.g. Shafranov 1967, p. 145). Focusing on resonant waves, we introduce a new slow variable

(2.17)\begin{equation} \psi \equiv \zeta - \frac{\omega }{n}t, \end{equation}

which represents the phase shift between the phase of the wave and the phase of the particle gyro-motion. Here, $n$ is the integer corresponding to the resonance of interest. The frequency $\omega$ is assumed to be positive, and we work with negatively charged particles. Equations for positively charged particles can be obtained by letting $\omega < 0$. A time average of (2.16) removes all non-resonant terms from the expansion series, resulting in

(2.18)\begin{align} \dot{\zeta} W & \equiv \frac{1}{2 T} \int_{{-}T}^{T} \sum_{i=x,y,z} q \dot{\boldsymbol{\rho}}\boldsymbol{\cdot} {\boldsymbol{A}}_{w,i} \,{\rm d}t \nonumber\\ & \approx\dot{\zeta} \frac{p_\perp}{2 \omega B} \left\{\vphantom{\left(n\psi + \varphi(\boldsymbol{R}) - n\frac{\rm \pi}{2}\right)} E_x(\boldsymbol{R}) [{\rm J}_{n-1}(b) + {\rm J}_{n+1}(b)] \sin\left(n\psi + \varphi(\boldsymbol{R}) - n\frac{\rm \pi}{2}\right)\right.\nonumber\\ & \quad \left.\vphantom{\left(n\psi + \varphi(\boldsymbol{R}) - n\frac{\rm \pi}{2}\right)}-E_y(\boldsymbol{R}) [{\rm J}_{n-1}(b) - {\rm J}_{n+1}(b)] \cos\left(n\psi + \varphi(\boldsymbol{R}) - n\frac{\rm \pi}{2}\right) \right\}. \end{align}

Here, we can replace $\dot {\zeta }\approx \omega /n$ since $\dot {\psi }/ \omega$ is small and $\omega |{\boldsymbol {A}_w}| / c B \sim \mathcal {O}(1)$.

The time average of $\dot {\boldsymbol {R}} \boldsymbol {\cdot } {\boldsymbol {A}}_{w,i}$ is computed analogously, but can be further simplified because ${\dot {\boldsymbol {R}}}_\perp$ is negligible. Only the $E_z$ term is of importance and $\sum \dot {\boldsymbol {R}} \boldsymbol {\cdot } {\boldsymbol {A}}_{w,i} \approx \dot {\boldsymbol {R}} \boldsymbol {\cdot } {\boldsymbol {A}}_{w,z}$, resulting in

(2.19)\begin{equation} \dot{\boldsymbol{R}} \boldsymbol{\cdot} {\bar{\boldsymbol{A}}}_{w} \equiv \frac{1}{2T}\int_{{-}T}^{T}\sum_{i=x,y,z} \dot{\boldsymbol{R}} \boldsymbol{\cdot} {\boldsymbol{A}}_{w,i} \,{\rm d} t \approx \dot{\boldsymbol{R}}\boldsymbol{\cdot} \hat{b}\frac{E_z}{\omega}{\rm J}_n(b) \sin\left(n\psi + \varphi(\boldsymbol{R}) - n\frac{\rm \pi}{2}\right). \end{equation}

The time average of $\tilde {\phi }_w$ is analogous to the time average of $\dot {\boldsymbol {R}} \boldsymbol {\cdot } {\boldsymbol {A}}_{w,z}$ and yields

(2.20)\begin{equation} \bar{\phi}_w\equiv \frac{1}{2T}\int_{{-}T}^{T}\tilde{\phi}_w \,{\rm d} t \approx \phi_w {\rm J}_n(b) \sin\left(n\psi + \varphi(\boldsymbol{R}) - n\frac{\rm \pi}{2}\right). \end{equation}

A formal approach to removal of the non-resonant terms is presented in Appendix B.

Combining these results, the full Lagrangian in (2.8) in guiding-centre coordinates becomes

(2.21)\begin{equation} L = L_w + L_{{\rm GC}} ={-} H + \frac{m \mu}{-q} \dot{\psi}+\left[q \boldsymbol{A}_B(\boldsymbol{R}, t)+ q {\bar{\boldsymbol{A}}}_{w}(\boldsymbol{R}, \psi, \mu) + p_\parallel \hat{b}(\boldsymbol{R}, t)\right] \boldsymbol{\cdot} \dot{\boldsymbol{R}} , \end{equation}

where the guiding-centre Hamiltonian is given by

(2.22)\begin{equation} H = m \mathrm{c}^2 \sqrt{1 + \frac{2 \mu B}{m \mathrm{c}^2} + \frac{p_\parallel^2}{m^2 \mathrm{c}^2}} - \frac{\omega}{n}\left(\frac{m \mu}{-q} + W\right) + q \left[\phi+\bar{\phi}_w\right]. \end{equation}

This Hamiltonian reduces to the one obtained in Suvorov & Tokman (1988), Taylor et al. (1988), Farina & Pozzoli (1991) and Litvak et al. (1993) for the cases studied therein. The resonance number $n$ is governed by the resonance condition $-n q B / (m \gamma ) + {k}_{\parallel } v_{\parallel } - \omega = 0$. Note that, far away from the resonance, the ‘resonant’ terms given by (2.18) and (2.19) decrease and become comparable to the other neglected terms of the corresponding series. The term $({\omega }/{n})({m \mu }/{-q} + W)$ originates from changing to a rotating frame of reference when introducing $\psi$ in (2.17).

In the case of multiple waves with different $\boldsymbol {k}$ or $\boldsymbol {E}$, their contributions can be accounted for in an additive manner, i.e. $L = L_{{\rm GC}} + \sum _i L_{w}^{(i)}$. No new independent variables need to be introduced in this case. If they have different $\omega$ (by factor of $\mathbb {R}\setminus \mathbb {Q}$) no common rotating frame of reference exists and the Hamiltonian becomes time dependent.

2.2. Equations of motion

By varying the Lagrangian in (2.16) with respect to ${p_{\parallel }}, \boldsymbol {R}, \mu$, and $\psi$, the following equations of motion are obtained:

(2.23a)\begin{gather} \hat{b}\boldsymbol{\cdot} {\dot{\boldsymbol{R}}}= \frac{{p_{{\parallel}}}}{m \gamma} \end{gather}

(2.23b)\begin{gather}\dot {p_{{\parallel}}} \hat{b} = q {\dot{\boldsymbol{R}}} \boldsymbol{\times} \boldsymbol{B}^* + q \boldsymbol{E} - {p_{{\parallel}}} \frac{\partial\hat{b}}{\partial t} - \frac{\mu \boldsymbol{\nabla} B}{\gamma} +\frac{\omega}{n} \boldsymbol{\nabla} W - q \boldsymbol{\nabla} \bar{\phi}_w - \dot{\mu} q \frac{\partial {\bar{\boldsymbol{A}}}_{w}}{\partial\mu} - \dot{\psi} q \frac{\partial{\bar{\boldsymbol{A}}}_{w}}{\partial\psi} \end{gather}

(2.23c)\begin{gather}\dot{\psi}={-}\frac{\omega}{n} \left(1 - \frac{q}{m} \frac{\partial W}{\partial \mu} + \frac{q^2 n}{ m \omega} \frac{\partial \bar{\phi}_w}{\partial \mu}\right) - \frac{q B}{m \gamma} + \frac{q^2}{m} {\dot{\boldsymbol{R}}} \boldsymbol{\cdot} \frac{\partial{\bar{\boldsymbol{A}}}_{w}}{\partial \mu} \end{gather}

(2.23d)\begin{gather}\dot{\mu}={-}\frac{q \omega}{m n} \frac{\partial W}{\partial \psi} + \frac{q^2}{m}\frac{\partial\bar{\phi}_w}{\partial \psi}- \frac{q^2}{m}{\dot{\boldsymbol{R}}} \boldsymbol{\cdot} \frac{\partial{\bar{\boldsymbol{A}}}_{w}}{\partial\psi}, \end{gather}

where the effective magnetic field is

(2.24)\begin{equation} \boldsymbol{B}^* \equiv \boldsymbol{B} + \frac{{p_{{\parallel}}}}{q} \boldsymbol{\nabla}\boldsymbol{\times} \hat{b} + \boldsymbol{\nabla}\boldsymbol{\times} {\bar{\boldsymbol{A}}}_{w}. \end{equation}

These equations of motion reduce to, for example, the ones in Litvak et al. (1993) for the case studied there.

Substituting $\dot {\psi }$ and $\dot {\mu }$ in (2.23b) it is simplified and takes the form

(2.25)\begin{equation} \dot{{p_{{\parallel}}}}\hat{b} = q {\dot{\boldsymbol{R}}} \boldsymbol{\times} \boldsymbol{B}^* + \boldsymbol{F}, \end{equation}

where the effective force is

(2.26)\begin{align} \boldsymbol{F} & \equiv q \boldsymbol{E} - {p_{{\parallel}}} \frac{\partial\hat{b}}{\partial t} - \frac{\mu}{\gamma} \boldsymbol{\nabla} B + \frac{\omega}{n}\boldsymbol{\nabla} W - q \boldsymbol{\nabla} \bar{\phi}_w\nonumber\\ & \quad +q \left(\frac{q B}{m \gamma} + \frac{\omega}{n}\right) \frac{\partial{\bar{\boldsymbol{A}}}_{w}}{\partial\psi} +\frac{q^2\omega}{m n} \left(\frac{\partial W}{\partial \psi}\frac{\partial {\bar{\boldsymbol{A}}}_{w}}{\partial \mu} - \frac{\partial W}{\partial \mu}\frac{\partial{\bar{\boldsymbol{A}}}_{w}}{\partial\psi}\right). \end{align}

We used

(2.27)\begin{equation} \left({\dot{\boldsymbol{R}}} \boldsymbol{\cdot} \frac{\partial{\bar{\boldsymbol{A}}}_{w}}{\partial\psi}\right) \frac{\partial{\bar{\boldsymbol{A}}}_{w}}{\partial\mu} - \left({\dot{\boldsymbol{R}}} \boldsymbol{\cdot} \frac{\partial {\bar{\boldsymbol{A}}}_{w}}{\partial\mu}\right) \frac{\partial{\bar{\boldsymbol{A}}}_{w}}{\partial\psi} = {\dot{\boldsymbol{R}}} \boldsymbol{\times} \left(\frac{\partial{\bar{\boldsymbol{A}}}_{w}}{\partial\mu} \boldsymbol{\times} \frac{\partial{\bar{\boldsymbol{A}}}_{w}}{\partial\psi}\right)= \boldsymbol{0}, \end{equation}

since ${\partial {\bar {\boldsymbol {A}}}_{w}}/{\partial \mu }$ and ${\partial {\bar {\boldsymbol {A}}}_{w}}/{\partial \psi }$ are parallel.

3. The X3 startup in the W7-X stellarator

Startup at the third harmonic is prohibitively difficult in homogeneous magnetic fields, due to a very week interaction. Farina (2018) demonstrated that, for slow particles, the nonlinear energy gain is well below 1 eV, which is not enough to support startup. In this section, we discuss numerical solutions of the equations of motion for electrons. These simulations account for both the wave field and the background magnetic field inhomogeneity. They show that the energy gain can be much larger than in a homogeneous background magnetic field.

For these numerical solutions, we use a background field structure relevant to a reduced B-field W7-X configuration. This field can be represented approximately by

(3.1)\begin{equation} \boldsymbol{A}_B = \left[B_0 + B_1 \cos\left(\frac{2 {\rm \pi}}{L}z - \alpha\right)\right] x \hat{y}, \end{equation}

and the electron trajectories lie approximately on $x=y=0$ (since the cross-field drifts are small during the time of one beam interaction). A typical mirror ratio in W7-X is of order $|B_{\max } - B_{\min }|/|B_{\min }| \approx 0.1$. We therefore let $B_1 = 0.069004\ {\rm T}$ and $B_0$ is varied slightly around $B(z=0) = {1.6671}\ {\rm T}$ depending on the exact desired location of the resonance within the structure given by (3.1).

The wave field in W7-X is created by 140 GHz gyrotrons. Such a gyrotron is assumed to create a beam with a Gaussian profile with elliptic polarisation and plane-wave phase. That is, the wave field is

(3.2)\begin{align} \omega \boldsymbol{A}_w & ={-}E_y \exp\left\{-\frac{r^2}{w^2}\right\}\hat{y} \cos(\boldsymbol{k} \boldsymbol{\cdot} \boldsymbol{r} - \omega t) \nonumber\\ & \quad + E_{x'}\exp\left\{-\frac{r^2}{w^2}\right\} (\hat{y} \boldsymbol{\times} \hat{k}) \sin(\boldsymbol{k} \boldsymbol{\cdot} \boldsymbol{r} - \omega t), \end{align}

where $r$ here is the radial distance from the centre axis of the beam, i.e. $r^2 = y^2 + (-x {k}_{\parallel }/k + z {k}_{\perp }/k)^2$ and $w = 2$ cm (Hailer et al. 2003). In a vacuum, the total field must be such that $\boldsymbol {\nabla }\boldsymbol {\cdot } \boldsymbol {E} = 0$. The Gaussian profile (3.2) has a small non-zero divergence

(3.3)\begin{equation} \boldsymbol{\nabla}\boldsymbol{\cdot} \boldsymbol{E} ={-}2 \frac{\partial \boldsymbol{A}_w}{\partial t} \boldsymbol{\cdot} \left(\frac{y}{w^2}\hat{y} + \frac{({-}x {k}_{{\parallel}}/k + z {k}_{{\perp}}/k)}{w^2}\hat{y} \boldsymbol{\times} \hat{k}\right), \end{equation}

and must be compensated with the scalar potential. This potential enters the equations of motion at one higher order in ${k}_{\perp } \rho$ than the field created by $\boldsymbol {A}_w$ and is therefore ignored (compare (2.20) and (2.18) where $b = {k}_{\perp } \rho$).

Expanding the Bessel functions in (2.23a) to (2.23d) in ${k}_{\perp } \rho \ll 1$, the wave term becomes

(3.4)\begin{equation} \frac{\omega}{n} W = m \mathrm{c}^2\left(\frac{\mu B}{m \mathrm{c}^2}\right)^{n/2} \epsilon(z) \sin(n \psi + {k}_{{\parallel}} z), \end{equation}

where the interaction parameter $\epsilon$ is

(3.5)\begin{equation} \epsilon = \begin{cases} \dfrac{m {k}_{{\perp}} \mathrm{c}}{2 \mathrm{e} B} \dfrac{E_-}{2 \mathrm{c} B} & \mathrm{for\ X2}\\[11pt] \mathrm{c} {k}_{{\perp}}^2 \dfrac{m^2}{9 \mathrm{e}^2 B^2} \dfrac{3 \sqrt{2} E_-}{8 B} & \mathrm{for\ X3}, \end{cases} \end{equation}

where

(3.6)\begin{equation} E_-\equiv E_{x'}(\hat{y} \boldsymbol{\times} \hat{k})\boldsymbol{\cdot}\hat{x} - E_y. \end{equation}

The other terms are of higher order. Then, the equations of motion to relevant order take the form

(3.7a)\begin{equation} \dot{z} = \frac{{p_{{\parallel}}}}{m \gamma} \end{equation}

(3.7b)\begin{align} \dot{{p_{{\parallel}}}} & ={-}\frac{\mu}{\gamma} \frac{{\rm d}B}{{\rm d}z} + \mu B \left(\frac{\mu B}{m \mathrm{c}^2}\right)^{{n}/{2}-1} \frac{{\rm d}\epsilon(z)}{{\rm d}z} \sin(n \psi + {k}_{{\parallel}} z)\nonumber\\ & \quad +{k}_{{\parallel}} \mu B \left(\frac{\mu B}{m \mathrm{c}^2}\right)^{{n}/{2}-1}\epsilon(z) \cos(n \psi + {k}_{{\parallel}} z) \end{align}

(3.7c)\begin{gather} \dot{\psi}= \frac{\mathrm{e} B}{m \gamma} - \frac{\omega}{n} - \frac{n \mathrm{e} B}{2 m} \left(\frac{\mu B}{m \mathrm{c}^2}\right)^{{n}/{2}-1} \epsilon(z) \sin(n \psi + {k}_{{\parallel}} z) \end{gather}

(3.7d)\begin{gather}\dot{\mu} = n \mathrm{e} \mathrm{c}^2 \left(\frac{\mu B}{m \mathrm{c}^2}\right)^{n/2} \epsilon(z) \cos(n \psi + {k}_{{\parallel}} z), \end{gather}

where the cross-field drifts are ignored together with terms containing $({{\rm d}B}/{{\rm d}z}) \epsilon (z)$.

This system is solved numerically using Runge–Kutta–Fehlberg 4,5 explicit scheme from the GNU science library (2009) with a fixed time step of $10 m/ \mathrm{e} B(z=0)$. This numerical scheme ensures conservation of the Hamiltonian to 12 decimal places (i.e. approximately ${0.5}\ {\mathrm {\mu }}{\rm eV}$). The evaluation is stopped when either $t \mathrm {e} B(z=0)/m = 4\times 10^{6}$ or when the particle leaves the beam, i.e. $|{z / w}| > 2$ for an X3 single beam, $|{z / w}| > 4$ for two X3 beams and $|{z/ w}| > 3$ for X2. This yields a single interaction energy gain.

Figure 1 (solid curves) shows an example trajectory of an electron interacting with the beam once. The perpendicular energy evolution is shown in the top graph together with the $z$ motion in the bottom graph. In this case, the cold resonance is located at $z={-1.32}\ {\rm cm}$ with $\alpha = 0.013538$ and the magnetic field is $B_0 = 1.598133$ T. The corresponding field inhomogeneity length scale is $B/\hat {b}\boldsymbol {\cdot } \boldsymbol {\nabla } B = 2045$ m. The beam centre is always at $z=0$ (see (3.2)). The initial perpendicular particle energy is 1.03 eV, whilst the initial parallel energy is very small at 0.25 meV. The initial phase of the particle is chosen to maximise the energy gain. The corresponding unperturbed trajectory is plotted as a dashed curve. The energy gain of the particle with the same initial conditions but in homogeneous magnetic field is also shown with the dashed–dotted curve. In this case, $B_0 = 1.667107$ T and $B_1 = 0$. We observe that the interaction is extended considerably in the inhomogeneous case, which results in much higher excursions during nonlinear trapping in the wave field and approximately a doubling in the single interaction energy gain. Note that this particle turns around near $z=0$ due to the mirror force. This particle has a very slow initial parallel velocity of $0.1 v_{th, 300\ {\rm K}}$.

Figure 1. Example electron trajectory in X3 wave (solid curves). The dash–dotted curve shows the same trajectory in a homogeneous case. The dashed curve represents the particle trajectory in the absence of the wave, highlighting that the bounce is caused by the increase in magnetic moment. These trajectories are for very slow parallel velocities of $0.1 v_{th, 300\ {\rm K}}$. A trajectory of a particle from inside the 80 eV contour of figure 2 is shown with the red dotted curve.

We also show a typical orbit for high energy gain at higher parallel velocity in dotted red. Because the beam travel time is shorter, the interaction strength must be stronger for a significant interaction. Because the interaction strength scales with $v_{\perp }^3$, see (3.7d), increasing initial $v_{\perp }$ achieves just that. The interaction is no longer several energy excursions but an interaction with an approximately stationary phase. The interaction is significantly extended compared with the homogeneous case because $\gamma$ and $B$ change in conjunction.

Figure 2 shows contours (in eV) of the single interaction energy gain for electrons with various initial energies and pitch angles. The energy gain is maximised over the initial phase. The inhomogeneous background field is the same as in figure 1 ($B_0 = 1.6671$). Positive parallel energy corresponds to electrons moving toward increasing $B$. The maximised energy gain in an analogous homogeneous situation is shown in figure 3. These calculations show that a small inhomogeneity not only increases the maximum gain to around 80 eV, but also significantly extends the phase-space region over which efficient interaction takes place. A factor of $4$ increase in energy gain can alternatively be achieved by a 10–100 times increase of the ECRH beam power if the ambient magnetic field is homogeneous. This is because the X3 interaction scales between $\sqrt {E_-}\sim P^{1/4}$ and $E_-\sim P^{1/2}$ (see (4.9)). However, for electrons, where the stationary phase is the major interaction, energy gain scales as $E_-\sim P^{1/2}$ and 16 times power would be required to achieve an energy increase of a factor 4.

Figure 2. Contours of the energy gain (eV), maximised over initial phase for a range parallel and perpendicular initial energy of the particles in an X3 wave. Inhomogeneous magnetic field as per (3.1) with $B_0 = 1.599343$ T, $B_1 = 0.069004$ T and $\alpha = 0.190400$. The 1 MW beam is assumed to have a Gaussian profile with 2 cm width.

Figure 3. Same as figure 2, but homogeneous field $B_0 = 1.667078$ T so resonance is fulfilled at 24 eV.

Note, however, that these results are quantitatively sensitive to the location of the resonance. They merely highlight a significant effect of the inhomogeneity on the energy gain. More general results are presented in the next sections.

The energy gain averaged over the initial phase is lower. It is shown in figure 4. The red contour corresponds to a gain of 13.6 eV, which is necessary for maintaining the ionisation avalanche process. However, this phase-space region is very narrow, in particular in $v_{\parallel }$. Because secondary electrons are distributed uniformly over the pitch angles during ionisation avalanche it is unlikely that such a beam can maintain ionisation.

Figure 4. Contours of the mean energy gain (eV), averaged over initial phase for the parameters of figure 2.

Another feature of the 13.6 eV contour in figure 4 is that its minimal initial electron energy is above 13.6 eV, i.e. an electron needs to already have more than 13.6 eV in order to gain significant energy. This feature (the location of the 13.6 eV phase-space contour), however, depends on the inhomogeneity length scale. This is discussed for in the next section (see figure 14).

3.1. Configuration with multiple beams

The energy gain required for the breakdown process during startup is approximately 13.6 eV. Robust breakdown requires that a significant fraction of particles are accelerated from below 13.6 eV to tens of eV during the interaction. As shown in the previous section, this is difficult to achieve with a single beam set-up. In the presence of multiple beams, an overlap of multiple resonances can lead to significantly larger overall gains. We consider such a scenario in this section.

The second beam is set up analogously to the first one with an extra shift along the field line, $z_0$,

(3.8)\begin{equation} \boldsymbol{E}^{(2)}(0,0,z) = E_0 \exp\left({-}k_{{\perp},2}^2 \frac{(z-z_0)^2}{k^2 w^2}\right). \end{equation}

The relative phase shift is generally important. Due to the chaotic nature of the slow phase drifts of the gyrotrons, we expect that all phase shifts are present during a startup scenario. The relative phase shift is indirectly controlled through $z_0$ and difference in ${k}_{\parallel }$. Therefore, we ignore the explicit relative phase shift to reduce the number of optimisation variables.

Figures 5 and 6 demonstrate the results of an optimisation procedure. In figure 5 the maximum single interaction energy gain is optimised, whereas in figure 6 optimisation is of energy gain maximised over initial $\psi$ and then averaged over initial $v_{\parallel }$ and $v_{\perp }$. Both results are in the presence of two beams. The conditions are similar to those of figure 2, with the optimisation parameters being $B_0$, $\alpha$ (i.e. $\hat {b}\boldsymbol {\cdot } \boldsymbol {\nabla } B / B$), ${k}_{\parallel }{}_1$, ${k}_{\parallel }{}_2$ and the second beam position $z_0$. The Nealder–Mead method with 50 random starting points and 250 000 trajectories per step is used.

Figure 5. Contours of maximum energy gain in a case of 2 X3 beams with injection geometry optimised for maximum energy gain.

Figure 6. Same as figure 5 but optimisation for the average maximum energy gain in $E_\perp \times E_\parallel \in [0, {13.6}\ {\rm eV}]\times [0, {4}\ {\rm eV}]$.

The first optimisation maximises the energy gain in $\mu B_0 \in [0, {13.6}\ {\rm eV}]$, and ${m v_{\parallel }^2}/{2} \in [0, {4}\ {\rm eV}]$. The best result is ${{k}_{\parallel } \mathrm{c}}/{\omega } = 0.243/3$, ${k_{\parallel,2} \mathrm{c}}/{\omega } = 0.214/3$, $1 - {m \omega }/{3 e B} = -5.28 / 511\,000$, $z_0 = -0.826 w$, $\alpha = 2.90$. The results are shown in figure 5. The maximum energy gain is ${\sim }{200}\ {\rm eV}$, which is approximately twice as high as that in the case of one beam. Moreover, the initial energy required for reaching 13.6 eV is now lower than 13.6 eV and the initial $v_{\parallel }$ range is increased significantly.

The second optimisation optimises energy gain maximised over initial $\psi$ and then averaged over initial $v_{\parallel }$ and $v_{\perp }$ in the phase-space area $\mu B_0\in [0,{13.6}\ {\rm eV}]$, and ${m v_{\parallel }^2}/{2} \in [0,{4}\ {\rm eV}]$. The best result is ${{k}_{\parallel } \mathrm{c}}/{\omega } = 0.0259/3$, ${k_{\parallel,2} \mathrm{c}}/{\omega } = 0.0193/3$, $1 - {m \omega }/{3 e B} = -0.8125 / 511\,000$, $z_0 = 0.741$, $\alpha = 0.0775$. The maximum energy gain is shown in figure 6. Although it was not possible to achieve mean energy gains comparable to those from the second harmonic interaction, which is several hundreds of eVs (see figure 8), the optimisation procedure has extended the range of $v_{\parallel }$ for which high gain is expected by at least an order of magnitude. Kinetic modelling of the ionisation avalanche is required in order to answer the question as to whether such double beam X3 particle energisation is efficient to sustain startup.

3.2. Effect of magnetic field inhomogeneity on X2 interaction

The X2 ECRH startup is routinely performed at W7-X. In this section, we look into effects of inhomogeneity on X2 interaction. In the second-harmonic case, the cold resonance is at 2.5 T for a 140 GHz W7-X gyrotron.

Once again, the equations (3.7) are solved numerically, with $n=2$ this time. Figures 7 and 8 show the mean (over initial gyro-phase) single interaction energy gain for the homogeneous and inhomogeneous cases, respectively. For the homogeneous case we set $\omega = 2 {\rm \pi}\times {140}\ {\rm GHz}$, and the magnetic field strength such that the resonance energy is $\mu B = {186.5}\ {\rm eV}$. For the inhomogeneous case, we set $B_1 = {0.1}\ {\rm T}$ and $B_0 \approx {2.5}\ {\rm T}$, so that the $\mu B = {186.5}\ {\rm eV}$ resonance is at $z = 0$. The inhomogeneity at $z=0$ is $B/\hat {b} \boldsymbol {\cdot } \boldsymbol {\nabla } B = 174$ m. We let ${k}_{\parallel } = 0$.

Figure 7. Contours of the energy gain (eV), averaged over initial phase, X2 homogeneous background field ($B_1 = 0$).

Figure 8. Same as figure 7, but with inhomogeneous magnetic field ($\alpha = {{\rm \pi} }/{2}, B_1 = {0.1}\ {\rm T}$).

As expected, the gain in both cases is much greater than for X3. In addition, the $v_{||}$ range is much broader as well: note the difference in $x$-axis scale between figures 4 and 8. A relatively strong effect of inhomogeneity on X2 mean energy gain is observed for low $v_{\parallel }$, where the nonlinear interaction is also extended considerably. The affected phase-space region is quite narrow for typical plasmas after startup, but quite large when considering low temperature plasma or breakdown. We therefore expect at least a small improvement of X2 interaction by the inhomogeneity.

These results are analysed in the next sections from the point of view of the Hamiltonian phase-space structure.

4. Phase-space structure

In the previous section we demonstrated that the ambient $B$-field inhomogeneity has a significant effect on the resonant electron dynamics and the energy gain of electrons. We will use the known weakly relativistic Hamiltonian expression to analyse these results.

The Hamiltonian (2.22) can be transformed and expanded into a weakly relativistic form to

(4.1)\begin{equation} \frac{H}{mc^2} = 1 + \varDelta_n \varPhi - (1-\xi^2)\frac{\varPhi^2}{2} + \varPhi^{n/2} \epsilon_* \cos(\chi) + \frac{P^2}{2} - \frac{P^4}{8}, \end{equation}

for the $X$ mode (Farina & Pozzoli 1991; Litvak et al. 1993; Farina 2018), where the normalised perpendicular energy $\varPhi = n P_\chi (-q B)/ m^2c^2$ is introduced together with the normalised canonical $Z$ momentum $P = P_Z / m c$. The canonical momentum $P_\chi$ is associated with the gyro-motion through

(4.2)\begin{equation} n P_\chi \equiv{-}\frac{m}{q} \mu, \end{equation}

and the canonical momentum $P_Z$ is associated with the parallel motion

(4.3)\begin{equation} P_Z \equiv p_\parallel{-} {k}_{{\parallel}} P_\chi + q\frac{E_z}{\omega} {\rm J}_n(b_z) \sin(\chi) + q \boldsymbol{A} \boldsymbol{\cdot} \hat{b}. \end{equation}

The wave-phase coordinate is $\chi = n \psi + \varphi (\boldsymbol {R}) - n ({{\rm \pi} }/{2})$. These canonical coordinates were introduced by the use of the generating function

(4.4)\begin{equation} F_2 = P_\chi \left(n \psi + \varphi(\boldsymbol{R}) - n \frac{\rm \pi}{2}\right) + \boldsymbol{R} \boldsymbol{\cdot} \hat{b} P_Z. \end{equation}

Resonant particles typically experience quick quasi-periodic motion in the ($\chi, P_\chi$) plane. The structure of the corresponding Hamiltonian contours provides important insights into the particle dynamics (see e.g. Neishtadt & Timofeev 1987; Farina & Pozzoli 1991; Kotel'Nikov & Stupakov 1991; Litvak et al. 1993). The shape of a given Hamiltonian contour in the ($\chi, P_\chi$) plane is set by the three remaining ‘slower changing’ parameters of (4.1). The first parameter is the relativistic frequency shift

(4.5)\begin{equation} \varDelta_n = 1 - \frac{\omega}{n \varOmega_0} - \frac{P_Z^2}{2 m^2 \mathrm{c}^2} + \frac{{k}_{{\parallel}} \mathrm{c}}{n \varOmega_0} \frac{P_Z}{m c}, \end{equation}

where $\varOmega _0 = {\mathrm {e} B}/{m}$ is the non-relativistic gyro-frequency. The second parameter characterises the Doppler shift $\xi _n = {k}_{\parallel } \mathrm{c} / n \varOmega _0$. The third parameter is the interaction strength as a function of the field strengths, $\epsilon _* = \epsilon (E_x, E_y)$, which is given by (3.5). It is assumed that $\epsilon >0$. If $\epsilon <0$, a redefinition of $\epsilon \mapsto - \epsilon$ and $\chi \mapsto \chi + {\rm \pi}$ restores the Hamiltonian to its form with $\epsilon >0$.

The contours of the Hamiltonian in (2.22) for typical W7-X parameters at the peak wave field are shown in figure 9 with the solid curves. Numerical solutions to the full orbit equations of motion from (2.1) are shown in dotted green. These solutions include fast time-scale wave effects, however, as discussed earlier, these effects have little effect on the general character of the resonant dynamics. The parameters of the X2 case are given by a plane wave with $E_y = {1.46\times 10^{-3}} B \mathrm{c}$, $E_x = E_z = 0$, ${k}_{\parallel } \mathrm{c} / \omega = 0$, $k \mathrm{c} / \omega = 1$, in a homogeneous magnetic field with the frequency relation $\omega = 2 \mathrm {e} B / m$. This corresponds to the maximum field created by a 1 MW gyrotron with a radius of 2 cm aimed at 2.5 T. The parameters of the X3 case are given by $E_y = {2\times 10^{-3}}B \mathrm{c}$, $E_x = E_z = 0$, ${k}_{\parallel } \mathrm{c} / \omega = 0.25$, ${k}_{\perp } \mathrm{c} / \omega = 0.968$, $\omega = 2.9999 \mathrm {e} B / m$. This corresponds to the maximum field created by a 1 MW gyrotron with a radius of 2 cm aimed at 1.8 T (or slightly lower than maximum electric field at 1.7 T).

Figure 9. Hamiltonian contours in X2 and X3. Centre of resonance in dash dotted, trapped region in dashed. Full solution to (2.1) in green; (a) X2 and (b) X3.

The trapped region can be determined analytically through singular points, see for e.g. Lichtenberg & Lieberman (2013), Farina & Pozzoli (1991), Litvak et al. (1993) and references therein. The second harmonic has a trapped region inside

(4.6)\begin{equation} \mu \in [\mu_{c} - \mu_{{\rm exc}}, \mu_{c} + \mu_{{\rm exc}}], \end{equation}

where the energy excursions are given by

(4.7)\begin{equation} \frac{\mu_{{\rm exc}} B}{m \mathrm{c}^2} = \begin{cases} \dfrac{2 \sqrt{\epsilon_{X2} \varDelta_2 }}{1 - \xi_2^2} & \dfrac{\varDelta_2 - \epsilon_{X2}}{1 - \xi_2^2} > 0\\[11pt] \dfrac{\mu_{c} B}{m \mathrm{c}^2} & \dfrac{\varDelta_2 - \epsilon_{X2}}{1 - \xi_2^2} < 0, \end{cases} \end{equation}

and centre by

(4.8)\begin{equation} \frac{\mu_{c} B}{m \mathrm{c}^2} = \frac{\varDelta_2 + \epsilon_{X2}}{1 - \xi_2^2}. \end{equation}

These analytical trapped regions are shown with dashed lines in figure 9.

The third-harmonic Hamiltonian is not a polynomial in $P_\chi$, so to work out the trapped region we work with $\beta ^2 \equiv 2 \varPhi$ instead. Centre of resonance is found normally. To find the maximum excursions we expand the Hamiltonian in perpendicular velocity around the centre to avoid solving a fourth degree polynomial. This yields the trapped region as

(4.9)\begin{equation} \frac{\mu B}{m \mathrm{c}^2} \in \left[\frac{1}{2}(\beta_c - \beta_{{\rm exc}})^2, \frac{1}{2}(\beta_c + \beta_{{\rm exc}})^2\right], \end{equation}

with

(4.10)\begin{equation} \beta_{{\rm exc}} = \sqrt{\frac{H_{{\rm sep}} - {H}|_{\beta=\beta_c,\chi=0}}{\dfrac{1}{2}\left.\dfrac{\partial^2H}{\partial\beta^{2}}\right|_{\beta=\beta_c,\chi=0} } }= \frac{\sqrt{q^{3/2}\epsilon_{X3}}}{\sqrt{2}|{1-\xi_3^2}|\sqrt{q + 3 \sqrt{q}\epsilon_{X3}}}, \end{equation}

and centre of resonance

(4.11)\begin{equation} \beta_c = \frac{3 \epsilon_{X3} + \sqrt{q}}{2 \sqrt{2}(1-\xi_3^2)}, \end{equation}

where

(4.12)\begin{equation} q = 9\epsilon_{X3}^2 + 16 \varDelta_3 (1-\xi_3^2), \end{equation}

and $H_{{\rm sep}}$ is the value of the Hamiltonian on the separatrix. These regions are shown in dashed lines of figure 9.

Figure 10 shows the width of the resonance as a function of $\varDelta _n$, which can be interpreted approximately as the “perpendicular relativistic Lorentz factor” $\gamma _\perp \equiv \sqrt {1+2 \varPhi }$ yielding perfect resonance. We use an electric field strength corresponding to the maximum field from a 1 MW beam spread over a disc with radius 2 cm. For X2 this is $E_-/\mathrm{c} B = {1.46\times 10^{-3}}$ (with $B = {2.5}\ {\rm T}$) whereas for X3 it corresponds to $E_-/\mathrm{c} B \approx {2.15\times 10^{-3}}$ (with $B = {1.7}\ {\rm T}$). A small parallel component of the wave vector is introduced, ${k}_{\parallel } \mathrm{c} / \omega = \sin (10^\circ )$ for both X2 and X3 cases, although ${k}_{\parallel }$ only plays a minor role until it approaches $\omega / \mathrm{c}$ (almost full parallel propagation). The $\Delta v_{\parallel }$ axis is calculated assuming $\varDelta _n=\xi _n P$ and is only valid for small $P$ as $\varDelta _n$ is also dependent on $P^2$. Figure 10 demonstrates a large resonance width for X2 (this is typical for a broad range of startup-relevant parameters). The resonance region reaches all the way to low initial particle energies and therefore no special conditions are necessary for X2 startup.

Figure 10. Resonance regions for resonance condition fulfilled at different perpendicular energies; X2 (a) and X3 (b).

For X3, the resonance width is much more narrow, and to sustain ionisation a careful selection of inhomogeneous ambient magnetic field and beam properties is required.

This is further evident from consideration of the resonance width as a function of power. Figure 11 shows the dependence of the resonance regions ((4.6) and (4.9)) on the beam power assuming W7-X magnetic field strengths and $\varDelta _n = {2\times 10^{-5}}$. The relation to power and electric field strength is taken as

(4.13)\begin{equation} E_{wave} = 2 \sqrt{\frac{P \times {376.73}{\varOmega}}{4 {\rm \pi}{\rm cm}^{2}}}. \end{equation}

Note that, in the case of X2, the trapped region scales differently with power depending on the sign of $({\varDelta _2 - \epsilon _{X2}})/({1 - \xi _2^2})$ (4.6). For small powers, the width scales as $P^{1/4}$, and for higher powers (in relation to $\varDelta _2$) it scales as $P^{1/2}$. Due to our choice of low $\varDelta _2$, only the $P^{1/2}$ is visible in figure 11.

Figure 11. Resonance regions for different power; X2 (a) and X3 (b).

With the analysis of the general differences between X2 and X3 introduced (based essentially on the homogeneous picture), we proceed to the analysis of our numerical results for the inhomogeneous cases presented in the previous section. We first consider X2 calculations presented in figures 7 and 8. These figures show that a significantly large phase space exhibits very efficient energy gain in the inhomogeneous case, specifically in low $v_{\parallel }$ region.

The value of the Hamiltonian is always conserved on particle trajectories, but the shape of the Hamiltonian contours in ($\chi, P_\chi$) plane evolves with the passage of the particle through higher field strengths. The character of the particle trajectory changes accordingly: a resonant particle becomes nonlinearly trapped in the wave field and will follow the closed contours instead. This occurs when the trapping region reaches the electron phase-space position. As the particle continues toward the weaker wave field the closed contours disappear, leaving the particle with new values of $P_\chi, P_Z$. This is demonstrated with a solid line in figure 1, where a sequence of spikes on the energy curve corresponds to quasi-periodic motion of the particle around the resonance.

Equation (4.1) has only two solutions for $\varPhi$ outside the beam for fixed $H, P, \varDelta _n, \xi _n$. If these quantities are conserved before and after the interaction, as they are for the case of constant field and adiabatic interaction (see for e.g. Farina 2018), then the jump in orthogonal energy $\varPhi$ is two times the distance to the line $\varPhi = \varDelta _n/(1-\xi _n^2)$. The $B$ field inhomogeneity changes $\varDelta _n$ and $P$ during the interaction so that the interaction is a complicated four-dimensional motion.

If $B$ increases as the electron transverses the magnetic field line, the resonance centre $\varDelta _n$ will move upwards and ultimately allow large energy gain. This is easiest observed in a plane-wave interaction. In this case, adiabacity forces a new constant of the motion $\oint P_\chi \,{\rm d}\chi$. We show constant Hamiltonian intersected with this constant in $z, P_\chi, \chi$ space in figure 12. Here, we clearly see the resonance centre moving upwards in energy, and the particle trajectory follows. Movement of the resonance centre plays a favourable role, regardless of adiabatic interaction or not.

Figure 12. An X2 toy example of the adiabatic case, inhomogeneous magnetic field, plane wave. Hamiltonian surface (red) and particle trajectory (blue).

If $B$ decreases instead, the resonance centre $\varDelta _n$ will come from above, and allow for large excursions and energy gains. These are larger than the homogeneous case because there typically exists a more optimal $\varDelta _n$ along the path than in the homogeneous case.

The adiabatic interaction is only valid for very low parallel velocities. Seol et al. (2009) calculate the frequency of revolving the nonlinear trapped region. Dividing this frequency with the beam travel time (the second fastest time scale) we find

(4.14)\begin{equation} \frac{f_{{\rm nl}} w}{v_{{\parallel}}} \approx 5 \sqrt{\frac{P}{k_B T_\parallel} \frac{{\rm eV}}{{\rm MW}}}, \end{equation}

where $k_B T_\parallel$ is the parallel kinetic energy and $P$ the beam power. The ratio is independent of beam width, and large only for very very low parallel velocities.

It is the beam structure that breaks the adiabatic condition. The beam shaping creates a finite ${k}_{\parallel }$ component of the wave vector, which breaks the conservation of $P_Z$ even in the case of ${k}_{\parallel } = 0$ in the wave phase. Generally, a small kick in $P_Z$ is allowed due to shaping of $\epsilon _{X2}$ in $z$. This allows for a larger energy gain compared with the adiabatic case, even for a very small kick $\delta P$ in $P=P_Z/mc$. This can be understood by perturbing the Hamiltonian with a small kick $\delta P$ and equating it with a kick $\delta P_\chi$. We find the energy change by solving

(4.15)\begin{equation} \delta \varPhi \frac{\partial H}{\partial\varPhi} + \delta \varPhi^2 \frac{1}{2} \frac{\partial^2 H}{\partial\varPhi^2} + \delta P \frac{\partial H}{\partial P} = 0, \end{equation}

which results in (for relativistic $P_Z$ only inside $\varDelta _n$)

(4.16)\begin{align} \delta\varPhi& \approx\frac{\varDelta_n - (1-\xi_n^2)\varPhi\pm\sqrt{[\varDelta_n - (1-\xi_n^2)\varPhi]^2 + 2 (1-\xi_n^2) (P+\xi_n) \delta P}}{1-\xi_n^2} \nonumber\\ & \sim \frac{(P+\xi_n) \delta P}{(1-\xi_n^2)\varPhi - \varDelta_n},\quad |{\varDelta_n - (1-\xi_n^2)\varPhi}| \ll |{4(1-\xi_n^2)(P+\xi_n) \delta P}|, \end{align}

due to $P_Z$ no longer being conserved. This change in $P_Z, P_\chi$ is the difference between figure 7 and an adiabatic interaction.

The X3 interaction is much weaker than the X2, so that several excursions for single beam pass is only possible for electrons with very low transverse energy (meV). As the consequence, if the resonance centre moves from above, the particles do not typically complete a single revolution around the resonance centre before the electron is outside the trapped region. Therefore, we see the larger asymmetry with respect to $v_{\parallel }$ in figures 2 and 4 to 6 than in figure 7 and 8.

In this type of interaction, the particle motion in the phase space coincides with the trapped region evolution such that the phase $\chi$ is approximately constant. This kind of interaction is very efficient. This ‘stationary phase’ regime of the interaction is demonstrated with the dotted red curve in figure 1. It should not be confused with the stationary phase approximation of the liner wave–particle interaction, since several nonlinear effects cancel to allow for a long interaction time in our case.

The main reason for the enhanced energy gain in X3 is extended period of the stationary phase, where $B$ and $\gamma$ changes in conjunction to extend the resonance interaction. The particle is then allowed to travel ‘up’ in figure 10, because $\varDelta _3$ changes accordingly. Long stationary phase is characterised by $\dot {\psi } = 0$ and $\ddot {\psi } = 0$ which, for ${k}_{\parallel } = 0$, is equivalent to

(4.17)\begin{equation} \frac{-q B}{m \gamma^2} \dot{\gamma} = \frac{-q}{m \gamma} \frac{{\rm d}B}{{\rm d}z} v_{{\parallel}}. \end{equation}

Approximating $\dot {\gamma }\approx \dot {\varPhi } \sim \epsilon _{X3} \varPhi ^{3/2} \sim \epsilon _{X3}({v_{\perp }^3}/{\mathrm{c}^3})$ we find

(4.18)\begin{equation} \epsilon_{X3} \frac{v_{{\perp}}^3}{\mathrm{c}^3} \sim \frac{1}{B^2}\frac{\partial B}{\partial z} v_{{\parallel}}, \end{equation}

so that, for the longer magnetic field length scales, lower energies satisfy the stationary phase condition. This scaling approximately yields the shape of the contours of figures 2 and 4. For example, the 13.6 eV line in figure 2 that starts at 0 energy and goes to 90 eV perpendicular energy at 0.04 eV parallel energy follows the scaling (4.18).

Numerical solution to (3.7) shows that the nonlinear energy gain scales approximately as a square with the maximum of $\epsilon _{X3}$. This quadratic scaling is shown in figure 13. Here, the average energy gain is shown as function of maximum $\epsilon _{X3}$. The rest of the parameters match those of figure 2, except $\alpha ={\rm \pi} /10$. This scaling sets the scaling of the average energy gain to be linear in beam power for fixed beam width and is expected from linear wave absorption theory.

Figure 13. Average energy gain as function of interaction parameter $\epsilon _{X3}$ (3.5).

5. Optimal $B$ field inhomogeneity

The discussion in the previous section hints at the existence of an optimal $B$ field inhomogeneity length scale for every characteristic parallel velocity and therefore every plasma temperature. The inhomogeneity length scale dependence of the minimal initial energy required for a significant gain is investigated in figure 14. Orange, blue and green curves correspond to gains of 5, 13.6 and 25 eV, respectively. These calculations demonstrate that, when the inhomogeneity length scale varies, electrons with as low energy as 2–3 eV can be accelerated to above 13.6 eV by a 1 MW beam in W7-X-like conditions. We also observe that a smaller magnetic field slope is favourable for lower initial energies, in agreement with the predictions of (4.18).

Figure 14. Minimal initial energy of an electron gaining 5 eV (dashed curve), 13.6 eV (solid curve) and 25 eV (dash–dotted curve) as a function of $B$ gradient.

In figure 14 we have set $B_0$, so that resonance at $z=0$ is at 2.58 eV. This then creates a maximum energy gain of around 5 eV at constant field. Moving the centre of resonance at $z=0$ to arbitrary energy then yields an absolute maximum energy gain of approximately the width of resonance, given approximately by the separatrix width, see figure 10. Thus, we could gain 13.6 eV at no magnetic field gradient. The cost is that the first particle that gains a substantial amount of energy must have an initial energy of approximately 10 eV, see figure 3. Therefore, resonance at around 2 eV is chosen as this is a typical low energy during the ionisation avalanche.

Figure 15 shows the effect of the inhomogeneity on the average energy gain from a single beam pass for a Maxwellian population of incoming particles. The varied parameters are the $B$ field gradient length scale and the plasma temperature. Because the beam typically propagates across field lines with different magnetic field strengths, for each magnetic field gradient we maximise over different magnetic field strengths at $z=0$.

Figure 15. Average energy gained in meV by electrons passing the beam once at different magnetic field inhomogeneities. The average energy gain was maximised over magnetic field strengths near cold resonance, motivated by that the beam cuts different field lines with slightly different field strengths at beam centre.

The contours show average energy gain in meV. Note that the maximum energy gain (reaching 100 eV) is much larger than the average, since only the narrow region of the phase space experiences the nonlinear enhancement from the inhomogeneity.

The gradients chosen are those approximately available to W7-X with a 10 % mirror ratio. Note that the maximum energy gained is not fully correlated with the average energy gain. Increasing the inhomogeneity length scale also forces particles to bounce, particularly with low $v_{\parallel }$, which had the strongest normal interaction at no field gradient. Although the inhomogeneity length scaled increased the maximum energy gained by a factor of 4 or more, the average energy gained increase is lower, partly because the phase-space area that gains energy is lower. We observe an optimum at magnetic field-scale gradients of the order of ${1}\ {\rm km}^{-1}$ to $3\ {\rm km}^{-1}$ for both average energy gain and lowest minimal energy required for 13.6 eV energy gain.

6. Conclusion

In this paper, we have considered electron orbits in W7-X-like background fields with microwave heating in the X2 and X3 startup scenarios. The main effect of the background magnetic field inhomogeneity is to extend the interaction, resulting in a significant increase of the maximum energy gain during the interaction. A large energy gain is made possible for lower initial energies.

In the adiabatic interaction regime, the particles would be trapped in the resonance, which follows the strength of the inhomogeneous $B$-field. Unfortunately, adiabatic interaction does not apply to the majority of orbits in X3, which complicates the analysis. Yet, the magnetic field inhomogeneity can be chosen favourably to increase both the overall energy gain and to extend the phase space of the efficient interaction. We find a 4-fold increase of the maximum energy gain of a few eV electrons with the introduction of a small inhomogeneity. To achieve similar increase in energy gain in homogeneous fields a 10 times higher beam power is required. Moreover, we find that the magnetic field gradient allows electrons with  2 eV to gain above 13.6 eV in W7-X-like conditions.

A scan in magnetic field gradient shows that the average energy gain can be increased by around a factor of 1.5–3 for electron temperatures in the eV range, when inhomogeneity is taken into account. The optimal beam inhomogeneity is found to be $1$ to $3\ {\rm km}^{-1}$. However, the single third-harmonic $X$ mode with a 1 MW wave is not sufficient to achieve breakdown in W7-X-like conditions – the mean energy gain remains much smaller than in the analogous X2 case.

When two 1 MW beams are present, their resonance regions can be combined. The beams’ focal points are placed next to each other. In this case, the maximum energy gain approaches the energy gain observed in a single beam X2 case (up to 200 eV compared with ${\sim }1$ keV), which is known to produce a startup in W7-X. However, the phase-space area for efficient interaction is still found to be much smaller than in an analogous X2 case. This area is limited by the parallel energy, and has a width of around 0.1 eV, whereas the corresponding width in X2 is of the order of 300 eV. The energy increase for low energy electrons is still stronger than using a single beam with twice the power.

We conclude that, while a B field inhomogeneity plays an important role in wave–particle interaction in startup conditions, yielding a noticeable increase of the electron energy gain, inhomogeneity alone is unlikely to achieve X3 startup in W7-X-like conditions. A careful design of a multi-wave set-up is shown to improve the situation considerably. A further work study is required to find an optimal scheme. Furthermore, a kinetic modelling of the ionisation process is needed for a predictive study of X3 and X2 startups.