Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T03:52:17.891Z Has data issue: false hasContentIssue false
  • English
  • Français

Electron-scale reduced fluid models with gyroviscous effects

Part of: Frontiers in Plasma Physics Conference

Published online by Cambridge University Press:  24 July 2017

T. Passot ,
P. L. Sulem  and
E. Tassi
T. Passot*
Affiliation:
Université Côte d’Azur, CNRS, Observatoire de la Côte d’Azur, Laboratoire J.L. Lagrange, Boulevard de l’Observatoire, CS 34229, 06304 Nice CEDEX 4, France
P. L. Sulem
Affiliation:
Université Côte d’Azur, CNRS, Observatoire de la Côte d’Azur, Laboratoire J.L. Lagrange, Boulevard de l’Observatoire, CS 34229, 06304 Nice CEDEX 4, France
E. Tassi
Affiliation:
Aix Marseille Univ, Univ Toulon, CNRS, CPT, Marseille, France
*
†Email address for correspondence: passot@oca.eu
Get access Rights & Permissions [Opens in a new window]

Abstract

Reduced fluid models for collisionless plasmas including electron inertia and finite Larmor radius corrections are derived for scales ranging from the ion to the electron gyroradii. Based either on pressure balance or on the incompressibility of the electron fluid, they respectively capture kinetic Alfvén waves (KAWs) or whistler waves (WWs), and can provide suitable tools for reconnection and turbulence studies. Both isothermal regimes and Landau fluid closures permitting anisotropic pressure fluctuations are considered. 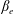For small values of the electron beta parameter $\unicode[STIX]{x1D6FD}_{e}$ , a perturbative computation of the gyroviscous force valid at scales comparable to the electron inertial length is performed at order 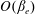$O(\unicode[STIX]{x1D6FD}_{e})$ , which requires second-order contributions in a scale expansion. Comparisons with kinetic theory are performed in the linear regime. The spectrum of transverse magnetic fluctuations for strong and weak turbulence energy cascades is also phenomenologically predicted for both types of waves. In the case of moderate ion to electron temperature ratio, a new regime of KAW turbulence at scales smaller than the electron inertial length is obtained, where the magnetic energy spectrum decays like 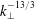$k_{\bot }^{-13/3}$ , thus faster than the 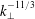$k_{\bot }^{-11/3}$ spectrum of WW turbulence.

Keywords

plasma dynamicsplasma nonlinear phenomenaspace plasma physics
Type
Research Article
Information
Journal of Plasma Physics , Volume 83 , Issue 4 , August 2017 , 715830402
Copyright
© Cambridge University Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abdelhamid, H. M., Lingam, M. & Mahajan, S. M. 2016 Extended MHD turbulence and its applications to the solar wind. Astrophys. J. 829, 87.Google Scholar
Andrés, N., Galtier, S. & Sahraoui, F. 2016a Exact scaling laws for helical three-dimensional two-fluid turbulent plasmas. Phys. Rev. E 94, 063206.Google ScholarPubMed
Andrés, N., Gonzalez, C., Martin, L., Dmitruk, P. & Gómez, D. 2014 Two-fluid turbulence including electron inertia. Phys. Plasmas 21, 122305.CrossRefGoogle Scholar
Andrés, N., Mininni, P. D., Dmitruk, P. & Gómez, D. O. 2016b von Kármán–Howarth equation for three-dimensional two-fluid plasmas. Phys. Rev. E 93, 063202.Google ScholarPubMed
Biskamp, D., Schwarz, E. & Drake, J. F. 1996 Two-dimensional electron magnetohydrodynamic turbulence. Phys. Rev. Lett. 76, 1264–1267.Google Scholar
Biskamp, D., Schwarz, E., Zeiler, A., Celani, A. & Drake, J. F. 1999 Electron magnetohydrodynamic turbulence. Phys. Plasmas 6, 751–758.Google Scholar
Boldyrev, S., Horaites, K., Xia, Q. & Perez, J. C. 2013 Toward a theory of astrophysical plasma turbulence at subproton scales. Astrophys. J. 777, 41.Google Scholar
Bulanov, S. V., Pegoraro, F. & Sakharov, A. S. 1992 Magnetic reconnection in electron magnetohydrodynamics. Phys. Fluids B 4, 2499–2508.Google Scholar
Cerri, S. S. & Califano, F. 2017 Reconnection and small-scale fields in 2d-3v hybrid-kinetic driven turbulence simulations. New J. Phys. 19, 025007.Google Scholar
Cerri, S. S., Califano, F., Jenko, F., Told, D. & Rincon, F. 2016 Subproton-scale cascades in solar wind turbulence: driven hybrid-kinetic simulations. Astrophys. J. Lett. 822, L12.Google Scholar
Chang, O., Gary, S. P. & Wang, J. 2011 Whistler turbulence forward cascade: three-dimensional particle-in-cell simulations. Geophys. Res. Lett. 38, L22102.CrossRefGoogle Scholar
Chang, O., Gary, S. P. & Wang, J. 2013 Whistler turbulence at variable electron beta: three-dimensional particle-in-cell simulations. J. Geophys. Res.: Space Phys. 118, 2824–2833.Google Scholar
Chaston, C. C., Salem, C., Bonnell, J. W., Carlson, C. W., Ergun, R. E., Strangeway, R. J. & McFadden, J. P. 2008 The turbulent Alfvénic aurora. Phys. Rev. Lett. 100, 175003.Google Scholar
Chen, C. H. K. & Boldyrev, S.2017 Nature of kinetic scale turbulence in the Earth’s magnetosheath. arXiv:1705.08558v1 [physics-space-ph] 23 May 2017.Google Scholar
Dagnelund, D. & Pavlenko, V. P. 2005 Hamiltonian description and stability of vortex flows in interchange mode turbulence. Phys. Scr. 71, 293–297.Google Scholar
Daughton, W., Roytershteyn, V., Karimabadi, H., Yin, L., Albright, B. J., Bergen, B. & Bowers, K. J. 2011 Role of electron physics in the development of turbulent magnetic reconnection in collisionless plasmas. Nat. Phys. 7, 539–542.Google Scholar
Galtier, S. & Bhattacharjee, A. 2003 Anisotropic weak whistler wave turbulence in electron magnetohydrodynamics. Phys. Plasmas 10, 3065–3075.CrossRefGoogle Scholar
Galtier, S. & Meyrand, R. 2015 Entanglement of helicity and energy in kinetic Alfvén wave/whistler turbulence. J. Plasma Phys. 81, 325810106.Google Scholar
Gary, S. P., Chang, O. & Wang, J. 2012 Forward cascade of whistler turbulence: three-dimensional particle in-cell simulations. Astrophys. J. 755, 142.CrossRefGoogle Scholar
Gary, S. P. & Smith, C. W 2009 Short-wavelength turbulence in the solar wind: linear theory of whistler and kinetic Alfvén fluctuations. J. Geophys. Res. 114, A12105.Google Scholar
Goswami, P., Passot, T. & Sulem, P. L. 2005 A Landau fluid model for warm collisionless plasmas. Phys. Plasmas 12, 102109.Google Scholar
Hammett, G. W. & Perkins, F. W. 1990 Fluid moment models for Landau damping with application to the ion-temperature gradient instability. Phys. Rev. Lett. 64, 3019–3022.Google Scholar
Hazeltine, R. D., Hsu, C. T. & Morrison, P. J. 1987 Hamiltonian four-field model for nonlinear tokamak dynamics. Phys. Fluids 30, 3204–3211.Google Scholar
Hazeltine, R. D. & Meiss, J. D. 1985 Shear-Alfvén dynamics of toroidally confined plasmas. Phys. Rep. 121, 1–164.CrossRefGoogle Scholar
Hesse, M., Kuznetsova, M. & Birn, J. 2004 The role of electron heat flux in guide-field magnetic reconnection. Phys. Plasmas 11, 5387–5397.Google Scholar
Hsu, C. T., Hazeltine, R. D. & Morrison, P. J. 1986 A generalized reduced fluid model with finite iongyroradius effects. Phys. Fluids 29, 1480–1487.CrossRefGoogle Scholar
Huang, S. Y., Sahraoui, F., Deng, X. H., He, J. S., Yuan, Z. G., Zhou, M., Pang, Y. & Fu, H. S. 2014 Kinetic turbulence in the terrestrial magnetosheath: cluster observations. Astrophys. J. Lett. 789, L28.Google Scholar
Izacard, O., Chandre, C., Tassi, E. & Ciraolo, G. 2011 Gyromap for a two-dimensional Hamiltonian fluid model derived from Braginskii’s closure for magnetized plasmas. Phys. Plasmas 18, 062105.Google Scholar
Kingsep, A. S., Chukbar, K. V. & Yan’kov, V. V. 1990 Electron electrohydrodynamics. Rev. Plasma Phys. 16, 243–291.Google Scholar
Krishan, V. & Mahajan, S. M. 2004 Magnetic fluctuations and Hall magnetohydrodynamic turbulence in the solar wind. J. Geophys. Res. 109, A11105.CrossRefGoogle Scholar
Krommes, J. A. 2002 Fundamental statistical descriptions of plasma turbulence in magnetic fields. Phys. Rep. 360, 1–352.Google Scholar
Kuvshinov, B. N., Westerhof, E., Schep, T. J. & Berning, M. 1998 Electron magnetohydrodynamics of magnetized, inhomogeneous plasmas. Phys. Lett. A 241, 287–292.Google Scholar
Lee, A., Daughton, W., Karimabadi, H. & Egedal, J. 2016 Hybrid simulations of magnetic reconnection with kinetic ions and fluid electron pressure anisotropy. Phys. Plasmas 23, 032114.Google Scholar
Loureiro, N. F., Schekochihin, A. A. & Zocco, A. 2013 Fast collisionless reconnection and electron heating in strongly magnetized plasmas. Phys. Rev. Lett. 111, 025002.Google Scholar
Lyutikov, M. 2013 Electron magnetohydrodynamics: dynamics and turbulence. Phys. Rev. E 88, 053103.Google ScholarPubMed
Matteini, L., Alexandrova, O., Chen, C. H. K. & Lacombe, C. 2017 Electric and magnetic spectra from MHD to electron scales in the magnetosheath. Mon. Not. R. Astron. Soc. 466, 945–951.Google Scholar
Mikhalovskii, A. B., Lakhin, V. P., Aburdzhaniya, G. D., Mikhailovskaya, L. A., Onishchenko, O. G. & Smolyakov, A. I. 1987 On the theory of Alfvén vortices. Plasma Phys. Control. Fusion 29, 1–25.Google Scholar
Miloshevich, G., Lingam, M. & Morrison, P. J. 2017 On the structure and statistical theory of turbulence of extended magnetohydrodynamics. New J. Phys. 19, 015007.Google Scholar
Morrison, P. J., Caldas, I. L. & Tasso, H. 1984 Hamiltonian formulation of two-dimensional gyroviscous MHD. Z. Naturforsch. A 39, 1023.Google Scholar
Morrison, P. J., Lingam, M. & Acevedo, R. 2014 Hamiltonian and action formalisms for two-dimensional gyroviscous magnetohydrodynamics. Phys. Plasmas 21, 082102.Google Scholar
Parashar, T. N., Salem, C., Wicks, R. T., Karimabadi, H., Gary, S. P. & Matthaeus, W. H. 2015 Turbulent dissipation challange: a community-driven effort. J. Plasma Phys. 81, 905810513.Google Scholar
Passot, T. & Sulem, P. L. 2007 Collisionless magnetohydrodynamics with gyrokinetic effects. Phys. Plasmas 14, 082502.Google Scholar
Passot, T. & Sulem, P. L. 2015 A model for the non-universal power-law of the solar wind sub-ion scale magnetic spectrum. Astrophys. J. Lett. 812, L37.Google Scholar
Passot, T., Sulem, P. L. & Hunana, P. 2012 Extending magnetohydrodynamics to the slow dynamics of collisionless plasmas. Phys. Plasmas 19, 082113.Google Scholar
Ramos, J. J. 2005a Fluid formalism for collisionless magnetized plasmas. Phys. Plasmas 12, 052102.Google Scholar
Ramos, J. J. 2005b General expression of the gyroviscous force. Phys. Plasmas 12, 112301.Google Scholar
Rogers, B. N., Denton, R. E., Drake, J. F. & Shay, M. A. 2001 Role of dispersive waves in collisionless magnetic reconnection. Phys. Rev. Lett. 87, 195004.Google Scholar
Rönnmark, K.1982 Waves in homogeneous, anisotropic multicomponent plasmas (WHAMP). Tech. Rep. 179, Kiruna Geophysical Institute.Google Scholar
Sahraoui, F., Belmont, G. & Goldstein, M. L. 2012 New insight into short-wavelength solar wind fluctuations from Vlasov theory. Astrophys. J. 748, 100.Google Scholar
Sahraoui, F., Goldstein, M. L., Belmont, G., Canu, P. & Rezeau, L. 2010 Three dimensional anisotropic $k$ spectra of turbulence at subproton scales in the solar wind. Phys. Rev. Lett. 105, 131101.Google Scholar
Sahraoui, F., Huang, S. Y., Belmont, G., Goldstein, M. L., Rétino, A., Robert, P. & De Patoul, J. 2013 Scaling of the electron dissipation range of solar wind turbulence. Astrophys. J. 777, 15.Google Scholar
Schekochihin, A. A., Cowley, S. C., Dorland, W., Hammett, G. W., Howes, G. G., Quataert, E. & Tatsuno, T. 2009 Astrophysical gyrokinetics: kinetic and fluid turbulent cascades in magnetized weakly collisional plasmas. Astrophys. J. Suppl. 182, 310–377.Google Scholar
Schekochihin, A. A., Cowley, S. C., Rincon, F. & Rosin, M. S. 2010 Magnetofluid dynamics of magnetized cosmic plasma: firehose and gyrothermal instabilities. Mon. Not. R. Astron. Soc. 405, 291–300.Google Scholar
Schep, J. T., Pegoraro, F. & Kuvshinov, B. N. 1994 Generalized two-fluid theory of nonlinear magnetic structures. Phys. Plasmas 1, 2843–2852.Google Scholar
Snyder, P. B., Hammett, G. W. & Dorland, W. 1997 Landau fluid models of collisionless magnetohydrodynamics. Phys. Plasmas 4, 3974–3985.Google Scholar
Sulem, P. L. & Passot, T. 2015 Landau fluid closures with nonlinear large-scale finite Larmor radius corrections for collisionless plasmas. J. Plasma Phys. 81, 325810103.Google Scholar
Sulem, P. L., Passot, T., Laveder, D. & Borgogno, D. 2016 Influence of the nonlinearity parameter on the solar wind sub-ion magnetic energy spectrum: FLR-Landau fluid simulations. Astrophys. J. 818, 66.CrossRefGoogle Scholar
Tassi, E., Sulem, P. L. & Passot, T. 2016 Reduced models accounting for parallel magnetic perturbations: gyrofluid and finite Larmor radius-Landau fluid approaches. J. Plasma Phys. 82, 705820601.Google Scholar
Treumann, R. A. & Baumjohann, W. 2013 Collisionless reconnection in space plasmas. Front. Phys. 1, 31.Google Scholar
Vaivads, A., Retinò, A., Soucek, J., Khotyaintsev, Y. V., Valentini, F., Escoubet, C. P., Alexandrova, O., André, M., Bale, S. D., Balikhin, M. et al. 2016 Turbulence Heating ObserveR – satellite mission proposal. J. Plasma Phys. 82 (5), 905820501.Google Scholar
Zocco, A. & Schekochihin, A. 2011 Reduced fluid-kinetic equations for low-frequency dynamics, magnetic reconnection, and electron heating in low-beta plasmas. Phys. Plasmas 18, 102309.Google Scholar
Zweibel, E. G. & Yamada, M. 2017 Perspectives on magnetic reconnection. Proc. R. Soc. Lond. A 472, 20160479.Google Scholar