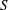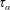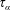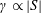1 Introduction
Magnetic fields are observed over a wide range of scales in various astrophysical objects (see, e.g. Han Reference Han2017). Their origins could be the result of turbulent dynamo processes which can lead to field generation on scales that are larger as well as smaller than the outer scale of the underlying turbulence (see, e.g. Moffatt Reference Moffatt1978; Parker Reference Parker1979; Krause & Rädler Reference Krause and Rädler1980; Zeldovich, Ruzmaikin & Sokolov Reference Zeldovich, Ruzmaikin and Sokolov1983; Ruzmaikin, Shukurov & Sokoloff Reference Ruzmaikin, Shukurov and Sokoloff1988; Brandenburg & Subramanian Reference Brandenburg and Subramanian2005). Of particular interest here is the subject of the large-scale dynamo (LSD), which may be studied in the framework of mean-field theory (Steenbeck, Krause & Rädler Reference Steenbeck, Krause and Rädler1966; Moffatt Reference Moffatt1978; Krause & Rädler Reference Krause and Rädler1980). The standard paradigm for LSD involves an
![]() $\unicode[STIX]{x1D6FC}$
-effect which arises when the background turbulence possesses mean kinetic helicity, thus breaking the mirror symmetry of turbulence (see, e.g. Brandenburg & Subramanian Reference Brandenburg and Subramanian2005). The problem becomes more interesting and complicated when the usual
$\unicode[STIX]{x1D6FC}$
-effect which arises when the background turbulence possesses mean kinetic helicity, thus breaking the mirror symmetry of turbulence (see, e.g. Brandenburg & Subramanian Reference Brandenburg and Subramanian2005). The problem becomes more interesting and complicated when the usual
![]() $\unicode[STIX]{x1D6FC}$
-effect is either absent or subcritical for dynamo growth. Mean velocity shear appears to play a vital role for LSD in such regimes of zero/subcritical
$\unicode[STIX]{x1D6FC}$
-effect is either absent or subcritical for dynamo growth. Mean velocity shear appears to play a vital role for LSD in such regimes of zero/subcritical
![]() $\unicode[STIX]{x1D6FC}$
. As most astrophysical bodies also possess mean differential rotation, it is natural to ask if large-scale magnetic fields could grow in the presence of a background shear flow when
$\unicode[STIX]{x1D6FC}$
. As most astrophysical bodies also possess mean differential rotation, it is natural to ask if large-scale magnetic fields could grow in the presence of a background shear flow when
![]() $\unicode[STIX]{x1D6FC}$
is a purely fluctuating quantity.
$\unicode[STIX]{x1D6FC}$
is a purely fluctuating quantity.
Early ideas of stochastically varying
![]() $\unicode[STIX]{x1D6FC}$
with zero mean suggested that it causes a decrement in turbulent diffusion (Kraichnan Reference Kraichnan1976; Moffatt Reference Moffatt1978). A number of subsequent studies then considered fluctuating
$\unicode[STIX]{x1D6FC}$
with zero mean suggested that it causes a decrement in turbulent diffusion (Kraichnan Reference Kraichnan1976; Moffatt Reference Moffatt1978). A number of subsequent studies then considered fluctuating
![]() $\unicode[STIX]{x1D6FC}$
as an important ingredient for the evolution of magnetic fields in objects, such as, the Sun (Silant’ev Reference Silant’ev2000; Proctor Reference Proctor2007), accretion disks (Vishniac & Brandenburg Reference Vishniac and Brandenburg1997), galaxies (Sokolov Reference Sokolov1997; Sur & Subramanian Reference Sur and Subramanian2009). Numerical demonstration of the shear dynamo problem (Brandenburg et al.
Reference Brandenburg, Rädler, Rheinhardt and Käpylä2008; Yousef et al.
Reference Yousef, Heinemann, Schekochihin, Kleeorin, Rogachevskii, Iskakov, Cowley and Mcwilliams2008a
,Reference Yousef, Heinemann, Rincon, Schekochihin, Kleeorin, Rogachevskii, Cowley and Mcwilliams
b
; Singh & Jingade Reference Singh and Jingade2015) where large-scale magnetic fields were generated due to non-helically forced turbulence in shear flows, and failure to understand these in terms of simple ideas involving a shear–current effect (Kleeorin & Rogachevskii Reference Kleeorin and Rogachevskii2008; Rogachevskii & Kleeorin Reference Rogachevskii and Kleeorin2008; Sridhar & Subramanian Reference Sridhar and Subramanian2009a
,Reference Sridhar and Subramanian
b
; Sridhar & Singh Reference Sridhar and Singh2010; Singh & Sridhar Reference Singh and Sridhar2011; Kolekar, Subramanian & Sridhar Reference Kolekar, Subramanian and Sridhar2012), brought the focus to a stochastic
$\unicode[STIX]{x1D6FC}$
as an important ingredient for the evolution of magnetic fields in objects, such as, the Sun (Silant’ev Reference Silant’ev2000; Proctor Reference Proctor2007), accretion disks (Vishniac & Brandenburg Reference Vishniac and Brandenburg1997), galaxies (Sokolov Reference Sokolov1997; Sur & Subramanian Reference Sur and Subramanian2009). Numerical demonstration of the shear dynamo problem (Brandenburg et al.
Reference Brandenburg, Rädler, Rheinhardt and Käpylä2008; Yousef et al.
Reference Yousef, Heinemann, Schekochihin, Kleeorin, Rogachevskii, Iskakov, Cowley and Mcwilliams2008a
,Reference Yousef, Heinemann, Rincon, Schekochihin, Kleeorin, Rogachevskii, Cowley and Mcwilliams
b
; Singh & Jingade Reference Singh and Jingade2015) where large-scale magnetic fields were generated due to non-helically forced turbulence in shear flows, and failure to understand these in terms of simple ideas involving a shear–current effect (Kleeorin & Rogachevskii Reference Kleeorin and Rogachevskii2008; Rogachevskii & Kleeorin Reference Rogachevskii and Kleeorin2008; Sridhar & Subramanian Reference Sridhar and Subramanian2009a
,Reference Sridhar and Subramanian
b
; Sridhar & Singh Reference Sridhar and Singh2010; Singh & Sridhar Reference Singh and Sridhar2011; Kolekar, Subramanian & Sridhar Reference Kolekar, Subramanian and Sridhar2012), brought the focus to a stochastic
![]() $\unicode[STIX]{x1D6FC}$
which could potentially lead to the dynamo action generically in shearing systems (Heinemann, McWilliams & Schekochihin Reference Heinemann, McWilliams and Schekochihin2011; McWilliams Reference Mcwilliams2012; Mitra & Brandenburg Reference Mitra and Brandenburg2012; Proctor Reference Proctor2012; Richardson & Proctor Reference Richardson and Proctor2012; Sridhar & Singh Reference Sridhar and Singh2014). There is still a need to verify the model predictions for the growth of the first moment of the mean magnetic field in such systems by performing more simulations.
$\unicode[STIX]{x1D6FC}$
which could potentially lead to the dynamo action generically in shearing systems (Heinemann, McWilliams & Schekochihin Reference Heinemann, McWilliams and Schekochihin2011; McWilliams Reference Mcwilliams2012; Mitra & Brandenburg Reference Mitra and Brandenburg2012; Proctor Reference Proctor2012; Richardson & Proctor Reference Richardson and Proctor2012; Sridhar & Singh Reference Sridhar and Singh2014). There is still a need to verify the model predictions for the growth of the first moment of the mean magnetic field in such systems by performing more simulations.
Squire & Bhattacharjee (Reference Squire and Bhattacharjee2015a
,Reference Squire and Bhattacharjee
b
) recently proposed a new mechanism, called the magnetic shear current effect, which leads to the generation of a large-scale magnetic field due to the combined action of shear and small-scale magnetic fluctuations, if these are sufficiently strong and are near equipartition levels of turbulent motions. Such strong magnetic fluctuations are expected to be naturally present due to small-scale dynamo (SSD) action in astrophysical plasmas, which typically have large magnetic Reynolds number (
![]() $\text{Rm}$
). This new effect thus raises the interesting possibility of the excitation of LSD due to SSD in presence of shear, and it challenges an understanding where SSD in high-
$\text{Rm}$
). This new effect thus raises the interesting possibility of the excitation of LSD due to SSD in presence of shear, and it challenges an understanding where SSD in high-
![]() $\text{Rm}$
systems is thought to weaken the LSD, which could survive only when SSD is suppressed due to shear (Tobias & Cattaneo Reference Tobias and Cattaneo2013; Pongkitiwanichakul et al.
Reference Pongkitiwanichakul, Nigro, Cattaneo and Tobias2016; Nigro et al.
Reference Nigro, Pongkitiwanichakul, Cattaneo and Tobias2017); but see also Kolokolov, Lebedev & Sizov (Reference Kolokolov, Lebedev and Sizov2011) and Singh, Rogachevskii & Brandenburg (Reference Singh, Rogachevskii and Brandenburg2017) where it is found that the shear supports and even enhances the growth rate of SSD. However, we are here more concerned with the excitation of a large-scale shear dynamo, quite independent of any small-scale dynamo or strong magnetic fluctuations, which are both absent in most numerical simulations that are relevant. These simulations typically had
$\text{Rm}$
systems is thought to weaken the LSD, which could survive only when SSD is suppressed due to shear (Tobias & Cattaneo Reference Tobias and Cattaneo2013; Pongkitiwanichakul et al.
Reference Pongkitiwanichakul, Nigro, Cattaneo and Tobias2016; Nigro et al.
Reference Nigro, Pongkitiwanichakul, Cattaneo and Tobias2017); but see also Kolokolov, Lebedev & Sizov (Reference Kolokolov, Lebedev and Sizov2011) and Singh, Rogachevskii & Brandenburg (Reference Singh, Rogachevskii and Brandenburg2017) where it is found that the shear supports and even enhances the growth rate of SSD. However, we are here more concerned with the excitation of a large-scale shear dynamo, quite independent of any small-scale dynamo or strong magnetic fluctuations, which are both absent in most numerical simulations that are relevant. These simulations typically had
![]() $\text{Rm}$
which were subcritical for SSD and the only source of magnetic fluctuations was due to the tangling of large-scale magnetic fields (Rogachevskii & Kleeorin Reference Rogachevskii and Kleeorin2007), and therefore these fluctuations could never be too strong in the kinematic regime of LSD.
$\text{Rm}$
which were subcritical for SSD and the only source of magnetic fluctuations was due to the tangling of large-scale magnetic fields (Rogachevskii & Kleeorin Reference Rogachevskii and Kleeorin2007), and therefore these fluctuations could never be too strong in the kinematic regime of LSD.
In the present paper we explore the possibility of large-scale dynamo action in presence of background shear flow, due to an
![]() $\unicode[STIX]{x1D6FC}$
that varies stochastically in space and time, with vanishing mean. Here we generalize the earlier work by Sridhar & Singh (Reference Sridhar and Singh2014), hereafter SS14, by including the full resistive term in determining the turbulent electromotive force (EMF). Such an extension in the absence of shear was done in Singh (Reference Singh2016). In § 2 we define our model by writing the dynamo equations in shearing coordinates. The integro-differential equation governing the evolution of the large-scale magnetic field is derived under a first-order smoothing approximation (FOSA) in § 3. This is non-perturbative in shearing rate
$\unicode[STIX]{x1D6FC}$
that varies stochastically in space and time, with vanishing mean. Here we generalize the earlier work by Sridhar & Singh (Reference Sridhar and Singh2014), hereafter SS14, by including the full resistive term in determining the turbulent electromotive force (EMF). Such an extension in the absence of shear was done in Singh (Reference Singh2016). In § 2 we define our model by writing the dynamo equations in shearing coordinates. The integro-differential equation governing the evolution of the large-scale magnetic field is derived under a first-order smoothing approximation (FOSA) in § 3. This is non-perturbative in shearing rate
![]() $S$
and the correlation time
$S$
and the correlation time
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
. Here we briefly review the exactly solvable limit of white-noise
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
. Here we briefly review the exactly solvable limit of white-noise
![]() $\unicode[STIX]{x1D6FC}$
fluctuations. In § 4 we reduce the evolution equation into a partial differential equation (PDE) for axisymmetric mean magnetic fields, by assuming small but non-zero
$\unicode[STIX]{x1D6FC}$
fluctuations. In § 4 we reduce the evolution equation into a partial differential equation (PDE) for axisymmetric mean magnetic fields, by assuming small but non-zero
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
. The dispersion relation giving the growth rate is then determined in § 5 where we present our results in different parameter regimes. We then discuss our findings and conclude in § 6.
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
. The dispersion relation giving the growth rate is then determined in § 5 where we present our results in different parameter regimes. We then discuss our findings and conclude in § 6.
2 The model
Let us begin with the standard dynamo equation in the presence of a background linear shear flow,
![]() $\boldsymbol{V}=SX_{1}\boldsymbol{e}_{2}$
, where meso-scale magnetic field
$\boldsymbol{V}=SX_{1}\boldsymbol{e}_{2}$
, where meso-scale magnetic field
![]() $\boldsymbol{B}$
evolves according to (see, Moffatt Reference Moffatt1978; Krause & Rädler Reference Krause and Rädler1980; Brandenburg & Subramanian Reference Brandenburg and Subramanian2005; Sridhar & Singh Reference Sridhar and Singh2014):
$\boldsymbol{B}$
evolves according to (see, Moffatt Reference Moffatt1978; Krause & Rädler Reference Krause and Rädler1980; Brandenburg & Subramanian Reference Brandenburg and Subramanian2005; Sridhar & Singh Reference Sridhar and Singh2014):
Here we follow the same notation as in Sridhar & Singh (Reference Sridhar and Singh2014) where the position vector is denoted by
![]() $\boldsymbol{X}=(X_{1},X_{2},X_{3})$
with components given in a fixed orthonormal frame
$\boldsymbol{X}=(X_{1},X_{2},X_{3})$
with components given in a fixed orthonormal frame
![]() $(\boldsymbol{e}_{1},\boldsymbol{e}_{2},\boldsymbol{e}_{3})$
, and
$(\boldsymbol{e}_{1},\boldsymbol{e}_{2},\boldsymbol{e}_{3})$
, and
![]() $\unicode[STIX]{x1D70F}$
is the time variable. The shear rate,
$\unicode[STIX]{x1D70F}$
is the time variable. The shear rate,
![]() $S$
, and total diffusivity,
$S$
, and total diffusivity,
![]() $\unicode[STIX]{x1D702}_{T}$
, are treated as constant parameters, whereas
$\unicode[STIX]{x1D702}_{T}$
, are treated as constant parameters, whereas
![]() $\unicode[STIX]{x1D6FC}(\boldsymbol{X},\unicode[STIX]{x1D70F})$
provides a measure of meso-scale kinetic helicity of turbulence. We recall that (2.1) governing the dynamics of a meso-scale magnetic field is obtained by averaging over an ensemble of random velocity fields,
$\unicode[STIX]{x1D6FC}(\boldsymbol{X},\unicode[STIX]{x1D70F})$
provides a measure of meso-scale kinetic helicity of turbulence. We recall that (2.1) governing the dynamics of a meso-scale magnetic field is obtained by averaging over an ensemble of random velocity fields,
![]() $\{\boldsymbol{v}(\boldsymbol{X},\unicode[STIX]{x1D70F})\}$
, which are assumed to have zero-mean isotropic fluctuations, uniform and constant kinetic energy density per unit mass and slow helicity fluctuations.
$\{\boldsymbol{v}(\boldsymbol{X},\unicode[STIX]{x1D70F})\}$
, which are assumed to have zero-mean isotropic fluctuations, uniform and constant kinetic energy density per unit mass and slow helicity fluctuations.
We employ here the double-averaging scheme (Kraichnan Reference Kraichnan1976; Moffatt Reference Moffatt1983; Sokolov Reference Sokolov1997) under which
![]() $\unicode[STIX]{x1D6FC}(\boldsymbol{X},\unicode[STIX]{x1D70F})$
itself is a random variable of space and time, thus making (2.1) a stochastic partial differential equation. It is drawn from a superensemble with zero mean,
$\unicode[STIX]{x1D6FC}(\boldsymbol{X},\unicode[STIX]{x1D70F})$
itself is a random variable of space and time, thus making (2.1) a stochastic partial differential equation. It is drawn from a superensemble with zero mean,
![]() $\overline{\unicode[STIX]{x1D6FC}(\boldsymbol{X},\unicode[STIX]{x1D70F})}=0$
. It’s statistical properties are given below in (2.11). Next, we separate the meso-scale field,
$\overline{\unicode[STIX]{x1D6FC}(\boldsymbol{X},\unicode[STIX]{x1D70F})}=0$
. It’s statistical properties are given below in (2.11). Next, we separate the meso-scale field,
![]() $\boldsymbol{B}=\overline{\boldsymbol{B}}+\boldsymbol{b}$
, into large-scale,
$\boldsymbol{B}=\overline{\boldsymbol{B}}+\boldsymbol{b}$
, into large-scale,
![]() $\overline{\boldsymbol{B}}$
, and fluctuating,
$\overline{\boldsymbol{B}}$
, and fluctuating,
![]() $\boldsymbol{b}$
, components, where the superensemble average of
$\boldsymbol{b}$
, components, where the superensemble average of
![]() $\boldsymbol{b}$
vanishes, i.e.
$\boldsymbol{b}$
vanishes, i.e.
![]() $\overline{\boldsymbol{b}}=\mathbf{0}$
. The governing equation for the large-scale magnetic field
$\overline{\boldsymbol{b}}=\mathbf{0}$
. The governing equation for the large-scale magnetic field
![]() $\overline{\boldsymbol{B}}$
can thus be obtained by Reynolds averaging the (2.1) over the superensemble:
$\overline{\boldsymbol{B}}$
can thus be obtained by Reynolds averaging the (2.1) over the superensemble:
In order to determine the mean electromotive force (EMF), we must solve for the fluctuating field
![]() $\boldsymbol{b}$
, which evolves as:
$\boldsymbol{b}$
, which evolves as:
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \left(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}+SX_{1}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}X_{2}}\right)\boldsymbol{b}-Sb_{1}\boldsymbol{e}_{2}=\unicode[STIX]{x1D735}\times [\unicode[STIX]{x1D6FC}\overline{\boldsymbol{B}}]+\unicode[STIX]{x1D735}\times [\unicode[STIX]{x1D6FC}\boldsymbol{b}-\overline{\unicode[STIX]{x1D6FC}\boldsymbol{b}}]+\unicode[STIX]{x1D702}_{T}\unicode[STIX]{x1D6FB}^{2}\boldsymbol{b},\\ \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{b}=0,\quad \text{with initial condition }\boldsymbol{b}(\boldsymbol{X},0)=\mathbf{0}.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \left(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}+SX_{1}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}X_{2}}\right)\boldsymbol{b}-Sb_{1}\boldsymbol{e}_{2}=\unicode[STIX]{x1D735}\times [\unicode[STIX]{x1D6FC}\overline{\boldsymbol{B}}]+\unicode[STIX]{x1D735}\times [\unicode[STIX]{x1D6FC}\boldsymbol{b}-\overline{\unicode[STIX]{x1D6FC}\boldsymbol{b}}]+\unicode[STIX]{x1D702}_{T}\unicode[STIX]{x1D6FB}^{2}\boldsymbol{b},\\ \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{b}=0,\quad \text{with initial condition }\boldsymbol{b}(\boldsymbol{X},0)=\mathbf{0}.\end{array}\right\}\end{eqnarray}$$
As (2.2) and (2.4) involve inhomogeneous terms, it is convenient to solve these in the shearing coordinates
![]() $(\boldsymbol{x},t)$
which are expressed in terms of the laboratory coordinates
$(\boldsymbol{x},t)$
which are expressed in terms of the laboratory coordinates
![]() $(\boldsymbol{X},\unicode[STIX]{x1D70F})$
as (see, Sridhar & Subramanian Reference Sridhar and Subramanian2009a
; Sridhar & Singh Reference Sridhar and Singh2010):
$(\boldsymbol{X},\unicode[STIX]{x1D70F})$
as (see, Sridhar & Subramanian Reference Sridhar and Subramanian2009a
; Sridhar & Singh Reference Sridhar and Singh2010):
The inverse transformation is:
Now we can write equations (2.2)–(2.4) in terms of new fields that are functions of
![]() $\boldsymbol{x}$
and
$\boldsymbol{x}$
and
![]() $t$
:
$t$
:
![]() $\overline{\boldsymbol{H}}(\boldsymbol{x},t)=\overline{\boldsymbol{B}}(\boldsymbol{X},\unicode[STIX]{x1D70F})$
;
$\overline{\boldsymbol{H}}(\boldsymbol{x},t)=\overline{\boldsymbol{B}}(\boldsymbol{X},\unicode[STIX]{x1D70F})$
;
![]() $\boldsymbol{h}(\boldsymbol{x},t)=\boldsymbol{b}(\boldsymbol{X},\unicode[STIX]{x1D70F})$
;
$\boldsymbol{h}(\boldsymbol{x},t)=\boldsymbol{b}(\boldsymbol{X},\unicode[STIX]{x1D70F})$
;
![]() $a(\boldsymbol{x},t)=\unicode[STIX]{x1D6FC}(\boldsymbol{X},\unicode[STIX]{x1D70F})$
; and
$a(\boldsymbol{x},t)=\unicode[STIX]{x1D6FC}(\boldsymbol{X},\unicode[STIX]{x1D70F})$
; and
![]() $\overline{\boldsymbol{E}}(\boldsymbol{x},t)=\overline{\boldsymbol{{\mathcal{E}}}}(\boldsymbol{X},\unicode[STIX]{x1D70F})$
. Equations (2.2)–(2.4) then take the form (Sridhar & Singh Reference Sridhar and Singh2014):
$\overline{\boldsymbol{E}}(\boldsymbol{x},t)=\overline{\boldsymbol{{\mathcal{E}}}}(\boldsymbol{X},\unicode[STIX]{x1D70F})$
. Equations (2.2)–(2.4) then take the form (Sridhar & Singh Reference Sridhar and Singh2014):
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \frac{\unicode[STIX]{x2202}\boldsymbol{h}}{\unicode[STIX]{x2202}t}-Sh_{1}\boldsymbol{e}_{2}=\unicode[STIX]{x1D735}\times [a\overline{\boldsymbol{H}}]+\unicode[STIX]{x1D735}\times [a\boldsymbol{h}-\overline{a\boldsymbol{h}}]+\unicode[STIX]{x1D702}_{T}\unicode[STIX]{x1D6FB}^{2}\boldsymbol{h},\\ \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{h}=0,\quad \text{with initial condition }\boldsymbol{h}(\boldsymbol{x},0)=\mathbf{0};\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \frac{\unicode[STIX]{x2202}\boldsymbol{h}}{\unicode[STIX]{x2202}t}-Sh_{1}\boldsymbol{e}_{2}=\unicode[STIX]{x1D735}\times [a\overline{\boldsymbol{H}}]+\unicode[STIX]{x1D735}\times [a\boldsymbol{h}-\overline{a\boldsymbol{h}}]+\unicode[STIX]{x1D702}_{T}\unicode[STIX]{x1D6FB}^{2}\boldsymbol{h},\\ \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{h}=0,\quad \text{with initial condition }\boldsymbol{h}(\boldsymbol{x},0)=\mathbf{0};\end{array}\right\}\end{eqnarray}$$
We complete defining our model by specifying the statistics of the
![]() $\unicode[STIX]{x1D6FC}$
fluctuations. We follow the exact same approach as given in detail in Sridhar & Singh (Reference Sridhar and Singh2014) and recall here only some key relevant points:
$\unicode[STIX]{x1D6FC}$
fluctuations. We follow the exact same approach as given in detail in Sridhar & Singh (Reference Sridhar and Singh2014) and recall here only some key relevant points:
(i) Shear flows possess a natural symmetry known as Galilean invariance, relating the measurements of correlation functions made by comoving observers whose origins with respect to the laboratory frame translate with the same speed as that of the linear shear flow (Sridhar & Subramanian Reference Sridhar and Subramanian2009a ,Reference Sridhar and Subramanian b ).
(ii) Here we are more interested in time-stationary Galilean-invariant
 $\unicode[STIX]{x1D6FC}$
statistics, which can be expressed in the shearing frame as (see Sridhar & Singh (Reference Sridhar and Singh2014) for a derivation): (2.10)
$\unicode[STIX]{x1D6FC}$
statistics, which can be expressed in the shearing frame as (see Sridhar & Singh (Reference Sridhar and Singh2014) for a derivation): (2.10) $$\begin{eqnarray}\displaystyle & \displaystyle \overline{a(\boldsymbol{x},t)a(\boldsymbol{x}^{\prime },t^{\prime })}=2{\mathcal{A}}\left(\boldsymbol{x}-\boldsymbol{x}^{\prime }+St^{\prime }(x_{1}-x_{1}^{\prime })\boldsymbol{e}_{2}\right){\mathcal{D}}(t-t^{\prime }),\quad \text{with} & \displaystyle\end{eqnarray}$$
(2.11)The correlation time for the
$$\begin{eqnarray}\displaystyle & \displaystyle \overline{a(\boldsymbol{x},t)a(\boldsymbol{x}^{\prime },t^{\prime })}=2{\mathcal{A}}\left(\boldsymbol{x}-\boldsymbol{x}^{\prime }+St^{\prime }(x_{1}-x_{1}^{\prime })\boldsymbol{e}_{2}\right){\mathcal{D}}(t-t^{\prime }),\quad \text{with} & \displaystyle\end{eqnarray}$$
(2.11)The correlation time for the $$\begin{eqnarray}\displaystyle & \displaystyle 2\int _{0}^{\infty }{\mathcal{D}}(t)\,\text{d}t=1,\quad {\mathcal{A}}(\mathbf{0})=\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}\geqslant 0. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle 2\int _{0}^{\infty }{\mathcal{D}}(t)\,\text{d}t=1,\quad {\mathcal{A}}(\mathbf{0})=\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}\geqslant 0. & \displaystyle\end{eqnarray}$$
 $\unicode[STIX]{x1D6FC}$
fluctuations is defined as, (2.12)The intrinsic anisotropy of the
$\unicode[STIX]{x1D6FC}$
fluctuations is defined as, (2.12)The intrinsic anisotropy of the $$\begin{eqnarray}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}=2\int _{0}^{\infty }\text{d}t\,t\,{\mathcal{D}}(t).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}=2\int _{0}^{\infty }\text{d}t\,t\,{\mathcal{D}}(t).\end{eqnarray}$$
 $\unicode[STIX]{x1D6FC}$
fluctuations is measured by the Moffatt drift velocity, (2.13)
$\unicode[STIX]{x1D6FC}$
fluctuations is measured by the Moffatt drift velocity, (2.13) $$\begin{eqnarray}\boldsymbol{V}_{M}=-\left(\frac{\unicode[STIX]{x2202}{\mathcal{A}}(\unicode[STIX]{x1D743})}{\unicode[STIX]{x2202}\unicode[STIX]{x1D743}}\right)_{\unicode[STIX]{x1D743}=\mathbf{0}}=\int _{0}^{\infty }\overline{\unicode[STIX]{x1D6FC}(\boldsymbol{X},\unicode[STIX]{x1D70F})\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FC}(\boldsymbol{X},0)}\,\text{d}\unicode[STIX]{x1D70F}.\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{V}_{M}=-\left(\frac{\unicode[STIX]{x2202}{\mathcal{A}}(\unicode[STIX]{x1D743})}{\unicode[STIX]{x2202}\unicode[STIX]{x1D743}}\right)_{\unicode[STIX]{x1D743}=\mathbf{0}}=\int _{0}^{\infty }\overline{\unicode[STIX]{x1D6FC}(\boldsymbol{X},\unicode[STIX]{x1D70F})\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FC}(\boldsymbol{X},0)}\,\text{d}\unicode[STIX]{x1D70F}.\end{eqnarray}$$
In the above, we noted two properties of the spatial correlation function,
![]() ${\mathcal{A}}$
, namely its value
${\mathcal{A}}$
, namely its value
![]() $\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}$
and gradient
$\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}$
and gradient
![]() $\boldsymbol{V}_{M}$
at zero separation. But we can associate one or more length scales relating to its variation in
$\boldsymbol{V}_{M}$
at zero separation. But we can associate one or more length scales relating to its variation in
![]() $\unicode[STIX]{x1D743}$
-space. In the estimates made below we use a single scale
$\unicode[STIX]{x1D743}$
-space. In the estimates made below we use a single scale
![]() $\ell$
to denote this correlation length. The temporal correlation function,
$\ell$
to denote this correlation length. The temporal correlation function,
![]() ${\mathcal{D}}$
is characterized by a single correlation time,
${\mathcal{D}}$
is characterized by a single correlation time,
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
. Hence the basic constant parameters of our model are
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
. Hence the basic constant parameters of our model are
![]() $(\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}},\boldsymbol{V}_{M},\ell ,\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}})$
.
$(\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}},\boldsymbol{V}_{M},\ell ,\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}})$
.
3 Evolution equation for the large-scale magnetic field
Here we derive a closed equation for the large-scale magnetic field by exploiting the homogeneity of the problem in the sheared coordinates
![]() $\boldsymbol{x}$
by working with its conjugate Fourier variable
$\boldsymbol{x}$
by working with its conjugate Fourier variable
![]() $\boldsymbol{k}$
. Let
$\boldsymbol{k}$
. Let
![]() $\widetilde{Q}(\boldsymbol{k},t)=\int \text{d}^{3}x\exp (-\text{i}\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{x})Q(\boldsymbol{x},t)$
be the Fourier transform of any quantity
$\widetilde{Q}(\boldsymbol{k},t)=\int \text{d}^{3}x\exp (-\text{i}\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{x})Q(\boldsymbol{x},t)$
be the Fourier transform of any quantity
![]() $Q(\boldsymbol{x},t)$
, with similar definition in terms of laboratory-frame coordinates, where
$Q(\boldsymbol{x},t)$
, with similar definition in terms of laboratory-frame coordinates, where
![]() $\boldsymbol{K}$
denotes the conjugate variable to
$\boldsymbol{K}$
denotes the conjugate variable to
![]() $\boldsymbol{X}$
. Note that the laboratory-frame wavevector
$\boldsymbol{X}$
. Note that the laboratory-frame wavevector
![]() $\boldsymbol{K}$
is time dependent and can be expressed in terms of sheared wavevectors
$\boldsymbol{K}$
is time dependent and can be expressed in terms of sheared wavevectors
![]() $\boldsymbol{k}$
as,
$\boldsymbol{k}$
as,
![]() $\boldsymbol{K}(\boldsymbol{k},t)=(k_{1}-Stk_{2},k_{2},k_{3})$
; see (2.9). We need to first solve for
$\boldsymbol{K}(\boldsymbol{k},t)=(k_{1}-Stk_{2},k_{2},k_{3})$
; see (2.9). We need to first solve for
![]() $\widetilde{\boldsymbol{h}}(\boldsymbol{k},t)$
as a functional of
$\widetilde{\boldsymbol{h}}(\boldsymbol{k},t)$
as a functional of
![]() $\widetilde{a}(\boldsymbol{k},t)$
and
$\widetilde{a}(\boldsymbol{k},t)$
and
![]() $\widetilde{\overline{\boldsymbol{H}}}(\boldsymbol{k},t)$
. This is in general a complicated problem by itself, so for a first attempt we use the standard approach of the first-order smoothing approximation (FOSA) wherein the term,
$\widetilde{\overline{\boldsymbol{H}}}(\boldsymbol{k},t)$
. This is in general a complicated problem by itself, so for a first attempt we use the standard approach of the first-order smoothing approximation (FOSA) wherein the term,
![]() $\unicode[STIX]{x1D735}\times [a\boldsymbol{h}-\overline{a\boldsymbol{h}}]$
, is dropped in (2.8). Analogous to (7.124) of Moffatt (Reference Moffatt1978), the condition for FOSA to be valid is:
$\unicode[STIX]{x1D735}\times [a\boldsymbol{h}-\overline{a\boldsymbol{h}}]$
, is dropped in (2.8). Analogous to (7.124) of Moffatt (Reference Moffatt1978), the condition for FOSA to be valid is:
where we recall that
![]() $\ell$
is the correlation length of the
$\ell$
is the correlation length of the
![]() $\unicode[STIX]{x1D6FC}$
fluctuations. The first term of these condition comes from the short correlation assumption by comparing
$\unicode[STIX]{x1D6FC}$
fluctuations. The first term of these condition comes from the short correlation assumption by comparing
![]() $\unicode[STIX]{x2202}\boldsymbol{h}/\unicode[STIX]{x2202}t$
with
$\unicode[STIX]{x2202}\boldsymbol{h}/\unicode[STIX]{x2202}t$
with
![]() $\unicode[STIX]{x1D735}\times [a\boldsymbol{h}-\overline{a\boldsymbol{h}}]$
;
$\unicode[STIX]{x1D735}\times [a\boldsymbol{h}-\overline{a\boldsymbol{h}}]$
;
![]() $\unicode[STIX]{x2202}\boldsymbol{h}/\unicode[STIX]{x2202}t$
is of the order
$\unicode[STIX]{x2202}\boldsymbol{h}/\unicode[STIX]{x2202}t$
is of the order
![]() $O(h_{0}/\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}})$
and
$O(h_{0}/\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}})$
and
![]() $\unicode[STIX]{x1D735}\times [a\boldsymbol{h}-\overline{a\boldsymbol{h}}]$
is of the order
$\unicode[STIX]{x1D735}\times [a\boldsymbol{h}-\overline{a\boldsymbol{h}}]$
is of the order
![]() $O(\unicode[STIX]{x1D6FC}_{0}h_{0}/\ell )$
. For FOSA to be valid,
$O(\unicode[STIX]{x1D6FC}_{0}h_{0}/\ell )$
. For FOSA to be valid,
![]() $\unicode[STIX]{x1D6FC}_{0}h_{0}/\ell \ll h_{0}/\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
. Using
$\unicode[STIX]{x1D6FC}_{0}h_{0}/\ell \ll h_{0}/\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
. Using
![]() $\unicode[STIX]{x1D6FC}_{0}^{2}\sim \unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}/\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
(from (2.11)), we can write the first condition in (3.1). Similarly, the second condition comes from comparing
$\unicode[STIX]{x1D6FC}_{0}^{2}\sim \unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}/\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
(from (2.11)), we can write the first condition in (3.1). Similarly, the second condition comes from comparing
![]() $\unicode[STIX]{x1D702}_{T}\unicode[STIX]{x1D6FB}^{2}\boldsymbol{h}$
with
$\unicode[STIX]{x1D702}_{T}\unicode[STIX]{x1D6FB}^{2}\boldsymbol{h}$
with
![]() $\unicode[STIX]{x1D735}\times [a\boldsymbol{h}-\overline{a\boldsymbol{h}}]$
in (2.8);
$\unicode[STIX]{x1D735}\times [a\boldsymbol{h}-\overline{a\boldsymbol{h}}]$
in (2.8);
![]() $\unicode[STIX]{x1D702}_{T}\unicode[STIX]{x1D6FB}^{2}\boldsymbol{h}$
is of the order
$\unicode[STIX]{x1D702}_{T}\unicode[STIX]{x1D6FB}^{2}\boldsymbol{h}$
is of the order
![]() $O(\unicode[STIX]{x1D702}_{T}h_{0}/\ell ^{2})$
, and so, for FOSA to be valid,
$O(\unicode[STIX]{x1D702}_{T}h_{0}/\ell ^{2})$
, and so, for FOSA to be valid,
![]() $\unicode[STIX]{x1D702}_{T}h_{0}/\ell ^{2}\gg \unicode[STIX]{x1D6FC}_{0}h_{0}/\ell$
, which yields the second condition in (3.1) after rearranging and squaring the terms.
$\unicode[STIX]{x1D702}_{T}h_{0}/\ell ^{2}\gg \unicode[STIX]{x1D6FC}_{0}h_{0}/\ell$
, which yields the second condition in (3.1) after rearranging and squaring the terms.
Then the fluctuating magnetic field evolves as:
where
![]() $\boldsymbol{M}(\boldsymbol{x},t)=a(\boldsymbol{x},t)\overline{\boldsymbol{H}}(\boldsymbol{x},t)$
is a source term for the fluctuating magnetic field, and
$\boldsymbol{M}(\boldsymbol{x},t)=a(\boldsymbol{x},t)\overline{\boldsymbol{H}}(\boldsymbol{x},t)$
is a source term for the fluctuating magnetic field, and
![]() $\unicode[STIX]{x1D735}$
is the time-dependent operator defined in (2.9). The FOSA solution for the fluctuating magnetic field in the Fourier space is given by (see appendix A for a derivation),
$\unicode[STIX]{x1D735}$
is the time-dependent operator defined in (2.9). The FOSA solution for the fluctuating magnetic field in the Fourier space is given by (see appendix A for a derivation),
where the sheared Green’s function in Fourier space:
This is derived in Sridhar & Singh (Reference Sridhar and Singh2010). It may be readily verified that (3.3) satisfies both constraints,
![]() $\boldsymbol{K}\boldsymbol{\cdot }\widetilde{\boldsymbol{h}}=0$
and
$\boldsymbol{K}\boldsymbol{\cdot }\widetilde{\boldsymbol{h}}=0$
and
![]() $\widetilde{\boldsymbol{h}}(\boldsymbol{k},0)=\mathbf{0}$
. By making use of (3.3), and time-stationary Galilean-invariant statistics for the
$\widetilde{\boldsymbol{h}}(\boldsymbol{k},0)=\mathbf{0}$
. By making use of (3.3), and time-stationary Galilean-invariant statistics for the
![]() $\unicode[STIX]{x1D6FC}$
fluctuations in Fourier space (see appendix B), we obtain the following expression for the mean EMF in Fourier space, after some straightforward algebra (see appendix C for a derivation):
$\unicode[STIX]{x1D6FC}$
fluctuations in Fourier space (see appendix B), we obtain the following expression for the mean EMF in Fourier space, after some straightforward algebra (see appendix C for a derivation):
where
is a complex velocity field.
Fourier transforming (2.7), the equation governing the large-scale field is:
Thus the set of (3.5)–(3.7) describes the evolution of the large-scale magnetic field,
![]() $\widetilde{\overline{\boldsymbol{H}}}(\boldsymbol{k},t)$
in terms of a closed, linear integro-differential equation, where both shear strength,
$\widetilde{\overline{\boldsymbol{H}}}(\boldsymbol{k},t)$
in terms of a closed, linear integro-differential equation, where both shear strength,
![]() $S$
, and the
$S$
, and the
![]() $\unicode[STIX]{x1D6FC}$
-correlation time,
$\unicode[STIX]{x1D6FC}$
-correlation time,
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
, are treated non-perturbatively. This is the principal general result of this paper, but solving these in full generality is beyond the scope of the present work, and we next pursue these equations analytically by making useful approximations.
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
, are treated non-perturbatively. This is the principal general result of this paper, but solving these in full generality is beyond the scope of the present work, and we next pursue these equations analytically by making useful approximations.
3.1 White-noise
 $\unicode[STIX]{x1D6FC}$
fluctuations
$\unicode[STIX]{x1D6FC}$
fluctuations
It is useful to recall basic properties of an exactly solvable limit of
![]() $\unicode[STIX]{x1D6FF}$
-correlated-in-time
$\unicode[STIX]{x1D6FF}$
-correlated-in-time
![]() $\unicode[STIX]{x1D6FC}$
fluctuations when the normalized correlation function
$\unicode[STIX]{x1D6FC}$
fluctuations when the normalized correlation function
![]() ${\mathcal{D}}_{\text{WN}}(t)=\unicode[STIX]{x1D6FF}(t)$
which is the Dirac delta function, giving
${\mathcal{D}}_{\text{WN}}(t)=\unicode[STIX]{x1D6FF}(t)$
which is the Dirac delta function, giving
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}=0$
from (2.12). Using this in (3.5) and (3.6), and noting that
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}=0$
from (2.12). Using this in (3.5) and (3.6), and noting that
![]() $\widetilde{G}_{\unicode[STIX]{x1D702}_{T}}(\boldsymbol{k}-\boldsymbol{k}^{\prime },t,t)=1$
from (3.4), we find the mean EMF:
$\widetilde{G}_{\unicode[STIX]{x1D702}_{T}}(\boldsymbol{k}-\boldsymbol{k}^{\prime },t,t)=1$
from (3.4), we find the mean EMF:
where the
![]() $\unicode[STIX]{x1D6FC}$
-diffusivity,
$\unicode[STIX]{x1D6FC}$
-diffusivity,
![]() $\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}={\mathcal{A}}(\mathbf{0})$
, is given in (2.11) and the Moffatt drift velocity
$\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}={\mathcal{A}}(\mathbf{0})$
, is given in (2.11) and the Moffatt drift velocity
![]() $\boldsymbol{V}_{M}$
is defined in (2.13). The Kraichnan diffusivity,
$\boldsymbol{V}_{M}$
is defined in (2.13). The Kraichnan diffusivity,
![]() $\unicode[STIX]{x1D702}_{K}$
, is defined as,
$\unicode[STIX]{x1D702}_{K}$
, is defined as,
![]() $\unicode[STIX]{x1D702}_{K}=\unicode[STIX]{x1D702}_{T}-\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}$
. Using these in (3.7) leads to the solution for the large-scale magnetic field (see Sridhar & Singh (Reference Sridhar and Singh2014) for more details):
$\unicode[STIX]{x1D702}_{K}=\unicode[STIX]{x1D702}_{T}-\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}$
. Using these in (3.7) leads to the solution for the large-scale magnetic field (see Sridhar & Singh (Reference Sridhar and Singh2014) for more details):
where
 $$\begin{eqnarray}\displaystyle \widetilde{{\mathcal{G}}}(\boldsymbol{k},t) & = & \displaystyle \exp \left\{-\int _{0}^{t}\,\text{d}t^{\prime }[\unicode[STIX]{x1D702}_{K}K^{2}(\boldsymbol{k},t^{\prime })+\text{i}\boldsymbol{V}_{M}\boldsymbol{\cdot }\boldsymbol{K}(\boldsymbol{k},t^{\prime })]\right\}\nonumber\\ \displaystyle & = & \displaystyle \exp \{-\unicode[STIX]{x1D702}_{K}[k^{2}t-Sk_{1}k_{2}t^{2}+(S^{2}/3)k_{2}^{2}t^{3}]-\text{i}[(\boldsymbol{V}_{M}\boldsymbol{\cdot }\boldsymbol{k})t-(S/2)V_{M1}k_{2}t^{2}]\}.\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widetilde{{\mathcal{G}}}(\boldsymbol{k},t) & = & \displaystyle \exp \left\{-\int _{0}^{t}\,\text{d}t^{\prime }[\unicode[STIX]{x1D702}_{K}K^{2}(\boldsymbol{k},t^{\prime })+\text{i}\boldsymbol{V}_{M}\boldsymbol{\cdot }\boldsymbol{K}(\boldsymbol{k},t^{\prime })]\right\}\nonumber\\ \displaystyle & = & \displaystyle \exp \{-\unicode[STIX]{x1D702}_{K}[k^{2}t-Sk_{1}k_{2}t^{2}+(S^{2}/3)k_{2}^{2}t^{3}]-\text{i}[(\boldsymbol{V}_{M}\boldsymbol{\cdot }\boldsymbol{k})t-(S/2)V_{M1}k_{2}t^{2}]\}.\qquad\end{eqnarray}$$
This solution is identical to the one obtained in Sridhar & Singh (Reference Sridhar and Singh2014). Thus we find that the inclusion of the turbulent diffusion term in determining the mean EMF makes no difference for the dynamo solution in the white-noise limit. In agreement with earlier findings (Kraichnan Reference Kraichnan1976; Moffatt Reference Moffatt1978; Sridhar & Singh Reference Sridhar and Singh2014), we see from above that the
![]() $\unicode[STIX]{x1D6FC}$
-diffusivity causes a reduction in the turbulent diffusion of the fields, and if it is sufficiently strong, i.e. when
$\unicode[STIX]{x1D6FC}$
-diffusivity causes a reduction in the turbulent diffusion of the fields, and if it is sufficiently strong, i.e. when
![]() $\unicode[STIX]{x1D702}_{K}<0$
, this can lead to an instability giving growth of the large-scale magnetic field. Also, the Moffatt drift does not couple to the dynamo growth/decay and contributes only to the phase.
$\unicode[STIX]{x1D702}_{K}<0$
, this can lead to an instability giving growth of the large-scale magnetic field. Also, the Moffatt drift does not couple to the dynamo growth/decay and contributes only to the phase.
4 Axisymmetric large-scale dynamo equation with finite
 $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
We now turn to the principal aim of this work where we are more interested in exploring the possibility of a large-scale dynamo even when the
![]() $\unicode[STIX]{x1D6FC}$
fluctuations are weak, i.e. when
$\unicode[STIX]{x1D6FC}$
fluctuations are weak, i.e. when
![]() $\unicode[STIX]{x1D702}_{K}>0$
, by taking the memory effects into account. Assuming a small but finite correlation time for
$\unicode[STIX]{x1D702}_{K}>0$
, by taking the memory effects into account. Assuming a small but finite correlation time for
![]() $\unicode[STIX]{x1D6FC}$
fluctuations,
$\unicode[STIX]{x1D6FC}$
fluctuations,
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}\neq 0$
, we reduce the general set of (3.5)–(3.7) into a partial differential equation governing the dynamics of the large-scale magnetic field which evolves over times much larger than
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}\neq 0$
, we reduce the general set of (3.5)–(3.7) into a partial differential equation governing the dynamics of the large-scale magnetic field which evolves over times much larger than
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
. In this case, the normalized time correlation function,
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
. In this case, the normalized time correlation function,
![]() ${\mathcal{D}}(t)$
, is significant only for times
${\mathcal{D}}(t)$
, is significant only for times
![]() $t\leqslant \unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
and it becomes negligible for larger times. The generalized mean EMF as given in (3.5) involves a time integral which can be solved under the small
$t\leqslant \unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
and it becomes negligible for larger times. The generalized mean EMF as given in (3.5) involves a time integral which can be solved under the small
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
approximation.
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
approximation.
Since the limit
![]() $\lim _{\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}\rightarrow 0}\widetilde{\overline{\boldsymbol{E}}}(\boldsymbol{k},t)=\widetilde{\overline{\boldsymbol{E}}}_{\text{WN}}(\boldsymbol{k},t)$
, given by (3.8), is non-singular, we proceed by making the following ansatz where, for small
$\lim _{\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}\rightarrow 0}\widetilde{\overline{\boldsymbol{E}}}(\boldsymbol{k},t)=\widetilde{\overline{\boldsymbol{E}}}_{\text{WN}}(\boldsymbol{k},t)$
, given by (3.8), is non-singular, we proceed by making the following ansatz where, for small
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
, the mean EMF can be expanded in a power series in
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
, the mean EMF can be expanded in a power series in
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
as:
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
as:
where
![]() $\widetilde{\overline{\boldsymbol{E}}}_{\text{WN}}(\boldsymbol{k},t)\sim O(1)$
and
$\widetilde{\overline{\boldsymbol{E}}}_{\text{WN}}(\boldsymbol{k},t)\sim O(1)$
and
![]() $\widetilde{\overline{\boldsymbol{E}}}^{(n)}(\boldsymbol{k},t)\sim O(\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}^{n})$
for
$\widetilde{\overline{\boldsymbol{E}}}^{(n)}(\boldsymbol{k},t)\sim O(\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}^{n})$
for
![]() $n\geqslant 1$
. Below we verify this ansatz up to
$n\geqslant 1$
. Below we verify this ansatz up to
![]() $n=1$
, for slowly varying magnetic fields. From (3.5) we determine
$n=1$
, for slowly varying magnetic fields. From (3.5) we determine
![]() $\widetilde{\overline{\boldsymbol{E}}}(\boldsymbol{k},t)$
to first order in
$\widetilde{\overline{\boldsymbol{E}}}(\boldsymbol{k},t)$
to first order in
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
, for
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
, for
![]() $t\gg \unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
, by (i) changing the integration variable from
$t\gg \unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
, by (i) changing the integration variable from
![]() $t^{\prime }$
to
$t^{\prime }$
to
![]() $s=t-t^{\prime }$
; (ii) setting the upper limit of the time integral to
$s=t-t^{\prime }$
; (ii) setting the upper limit of the time integral to
![]() $+\infty$
, since
$+\infty$
, since
![]() ${\mathcal{D}}(s)$
is significant only for times
${\mathcal{D}}(s)$
is significant only for times
![]() $s\leqslant \unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
as mentioned above, suggesting that only short times
$s\leqslant \unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
as mentioned above, suggesting that only short times
![]() $0\leqslant s<\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
contribute appreciably to the integral in (3.5); and (iii) keeping the terms inside the
$0\leqslant s<\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
contribute appreciably to the integral in (3.5); and (iii) keeping the terms inside the
![]() $\{\;\}$
in the integrand of (3.5) up to only first order in
$\{\;\}$
in the integrand of (3.5) up to only first order in
![]() $s$
. To be able to expand in
$s$
. To be able to expand in
![]() $s$
, we need to first express the (3.6) in the laboratory-frame wavevector
$s$
, we need to first express the (3.6) in the laboratory-frame wavevector
![]() $\boldsymbol{K}=\boldsymbol{K}(\boldsymbol{k},t^{\prime })=\boldsymbol{K}(\boldsymbol{k},t-s)$
, so that the Green’s function in (3.4) and therefore the complex velocity field
$\boldsymbol{K}=\boldsymbol{K}(\boldsymbol{k},t^{\prime })=\boldsymbol{K}(\boldsymbol{k},t-s)$
, so that the Green’s function in (3.4) and therefore the complex velocity field
![]() $\widetilde{\boldsymbol{U}}$
in (3.6) becomes time-translational symmetric.Footnote
1
$\widetilde{\boldsymbol{U}}$
in (3.6) becomes time-translational symmetric.Footnote
1
We first rewrite the mean EMF, given in (3.5), as
where the complex velocity field,
![]() $\widetilde{\boldsymbol{U}}$
, is
$\widetilde{\boldsymbol{U}}$
, is
Equation (4.3) is obtained by changing the integration variable in (3.6) to
![]() $\boldsymbol{K}^{\prime }=\boldsymbol{K}(\boldsymbol{k}^{\prime },t^{\prime })=(k_{1}^{\prime }-S(t-s)k_{2}^{\prime },k_{2}^{\prime },k_{3}^{\prime })$
– which has unit Jacobian, giving
$\boldsymbol{K}^{\prime }=\boldsymbol{K}(\boldsymbol{k}^{\prime },t^{\prime })=(k_{1}^{\prime }-S(t-s)k_{2}^{\prime },k_{2}^{\prime },k_{3}^{\prime })$
– which has unit Jacobian, giving
![]() $\text{d}^{3}k^{\prime }=\text{d}^{3}K^{\prime }$
.
$\text{d}^{3}k^{\prime }=\text{d}^{3}K^{\prime }$
.
We make further simplification by considering only axisymmetric modes for which
![]() $k_{2}=0$
. Note that for the non-axisymmetric modes,
$k_{2}=0$
. Note that for the non-axisymmetric modes,
![]() $\boldsymbol{K}(\boldsymbol{k},t)=\boldsymbol{e}_{1}(k_{1}-Stk_{2})+\boldsymbol{e}_{2}k_{2}+\boldsymbol{e}_{3}k_{3}$
increases monotonically with time, increasing the wavenumber, which would eventually decay by turbulent diffusivity. Therefore we focus our attention only on axisymmetric modes, for which
$\boldsymbol{K}(\boldsymbol{k},t)=\boldsymbol{e}_{1}(k_{1}-Stk_{2})+\boldsymbol{e}_{2}k_{2}+\boldsymbol{e}_{3}k_{3}$
increases monotonically with time, increasing the wavenumber, which would eventually decay by turbulent diffusivity. Therefore we focus our attention only on axisymmetric modes, for which
![]() $\boldsymbol{K}(\boldsymbol{k},t-s)=\boldsymbol{K}(\boldsymbol{k},t)=\boldsymbol{k}=(k_{1},0,k_{3})$
.
$\boldsymbol{K}(\boldsymbol{k},t-s)=\boldsymbol{K}(\boldsymbol{k},t)=\boldsymbol{k}=(k_{1},0,k_{3})$
.
Let us first work out
![]() $\widetilde{\boldsymbol{U}}(\boldsymbol{k},s)$
and
$\widetilde{\boldsymbol{U}}(\boldsymbol{k},s)$
and
![]() $\widetilde{\overline{\boldsymbol{H}}}(\boldsymbol{k},t-s)$
correct up to
$\widetilde{\overline{\boldsymbol{H}}}(\boldsymbol{k},t-s)$
correct up to
![]() $O(s)$
.
$O(s)$
.
![]() $(1)\;\;\text{}\underline{\widetilde{\boldsymbol{U}}(\boldsymbol{k},s)\;\text{to}\;O(s):}$
Taylor expanding
$(1)\;\;\text{}\underline{\widetilde{\boldsymbol{U}}(\boldsymbol{k},s)\;\text{to}\;O(s):}$
Taylor expanding
![]() $\widetilde{\boldsymbol{U}}(\boldsymbol{k},s)$
gives,
$\widetilde{\boldsymbol{U}}(\boldsymbol{k},s)$
gives,
Equation (4.6) is obtained by differentiating equation (4.3) with respect to
![]() $s$
and taking the limit
$s$
and taking the limit
![]() $s\rightarrow 0$
; note that
$s\rightarrow 0$
; note that
![]() $\boldsymbol{K}=\boldsymbol{k}$
, since
$\boldsymbol{K}=\boldsymbol{k}$
, since
![]() $k_{2}=0$
. Using the Fourier transform for
$k_{2}=0$
. Using the Fourier transform for
![]() $\widetilde{{\mathcal{A}}}$
, together with the properties of the
$\widetilde{{\mathcal{A}}}$
, together with the properties of the
![]() $\unicode[STIX]{x1D6FF}$
-function, we get
$\unicode[STIX]{x1D6FF}$
-function, we get
 $$\begin{eqnarray}\displaystyle \left.\frac{\unicode[STIX]{x2202}\widetilde{\boldsymbol{U}}}{\unicode[STIX]{x2202}s}\right|_{s=0} & = & \displaystyle -\text{i}\unicode[STIX]{x1D702}_{T}\!\left\{k^{2}(\boldsymbol{k}{\mathcal{A}}(\unicode[STIX]{x1D743})+\text{i}[\unicode[STIX]{x1D735}{\mathcal{A}}(\unicode[STIX]{x1D743})])+2\text{i}\boldsymbol{k}(\boldsymbol{k}\boldsymbol{\cdot }[\unicode[STIX]{x1D735}{\mathcal{A}}(\unicode[STIX]{x1D743})])\right.\nonumber\\ \displaystyle & & \displaystyle -\left.\boldsymbol{k}[\unicode[STIX]{x1D6FB}^{2}{\mathcal{A}}(\unicode[STIX]{x1D743})]-\text{i}[\unicode[STIX]{x1D6FB}^{2}\{\unicode[STIX]{x1D735}{\mathcal{A}}(\unicode[STIX]{x1D743})\}]-2(\boldsymbol{k}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\{\unicode[STIX]{x1D735}{\mathcal{A}}(\unicode[STIX]{x1D743})\}\right\}_{\unicode[STIX]{x1D743}=0}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\frac{\unicode[STIX]{x2202}\widetilde{\boldsymbol{U}}}{\unicode[STIX]{x2202}s}\right|_{s=0} & = & \displaystyle -\text{i}\unicode[STIX]{x1D702}_{T}\!\left\{k^{2}(\boldsymbol{k}{\mathcal{A}}(\unicode[STIX]{x1D743})+\text{i}[\unicode[STIX]{x1D735}{\mathcal{A}}(\unicode[STIX]{x1D743})])+2\text{i}\boldsymbol{k}(\boldsymbol{k}\boldsymbol{\cdot }[\unicode[STIX]{x1D735}{\mathcal{A}}(\unicode[STIX]{x1D743})])\right.\nonumber\\ \displaystyle & & \displaystyle -\left.\boldsymbol{k}[\unicode[STIX]{x1D6FB}^{2}{\mathcal{A}}(\unicode[STIX]{x1D743})]-\text{i}[\unicode[STIX]{x1D6FB}^{2}\{\unicode[STIX]{x1D735}{\mathcal{A}}(\unicode[STIX]{x1D743})\}]-2(\boldsymbol{k}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\{\unicode[STIX]{x1D735}{\mathcal{A}}(\unicode[STIX]{x1D743})\}\right\}_{\unicode[STIX]{x1D743}=0}.\end{eqnarray}$$
Equation (4.7) can be evaluated once we know the functional form for spatial correlator
![]() ${\mathcal{A}}(\unicode[STIX]{x1D743})$
. Neglecting derivatives of
${\mathcal{A}}(\unicode[STIX]{x1D743})$
. Neglecting derivatives of
![]() ${\mathcal{A}}$
that are higher than the first order – see Singh (Reference Singh2016) for detail – we have:
${\mathcal{A}}$
that are higher than the first order – see Singh (Reference Singh2016) for detail – we have:
Equation (4.5) and (4.8) together thus provide the function
![]() $\widetilde{\boldsymbol{U}}(\boldsymbol{k},s)$
correct up to
$\widetilde{\boldsymbol{U}}(\boldsymbol{k},s)$
correct up to
![]() $O(s)$
.
$O(s)$
.
![]() $(2)\;\;\text{}\underline{\widetilde{\overline{\boldsymbol{H}}}(\boldsymbol{k},t-s)\;\text{to}\;O(s):}$
We write as,
$(2)\;\;\text{}\underline{\widetilde{\overline{\boldsymbol{H}}}(\boldsymbol{k},t-s)\;\text{to}\;O(s):}$
We write as,
where it is assumed that
![]() $|\widetilde{\overline{\boldsymbol{H}}}|\gg s|\unicode[STIX]{x2202}\widetilde{\overline{\boldsymbol{H}}}/\unicode[STIX]{x2202}t|\gg s^{2}|\unicode[STIX]{x2202}^{2}\widetilde{\overline{\boldsymbol{H}}}/\unicode[STIX]{x2202}t^{2}|,\text{etc}$
. In (4.9), we need
$|\widetilde{\overline{\boldsymbol{H}}}|\gg s|\unicode[STIX]{x2202}\widetilde{\overline{\boldsymbol{H}}}/\unicode[STIX]{x2202}t|\gg s^{2}|\unicode[STIX]{x2202}^{2}\widetilde{\overline{\boldsymbol{H}}}/\unicode[STIX]{x2202}t^{2}|,\text{etc}$
. In (4.9), we need
![]() $\unicode[STIX]{x2202}\widetilde{\overline{\boldsymbol{H}}}/\unicode[STIX]{x2202}t$
only up to
$\unicode[STIX]{x2202}\widetilde{\overline{\boldsymbol{H}}}/\unicode[STIX]{x2202}t$
only up to
![]() $O(1)$
to find
$O(1)$
to find
![]() $\widetilde{\overline{\boldsymbol{H}}}(\boldsymbol{k},t-s)$
up to
$\widetilde{\overline{\boldsymbol{H}}}(\boldsymbol{k},t-s)$
up to
![]() $O(s)$
. We write this by substituting (3.8) in (3.7) and using
$O(s)$
. We write this by substituting (3.8) in (3.7) and using
![]() $\widetilde{\boldsymbol{U}}_{\text{WN}}(\boldsymbol{k},t)=\widetilde{\boldsymbol{U}}_{\text{WN}}(\boldsymbol{k})=\text{i}\boldsymbol{k}\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}+\boldsymbol{V}_{M}$
:
$\widetilde{\boldsymbol{U}}_{\text{WN}}(\boldsymbol{k},t)=\widetilde{\boldsymbol{U}}_{\text{WN}}(\boldsymbol{k})=\text{i}\boldsymbol{k}\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}+\boldsymbol{V}_{M}$
:
 $$\begin{eqnarray}\left.\frac{\unicode[STIX]{x2202}\widetilde{\overline{\boldsymbol{H}}}}{\unicode[STIX]{x2202}t}\right|_{O(1)}=S\widetilde{\overline{H}_{1}}\boldsymbol{e}_{2}+\text{i}\boldsymbol{k}\times \widetilde{\overline{\boldsymbol{E}}}_{\text{WN}}-\unicode[STIX]{x1D702}_{T}k^{2}\,\widetilde{\overline{\boldsymbol{H}}}=S\widetilde{\overline{H}_{1}}\boldsymbol{e}_{2}-(\unicode[STIX]{x1D702}_{K}k^{2}+\text{i}\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{V}_{\text{M}})\widetilde{\overline{\boldsymbol{H}}}.\end{eqnarray}$$
$$\begin{eqnarray}\left.\frac{\unicode[STIX]{x2202}\widetilde{\overline{\boldsymbol{H}}}}{\unicode[STIX]{x2202}t}\right|_{O(1)}=S\widetilde{\overline{H}_{1}}\boldsymbol{e}_{2}+\text{i}\boldsymbol{k}\times \widetilde{\overline{\boldsymbol{E}}}_{\text{WN}}-\unicode[STIX]{x1D702}_{T}k^{2}\,\widetilde{\overline{\boldsymbol{H}}}=S\widetilde{\overline{H}_{1}}\boldsymbol{e}_{2}-(\unicode[STIX]{x1D702}_{K}k^{2}+\text{i}\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{V}_{\text{M}})\widetilde{\overline{\boldsymbol{H}}}.\end{eqnarray}$$
The time integral in (4.2) is then solved by using the definitions provided in (2.11) and (2.12) when we substitute the expressions derived above for the terms in
![]() $\{\;\}$
in (4.2). We get, after straightforward algebra, the following expression for the mean EMF, which is correct up to
$\{\;\}$
in (4.2). We get, after straightforward algebra, the following expression for the mean EMF, which is correct up to
![]() $O(\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}})$
:
$O(\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}})$
:
This verifies the ansatz of (4.1) up to
![]() $n=1$
, as claimed. It is important to note that the (4.11) is valid only for slowly varying large-scale magnetic fields. To lowest order this condition can be explicitly stated as:
$n=1$
, as claimed. It is important to note that the (4.11) is valid only for slowly varying large-scale magnetic fields. To lowest order this condition can be explicitly stated as:
![]() $|\widetilde{\overline{\boldsymbol{H}}}|\gg \unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}|\unicode[STIX]{x2202}\widetilde{\overline{\boldsymbol{H}}}/\unicode[STIX]{x2202}t|$
. To obtain the sufficient condition for the validity of (4.11), use (4.10) for
$|\widetilde{\overline{\boldsymbol{H}}}|\gg \unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}|\unicode[STIX]{x2202}\widetilde{\overline{\boldsymbol{H}}}/\unicode[STIX]{x2202}t|$
. To obtain the sufficient condition for the validity of (4.11), use (4.10) for
![]() $\unicode[STIX]{x2202}\widetilde{\overline{\boldsymbol{H}}}/\unicode[STIX]{x2202}t$
to get the following conditions for three dimensionless quantities which need to be small:
$\unicode[STIX]{x2202}\widetilde{\overline{\boldsymbol{H}}}/\unicode[STIX]{x2202}t$
to get the following conditions for three dimensionless quantities which need to be small:
Since we have expanded EMF in small
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
, it is only the first of the two FOSA conditions in (3.1) that becomes relevant. This must be added to the above three conditions for (4.11) to be valid. Using (4.11) in (3.7) we obtain:
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
, it is only the first of the two FOSA conditions in (3.1) that becomes relevant. This must be added to the above three conditions for (4.11) to be valid. Using (4.11) in (3.7) we obtain:
 $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}\widetilde{\overline{\boldsymbol{H}}}}{\unicode[STIX]{x2202}t} & = & \displaystyle [S\widetilde{\overline{H}}_{1}\boldsymbol{e}_{2}+\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}k^{2}\widetilde{\overline{\boldsymbol{H}}}-\text{i}(\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{V}_{M})\widetilde{\overline{\boldsymbol{H}}}][1+\text{i}(\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{V}_{M})\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}-\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}k^{2}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}]-\unicode[STIX]{x1D702}_{T}k^{2}\widetilde{\overline{\boldsymbol{H}}}\nonumber\\ \displaystyle & & \displaystyle +\,2\text{i}\unicode[STIX]{x1D702}_{T}k^{2}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}(\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{V}_{M})\widetilde{\overline{\boldsymbol{H}}}+S\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}[V_{M2}\widetilde{\overline{H}}_{3}-V_{M3}\widetilde{\overline{H}}_{2}-\text{i}\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}k_{3}\widetilde{\overline{H}}_{2}][-\text{i}k_{3}\boldsymbol{e}_{1}+\text{i}k_{1}\boldsymbol{e}_{3}],\nonumber\\ \displaystyle & & \displaystyle \text{with }\boldsymbol{k}=(k_{1},0,k_{3}),\;\text{and}\;k_{1}\widetilde{\overline{H}}_{1}+k_{3}\widetilde{\overline{H}}_{3}=0.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}\widetilde{\overline{\boldsymbol{H}}}}{\unicode[STIX]{x2202}t} & = & \displaystyle [S\widetilde{\overline{H}}_{1}\boldsymbol{e}_{2}+\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}k^{2}\widetilde{\overline{\boldsymbol{H}}}-\text{i}(\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{V}_{M})\widetilde{\overline{\boldsymbol{H}}}][1+\text{i}(\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{V}_{M})\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}-\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}k^{2}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}]-\unicode[STIX]{x1D702}_{T}k^{2}\widetilde{\overline{\boldsymbol{H}}}\nonumber\\ \displaystyle & & \displaystyle +\,2\text{i}\unicode[STIX]{x1D702}_{T}k^{2}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}(\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{V}_{M})\widetilde{\overline{\boldsymbol{H}}}+S\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}[V_{M2}\widetilde{\overline{H}}_{3}-V_{M3}\widetilde{\overline{H}}_{2}-\text{i}\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}k_{3}\widetilde{\overline{H}}_{2}][-\text{i}k_{3}\boldsymbol{e}_{1}+\text{i}k_{1}\boldsymbol{e}_{3}],\nonumber\\ \displaystyle & & \displaystyle \text{with }\boldsymbol{k}=(k_{1},0,k_{3}),\;\text{and}\;k_{1}\widetilde{\overline{H}}_{1}+k_{3}\widetilde{\overline{H}}_{3}=0.\end{eqnarray}$$
Equation (4.13) is the linear partial differential equation obtained by reducing the linear integro-differential equation (see (3.5)–(3.7)) under the condition of (4.12). It describes the evolution of an axisymmetric, large-scale magnetic field over times that are much larger than
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
. It depends on (i) the diffusivity
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
. It depends on (i) the diffusivity
![]() $\unicode[STIX]{x1D702}_{T}$
; (ii) properties of the
$\unicode[STIX]{x1D702}_{T}$
; (ii) properties of the
![]() $\unicode[STIX]{x1D6FC}$
correlation in terms of
$\unicode[STIX]{x1D6FC}$
correlation in terms of
![]() $\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}$
,
$\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}$
,
![]() $\boldsymbol{V}_{M}$
and
$\boldsymbol{V}_{M}$
and
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
; (iii) shear
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
; (iii) shear
![]() $S$
. These must satisfy the three conditions given in (4.12) and the first condition in (3.1) for the validity of (4.13). We note here again that the set of (3.5)–(3.7) is non-perturbative in both
$S$
. These must satisfy the three conditions given in (4.12) and the first condition in (3.1) for the validity of (4.13). We note here again that the set of (3.5)–(3.7) is non-perturbative in both
![]() $S$
and
$S$
and
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
, whereas (4.13) is valid only when
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
, whereas (4.13) is valid only when
![]() $|S\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}|\ll 1$
.
$|S\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}|\ll 1$
.
5 Growth rate of modes when
 $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
is non-zero
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
is non-zero
As usual in numerical works on the related subject (see, e.g. Brandenburg et al.
Reference Brandenburg, Rädler, Rheinhardt and Käpylä2008; Singh & Jingade Reference Singh and Jingade2015) where ‘horizontal’ (plane of shear; in this case the
![]() $X_{1}-X_{2}$
plane) averages are performed to define the large-scale magnetic fields, it is useful to consider one-dimensional propagating modes. This is equivalent to setting
$X_{1}-X_{2}$
plane) averages are performed to define the large-scale magnetic fields, it is useful to consider one-dimensional propagating modes. This is equivalent to setting
![]() $K_{1}$
and
$K_{1}$
and
![]() $K_{2}$
equal to zero. Here we only need to set
$K_{2}$
equal to zero. Here we only need to set
![]() $k_{1}=0$
in (4.13). In this case the wavevector
$k_{1}=0$
in (4.13). In this case the wavevector
![]() $\boldsymbol{k}=(0,0,k)$
points along the ‘vertical’ (
$\boldsymbol{k}=(0,0,k)$
points along the ‘vertical’ (
![]() $\pm \boldsymbol{e}_{3}$
) direction, thus resulting in a uniform
$\pm \boldsymbol{e}_{3}$
) direction, thus resulting in a uniform
![]() $\widetilde{\overline{H}}_{3}$
which is of no interest for dynamo action. Hence we set
$\widetilde{\overline{H}}_{3}$
which is of no interest for dynamo action. Hence we set
![]() $\widetilde{\overline{H}}_{3}=0$
, and take
$\widetilde{\overline{H}}_{3}=0$
, and take
![]() $\widetilde{\overline{\boldsymbol{H}}}(k,t)=\widetilde{\overline{H}}_{1}(k,t)\boldsymbol{e}_{1}+\widetilde{\overline{H}}_{2}(k,t)\boldsymbol{e}_{2}$
. Making these substitutions in (4.13) we find:
$\widetilde{\overline{\boldsymbol{H}}}(k,t)=\widetilde{\overline{H}}_{1}(k,t)\boldsymbol{e}_{1}+\widetilde{\overline{H}}_{2}(k,t)\boldsymbol{e}_{2}$
. Making these substitutions in (4.13) we find:
 $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}\widetilde{\overline{\boldsymbol{H}}}}{\unicode[STIX]{x2202}t} & = & \displaystyle [S\widetilde{\overline{H}}_{1}\boldsymbol{e}_{2}+\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}k^{2}\widetilde{\overline{\boldsymbol{H}}}-\text{i}kV_{M3}\widetilde{\overline{\boldsymbol{H}}}][1+\text{i}kV_{M3}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}-\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}k^{2}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}]-\unicode[STIX]{x1D702}_{T}k^{2}\widetilde{\overline{\boldsymbol{H}}}\nonumber\\ \displaystyle & & \displaystyle +\,2\text{i}\unicode[STIX]{x1D702}_{T}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}(k^{3}V_{M3})\widetilde{\overline{\boldsymbol{H}}}+S[\text{i}kV_{M3}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}-\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}k^{2}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}]\widetilde{\overline{H}}_{2}\boldsymbol{e}_{1}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}\widetilde{\overline{\boldsymbol{H}}}}{\unicode[STIX]{x2202}t} & = & \displaystyle [S\widetilde{\overline{H}}_{1}\boldsymbol{e}_{2}+\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}k^{2}\widetilde{\overline{\boldsymbol{H}}}-\text{i}kV_{M3}\widetilde{\overline{\boldsymbol{H}}}][1+\text{i}kV_{M3}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}-\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}k^{2}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}]-\unicode[STIX]{x1D702}_{T}k^{2}\widetilde{\overline{\boldsymbol{H}}}\nonumber\\ \displaystyle & & \displaystyle +\,2\text{i}\unicode[STIX]{x1D702}_{T}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}(k^{3}V_{M3})\widetilde{\overline{\boldsymbol{H}}}+S[\text{i}kV_{M3}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}-\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}k^{2}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}]\widetilde{\overline{H}}_{2}\boldsymbol{e}_{1}.\end{eqnarray}$$
Seeking modal solutions of the form,
and substituting this in (5.1) we get the following dispersion relation:
We are more interested in the growth rate
![]() $\unicode[STIX]{x1D6FE}=\text{Re}\{\unicode[STIX]{x1D706}\}$
, as the dynamo action corresponds to the case when
$\unicode[STIX]{x1D6FE}=\text{Re}\{\unicode[STIX]{x1D706}\}$
, as the dynamo action corresponds to the case when
![]() $\unicode[STIX]{x1D6FE}>0$
. From the dispersion relation (5.3) we have:
$\unicode[STIX]{x1D6FE}>0$
. From the dispersion relation (5.3) we have:
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \unicode[STIX]{x1D6FE}_{\pm }=\text{Re}\{\unicode[STIX]{x1D706}_{\pm }\}=-\unicode[STIX]{x1D702}_{K}k^{2}-\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}^{2}k^{4}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}+(kV_{M3})^{2}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}\pm |S|[\unicode[STIX]{x1D712}_{R}^{2}+\unicode[STIX]{x1D712}_{I}^{2}]^{1/4}\cos (\unicode[STIX]{x1D713}/2),\\ \displaystyle \text{where }\cos (\unicode[STIX]{x1D713})=\frac{\unicode[STIX]{x1D712}_{R}}{(\unicode[STIX]{x1D712}_{R}^{2}+\unicode[STIX]{x1D712}_{I}^{2})^{1/2}},\quad \cos (\unicode[STIX]{x1D713}/2)=\frac{\sqrt{\unicode[STIX]{x1D712}_{R}+\sqrt{\unicode[STIX]{x1D712}_{R}^{2}+\unicode[STIX]{x1D712}_{I}^{2}}}}{\sqrt{2}(\unicode[STIX]{x1D712}_{R}^{2}+\unicode[STIX]{x1D712}_{I}^{2})^{1/4}},\\ \displaystyle \unicode[STIX]{x1D712}_{R}=\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}k^{2}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}k^{2}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}-1)-(kV_{M3}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}})^{2},\quad \unicode[STIX]{x1D712}_{I}=-kV_{M3}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}(2\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}k^{2}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}-1).\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \unicode[STIX]{x1D6FE}_{\pm }=\text{Re}\{\unicode[STIX]{x1D706}_{\pm }\}=-\unicode[STIX]{x1D702}_{K}k^{2}-\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}^{2}k^{4}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}+(kV_{M3})^{2}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}\pm |S|[\unicode[STIX]{x1D712}_{R}^{2}+\unicode[STIX]{x1D712}_{I}^{2}]^{1/4}\cos (\unicode[STIX]{x1D713}/2),\\ \displaystyle \text{where }\cos (\unicode[STIX]{x1D713})=\frac{\unicode[STIX]{x1D712}_{R}}{(\unicode[STIX]{x1D712}_{R}^{2}+\unicode[STIX]{x1D712}_{I}^{2})^{1/2}},\quad \cos (\unicode[STIX]{x1D713}/2)=\frac{\sqrt{\unicode[STIX]{x1D712}_{R}+\sqrt{\unicode[STIX]{x1D712}_{R}^{2}+\unicode[STIX]{x1D712}_{I}^{2}}}}{\sqrt{2}(\unicode[STIX]{x1D712}_{R}^{2}+\unicode[STIX]{x1D712}_{I}^{2})^{1/4}},\\ \displaystyle \unicode[STIX]{x1D712}_{R}=\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}k^{2}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}k^{2}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}-1)-(kV_{M3}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}})^{2},\quad \unicode[STIX]{x1D712}_{I}=-kV_{M3}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}(2\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}k^{2}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}-1).\end{array}\right\}\end{eqnarray}$$
Below, we make some comments about the growth rate derived above.
(i) The growth rate
 $\unicode[STIX]{x1D6FE}$
of the large-scale dynamo is linear in the shear rate
$\unicode[STIX]{x1D6FE}$
of the large-scale dynamo is linear in the shear rate
 $|S|$
, assuming that the parameters (
$|S|$
, assuming that the parameters (
 $\unicode[STIX]{x1D702}_{K},\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}},V_{M3},\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
) are all independent of
$\unicode[STIX]{x1D702}_{K},\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}},V_{M3},\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
) are all independent of
 $S$
. This linear scaling is observed in earlier numerical works (Brandenburg et al.
Reference Brandenburg, Rädler, Rheinhardt and Käpylä2008; Yousef et al.
Reference Yousef, Heinemann, Schekochihin, Kleeorin, Rogachevskii, Iskakov, Cowley and Mcwilliams2008a
,Reference Yousef, Heinemann, Rincon, Schekochihin, Kleeorin, Rogachevskii, Cowley and Mcwilliams
b
; Singh & Jingade Reference Singh and Jingade2015).
$S$
. This linear scaling is observed in earlier numerical works (Brandenburg et al.
Reference Brandenburg, Rädler, Rheinhardt and Käpylä2008; Yousef et al.
Reference Yousef, Heinemann, Schekochihin, Kleeorin, Rogachevskii, Iskakov, Cowley and Mcwilliams2008a
,Reference Yousef, Heinemann, Rincon, Schekochihin, Kleeorin, Rogachevskii, Cowley and Mcwilliams
b
; Singh & Jingade Reference Singh and Jingade2015).(ii) For zero shear, the growth rate as given from (5.4) becomes identical to the one derived in Singh (Reference Singh2016), where the generalization to the Kraichnan problem as well as the possibility of Moffatt drift driven dynamos were explored in detail.
(iii) The last term involving shear in (5.4) is identical to the corresponding term in the expression for the growth rate derived in Sridhar & Singh (Reference Sridhar and Singh2014), with an important difference being that there the angle
 $\unicode[STIX]{x1D713}$
was defined using the tangent function, which introduces an error when either of the two,
$\unicode[STIX]{x1D713}$
was defined using the tangent function, which introduces an error when either of the two,
 $\unicode[STIX]{x1D712}_{R}$
and
$\unicode[STIX]{x1D712}_{R}$
and
 $\unicode[STIX]{x1D712}_{I}$
, take negative values. Here we correct this by explicitly writing
$\unicode[STIX]{x1D712}_{I}$
, take negative values. Here we correct this by explicitly writing
 $\cos (\unicode[STIX]{x1D713}/2)$
in terms of
$\cos (\unicode[STIX]{x1D713}/2)$
in terms of
 $\unicode[STIX]{x1D712}_{R}$
and
$\unicode[STIX]{x1D712}_{R}$
and
 $\unicode[STIX]{x1D712}_{I}$
.
$\unicode[STIX]{x1D712}_{I}$
.
5.1 Dimensionless growth rate function
The growth rate function
![]() $\unicode[STIX]{x1D6E4}$
is defined using dimensionless quantities,
$\unicode[STIX]{x1D6E4}$
is defined using dimensionless quantities,
where
![]() $\unicode[STIX]{x1D6FD}$
and
$\unicode[STIX]{x1D6FD}$
and
![]() $\unicode[STIX]{x1D700}_{K}$
measure the wavenumber of modal mean magnetic field in terms of
$\unicode[STIX]{x1D700}_{K}$
measure the wavenumber of modal mean magnetic field in terms of
![]() $\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}$
and
$\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}$
and
![]() $\unicode[STIX]{x1D702}_{K}$
, respectively. With the first condition of (3.1),
$\unicode[STIX]{x1D702}_{K}$
, respectively. With the first condition of (3.1),
![]() $\unicode[STIX]{x1D6FD}/k^{2}=\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}\ll \ell ^{2}$
. These parameters can vary as,
$\unicode[STIX]{x1D6FD}/k^{2}=\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}\ll \ell ^{2}$
. These parameters can vary as,
The parameter
![]() $\unicode[STIX]{x1D6FD}$
can be larger or smaller than unity depending on whether the mean-field varies over scales smaller or larger than
$\unicode[STIX]{x1D6FD}$
can be larger or smaller than unity depending on whether the mean-field varies over scales smaller or larger than
![]() $\ell$
, respectively. The second condition comes from
$\ell$
, respectively. The second condition comes from
![]() $\unicode[STIX]{x1D6FD}+\unicode[STIX]{x1D700}_{K}=\unicode[STIX]{x1D702}_{T}k^{2}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}>0$
, and last three constraints come from (4.12). Multiplying the expression for
$\unicode[STIX]{x1D6FD}+\unicode[STIX]{x1D700}_{K}=\unicode[STIX]{x1D702}_{T}k^{2}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}>0$
, and last three constraints come from (4.12). Multiplying the expression for
![]() $\unicode[STIX]{x1D6FE}_{\pm }$
in (5.4) by
$\unicode[STIX]{x1D6FE}_{\pm }$
in (5.4) by
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
, and denoting by
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
, and denoting by
![]() $\unicode[STIX]{x1D6E4}_{{>}}$
(
$\unicode[STIX]{x1D6E4}_{{>}}$
(
![]() $\unicode[STIX]{x1D6E4}_{{<}}$
) the larger (smaller) of
$\unicode[STIX]{x1D6E4}_{{<}}$
) the larger (smaller) of
![]() $\unicode[STIX]{x1D6E4}_{+}$
and
$\unicode[STIX]{x1D6E4}_{+}$
and
![]() $\unicode[STIX]{x1D6E4}_{-}$
, we get
$\unicode[STIX]{x1D6E4}_{-}$
, we get
Note that the radicand in (5.7) is greater than zero. In figure 1 we show the behaviour of
![]() $\unicode[STIX]{x1D6E4}$
as a function of
$\unicode[STIX]{x1D6E4}$
as a function of
![]() $\unicode[STIX]{x1D6FD}$
by keeping other parameters fixed. Below we list some properties of the growth rate function as defined in (5.7).
$\unicode[STIX]{x1D6FD}$
by keeping other parameters fixed. Below we list some properties of the growth rate function as defined in (5.7).
(i) For fixed
 $\unicode[STIX]{x1D700}_{K}$
,
$\unicode[STIX]{x1D700}_{K}$
,
 $\unicode[STIX]{x1D6FD}$
and
$\unicode[STIX]{x1D6FD}$
and
 $\unicode[STIX]{x1D700}_{M}$
,
$\unicode[STIX]{x1D700}_{M}$
,
 $\unicode[STIX]{x1D6E4}_{{>}}$
(
$\unicode[STIX]{x1D6E4}_{{>}}$
(
 $\unicode[STIX]{x1D6E4}_{{<}}$
) increases (decreases) monotonically with shear.
$\unicode[STIX]{x1D6E4}_{{<}}$
) increases (decreases) monotonically with shear.(ii) When
 $\unicode[STIX]{x1D700}_{M}$
is non-zero, then the radicand in (5.7) vanishes at
$\unicode[STIX]{x1D700}_{M}$
is non-zero, then the radicand in (5.7) vanishes at
 $\unicode[STIX]{x1D6FD}=1/2$
, where the two roots coincide; see green solid and dashed curves in figure 1. Both roots are identical for
$\unicode[STIX]{x1D6FD}=1/2$
, where the two roots coincide; see green solid and dashed curves in figure 1. Both roots are identical for
 $0\leqslant \unicode[STIX]{x1D6FD}\leqslant 1$
when
$0\leqslant \unicode[STIX]{x1D6FD}\leqslant 1$
when
 $\unicode[STIX]{x1D700}_{M}=0$
and branch out for
$\unicode[STIX]{x1D700}_{M}=0$
and branch out for
 $\unicode[STIX]{x1D6FD}>1$
; see red solid and dashed curves.
$\unicode[STIX]{x1D6FD}>1$
; see red solid and dashed curves.(iii) In the absence of the Moffatt drift, the necessary condition for dynamo action is that the
 $\unicode[STIX]{x1D6FC}$
fluctuations must be strong, i.e.
$\unicode[STIX]{x1D6FC}$
fluctuations must be strong, i.e.
 $\unicode[STIX]{x1D700}_{K}<0$
, regardless of the strength of the shear parameter
$\unicode[STIX]{x1D700}_{K}<0$
, regardless of the strength of the shear parameter
 $|\unicode[STIX]{x1D700}_{S}|$
which should be kept smaller than unity in the present model. The dynamo is then driven through the
$|\unicode[STIX]{x1D700}_{S}|$
which should be kept smaller than unity in the present model. The dynamo is then driven through the
 $-\unicode[STIX]{x1D700}_{K}$
term in (5.7) by the process of negative diffusion first suggested by Kraichnan (Reference Kraichnan1976).
$-\unicode[STIX]{x1D700}_{K}$
term in (5.7) by the process of negative diffusion first suggested by Kraichnan (Reference Kraichnan1976).(iv) Moffatt drift always contributes positively to the dynamo growth. Considering the case of zero shear, we see from (5.7) that
 $\unicode[STIX]{x1D700}_{M}>\unicode[STIX]{x1D700}_{M}^{\text{crit}}$
, with
$\unicode[STIX]{x1D700}_{M}>\unicode[STIX]{x1D700}_{M}^{\text{crit}}$
, with
 $\unicode[STIX]{x1D700}_{M}^{\text{crit}}=\sqrt{\unicode[STIX]{x1D700}_{K}+\unicode[STIX]{x1D6FD}^{2}}$
, can always facilitate LSD in both the weak and strong
$\unicode[STIX]{x1D700}_{M}^{\text{crit}}=\sqrt{\unicode[STIX]{x1D700}_{K}+\unicode[STIX]{x1D6FD}^{2}}$
, can always facilitate LSD in both the weak and strong
 $\unicode[STIX]{x1D6FC}$
fluctuation regimes, for sufficiently low values of
$\unicode[STIX]{x1D6FC}$
fluctuation regimes, for sufficiently low values of
 $\unicode[STIX]{x1D6FD}$
such that
$\unicode[STIX]{x1D6FD}$
such that
 $\unicode[STIX]{x1D700}_{M}^{\text{crit}}\ll 1$
.
$\unicode[STIX]{x1D700}_{M}^{\text{crit}}\ll 1$
.(v) The growth rate is always negative for
 $\unicode[STIX]{x1D6FD}\gg 1$
due to the
$\unicode[STIX]{x1D6FD}\gg 1$
due to the
 $-\unicode[STIX]{x1D6FD}^{2}$
term in (5.7), as is also shown in figure 1.
$-\unicode[STIX]{x1D6FD}^{2}$
term in (5.7), as is also shown in figure 1.(vi) The growth rate for
 $\unicode[STIX]{x1D6FD}\approx 0$
i.e. largest scale possible is given for small values of
$\unicode[STIX]{x1D6FD}\approx 0$
i.e. largest scale possible is given for small values of
 $\unicode[STIX]{x1D700}_{M}\ll 1$
as, (5.8)which implies Moffatt drift couples strongly with shear and growth is possible for weak
$\unicode[STIX]{x1D700}_{M}\ll 1$
as, (5.8)which implies Moffatt drift couples strongly with shear and growth is possible for weak $$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{{>}}\simeq -\unicode[STIX]{x1D700}_{K}+\frac{|\unicode[STIX]{x1D700}_{S}|}{\sqrt{2}}|\unicode[STIX]{x1D700}_{M}|^{1/2},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{{>}}\simeq -\unicode[STIX]{x1D700}_{K}+\frac{|\unicode[STIX]{x1D700}_{S}|}{\sqrt{2}}|\unicode[STIX]{x1D700}_{M}|^{1/2},\end{eqnarray}$$
 $\unicode[STIX]{x1D6FC}$
-fluctuations i.e.
$\unicode[STIX]{x1D6FC}$
-fluctuations i.e.
 $\unicode[STIX]{x1D700}_{K}>0$
when
$\unicode[STIX]{x1D700}_{K}>0$
when
 $|\unicode[STIX]{x1D700}_{S}||\unicode[STIX]{x1D700}_{M}|^{1/2}>\sqrt{2}\unicode[STIX]{x1D700}_{K}$
.
$|\unicode[STIX]{x1D700}_{S}||\unicode[STIX]{x1D700}_{M}|^{1/2}>\sqrt{2}\unicode[STIX]{x1D700}_{K}$
.

Figure 1. The two roots,
![]() $\unicode[STIX]{x1D6E4}_{{>}}$
(solid) and
$\unicode[STIX]{x1D6E4}_{{>}}$
(solid) and
![]() $\unicode[STIX]{x1D6E4}_{{<}}$
(dashed), of the growth rate function defined in (5.7) are shown as a function of
$\unicode[STIX]{x1D6E4}_{{<}}$
(dashed), of the growth rate function defined in (5.7) are shown as a function of
![]() $\unicode[STIX]{x1D6FD}$
for
$\unicode[STIX]{x1D6FD}$
for
![]() $\unicode[STIX]{x1D700}_{M}=0$
(red; thick) and
$\unicode[STIX]{x1D700}_{M}=0$
(red; thick) and
![]() $0.3$
(green; thin) with
$0.3$
(green; thin) with
![]() $|\unicode[STIX]{x1D700}_{S}|=0.5$
, where (a) and (b) correspond to weak (
$|\unicode[STIX]{x1D700}_{S}|=0.5$
, where (a) and (b) correspond to weak (
![]() $\unicode[STIX]{x1D700}_{K}=0.1$
) and strong (
$\unicode[STIX]{x1D700}_{K}=0.1$
) and strong (
![]() $\unicode[STIX]{x1D700}_{K}=-0.1$
)
$\unicode[STIX]{x1D700}_{K}=-0.1$
)
![]() $\unicode[STIX]{x1D6FC}$
fluctuations, respectively.
$\unicode[STIX]{x1D6FC}$
fluctuations, respectively.
5.2 Growth rates as functions of the wavenumber
We henceforth consider only the dominant root
![]() $\unicode[STIX]{x1D6E4}_{{>}}$
and study its wavenumber dependence. Following SS14, we first identify natural length and time scales whose corresponding wavenumber and frequency are defined as,
$\unicode[STIX]{x1D6E4}_{{>}}$
and study its wavenumber dependence. Following SS14, we first identify natural length and time scales whose corresponding wavenumber and frequency are defined as,
where
![]() $k_{\unicode[STIX]{x1D6FC}}$
can be recognized as an inverse diffusion length due to
$k_{\unicode[STIX]{x1D6FC}}$
can be recognized as an inverse diffusion length due to
![]() $\unicode[STIX]{x1D6FC}$
-diffusivity
$\unicode[STIX]{x1D6FC}$
-diffusivity
![]() $\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}$
. Here
$\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}$
. Here
![]() $|k|>k_{\unicode[STIX]{x1D6FC}}$
and
$|k|>k_{\unicode[STIX]{x1D6FC}}$
and
![]() $|k|<k_{\unicode[STIX]{x1D6FC}}$
are called high and low wavenumbers, respectively. From (5.5) and (5.9) we see that
$|k|<k_{\unicode[STIX]{x1D6FC}}$
are called high and low wavenumbers, respectively. From (5.5) and (5.9) we see that
![]() $\unicode[STIX]{x1D6FD}=(k/k_{\unicode[STIX]{x1D6FC}})^{2}$
. Since the parameters
$\unicode[STIX]{x1D6FD}=(k/k_{\unicode[STIX]{x1D6FC}})^{2}$
. Since the parameters
![]() $\unicode[STIX]{x1D700}_{K}$
and
$\unicode[STIX]{x1D700}_{K}$
and
![]() $\unicode[STIX]{x1D700}_{M}$
involve the wavenumber
$\unicode[STIX]{x1D700}_{M}$
involve the wavenumber
![]() $k$
in their definitions, we find it better to rewrite an expression for
$k$
in their definitions, we find it better to rewrite an expression for
![]() $\unicode[STIX]{x1D6E4}_{{>}}$
using new dimensionless dynamo numbers, which are defined in terms of known constants:
$\unicode[STIX]{x1D6E4}_{{>}}$
using new dimensionless dynamo numbers, which are defined in terms of known constants:
We first make use of (5.4)–(5.10) to express the growth rates as a function of wavenumber and constant dynamo parameters in the weak and strong regimes of
![]() $\unicode[STIX]{x1D6FC}$
-fluctuations.
$\unicode[STIX]{x1D6FC}$
-fluctuations.

Figure 2. Normalized growth rate
![]() $\unicode[STIX]{x1D6FE}_{{>}}/\unicode[STIX]{x1D70E}$
as a function of
$\unicode[STIX]{x1D6FE}_{{>}}/\unicode[STIX]{x1D70E}$
as a function of
![]() $|k/k_{\unicode[STIX]{x1D6FC}}|$
for
$|k/k_{\unicode[STIX]{x1D6FC}}|$
for
![]() ${\mathcal{D}}_{M}=0.2$
. (a) and (b) correspond to weak (
${\mathcal{D}}_{M}=0.2$
. (a) and (b) correspond to weak (
![]() ${\mathcal{D}}_{\unicode[STIX]{x1D6FC}}=0.5$
) and strong (
${\mathcal{D}}_{\unicode[STIX]{x1D6FC}}=0.5$
) and strong (
![]() ${\mathcal{D}}_{\unicode[STIX]{x1D6FC}}=1.5$
)
${\mathcal{D}}_{\unicode[STIX]{x1D6FC}}=1.5$
)
![]() $\unicode[STIX]{x1D6FC}$
fluctuations respectively. Solid, dashed, dash-dotted and dotted curves correspond to
$\unicode[STIX]{x1D6FC}$
fluctuations respectively. Solid, dashed, dash-dotted and dotted curves correspond to
![]() $\unicode[STIX]{x1D700}_{S}=0.6$
, 0.4, 0.2 and 0, respectively.
$\unicode[STIX]{x1D700}_{S}=0.6$
, 0.4, 0.2 and 0, respectively.
Weak
![]() $\unicode[STIX]{x1D6FC}$
fluctuations: Here,
$\unicode[STIX]{x1D6FC}$
fluctuations: Here,
![]() $\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}<\unicode[STIX]{x1D702}_{T}$
, i.e.
$\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}<\unicode[STIX]{x1D702}_{T}$
, i.e.
![]() ${\mathcal{D}}_{\unicode[STIX]{x1D6FC}}<1$
and
${\mathcal{D}}_{\unicode[STIX]{x1D6FC}}<1$
and
![]() $|\unicode[STIX]{x1D702}_{K}|=+\unicode[STIX]{x1D702}_{K}=\unicode[STIX]{x1D702}_{T}-\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}$
, giving
$|\unicode[STIX]{x1D702}_{K}|=+\unicode[STIX]{x1D702}_{K}=\unicode[STIX]{x1D702}_{T}-\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}$
, giving
 $$\begin{eqnarray}\displaystyle & \displaystyle \text{and }{\mathcal{R}}_{b}(k)=\left(\left\{\left[\left(\frac{k}{k_{\unicode[STIX]{x1D6FC}}}\right)^{2}-1\right]+{\mathcal{D}}_{M}\left(\frac{k}{k_{\unicode[STIX]{x1D6FC}}}\right)^{2}\right\}^{2}+{\mathcal{D}}_{M}\left(\frac{k}{k_{\unicode[STIX]{x1D6FC}}}\right)^{2}\right)^{1/2}. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \text{and }{\mathcal{R}}_{b}(k)=\left(\left\{\left[\left(\frac{k}{k_{\unicode[STIX]{x1D6FC}}}\right)^{2}-1\right]+{\mathcal{D}}_{M}\left(\frac{k}{k_{\unicode[STIX]{x1D6FC}}}\right)^{2}\right\}^{2}+{\mathcal{D}}_{M}\left(\frac{k}{k_{\unicode[STIX]{x1D6FC}}}\right)^{2}\right)^{1/2}. & \displaystyle\end{eqnarray}$$
In figure 2(a) we show the wavenumber dependence of the normalized growth rate
![]() $\unicode[STIX]{x1D6FE}_{{>}}/\unicode[STIX]{x1D70E}$
for different choices of the shear parameter, at fixed
$\unicode[STIX]{x1D6FE}_{{>}}/\unicode[STIX]{x1D70E}$
for different choices of the shear parameter, at fixed
![]() ${\mathcal{D}}_{\unicode[STIX]{x1D6FC}}$
and
${\mathcal{D}}_{\unicode[STIX]{x1D6FC}}$
and
![]() ${\mathcal{D}}_{M}$
, when the
${\mathcal{D}}_{M}$
, when the
![]() $\unicode[STIX]{x1D6FC}$
fluctuations are weak. Interestingly, the growth rate is positive for fairly small wavenumbers, thus facilitating a truly large-scale dynamo, with a wavenumber cutoff beyond which the growth rate turns negative. At much larger wavenumbers, The growth rate varies as
$\unicode[STIX]{x1D6FC}$
fluctuations are weak. Interestingly, the growth rate is positive for fairly small wavenumbers, thus facilitating a truly large-scale dynamo, with a wavenumber cutoff beyond which the growth rate turns negative. At much larger wavenumbers, The growth rate varies as
![]() $\unicode[STIX]{x1D6FE}\propto -k^{4}$
due to the
$\unicode[STIX]{x1D6FE}\propto -k^{4}$
due to the
![]() $\unicode[STIX]{x1D702}_{T}$
-correction in the present model. Shear boosts the growth rates at all wavenumbers, and thus it can support the dynamo action for sufficiently strong Moffatt drift.
$\unicode[STIX]{x1D702}_{T}$
-correction in the present model. Shear boosts the growth rates at all wavenumbers, and thus it can support the dynamo action for sufficiently strong Moffatt drift.
Strong
![]() $\unicode[STIX]{x1D6FC}$
fluctuations: In this case,
$\unicode[STIX]{x1D6FC}$
fluctuations: In this case,
![]() $\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}>\unicode[STIX]{x1D702}_{T}$
, i.e.
$\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}>\unicode[STIX]{x1D702}_{T}$
, i.e.
![]() ${\mathcal{D}}_{\unicode[STIX]{x1D6FC}}>1$
and
${\mathcal{D}}_{\unicode[STIX]{x1D6FC}}>1$
and
![]() $|\unicode[STIX]{x1D702}_{K}|=-\unicode[STIX]{x1D702}_{K}$
, giving
$|\unicode[STIX]{x1D702}_{K}|=-\unicode[STIX]{x1D702}_{K}$
, giving
Here the small wavenumbers grow as all the effects, Kraichnan diffusivity, Moffatt drift and shear, contribute positively to the dynamo action; see figure 2(b). Similar to the case of weak
![]() $\unicode[STIX]{x1D6FC}$
fluctuations, the growth rate here too is a non-monotonic function of
$\unicode[STIX]{x1D6FC}$
fluctuations, the growth rate here too is a non-monotonic function of
![]() $k$
and it becomes negative for sufficiently large wavenumbers.
$k$
and it becomes negative for sufficiently large wavenumbers.
5.2.1 Dynamo action for zero Moffatt drift
This corresponds to the Kraichnan problem, extended to include a non-zero
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
. There are two cases to consider, the one in the absence of shear and the other when shear is present.
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
. There are two cases to consider, the one in the absence of shear and the other when shear is present.
1. Shear absent (only
![]() $\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}$
and
$\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}$
and
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
non-zero)
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
non-zero)
Using (5.11)–(5.14) by setting
![]() ${\mathcal{D}}_{M}=0$
and
${\mathcal{D}}_{M}=0$
and
![]() $|\unicode[STIX]{x1D700}_{S}|=0$
the normalized growth rate can be expressed as, for
$|\unicode[STIX]{x1D700}_{S}|=0$
the normalized growth rate can be expressed as, for
Weak
![]() $\unicode[STIX]{x1D6FC}$
fluctuations: when
$\unicode[STIX]{x1D6FC}$
fluctuations: when
![]() $0<\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}<\unicode[STIX]{x1D702}_{T}$
, i.e.
$0<\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}<\unicode[STIX]{x1D702}_{T}$
, i.e.
![]() ${\mathcal{D}}_{\unicode[STIX]{x1D6FC}}<1$
,
${\mathcal{D}}_{\unicode[STIX]{x1D6FC}}<1$
,
Here, the growth is negative definite for all values of
![]() $k$
and a monotonically decreasing function of
$k$
and a monotonically decreasing function of
![]() $k$
. At large wavenumbers, it varies as
$k$
. At large wavenumbers, it varies as
![]() $\unicode[STIX]{x1D6FE}\propto -k^{4}$
, a correction due to finite
$\unicode[STIX]{x1D6FE}\propto -k^{4}$
, a correction due to finite
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
and inclusion of a finite resistive term in the fluctuating field equation. The first term in the (5.15) is due to Kraichnan diffusivity (compare it with (3.10) by setting
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
and inclusion of a finite resistive term in the fluctuating field equation. The first term in the (5.15) is due to Kraichnan diffusivity (compare it with (3.10) by setting
![]() $S=0$
and
$S=0$
and
![]() $\boldsymbol{V}_{M}=0$
).
$\boldsymbol{V}_{M}=0$
).
Strong
![]() $\unicode[STIX]{x1D6FC}$
fluctuations: when
$\unicode[STIX]{x1D6FC}$
fluctuations: when
![]() $0<\unicode[STIX]{x1D702}_{T}<\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}$
, i.e.
$0<\unicode[STIX]{x1D702}_{T}<\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}$
, i.e.
![]() ${\mathcal{D}}_{\unicode[STIX]{x1D6FC}}>1$
,
${\mathcal{D}}_{\unicode[STIX]{x1D6FC}}>1$
,
In this regime, the growth rate is positive for a certain range of wavenumbers and it becomes negative for large wavenumbers as mentioned above. In figure 3 we compare our model (which has non-zero
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
) with the original Kraichnan model – we see that a non-zero
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
) with the original Kraichnan model – we see that a non-zero
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
introduces a high wavenumber cutoff in the case of strong
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
introduces a high wavenumber cutoff in the case of strong
![]() $\unicode[STIX]{x1D6FC}$
-fluctuations, which agrees with the conclusions of Singh (Reference Singh2016).
$\unicode[STIX]{x1D6FC}$
-fluctuations, which agrees with the conclusions of Singh (Reference Singh2016).

Figure 3. Normalized growth rate when Moffatt drift and shear are zero. Plotted as a function of
![]() $|k/k_{\unicode[STIX]{x1D6FC}}|$
. Solid curve shows finite
$|k/k_{\unicode[STIX]{x1D6FC}}|$
. Solid curve shows finite
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
correction and dashed-dotted curve is for the white-noise case.
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
correction and dashed-dotted curve is for the white-noise case.
2. The effect of shear
Using (5.7) we rewrite the growth rate function more explicitly as:
We note that the shear does not couple to the dynamo growth rate when
![]() $\unicode[STIX]{x1D6FD}$
is smaller than or equal to unity, or in other words, when
$\unicode[STIX]{x1D6FD}$
is smaller than or equal to unity, or in other words, when
![]() $|k|<k_{\unicode[STIX]{x1D6FC}}$
.Footnote
2
Since
$|k|<k_{\unicode[STIX]{x1D6FC}}$
.Footnote
2
Since
![]() $|\unicode[STIX]{x1D700}_{S}|\ll 1$
, the dominant term in (5.18) is
$|\unicode[STIX]{x1D700}_{S}|\ll 1$
, the dominant term in (5.18) is
![]() $-\unicode[STIX]{x1D6FD}^{2}$
for
$-\unicode[STIX]{x1D6FD}^{2}$
for
![]() $k>k_{\unicode[STIX]{x1D6FC}}$
, which makes the growth rate negative definite. Thus, for weak
$k>k_{\unicode[STIX]{x1D6FC}}$
, which makes the growth rate negative definite. Thus, for weak
![]() $\unicode[STIX]{x1D6FC}$
fluctuations which have
$\unicode[STIX]{x1D6FC}$
fluctuations which have
![]() $\unicode[STIX]{x1D700}_{K}>0$
, shear alone cannot drive a large-scale dynamo at any wavenumber. Therefore, the necessary condition for dynamo action in this case is that the
$\unicode[STIX]{x1D700}_{K}>0$
, shear alone cannot drive a large-scale dynamo at any wavenumber. Therefore, the necessary condition for dynamo action in this case is that the
![]() $\unicode[STIX]{x1D6FC}$
fluctuations must be strong. We now look at the properties of growth rate as a function of wavenumber.
$\unicode[STIX]{x1D6FC}$
fluctuations must be strong. We now look at the properties of growth rate as a function of wavenumber.
Weak
![]() $\unicode[STIX]{x1D6FC}$
fluctuations: Here,
$\unicode[STIX]{x1D6FC}$
fluctuations: Here,
![]() $\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}<\unicode[STIX]{x1D702}_{T}$
, i.e.
$\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}<\unicode[STIX]{x1D702}_{T}$
, i.e.
![]() ${\mathcal{D}}_{\unicode[STIX]{x1D6FC}}<1$
and
${\mathcal{D}}_{\unicode[STIX]{x1D6FC}}<1$
and
![]() $|\unicode[STIX]{x1D702}_{K}|=+\unicode[STIX]{x1D702}_{K}=\unicode[STIX]{x1D702}_{T}-\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}$
, giving
$|\unicode[STIX]{x1D702}_{K}|=+\unicode[STIX]{x1D702}_{K}=\unicode[STIX]{x1D702}_{T}-\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}$
, giving
 $$\begin{eqnarray}\displaystyle & = & \displaystyle -\left(\frac{k}{k_{\unicode[STIX]{x1D6FC}}}\right)^{2}+\frac{{\mathcal{D}}_{\unicode[STIX]{x1D6FC}}}{1-{\mathcal{D}}_{\unicode[STIX]{x1D6FC}}}\left[-\left(\frac{k}{k_{\unicode[STIX]{x1D6FC}}}\right)^{4}+|\unicode[STIX]{x1D700}_{S}|\sqrt{\left(\frac{k}{k_{\unicode[STIX]{x1D6FC}}}\right)^{2}\left[\left(\frac{k}{k_{\unicode[STIX]{x1D6FC}}}\right)^{2}-1\right]}\right],\nonumber\\ \displaystyle & & \displaystyle \text{when }|k|>k_{\unicode[STIX]{x1D6FC}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & = & \displaystyle -\left(\frac{k}{k_{\unicode[STIX]{x1D6FC}}}\right)^{2}+\frac{{\mathcal{D}}_{\unicode[STIX]{x1D6FC}}}{1-{\mathcal{D}}_{\unicode[STIX]{x1D6FC}}}\left[-\left(\frac{k}{k_{\unicode[STIX]{x1D6FC}}}\right)^{4}+|\unicode[STIX]{x1D700}_{S}|\sqrt{\left(\frac{k}{k_{\unicode[STIX]{x1D6FC}}}\right)^{2}\left[\left(\frac{k}{k_{\unicode[STIX]{x1D6FC}}}\right)^{2}-1\right]}\right],\nonumber\\ \displaystyle & & \displaystyle \text{when }|k|>k_{\unicode[STIX]{x1D6FC}}.\end{eqnarray}$$
We can see from (5.19) that the growth rate is negative definite in the range
![]() $0<|k|<k_{\unicode[STIX]{x1D6FC}}$
, as inferred above. Dynamo action is not possible for
$0<|k|<k_{\unicode[STIX]{x1D6FC}}$
, as inferred above. Dynamo action is not possible for
![]() $|k|>k_{\unicode[STIX]{x1D6FC}}$
for the following reason. When
$|k|>k_{\unicode[STIX]{x1D6FC}}$
for the following reason. When
![]() $|k|>k_{\unicode[STIX]{x1D6FC}}$
, shear contributes to the growth rate (see (5.20)). Since the model is valid for
$|k|>k_{\unicode[STIX]{x1D6FC}}$
, shear contributes to the growth rate (see (5.20)). Since the model is valid for
![]() $|\unicode[STIX]{x1D700}_{S}|\ll 1$
, in order to increase the strength of that term we can increase
$|\unicode[STIX]{x1D700}_{S}|\ll 1$
, in order to increase the strength of that term we can increase
![]() ${\mathcal{D}}_{\unicode[STIX]{x1D6FC}}$
(while keeping it less than unity), but this will also strengthen the second term, which is
${\mathcal{D}}_{\unicode[STIX]{x1D6FC}}$
(while keeping it less than unity), but this will also strengthen the second term, which is
![]() $\propto -k^{4}$
, due to the finite
$\propto -k^{4}$
, due to the finite
![]() $\unicode[STIX]{x1D702}_{T}$
correction in the fluctuating field equation, thereby killing dynamo action.
$\unicode[STIX]{x1D702}_{T}$
correction in the fluctuating field equation, thereby killing dynamo action.

Figure 4. Normalized growth rate
![]() $\unicode[STIX]{x1D6FE}_{{>}}/\unicode[STIX]{x1D70E}$
as a function of
$\unicode[STIX]{x1D6FE}_{{>}}/\unicode[STIX]{x1D70E}$
as a function of
![]() $|k/k_{\unicode[STIX]{x1D6FC}}|$
for
$|k/k_{\unicode[STIX]{x1D6FC}}|$
for
![]() $|\unicode[STIX]{x1D700}_{S}|=0.3$
. (a,b) Correspond to weak (
$|\unicode[STIX]{x1D700}_{S}|=0.3$
. (a,b) Correspond to weak (
![]() ${\mathcal{D}}_{\unicode[STIX]{x1D6FC}}=0.5$
) and strong (
${\mathcal{D}}_{\unicode[STIX]{x1D6FC}}=0.5$
) and strong (
![]() ${\mathcal{D}}_{\unicode[STIX]{x1D6FC}}=1.8$
)
${\mathcal{D}}_{\unicode[STIX]{x1D6FC}}=1.8$
)
![]() $\unicode[STIX]{x1D6FC}$
fluctuations, respectively. Solid and dashed curves correspond to this work and SS14, respectively.
$\unicode[STIX]{x1D6FC}$
fluctuations, respectively. Solid and dashed curves correspond to this work and SS14, respectively.
Strong
![]() $\unicode[STIX]{x1D6FC}$
fluctuations: Here,
$\unicode[STIX]{x1D6FC}$
fluctuations: Here,
![]() $\unicode[STIX]{x1D702}_{T}<\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}$
, i.e.
$\unicode[STIX]{x1D702}_{T}<\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}$
, i.e.
![]() ${\mathcal{D}}_{\unicode[STIX]{x1D6FC}}>1$
and
${\mathcal{D}}_{\unicode[STIX]{x1D6FC}}>1$
and
![]() $|\unicode[STIX]{x1D702}_{K}|=-\unicode[STIX]{x1D702}_{K}=\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}-\unicode[STIX]{x1D702}_{T}$
, giving
$|\unicode[STIX]{x1D702}_{K}|=-\unicode[STIX]{x1D702}_{K}=\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}-\unicode[STIX]{x1D702}_{T}$
, giving
 $$\begin{eqnarray}\displaystyle & = & \displaystyle \left(\frac{k}{k_{\unicode[STIX]{x1D6FC}}}\right)^{2}+\frac{{\mathcal{D}}_{\unicode[STIX]{x1D6FC}}}{{\mathcal{D}}_{\unicode[STIX]{x1D6FC}}-1}\left[-\left(\frac{k}{k_{\unicode[STIX]{x1D6FC}}}\right)^{4}+|\unicode[STIX]{x1D700}_{S}|\sqrt{\left(\frac{k}{k_{\unicode[STIX]{x1D6FC}}}\right)^{2}\left[\left(\frac{k}{k_{\unicode[STIX]{x1D6FC}}}\right)^{2}-1\right]}\right],\nonumber\\ \displaystyle & & \displaystyle \text{when }|k|>|k_{\unicode[STIX]{x1D6FC}}|.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & = & \displaystyle \left(\frac{k}{k_{\unicode[STIX]{x1D6FC}}}\right)^{2}+\frac{{\mathcal{D}}_{\unicode[STIX]{x1D6FC}}}{{\mathcal{D}}_{\unicode[STIX]{x1D6FC}}-1}\left[-\left(\frac{k}{k_{\unicode[STIX]{x1D6FC}}}\right)^{4}+|\unicode[STIX]{x1D700}_{S}|\sqrt{\left(\frac{k}{k_{\unicode[STIX]{x1D6FC}}}\right)^{2}\left[\left(\frac{k}{k_{\unicode[STIX]{x1D6FC}}}\right)^{2}-1\right]}\right],\nonumber\\ \displaystyle & & \displaystyle \text{when }|k|>|k_{\unicode[STIX]{x1D6FC}}|.\end{eqnarray}$$
The growth rate
![]() $\unicode[STIX]{x1D6FE}$
becomes positive for a certain range of wavenumber depending upon the strength of the
$\unicode[STIX]{x1D6FE}$
becomes positive for a certain range of wavenumber depending upon the strength of the
![]() $\unicode[STIX]{x1D6FC}$
-fluctuations, eventually becoming negative at large wavenumbers due to the
$\unicode[STIX]{x1D6FC}$
-fluctuations, eventually becoming negative at large wavenumbers due to the
![]() $-k^{4}$
term arising due to the finite
$-k^{4}$
term arising due to the finite
![]() $\unicode[STIX]{x1D702}_{T}$
correction. This behaviour is compared in figure 4 with Sridhar & Singh (Reference Sridhar and Singh2014); we can see that there is good agreement at low wavenumbers whereas at large wavenumbers there is a difference. The derivation of Sridhar & Singh (Reference Sridhar and Singh2014) had neglected the effect of turbulent resistivity on the fluctuating component of the magnetic field, and they had noted that this would lead to an overestimation of growth rates at large wavenumbers. This is what we find in the present work: retaining this term makes the growth rate negative at large wavenumbers and, for weak
$\unicode[STIX]{x1D702}_{T}$
correction. This behaviour is compared in figure 4 with Sridhar & Singh (Reference Sridhar and Singh2014); we can see that there is good agreement at low wavenumbers whereas at large wavenumbers there is a difference. The derivation of Sridhar & Singh (Reference Sridhar and Singh2014) had neglected the effect of turbulent resistivity on the fluctuating component of the magnetic field, and they had noted that this would lead to an overestimation of growth rates at large wavenumbers. This is what we find in the present work: retaining this term makes the growth rate negative at large wavenumbers and, for weak
![]() $\unicode[STIX]{x1D6FC}$
-fluctuations, the behaviour is indeed qualitatively different. Therefore, including the
$\unicode[STIX]{x1D6FC}$
-fluctuations, the behaviour is indeed qualitatively different. Therefore, including the
![]() $\unicode[STIX]{x1D702}_{T}$
term gives a bonafide large-scale dynamo action by predicting the high wavenumber cutoff. Thus, in the absence of Moffatt drift, the necessary condition for the large-scale dynamo when shear is present is the same as the case when it is absent.
$\unicode[STIX]{x1D702}_{T}$
term gives a bonafide large-scale dynamo action by predicting the high wavenumber cutoff. Thus, in the absence of Moffatt drift, the necessary condition for the large-scale dynamo when shear is present is the same as the case when it is absent.
6 Conclusions
We have studied the effect of
![]() $\unicode[STIX]{x1D6FC}$
fluctuations on the growth of large-scale magnetic fields in a shearing background. Our derivation of the mean electromotive force is based on the first-order smoothing approximation (FOSA), whose range of validity is given in (3.1). These are such that FOSA is, in general, valid for all ‘weak’
$\unicode[STIX]{x1D6FC}$
fluctuations on the growth of large-scale magnetic fields in a shearing background. Our derivation of the mean electromotive force is based on the first-order smoothing approximation (FOSA), whose range of validity is given in (3.1). These are such that FOSA is, in general, valid for all ‘weak’
![]() $\unicode[STIX]{x1D6FC}$
fluctuations (
$\unicode[STIX]{x1D6FC}$
fluctuations (
![]() $\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}<\unicode[STIX]{x1D702}_{T}$
), which is the case of primary interest for dynamo action. We have extended the analysis of Sridhar & Singh (Reference Sridhar and Singh2014) by including the effect of the turbulent resistivity,
$\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}<\unicode[STIX]{x1D702}_{T}$
), which is the case of primary interest for dynamo action. We have extended the analysis of Sridhar & Singh (Reference Sridhar and Singh2014) by including the effect of the turbulent resistivity,
![]() $\unicode[STIX]{x1D702}_{T}$
, on the fluctuating component of the magnetic field. We derived the integro-differential equation for the large-scale magnetic field, which is non-perturbative in shear strength,
$\unicode[STIX]{x1D702}_{T}$
, on the fluctuating component of the magnetic field. We derived the integro-differential equation for the large-scale magnetic field, which is non-perturbative in shear strength,
![]() $S$
, and the
$S$
, and the
![]() $\unicode[STIX]{x1D6FC}$
-correlation time,
$\unicode[STIX]{x1D6FC}$
-correlation time,
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
, similar to Sridhar & Singh (Reference Sridhar and Singh2014). For the exactly solvable case of white-noise
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
, similar to Sridhar & Singh (Reference Sridhar and Singh2014). For the exactly solvable case of white-noise
![]() $\unicode[STIX]{x1D6FC}$
-fluctuations, dynamo action is possible only when the
$\unicode[STIX]{x1D6FC}$
-fluctuations, dynamo action is possible only when the
![]() $\unicode[STIX]{x1D6FC}$
-fluctuations are strong; this is also similar to Sridhar & Singh (Reference Sridhar and Singh2014). In order to explore dynamo action in the regime of weak
$\unicode[STIX]{x1D6FC}$
-fluctuations are strong; this is also similar to Sridhar & Singh (Reference Sridhar and Singh2014). In order to explore dynamo action in the regime of weak
![]() $\unicode[STIX]{x1D6FC}$
-fluctuations it is necessary to consider a non-zero
$\unicode[STIX]{x1D6FC}$
-fluctuations it is necessary to consider a non-zero
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
. Considering a small but non-zero
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
. Considering a small but non-zero
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
and a slowly varying large-scale magnetic field, we reduced the integro-differential equation to a partial differential equation. We present an expression for the mean EMF, correct up to first order in
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
and a slowly varying large-scale magnetic field, we reduced the integro-differential equation to a partial differential equation. We present an expression for the mean EMF, correct up to first order in
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
. We also corrected an error in Sridhar & Singh (Reference Sridhar and Singh2014) in the expression for the growth rate,
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
. We also corrected an error in Sridhar & Singh (Reference Sridhar and Singh2014) in the expression for the growth rate,
![]() $\unicode[STIX]{x1D6FE}$
. Our salient conclusions are listed below:
$\unicode[STIX]{x1D6FE}$
. Our salient conclusions are listed below:
(i) In the absence of Moffatt drift (i.e.
 $\boldsymbol{V}_{M}=0$
) the growth rate is independent of shear when
$\boldsymbol{V}_{M}=0$
) the growth rate is independent of shear when
 $0<|k|<k_{\unicode[STIX]{x1D6FC}}$
, and there is no dynamo action for weak
$0<|k|<k_{\unicode[STIX]{x1D6FC}}$
, and there is no dynamo action for weak
 $\unicode[STIX]{x1D6FC}$
-fluctuations even when
$\unicode[STIX]{x1D6FC}$
-fluctuations even when
 $|k|>k_{\unicode[STIX]{x1D6FC}}$
for moderately small shear (i.e.
$|k|>k_{\unicode[STIX]{x1D6FC}}$
for moderately small shear (i.e.
 $|\unicode[STIX]{x1D700}_{S}|\ll 1$
) – see figure 4(a).
$|\unicode[STIX]{x1D700}_{S}|\ll 1$
) – see figure 4(a).(ii) For dynamo action with weak
 $\unicode[STIX]{x1D6FC}$
-fluctuations, it is necessary that
$\unicode[STIX]{x1D6FC}$
-fluctuations, it is necessary that
 $\boldsymbol{V}_{M}\neq 0$
: Moffatt drift couples strongly to shear and excites dynamo modes for
$\boldsymbol{V}_{M}\neq 0$
: Moffatt drift couples strongly to shear and excites dynamo modes for
 $|k|<k_{\unicode[STIX]{x1D6FC}}$
– see item (iv) in § 5.1 and figure 2.
$|k|<k_{\unicode[STIX]{x1D6FC}}$
– see item (iv) in § 5.1 and figure 2.
We briefly comment on different approaches adopted in some related earlier works involving
![]() $\unicode[STIX]{x1D6FC}$
fluctuations in a shearing background. Heinemann et al. (Reference Heinemann, McWilliams and Schekochihin2011) considered tensorial
$\unicode[STIX]{x1D6FC}$
fluctuations in a shearing background. Heinemann et al. (Reference Heinemann, McWilliams and Schekochihin2011) considered tensorial
![]() $\hat{\unicode[STIX]{x1D736}}$
-fluctuations due to a quasi-two-dimensional velocity field, whose dynamics is governed by the Navier–Stokes equation at low Reynolds number, where the stochastic motions occur due to a Gaussian random forcing which is
$\hat{\unicode[STIX]{x1D736}}$
-fluctuations due to a quasi-two-dimensional velocity field, whose dynamics is governed by the Navier–Stokes equation at low Reynolds number, where the stochastic motions occur due to a Gaussian random forcing which is
![]() $\unicode[STIX]{x1D6FF}$
-correlated in time. A double-averaging scheme was employed, first over the ‘horizontal’ (or
$\unicode[STIX]{x1D6FF}$
-correlated in time. A double-averaging scheme was employed, first over the ‘horizontal’ (or
![]() $xy$
) coordinates, and second over the statistics of the forcing function. They found that the first moment of the magnetic field does not grow, while there is a growth of the mean-squared magnetic field. Note that the spatial fluctuations in
$xy$
) coordinates, and second over the statistics of the forcing function. They found that the first moment of the magnetic field does not grow, while there is a growth of the mean-squared magnetic field. Note that the spatial fluctuations in
![]() $\hat{\unicode[STIX]{x1D736}}$
were ignored there, and the correlation time of only temporally fluctuating
$\hat{\unicode[STIX]{x1D736}}$
were ignored there, and the correlation time of only temporally fluctuating
![]() $\hat{\unicode[STIX]{x1D736}}$
was assumed to be the same as that of the velocity field. Mitra & Brandenburg (Reference Mitra and Brandenburg2012) also studied a model with tensorial
$\hat{\unicode[STIX]{x1D736}}$
was assumed to be the same as that of the velocity field. Mitra & Brandenburg (Reference Mitra and Brandenburg2012) also studied a model with tensorial
![]() $\hat{\unicode[STIX]{x1D736}}$
and allowed only temporal fluctuations which were further restricted to be
$\hat{\unicode[STIX]{x1D736}}$
and allowed only temporal fluctuations which were further restricted to be
![]() $\unicode[STIX]{x1D6FF}$
-correlated in time. When cross-correlations between different
$\unicode[STIX]{x1D6FF}$
-correlated in time. When cross-correlations between different
![]() $\hat{\unicode[STIX]{x1D736}}$
components were assumed to be zero, they found growing solutions for the second moment of the mean magnetic field, but not for the first moment. However, when cross-correlations were allowed, large enough shear promoted the growth of even the mean magnetic field. Ignoring spatial structures and memory effects of the stochastic
$\hat{\unicode[STIX]{x1D736}}$
components were assumed to be zero, they found growing solutions for the second moment of the mean magnetic field, but not for the first moment. However, when cross-correlations were allowed, large enough shear promoted the growth of even the mean magnetic field. Ignoring spatial structures and memory effects of the stochastic
![]() $\unicode[STIX]{x1D6FC}$
appear to be a serious limitation. We remedy this in the present investigation where an essential generalization is made to explore new physical mechanisms driving large-scale dynamos, but by focussing here on the scalar
$\unicode[STIX]{x1D6FC}$
appear to be a serious limitation. We remedy this in the present investigation where an essential generalization is made to explore new physical mechanisms driving large-scale dynamos, but by focussing here on the scalar
![]() $\unicode[STIX]{x1D6FC}$
fluctuations to keep the analysis simple.
$\unicode[STIX]{x1D6FC}$
fluctuations to keep the analysis simple.
Thus, our model is a minimal extension of Kraichnan (Reference Kraichnan1976) and Moffatt (Reference Moffatt1978), where
![]() $\unicode[STIX]{x1D6FC}$
is assumed to be a fluctuating pseudo-scalar field, and
$\unicode[STIX]{x1D6FC}$
is assumed to be a fluctuating pseudo-scalar field, and
![]() $\unicode[STIX]{x1D702}_{T}$
is constant. We have constructed a model of large-scale dynamo action with essential roles played by the Moffatt drift and a non-zero correlation time. Hence our focus has been to keep the tensorial structure of
$\unicode[STIX]{x1D702}_{T}$
is constant. We have constructed a model of large-scale dynamo action with essential roles played by the Moffatt drift and a non-zero correlation time. Hence our focus has been to keep the tensorial structure of
![]() $\unicode[STIX]{x1D6FC}$
as simple as possible, while exploring the effect of spatio-temporal variations that are natural to turbulent flows. We note that our work is almost completely complementary to Mitra & Brandenburg (Reference Mitra and Brandenburg2012), wherein
$\unicode[STIX]{x1D6FC}$
as simple as possible, while exploring the effect of spatio-temporal variations that are natural to turbulent flows. We note that our work is almost completely complementary to Mitra & Brandenburg (Reference Mitra and Brandenburg2012), wherein
![]() $\unicode[STIX]{x1D6FC}$
fluctuations are tensorial but have very restrictive space–time properties: no spatial variation at all and with a zero correlation time. Indeed non-zero correlation times and non-trivial spatial statistics appear essential for dynamo action, as emphasized in item (2) above. We note here that there seems to be some numerical evidence for pseudo-tensorial
$\unicode[STIX]{x1D6FC}$
fluctuations are tensorial but have very restrictive space–time properties: no spatial variation at all and with a zero correlation time. Indeed non-zero correlation times and non-trivial spatial statistics appear essential for dynamo action, as emphasized in item (2) above. We note here that there seems to be some numerical evidence for pseudo-tensorial
![]() $\unicode[STIX]{x1D6FC}$
and tensorial
$\unicode[STIX]{x1D6FC}$
and tensorial
![]() $\unicode[STIX]{x1D702}_{T}$
fluctuations (Brandenburg et al.
Reference Brandenburg, Rädler, Rheinhardt and Käpylä2008; Rheinhardt et al.
Reference Rheinhardt, Devlen, Rdler and Brandenburg2014; Singh & Jingade Reference Singh and Jingade2015). Our results, obtained for pseudo-scalar
$\unicode[STIX]{x1D702}_{T}$
fluctuations (Brandenburg et al.
Reference Brandenburg, Rädler, Rheinhardt and Käpylä2008; Rheinhardt et al.
Reference Rheinhardt, Devlen, Rdler and Brandenburg2014; Singh & Jingade Reference Singh and Jingade2015). Our results, obtained for pseudo-scalar
![]() $\unicode[STIX]{x1D6FC}$
, can be readily extended to tensorial fields.
$\unicode[STIX]{x1D6FC}$
, can be readily extended to tensorial fields.
Our analytical results for the growth rates of modes relies on a perturbative expansion in
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
, which could also be generalized. Another important assumption is the role of the shear in the statistics of the
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
, which could also be generalized. Another important assumption is the role of the shear in the statistics of the
![]() $\unicode[STIX]{x1D6FC}$
fluctuations: these fluctuations have been specified by a Galilean-invariant two-point correlation function in factored form
$\unicode[STIX]{x1D6FC}$
fluctuations: these fluctuations have been specified by a Galilean-invariant two-point correlation function in factored form
![]() ${\mathcal{A}}(\boldsymbol{R}){\mathcal{D}}(t)$
, where
${\mathcal{A}}(\boldsymbol{R}){\mathcal{D}}(t)$
, where
![]() $\boldsymbol{R}=\boldsymbol{x}-\boldsymbol{x}^{\prime }+St^{\prime }(x_{1}-x_{1}^{\prime })\boldsymbol{e}_{2}$
. Even though the functional form of
$\boldsymbol{R}=\boldsymbol{x}-\boldsymbol{x}^{\prime }+St^{\prime }(x_{1}-x_{1}^{\prime })\boldsymbol{e}_{2}$
. Even though the functional form of
![]() ${\mathcal{A}}$
has dependence on shear through the argument
${\mathcal{A}}$
has dependence on shear through the argument
![]() $\boldsymbol{R}$
, to the first-order expansion in
$\boldsymbol{R}$
, to the first-order expansion in
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
, neither
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$
, neither
![]() ${\mathcal{A}}(0)=\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}$
nor
${\mathcal{A}}(0)=\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}$
nor
![]() $\boldsymbol{V}_{M}$
depends on shear explicitly. This is a limitation, since we can expect a background shear flow to introduce anisotropy in the turbulent flow which is the source of the fluctuations. Future modelling must seek to be guided by numerical simulations that are designed to measure the statistics of
$\boldsymbol{V}_{M}$
depends on shear explicitly. This is a limitation, since we can expect a background shear flow to introduce anisotropy in the turbulent flow which is the source of the fluctuations. Future modelling must seek to be guided by numerical simulations that are designed to measure the statistics of
![]() $\unicode[STIX]{x1D6FC}$
fluctuations.
$\unicode[STIX]{x1D6FC}$
fluctuations.
Appendix A. Derivation of (3.3)
Fourier transforming (3.2), we obtain:
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \left(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}+\unicode[STIX]{x1D702}_{T}K^{2}\right)\widetilde{\boldsymbol{h}}-S\widetilde{h}_{1}\boldsymbol{e}_{2}=\text{i}\boldsymbol{K}\times \widetilde{\boldsymbol{M}},\quad \boldsymbol{K}\boldsymbol{\cdot }\widetilde{\boldsymbol{h}}=0,\quad \widetilde{\boldsymbol{h}}(\boldsymbol{k},0)=\mathbf{0},\\ \displaystyle \text{with }\boldsymbol{K}(\boldsymbol{k},t)=\boldsymbol{e}_{1}(k_{1}-Stk_{2})+\boldsymbol{e}_{2}k_{2}+\boldsymbol{e}_{3}k_{3},\\ \displaystyle \text{and}\quad \widetilde{\boldsymbol{M}}(\boldsymbol{k},t)=\frac{1}{(2\unicode[STIX]{x03C0})^{3}}\int \text{d}^{3}k^{\prime }\widetilde{a}^{\ast }(\boldsymbol{k}^{\prime },t)\,\widetilde{\overline{\boldsymbol{H}}}(\boldsymbol{k}+\boldsymbol{k}^{\prime },t).\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \left(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}+\unicode[STIX]{x1D702}_{T}K^{2}\right)\widetilde{\boldsymbol{h}}-S\widetilde{h}_{1}\boldsymbol{e}_{2}=\text{i}\boldsymbol{K}\times \widetilde{\boldsymbol{M}},\quad \boldsymbol{K}\boldsymbol{\cdot }\widetilde{\boldsymbol{h}}=0,\quad \widetilde{\boldsymbol{h}}(\boldsymbol{k},0)=\mathbf{0},\\ \displaystyle \text{with }\boldsymbol{K}(\boldsymbol{k},t)=\boldsymbol{e}_{1}(k_{1}-Stk_{2})+\boldsymbol{e}_{2}k_{2}+\boldsymbol{e}_{3}k_{3},\\ \displaystyle \text{and}\quad \widetilde{\boldsymbol{M}}(\boldsymbol{k},t)=\frac{1}{(2\unicode[STIX]{x03C0})^{3}}\int \text{d}^{3}k^{\prime }\widetilde{a}^{\ast }(\boldsymbol{k}^{\prime },t)\,\widetilde{\overline{\boldsymbol{H}}}(\boldsymbol{k}+\boldsymbol{k}^{\prime },t).\end{array}\right\}\end{eqnarray}$$
We integrate (A 1) component-wise to write the following solution, satisfying both constraints,
![]() $\boldsymbol{K}\boldsymbol{\cdot }\widetilde{\boldsymbol{h}}=0$
and
$\boldsymbol{K}\boldsymbol{\cdot }\widetilde{\boldsymbol{h}}=0$
and
![]() $\widetilde{\boldsymbol{h}}(\boldsymbol{k},0)=\mathbf{0}$
:
$\widetilde{\boldsymbol{h}}(\boldsymbol{k},0)=\mathbf{0}$
:
 $$\begin{eqnarray}\displaystyle \widetilde{\boldsymbol{h}}(\boldsymbol{k},t) & = & \displaystyle \int _{0}^{t}\text{d}t^{\prime }\,\widetilde{G}_{\unicode[STIX]{x1D702}_{T}}(\boldsymbol{k},t,t^{\prime })[\text{i}\boldsymbol{K}(\boldsymbol{k},t^{\prime })\times \widetilde{\boldsymbol{M}}(\boldsymbol{k},t^{\prime })]\nonumber\\ \displaystyle & & \displaystyle +\,\boldsymbol{e}_{2}S\int _{0}^{t}\text{d}t^{\prime }\int _{0}^{t^{\prime }}\text{d}t^{\prime \prime }\,\widetilde{G}_{\unicode[STIX]{x1D702}_{T}}(\boldsymbol{k},t,t^{\prime \prime })[\text{i}\boldsymbol{K}(\boldsymbol{k},t^{\prime \prime })\times \widetilde{\boldsymbol{M}}(\boldsymbol{k},t^{\prime \prime })]_{1}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widetilde{\boldsymbol{h}}(\boldsymbol{k},t) & = & \displaystyle \int _{0}^{t}\text{d}t^{\prime }\,\widetilde{G}_{\unicode[STIX]{x1D702}_{T}}(\boldsymbol{k},t,t^{\prime })[\text{i}\boldsymbol{K}(\boldsymbol{k},t^{\prime })\times \widetilde{\boldsymbol{M}}(\boldsymbol{k},t^{\prime })]\nonumber\\ \displaystyle & & \displaystyle +\,\boldsymbol{e}_{2}S\int _{0}^{t}\text{d}t^{\prime }\int _{0}^{t^{\prime }}\text{d}t^{\prime \prime }\,\widetilde{G}_{\unicode[STIX]{x1D702}_{T}}(\boldsymbol{k},t,t^{\prime \prime })[\text{i}\boldsymbol{K}(\boldsymbol{k},t^{\prime \prime })\times \widetilde{\boldsymbol{M}}(\boldsymbol{k},t^{\prime \prime })]_{1}.\end{eqnarray}$$
Green’s function
![]() $\widetilde{G}_{\unicode[STIX]{x1D702}_{T}}(\boldsymbol{k},t,t^{\prime })$
is given in (3.4), from where we can see a property that
$\widetilde{G}_{\unicode[STIX]{x1D702}_{T}}(\boldsymbol{k},t,t^{\prime })$
is given in (3.4), from where we can see a property that
![]() $\widetilde{G}_{\unicode[STIX]{x1D702}_{T}}(\boldsymbol{k},t,t^{\prime })\times \widetilde{G}_{\unicode[STIX]{x1D702}_{T}}(\boldsymbol{k},t,t^{\prime \prime })=\widetilde{G}_{\unicode[STIX]{x1D702}_{T}}(\boldsymbol{k},t,t^{\prime \prime })$
, which is used in getting (A 2). Reducing the double time integral in (A 2) to a single time integral by using,
$\widetilde{G}_{\unicode[STIX]{x1D702}_{T}}(\boldsymbol{k},t,t^{\prime })\times \widetilde{G}_{\unicode[STIX]{x1D702}_{T}}(\boldsymbol{k},t,t^{\prime \prime })=\widetilde{G}_{\unicode[STIX]{x1D702}_{T}}(\boldsymbol{k},t,t^{\prime \prime })$
, which is used in getting (A 2). Reducing the double time integral in (A 2) to a single time integral by using,
we obtain the FOSA solution for the fluctuating magnetic field as given in (3.3).
Appendix B. Two-point
 $\unicode[STIX]{x1D6FC}$
-correlator in Fourier space
$\unicode[STIX]{x1D6FC}$
-correlator in Fourier space
Here we derive a general expression for time-stationary Galilean-invariant two-point
![]() $\unicode[STIX]{x1D6FC}$
-correlator in Fourier space, where (2.11) transforms to:
$\unicode[STIX]{x1D6FC}$
-correlator in Fourier space, where (2.11) transforms to:
 $$\begin{eqnarray}\displaystyle & & \displaystyle \overline{\widetilde{a}(\boldsymbol{k}_{1},t)\widetilde{a}^{\ast }(\boldsymbol{k}_{3},t^{\prime })}=\int \text{d}^{3}x_{1}\text{d}^{3}x_{3}\exp (-\text{i}\boldsymbol{k}_{1}\boldsymbol{\cdot }\boldsymbol{x}_{1}+\text{i}\boldsymbol{k}_{3}\boldsymbol{\cdot }\boldsymbol{x}_{3})\overline{a(\boldsymbol{x}_{1},t)a(\boldsymbol{x}_{3},t^{\prime })}\nonumber\\ \displaystyle & & \displaystyle \quad =2{\mathcal{D}}(t-t^{\prime })\int \text{d}^{3}x_{1}\,\text{d}^{3}x_{3}\exp [-\text{i}(\boldsymbol{k}_{1}\boldsymbol{\cdot }\boldsymbol{x}_{1}-\boldsymbol{k}_{3}\boldsymbol{\cdot }\boldsymbol{x}_{3})]{\mathcal{A}}(\boldsymbol{x}_{1}-\boldsymbol{x}_{3}+St^{\prime }(x_{11}-x_{31})\boldsymbol{e}_{2}).\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \overline{\widetilde{a}(\boldsymbol{k}_{1},t)\widetilde{a}^{\ast }(\boldsymbol{k}_{3},t^{\prime })}=\int \text{d}^{3}x_{1}\text{d}^{3}x_{3}\exp (-\text{i}\boldsymbol{k}_{1}\boldsymbol{\cdot }\boldsymbol{x}_{1}+\text{i}\boldsymbol{k}_{3}\boldsymbol{\cdot }\boldsymbol{x}_{3})\overline{a(\boldsymbol{x}_{1},t)a(\boldsymbol{x}_{3},t^{\prime })}\nonumber\\ \displaystyle & & \displaystyle \quad =2{\mathcal{D}}(t-t^{\prime })\int \text{d}^{3}x_{1}\,\text{d}^{3}x_{3}\exp [-\text{i}(\boldsymbol{k}_{1}\boldsymbol{\cdot }\boldsymbol{x}_{1}-\boldsymbol{k}_{3}\boldsymbol{\cdot }\boldsymbol{x}_{3})]{\mathcal{A}}(\boldsymbol{x}_{1}-\boldsymbol{x}_{3}+St^{\prime }(x_{11}-x_{31})\boldsymbol{e}_{2}).\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
Using new integration variables,
![]() $\boldsymbol{r}=\boldsymbol{x}_{1}-\boldsymbol{x}_{3}$
and
$\boldsymbol{r}=\boldsymbol{x}_{1}-\boldsymbol{x}_{3}$
and
![]() $\boldsymbol{r}^{\prime }=(\boldsymbol{x}_{1}+\boldsymbol{x}_{3})/2$
, we get
$\boldsymbol{r}^{\prime }=(\boldsymbol{x}_{1}+\boldsymbol{x}_{3})/2$
, we get
 $$\begin{eqnarray}\displaystyle \overline{\widetilde{a}(\boldsymbol{k}_{1},t)\widetilde{a}^{\ast }(\boldsymbol{k}_{3},t^{\prime })} & = & \displaystyle 2{\mathcal{D}}(t-t^{\prime })\int \text{d}^{3}r\,\text{d}^{3}r^{\prime }\exp \left[-\text{i}(\boldsymbol{k}_{1}-\boldsymbol{k}_{3})\boldsymbol{\cdot }\boldsymbol{r}^{\prime }-\frac{\text{i}}{2}(\boldsymbol{k}_{1}+\boldsymbol{k}_{3})\boldsymbol{\cdot }\boldsymbol{r}\right]\nonumber\\ \displaystyle & & \displaystyle \times \,{\mathcal{A}}(\boldsymbol{r}+St^{\prime }r_{1}\boldsymbol{e}_{2})=2{\mathcal{D}}(t-t^{\prime })(2\unicode[STIX]{x03C0})^{3}\unicode[STIX]{x1D6FF}(\boldsymbol{k}_{1}-\boldsymbol{k}_{3})\nonumber\\ \displaystyle & & \displaystyle \times \,\int \text{d}^{3}r\exp (-\text{i}\boldsymbol{k}_{1}\boldsymbol{\cdot }\boldsymbol{r}){\mathcal{A}}(\boldsymbol{r}+St^{\prime }r_{1}\boldsymbol{e}_{2}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \overline{\widetilde{a}(\boldsymbol{k}_{1},t)\widetilde{a}^{\ast }(\boldsymbol{k}_{3},t^{\prime })} & = & \displaystyle 2{\mathcal{D}}(t-t^{\prime })\int \text{d}^{3}r\,\text{d}^{3}r^{\prime }\exp \left[-\text{i}(\boldsymbol{k}_{1}-\boldsymbol{k}_{3})\boldsymbol{\cdot }\boldsymbol{r}^{\prime }-\frac{\text{i}}{2}(\boldsymbol{k}_{1}+\boldsymbol{k}_{3})\boldsymbol{\cdot }\boldsymbol{r}\right]\nonumber\\ \displaystyle & & \displaystyle \times \,{\mathcal{A}}(\boldsymbol{r}+St^{\prime }r_{1}\boldsymbol{e}_{2})=2{\mathcal{D}}(t-t^{\prime })(2\unicode[STIX]{x03C0})^{3}\unicode[STIX]{x1D6FF}(\boldsymbol{k}_{1}-\boldsymbol{k}_{3})\nonumber\\ \displaystyle & & \displaystyle \times \,\int \text{d}^{3}r\exp (-\text{i}\boldsymbol{k}_{1}\boldsymbol{\cdot }\boldsymbol{r}){\mathcal{A}}(\boldsymbol{r}+St^{\prime }r_{1}\boldsymbol{e}_{2}).\end{eqnarray}$$
Another change of the integration variable to
![]() $\boldsymbol{R}=\boldsymbol{r}+St^{\prime }r_{1}\boldsymbol{e}_{2}$
gives us a compact form for the two-point correlator:
$\boldsymbol{R}=\boldsymbol{r}+St^{\prime }r_{1}\boldsymbol{e}_{2}$
gives us a compact form for the two-point correlator:
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \overline{\widetilde{a}(\boldsymbol{k}_{1},t)\widetilde{a}^{\ast }(\boldsymbol{k}_{3},t^{\prime })}=2{\mathcal{D}}(t-t^{\prime })(2\unicode[STIX]{x03C0})^{3}\unicode[STIX]{x1D6FF}(\boldsymbol{k}_{1}-\boldsymbol{k}_{3})\,\widetilde{{\mathcal{A}}}(\boldsymbol{K}(\boldsymbol{k}_{1},t^{\prime })),\\ \displaystyle \text{where }\widetilde{{\mathcal{A}}}(\boldsymbol{K})=\int \text{d}^{3}R\exp (-\text{i}\boldsymbol{K}\boldsymbol{\cdot }\boldsymbol{R}){\mathcal{A}}(\boldsymbol{R}).\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \overline{\widetilde{a}(\boldsymbol{k}_{1},t)\widetilde{a}^{\ast }(\boldsymbol{k}_{3},t^{\prime })}=2{\mathcal{D}}(t-t^{\prime })(2\unicode[STIX]{x03C0})^{3}\unicode[STIX]{x1D6FF}(\boldsymbol{k}_{1}-\boldsymbol{k}_{3})\,\widetilde{{\mathcal{A}}}(\boldsymbol{K}(\boldsymbol{k}_{1},t^{\prime })),\\ \displaystyle \text{where }\widetilde{{\mathcal{A}}}(\boldsymbol{K})=\int \text{d}^{3}R\exp (-\text{i}\boldsymbol{K}\boldsymbol{\cdot }\boldsymbol{R}){\mathcal{A}}(\boldsymbol{R}).\end{array}\right\}\end{eqnarray}$$
Note that
![]() $\widetilde{{\mathcal{A}}}(-\boldsymbol{K})=\widetilde{{\mathcal{A}}}^{\ast }(\boldsymbol{K})$
because
$\widetilde{{\mathcal{A}}}(-\boldsymbol{K})=\widetilde{{\mathcal{A}}}^{\ast }(\boldsymbol{K})$
because
![]() ${\mathcal{A}}(\boldsymbol{R})$
is a real function and that the argument of the complex spatial power spectrum
${\mathcal{A}}(\boldsymbol{R})$
is a real function and that the argument of the complex spatial power spectrum
![]() $\widetilde{{\mathcal{A}}}(\boldsymbol{K})$
is a time-dependent wavevector.
$\widetilde{{\mathcal{A}}}(\boldsymbol{K})$
is a time-dependent wavevector.
Appendix C. Derivation of (3.5) and (3.6)
We derive an expression for the mean EMF in Fourier space by using (3.3) as:
 $$\begin{eqnarray}\displaystyle \widetilde{\overline{\boldsymbol{E}}}(\boldsymbol{k},t) & = & \displaystyle \int \text{d}^{3}x\exp (-\text{i}\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{x})\,\overline{\boldsymbol{E}}(\boldsymbol{x},t)=\int \text{d}^{3}x\exp (-\text{i}\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{x})\,\overline{a(\boldsymbol{x},t)\boldsymbol{h}(\boldsymbol{x},t)}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{(2\unicode[STIX]{x03C0})^{3}}\int \text{d}^{3}k^{\prime }\text{d}^{3}k^{\prime \prime }\unicode[STIX]{x1D6FF}(\boldsymbol{k}^{\prime }+\boldsymbol{k}^{\prime \prime }-\boldsymbol{k})\,\overline{\widetilde{a}(\boldsymbol{k}^{\prime },t)\,\widetilde{\boldsymbol{h}}(\boldsymbol{k}^{\prime \prime },t)}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{(2\unicode[STIX]{x03C0})^{3}}\int \text{d}^{3}k^{\prime }\,\text{d}^{3}k^{\prime \prime }\unicode[STIX]{x1D6FF}(\boldsymbol{k}^{\prime }+\boldsymbol{k}^{\prime \prime }-\boldsymbol{k})\int _{0}^{t}\text{d}t^{\prime }\,\widetilde{G}_{\unicode[STIX]{x1D702}_{T}}(\boldsymbol{k}^{\prime \prime },t,t^{\prime })\nonumber\\ \displaystyle & & \displaystyle \times \,\{[\text{i}\boldsymbol{K}(\boldsymbol{k}^{\prime \prime },t^{\prime })\times \overline{\widetilde{a}(\boldsymbol{k}^{\prime },t)\widetilde{\boldsymbol{M}}(\boldsymbol{k}^{\prime \prime },t^{\prime })}]+\boldsymbol{e}_{2}S(t-t^{\prime })[\text{i}\boldsymbol{K}(\boldsymbol{k}^{\prime \prime },t^{\prime })\times \overline{\widetilde{a}(\boldsymbol{k}^{\prime },t)\widetilde{\boldsymbol{M}}(\boldsymbol{k}^{\prime \prime },t^{\prime })}]_{1}\}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widetilde{\overline{\boldsymbol{E}}}(\boldsymbol{k},t) & = & \displaystyle \int \text{d}^{3}x\exp (-\text{i}\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{x})\,\overline{\boldsymbol{E}}(\boldsymbol{x},t)=\int \text{d}^{3}x\exp (-\text{i}\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{x})\,\overline{a(\boldsymbol{x},t)\boldsymbol{h}(\boldsymbol{x},t)}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{(2\unicode[STIX]{x03C0})^{3}}\int \text{d}^{3}k^{\prime }\text{d}^{3}k^{\prime \prime }\unicode[STIX]{x1D6FF}(\boldsymbol{k}^{\prime }+\boldsymbol{k}^{\prime \prime }-\boldsymbol{k})\,\overline{\widetilde{a}(\boldsymbol{k}^{\prime },t)\,\widetilde{\boldsymbol{h}}(\boldsymbol{k}^{\prime \prime },t)}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{(2\unicode[STIX]{x03C0})^{3}}\int \text{d}^{3}k^{\prime }\,\text{d}^{3}k^{\prime \prime }\unicode[STIX]{x1D6FF}(\boldsymbol{k}^{\prime }+\boldsymbol{k}^{\prime \prime }-\boldsymbol{k})\int _{0}^{t}\text{d}t^{\prime }\,\widetilde{G}_{\unicode[STIX]{x1D702}_{T}}(\boldsymbol{k}^{\prime \prime },t,t^{\prime })\nonumber\\ \displaystyle & & \displaystyle \times \,\{[\text{i}\boldsymbol{K}(\boldsymbol{k}^{\prime \prime },t^{\prime })\times \overline{\widetilde{a}(\boldsymbol{k}^{\prime },t)\widetilde{\boldsymbol{M}}(\boldsymbol{k}^{\prime \prime },t^{\prime })}]+\boldsymbol{e}_{2}S(t-t^{\prime })[\text{i}\boldsymbol{K}(\boldsymbol{k}^{\prime \prime },t^{\prime })\times \overline{\widetilde{a}(\boldsymbol{k}^{\prime },t)\widetilde{\boldsymbol{M}}(\boldsymbol{k}^{\prime \prime },t^{\prime })}]_{1}\}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
This is given in terms of the quantity
![]() $\overline{\widetilde{a}(\boldsymbol{k}^{\prime },t)\widetilde{\boldsymbol{M}}(\boldsymbol{k}^{\prime \prime },t^{\prime })}$
, which can be determined by using the definition of
$\overline{\widetilde{a}(\boldsymbol{k}^{\prime },t)\widetilde{\boldsymbol{M}}(\boldsymbol{k}^{\prime \prime },t^{\prime })}$
, which can be determined by using the definition of
![]() $\widetilde{\boldsymbol{M}}$
from (A 1) and then using the time-stationary Galilean-invariant expression for the two-point
$\widetilde{\boldsymbol{M}}$
from (A 1) and then using the time-stationary Galilean-invariant expression for the two-point
![]() $\widetilde{a}$
-correlator as given by (B 3). We get
$\widetilde{a}$
-correlator as given by (B 3). We get
 $$\begin{eqnarray}\displaystyle \overline{\widetilde{a}(\boldsymbol{k}^{\prime },t)\widetilde{\boldsymbol{M}}(\boldsymbol{k}^{\prime \prime },t^{\prime })} & = & \displaystyle \frac{1}{(2\unicode[STIX]{x03C0})^{3}}\int \text{d}^{3}k^{\prime \prime \prime }\,\overline{\widetilde{a}(\boldsymbol{k}^{\prime },t)\widetilde{a}^{\ast }(\boldsymbol{k}^{\prime \prime \prime },t^{\prime })}\,\widetilde{\overline{\boldsymbol{H}}}(\boldsymbol{k}^{\prime \prime }+\boldsymbol{k}^{\prime \prime \prime },t^{\prime })\nonumber\\ \displaystyle & = & \displaystyle 2{\mathcal{D}}(t-t^{\prime })\,\widetilde{{\mathcal{A}}}(\boldsymbol{K}(\boldsymbol{k}^{\prime },t^{\prime }))\,\widetilde{\overline{\boldsymbol{H}}}(\boldsymbol{k}^{\prime }+\boldsymbol{k}^{\prime \prime },t^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \overline{\widetilde{a}(\boldsymbol{k}^{\prime },t)\widetilde{\boldsymbol{M}}(\boldsymbol{k}^{\prime \prime },t^{\prime })} & = & \displaystyle \frac{1}{(2\unicode[STIX]{x03C0})^{3}}\int \text{d}^{3}k^{\prime \prime \prime }\,\overline{\widetilde{a}(\boldsymbol{k}^{\prime },t)\widetilde{a}^{\ast }(\boldsymbol{k}^{\prime \prime \prime },t^{\prime })}\,\widetilde{\overline{\boldsymbol{H}}}(\boldsymbol{k}^{\prime \prime }+\boldsymbol{k}^{\prime \prime \prime },t^{\prime })\nonumber\\ \displaystyle & = & \displaystyle 2{\mathcal{D}}(t-t^{\prime })\,\widetilde{{\mathcal{A}}}(\boldsymbol{K}(\boldsymbol{k}^{\prime },t^{\prime }))\,\widetilde{\overline{\boldsymbol{H}}}(\boldsymbol{k}^{\prime }+\boldsymbol{k}^{\prime \prime },t^{\prime }).\end{eqnarray}$$
Substituting (C 2) in (C 1) and solving the
![]() $k^{\prime \prime }$
-integral using the property of the
$k^{\prime \prime }$
-integral using the property of the
![]() $\unicode[STIX]{x1D6FF}$
-function, we immediately find the expression for mean EMF as given in (3.5) in terms of a generalized complex velocity vector
$\unicode[STIX]{x1D6FF}$
-function, we immediately find the expression for mean EMF as given in (3.5) in terms of a generalized complex velocity vector
![]() $\widetilde{\boldsymbol{U}}$
defined by (3.6).
$\widetilde{\boldsymbol{U}}$
defined by (3.6).