Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-14T17:29:03.157Z Has data issue: false hasContentIssue false
  • English
  • Français

Global calculation of neoclassical impurity transport including the variation of electrostatic potential

Part of: Focus on Fusion

Published online by Cambridge University Press:  25 June 2020

Keiji Fujita Open the ORCID record for Keiji Fujita [Opens in a new window] ,
S. Satake ,
R. Kanno ,
M. Nunami ,
M. Nakata ,
J. M. García-Regaña ,
J. L. Velasco  and
I. Calvo
Keiji Fujita*
Affiliation:
The Graduate University for Advanced Studies (SOKENDAI), 322-6Oroshi-cho, Toki, Japan
S. Satake
Affiliation:
The Graduate University for Advanced Studies (SOKENDAI), 322-6Oroshi-cho, Toki, Japan National Institute for Fusion Science, 322-6Oroshi-cho, Toki, Japan
R. Kanno
Affiliation:
The Graduate University for Advanced Studies (SOKENDAI), 322-6Oroshi-cho, Toki, Japan National Institute for Fusion Science, 322-6Oroshi-cho, Toki, Japan
M. Nunami
Affiliation:
The Graduate University for Advanced Studies (SOKENDAI), 322-6Oroshi-cho, Toki, Japan National Institute for Fusion Science, 322-6Oroshi-cho, Toki, Japan
M. Nakata
Affiliation:
The Graduate University for Advanced Studies (SOKENDAI), 322-6Oroshi-cho, Toki, Japan National Institute for Fusion Science, 322-6Oroshi-cho, Toki, Japan
J. M. García-Regaña
Affiliation:
Laboratorio Nacional de Fusión, CIEMAT, Avenida Complutense, 40, 28040, Madrid, Spain
J. L. Velasco
Affiliation:
Laboratorio Nacional de Fusión, CIEMAT, Avenida Complutense, 40, 28040, Madrid, Spain
I. Calvo
Affiliation:
Laboratorio Nacional de Fusión, CIEMAT, Avenida Complutense, 40, 28040, Madrid, Spain
*
†Email address for correspondence: fujita.keiji@nifs.ac.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

Recently, the validity range of the approximations commonly used in neoclassical calculation has been reconsidered. One of the primary motivations behind this trend is observation of an impurity hole in LHD (Large Helical Device), i.e. the formation of an extremely hollow density profile of an impurity ion species, such as carbon 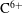$\text{C}^{6+}$, in the plasma core region where a negative radial electric field (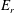$E_{r}$) is expected to exist. Recent studies have shown that the variation of electrostatic potential on the flux surface, 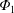$\unicode[STIX]{x1D6F7}_{1}$, has significant impact on neoclassical impurity transport. Nevertheless, the effect of 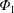$\unicode[STIX]{x1D6F7}_{1}$ has been studied with radially local codes and the necessity of global calculation has been suggested. Thus, we have extended a global neoclassical code, FORTEC-3D, to simulate impurity transport in an impurity hole plasma including 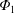$\unicode[STIX]{x1D6F7}_{1}$ globally. Independently of the 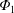$\unicode[STIX]{x1D6F7}_{1}$ effect, an electron root of the ambipolar condition for the impurity hole plasma has been found by global simulation. Hence, we have considered two different cases, each with a positive (global) and a negative (local) solution of the ambipolar condition, respectively. Our result provides another support that 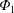$\unicode[STIX]{x1D6F7}_{1}$ has non-negligible impact on impurity transport. However, for the ion-root case, the radial 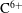$\text{C}^{6+}$ flux is driven further inwardly by 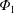$\unicode[STIX]{x1D6F7}_{1}$. For the electron-root case, on the other hand, the radial particle 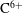$\text{C}^{6+}$ flux is outwardly enhanced by 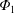$\unicode[STIX]{x1D6F7}_{1}$. These results indicate that how 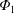$\unicode[STIX]{x1D6F7}_{1}$ affects the radial particle transport crucially depends on the profile of the ambipolar-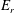$E_{r}$, which is found to be susceptible to 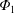$\unicode[STIX]{x1D6F7}_{1}$ itself and the global effects.

Keywords

fusion plasmaplasma confinementplasma simulation
Type
Research Article
Information
Journal of Plasma Physics , Volume 86 , Issue 3 , June 2020 , 905860319
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Boozer, A. H. 1981 Plasma equilibrium with rational magnetic surfaces. Phys. Fluids 24 (11), 1999–2003.CrossRefGoogle Scholar
Brunner, S., Valeo, E. & Krommes, J. A. 1999 Collisional delta-f scheme with evolving background for transport time scale simulations. Phys. Plasmas 6 (12), 4504–4521.CrossRefGoogle Scholar
Buller, S., Smith, H., Helander, P., Mollén, A., Newton, S. & Pusztai, I. 2018 Collisional transport of impurities with flux-surface varying density in stellarators. J. Plasma Phys. 84 (4), 905840409.CrossRefGoogle Scholar
Burhenn, R., Feng, Y., Ida, K., Maassberg, H., McCarthy, K. J., Kalinina, D., Kobayashi, M., Morita, S., Nakamura, Y., Nozato, H. et al. 2009 On impurity handling in high performance stellarator/heliotron plasmas. Nucl. Fusion 49 (6), 065005.CrossRefGoogle Scholar
Calvo, I., Parra, F. I., Velasco, J. L. & Alonso, J. A. 2017 The effect of tangential drifts on neoclassical transport in stellarators close to omnigeneity. Plasma Phys. Control. Fusion 59 (5), 055014.CrossRefGoogle Scholar
Calvo, I., Parra, F. I., Velasco, J. L., Alonso, J. A. & García-Regaña, J. M. 2018a Stellarator impurity flux driven by electric fields tangent to magnetic surfaces. Nucl. Fusion 58 (12), 124005.CrossRefGoogle Scholar
Calvo, I., Parra, F. I., Velasco, J. L. & García-Regaña, J. M. 2020 Impact of main ion pressure anisotropy on stellarator impurity transport. Nucl. Fusion 60 (1), 016035.CrossRefGoogle Scholar
Calvo, I., Velasco, J., Parra, F., Alonso, J. & García-Regaña, J. 2018b Electrostatic potential variations on stellarator magnetic surfaces in low collisionality regimes. J. Plasma Phys. 84 (4), 905840407.CrossRefGoogle Scholar
Estrada, T., Sánchez, E., García-Regaña, J. M., Alonso, J. A., Ascasíbar, E., Calvo, I., Cappa, A., Carralero, D., Hidalgo, C., Liniers, M. et al. 2019 Turbulence and perpendicular plasma flow asymmetries measured at TJ-II plasmas. Nucl. Fusion 59 (7), 076021.CrossRefGoogle Scholar
Fujita, K., Satake, S., Kanno, R., Nunami, M., Nakata, M. & García-Regaña, J. M. 2019 Global effects on the variation of ion density and electrostatic potential on the flux surface in helical plasmas. Plasma Fusion Res. 14, 3403102.CrossRefGoogle Scholar
García-Regaña, J.M., Beidler, C.D., Kleiber, R., Helander, P., Mollén, A., Alonso, J.A., Landreman, M., Maassberg, H., Smith, H. M., Turkin, Y. et al. 2017 Electrostatic potential variation on the flux surface and its impact on impurity transport. Nucl. Fusion 57 (5), 056004.CrossRefGoogle Scholar
García-Regaña, J.M., Estrada, T., Calvo, I., Velasco, J.L., Alonso, J.A., Carralero, D., Kleiber, R., Landreman, M., Mollén, A., Sánchez, E. et al. 2018 On-surface potential and radial electric field variations in electron root stellarator plasmas. Plasma Phys. Control. Fusion 60 (10), 104002.CrossRefGoogle Scholar
García-Regaña, J. M., Kleiber, R., Beidler, C. D., Turkin, Y., Maassberg, H. & Helander, P. 2013 On neoclassical impurity transport in stellarator geometry. Plasma Phys. Control. Fusion 55 (7), 074008.CrossRefGoogle Scholar
Helander, P., Newton, S. L., Mollén, A. & Smith, H. M. 2017 Impurity transport in a mixed-collisionality stellarator plasma. Phys. Rev. Lett. 118 (15), 155002.CrossRefGoogle Scholar
Huang, B., Satake, S., Kanno, R., Sugama, H. & Matsuoka, S. 2017 Benchmark of the local drift-kinetic models for neoclassical transport simulation in helical plasmas. Phys. Plasmas 24 (2), 022503.CrossRefGoogle Scholar
Ida, K., Yoshinuma, M., Osakabe, M., Nagaoka, K., Yokoyama, M., Funaba, H., Suzuki, C., Ido, T., Shimizu, A., Murakami, I. et al. 2009 Observation of an impurity hole in a plasma with an ion internal transport barrier in the large helical device. Phys. Plasmas 16 (5), 056111.CrossRefGoogle Scholar
Ido, T., Shimizu, A., Nishiura, M., Nagaoka, K., Yokoyama, M., Ida, K., Yoshinuma, M., Toi, K., Itoh, K., Nakano, H. et al. 2010 Experimental study of radial electric field and electrostatic potential fluctuation in the large helical device. Plasma Phys. Control. Fusion 52 (12), 124025.CrossRefGoogle Scholar
Landreman, M., Smith, H. M., Mollén, A. & Helander, P. 2014 Comparison of particle trajectories and collision operators for collisional transport in nonaxisymmetric plasmas. Phys. Plasmas 21 (4), 042503.CrossRefGoogle Scholar
Littlejohn, R. G. 1983 Variational principles of guiding centre motion. J. Plasma Phys. 29 (1), 111–125.CrossRefGoogle Scholar
Matsuoka, S., Satake, S., Kanno, R. & Sugama, H. 2015 Effects of magnetic drift tangential to magnetic surfaces on neoclassical transport in non-axisymmetric plasmas. Phys. Plasmas 22 (7), 072511.CrossRefGoogle Scholar
Mollén, A., Landreman, M., Smith, H. M., García-Regaña, J. M. & Nunami, M. 2018 Flux-surface variations of the electrostatic potential in stellarators: impact on the radial electric field and neoclassical impurity transport. Plasma Phys. Control. Fusion 60 (8), 084001.CrossRefGoogle Scholar
Nakamura, Y., Tamura, N., Yoshinuma, M., Suzuki, C., Yoshimura, S., Kobayashi, M., Yokoyama, M., Nunami, M., Nakata, M., Nagaoka, K. et al. 2017 Strong suppression of impurity accumulation in steady-state hydrogen discharges with high power NBI heating on LHD. Nucl. Fusion 57 (5), 056003.CrossRefGoogle Scholar
Newton, S., Helander, P., Mollén, A. & Smith, H. 2017 Impurity transport and bulk ion flow in a mixed collisionality stellarator plasma. J. Plasma Phys. 83 (5), 905830505.CrossRefGoogle Scholar
Nunami, M., Nakata, M., Sato, M., Toda, S., Yamaguchi, H., Sugama, H. & Yokoyama, M. 2017 Kinetic simulation studies on multi-ion-species plasma transport in helical systems. In 27th IAEA Fusion Energy Conference (FEC 2018) 22–27 October 2018, Gandhinagar (nearest Airport: Ahmedabad), India. https://www.iaea.org/events/fec-2018.Google Scholar
Nunami, M., Nakata, M., Toda, S. & Sugama, H. 2020 Gyrokinetic simulations for turbulent transport of multi-ion-species plasmas in helical systems. Phys. Plasmas 27 (5), 052501.CrossRefGoogle Scholar
Nunami, M., Satake, S., Fujita, K., Yamaguchi, H., Matsuoka, S., Sato, M., Toda, S. & Sugama, H. 2019 Particle balance in turbulent and neoclassical transport of helical plasmas. In 22nd ISHW (22nd International Stellarator and Heliotron Workshop) September 23–27, 2019. University of Wisconsin-Madison.Google Scholar
Nunami, M., Sugama, H., Velasco, J. L., Yokoyama, M., Sato, M., Nakata, M. & Satake, S. 2016 Anomalous and neoclassical transport of hydrogen isotope and impurity ions in LHD plasmas. In 26th IAEA Fusion Energy Conference, 17–22 October 2016, Kyoto, Japan. Conference ID: 48315 (CN-234). https://www-pub.iaea.org/iaeameetings/48315/26th-IAEA-Fusion-Energy-Conference.Google Scholar
Pedrosa, M. A., Alonso, J. A., García-Regaña, J. M., Hidalgo, C., Velasco, J. L., Calvo, I., Kleiber, R., Silva, C. & Helander, P. 2015 Electrostatic potential variations along flux surfaces in stellarators. Nucl. Fusion 55 (5), 052001.CrossRefGoogle Scholar
Satake, S., Idomura, Y., Sugama, H. & Watanabe, T.-H. 2010 Benchmark test of drift-kinetic and gyrokinetic codes through neoclassical transport simulations. Comput. Phys. Comm. 181 (6), 1069–1076.CrossRefGoogle Scholar
Satake, S., Kanno, R. & Sugama, H. 2008 Development of a non-local neoclassical transport code for helical configurations. Plasma Fusion Res. 3, S1062.CrossRefGoogle Scholar
Satake, S., Nakata, M., Pianpanit, T., Sugama, H., Nunami, M., Matsuoka, S., Ishiguro, S. & Kanno, R. 2020 Benchmark of a new multi-ion-species collision operator for $\unicode[STIX]{x1D6FF}f$ Monte Carlo neoclassical simulation. Comput. Phys. Commun. 255, 107249.CrossRefGoogle Scholar
Sugama, H., Matsuoka, S., Satake, S., Nunami, M. & Watanabe, T.-H. 2019 Improved linearized model collision operator for the highly collisional regime. Phys. Plasmas 26 (10), 102108.CrossRefGoogle Scholar
Sugama, H., Watanabe, T.-H. & Nunami, M. 2009 Linearized model collision operators for multiple ion species plasmas and gyrokinetic entropy balance equations. Phys. Plasmas 16 (11), 112503.CrossRefGoogle Scholar
Velasco, J.L., Calvo, I., García-Regaña, J.M., Parra, F.I., Satake, S. & Alonso, J.A. 2018 Large tangential electric fields in plasmas close to temperature screening. Plasma Phys. Control. Fusion 60 (7), 074004.CrossRefGoogle Scholar
Velasco, J. L., Calvo, I., Parra, F. I., Alonso, J. A., Carralero, D., Estrada, T., García-Regañ, J. M., Huang, X., Morita, S., Satake, S. et al. 2019 Fast calculation of neoclassical transport of energy and impurities in arbitrary stellarator geometry with the code KNOSOS. In 22nd ISHW (22nd International Stellarator and Heliotron Workshop) September 23–27, 2019. University of Wisconsin-Madison.Google Scholar
Velasco, J. L., Calvo, I., Parra, F. I. & García-Regana, J. M. 2020 KNOSOS: a fast orbit-averaging neoclassical code for arbitrary stellarator geometry. J. Comput. Phys. 109512. doi:10.1016/j.jcp.2020.109512.CrossRefGoogle Scholar
Velasco, J. L., Calvo, I., Satake, S., Alonso, A., Nunami, M., Yokoyama, M., Sato, M., Estrada, T., Fontdecaba, J. M., Liniers, M. et al. 2017 Moderation of neoclassical impurity accumulation in high temperature plasmas of helical devices. Nucl. Fusion 57, 016016.CrossRefGoogle Scholar
Wang, W. X., Nakajima, N., Okamoto, M. & Murakami, S. 1999 A new f method for neoclassical transport studies. Plasma Phys. Control. Fusion 41 (9), 1091.CrossRefGoogle Scholar
White, R. B. 2014 The Theory of Toroidally Confined Plasmas, 3rd edn.World Scientific.CrossRefGoogle Scholar
Yoshinuma, M., Ida, K. & Yokoyama, M.2010 Impurity transport of ion ITB plasmas on LHD. Tech. Rep., National Institute for Fusion Science.Google Scholar