Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T04:00:14.308Z Has data issue: false hasContentIssue false
  • English
  • Français

Godbillon-Vey helicity and magnetic helicity in magnetohydrodynamics

Part of: PLA Topological Methods in MHD, Fluids, and Plasmas

Published online by Cambridge University Press:  10 October 2019

G. M. Webb Open the ORCID record for G. M. Webb [Opens in a new window] ,
A. Prasad Open the ORCID record for A. Prasad [Opens in a new window] ,
S. C. Anco Open the ORCID record for S. C. Anco [Opens in a new window]  and
Q. Hu Open the ORCID record for Q. Hu [Opens in a new window]
G. M. Webb*
Affiliation:
Center for Space Plasma and Aeronomic Research, The University of Alabama in Huntsville, Huntsville, AL 35805, USA
A. Prasad
Affiliation:
Center for Space Plasma and Aeronomic Research, The University of Alabama in Huntsville, Huntsville, AL 35805, USA
S. C. Anco
Affiliation:
Department of Mathematics, Brock University, St. Catharines, ON L2S 3A1, Canada
Q. Hu
Affiliation:
Center for Space Plasma and Aeronomic Research, The University of Alabama in Huntsville, Huntsville, AL 35805, USA Department of Space Science, The University of Alabama in Huntsville, Huntsville, AL 35899, USA
*
†Email address for correspondence: gmw0002@uah.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

The Godbillon–Vey invariant occurs in homology theory, and algebraic topology, when conditions for a co-dimension 1, foliation of a three-dimensional manifold are satisfied. The magnetic Godbillon–Vey helicity invariant in magnetohydrodynamics (MHD) is a higher-order helicity invariant that occurs for flows in which the magnetic helicity density 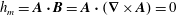$h_{m}=\boldsymbol{A}\boldsymbol{\cdot }\boldsymbol{B}=\boldsymbol{A}\boldsymbol{\cdot }(\unicode[STIX]{x1D735}\times \boldsymbol{A})=0$, where 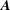$\boldsymbol{A}$ is the magnetic vector potential and 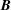$\boldsymbol{B}$ is the magnetic induction. This paper obtains evolution equations for the magnetic Godbillon–Vey field 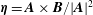$\unicode[STIX]{x1D6C8}=\boldsymbol{A}\times \boldsymbol{B}/|\boldsymbol{A}|^{2}$ and the Godbillon–Vey helicity density 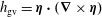$h_{\text{gv}}=\unicode[STIX]{x1D6C8}\boldsymbol{\cdot }(\unicode[STIX]{x1D735}\times \unicode[STIX]{x1D6C8})$ in general MHD flows in which either 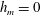$h_{m}=0$ or 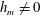$h_{m}\neq 0$. A conservation law for 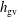$h_{\text{gv}}$ occurs in flows for which 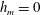$h_{m}=0$. For 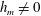$h_{m}\neq 0$ the evolution equation for 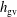$h_{\text{gv}}$ contains a source term in which 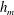$h_{m}$ is coupled to 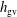$h_{\text{gv}}$ via the shear tensor of the background flow. The transport equation for 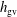$h_{\text{gv}}$ also depends on the electric field potential 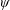$\unicode[STIX]{x1D713}$, which is related to the gauge for 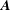$\boldsymbol{A}$, which takes its simplest form for the advected 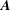$\boldsymbol{A}$ gauge in which 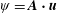$\unicode[STIX]{x1D713}=\boldsymbol{A}\boldsymbol{\cdot }\boldsymbol{u}$ where $\boldsymbol{u}$ is the fluid velocity. An application of the Godbillon–Vey magnetic helicity to nonlinear force-free magnetic fields used in solar physics is investigated. The possible uses of the Godbillon–Vey helicity in zero helicity flows in ideal fluid mechanics, and in zero helicity Lagrangian kinematics of three-dimensional advection, are discussed.

Keywords

astrophysical plasmasplasma flowsspace plasma physics
Type
Research Article
Information
Journal of Plasma Physics , Volume 85 , Issue 5 , October 2019 , 775850502
Copyright
© Cambridge University Press 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akmet’ev, P. M., Candelaresi, S. & Smirnov, A. Y. 2017 Calculations for the practical applications of quadratic helicity in MHD. Phys. Plasmas 24 (10), 102128.Google Scholar
Anco, S. C. & Dar, A. 2009 Classification of conservation laws of compressible isentropic fluid flow in $n>1$ spatial dimensions. Proc. R. Soc. Lond. A 464, 2641–2488.1$+spatial+dimensions.+Proc.+R.+Soc.+Lond.+A+464,+2641–2488.>Google Scholar
Anco, S. C. & Dar, A. 2010 Conservation laws of inviscid non-isentropic compressible fluid flow in $n>1$ space dimensions. Proc. R. Soc. Lond. A 466, 2605–2632.1$+space+dimensions.+Proc.+R.+Soc.+Lond.+A+466,+2605–2632.>Google Scholar
Anco, S. C. & Webb, G. M. 2018 Hierarchies of Vorticity invariants and related conserved helicity and cross helicity integrals in inviscid fluid flow. J. Fluid Mech. submitted arXiv:1809.01544 (physics:flu-dyn).Google Scholar
Arnold, V. I. & Khesin, B. A. 1998 Topological Methods in Hydrodynamics, Applied Mathematical Sciences, Series, vol. 125. Springer.Google Scholar
Balsara, D. 2004 Second order accurate schemes for magnetohydrodynamics with divergence free reconstruction. Astrophys. J. Suppl. 151, 149–184.Google Scholar
Blackman, E. G. 2015 Magnetic helicity and large scale magnetic fields: a primer. Space Sci. Rev. 188 (1–4), 59–91.Google Scholar
Berger, M. A. & Field, G. B. 1984 The topological properties of magnetic helicity. J. Fluid Mech. 147, 133–148.Google Scholar
Berger, M. A. & Hornig, G. 2018 A generalized poloidal and toroidal decomposition and an absolute measure of helicity. J. Phys. A: Math. Theor. 51, 495501 (22p).Google Scholar
Bieber, J. W., Evenson, P. A. & Matthaeus, W. H. 1987 Magnetic helicity of the Parker field. Astrophys. J. 315, 700.Google Scholar
Bishop, R. L. 1975 There is more than one way to frame a curve. Am. Math. Mon. 82, 246–251.Google Scholar
Boyd, T. J. M. & Sanderson, J. J. 1969 Plasma Dynamics. Barnes and Noble.Google Scholar
Boozer, A. H. 1983 Evaluation of the structure of ergodic fields. Phys. Fluids 26 (5), 1288–1291.Google Scholar
Boozer, A. H. 2004 Physics of magnetically confined plasmas. Rev. Mod. Phys. 76, 1071–1138.Google Scholar
Besse, N. & Frisch, U. 2017 Geometric formulation of the Cauchy invariants for incompressible Euler flow in flat and curved spaces. J. Fluid Mech. 825, 412–478.Google Scholar
Calkin, M. G. 1963 An action principle for magnetohydrodynamics. Can. J. Phys. 41, 2241–2251.Google Scholar
Chandrasekhar, S. 1956 On force-free magnetic fields. Proc. Natl Acad. Sci. USA 42, 1–5.Google Scholar
Chandrasekhar, S. & Kendall, P. C. 1957 On force-free magnetic fields. Astrophys. J. 126, 457–460.Google Scholar
Cotter, C. J., Holm, D. D. & Hydon, P. E. 2007 Multi-symplectic formulation of fluid dynamics using the inverse map. Proc. R. Soc. Lond. A 463, 2617–2687.Google Scholar
Dombre, T., Frisch, U., Green, J. M., Henon, M., Mehr, A. & Soward, A. M. 1986 Chaotic streamlines in ABC flows. J. Fluid Mech. 167, 353–391.Google Scholar
Dedner, A., Kemm, F., Kröner, D., Munz, C., Schnitzer, T. & Wesenberg, M. 2002 Hyperbolic divergence cleaning for the MHD equations. J. Comput. Phys. 175, 645–673.Google Scholar
Elsässer, W. M. 1956 Hydromagnetic dynamo theory. Rev. Mod. Phys. 28 (2), 135–163.Google Scholar
Evans, C. R. & Hawley, J. F. 1988 Simulation of magnetohydrodynamic flows: a constrained transport method. Astrophys. J. 332, 659–677.Google Scholar
Finn, J. H. & Antonsen, T. M. 1985 Magnetic helicity: what is it and what is it good for? Comment Plasma Phys. Control. Fusion 9 (3), 111.Google Scholar
Finn, J. M. & Antonsen, T. M. 1988 Magnetic helicity injection for configurations with field errors. Phys. Fluids 31 (10), 3012–3017.Google Scholar
Flanders, H. 1963 Differential Forms (ed. Bellman, R.), Mathematics in Science and Engineering Series, vol. 11. Academic Press.Google Scholar
Fulton, W. 1995 Algebraic Topology, Graduate Texts in Mathematics, vol. 153. Springer.Google Scholar
Ghys, E.2014 Foliations: What’s next after Thurston? Bill Thurston Legacy Conference, June 23–27, 2014 at Cornell University. Slides for talk available at http://www.pi.math.cornell.edu/∼thurston/slides/ghys.pdf). video of talk also available on the web.Google Scholar
Godbillon, C. & Vey, J. 1971 Un invariant des Feuilletages, 1. C. R. Acad. Sci. Paris Ser. A-B 273, A92–A95; MR 44 number 11046.Google Scholar
Goldstein, H. 1980 Classical Mechanics, 2nd edn. Addison Wesley.Google Scholar
Golovin, S. V. 2011 Natural curvilinear coordinates for ideal MHD equations. Nonstationary flows with constant total pressure. Phys. Lett. A 375, 283–290.Google Scholar
Gordin, V. A. & Petviashvili, V. I. 1987 Equation of continuity for the helicity in media with an infinite conductivity. JETP Lett. 45 (5), 266–267.Google Scholar
Gordin, V. A. & Petviashvili, V. I. 1989 Lyapunov instability of MHD equilibrium of a plasma with nonvanishing pressure. Sov. Phy. JETP 68 (5), 988–994.Google Scholar
Hameiri, E. 2004 The complete set of Casimir constants of the motion in magnetohydrodynamics. Phys. Plasmas 11, 3423–3431.Google Scholar
Hatcher, A. E. 2002 Algebraic Topology. Cambridge University Press.Google Scholar
Holm, D. D. & Kimura, Y. 1991 Zero helicity Lagrangian kinematics of three-dimensional advection. Phys. Fluids A 3 (5), 1033–1038.Google Scholar
Holm, D. D. & Kupershmidt, B. A. 1983a Poisson brackets and Clebsch representations for magnetohydrodynamics, multi-fluid plasmas and elasticity. Physica D 6D, 347–363.Google Scholar
Holm, D. D. & Kupershmidt, B. A. 1983b Noncanonical Hamiltonian formulation of ideal magnetohydrodynamics. Physica D 7D, 330–333.Google Scholar
Holm, D. D. 2008 Geometric Mechanics, Part I, Dynamics and Symmetry, Part II Rotating, Translating and Rolling. Imperial College Press; Distributed by World Scientific Co., Singapore, New Jersey, London.Google Scholar
Holm, D. D., Marsden, J. E., Ratiu, T. & Weinstein, A. 1985 Nonlinear stability of fluid and plasma equilibria. Phys. Rep. 123 (1–2), 1–116.Google Scholar
Holm, D. D., Marsden, J. E. & Ratiu, T. S. 1998 The Euler–Lagrange equations and semiproducts with application to continuum theories. Adv. Math. 137 (1), 1–81.Google Scholar
Hurder, S. 2000 Godbillon-Vey classes: a history and survey. In Foliations: Geometry and Dynamics (Warsaw, 2000) (ed. Walczack, P. et al. ), pp. 29–60. World Scientific.Google Scholar
Janhunen, P. 2000 A positive conservative method for magnetohydrodynamics based on HLL and Roe methods. J. Comput. Phys. 160, 649–661.Google Scholar
Kamchatnov, A. M. 1982 Topological soliton in magnetohydrodynamics. Sov. Phys. JETP 82, 117–124.Google Scholar
Kats, A. V. 2003 Variational principle in canonical variables, Weber transformation and complete set of local integrals of motion for dissipation-free magnetohydrodynamics. JETP Lett. 77 (12), 657–661.Google Scholar
Kobayashi, S. & Nomizu, K. 1963 Foundations of Differential Geometry, vol. 1. Interscience Publishers, a division of John Wiley and Sons.Google Scholar
Kruskal, M. D. & Kulsrud, R. M. 1958 Equilibrium of a magnetically confined plasma in a toroid. Phys. Fluids 1, 265.Google Scholar
Lee, J. M. 1997 Riemannian Manifolds: An Introduction to Curvature (ed. Axler, S., Gehring, F. W. & Halmos, P. R.), Graduate Texts in Mathematics, vol. 176. Springer.Google Scholar
Lipschutz, M. M. 1969 Theory and Problems of Differential Geometry, Schaum Outline Series. McGraw-Hill.Google Scholar
Longcope, D. W. & Malanuschenko, A. 2008 Defining and calculating self-helicity in coronal magnetic fields. Astrophys. J. 674, 1130–1143.Google Scholar
Low, B. C. 2006 Magnetic helicity in a two-flux partitioning of an ideal hydromagnetic fluid. Astrophys. J. 646, 1288–1302.Google Scholar
Low, B. C. 2011 Absolute magnetic helicity and the cylindrical magnetic field. Phys. Plasmas 18, 052901.Google Scholar
Low, B. C. & Lou, Y. Q. 1990 Modeling solar force-free magnetic fields. Astrophys. J. 352, 343–352.Google Scholar
Marsden, J. E. & Ratiu, T. S. 1994 Introduction to Mechanics and Symmetry, Texts in Applied Math., vol. 17. chap. 4. Springer.Google Scholar
Mihalas, D. & Mihalas, B. W. 1984 Foundations of Radiation Hydrodynamics. Oxford University Press.Google Scholar
Moffatt, H. K. 1969 The degree of knottedness of tangled vortex lines. J. Fluid Mech. 35, 117.Google Scholar
Moffatt, H. K. 1978 Magnetic Field Generation in Electrically Conducting Fluids. Cambridge University Press.Google Scholar
Moffatt, H. K. & Ricca, R. L. 1992 Helicity and the Calugareanu invariant. Proc. R. Soc. Lond. A 439, 411.Google Scholar
Moiseev, S. S., Sagdeev, R. Z., Tur, A. V. & Yanovskii, V. V. 1982 On the freezing-in integrals and Lagrange invariants in hydrodynamic models. Sov. Phys. JETP 56 (1), 117–123.Google Scholar
Morrison, P. J. 1982 Poisson brackets for fluids and plasmas. In Mathematical Methods in Hydrodynamics and Integrability of Dynamical Systems (ed. Tabor, M. & Treve, Y. M.), AIP Proc. Conf., vol. 88, pp. 13–46.Google Scholar
Morrison, P. J. 1998 Hamiltonian description of the ideal fluid. Rev. Mod. Phys. 70 (2), 467–521.Google Scholar
Okhitani, K. 2018 Study of the 3D Euler equation using Clebsch potentials: dual mechanisms of geometric depletion. Nonlinearity 31, R25–R51; ibid., Addendum, 31, 3973–3973.Google Scholar
Padhye, N. & Morrison, P. J. 1996a Fluid element relabeling symmetry. Phys. Lett. A 219, 287–292.Google Scholar
Padhye, N. & Morrison, P. J. 1996b Relabeling symmetries in hydrodynamics and magnetohydrodynamics. Plasma Phys. Rep. 22 (10), 869–877.Google Scholar
Pontryagin, L. S. 1952 Foundations of Combinatorial Topology. Graylock Press.Google Scholar
Powell, K. G., Roe, P. L., Linde, T. J., Gombosi, T. I. & De Zeeuw, D. 1999 A solution adaptive upwind scheme for ideal magnetohydrodynamics. J. Comput. Phys. 154, 284–309.Google Scholar
Prasad, A., Mangalam, A. & Ravindra, B. 2014 Separable solutions of force-free spheres and applications to solar active regions. Astrophys. J. 768 (81), (23pp).Google Scholar
Prior, C. & Yeates, A. R. 2014 On the helicity of open magnetic fields. Astrophys. J. 787, 100 13pp.Google Scholar
Reinhart, B. L. & Wood, J. W. 1973 A metric formula for the Godbillon-Vey invariant for foliations. Proc. Am. Math. Soc. 38 (2), 427–430.Google Scholar
Rovenski, V. & Walczak, P. 2019a A Godbillon-Vey type invariant for a 3-dimensional manifold with a plane field. Differential Geometry and its Applications 66, 212–230; arXiv:1707.04847v2[math.DG], Feb. 4.Google Scholar
Rovenski, V. & Walczak, P. 2019b Variations of the Godbillon-Vey invariant of foliated 3-manifolds. Complex Anal. Oper. Theory 13, 2917–2937. doi:10.1007/s11785-018-871-9.Google Scholar
Sagdeev, R. Z., Tur, A. V. & Yanovsky, V. V. 1990 Construction of frozen in integrals, Lagrangian and topological invariants in hydrodynamical models. In Proceedings of the IUTAM Symposium (ed. Moffatt, H. K. & Tsinober, A.), Topological Fluid dynamics, pp. 421–428. Cambridge University Press.Google Scholar
Sakurai, T. 1979 A new approach to the force-free magnetic field and its application to the magnetic field of solar active regions. Publ. Astron. Soc. Japan 31, 209–230.Google Scholar
Salmon, R. 1982 Hamilton’s principle and Ertel’s theorem. AIP Conf. Proc. 88, 127–135.Google Scholar
Salmon, R. 1988 Hamiltonian fluid mechanics. Annu. Rev. Fluid Mech. 20, 225–256.Google Scholar
Semenov, V. S., Korovinski, D. B. & Biernat, H. K. 2002 Euler potentials for the MHD-Kamchatnov-Hopf soliton solution. Nonlin. Process. Geophys. 9, 347–354.Google Scholar
Sneddon, I. N. 1957 Elements of Partial Differential Equations, International Student Edition (ed. Martin, W. T.), International Series in Pure and Applied Mathematics. McGraw Hill.Google Scholar
Stone, J. M. & Gardiner, T. 2009 A simple unsplit Godunov method for multi-dimensional MHD. New Astron. 14, 139–148.Google Scholar
Tanehashi, K. & Yoshida, Z. 2015 Gauge symmetries and Noether charges in Clebsch-parameterized magnetohydrodynamics. J. Phys. A: Math. Theor. 48 (2015), 495501 (20pp).Google Scholar
Taylor, J. B. 1986 Relaxation and magnetic reconnection in plasmas. Rev. Mod. Phys. 58, 741–763.Google Scholar
Thurston, W. 1972 Noncobordant foliations of $S^{3}$ . Bull. AMS 78 (4), 511–514.Google Scholar
Tur, A. V. & Yanovsky, V. V. 1993 Invariants for dissipationless hydrodynamic media. J. Fluid Mech. 248, 67–106.Google Scholar
Webb, G. M. 2018 Magnetohydrodynamics and Fluid Dynamics: Action Principles and Conservation Laws, Lecture Notes in Physics, vol. 946. Springer.Google Scholar
Webb, G. M. & Anco, S. C. 2017 On magnetohydrodynamic gauge field theory. J. Phys. A: Math. Theor. 50, 255501 (34pp).Google Scholar
Webb, G. M., Jokipii, J. R. & Morfill, G. E. 1994 Green’s formula and variational principles for cosmic ray transport with application to rotating and shearing flows. Astrophys. J. 424, 158–180.Google Scholar
Webb, G. M., Pogorelov, N. V. & Zank, G. P. 2010 MHD simple waves and the divergence wave. In Solar Wind 12, AIP Proc. Conference, vol. 1216, pp. 300–303. American Institute of Physics.Google Scholar
Webb, G. M., Hu, Q., Dasgupta, B. & Zank, G. P. 2010 Homotopy formulas for the magnetic vector potential and magnetic helicity: the Parker spiral interplanetary magnetic field and magnetic flux ropes. J. Geophys. Res. 115, A10112; Corrections: J. Geophys. Res. 116, A11102, doi:10.1029/2011JA017286, 22nd November 2011.Google Scholar
Webb, G. M., Dasgupta, B., McKenzie, J. F., Hu, Q. & Zank, G. P. 2014a Local and nonlocal advected invariants and helicities in magnetohydrodynamics and gas dynamics, I, Lie dragging approach. J. Phys. A: Math. Theor. 47, 095501 (33pp).Google Scholar
Webb, G. M., Dasgupta, B., McKenzie, J. F., Hu, Q. & Zank, G. P. 2014b Local and nonlocal advected invariants and helicities in magnetohydrodynamics and gas dynamics, II, Noether’s theorems and Casimirs. J. Phys. A: Math. Theor. 47, 095502 (31pp).Google Scholar
Wiegelmann, T. & Sakurai, T. 2012 Solar force-free magnetic fields. Living Rev. Solar Phys. 9, 5 (pp. 49).Google Scholar
Woltjer, L. 1958 A theorem on force-free magnetic fields. Proc. Natl Acad. Sci. USA 44, 489.Google Scholar
Yahalom, A. 2013 Aharonov–Bohm effects in magnetohydrodynamics. Phys. Lett. A 377, 1898–1904.Google Scholar
Yahalom, A. 2017a A conserved cross helicity for non-barotropic MHD. Geophys. Astrophys. Fluid Dyn. 111, 131.Google Scholar
Yahalom, A. 2017b Non barotropic cross helicity conservation and the Aharonov–Bohm effect in magnetohydrodynamics. Fluid Dyn. Res. 50, 011406 (27pp).Google Scholar
Zank, G. P., Dosch, A., Hunana, P., Florinski, V., Matthaeus, W. H. & Webb, G. M. 2012 The transport of low frequency turbulence in astrophysical flows. Part I. Governing equations. Astrophys. J. 745, 35 (20pp).Google Scholar
Zhou, Y. & Matthaeus, W. H. 1990a Transport and turbulence modeling of solar wind fluctuations. J. Geophys. Res. 95 (A7), 10291–10311.Google Scholar
Zhou, Y. & Matthaeus, W. H. 1990b Models of inertial range spectra of interplanetary magnetohydrodynamic turbulence. J. Geophys. Res. 95 (A9), 14881–14892.Google Scholar