Published online by Cambridge University Press: 13 March 2009
For relativistic amplitudes (‘intense propagation’), modulations of electromagnetic (EM) waves in a cold plasma are strongly coupled to longitudinal modes via the ponderomotive force, even if the unmodulated wave is purely transverse. The effect of longitudinal motions is comparable to that of relativistic nonlinearities. Hence a correct and proper expansion procedure requires solution of all the field equations up the appropriate order, including the longitudinal equations. (The plasma is assumed to be fully ionized and cold, with no net charge. The positive component may consist of either positrons or singularly charged ions. Quasi-neutrality is not imposed, but deviations are shown to be small for slow modulations.) We begin by deriving envelope equations (i.e. a reduced set of partial differential equations) governing modulations of intensely propagating, circularly polarized, plane EM plasma waves. (Here the envelope equations are not merely accurate to the appropriate order, but in fact exact.) We then analyse their modulational instabilities. Since the envelope equations are exact, they include the weakly relativistic case (transverse velocities ≪ c) as a limit. We first verify that, in this limit, the envelope equations yield the nonlinear Schrödinger equation (NLS) complete with the correct coefficients and thus the correct modulational instability conditions. Next, although the NLS does not hold for the general case of fully relativistic systems (transverse velocities comparable to c), we still succeed in deriving the modulational instability properties of intensely propagating EM waves in the fully relativistic case directly from the envelope equations, again, reproducing the weakly relativistic case as a test of the perturbation method used. Finally, we apply the results in special cases. For example, in the ultrarelativistic limit (transverse velocities close to c) of either an electron—positron or ion—electron plasma, waves with frequencies below twice the relativistic plasma frequency ωp, where 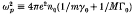 , are unstable. The time scale for growth is comparable to the time for a wave packet to move past a fixed point. (This time scale is much shorter than in the weakly relativistic case, where the time scale for instability is that of the spreading of the wave packet due to linear dispersion.) Our results have important consequences for observations of pulsar micropulses, possible technological applications, and general implications for applications of Whitham theory.
, are unstable. The time scale for growth is comparable to the time for a wave packet to move past a fixed point. (This time scale is much shorter than in the weakly relativistic case, where the time scale for instability is that of the spreading of the wave packet due to linear dispersion.) Our results have important consequences for observations of pulsar micropulses, possible technological applications, and general implications for applications of Whitham theory.