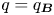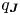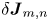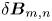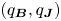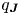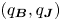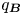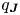1 Introduction
In a magnetic confinement fusion (MCF) plasma, alpha particles produced from fusion reactions will be confined by the magnetic field and heat back the plasma species, and primarily electrons, through collisions. To ignite the plasma, the rate of alpha heating must exceed (and at least match) the rate at which plasma loses energy. Finding scenarios that minimize plasma losses is thus crucial for optimizing the achievement of the conditions necessary for fusion and sustained ignition. A well-known prime reservoir for the minimization of plasma losses lies in the electron energy channel since the electron heat transport is anomalous. This arises from the fact that, being the least massive charged particles, electrons are also the most magnetized and thus the most sensitive to the non-regularity of magnetic field lines. Understanding, controlling and ideally reducing electron heat transport has thus been a major objective of MCF research so far.
A picture that emerged long ago is that the magnetic topology impacts then the electron collective behaviour. Ideally, the magnetic field within a tokamak should be axisymmetric with smooth magnetic field lines spiralling about the magnetic axis. Yet, departures from axisymmetry caused by three-dimensional effects manifesting through the overlap of magnetic resonances break the smoothness of the magnetic field lines and introduce, at least locally, some stochasticity. Although a rigorously exact self-consistent analysis of electron heat transport may still be mathematically out of reach, some relevant estimates obtained using simplifying assumptions have existed for a long time. A significant breakthrough occurred when Rechester & Rosenbluth (Reference Rechester and Rosenbluth1978) showed that, because electrons are strongly magnetized, even a slight braiding of magnetic field lines could result in a noticeable increase in perpendicular heat transport. This means that the magnetic field line diffusivity transfers to the electron thermal diffusivity. This derivation was done under the assumption of stationary magnetic fluctuations and prompted numerous theoretical studies aiming to clarify its application regime. Later, Isichenko notably included the decorrelation effects produced by time-varying magnetic perturbations (Isichenko Reference Isichenko1991a,Reference Isichenkob). It emerges from this careful analysis that, except for the extreme case of quick decorrelation where the characteristic frequency of magnetic turbulence would be much greater than the ratio of the electron thermal velocity, $v_{e}$![]() , to the magnetic exponentiation length, the electron thermal diffusivity is proportional to the magnetic line diffusivity $D_{m}$
, to the magnetic exponentiation length, the electron thermal diffusivity is proportional to the magnetic line diffusivity $D_{m}$![]() . Furthermore, in the collisionless limit, it approximates to $v_{e} D_{m}$
. Furthermore, in the collisionless limit, it approximates to $v_{e} D_{m}$![]() .
.
Critical to the anomalous electron transport is thus the existence of resonant magnetic perturbations. This calls for an examination of the source of these resonant magnetic perturbations. In addition to some possible curl-free magnetic perturbations coming from external sources, e.g. due to ripple effects, the magnetic perturbations are associated by Ampère's law with plasma current density perturbations. This naturally introduces a plasma current density approach that has been left apart up to now. Indeed, in a tokamak plasma, the displacement current is largely negligible in front of the plasma current so that the plasma current density, $\boldsymbol {J}$![]() , can be approximated as a divergence-free field satisfying
, can be approximated as a divergence-free field satisfying
Equation (1.1), together with the Maxwell-flux equation for the magnetic field $\boldsymbol {B}$![]()
form then a closed set of equations. It is the aim of the present Letter to explore the implications of the divergence-free nature of the magnetic and current density fields linked by Ampère's law (1.1) in driven MCF ideally axisymmetric devices such as tokamaks.
2 Hamiltonian representation of divergence-free field lines
At each given time, (1.2) is universally valid and (1.1) is a strongly relevant approximation in tokamak plasmas since the magnitude of the displacement current density $\boldsymbol {J}_{d}=c^{-2}\partial _{t}\boldsymbol {E}$![]() is at least eleven orders smaller than that of the plasma current density (Boozer Reference Boozer2015). Yet, the field lines of any solenoidal (i.e. divergence-free) field can be identified to the trajectories of a one-and-a-half degrees of freedom Hamiltonian system. Here, this means that, at each given time $t$
is at least eleven orders smaller than that of the plasma current density (Boozer Reference Boozer2015). Yet, the field lines of any solenoidal (i.e. divergence-free) field can be identified to the trajectories of a one-and-a-half degrees of freedom Hamiltonian system. Here, this means that, at each given time $t$![]() , magnetic and current density field lines are the respective trajectories of two Hamiltonian systems $H_{\boldsymbol {B}}^{t}$
, magnetic and current density field lines are the respective trajectories of two Hamiltonian systems $H_{\boldsymbol {B}}^{t}$![]() and $H_{\boldsymbol {J}}^{t}$
and $H_{\boldsymbol {J}}^{t}$![]() depending on three space coordinates. In a simple toroid, the divergence-free vector fields $\boldsymbol {B}$
depending on three space coordinates. In a simple toroid, the divergence-free vector fields $\boldsymbol {B}$![]() and $\boldsymbol {J}$
and $\boldsymbol {J}$![]() may be represented in the general canonical forms, see Boozer (Reference Boozer1983), Hatori et al. (Reference Hatori, Irie, Abe and Urata1989) and Yoshida (Reference Yoshida1994),
may be represented in the general canonical forms, see Boozer (Reference Boozer1983), Hatori et al. (Reference Hatori, Irie, Abe and Urata1989) and Yoshida (Reference Yoshida1994),
where $\theta$![]() and $\varphi$
and $\varphi$![]() are independent appropriate poloidal and toroidal angles. The differential equations to solve to obtain the magnetic field lines are
are independent appropriate poloidal and toroidal angles. The differential equations to solve to obtain the magnetic field lines are

with similar equations for $\boldsymbol {J}$![]() -field lines. Generically, the Hamiltonian $H_{\boldsymbol {B}}^{t}(\psi _{\boldsymbol {B}},\theta,\varphi )$
-field lines. Generically, the Hamiltonian $H_{\boldsymbol {B}}^{t}(\psi _{\boldsymbol {B}},\theta,\varphi )$![]() can be Fourier decomposed into an axisymmetric equilibrium part depending on the flux function $\psi _{\boldsymbol {B}}$
can be Fourier decomposed into an axisymmetric equilibrium part depending on the flux function $\psi _{\boldsymbol {B}}$![]() and a non-axisymmetric perturbation part such that
and a non-axisymmetric perturbation part such that
For simplicity's sake, the time $t$![]() index will be dropped in the following. The axisymmetric contribution is dominant in tokamak plasmas and yields integrable magnetic and density field lines spiralling on flux surfaces given by
index will be dropped in the following. The axisymmetric contribution is dominant in tokamak plasmas and yields integrable magnetic and density field lines spiralling on flux surfaces given by

defining the magnetic and current density ‘safety factor’ functions $q_{\boldsymbol {B}}=q$![]() and $q_{\boldsymbol {J}}$
and $q_{\boldsymbol {J}}$![]() . Let us note here that, under the usual assumption that the Grad–Shafranov equation holds at equilibrium, both magnetic and current density flux surfaces are constant pressure surfaces which allows us to construct a common set of canonical coordinates to express $\boldsymbol {B}$
. Let us note here that, under the usual assumption that the Grad–Shafranov equation holds at equilibrium, both magnetic and current density flux surfaces are constant pressure surfaces which allows us to construct a common set of canonical coordinates to express $\boldsymbol {B}$![]() and $\boldsymbol {J}$
and $\boldsymbol {J}$![]() , such as Hamada coordinates (Hamada Reference Hamada1962; Kikuchi Reference Kikuchi2011). For the present analysis, it is sufficient that the same poloidal and toroidal coordinates be shared by $\boldsymbol {B}$
, such as Hamada coordinates (Hamada Reference Hamada1962; Kikuchi Reference Kikuchi2011). For the present analysis, it is sufficient that the same poloidal and toroidal coordinates be shared by $\boldsymbol {B}$![]() and $\boldsymbol {J}$
and $\boldsymbol {J}$![]() canonical descriptions. Let us note also that, in fusion-relevant tokamaks, diamagnetic effects ensure that $q_{\boldsymbol {J}}$
canonical descriptions. Let us note also that, in fusion-relevant tokamaks, diamagnetic effects ensure that $q_{\boldsymbol {J}}$![]() is not trivial.
is not trivial.
3 Topology and classification of modes
Let us consider a perturbation to the axisymmetric state by a single mode $(m_0,n_0)$![]() . The generic form of the Hamiltonian, for the $\boldsymbol {B}$
. The generic form of the Hamiltonian, for the $\boldsymbol {B}$![]() - or $\boldsymbol {J}$
- or $\boldsymbol {J}$![]() -field lines, is then
-field lines, is then
Resonance occurs when the insertion of the $\mathcal {O}(\varepsilon ^{0})$![]() axisymmetric solution produces a secular forcing resulting in a linear increase of $\psi$
axisymmetric solution produces a secular forcing resulting in a linear increase of $\psi$![]() with $\varphi$
with $\varphi$![]() . This happens when there exists some $\psi ^{*}$
. This happens when there exists some $\psi ^{*}$![]() such that $q(\psi ^{*})=m_0/n_0$
such that $q(\psi ^{*})=m_0/n_0$![]() . Figure 1 considers an instantaneous axisymmetric plasma state with arbitrary magnetic and current density safety profiles. The plot on the right highlights the possible resonant modes for $\boldsymbol {B}$
. Figure 1 considers an instantaneous axisymmetric plasma state with arbitrary magnetic and current density safety profiles. The plot on the right highlights the possible resonant modes for $\boldsymbol {B}$![]() (in blue) and for $\boldsymbol {J}$
(in blue) and for $\boldsymbol {J}$![]() (in red). In this example, there are modes that are both resonant for $\boldsymbol {B}$
(in red). In this example, there are modes that are both resonant for $\boldsymbol {B}$![]() and $\boldsymbol {J}$
and $\boldsymbol {J}$![]() in the overlapping (violet) cone. By virtue of the linearity of Ampère's equation (1.1), some $(m_0,n_0)$
in the overlapping (violet) cone. By virtue of the linearity of Ampère's equation (1.1), some $(m_0,n_0)$![]() current perturbation $\boldsymbol {\delta } \boldsymbol {J}_{m_0,n_0}$
current perturbation $\boldsymbol {\delta } \boldsymbol {J}_{m_0,n_0}$![]() is associated with some $(m_0,n_0)$
is associated with some $(m_0,n_0)$![]() magnetic perturbation $\boldsymbol {\delta } \boldsymbol {B}_{m_0,n_0}$
magnetic perturbation $\boldsymbol {\delta } \boldsymbol {B}_{m_0,n_0}$![]() . Reciprocally, there could exist vacuum magnetic perturbations that have no manifestation on the current density. Since our interest lies in the magnetic perturbations originating from plasma current density perturbations, we focus on the current density modes.
. Reciprocally, there could exist vacuum magnetic perturbations that have no manifestation on the current density. Since our interest lies in the magnetic perturbations originating from plasma current density perturbations, we focus on the current density modes.

Figure 1. (a) Example of two arbitrary magnetic and current density safety factor profiles as a function of respectively normalized flux coordinates $\hat {\psi }_{\boldsymbol {B}}$![]() and $\hat {\psi }_{\boldsymbol {J}}$
and $\hat {\psi }_{\boldsymbol {J}}$![]() . (b) Each dot represents an $(m,n)$
. (b) Each dot represents an $(m,n)$![]() mode. It is a resonant mode for $\boldsymbol {B}$
mode. It is a resonant mode for $\boldsymbol {B}$![]() if it is in the blue cone bounded by the lines $y=q_{\boldsymbol {B}\min } x$
if it is in the blue cone bounded by the lines $y=q_{\boldsymbol {B}\min } x$![]() and $y=q_{\boldsymbol {B}\max } x$
and $y=q_{\boldsymbol {B}\max } x$![]() and/or for $\boldsymbol {J}$
and/or for $\boldsymbol {J}$![]() if it is in the red cone bounded by the lines $y=q_{\boldsymbol {J}\min } x$
if it is in the red cone bounded by the lines $y=q_{\boldsymbol {J}\min } x$![]() and $y=q_{\boldsymbol {J}\max } x$
and $y=q_{\boldsymbol {J}\max } x$![]() . The violet intersection cone contains modes that are both resonant to $\boldsymbol {B}$
. The violet intersection cone contains modes that are both resonant to $\boldsymbol {B}$![]() and $\boldsymbol {J}$
and $\boldsymbol {J}$![]() . The white cone contains modes that are non-resonant to $\boldsymbol {B}$
. The white cone contains modes that are non-resonant to $\boldsymbol {B}$![]() and non-resonant to $\boldsymbol {J}$
and non-resonant to $\boldsymbol {J}$![]() .
.
Any mode of a divergence-free vector field with a rotational transform is either resonant or non-resonant. Considering the current density field $\boldsymbol {J}$![]() , a mode $(m_{0},n_{0})$
, a mode $(m_{0},n_{0})$![]() is resonant if there exists some $\psi _{\boldsymbol {J}}^{*}$
is resonant if there exists some $\psi _{\boldsymbol {J}}^{*}$![]() such that $q(\psi _{\boldsymbol {J}}^{*})=m_0/n_0$
such that $q(\psi _{\boldsymbol {J}}^{*})=m_0/n_0$![]() ; if not, it is non-resonant. In the first case, a poloidal cross-section cut of the current density field lines reveals that, around the current flux surface $\psi _{\boldsymbol {J}}^{*}$
; if not, it is non-resonant. In the first case, a poloidal cross-section cut of the current density field lines reveals that, around the current flux surface $\psi _{\boldsymbol {J}}^{*}$![]() , even a tiny amplitude $(m_{0},n_{0})$
, even a tiny amplitude $(m_{0},n_{0})$![]() perturbation produces a change in the topology of current density field lines with the apparition of a vortex (island). In three dimensions, such a resonant mode for the current density exhibits then a filamentary structure such as in the example of figure 2. On the contrary, a non-resonant mode manifests only through smooth deformations of flux contours. To be more specific, a resonant mode $(m_{0},n_{0})$
perturbation produces a change in the topology of current density field lines with the apparition of a vortex (island). In three dimensions, such a resonant mode for the current density exhibits then a filamentary structure such as in the example of figure 2. On the contrary, a non-resonant mode manifests only through smooth deformations of flux contours. To be more specific, a resonant mode $(m_{0},n_{0})$![]() for $\boldsymbol {B}$
for $\boldsymbol {B}$![]() originating from a current density perturbation can have for source either a $\boldsymbol {J}$
originating from a current density perturbation can have for source either a $\boldsymbol {J}$![]() -resonant filament-like mode if there exists some $\psi ^{*}_{\boldsymbol {J}}$
-resonant filament-like mode if there exists some $\psi ^{*}_{\boldsymbol {J}}$![]() such that $q(\psi _{\boldsymbol {J}}^{*})=m_0/n_0$
such that $q(\psi _{\boldsymbol {J}}^{*})=m_0/n_0$![]() (this is the case for modes in the violet cone of figure 1), or a non-resonant $\boldsymbol {J}$
(this is the case for modes in the violet cone of figure 1), or a non-resonant $\boldsymbol {J}$![]() mode if not (this is the case for modes in the blue region of figure 1). Non-resonant modes include collective modes of deformation of the current density radial contours.
mode if not (this is the case for modes in the blue region of figure 1). Non-resonant modes include collective modes of deformation of the current density radial contours.

Figure 2. When there exists some $\psi ^{*}_{\boldsymbol {J}}$![]() such that $q(\psi _{\boldsymbol {J}}^{*})=m_0/n_0$
such that $q(\psi _{\boldsymbol {J}}^{*})=m_0/n_0$![]() , i.e. the mode $(m_0,n_0)$
, i.e. the mode $(m_0,n_0)$![]() is resonant for $\boldsymbol {J}$
is resonant for $\boldsymbol {J}$![]() , then a current filament flows within the current ‘flux tubes’ attached to elliptic surfaces. In the representation, $m_0=5$
, then a current filament flows within the current ‘flux tubes’ attached to elliptic surfaces. In the representation, $m_0=5$![]() and $n_0=3$
and $n_0=3$![]() .
.
4 Illustration in cylindrical geometry of the interplay between magnetic and current density field topologies
Let us examine this further by deriving the magnetic and current density field lines corresponding to some axisymmetric state, defined by given $q_{\boldsymbol { B}}$![]() and $q_{\boldsymbol {J}}$
and $q_{\boldsymbol {J}}$![]() , perturbed by a single mode with poloidal mode number $m_{0}$
, perturbed by a single mode with poloidal mode number $m_{0}$![]() and toroidal mode number $n_{0}$
and toroidal mode number $n_{0}$![]() . Here, we shall consider a cylinder configuration with length $2 {\rm \pi}R$
. Here, we shall consider a cylinder configuration with length $2 {\rm \pi}R$![]() with periodic boundary conditions ($z=R \varphi$
with periodic boundary conditions ($z=R \varphi$![]() ) to simplify calculations without affecting the conclusions. One simplification of cylindrical geometry is that the action variable $\psi$
) to simplify calculations without affecting the conclusions. One simplification of cylindrical geometry is that the action variable $\psi$![]() only depends on the radius $r$
only depends on the radius $r$![]() so that we can directly use $r$
so that we can directly use $r$![]() to compare $q_{\boldsymbol {B}}$
to compare $q_{\boldsymbol {B}}$![]() and $q_{\boldsymbol {J}}$
and $q_{\boldsymbol {J}}$![]() .
.
The axisymmetric axial component of the magnetic field is denoted by $B_{0}(r)$![]() and $B_{0}(0)\equiv B_{0}$
and $B_{0}(0)\equiv B_{0}$![]() . The total magnetic field amounts to $\boldsymbol {B}=B_{\theta }(r)\boldsymbol {e}_{\theta }+B_{0}(r)\boldsymbol {e}_{z}+\boldsymbol {\delta } \boldsymbol {B}(r,\theta,z)$
. The total magnetic field amounts to $\boldsymbol {B}=B_{\theta }(r)\boldsymbol {e}_{\theta }+B_{0}(r)\boldsymbol {e}_{z}+\boldsymbol {\delta } \boldsymbol {B}(r,\theta,z)$![]() with $\boldsymbol {\delta } \boldsymbol {B}(r,\theta,z)=\boldsymbol {\nabla }\times \boldsymbol {\delta } \boldsymbol {A}$
with $\boldsymbol {\delta } \boldsymbol {B}(r,\theta,z)=\boldsymbol {\nabla }\times \boldsymbol {\delta } \boldsymbol {A}$![]() with $\boldsymbol {\delta } \boldsymbol {A}=\varepsilon _{m_{0},n_{0}} f(r) \cos (m_{0} \theta -n_{0} \varphi )\boldsymbol {e}_{z}$
with $\boldsymbol {\delta } \boldsymbol {A}=\varepsilon _{m_{0},n_{0}} f(r) \cos (m_{0} \theta -n_{0} \varphi )\boldsymbol {e}_{z}$![]() , for some waveform $f(r)$
, for some waveform $f(r)$![]() . The total current density field is obtained from Ampère's law (1.1). The equations of the magnetic field lines derive from $\boldsymbol {B}\times d\boldsymbol {OM}=\boldsymbol {0}$
. The total current density field is obtained from Ampère's law (1.1). The equations of the magnetic field lines derive from $\boldsymbol {B}\times d\boldsymbol {OM}=\boldsymbol {0}$![]() with $d\boldsymbol {OM}=dr \boldsymbol {e}_{r}+r d\theta \boldsymbol {e}_{\theta }+ dz \boldsymbol {e}_{z}$
with $d\boldsymbol {OM}=dr \boldsymbol {e}_{r}+r d\theta \boldsymbol {e}_{\theta }+ dz \boldsymbol {e}_{z}$![]() and similarly for the current density field lines. For the equilibrium axisymmetric part, one obtains the expressions of $q_{\boldsymbol {B}}$
and similarly for the current density field lines. For the equilibrium axisymmetric part, one obtains the expressions of $q_{\boldsymbol {B}}$![]() and $q_{\boldsymbol {J}}$
and $q_{\boldsymbol {J}}$![]() as functions of the magnetic field components
as functions of the magnetic field components
Considering given radial profiles $q_{\boldsymbol {B}}(r)$![]() and $q_{\boldsymbol {J}}(r)$
and $q_{\boldsymbol {J}}(r)$![]() , the system (4.1)–(4.2) allows us to obtain the axisymmetric magnetic field components as $B_{\theta }(r)=r B_{0}(r)/(R q_{\boldsymbol {B}}(r))$
, the system (4.1)–(4.2) allows us to obtain the axisymmetric magnetic field components as $B_{\theta }(r)=r B_{0}(r)/(R q_{\boldsymbol {B}}(r))$![]() with the axial component $B_{0}(r)$
with the axial component $B_{0}(r)$![]() solving a first-order differential equation as
solving a first-order differential equation as
The winding properties of the axisymmetric equilibrium magnetic and current density fields are specified by the pair $(q_{\boldsymbol {B}}, q_{\boldsymbol {J}})$![]() . In figure 3, a safety profile $q_{\boldsymbol {B}}$
. In figure 3, a safety profile $q_{\boldsymbol {B}}$![]() has been chosen. We consider the effect of a small perturbation having $m_0=5$
has been chosen. We consider the effect of a small perturbation having $m_0=5$![]() and $n_0=3$
and $n_0=3$![]() that is resonant for the magnetic field because there exists some minor radius at which $q_{\boldsymbol {B}}=5/3$
that is resonant for the magnetic field because there exists some minor radius at which $q_{\boldsymbol {B}}=5/3$![]() . This determines the Poincaré plot of magnetic field lines, shown in blue in figure 3(c). The Poincaré plots of the current density field lines are plotted in red and vary according to the $q_{\boldsymbol {J}}$
. This determines the Poincaré plot of magnetic field lines, shown in blue in figure 3(c). The Poincaré plots of the current density field lines are plotted in red and vary according to the $q_{\boldsymbol {J}}$![]() profile. For each $q_{\boldsymbol {J}}$
profile. For each $q_{\boldsymbol {J}}$![]() , the components of the magnetic field (normalized to $B_{0}$
, the components of the magnetic field (normalized to $B_{0}$![]() ) are fully known and are plotted for the sake of completeness in figure 3(b). Depending on $q_{\boldsymbol {J}}$
) are fully known and are plotted for the sake of completeness in figure 3(b). Depending on $q_{\boldsymbol {J}}$![]() , the magnetic island is associated either with a current density island (or filamentation mode), if there exists one radial coordinate at which $q_{\boldsymbol {J}}=m_{0}/n_{0}$
, the magnetic island is associated either with a current density island (or filamentation mode), if there exists one radial coordinate at which $q_{\boldsymbol {J}}=m_{0}/n_{0}$![]() (case $q_{\boldsymbol {J}1}$
(case $q_{\boldsymbol {J}1}$![]() ) or more than one (case $q_{\boldsymbol {J}2}$
) or more than one (case $q_{\boldsymbol {J}2}$![]() ). Let us note that the radial locations of the magnetic and current density islands differ when $q_{\boldsymbol {B}}$
). Let us note that the radial locations of the magnetic and current density islands differ when $q_{\boldsymbol {B}}$![]() and $q_{\boldsymbol {J}}$
and $q_{\boldsymbol {J}}$![]() do not coincide, which is the case considered here. Alternatively, the magnetic island may be associated with a non-resonant current density mode when $q_{\boldsymbol {J}}$
do not coincide, which is the case considered here. Alternatively, the magnetic island may be associated with a non-resonant current density mode when $q_{\boldsymbol {J}}$![]() does not take the value $m_{0}/n_{0}$
does not take the value $m_{0}/n_{0}$![]() (cases 3 and 5). Case 4 corresponds to a limiting case when $q_{\boldsymbol {J}}$
(cases 3 and 5). Case 4 corresponds to a limiting case when $q_{\boldsymbol {J}}$![]() reaches the value $m_{0}/n_{0}$
reaches the value $m_{0}/n_{0}$![]() at the border.
at the border.

Figure 3. Examples of the impact on magnetic and current density field lines of a small three-dimensional perturbation, having here poloidal $m_{0}=5$![]() and toroidal $n_{0}=3$
and toroidal $n_{0}=3$![]() mode numbers. The arbitrarily chosen safety profile $q_{\boldsymbol {B}}$
mode numbers. The arbitrarily chosen safety profile $q_{\boldsymbol {B}}$![]() is plotted in blue in (a). The Poincaré's plot of the magnetic field lines is shown in (c) and shows that the perturbation is magnetically resonant. One considers five arbitrary $q_{\boldsymbol {J}}$
is plotted in blue in (a). The Poincaré's plot of the magnetic field lines is shown in (c) and shows that the perturbation is magnetically resonant. One considers five arbitrary $q_{\boldsymbol {J}}$![]() -profiles, noted $q_{\boldsymbol {J}1}$
-profiles, noted $q_{\boldsymbol {J}1}$![]() to $q_{\boldsymbol {J}5}$
to $q_{\boldsymbol {J}5}$![]() , plotted in red in (a). The corresponding current density field lines are plotted in (d–h). Knowing $q_{\boldsymbol {B}}$
, plotted in red in (a). The corresponding current density field lines are plotted in (d–h). Knowing $q_{\boldsymbol {B}}$![]() and $q_{\boldsymbol {J}}$
and $q_{\boldsymbol {J}}$![]() provides the full axisymmetric magnetic configuration (b) (normalized to $B_{0}$
provides the full axisymmetric magnetic configuration (b) (normalized to $B_{0}$![]() ). Here, $\hat {r}$
). Here, $\hat {r}$![]() denotes the radial variable normalized to the minor radius.
denotes the radial variable normalized to the minor radius.
It has been shown that providing the pair $(q_{\boldsymbol {B}}, q_{\boldsymbol {J}})$![]() allows for a comprehensive characterization of the modes. This requires us to reconstruct in real time not only the safety profile, $q_{\boldsymbol {B}}$
allows for a comprehensive characterization of the modes. This requires us to reconstruct in real time not only the safety profile, $q_{\boldsymbol {B}}$![]() , but also $q_{\boldsymbol {J}}$
, but also $q_{\boldsymbol {J}}$![]() . To facilitate this in the realistic toroidal geometry, their expressions in flux coordinates are derived now.
. To facilitate this in the realistic toroidal geometry, their expressions in flux coordinates are derived now.
5 Analytic expressions of the magnetic ($q_{\boldsymbol {B}}$ ) and current density ($q_{\boldsymbol {J}}$
) and current density ($q_{\boldsymbol {J}}$ ) profiles in flux coordinates
) profiles in flux coordinates
In the Hamada set of variables $( v,\theta,\zeta )$![]() , with $v$
, with $v$![]() the volume enclosed by the flux surface, and $\zeta$
the volume enclosed by the flux surface, and $\zeta$![]() and $\theta$
and $\theta$![]() the toroidal and poloidal coordinates (chosen here to have period 1, not $2 {\rm \pi}$
the toroidal and poloidal coordinates (chosen here to have period 1, not $2 {\rm \pi}$![]() ), both equilibrium magnetic and current density field lines are straight with
), both equilibrium magnetic and current density field lines are straight with

This is a canonical set of variables for both the magnetic and current density field lines. It is, however, not easy to accommodate because the toroidal and poloidal coordinates are not the usual geometrical angles. Nevertheless, the previous illustration (in figure 3) as well as the diagram (in figure 1) show that, in order to classify modes, we essentially need to compare the equilibrium windings of the magnetic field and the current density field. Using the explicit transformation between Hamada coordinates $( v,\theta,\zeta )$![]() and the flux coordinates $( \psi,\theta _{g},\varphi _{g} )$
and the flux coordinates $( \psi,\theta _{g},\varphi _{g} )$![]() , where $\theta _{g}$
, where $\theta _{g}$![]() and $\varphi _{g}$
and $\varphi _{g}$![]() are respectively the poloidal and toroidal geometrical angles, it was shown in Hua et al. (Reference Hua, Chapman, Field, Hastie and Pinches2010) that $q_{\boldsymbol {B}}(v)$
are respectively the poloidal and toroidal geometrical angles, it was shown in Hua et al. (Reference Hua, Chapman, Field, Hastie and Pinches2010) that $q_{\boldsymbol {B}}(v)$![]() is the usual safety factor, namely
is the usual safety factor, namely
Moreover, using $\boldsymbol {B}=F(\psi )\boldsymbol {\nabla }\varphi _{g} +\boldsymbol {\nabla } \psi \times \boldsymbol {\nabla }\varphi _{g}$![]() where $F(\psi )=RB_{\varphi _{g} }$
where $F(\psi )=RB_{\varphi _{g} }$![]() is the diamagnetic function, and defining the flux surface average
is the diamagnetic function, and defining the flux surface average

yields
Now let us also consider here $q_{\boldsymbol {J}}$![]() . We have
. We have

Moreover,

implying
We have, from (5.5) and (5.6),
Let us use the fact that we can average ‘for free’ this function on $\theta$![]() as it only depends on $v$
as it only depends on $v$![]() . We have, for the first member of the right-hand side
. We have, for the first member of the right-hand side
For the second member of the right-hand side, we have
by definition of the flux surface average (5.3). This gives the result
Let us now use the Grad–Shafranov equation to get an explicit expression. This gives
From $\mu _{0}\boldsymbol {J}\boldsymbol {\cdot }\boldsymbol {\nabla }\theta _{g}\,{=}\,( \boldsymbol {\nabla } F\,{\times}\, \boldsymbol {\nabla }\varphi _{g} ) \boldsymbol {\cdot }\boldsymbol {\nabla }\theta _{g}$![]() , $\boldsymbol {B}\boldsymbol {\cdot } \boldsymbol {\nabla }\theta _{g}\,{=}\,( \boldsymbol {\nabla }\psi \,{\times}\, \boldsymbol { \nabla }\varphi _{g} ) \boldsymbol {\cdot }\boldsymbol {\nabla }\theta _{g}$
, $\boldsymbol {B}\boldsymbol {\cdot } \boldsymbol {\nabla }\theta _{g}\,{=}\,( \boldsymbol {\nabla }\psi \,{\times}\, \boldsymbol { \nabla }\varphi _{g} ) \boldsymbol {\cdot }\boldsymbol {\nabla }\theta _{g}$![]() and $\boldsymbol {\nabla } F\,{=}\,F^{\prime }(\psi )\boldsymbol {\nabla }\psi$
and $\boldsymbol {\nabla } F\,{=}\,F^{\prime }(\psi )\boldsymbol {\nabla }\psi$![]() , one gets $\boldsymbol {J}\boldsymbol {\cdot }\boldsymbol {\nabla } \theta _{g}=\mu _{0}^{-1}F^{\prime }(\psi )\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla }\theta _{g}$
, one gets $\boldsymbol {J}\boldsymbol {\cdot }\boldsymbol {\nabla } \theta _{g}=\mu _{0}^{-1}F^{\prime }(\psi )\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla }\theta _{g}$![]() . Consequently,
. Consequently,

This yields from (5.3) and (5.4)
that is, choosing the flux label $\psi$![]() instead of $v$
instead of $v$![]() ,
,
To the author's knowledge, this is the first expression of the $q_{\boldsymbol {J}}$![]() profile in flux coordinates. We are indeed in the same situation as in the previous cylindrical illustration where the action variable depends only on the radius $r$
profile in flux coordinates. We are indeed in the same situation as in the previous cylindrical illustration where the action variable depends only on the radius $r$![]() : here, the action variable $v$
: here, the action variable $v$![]() in the Hamada set depends only on $\psi$
in the Hamada set depends only on $\psi$![]() ($v=v(\psi )$
($v=v(\psi )$![]() ). One can then do the comparison between the $q_{\boldsymbol {B}}$
). One can then do the comparison between the $q_{\boldsymbol {B}}$![]() and $q_{\boldsymbol {J}}$
and $q_{\boldsymbol {J}}$![]() profiles with flux coordinates. This can serve to figure out whether the modes resonant to the current density, namely the current filamentary modes, produce magnetic perturbations that are resonant to the magnetic field.
profiles with flux coordinates. This can serve to figure out whether the modes resonant to the current density, namely the current filamentary modes, produce magnetic perturbations that are resonant to the magnetic field.
6 Implications, perspectives and conclusions
In the case of a zero-$\beta$![]() (constant zero pressure) plasma, (5.15) shows that $q_{\boldsymbol {B}}$
(constant zero pressure) plasma, (5.15) shows that $q_{\boldsymbol {B}}$![]() and $q_{\boldsymbol {J}}$
and $q_{\boldsymbol {J}}$![]() coincide. In this special case, $(m,n)$
coincide. In this special case, $(m,n)$![]() current filaments flow within $(m,n)$
current filaments flow within $(m,n)$![]() magnetic islands. This case is not relevant to fusion conditions. Indeed, in ITER, to attain $Q \simeq 10$
magnetic islands. This case is not relevant to fusion conditions. Indeed, in ITER, to attain $Q \simeq 10$![]() , plasmas will need to have a normalized beta $\beta _{N}>1.8$
, plasmas will need to have a normalized beta $\beta _{N}>1.8$![]() with $\beta _{N}=\beta /I/aB$
with $\beta _{N}=\beta /I/aB$![]() , with $I$
, with $I$![]() the plasma current, $a$
the plasma current, $a$![]() the minor radius and $\beta \equiv p/B^{2}/(2\mu _{0})$
the minor radius and $\beta \equiv p/B^{2}/(2\mu _{0})$![]() (Shimada et al. Reference Shimada2007). Consequently, the $q_{\boldsymbol {J}}$
(Shimada et al. Reference Shimada2007). Consequently, the $q_{\boldsymbol {J}}$![]() profile will be somehow separated from the $q_{\boldsymbol {B}}$
profile will be somehow separated from the $q_{\boldsymbol {B}}$![]() profile according to (5.15). In view of the one-and-a-half Hamiltonian picture of the field lines, this means that a MCF device needs to drive the magnetic and current density channels apart. The present study should thus have important implications:
profile according to (5.15). In view of the one-and-a-half Hamiltonian picture of the field lines, this means that a MCF device needs to drive the magnetic and current density channels apart. The present study should thus have important implications:
(i) Add the calculation of $q_{\boldsymbol {J}}$
 to equilibrium reconstruction codes to diagnose the separation of the magnetic and current density channels.
to equilibrium reconstruction codes to diagnose the separation of the magnetic and current density channels.The kinetic equilibrium reconstruction codes presently serve to monitor in real time the magnetics in modern tokamaks. This involves the resolution of the elliptic nonlinear Grad–Shafranov differential equation to determine the magnetic equilibrium configuration from the measurement data. This has been a challenging and fundamental MCF research topic for around four decades, involving the collaborative contributions of physicists, mathematicians and computer scientists (Lao et al. Reference Lao, John, Stambaugh, Kellman and Pfeiffer1985, Reference Lao, Ferron, Groebner, Howl, John, Strait and Taylor1990; Lütjens, Bondeson & Sauter Reference Lütjens, Bondeson and Sauter1996; Ferron et al. Reference Ferron, Walker, Lao, John, Humphreys and Leuer1998; Lao et al. Reference Lao, John, Peng, Ferron, Strait, Taylor, Meyer, Zhang and You2005; Blum, Boulbe & Faugeras Reference Blum, Boulbe and Faugeras2007; Katsuro-Hopkins et al. Reference Katsuro-Hopkins2010; Blum, Boulbe & Faugeras Reference Blum, Boulbe and Faugeras2012; Li et al. Reference Li, Ren, Qian, Lao, Ding, Chen, Liu, Lu and Zang2013; Faugeras et al. Reference Faugeras and Orsitto2018; Xing et al. Reference Xing, Eldon, Nelson, Roelofs, Eggert, Izacard, Glasser, Logan, Meneghini, Smith, Nazikian and Kolemen2021; Zheng et al. Reference Zheng, Kotschenreuther, Waelbroeck and Todo2022; Hansen et al. Reference Hansen, Stewart, Burgess, Pharr, Guizzo, Logak, Nelson and Paz-Soldan2024), with recent contributions from fast-parallel computing (Huang, Xiao & Luo Reference Huang, Xiao and Luo2017), artificial intelligence and neural networks (Ma et al. Reference Ma, Xia, Ling and Li2018; Joung et al. Reference Joung, Kim, Kwak, Bak, Lee, Han, Kim, Lee, Kwon and Ghim2019; Kaltsas & Throumoulopoulos Reference Kaltsas and Throumoulopoulos2022; Lao et al. Reference Lao2022; Pavone et al. Reference Pavone, Merlo, Kwak and Svensson2023).
One outcome of these codes is the real-time computation of the safety factor profile $q$
 (that is, $q_{\boldsymbol {B}}$
(that is, $q_{\boldsymbol {B}}$ ). The analysis presented here highlights the value of including the computation of the current density $q_{\boldsymbol {J}}$
). The analysis presented here highlights the value of including the computation of the current density $q_{\boldsymbol {J}}$ profile. It is shown by (5.15) that this amounts to adding just a line to existing codes. Then, the knowledge of the pair $(q_{\boldsymbol {B}}, q_{\boldsymbol {J}})$
profile. It is shown by (5.15) that this amounts to adding just a line to existing codes. Then, the knowledge of the pair $(q_{\boldsymbol {B}}, q_{\boldsymbol {J}})$ will enable the complete identification of the electromagnetic, not purely electrostatic, modes, both in terms of their magnetic contribution and their contribution to the current density, as exemplified in figure 1.
will enable the complete identification of the electromagnetic, not purely electrostatic, modes, both in terms of their magnetic contribution and their contribution to the current density, as exemplified in figure 1.Let us here note that the expression for $q_{\boldsymbol {J}}$
 in (5.15) has been obtained under the usual assumption that the plasma equilibrium is governed by the Grad–Shafranov equation. This derives from the steady-state Navier–Stokes equation in which one neglects the plasma velocity field. If this steady-state plasma velocity field happens to be non-negligible, then plasma rotation could also contribute to separating the magnetic and current density channels. Nevertheless, one can reasonably expect the Grad–Shafranov equation to give the dominant contribution to $q_{\boldsymbol {J}}$
in (5.15) has been obtained under the usual assumption that the plasma equilibrium is governed by the Grad–Shafranov equation. This derives from the steady-state Navier–Stokes equation in which one neglects the plasma velocity field. If this steady-state plasma velocity field happens to be non-negligible, then plasma rotation could also contribute to separating the magnetic and current density channels. Nevertheless, one can reasonably expect the Grad–Shafranov equation to give the dominant contribution to $q_{\boldsymbol {J}}$ .
.(ii) Investigate the relationship between the interplay of the $q_{\boldsymbol {B}}$
 and $q_{\boldsymbol {J}}$
and $q_{\boldsymbol {J}}$ profiles and the confinement properties.
profiles and the confinement properties.Any experimentally unavoidable perturbation to the axisymmetric current density gives rise, through Fourier mode decomposition, to a spectrum of current density modes. In particular, there exists, at any time, a spectrum of tiny filamentation modes, that are modes for which $q_{\boldsymbol {J}}$
 is rational. Obviously, linear theory may favour some specific modes. The point here is just to stress that there should exist at all times a spectrum of non-vanishing current density filaments that comes up, by virtue of Ampère's law, with a spectrum of magnetic perturbations.
is rational. Obviously, linear theory may favour some specific modes. The point here is just to stress that there should exist at all times a spectrum of non-vanishing current density filaments that comes up, by virtue of Ampère's law, with a spectrum of magnetic perturbations.Let us consider, for example, a situation where the images of the functions $q_{\boldsymbol {B}}$
 and $q_{\boldsymbol {J}}$
and $q_{\boldsymbol {J}}$ are disjoint. Then, the resonant modes for the current density (i.e. the filamentary modes) do not impact the magnetic field topology. They are not associated with magnetic islands, but with non-resonant magnetic modes. In this case, only collective modes of deformation of the current density, that do not change the topology of the current density field lines, can be associated with magnetic islands. It remains to be explored to what extent such a configuration, where the spectrum of tiny current density filaments produces a spectrum of magnetic modes that has practically no effect on heat transport, is beneficial.
are disjoint. Then, the resonant modes for the current density (i.e. the filamentary modes) do not impact the magnetic field topology. They are not associated with magnetic islands, but with non-resonant magnetic modes. In this case, only collective modes of deformation of the current density, that do not change the topology of the current density field lines, can be associated with magnetic islands. It remains to be explored to what extent such a configuration, where the spectrum of tiny current density filaments produces a spectrum of magnetic modes that has practically no effect on heat transport, is beneficial.(iii) Explore the possibility of controlling the current transport and preventing disruptions by playing on the current density profile.
In MCF devices such as tokamaks, apart from magnetic perturbations due to the vacuum configuration, such as the ripple-induced magnetic disturbances, one can consider the current density channel as the driver for magnetic perturbations. By separating the $q_{\boldsymbol {B}}$
 and $q_{\boldsymbol {J}}$
and $q_{\boldsymbol {J}}$ profiles, one can prevent the magnetic perturbations due to the aforementioned tiny current filaments from contributing to magnetic diffusivity. Ultimately, the current path might also be controlled by monitoring and playing on the shear of the $q_{\boldsymbol {J}}$
profiles, one can prevent the magnetic perturbations due to the aforementioned tiny current filaments from contributing to magnetic diffusivity. Ultimately, the current path might also be controlled by monitoring and playing on the shear of the $q_{\boldsymbol {J}}$ profile, with potentially important implications.
profile, with potentially important implications.In conclusion, this Letter points to the benefits of monitoring both the $q_{\boldsymbol {B}}$
 and $q_{\boldsymbol {J}}$
and $q_{\boldsymbol {J}}$ profiles to get a full, real-time, picture of the magnetic and current density channels in MCF devices. Some reconstruction of the $q_{\boldsymbol {J}}$
profiles to get a full, real-time, picture of the magnetic and current density channels in MCF devices. Some reconstruction of the $q_{\boldsymbol {J}}$ profile from experimental data will be presented and analysed in a forthcoming study.
profile from experimental data will be presented and analysed in a forthcoming study.
Acknowledgements
Editor Tünde Fülöp thanks the referees for their advice in evaluating this article.
Funding
M.-C.F. acknowledges support from EUROfusion H-Europe/WP24 (TRED).
Declaration of interests
The author reports no conflict of interest.