Article contents
Lane formation in 3D driven pair-ion plasmas: I Parallel External Forcing
Published online by Cambridge University Press: 05 May 2023
Abstract
Lane formation dynamics of driven three-dimensional pair-ion plasmas (PIP) is investigated. Extensive Langevin dynamics simulation is performed to study the influence of an external electric field on the behaviour of the PIP system. In our model, one half of the particles are pushed into the field direction by an external force $\boldsymbol {F}_{A}$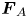 while the other half are pulled into the opposite direction by an external force $\boldsymbol {F}_{B}$
while the other half are pulled into the opposite direction by an external force $\boldsymbol {F}_{B}$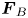 . We show that if $\boldsymbol {F}_{A}$
. We show that if $\boldsymbol {F}_{A}$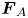 and $\boldsymbol {F}_{B}$
and $\boldsymbol {F}_{B}$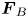 are parallel, the system undergoes a non-equilibrium phase transition from a disordered state to a lane formation state parallel to the field direction with increasing field strength. The lanes are formed by the same kind of particles moving collectively with the field. The lane order parameter has been implemented to detect phase transition. Further, we show the lane formation in the presence of a time-varying external electric field. In particular, the effect of parallel forces are investigated. Unlike the previously reported two-dimensional case (Sarma, et al., Phys. Plasmas, vol. 27, 2020, p. 012106; Baruah, et al., J. Plasma Phys., vol. 87, issue 2, 2021, p. 905870202), for the time-varying electric field case, spontaneous formation and the breaking of lanes are not observed for all values of applied frequencies; however, the orderness varies and spontaneous formation and breaking of lanes is observed for values close to a critical frequency $\omega _c$
are parallel, the system undergoes a non-equilibrium phase transition from a disordered state to a lane formation state parallel to the field direction with increasing field strength. The lanes are formed by the same kind of particles moving collectively with the field. The lane order parameter has been implemented to detect phase transition. Further, we show the lane formation in the presence of a time-varying external electric field. In particular, the effect of parallel forces are investigated. Unlike the previously reported two-dimensional case (Sarma, et al., Phys. Plasmas, vol. 27, 2020, p. 012106; Baruah, et al., J. Plasma Phys., vol. 87, issue 2, 2021, p. 905870202), for the time-varying electric field case, spontaneous formation and the breaking of lanes are not observed for all values of applied frequencies; however, the orderness varies and spontaneous formation and breaking of lanes is observed for values close to a critical frequency $\omega _c$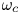 . Further, some aspects of the lane formation dynamics of a PIP system are also studied in the presence of an external magnetic field, which reveals that the presence of an external magnetic field accelerates the lane formation process and introduces a drift of the lanes in a direction perpendicular to both electric and magnetic fields.
. Further, some aspects of the lane formation dynamics of a PIP system are also studied in the presence of an external magnetic field, which reveals that the presence of an external magnetic field accelerates the lane formation process and introduces a drift of the lanes in a direction perpendicular to both electric and magnetic fields.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © The Author(s), 2023. Published by Cambridge University Press
References
- 3
- Cited by


