No CrossRef data available.
Published online by Cambridge University Press: 18 May 2023
In Part 1 of the companion paper, we have investigated lane formation dynamics of driven three-dimensional (3-D) pair-ion plasmas (PIP) in the presence of parallel external forcing using extensive Langevin dynamics (LD) simulation. In continuation of the work, in this Part 2, we investigate lane formation dynamics in the presence of non-parallel external forcing, and the effect of both constant and time varying forces are studied. In our model, positively charged PIP particles are pushed into the field direction by an external force $\boldsymbol{F}_{A} = E_A\cos \omega _At$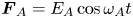 while the negatively charged PIP particles are pulled by an external force $\boldsymbol{F}_{B} = E_B\cos \omega _Bt$
while the negatively charged PIP particles are pulled by an external force $\boldsymbol{F}_{B} = E_B\cos \omega _Bt$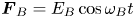 in a direction perpendicular to the external force $\boldsymbol{F}_{A}$
in a direction perpendicular to the external force $\boldsymbol{F}_{A}$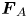 . We show that in the case of non-parallel forces, the lanes are observed with an orientation (characterised by angle of inclination $\theta$
. We show that in the case of non-parallel forces, the lanes are observed with an orientation (characterised by angle of inclination $\theta$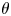 ) tilted in the direction of the force difference vector ($\boldsymbol{F}_{A} - \boldsymbol{F}_{B}$
) tilted in the direction of the force difference vector ($\boldsymbol{F}_{A} - \boldsymbol{F}_{B}$ ). The instantaneous lane order parameter, order parameter with gradient of angle of inclination ($\phi (\theta )$
). The instantaneous lane order parameter, order parameter with gradient of angle of inclination ($\phi (\theta )$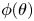 ) and distribution function of $\Delta \theta$
) and distribution function of $\Delta \theta$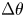 have been implemented to characterise the phase transition. A spontaneous formation and breaking of lanes are observed when under the influence of time-varying forces. The effect is further investigated for three different situations: first, when $\omega _A \neq 0$
have been implemented to characterise the phase transition. A spontaneous formation and breaking of lanes are observed when under the influence of time-varying forces. The effect is further investigated for three different situations: first, when $\omega _A \neq 0$ and $\omega _B = 0$
and $\omega _B = 0$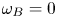 ; second, when $\omega _A = \omega _B \neq 0$
; second, when $\omega _A = \omega _B \neq 0$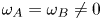 ; and third, for $\omega _A \neq \omega _B \neq 0$
; and third, for $\omega _A \neq \omega _B \neq 0$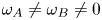 . Our study reveals that for the first case, a periodic oscillation of angle of inclination is observed. If oscillating forces of the same frequency are applied, the oscillation in angle of inclination disappears, and spontaneous formation and breaking of lanes is observed. However, in the presence of forces with different frequencies, flipping of lane inclination between the positive and negative domain of $\theta$
. Our study reveals that for the first case, a periodic oscillation of angle of inclination is observed. If oscillating forces of the same frequency are applied, the oscillation in angle of inclination disappears, and spontaneous formation and breaking of lanes is observed. However, in the presence of forces with different frequencies, flipping of lane inclination between the positive and negative domain of $\theta$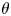 is observed. Further, some aspects of the lane formation dynamics of a PIP system is also studied in the presence of an external magnetic field where the lane formation dynamics is found to be accelerated.
is observed. Further, some aspects of the lane formation dynamics of a PIP system is also studied in the presence of an external magnetic field where the lane formation dynamics is found to be accelerated.