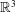1 Introduction
The classical definition of magnetic helicity in magnetohydrodynamics (MHD) is for a bounded simply connected domain. Let
![]() $\unicode[STIX]{x1D6FA}$
be such a domain with boundary
$\unicode[STIX]{x1D6FA}$
be such a domain with boundary
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}$
and outward unit normal
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}$
and outward unit normal
![]() $\boldsymbol{n}$
. Consider a magnetic field
$\boldsymbol{n}$
. Consider a magnetic field
![]() $\boldsymbol{B}$
in the space
$\boldsymbol{B}$
in the space
Then the magnetic helicity (hereafter helicity) is
where
![]() $\boldsymbol{B}=\text{curl}\,\boldsymbol{A}$
. It is well known that
$\boldsymbol{B}=\text{curl}\,\boldsymbol{A}$
. It is well known that
![]() $H$
is an invariant of ideal MHD (Woltjer Reference Woltjer1958) and is also well conserved in resistive MHD with very small magnetic diffusion (Berger Reference Berger1984; Faraco & Lindberg Reference Faraco and Lindberg2018). It is also well known that
$H$
is an invariant of ideal MHD (Woltjer Reference Woltjer1958) and is also well conserved in resistive MHD with very small magnetic diffusion (Berger Reference Berger1984; Faraco & Lindberg Reference Faraco and Lindberg2018). It is also well known that
![]() $H$
is gauge invariant, that is,
$H$
is gauge invariant, that is,
![]() $H$
is not affected by the change
$H$
is not affected by the change
![]() $\boldsymbol{A}\rightarrow \boldsymbol{A}+\text{grad}\,\unicode[STIX]{x1D712}$
, for some scalar function
$\boldsymbol{A}\rightarrow \boldsymbol{A}+\text{grad}\,\unicode[STIX]{x1D712}$
, for some scalar function
![]() $\unicode[STIX]{x1D712}$
.
$\unicode[STIX]{x1D712}$
.
The topological interpretation of
![]() $H$
is due, originally, to Moffatt (Reference Moffatt1969). By considering the Coulomb gauge,
$H$
is due, originally, to Moffatt (Reference Moffatt1969). By considering the Coulomb gauge,
![]() $\text{div}\,\boldsymbol{A}=0$
, Moffatt (Reference Moffatt1969) showed that
$\text{div}\,\boldsymbol{A}=0$
, Moffatt (Reference Moffatt1969) showed that
![]() $H$
could be interpreted in terms of the Gauss linking number weighted by magnetic flux. The linking number can refer to the linkage of thin flux tubes (e.g. Moffatt Reference Moffatt1969) or field lines (e.g. Arnold & Khesin Reference Arnold and Khesin1992). Since both helicity and magnetic flux are invariants of ideal MHD, this linkage is also invariant. The topology of field lines has also been studied in magnetic fields that are not everywhere tangent to the domain boundary (e.g. Berger & Field Reference Berger and Field1984) but we will not consider such fields in this work.
$H$
could be interpreted in terms of the Gauss linking number weighted by magnetic flux. The linking number can refer to the linkage of thin flux tubes (e.g. Moffatt Reference Moffatt1969) or field lines (e.g. Arnold & Khesin Reference Arnold and Khesin1992). Since both helicity and magnetic flux are invariants of ideal MHD, this linkage is also invariant. The topology of field lines has also been studied in magnetic fields that are not everywhere tangent to the domain boundary (e.g. Berger & Field Reference Berger and Field1984) but we will not consider such fields in this work.
Moving to multiply connected domains, there have been two general approaches to determining helicity. The first comes from plasma physics and focuses on a toroidal domain suitable for fusion devices (e.g. Taylor & Newton Reference Taylor and Newton2015). This domain is not simply connected and
![]() $H$
from (1.2) is not (in general) gauge invariant in such a domain. The main reference in the plasma physics literature to the gauge-invariant form of helicity in a torus is Bevir & Gray (Reference Bevir and Gray1980), who state that the correct form of helicity is
$H$
from (1.2) is not (in general) gauge invariant in such a domain. The main reference in the plasma physics literature to the gauge-invariant form of helicity in a torus is Bevir & Gray (Reference Bevir and Gray1980), who state that the correct form of helicity is
where
![]() $\unicode[STIX]{x1D6FA}$
no longer refers to a simply connected domain (which will be assumed for the rest of this work),
$\unicode[STIX]{x1D6FA}$
no longer refers to a simply connected domain (which will be assumed for the rest of this work),
![]() $\unicode[STIX]{x1D6FE}_{1}$
and
$\unicode[STIX]{x1D6FE}_{1}$
and
![]() $\unicode[STIX]{x1D6FE}_{2}$
are closed paths on
$\unicode[STIX]{x1D6FE}_{2}$
are closed paths on
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}$
travelling around the major and minor circumferences of the torus, respectively, and
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}$
travelling around the major and minor circumferences of the torus, respectively, and
![]() $\boldsymbol{t}_{1}$
and
$\boldsymbol{t}_{1}$
and
![]() $\boldsymbol{t}_{2}$
are the associated unit tangent vectors of the paths. The derivation of (1.3), which we refer to as the Bevir–Gray formula, in the plasma physics literature is based on making the transformation
$\boldsymbol{t}_{2}$
are the associated unit tangent vectors of the paths. The derivation of (1.3), which we refer to as the Bevir–Gray formula, in the plasma physics literature is based on making the transformation
![]() $\boldsymbol{A}\rightarrow \boldsymbol{A}+\text{grad}\,\unicode[STIX]{x1D712}$
but with
$\boldsymbol{A}\rightarrow \boldsymbol{A}+\text{grad}\,\unicode[STIX]{x1D712}$
but with
![]() $\unicode[STIX]{x1D712}$
now being multivalued (e.g. Biskamp Reference Biskamp1993; Marsh Reference Marsh1996). After the transformation is performed, the domain is cut in order to make
$\unicode[STIX]{x1D712}$
now being multivalued (e.g. Biskamp Reference Biskamp1993; Marsh Reference Marsh1996). After the transformation is performed, the domain is cut in order to make
![]() $\unicode[STIX]{x1D712}$
single-valued, and the result is the second term on the right-hand side of (1.3). This approach is difficult to generalize to domains of more complex topology. Later, we will derive a generalized version of the Bevir–Gray formula by means of the Helmholtz decomposition of vectors in multiply connected domains.
$\unicode[STIX]{x1D712}$
single-valued, and the result is the second term on the right-hand side of (1.3). This approach is difficult to generalize to domains of more complex topology. Later, we will derive a generalized version of the Bevir–Gray formula by means of the Helmholtz decomposition of vectors in multiply connected domains.
Whereas the approach in plasma physics has been to focus on a particular domain and not specify a particular vector potential, the second approach to determining helicity in multiply connected domains has been to specify the vector potential and consider arbitrary domains. In a series of papers by Cantarella and collaborators (Cantarella Reference Cantarella2000; Cantarella et al. Reference Cantarella, DeTurck, Gluck and Teytel2000; Cantarella, DeTurck & Gluck Reference Cantarella, DeTurck and Gluck2001, Reference Cantarella, DeTurck and Gluck2002), the vector potential is chosen to satisfy the Coulomb gauge and takes the form of the Biot–Savart operator,
This operator appears in other contexts in electromagnetism and, as mentioned previously, was used in Moffatt (Reference Moffatt1969) to interpret helicity in terms of the Gauss linking number.Footnote 1 One particularly interesting property of the Biot–Savart operator is that it can be made self-adjoint, leading to the application of spectral theory where magnetic fields that maximize the helicity in a domain correspond to linear force-free fields (e.g. Cantarella et al. Reference Cantarella, DeTurck, Gluck and Teytel2000; Valli Reference Valli2019). In this paper, we will refer to helicity expressed in terms of the Biot–Savart operator as Biot–Savart helicity. This term is purely for convenience and does not imply a new object: Biot–Savart helicity is still helicity but written in a particular way.
In this work we show that the two approaches to finding helicity in multiply connected domains, described above, can be unified. We first generalize (1.3) to connected domains of arbitrary topology in a systematic way. We then show how the gauge-invariant helicity in multiply connected domains is coincident with Biot–Savart helicity. This leads to a discussion of how the (often quoted) mutual helicity (Moffatt Reference Moffatt1969; Laurence & Avellaneda Reference Laurence and Avellaneda1993; Cantarella Reference Cantarella2000) follows from the general helicity formula. The paper ends with a summary and a discussion of the interpretation of helicity in periodic domains.
2 Helicity in multiply connected domains
2.1 Geometrical set-up
We now describe the general geometrical set-up and introduce ideas from homology which are necessary for treating multiply connected domains. A comprehensive review of the application of homology to magnetic fields can be found in Blank, Friedrichs & Grad (Reference Blank, Friedrichs and Grad1957). A more recent and accessible account can be found in Cantarella et al. (Reference Cantarella, DeTurck and Gluck2002).
We consider a domain
![]() $\unicode[STIX]{x1D6FA}\in \mathbb{R}^{3}$
that is a bounded open connected set with Lipschitz continuous boundary
$\unicode[STIX]{x1D6FA}\in \mathbb{R}^{3}$
that is a bounded open connected set with Lipschitz continuous boundary
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}$
and outer unit normal vector
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}$
and outer unit normal vector
![]() $\boldsymbol{n}$
. If the first Betti number of
$\boldsymbol{n}$
. If the first Betti number of
![]() $\unicode[STIX]{x1D6FA}$
is (the genus)
$\unicode[STIX]{x1D6FA}$
is (the genus)
![]() $g>0$
, then the first Betti number of
$g>0$
, then the first Betti number of
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}$
is
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}$
is
![]() $2g$
(e.g. Cantarella et al.
Reference Cantarella, DeTurck and Gluck2002). We can consider
$2g$
(e.g. Cantarella et al.
Reference Cantarella, DeTurck and Gluck2002). We can consider
![]() $2g$
non-bounding cycles on
$2g$
non-bounding cycles on
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}$
,
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}$
,
![]() $\{\unicode[STIX]{x1D6FE}_{j}\}_{j=1}^{g}\cup \{\unicode[STIX]{x1D6FE}_{j}^{\prime }\}_{j=1}^{g}$
, that represent the generators of the first homology group of
$\{\unicode[STIX]{x1D6FE}_{j}\}_{j=1}^{g}\cup \{\unicode[STIX]{x1D6FE}_{j}^{\prime }\}_{j=1}^{g}$
, that represent the generators of the first homology group of
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}$
. Each set of cycles is associated with the closed domain and its complement in a ball containing the domain. The
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}$
. Each set of cycles is associated with the closed domain and its complement in a ball containing the domain. The
![]() $\{\unicode[STIX]{x1D6FE}_{j}\}_{j=1}^{g}$
represent the generators of the first homology group of
$\{\unicode[STIX]{x1D6FE}_{j}\}_{j=1}^{g}$
represent the generators of the first homology group of
![]() $\overline{\unicode[STIX]{x1D6FA}}$
and have unit tangent vectors denoted by
$\overline{\unicode[STIX]{x1D6FA}}$
and have unit tangent vectors denoted by
![]() $\boldsymbol{t}_{j}$
. The
$\boldsymbol{t}_{j}$
. The
![]() $\{\unicode[STIX]{x1D6FE}_{j}^{\prime }\}_{j=1}^{g}$
represent the generators of the first homology group of
$\{\unicode[STIX]{x1D6FE}_{j}^{\prime }\}_{j=1}^{g}$
represent the generators of the first homology group of
![]() $\overline{\unicode[STIX]{x1D6FA}^{\prime }}$
, where
$\overline{\unicode[STIX]{x1D6FA}^{\prime }}$
, where
![]() $\unicode[STIX]{x1D6FA}^{\prime }=B\setminus \overline{\unicode[STIX]{x1D6FA}}$
and
$\unicode[STIX]{x1D6FA}^{\prime }=B\setminus \overline{\unicode[STIX]{x1D6FA}}$
and
![]() $B$
is an open ball containing
$B$
is an open ball containing
![]() $\overline{\unicode[STIX]{x1D6FA}}$
. The unit tangent vector of a cycle
$\overline{\unicode[STIX]{x1D6FA}}$
. The unit tangent vector of a cycle
![]() $\unicode[STIX]{x1D6FE}_{j}^{\prime }$
is denoted
$\unicode[STIX]{x1D6FE}_{j}^{\prime }$
is denoted
![]() $\boldsymbol{t}_{j}^{\prime }$
.
$\boldsymbol{t}_{j}^{\prime }$
.
In
![]() $\unicode[STIX]{x1D6FA}$
there are
$\unicode[STIX]{x1D6FA}$
there are
![]() $g$
cutting surfaces,
$g$
cutting surfaces,
![]() $\{\unicode[STIX]{x1D6F4}\}_{j=1}^{g}$
, that are connected orientable Lipschitz surfaces satisfying
$\{\unicode[STIX]{x1D6F4}\}_{j=1}^{g}$
, that are connected orientable Lipschitz surfaces satisfying
![]() $\unicode[STIX]{x1D6F4}_{j}\subset \unicode[STIX]{x1D6FA}$
and
$\unicode[STIX]{x1D6F4}_{j}\subset \unicode[STIX]{x1D6FA}$
and
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D6F4}_{j}\subset \unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}$
. Each surface
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6F4}_{j}\subset \unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}$
. Each surface
![]() $\unicode[STIX]{x1D6F4}_{j}$
satisfies
$\unicode[STIX]{x1D6F4}_{j}$
satisfies
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D6F4}_{j}=\unicode[STIX]{x1D6FE}_{j}^{\prime }$
and cuts the cycle
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6F4}_{j}=\unicode[STIX]{x1D6FE}_{j}^{\prime }$
and cuts the cycle
![]() $\unicode[STIX]{x1D6FE}_{j}$
. A similar set of cutting surfaces,
$\unicode[STIX]{x1D6FE}_{j}$
. A similar set of cutting surfaces,
![]() $\{\unicode[STIX]{x1D6F4}^{\prime }\}_{j=1}^{g}$
, exists in
$\{\unicode[STIX]{x1D6F4}^{\prime }\}_{j=1}^{g}$
, exists in
![]() $\unicode[STIX]{x1D6FA}^{\prime }$
. An illustration of the geometrical set-up for a domain with
$\unicode[STIX]{x1D6FA}^{\prime }$
. An illustration of the geometrical set-up for a domain with
![]() $g=2$
is shown in figure 1. For the sake of definiteness, we choose the unit normal vector
$g=2$
is shown in figure 1. For the sake of definiteness, we choose the unit normal vector
![]() $\boldsymbol{n}_{\unicode[STIX]{x1D6F4}_{j}}$
on
$\boldsymbol{n}_{\unicode[STIX]{x1D6F4}_{j}}$
on
![]() $\unicode[STIX]{x1D6F4}_{j}$
oriented in such a way that (i) the unit tangent vector
$\unicode[STIX]{x1D6F4}_{j}$
oriented in such a way that (i) the unit tangent vector
![]() $\boldsymbol{t}_{j}^{\prime }$
on
$\boldsymbol{t}_{j}^{\prime }$
on
![]() $\unicode[STIX]{x1D6FE}_{j}^{\prime }=\unicode[STIX]{x2202}\unicode[STIX]{x1D6F4}_{j}$
is oriented counterclockwise with respect to
$\unicode[STIX]{x1D6FE}_{j}^{\prime }=\unicode[STIX]{x2202}\unicode[STIX]{x1D6F4}_{j}$
is oriented counterclockwise with respect to
![]() $\boldsymbol{n}_{\unicode[STIX]{x1D6F4}_{j}}$
(the ‘right-hand rule’) and (ii) the unit tangent vector
$\boldsymbol{n}_{\unicode[STIX]{x1D6F4}_{j}}$
(the ‘right-hand rule’) and (ii) the unit tangent vector
![]() $\boldsymbol{t}_{j}$
crosses
$\boldsymbol{t}_{j}$
crosses
![]() $\unicode[STIX]{x1D6F4}_{j}$
consistently with the direction of
$\unicode[STIX]{x1D6F4}_{j}$
consistently with the direction of
![]() $\boldsymbol{n}_{\unicode[STIX]{x1D6F4}_{j}}$
.
$\boldsymbol{n}_{\unicode[STIX]{x1D6F4}_{j}}$
.
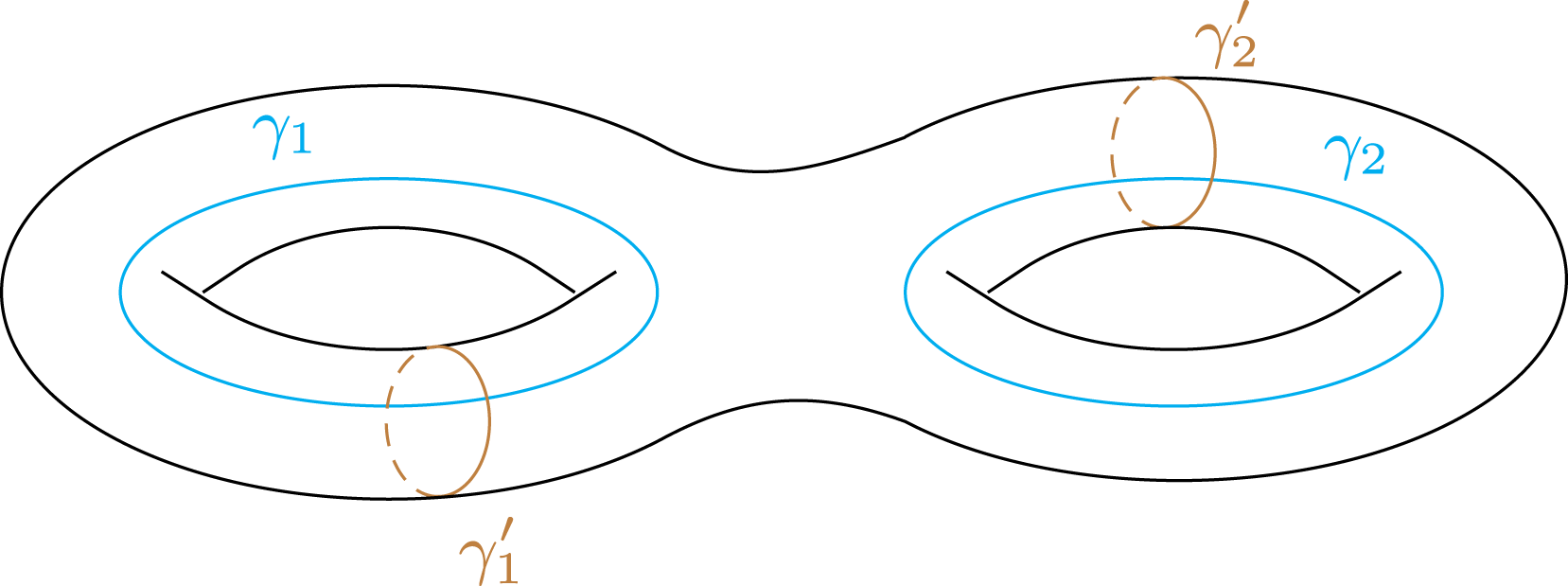
Figure 1. A domain with
![]() $g=2$
. The cycles are shown in brown and cyan, following the notation in the main text. The oriented surfaces bounded by the cycles
$g=2$
. The cycles are shown in brown and cyan, following the notation in the main text. The oriented surfaces bounded by the cycles
![]() $\unicode[STIX]{x1D6FE}_{j}^{\prime }$
and
$\unicode[STIX]{x1D6FE}_{j}^{\prime }$
and
![]() $\unicode[STIX]{x1D6FE}_{j}$
define the cutting surfaces
$\unicode[STIX]{x1D6FE}_{j}$
define the cutting surfaces
![]() $\unicode[STIX]{x1D6F4}_{j}$
and
$\unicode[STIX]{x1D6F4}_{j}$
and
![]() $\unicode[STIX]{x1D6F4}_{j}^{\prime }$
, respectively.
$\unicode[STIX]{x1D6F4}_{j}^{\prime }$
, respectively.
In the above description, if the boundary of
![]() $\unicode[STIX]{x1D6FA}$
is not connected then some care needs to be taken to make sure that a particular cutting surface remains in
$\unicode[STIX]{x1D6FA}$
is not connected then some care needs to be taken to make sure that a particular cutting surface remains in
![]() $\unicode[STIX]{x1D6FA}$
or
$\unicode[STIX]{x1D6FA}$
or
![]() $\unicode[STIX]{x1D6FA}^{\prime }$
but not in both. For the
$\unicode[STIX]{x1D6FA}^{\prime }$
but not in both. For the
![]() $n$
-holed torus, such as the two-holed torus in figure 1, this is not an issue. For a toroidal shell (e.g. O’Neil & Cerfon Reference O’Neil and Cerfon2018), however, the boundary is not connected, that is, the outer boundary of the solid torus is separated from the inner boundary of the toroidal hole. A toroidal shell has
$n$
-holed torus, such as the two-holed torus in figure 1, this is not an issue. For a toroidal shell (e.g. O’Neil & Cerfon Reference O’Neil and Cerfon2018), however, the boundary is not connected, that is, the outer boundary of the solid torus is separated from the inner boundary of the toroidal hole. A toroidal shell has
![]() $g=2$
and so there are two cycles for
$g=2$
and so there are two cycles for
![]() $\unicode[STIX]{x1D6FA}$
and two for
$\unicode[STIX]{x1D6FA}$
and two for
![]() $\unicode[STIX]{x1D6FA}^{\prime }$
. It is easy to see that the cutting surfaces
$\unicode[STIX]{x1D6FA}^{\prime }$
. It is easy to see that the cutting surfaces
![]() $\unicode[STIX]{x1D6F4}_{j}^{\prime }$
, corresponding to the
$\unicode[STIX]{x1D6F4}_{j}^{\prime }$
, corresponding to the
![]() $\unicode[STIX]{x1D6FE}_{j}$
, lie entirely in
$\unicode[STIX]{x1D6FE}_{j}$
, lie entirely in
![]() $\unicode[STIX]{x1D6FA}^{\prime }$
. Naively performing the same procedure for the cutting surfaces
$\unicode[STIX]{x1D6FA}^{\prime }$
. Naively performing the same procedure for the cutting surfaces
![]() $\unicode[STIX]{x1D6F4}_{j}$
of the
$\unicode[STIX]{x1D6F4}_{j}$
of the
![]() $\unicode[STIX]{x1D6FE}_{j}^{\prime }$
, however, results in their overlapping with parts of the complementary domain
$\unicode[STIX]{x1D6FE}_{j}^{\prime }$
, however, results in their overlapping with parts of the complementary domain
![]() $\unicode[STIX]{x1D6FA}^{\prime }$
. Restricting the
$\unicode[STIX]{x1D6FA}^{\prime }$
. Restricting the
![]() $\unicode[STIX]{x1D6F4}_{j}$
to lie entirely in
$\unicode[STIX]{x1D6F4}_{j}$
to lie entirely in
![]() $\unicode[STIX]{x1D6FA}$
can be achieved using homological properties. We explain the procedure by describing the cutting surfaces for the cycles,
$\unicode[STIX]{x1D6FA}$
can be achieved using homological properties. We explain the procedure by describing the cutting surfaces for the cycles,
![]() $\unicode[STIX]{x1D6FE}_{1}^{\prime }$
and
$\unicode[STIX]{x1D6FE}_{1}^{\prime }$
and
![]() $\unicode[STIX]{x1D6FE}_{2}^{\prime }$
, which orbit the central hole of the torus and the toroidal hole, respectively. This situation is illustrated in figure 2.
$\unicode[STIX]{x1D6FE}_{2}^{\prime }$
, which orbit the central hole of the torus and the toroidal hole, respectively. This situation is illustrated in figure 2.
Figure 2. Toroidal shell with cutting surfaces. (a) A three-dimensional illustration of a toroidal shell cut in half. The cutting surfaces
![]() $\unicode[STIX]{x1D6F4}_{1}$
and
$\unicode[STIX]{x1D6F4}_{1}$
and
![]() $\unicode[STIX]{x1D6F4}_{2}$
are indicated. (b) The major cross-section (toroidal hole shown as dashed lines) where
$\unicode[STIX]{x1D6F4}_{2}$
are indicated. (b) The major cross-section (toroidal hole shown as dashed lines) where
![]() $\unicode[STIX]{x1D6FE}_{1}^{\prime }$
is the boundary of the annulus
$\unicode[STIX]{x1D6FE}_{1}^{\prime }$
is the boundary of the annulus
![]() $\unicode[STIX]{x1D6F4}_{1}$
represented by the blue and red cycles. (c) The minor cross-section where
$\unicode[STIX]{x1D6F4}_{1}$
represented by the blue and red cycles. (c) The minor cross-section where
![]() $\unicode[STIX]{x1D6FE}_{2}^{\prime }$
is the boundary of the annulus
$\unicode[STIX]{x1D6FE}_{2}^{\prime }$
is the boundary of the annulus
![]() $\unicode[STIX]{x1D6F4}_{2}$
represented by the orange and green cycles. Note that the cross-sections are not to scale.
$\unicode[STIX]{x1D6F4}_{2}$
represented by the orange and green cycles. Note that the cross-sections are not to scale.
The boundary of the first cutting surface,
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D6F4}_{1}=\unicode[STIX]{x1D6FE}_{1}^{\prime }$
, is indicated in figure 2(b) by the red and blue cycles. Similarly, the boundary of the other cutting surface,
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6F4}_{1}=\unicode[STIX]{x1D6FE}_{1}^{\prime }$
, is indicated in figure 2(b) by the red and blue cycles. Similarly, the boundary of the other cutting surface,
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D6F4}_{2}=\unicode[STIX]{x1D6FE}_{2}^{\prime }$
, is indicated in figure 2(c) by orange and green cycles. The surfaces
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6F4}_{2}=\unicode[STIX]{x1D6FE}_{2}^{\prime }$
, is indicated in figure 2(c) by orange and green cycles. The surfaces
![]() $\unicode[STIX]{x1D6F4}_{1}$
and
$\unicode[STIX]{x1D6F4}_{1}$
and
![]() $\unicode[STIX]{x1D6F4}_{2}$
lie entirely in
$\unicode[STIX]{x1D6F4}_{2}$
lie entirely in
![]() $\unicode[STIX]{x1D6FA}$
and are annuli.
$\unicode[STIX]{x1D6FA}$
and are annuli.
For a given orientation of the normal
![]() $\boldsymbol{n}_{1}$
of
$\boldsymbol{n}_{1}$
of
![]() $\unicode[STIX]{x1D6F4}_{1}$
,
$\unicode[STIX]{x1D6F4}_{1}$
,
where
![]() $\boldsymbol{w}$
is a vector field and ‘blue’ and ‘red’ represent the cycles displayed in figure 2(b). A similar result holds for
$\boldsymbol{w}$
is a vector field and ‘blue’ and ‘red’ represent the cycles displayed in figure 2(b). A similar result holds for
![]() $\unicode[STIX]{x1D6F4}_{2}$
. Note, however, that the red cycle is bounding in
$\unicode[STIX]{x1D6F4}_{2}$
. Note, however, that the red cycle is bounding in
![]() $\unicode[STIX]{x1D6FA}^{\prime }$
, thus
$\unicode[STIX]{x1D6FA}^{\prime }$
, thus
![]() $\unicode[STIX]{x1D6FE}_{1}^{\prime }$
and the blue cycle are equivalent homologically. The same is true for
$\unicode[STIX]{x1D6FE}_{1}^{\prime }$
and the blue cycle are equivalent homologically. The same is true for
![]() $\unicode[STIX]{x1D6FE}_{2}^{\prime }$
and the green cycle in figure 2(c).
$\unicode[STIX]{x1D6FE}_{2}^{\prime }$
and the green cycle in figure 2(c).
In this paper we will focus on (
![]() $n$
-holed) tori and toroidal shells since these domains have the most immediate applications, both as domains in their own right (e.g. Dewar et al.
Reference Dewar, Yoshida, Bhattacharjee and Hudson2015; O’Neil & Cerfon Reference O’Neil and Cerfon2018) and in their connection to the common simulation domains of periodic and doubly periodic cubes (we will return to discuss helicity in periodic domains later). The ‘cut’ domains (those formed by removing the cutting surfaces) for these cases are simply connected. This fact, however, is not true of all domains in
$n$
-holed) tori and toroidal shells since these domains have the most immediate applications, both as domains in their own right (e.g. Dewar et al.
Reference Dewar, Yoshida, Bhattacharjee and Hudson2015; O’Neil & Cerfon Reference O’Neil and Cerfon2018) and in their connection to the common simulation domains of periodic and doubly periodic cubes (we will return to discuss helicity in periodic domains later). The ‘cut’ domains (those formed by removing the cutting surfaces) for these cases are simply connected. This fact, however, is not true of all domains in
![]() $\mathbb{R}^{3}$
. For example, consider a domain
$\mathbb{R}^{3}$
. For example, consider a domain
![]() $\unicode[STIX]{x1D6FA}=B\setminus K$
where
$\unicode[STIX]{x1D6FA}=B\setminus K$
where
![]() $B$
is a ball, as before, and
$B$
is a ball, as before, and
![]() $K$
is a trefoil knot (Benedetti, Frigerio & Ghiloni Reference Benedetti, Frigerio and Ghiloni2012; Alonso Rodríguez et al.
Reference Alonso Rodríguez, Camaño, Rodríguez, Valli and Venegas2018). An illustration of such a domain is displayed in figure 3. The procedure that we will now describe can cope with all the cases described above, including this last one.
$K$
is a trefoil knot (Benedetti, Frigerio & Ghiloni Reference Benedetti, Frigerio and Ghiloni2012; Alonso Rodríguez et al.
Reference Alonso Rodríguez, Camaño, Rodríguez, Valli and Venegas2018). An illustration of such a domain is displayed in figure 3. The procedure that we will now describe can cope with all the cases described above, including this last one.

Figure 3. An example of a ‘cut’ domain that is not simply connected. Following the description in the main text, the orange domain is the trefoil knot
![]() $K$
. The green surface is one of the cutting surfaces, shown here as two ‘discs’ with three ‘twisting bands’. This image was produced with SeifertView (Jarke J. van Wijk, Technische Universiteit Eindhoven).
$K$
. The green surface is one of the cutting surfaces, shown here as two ‘discs’ with three ‘twisting bands’. This image was produced with SeifertView (Jarke J. van Wijk, Technische Universiteit Eindhoven).
2.2 Helmholtz decomposition and Neumann harmonic vector fields
The gauge transformation normally used in helicity studies,
![]() $\boldsymbol{A}\rightarrow \boldsymbol{A}+\text{grad}\,\unicode[STIX]{x1D712}$
, is only applicable in simply connected domains if
$\boldsymbol{A}\rightarrow \boldsymbol{A}+\text{grad}\,\unicode[STIX]{x1D712}$
, is only applicable in simply connected domains if
![]() $\unicode[STIX]{x1D712}$
is to remain single-valued. For the regions under consideration with more complex topologies, we require the full Helmholtz decomposition (e.g. Blank et al.
Reference Blank, Friedrichs and Grad1957; Cantarella et al.
Reference Cantarella, DeTurck and Gluck2002).
$\unicode[STIX]{x1D712}$
is to remain single-valued. For the regions under consideration with more complex topologies, we require the full Helmholtz decomposition (e.g. Blank et al.
Reference Blank, Friedrichs and Grad1957; Cantarella et al.
Reference Cantarella, DeTurck and Gluck2002).
Theorem 1 (Helmholtz).
Any
![]() $\boldsymbol{u}\in (L^{2}(\unicode[STIX]{x1D6FA}))^{3}$
can be decomposed as
$\boldsymbol{u}\in (L^{2}(\unicode[STIX]{x1D6FA}))^{3}$
can be decomposed as
where
![]() $\boldsymbol{P}$
is a vector field,
$\boldsymbol{P}$
is a vector field,
![]() $\unicode[STIX]{x1D719}$
a single-valued scalar function and
$\unicode[STIX]{x1D719}$
a single-valued scalar function and
![]() $\unicode[STIX]{x1D746}$
is in the space of Neumann harmonic fields
$\unicode[STIX]{x1D746}$
is in the space of Neumann harmonic fields
![]() ${\mathcal{H}}$
, defined as
${\mathcal{H}}$
, defined as
In order to make use of
![]() ${\mathcal{H}}$
, we need its basis
${\mathcal{H}}$
, we need its basis
![]() $\{\unicode[STIX]{x1D746}_{j}\}_{j=1}^{g}$
. This can be found, for both
$\{\unicode[STIX]{x1D746}_{j}\}_{j=1}^{g}$
. This can be found, for both
![]() $\unicode[STIX]{x1D6FA}$
and
$\unicode[STIX]{x1D6FA}$
and
![]() $\unicode[STIX]{x1D6FA}^{\prime }$
separately, by finding the solutions
$\unicode[STIX]{x1D6FA}^{\prime }$
separately, by finding the solutions
![]() $\unicode[STIX]{x1D719}_{j}$
of suitable elliptic problems where the appropriate cutting surfaces are removed from the domain under study. The basis functions for the space of harmonic fields in
$\unicode[STIX]{x1D719}_{j}$
of suitable elliptic problems where the appropriate cutting surfaces are removed from the domain under study. The basis functions for the space of harmonic fields in
![]() $\unicode[STIX]{x1D6FA}$
take the form
$\unicode[STIX]{x1D6FA}$
take the form
![]() $\unicode[STIX]{x1D746}_{j}=\widetilde{\text{grad}\,}\unicode[STIX]{x1D719}_{j}$
, where
$\unicode[STIX]{x1D746}_{j}=\widetilde{\text{grad}\,}\unicode[STIX]{x1D719}_{j}$
, where
![]() $\widetilde{\text{grad}\,}\unicode[STIX]{x1D719}_{j}$
is the extension of
$\widetilde{\text{grad}\,}\unicode[STIX]{x1D719}_{j}$
is the extension of
![]() $\text{grad}\,\unicode[STIX]{x1D719}_{j}$
to
$\text{grad}\,\unicode[STIX]{x1D719}_{j}$
to
![]() $(L^{2}(\unicode[STIX]{x1D6FA}))^{3}$
and each
$(L^{2}(\unicode[STIX]{x1D6FA}))^{3}$
and each
![]() $\unicode[STIX]{x1D719}_{j}$
has a jump equal to 1 on the corresponding cutting surface. The basis functions of the space of harmonic fields in
$\unicode[STIX]{x1D719}_{j}$
has a jump equal to 1 on the corresponding cutting surface. The basis functions of the space of harmonic fields in
![]() $\unicode[STIX]{x1D6FA}^{\prime }$
are constructed in a similar way and are denoted by
$\unicode[STIX]{x1D6FA}^{\prime }$
are constructed in a similar way and are denoted by
![]() $\{\unicode[STIX]{x1D746}_{j}^{\prime }\}_{j=1}^{g}$
. For more details on the construction of the basis functions, we direct the reader to Alonso Rodríguez et al. (Reference Alonso Rodríguez, Camaño, Rodríguez, Valli and Venegas2018).
$\{\unicode[STIX]{x1D746}_{j}^{\prime }\}_{j=1}^{g}$
. For more details on the construction of the basis functions, we direct the reader to Alonso Rodríguez et al. (Reference Alonso Rodríguez, Camaño, Rodríguez, Valli and Venegas2018).
2.3 Zero flux magnetic fields
Consider two different vector potentials
![]() $\boldsymbol{A}_{1}$
and
$\boldsymbol{A}_{1}$
and
![]() $\boldsymbol{A}_{2}$
for
$\boldsymbol{A}_{2}$
for
![]() $\boldsymbol{B}\in {\mathcal{V}}$
. Since
$\boldsymbol{B}\in {\mathcal{V}}$
. Since
![]() $\text{curl}\,(\boldsymbol{A}_{1}-\boldsymbol{A}_{2})=\mathbf{0}$
in
$\text{curl}\,(\boldsymbol{A}_{1}-\boldsymbol{A}_{2})=\mathbf{0}$
in
![]() $\unicode[STIX]{x1D6FA}$
, it follows from Theorem 1 that we can write
$\unicode[STIX]{x1D6FA}$
, it follows from Theorem 1 that we can write
where
![]() $\unicode[STIX]{x1D712}$
is a scalar function and
$\unicode[STIX]{x1D712}$
is a scalar function and
![]() $\unicode[STIX]{x1D746}\in {\mathcal{H}}$
. Some simple manipulation reveals
$\unicode[STIX]{x1D746}\in {\mathcal{H}}$
. Some simple manipulation reveals
Therefore, if
![]() $\boldsymbol{B}\bot {\mathcal{H}}$
then helicity is independent of the vector potential. Writing
$\boldsymbol{B}\bot {\mathcal{H}}$
then helicity is independent of the vector potential. Writing
![]() $\unicode[STIX]{x1D746}$
in terms of its basis functions, we require that
$\unicode[STIX]{x1D746}$
in terms of its basis functions, we require that
This statement is nothing more than enforcing zero magnetic flux through every cutting surface,
 $$\begin{eqnarray}\displaystyle \int _{\unicode[STIX]{x1D6FA}}\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D746}_{j} & = & \displaystyle \int _{\unicode[STIX]{x1D6FA}\setminus \unicode[STIX]{x1D6F4}_{j}}\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D746}_{j}=\int _{\unicode[STIX]{x1D6FA}\setminus \unicode[STIX]{x1D6F4}_{j}}\boldsymbol{B}\boldsymbol{\cdot }\text{grad}\,\unicode[STIX]{x1D719}_{j}\nonumber\\ \displaystyle & = & \displaystyle \int _{\unicode[STIX]{x2202}(\unicode[STIX]{x1D6FA}\setminus \unicode[STIX]{x1D6F4}_{j})}\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{n}_{j}\unicode[STIX]{x1D719}_{j}-\int _{\unicode[STIX]{x1D6FA}\setminus \unicode[STIX]{x1D6F4}_{j}}(\text{div}\,\boldsymbol{B})\unicode[STIX]{x1D719}_{j}\nonumber\\ \displaystyle & = & \displaystyle \int _{\unicode[STIX]{x1D6F4}_{j}}\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{n}_{j}[[\unicode[STIX]{x1D719}_{j}]]=\int _{\unicode[STIX]{x1D6F4}_{j}}\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{n}_{j},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{\unicode[STIX]{x1D6FA}}\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D746}_{j} & = & \displaystyle \int _{\unicode[STIX]{x1D6FA}\setminus \unicode[STIX]{x1D6F4}_{j}}\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D746}_{j}=\int _{\unicode[STIX]{x1D6FA}\setminus \unicode[STIX]{x1D6F4}_{j}}\boldsymbol{B}\boldsymbol{\cdot }\text{grad}\,\unicode[STIX]{x1D719}_{j}\nonumber\\ \displaystyle & = & \displaystyle \int _{\unicode[STIX]{x2202}(\unicode[STIX]{x1D6FA}\setminus \unicode[STIX]{x1D6F4}_{j})}\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{n}_{j}\unicode[STIX]{x1D719}_{j}-\int _{\unicode[STIX]{x1D6FA}\setminus \unicode[STIX]{x1D6F4}_{j}}(\text{div}\,\boldsymbol{B})\unicode[STIX]{x1D719}_{j}\nonumber\\ \displaystyle & = & \displaystyle \int _{\unicode[STIX]{x1D6F4}_{j}}\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{n}_{j}[[\unicode[STIX]{x1D719}_{j}]]=\int _{\unicode[STIX]{x1D6F4}_{j}}\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{n}_{j},\end{eqnarray}$$
where
![]() $[[\unicode[STIX]{x1D719}_{j}]]=\unicode[STIX]{x1D719}_{j}|_{\unicode[STIX]{x1D6F4}_{j}^{+}}-\unicode[STIX]{x1D719}_{j}|_{\unicode[STIX]{x1D6F4}_{j}^{-}}=1$
, from the construction of the basis functions (Alonso Rodríguez et al.
Reference Alonso Rodríguez, Camaño, Rodríguez, Valli and Venegas2018). Thus, by enforcing zero magnetic flux through all the cutting surfaces of
$[[\unicode[STIX]{x1D719}_{j}]]=\unicode[STIX]{x1D719}_{j}|_{\unicode[STIX]{x1D6F4}_{j}^{+}}-\unicode[STIX]{x1D719}_{j}|_{\unicode[STIX]{x1D6F4}_{j}^{-}}=1$
, from the construction of the basis functions (Alonso Rodríguez et al.
Reference Alonso Rodríguez, Camaño, Rodríguez, Valli and Venegas2018). Thus, by enforcing zero magnetic flux through all the cutting surfaces of
![]() $\unicode[STIX]{x1D6FA}$
, the helicity in the domain can be written as in (1.2).
$\unicode[STIX]{x1D6FA}$
, the helicity in the domain can be written as in (1.2).
This approach to defining helicity in multiply connected domains has been used in several theoretical works (e.g. Jordan, Yoshida & Ito Reference Jordan, Yoshida and Ito1998; Faraco & Lindberg Reference Faraco and Lindberg2018). For cases where there is non-zero magnetic flux, more work is needed to produce a gauge-invariant helicity. We will now derive a more general formula which includes the zero flux condition as a special case.
2.4 Generalized Bevir–Gray formula
Let us consider the following quantities,
where
![]() $\boldsymbol{B}=\text{curl}\,\boldsymbol{A}_{1}$
and
$\boldsymbol{B}=\text{curl}\,\boldsymbol{A}_{1}$
and
![]() $\boldsymbol{B}=\text{curl}\,\boldsymbol{A}_{2}$
, respectively. Without the zero flux condition,
$\boldsymbol{B}=\text{curl}\,\boldsymbol{A}_{2}$
, respectively. Without the zero flux condition,
![]() $H_{1}$
and
$H_{1}$
and
![]() $H_{2}$
are not, in general, gauge invariant in multiply connected domains. Considering the difference of these quantities,
$H_{2}$
are not, in general, gauge invariant in multiply connected domains. Considering the difference of these quantities,
 $$\begin{eqnarray}\displaystyle H_{1}-H_{2} & = & \displaystyle \int _{\unicode[STIX]{x1D6FA}}\boldsymbol{B}\boldsymbol{\cdot }(\boldsymbol{A}_{1}-\boldsymbol{A}_{2})=\int _{\unicode[STIX]{x1D6FA}}\text{curl}\,\boldsymbol{A}_{1}\boldsymbol{\cdot }(\boldsymbol{A}_{1}-\boldsymbol{A}_{2})\nonumber\\ \displaystyle & = & \displaystyle \int _{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}}\boldsymbol{n}\times \boldsymbol{A}_{1}\boldsymbol{\cdot }(\boldsymbol{A}_{1}-\boldsymbol{A}_{2})=\int _{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}}\boldsymbol{A}_{1}\times \boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{A}_{2}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle H_{1}-H_{2} & = & \displaystyle \int _{\unicode[STIX]{x1D6FA}}\boldsymbol{B}\boldsymbol{\cdot }(\boldsymbol{A}_{1}-\boldsymbol{A}_{2})=\int _{\unicode[STIX]{x1D6FA}}\text{curl}\,\boldsymbol{A}_{1}\boldsymbol{\cdot }(\boldsymbol{A}_{1}-\boldsymbol{A}_{2})\nonumber\\ \displaystyle & = & \displaystyle \int _{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}}\boldsymbol{n}\times \boldsymbol{A}_{1}\boldsymbol{\cdot }(\boldsymbol{A}_{1}-\boldsymbol{A}_{2})=\int _{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}}\boldsymbol{A}_{1}\times \boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{A}_{2}.\end{eqnarray}$$
The second line follows from integration by parts and using
![]() $\text{curl}\,(\boldsymbol{A}_{1}-\boldsymbol{A}_{2})=\mathbf{0}$
. Since
$\text{curl}\,(\boldsymbol{A}_{1}-\boldsymbol{A}_{2})=\mathbf{0}$
. Since
![]() $\text{curl}\,\boldsymbol{A}_{1}\boldsymbol{\cdot }\boldsymbol{n}=0=\text{curl}\,\boldsymbol{A}_{2}\boldsymbol{\cdot }\boldsymbol{n}$
, the tangential traces
$\text{curl}\,\boldsymbol{A}_{1}\boldsymbol{\cdot }\boldsymbol{n}=0=\text{curl}\,\boldsymbol{A}_{2}\boldsymbol{\cdot }\boldsymbol{n}$
, the tangential traces
![]() $\boldsymbol{A}_{1}\times \boldsymbol{n}$
and
$\boldsymbol{A}_{1}\times \boldsymbol{n}$
and
![]() $\boldsymbol{A}_{2}\times \boldsymbol{n}$
can be expressed, via a Helmholtz decomposition on
$\boldsymbol{A}_{2}\times \boldsymbol{n}$
can be expressed, via a Helmholtz decomposition on
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}$
(e.g. Hiptmair, Kotiuga & Tordeux Reference Hiptmair, Kotiuga and Tordeux2012; Alonso Rodríguez et al.
Reference Alonso Rodríguez, Camaño, Rodríguez, Valli and Venegas2018), as
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}$
(e.g. Hiptmair, Kotiuga & Tordeux Reference Hiptmair, Kotiuga and Tordeux2012; Alonso Rodríguez et al.
Reference Alonso Rodríguez, Camaño, Rodríguez, Valli and Venegas2018), as
where
![]() $\unicode[STIX]{x1D702}$
,
$\unicode[STIX]{x1D702}$
,
![]() $\unicode[STIX]{x1D709}$
are scalar functions and
$\unicode[STIX]{x1D709}$
are scalar functions and
![]() $\unicode[STIX]{x1D6FC}_{j},\unicode[STIX]{x1D6FD}_{j},\unicode[STIX]{x1D6FF}_{j},\unicode[STIX]{x1D707}_{j}\in \mathbb{R}~(j=1,\ldots ,g)$
. Alonso Rodríguez et al. (Reference Alonso Rodríguez, Camaño, Rodríguez, Valli and Venegas2018) derived the following useful identities:
$\unicode[STIX]{x1D6FC}_{j},\unicode[STIX]{x1D6FD}_{j},\unicode[STIX]{x1D6FF}_{j},\unicode[STIX]{x1D707}_{j}\in \mathbb{R}~(j=1,\ldots ,g)$
. Alonso Rodríguez et al. (Reference Alonso Rodríguez, Camaño, Rodríguez, Valli and Venegas2018) derived the following useful identities:
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \int _{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}}\text{grad}\,\unicode[STIX]{x1D702}\times \boldsymbol{n}\boldsymbol{\cdot }\text{grad}\,\unicode[STIX]{x1D709}=0,\\[5.0pt] \displaystyle \int _{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}}\text{grad}\,\unicode[STIX]{x1D702}\times \boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D746}_{j}=0,\quad \displaystyle \int _{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}}\text{grad}\,\unicode[STIX]{x1D702}\times \boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D746}_{i}^{\prime }=0,\\[10.0pt] \displaystyle \int _{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D746}_{i}\times \boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D746}_{j}=0,\quad \displaystyle \int _{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D746}_{i}^{\prime }\times \boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D746}_{j}^{\prime }=0,\\[10.0pt] \displaystyle \int _{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D746}_{j}\times \boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D746}_{i}^{\prime }=\unicode[STIX]{x1D6FF}_{ij}=\displaystyle -\int _{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D746}_{i}^{\prime }\times \boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D746}_{j},\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \int _{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}}\text{grad}\,\unicode[STIX]{x1D702}\times \boldsymbol{n}\boldsymbol{\cdot }\text{grad}\,\unicode[STIX]{x1D709}=0,\\[5.0pt] \displaystyle \int _{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}}\text{grad}\,\unicode[STIX]{x1D702}\times \boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D746}_{j}=0,\quad \displaystyle \int _{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}}\text{grad}\,\unicode[STIX]{x1D702}\times \boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D746}_{i}^{\prime }=0,\\[10.0pt] \displaystyle \int _{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D746}_{i}\times \boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D746}_{j}=0,\quad \displaystyle \int _{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D746}_{i}^{\prime }\times \boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D746}_{j}^{\prime }=0,\\[10.0pt] \displaystyle \int _{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D746}_{j}\times \boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D746}_{i}^{\prime }=\unicode[STIX]{x1D6FF}_{ij}=\displaystyle -\int _{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D746}_{i}^{\prime }\times \boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D746}_{j},\end{array}\right\} & & \displaystyle\end{eqnarray}$$
for
![]() $1\leqslant i,j\leqslant g$
. Note that
$1\leqslant i,j\leqslant g$
. Note that
![]() $\unicode[STIX]{x1D6FF}_{ij}$
is the Kronecker delta. By making use of (2.10) and (2.11) and the above identities, it can be shown that
$\unicode[STIX]{x1D6FF}_{ij}$
is the Kronecker delta. By making use of (2.10) and (2.11) and the above identities, it can be shown that
where
Since
![]() $\unicode[STIX]{x1D6FE}_{j}^{\prime }=\unicode[STIX]{x2202}\unicode[STIX]{x1D6F4}_{j}$
, we have, by Stokes’s theorem,
$\unicode[STIX]{x1D6FE}_{j}^{\prime }=\unicode[STIX]{x2202}\unicode[STIX]{x1D6F4}_{j}$
, we have, by Stokes’s theorem,
By exactly the same reasoning,
Putting all these results together, we can now write
An alternative route to (2.18) is to consider a result from Blank et al. (Reference Blank, Friedrichs and Grad1957). Based on the consideration of vector identities, they derive a particular formula (see their formula (6.5) on page 65) for the inner product of an irrotational vector
![]() $\boldsymbol{x}$
and a solenoidal vector
$\boldsymbol{x}$
and a solenoidal vector
![]() $\boldsymbol{y}$
,
$\boldsymbol{y}$
,
where the notation for cycles and surfaces is as before and the vector fields are everywhere tangent to the boundary. In our application,
![]() $\boldsymbol{x}=\boldsymbol{A}_{1}-\boldsymbol{A}_{2}$
and
$\boldsymbol{x}=\boldsymbol{A}_{1}-\boldsymbol{A}_{2}$
and
![]() $\boldsymbol{y}=\boldsymbol{B}$
.
$\boldsymbol{y}=\boldsymbol{B}$
.
Returning to (2.18), it is clear that the quantity
is independent of the choice of vector potential. We are, therefore, led to define the gauge-invariant magnetic helicity as
It is clear that for
![]() $g=1$
, equation (2.21) reduces to the Bevir–Gray formula. Also, if
$g=1$
, equation (2.21) reduces to the Bevir–Gray formula. Also, if
![]() $\boldsymbol{B}\bot {\mathcal{H}}$
(zero flux), the helicity reduces to
$\boldsymbol{B}\bot {\mathcal{H}}$
(zero flux), the helicity reduces to
This is also the case for simply connected domains, for which
![]() ${\mathcal{H}}=\{\mathbf{0}\}$
.
${\mathcal{H}}=\{\mathbf{0}\}$
.
2.5 Biot–Savart helicity
As mentioned before, apart from the application of the Bevir–Gray formula in toroidal domains, helicity in multiply connected domains has, generally, taken the form of Biot–Savart helicity,
The Biot–Savart helicity formula resembles that of helicity in simply connected domains, that is to say, the second term on the right-hand side of (2.21) is missing. We will now show that (2.21) and (2.23) are coincident. Following Cantarella et al. (Reference Cantarella, DeTurck and Gluck2001) and Valli (Reference Valli2019), it can be shown that the Biot–Savart operator, defined on
![]() $\unicode[STIX]{x1D6FA}$
, can be extended to
$\unicode[STIX]{x1D6FA}$
, can be extended to
![]() $\mathbb{R}^{3}$
.
$\mathbb{R}^{3}$
.
For
![]() $\boldsymbol{B}\in {\mathcal{V}}$
,
$\boldsymbol{B}\in {\mathcal{V}}$
,
![]() $\text{BS}(\boldsymbol{B})\in {\mathcal{V}}$
. Since
$\text{BS}(\boldsymbol{B})\in {\mathcal{V}}$
. Since
![]() $\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{n}=0$
on
$\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{n}=0$
on
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}$
and
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}$
and
![]() $\text{div}\,\boldsymbol{B}=0$
in
$\text{div}\,\boldsymbol{B}=0$
in
![]() $\unicode[STIX]{x1D6FA}$
, the extended magnetic field
$\unicode[STIX]{x1D6FA}$
, the extended magnetic field
satisfies
![]() $\text{div}\,\widetilde{\boldsymbol{B}}=0$
in
$\text{div}\,\widetilde{\boldsymbol{B}}=0$
in
![]() $\mathbb{R}^{3}$
.
$\mathbb{R}^{3}$
.
Equation (1.4) can be modified to
We know from Cantarella et al. (Reference Cantarella, DeTurck and Gluck2001) that
![]() $\text{curl}\,\text{BS}(\boldsymbol{B})=\widetilde{\boldsymbol{B}}$
and
$\text{curl}\,\text{BS}(\boldsymbol{B})=\widetilde{\boldsymbol{B}}$
and
![]() $\text{div}\,\boldsymbol{B}=0$
in
$\text{div}\,\boldsymbol{B}=0$
in
![]() $\mathbb{R}^{3}$
. Therefore, we can consider line integrals along closed paths and apply Stokes’s theorem.
$\mathbb{R}^{3}$
. Therefore, we can consider line integrals along closed paths and apply Stokes’s theorem.
2.5.1
 $n$
-holed tori
$n$
-holed tori
We know that each
![]() $\unicode[STIX]{x1D6F4}_{j}^{\prime }\subset \unicode[STIX]{x1D6FA}^{\prime }~(j=1,\ldots ,g)$
is a surface bounded by a simple cycle
$\unicode[STIX]{x1D6F4}_{j}^{\prime }\subset \unicode[STIX]{x1D6FA}^{\prime }~(j=1,\ldots ,g)$
is a surface bounded by a simple cycle
![]() $\unicode[STIX]{x1D6FE}_{j}$
(one with a connected boundary). We then have
$\unicode[STIX]{x1D6FE}_{j}$
(one with a connected boundary). We then have
since
![]() $\text{curl}\,\text{BS}(\boldsymbol{B})=\mathbf{0}$
in
$\text{curl}\,\text{BS}(\boldsymbol{B})=\mathbf{0}$
in
![]() $\unicode[STIX]{x1D6FA}^{\prime }$
. Thus, choosing
$\unicode[STIX]{x1D6FA}^{\prime }$
. Thus, choosing
![]() $\boldsymbol{A}=\text{BS}(\boldsymbol{B})$
in (2.21), the helicity reduces to
$\boldsymbol{A}=\text{BS}(\boldsymbol{B})$
in (2.21), the helicity reduces to
Note that (2.27) can also be used for magnetic fields with zero flux, without having to impose this as a condition to ensure gauge invariance.
In above approach to deriving (2.27) we have made the standard construction of extending the Biot–Savart operator to
![]() $\mathbb{R}^{3}$
by assuming that the magnetic field is zero outside the domain. By virtue of (2.27), the magnetic field in the domain can inherit the field line topology interpretation of Moffatt (Reference Moffatt1969) and Arnold & Khesin (Reference Arnold and Khesin1992). For applications where linkage with magnetic field outside the domain is important, see § 2.6 below. First, however, we will investigate how the Biot–Savart operator can be used to understand the linkage of field lines on the surface of the domain with the domain itself.
$\mathbb{R}^{3}$
by assuming that the magnetic field is zero outside the domain. By virtue of (2.27), the magnetic field in the domain can inherit the field line topology interpretation of Moffatt (Reference Moffatt1969) and Arnold & Khesin (Reference Arnold and Khesin1992). For applications where linkage with magnetic field outside the domain is important, see § 2.6 below. First, however, we will investigate how the Biot–Savart operator can be used to understand the linkage of field lines on the surface of the domain with the domain itself.
2.5.2 Field line helicity on a toroidal boundary
Although the second term on the right-hand side of (2.21), related to the domain topology, is zero for Biot–Savart helicity, this does not mean that integrals on the domain boundary are unimportant. For the case of a standard torus
![]() $(g=1)$
, the property in (2.26) can be extended to define the field line helicity (e.g. Berger Reference Berger1988; Yeates & Hornig Reference Yeates and Hornig2013) on the boundary when the path of integration follows a closed field line. Such field lines are possible everywhere on the boundary of a torus as the Euler characteristic of the boundary is zero. A prominent example of such a field line is a torus knot (e.g. Oberti & Ricca Reference Oberti and Ricca2018). For domains with
$(g=1)$
, the property in (2.26) can be extended to define the field line helicity (e.g. Berger Reference Berger1988; Yeates & Hornig Reference Yeates and Hornig2013) on the boundary when the path of integration follows a closed field line. Such field lines are possible everywhere on the boundary of a torus as the Euler characteristic of the boundary is zero. A prominent example of such a field line is a torus knot (e.g. Oberti & Ricca Reference Oberti and Ricca2018). For domains with
![]() $g>1$
, closed field lines on the boundary are possible, but not everywhere on the boundary. This is due to the Euler characteristic being non-zero and, as a consequence of the ‘hairy ball’ theorem (e.g. Frankel Reference Frankel2004), smooth vector fields on the surfaces of these domains must have at least one point where they vanish.
$g>1$
, closed field lines on the boundary are possible, but not everywhere on the boundary. This is due to the Euler characteristic being non-zero and, as a consequence of the ‘hairy ball’ theorem (e.g. Frankel Reference Frankel2004), smooth vector fields on the surfaces of these domains must have at least one point where they vanish.
A closed path
![]() $\unicode[STIX]{x1D6FE}$
on the surface of a torus
$\unicode[STIX]{x1D6FE}$
on the surface of a torus
![]() $\unicode[STIX]{x1D6FA}$
can be expressed in terms of the basis cycles
$\unicode[STIX]{x1D6FA}$
can be expressed in terms of the basis cycles
![]() $\unicode[STIX]{x1D6FE}_{1}$
and
$\unicode[STIX]{x1D6FE}_{1}$
and
![]() $\unicode[STIX]{x1D6FE}_{1}^{\prime }$
as
$\unicode[STIX]{x1D6FE}_{1}^{\prime }$
as
up to bounding cycles on
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}$
, that are homologically trivial. Here
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}$
, that are homologically trivial. Here
![]() $L^{\prime }\in \mathbb{Z}$
is the linking number between
$L^{\prime }\in \mathbb{Z}$
is the linking number between
![]() $\unicode[STIX]{x1D6FE}$
and
$\unicode[STIX]{x1D6FE}$
and
![]() $\unicode[STIX]{x1D6FE}_{1}^{\prime }$
(slightly deformed outside
$\unicode[STIX]{x1D6FE}_{1}^{\prime }$
(slightly deformed outside
![]() $\unicode[STIX]{x1D6FA}$
, in order that there is no intersection with
$\unicode[STIX]{x1D6FA}$
, in order that there is no intersection with
![]() $\unicode[STIX]{x1D6FE}$
); similarly,
$\unicode[STIX]{x1D6FE}$
); similarly,
![]() $L\in \mathbb{Z}$
is the linking number between
$L\in \mathbb{Z}$
is the linking number between
![]() $\unicode[STIX]{x1D6FE}$
and
$\unicode[STIX]{x1D6FE}$
and
![]() $\unicode[STIX]{x1D6FE}_{1}$
(slightly deformed inside
$\unicode[STIX]{x1D6FE}_{1}$
(slightly deformed inside
![]() $\unicode[STIX]{x1D6FA}$
, in order that there is no intersection with
$\unicode[STIX]{x1D6FA}$
, in order that there is no intersection with
![]() $\unicode[STIX]{x1D6FE}$
). Therefore, if
$\unicode[STIX]{x1D6FE}$
). Therefore, if
![]() $\boldsymbol{w}$
is a vector field such that
$\boldsymbol{w}$
is a vector field such that
![]() $\text{curl}\,\boldsymbol{w}\boldsymbol{\cdot }\boldsymbol{n}=0$
on
$\text{curl}\,\boldsymbol{w}\boldsymbol{\cdot }\boldsymbol{n}=0$
on
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}$
and
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}$
and
![]() $\boldsymbol{t}$
is the unit tangent vector on
$\boldsymbol{t}$
is the unit tangent vector on
![]() $\unicode[STIX]{x1D6FE}$
,
$\unicode[STIX]{x1D6FE}$
,
Applying this result to the Biot–Savart vector field
![]() $\text{BS}(\boldsymbol{B})$
, for which (from (2.26)),
$\text{BS}(\boldsymbol{B})$
, for which (from (2.26)),
it follows that
Thus, by Stokes’s theorem,
where
![]() $\unicode[STIX]{x1D6F4}_{1}$
is a cutting surface of
$\unicode[STIX]{x1D6F4}_{1}$
is a cutting surface of
![]() $\unicode[STIX]{x1D6FA}$
with
$\unicode[STIX]{x1D6FA}$
with
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D6F4}_{1}=\unicode[STIX]{x1D6FE}_{1}^{\prime }$
. The value
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6F4}_{1}=\unicode[STIX]{x1D6FE}_{1}^{\prime }$
. The value
![]() $L$
can be interpreted as the number of loops of
$L$
can be interpreted as the number of loops of
![]() $\unicode[STIX]{x1D6FE}$
around the minor cross-section of the torus (say, the ‘linking number’ of the field line with the torus).
$\unicode[STIX]{x1D6FE}$
around the minor cross-section of the torus (say, the ‘linking number’ of the field line with the torus).
It is interesting to note that the field line helicity (the integral on the left-hand side of (2.32)) ‘knows’ about the linkage of the boundary curve with field lines inside the torus, by virtue of (2.25). This result is true for any magnetic field inside the torus, no matter how complex the field line topology. The value of the field line helicity, however, depends simply on the magnetic flux and a purely topological quantity depending only on the curve and the domain. Equation (2.32) is analogous to the voltage formula of a transformer (for a topological perspective on this formula, see Gross & Kotiuga Reference Gross and Kotiuga2004).
2.5.3 Field line helicity on the boundary of a toroidal shell
The Biot–Savart helicity is coincident with the general helicity, equation (2.21), in a toroidal shell by the same procedure as described for
![]() $n$
-tori. The toroidal shell does, however, have some extra physical interpretations related to the cutting surfaces and field line helicities on the boundaries.
$n$
-tori. The toroidal shell does, however, have some extra physical interpretations related to the cutting surfaces and field line helicities on the boundaries.
As described in § 2.1, some care is required in order to identify the
![]() $\unicode[STIX]{x1D6F4}_{j}$
cutting surfaces. Given suitable cutting surfaces, the helicity for a toroidal shell is
$\unicode[STIX]{x1D6F4}_{j}$
cutting surfaces. Given suitable cutting surfaces, the helicity for a toroidal shell is
where the notation is standard. The cutting surface
![]() $\unicode[STIX]{x1D6F4}_{1}$
is that shown in figure 2(b) and
$\unicode[STIX]{x1D6F4}_{1}$
is that shown in figure 2(b) and
![]() $\unicode[STIX]{x1D6F4}_{2}$
is that shown in figure 2(c). Therefore, we can label the fluxes as
$\unicode[STIX]{x1D6F4}_{2}$
is that shown in figure 2(c). Therefore, we can label the fluxes as
where
![]() $\unicode[STIX]{x1D6F9}_{P}$
and
$\unicode[STIX]{x1D6F9}_{P}$
and
![]() $\unicode[STIX]{x1D6F9}_{T}$
are the poloidal and toroidal fluxes respectively. If we select
$\unicode[STIX]{x1D6F9}_{T}$
are the poloidal and toroidal fluxes respectively. If we select
![]() $\boldsymbol{A}=\text{BS}(\boldsymbol{B})$
, then the general helicity formula naturally reduces to the form of (2.27) due to the property in (2.26).
$\boldsymbol{A}=\text{BS}(\boldsymbol{B})$
, then the general helicity formula naturally reduces to the form of (2.27) due to the property in (2.26).
Considering the field line helicity in (2.32), there are now two separate boundaries for a (closed) field line to lie on. For a field line lying on the outer boundary of a toroidal shell, the interpretation is the same as that of a standard torus. That is, a field line twisting around the minor circumference of the torus
![]() $L$
times will have a field line helicity of
$L$
times will have a field line helicity of
![]() $L\unicode[STIX]{x1D6F9}_{T}$
. For a field line on the inner boundary, the path of the line integral can also be deformed into a union of circles around the major and minor circumferences of the toroidal hole. This time, however, due to the property in (2.26), the contribution to the integral from circles around the minor cross-section of the hole is zero. The non-zero contribution comes from the major cross-section, and if a field line on the inner boundary wraps around the major cross-section
$L\unicode[STIX]{x1D6F9}_{T}$
. For a field line on the inner boundary, the path of the line integral can also be deformed into a union of circles around the major and minor circumferences of the toroidal hole. This time, however, due to the property in (2.26), the contribution to the integral from circles around the minor cross-section of the hole is zero. The non-zero contribution comes from the major cross-section, and if a field line on the inner boundary wraps around the major cross-section
![]() $L$
times, its field line helicity is
$L$
times, its field line helicity is
![]() $L\unicode[STIX]{x1D6F9}_{P}$
.
$L\unicode[STIX]{x1D6F9}_{P}$
.
2.6 Mutual helicity
Through the summation term on the right-hand side of (2.21), the domain topology enters explicitly into the helicity formula for multiply connected domains. This term is related to the mutual helicity (Laurence & Avellaneda Reference Laurence and Avellaneda1993; Cantarella Reference Cantarella2000), a quantity that measures the linkage of the magnetic field in two domains,
![]() $\unicode[STIX]{x1D6FA}$
and
$\unicode[STIX]{x1D6FA}$
and
![]() $\unicode[STIX]{x1D6FA}^{\prime }$
, say. Indeed, through (2.21) we can prove a representation formula for the mutual helicity which is equivalent to that obtained by Cantarella (Reference Cantarella2000) for domains
$\unicode[STIX]{x1D6FA}^{\prime }$
, say. Indeed, through (2.21) we can prove a representation formula for the mutual helicity which is equivalent to that obtained by Cantarella (Reference Cantarella2000) for domains
![]() $\unicode[STIX]{x1D6FA}$
,
$\unicode[STIX]{x1D6FA}$
,
![]() $\unicode[STIX]{x1D6FA}^{\prime }\subset \mathbb{R}^{3}$
of arbitrary topology.
$\unicode[STIX]{x1D6FA}^{\prime }\subset \mathbb{R}^{3}$
of arbitrary topology.
With its topological connection to the Gauss linking number (e.g. Moffatt Reference Moffatt1969; Laurence & Avellaneda Reference Laurence and Avellaneda1993), helicity is often written as
where
![]() $U$
is a bounded open set (but not necessarily connected) and
$U$
is a bounded open set (but not necessarily connected) and
![]() $\boldsymbol{B}$
is a magnetic field tangent to
$\boldsymbol{B}$
is a magnetic field tangent to
![]() $\unicode[STIX]{x2202}U$
. If we consider two disjoint bounded domains
$\unicode[STIX]{x2202}U$
. If we consider two disjoint bounded domains
![]() $M$
and
$M$
and
![]() $N$
and we set
$N$
and we set
![]() $U=M\cup N$
and
$U=M\cup N$
and
![]() $\boldsymbol{B}_{M}=\boldsymbol{B}_{|M}$
,
$\boldsymbol{B}_{M}=\boldsymbol{B}_{|M}$
,
![]() $\boldsymbol{B}_{N}=\boldsymbol{B}_{|N}$
, then it is easily checked that
$\boldsymbol{B}_{N}=\boldsymbol{B}_{|N}$
, then it is easily checked that
where
is the mutual helicity. The self-helicities,
![]() $H_{M}(\boldsymbol{B}_{M})$
and
$H_{M}(\boldsymbol{B}_{M})$
and
![]() $H_{N}(\boldsymbol{B}_{N})$
, can be readily expressed by means of the Biot–Savart operator,
$H_{N}(\boldsymbol{B}_{N})$
, can be readily expressed by means of the Biot–Savart operator,
Consider an open cube
![]() $Q$
such that
$Q$
such that
![]() $\overline{M\cup N}\subset Q$
. In this domain, we extend
$\overline{M\cup N}\subset Q$
. In this domain, we extend
![]() $\boldsymbol{B}$
by
$\boldsymbol{B}$
by
![]() $\mathbf{0}$
in
$\mathbf{0}$
in
![]() $Q\setminus \overline{M\cup N}$
. We label this extension
$Q\setminus \overline{M\cup N}$
. We label this extension
![]() $\widehat{\boldsymbol{B}}$
and note that it is divergence-free in
$\widehat{\boldsymbol{B}}$
and note that it is divergence-free in
![]() $Q$
and tangent to
$Q$
and tangent to
![]() $\unicode[STIX]{x2202}Q$
. Further, its helicity in
$\unicode[STIX]{x2202}Q$
. Further, its helicity in
![]() $Q$
coincides with that of
$Q$
coincides with that of
![]() $\boldsymbol{B}$
in
$\boldsymbol{B}$
in
![]() $M\cup N$
,
$M\cup N$
,
Since
![]() $Q$
is simply connected, we can use (2.21) with
$Q$
is simply connected, we can use (2.21) with
![]() $g=0$
to write
$g=0$
to write
where
![]() $\widehat{\boldsymbol{A}}$
is any vector potential of
$\widehat{\boldsymbol{A}}$
is any vector potential of
![]() $\widehat{\boldsymbol{B}}$
in
$\widehat{\boldsymbol{B}}$
in
![]() $Q$
. Since
$Q$
. Since
![]() $\widehat{\boldsymbol{B}}$
is vanishing outside
$\widehat{\boldsymbol{B}}$
is vanishing outside
![]() $M\cup N$
, it follows that
$M\cup N$
, it follows that
Using (2.21) in
![]() $M$
(with genus
$M$
(with genus
![]() $g_{M}$
) and in
$g_{M}$
) and in
![]() $N$
(with genus
$N$
(with genus
![]() $g_{N}$
), we have
$g_{N}$
), we have
and
Using (2.27),
![]() $H_{M}(\boldsymbol{B}_{M})=\unicode[STIX]{x1D6F6}(\boldsymbol{B}_{M})$
and
$H_{M}(\boldsymbol{B}_{M})=\unicode[STIX]{x1D6F6}(\boldsymbol{B}_{M})$
and
![]() $H_{N}(\boldsymbol{B}_{N})=\unicode[STIX]{x1D6F6}(\boldsymbol{B}_{N})$
. Substituting these results into (2.42) and (2.43) and then substituting these into (2.36), the mutual helicity is found to be
$H_{N}(\boldsymbol{B}_{N})=\unicode[STIX]{x1D6F6}(\boldsymbol{B}_{N})$
. Substituting these results into (2.42) and (2.43) and then substituting these into (2.36), the mutual helicity is found to be
 $$\begin{eqnarray}\displaystyle H(\boldsymbol{B}_{M},\boldsymbol{B}_{N}) & = & \displaystyle \frac{1}{2}\left[\mathop{\sum }_{j=1}^{g_{M}}\left(\oint _{\unicode[STIX]{x1D6FE}_{j}^{M}}\widehat{\boldsymbol{A}}_{|M}\boldsymbol{\cdot }\boldsymbol{t}_{j}^{M}\right)\left(\int _{\unicode[STIX]{x1D6F4}_{j}^{M}}\boldsymbol{B}_{M}\boldsymbol{\cdot }\boldsymbol{n}_{j}^{M}\right)\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\mathop{\sum }_{l=1}^{g_{N}}\left(\oint _{\unicode[STIX]{x1D6FE}_{l}^{N}}\widehat{\boldsymbol{A}}_{|N}\boldsymbol{\cdot }\boldsymbol{t}_{l}^{N}\right)\left(\int _{\unicode[STIX]{x1D6F4}_{l}^{N}}\boldsymbol{B}_{N}\boldsymbol{\cdot }\boldsymbol{n}_{l}^{N}\right)\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle H(\boldsymbol{B}_{M},\boldsymbol{B}_{N}) & = & \displaystyle \frac{1}{2}\left[\mathop{\sum }_{j=1}^{g_{M}}\left(\oint _{\unicode[STIX]{x1D6FE}_{j}^{M}}\widehat{\boldsymbol{A}}_{|M}\boldsymbol{\cdot }\boldsymbol{t}_{j}^{M}\right)\left(\int _{\unicode[STIX]{x1D6F4}_{j}^{M}}\boldsymbol{B}_{M}\boldsymbol{\cdot }\boldsymbol{n}_{j}^{M}\right)\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\mathop{\sum }_{l=1}^{g_{N}}\left(\oint _{\unicode[STIX]{x1D6FE}_{l}^{N}}\widehat{\boldsymbol{A}}_{|N}\boldsymbol{\cdot }\boldsymbol{t}_{l}^{N}\right)\left(\int _{\unicode[STIX]{x1D6F4}_{l}^{N}}\boldsymbol{B}_{N}\boldsymbol{\cdot }\boldsymbol{n}_{l}^{N}\right)\right].\end{eqnarray}$$
A careful analysis of the values of the linking numbers between
![]() $\unicode[STIX]{x1D6FE}_{j}^{M}$
and
$\unicode[STIX]{x1D6FE}_{j}^{M}$
and
![]() $\unicode[STIX]{x1D6FE}_{l}^{N}$
would show that this formula is equivalent to that given in Cantarella (Reference Cantarella2000). For simplicity, let us show that this is true in the case of two linked solid tori (Moffatt Reference Moffatt1969; Laurence & Avellaneda Reference Laurence and Avellaneda1993; Cantarella Reference Cantarella2000). We have
$\unicode[STIX]{x1D6FE}_{l}^{N}$
would show that this formula is equivalent to that given in Cantarella (Reference Cantarella2000). For simplicity, let us show that this is true in the case of two linked solid tori (Moffatt Reference Moffatt1969; Laurence & Avellaneda Reference Laurence and Avellaneda1993; Cantarella Reference Cantarella2000). We have
![]() $g_{M}=1$
and
$g_{M}=1$
and
![]() $g_{N}=1$
; the cycle
$g_{N}=1$
; the cycle
![]() $\unicode[STIX]{x1D6FE}_{1}^{M}$
is the boundary of a surface
$\unicode[STIX]{x1D6FE}_{1}^{M}$
is the boundary of a surface
![]() $\unicode[STIX]{x1D6F4}_{M}^{\prime }$
, contained in
$\unicode[STIX]{x1D6F4}_{M}^{\prime }$
, contained in
![]() $Q\setminus \overline{M}$
, and the cycle
$Q\setminus \overline{M}$
, and the cycle
![]() $\unicode[STIX]{x1D6FE}_{1}^{N}$
is the boundary of a surface
$\unicode[STIX]{x1D6FE}_{1}^{N}$
is the boundary of a surface
![]() $\unicode[STIX]{x1D6F4}_{N}^{\prime }$
, contained in
$\unicode[STIX]{x1D6F4}_{N}^{\prime }$
, contained in
![]() $Q\setminus \overline{N}$
. Let us also assume that the unit tangent vector
$Q\setminus \overline{N}$
. Let us also assume that the unit tangent vector
![]() $\boldsymbol{t}_{1}^{M}$
crosses
$\boldsymbol{t}_{1}^{M}$
crosses
![]() $\unicode[STIX]{x1D6F4}_{M}$
, the cross-section of the torus
$\unicode[STIX]{x1D6F4}_{M}$
, the cross-section of the torus
![]() $M$
, consistently with the direction of normal vector
$M$
, consistently with the direction of normal vector
![]() $\boldsymbol{n}_{\unicode[STIX]{x1D6F4}_{M}}$
on it, and similarly for
$\boldsymbol{n}_{\unicode[STIX]{x1D6F4}_{M}}$
on it, and similarly for
![]() $\boldsymbol{t}_{1}^{N}$
and the cross-section of
$\boldsymbol{t}_{1}^{N}$
and the cross-section of
![]() $N$
. In this way the linking number of
$N$
. In this way the linking number of
![]() $M$
and
$M$
and
![]() $N$
has value 1. By Stokes’s theorem,
$N$
has value 1. By Stokes’s theorem,
Since
![]() $\widehat{\boldsymbol{B}}=\mathbf{0}$
outside
$\widehat{\boldsymbol{B}}=\mathbf{0}$
outside
![]() $M\cup N$
, it follows that
$M\cup N$
, it follows that
Similarly,
and we obtain
3 Summary
In this paper we have unified the main approaches to calculating magnetic helicity in multiply connected domains. The correct approach for determining a gauge-invariant helicity is to consider the full Helmholtz decomposition, rather than the standard gauge transformation suitable for simply connected domains. We derive a gauge-invariant expression for helicity that generalizes the Bevir–Gray formula for a torus and is suitable for any connected, bounded domain in
![]() $\mathbb{R}^{3}$
, no matter how complicated the topology.
$\mathbb{R}^{3}$
, no matter how complicated the topology.
The discovery of magnetic helicity as a topological quantity was originally made by examining Biot–Savart helicity (Moffatt Reference Moffatt1969). We show that the general helicity formula, which holds for any vector potential, can naturally reduce to Biot–Savart helicity. The line integrals of the Biot–Savart operator on closed paths on the domain boundary can be interpreted as field line helicities, and these arise naturally from the general formula (2.21). The general form for mutual helicity is also shown to follow directly from (2.21).
In several works, a gauge-invariant helicity is found by imposing the constraint of zero flux outside the domain in question; see, for example, Chui & Moffatt (Reference Chui and Moffatt1995) for knotted domains and Taylor & Newton (Reference Taylor and Newton2015), Hussain, Browning & Hood (Reference Hussain, Browning and Hood2017) for periodic toroidal domains. The helicities in these works are coincident with Biot–Savart helicity by virtue of the property in (2.26).
What is clear from the general helicity formula is that the topology of the domain must be taken into account for a correct interpretation of quantities in the domain. Multiply connected domains are widely used in the context of MHD simulations. For example, a cube with two identified boundaries is equivalent to a torus topologically. Similarly, a cube with two pairs of identified boundaries is equivalent to a toroidal shell topologically. If, in such periodic domains, the magnetic field is tangent to the non-periodic boundaries, then the helicity can be interpreted in terms of (2.21) and, by extension, the Biot–Savart helicity (2.23). Care must be taken, however, when interpreting helicity (and other quantities) for evolving magnetic fields in periodic domains. For example, Berger (Reference Berger1997) discusses how periodic domains lead to strange results, such as magnetic flux ropes turning themselves inside out through magnetic reconnection. The issue here is one of mathematical modelling. That is, if a periodic domain is used to model a magnetic field in a simply connected domain, then there may be some unwanted effects due to the topology of the domain. For the (2D) flux tube example in Berger (Reference Berger1997, Figure 3), the behaviour shown makes perfect sense when considering the topology of the domain, the surface of a torus in this case. The behaviour, however, is physically unrealistic for a simply connected domain.
Another periodic domain that is popular in MHD simulations is the triply periodic cube. This domain, however, cannot be embedded in
![]() $\mathbb{R}^{3}$
and (2.21) does not apply in this case. Although it is possible to develop topological invariants in this domain (e.g. DeTurck et al.
Reference DeTurck, Gluck, Komendarczyk, Melvin, Shonkwiler and Vela-Vick2013), the physical significance of these quantities remains to investigated in depth.
$\mathbb{R}^{3}$
and (2.21) does not apply in this case. Although it is possible to develop topological invariants in this domain (e.g. DeTurck et al.
Reference DeTurck, Gluck, Komendarczyk, Melvin, Shonkwiler and Vela-Vick2013), the physical significance of these quantities remains to investigated in depth.