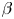1. Introduction
The quest for controlled thermonuclear fusion has seen renewed interest over the last decade. This has led to a revival of concepts other than the tokamak. The latter relies on toroidal magnetic fields with a spatial toroidal symmetry to confine a hot plasma within (Mukhovatov & Shafranov Reference Mukhovatov and Shafranov1971; Wesson Reference Wesson2011). It is useful to consider devices in which this symmetry requirement is relaxed, i.e. stellarators (Spitzer Reference Spitzer1958; Boozer Reference Boozer1998; Helander Reference Helander2014). The three-dimensional nature of stellarators provides them with a freedom necessary to avoid many limiting features of axisymmetric magnetic fields. Most importantly, large currents are no longer needed to hold the plasma, thus minimising the possibility of violent disruptions (Schuller Reference Schuller1995).
Finding attractive forms of stellarators that serve as magnetic confinement devices requires a dedicated effort. At the most basic level, the fields must be capable of confining collisionless charged particles for long enough (Mynick Reference Mynick2006). This requirement significantly restricts the space of stellarators, singling out a particular class of fields labelled omnigeneous (Hall & McNamara Reference Hall and McNamara1975; Bernardin, Moses & Tataronis Reference Bernardin, Moses and Tataronis1986; Cary & Shasharina Reference Cary and Shasharina1997; Landreman & Catto Reference Landreman and Catto2012; Helander Reference Helander2014). In this paper, we consider a particular group of omnigeneous stellarators, a most immediate generalisation of axisymmetry, known as quasisymmetric stellarators (Boozer Reference Boozer1983; Nührenberg & Zille Reference Nührenberg and Zille1988b; Burby, Kallinikos & MacKay Reference Burby, Kallinikos and MacKay2020; Rodríguez, Helander & Bhattacharjee Reference Rodríguez, Helander and Bhattacharjee2020). The defining property of this class is a particular form of hidden symmetry, which makes the magnitude of the magnetic field, ![]() $|\boldsymbol {B}|$, symmetric, but not necessarily
$|\boldsymbol {B}|$, symmetric, but not necessarily ![]() $\boldsymbol {B}$. By Noether's theorem, such partial symmetry is sufficient to prevent rapid loss of particles in the small-gyroradius limit.
$\boldsymbol {B}$. By Noether's theorem, such partial symmetry is sufficient to prevent rapid loss of particles in the small-gyroradius limit.
Confinement of single particles is not the only property desired of the stellarator: plasma stability, coil complexity, turbulent transport, etc., are also aspects of importance. This list of properties, alongside advances in computation, have naturally led to optimisation as the primary approach to the design of stellarators. This approach has proven to yield practical results (Beidler et al. Reference Beidler, Grieger, Herrnegger, Harmeyer, Kisslinger, Lotz, Maassberg, Merkel, Nührenberg and Rau1990; Anderson et al. Reference Anderson, Almagri, Anderson, Matthews, Talmadge and Shohet1995; Zarnstorff et al. Reference Zarnstorff2001; Garabedian Reference Garabedian2008; Najmabadi et al. Reference Najmabadi, Raffray, Abdel-Khalik, Bromberg, Crosatti, El-Guebaly, Garabedian, Grossman, Henderson and Ibrahim2008). However, it is not entirely satisfactory. The complexity of optimisation is prohibitive when attempting to comprehend the origin of the obtained designs (Rodríguez, Paul & Bhattacharjee Reference Rodríguez, Paul and Bhattacharjee2022a). This is partly a result of the space of optimisation having many local minima (Bader et al. Reference Bader, Drevlak, Anderson, Faber, Hegna, Likin, Schmitt and Talmadge2019; Henneberg, Helander & Drevlak Reference Henneberg, Helander and Drevlak2021). Some fundamental insight is necessary to interpret results and guide optimisation in such a space.
Understanding the relation between the properties imposed on stellarators is crucial. If two properties require similar or opposite magnetic field features, we should know it and perform optimisation accordingly. Intuition on these property trade-offs has developed over years of optimisation efforts. It is, for instance, believed that bean shapes (i.e. sizeable positive triangularity) favour magnetohydrodynamic (MHD) stability. This general wisdom accrued over years of stellarator optimisation (Nührenberg Reference Nührenberg2010) which regularly found these features, as well as more dedicated works (Lortz & Nührenberg Reference Lortz and Nührenberg1976; Nührenberg & Zille Reference Nührenberg and Zille1986). We put this observation to the test in this paper for axisymmetric and quasisymmetric stellarators.
To explore the question, we use two main ingredients. First, as a measure of MHD stability, we employ the Mercier criterion. We present the basics of this measure in § 2, together with the main theoretical framework for the paper: the near-axis expansion in inverse coordinates. The latter provides a simplifying description of the geometry and governing equations asymptotically in the distance from the centre of the stellarator. This framework becomes an ideal basis for analysing the problem. Section 3 considers the case of axisymmetry, which is often taken as reference to develop intuition on property trade-offs. We show that there is indeed a positive link between positive triangularity and stability in this scenario, reproducing the results of existing literature. That enables us to treat the case of quasisymmetric stellarators in § 4 analogously. Conventional shaping-stability intuition generally fails there, with negative triangularity being stabilising in practical examples. We close with some concluding remarks.
2. Mercier criterion and near-axis framework
For the purpose of this paper we consider static equilibria with isotropic pressure (Wesson Reference Wesson2011; Freidberg Reference Freidberg2014), in which magnetic field lines live on nested toroidal magnetic flux surfaces (Grad Reference Grad1967; Helander Reference Helander2014), labelled by the variable ![]() $\psi$ (
$\psi$ (![]() $1/2{\rm \pi}$ the toroidal magnetic flux). Given such an equilibrium, we are interested in knowing whether it is MHD-unstable or not. Although stellarators have proven certain nonlinear resilience to instability, an unstable configuration still represents a physically unattainable configuration. Knowing this is important at least to understand if the stellarator properties carefully designed will reliably hold or not.
$1/2{\rm \pi}$ the toroidal magnetic flux). Given such an equilibrium, we are interested in knowing whether it is MHD-unstable or not. Although stellarators have proven certain nonlinear resilience to instability, an unstable configuration still represents a physically unattainable configuration. Knowing this is important at least to understand if the stellarator properties carefully designed will reliably hold or not.
There is not a single way to study MHD stability. In this paper we turn to two scalar criteria for instability: the magnetic well, ![]() $V''>0$ (Greene Reference Greene1997), and the Mercier criterion,
$V''>0$ (Greene Reference Greene1997), and the Mercier criterion, ![]() $D_{\rm Merc}<0$ (Greene & Johnson Reference Greene and Johnson1962; Mercier Reference Mercier1962, Reference Mercier1974; Bauer, Betancourt & Garabedian Reference Bauer, Betancourt and Garabedian2012; Freidberg Reference Freidberg2014). The latter is a sufficient condition for the occurrence of an interchange instability, namely an instability that displaces the plasma without significantly bending field lines. A configuration is necessarily unstable if
$D_{\rm Merc}<0$ (Greene & Johnson Reference Greene and Johnson1962; Mercier Reference Mercier1962, Reference Mercier1974; Bauer, Betancourt & Garabedian Reference Bauer, Betancourt and Garabedian2012; Freidberg Reference Freidberg2014). The latter is a sufficient condition for the occurrence of an interchange instability, namely an instability that displaces the plasma without significantly bending field lines. A configuration is necessarily unstable if ![]() $D_{\rm Merc}<0$ (but
$D_{\rm Merc}<0$ (but ![]() $D_{\rm Merc}>0$ does not guarantee stability, as it does not negate ballooning instability; Connor, Hastie & Taylor Reference Connor, Hastie and Taylor1978; Correa-Restrepo Reference Correa-Restrepo1978; Dewar & Glasser Reference Dewar and Glasser1983; Nührenberg & Zille Reference Nührenberg and Zille1988a; Freidberg Reference Freidberg2014). The scalar
$D_{\rm Merc}>0$ does not guarantee stability, as it does not negate ballooning instability; Connor, Hastie & Taylor Reference Connor, Hastie and Taylor1978; Correa-Restrepo Reference Correa-Restrepo1978; Dewar & Glasser Reference Dewar and Glasser1983; Nührenberg & Zille Reference Nührenberg and Zille1988a; Freidberg Reference Freidberg2014). The scalar ![]() $D_{\rm Merc}$ involves multiple integrals over the fields and geometry of the configuration and can be found in the literature (Greene & Johnson Reference Greene and Johnson1962; Correa-Restrepo Reference Correa-Restrepo1978; Nührenberg & Zille Reference Nührenberg and Zille1988a; Bauer et al. Reference Bauer, Betancourt and Garabedian2012; Zocco, Aleynikova & Xanthopoulos Reference Zocco, Aleynikova and Xanthopoulos2018) (we include it in Appendix A for completeness). The magnetic well criterion (Greene Reference Greene1997) is nothing but the small-plasma-
$D_{\rm Merc}$ involves multiple integrals over the fields and geometry of the configuration and can be found in the literature (Greene & Johnson Reference Greene and Johnson1962; Correa-Restrepo Reference Correa-Restrepo1978; Nührenberg & Zille Reference Nührenberg and Zille1988a; Bauer et al. Reference Bauer, Betancourt and Garabedian2012; Zocco, Aleynikova & Xanthopoulos Reference Zocco, Aleynikova and Xanthopoulos2018) (we include it in Appendix A for completeness). The magnetic well criterion (Greene Reference Greene1997) is nothing but the small-plasma-![]() $\beta$, zero-magnetic-shear limit of the Mercier criterion. The complexity of both expressions in these stability criteria naturally requires a simplified framework in which to understand their underlying structure and relation to field properties.
$\beta$, zero-magnetic-shear limit of the Mercier criterion. The complexity of both expressions in these stability criteria naturally requires a simplified framework in which to understand their underlying structure and relation to field properties.
We adopt for that purpose the so-called near-axis framework, pioneered by Mercier (Reference Mercier1962) and Solov'ev & Shafranov (Reference Solov'ev and Shafranov1970), in which the stellarator is considered asymptotically near its magnetic axis, where the stellarator is particularly simple. This way of approaching the problem has seen a recent revival for theoretical and practical stellarator design (Garren & Boozer Reference Garren and Boozer1991b; Landreman & Sengupta Reference Landreman and Sengupta2019; Jorge, Sengupta & Landreman Reference Jorge, Sengupta and Landreman2020; Landreman Reference Landreman2022; Rodríguez, Sengupta & Bhattacharjee Reference Rodríguez, Sengupta and Bhattacharjee2022b). In its original form, often referred to as the direct-coordinate approach, one expands all the equations governing the magnetic field in the distance from the axis involving the shape of flux surfaces directly. That way, shaping and stability were related, through the Mercier criterion, by the works of Solov'ev & Shafranov (Reference Solov'ev and Shafranov1970), Lortz & Nührenberg (Reference Lortz and Nührenberg1976), Mikhailovskii & Aburdzhaniya (Reference Mikhailovskii and Aburdzhaniya1979), Shafranov (Reference Shafranov1983) and Freidberg (Reference Freidberg2014), and most recently of Jorge & Landreman (Reference Jorge and Landreman2020) and Kim, Jorge & Dorland (Reference Kim, Jorge and Dorland2021). The emphasis on the geometry of the stellarator in this asymptotic description does not, however, lend itself straightforwardly to describing stability and guiding centre dynamics. The latter naturally involves ![]() $|\boldsymbol {B}|$, which is a quantity not readily accessible in this framework. In particular, this complication makes the description of optimised stellarators, such as omnigeneous (Hall & McNamara Reference Hall and McNamara1975; Bernardin et al. Reference Bernardin, Moses and Tataronis1986; Cary & Shasharina Reference Cary and Shasharina1997; Landreman & Catto Reference Landreman and Catto2012) or quasisymmetric (Boozer Reference Boozer1983; Nührenberg & Zille Reference Nührenberg and Zille1988b; Rodríguez et al. Reference Rodríguez, Helander and Bhattacharjee2020) ones, challenging.
$|\boldsymbol {B}|$, which is a quantity not readily accessible in this framework. In particular, this complication makes the description of optimised stellarators, such as omnigeneous (Hall & McNamara Reference Hall and McNamara1975; Bernardin et al. Reference Bernardin, Moses and Tataronis1986; Cary & Shasharina Reference Cary and Shasharina1997; Landreman & Catto Reference Landreman and Catto2012) or quasisymmetric (Boozer Reference Boozer1983; Nührenberg & Zille Reference Nührenberg and Zille1988b; Rodríguez et al. Reference Rodríguez, Helander and Bhattacharjee2020) ones, challenging.
To bypass these limitations and describe axisymmetric and quasisymmetric stellarators in this paper, we adopt the inverse-coordinate near-axis expansion (Garren & Boozer Reference Garren and Boozer1991b; Landreman & Sengupta Reference Landreman and Sengupta2018, Reference Landreman and Sengupta2019). Its main difference from the direct-coordinate approach is that it involves ![]() $|\boldsymbol {B}|$ explicitly in the problem, rather than the geometry of flux surfaces. It does so by treating Boozer coordinates (Boozer Reference Boozer1981)
$|\boldsymbol {B}|$ explicitly in the problem, rather than the geometry of flux surfaces. It does so by treating Boozer coordinates (Boozer Reference Boozer1981) ![]() $\{\psi,\theta,\phi \}$ as an independent set, enabling the use of
$\{\psi,\theta,\phi \}$ as an independent set, enabling the use of ![]() $\epsilon =\sqrt {2\psi /\bar {B}_0}$ (a pseudo-radial coordinate) as an expansion parameter. Here
$\epsilon =\sqrt {2\psi /\bar {B}_0}$ (a pseudo-radial coordinate) as an expansion parameter. Here ![]() $\bar {B}_0$ is the average magnetic field magnitude along the magnetic axis and
$\bar {B}_0$ is the average magnetic field magnitude along the magnetic axis and ![]() $\psi =0$ on it. In terms of this
$\psi =0$ on it. In terms of this ![]() $\epsilon$, in the near-axis expansion all fields are expanded in power series of the form
$\epsilon$, in the near-axis expansion all fields are expanded in power series of the form
 \begin{equation} f(\psi,\theta,\phi)=\sum_{n=0}^\infty\epsilon^n\sum_m^n{}' [f_{nm}^c(\phi)\cos m\theta+f_{nm}^s(\phi)\sin m\theta], \end{equation}
\begin{equation} f(\psi,\theta,\phi)=\sum_{n=0}^\infty\epsilon^n\sum_m^n{}' [f_{nm}^c(\phi)\cos m\theta+f_{nm}^s(\phi)\sin m\theta], \end{equation}
where the sum ![]() $\sum '$ is over even or odd positive numbers (including 0) up to
$\sum '$ is over even or odd positive numbers (including 0) up to ![]() $n$ depending on the parity of
$n$ depending on the parity of ![]() $n$ (Garren & Boozer Reference Garren and Boozer1991b). As the paper focuses on axisymmetric and quasisymmetric configurations, the magnetic field magnitude has expansion parameters independent of the toroidal angle:
$n$ (Garren & Boozer Reference Garren and Boozer1991b). As the paper focuses on axisymmetric and quasisymmetric configurations, the magnetic field magnitude has expansion parameters independent of the toroidal angle:
Here the helical angle ![]() $\chi =\theta -N\phi$ takes the place of
$\chi =\theta -N\phi$ takes the place of ![]() $\theta$, where
$\theta$, where ![]() $N\in \mathbb {N}$ is the self-linking number of the magnetic axis (Rodríguez et al. Reference Rodríguez, Sengupta and Bhattacharjee2022b). This form allows us to include quasihelical configurations in the formalism (quasisymmetric stellarators in which the contours of
$N\in \mathbb {N}$ is the self-linking number of the magnetic axis (Rodríguez et al. Reference Rodríguez, Sengupta and Bhattacharjee2022b). This form allows us to include quasihelical configurations in the formalism (quasisymmetric stellarators in which the contours of ![]() $|\boldsymbol {B}|$ close helically for
$|\boldsymbol {B}|$ close helically for ![]() $N\neq 0$).
$N\neq 0$).
Using the inverse-coordinate approach relegates the shaping of magnetic flux surfaces to a secondary role. Flux surfaces are nevertheless described around the magnetic axis, using the Frenet–Serret vectors of the axis (see Landreman & Sengupta Reference Landreman and Sengupta2019) as a basis, as
for all ![]() $\chi$ and
$\chi$ and ![]() $\phi$ (at constant
$\phi$ (at constant ![]() $\psi$), where
$\psi$), where ![]() $\boldsymbol {r}_0$ represents the magnetic axis,
$\boldsymbol {r}_0$ represents the magnetic axis, ![]() $\hat {\kappa }$ is the normal to the curve,
$\hat {\kappa }$ is the normal to the curve, ![]() $\hat {\tau }$ the binormal and
$\hat {\tau }$ the binormal and ![]() $\hat {\boldsymbol {b}}$ its tangent. In any plane normal to the axis (and disregarding the function
$\hat {\boldsymbol {b}}$ its tangent. In any plane normal to the axis (and disregarding the function ![]() $Z$),
$Z$), ![]() $X$ and
$X$ and ![]() $Y$ describe the shape of the cross-sections. Our task in this paper is then to interpret the shaping through
$Y$ describe the shape of the cross-sections. Our task in this paper is then to interpret the shaping through ![]() $X$,
$X$, ![]() $Y$ and
$Y$ and ![]() $Z$, and relate it to the Mercier criterion.
$Z$, and relate it to the Mercier criterion.
Details of the near-axis expansion in the so-called inverse-coordinate approach may be found in the original paper by Garren & Boozer (Reference Garren and Boozer1991b), or later applications and extensions (Landreman & Sengupta Reference Landreman and Sengupta2018, Reference Landreman and Sengupta2019; Rodríguez & Bhattacharjee Reference Rodríguez and Bhattacharjee2021a). Here we do not rederive these results but rather apply them; the reader may refer to these if necessary. The magnetic well on axis (Landreman & Jorge Reference Landreman and Jorge2020) is
where the pressure gradient (to leading order) is given by ![]() $p_2$ (from
$p_2$ (from ![]() $p=p_0+\epsilon ^2 p_2+\cdots$, which includes for simplicity a factor of
$p=p_0+\epsilon ^2 p_2+\cdots$, which includes for simplicity a factor of ![]() $\mu _0$) and
$\mu _0$) and ![]() $G_0$ is the poloidal current linked to the torus. As we have hinted, the expression is simple and involves
$G_0$ is the poloidal current linked to the torus. As we have hinted, the expression is simple and involves ![]() $|\boldsymbol {B}|$ quite directly. Here the parameter
$|\boldsymbol {B}|$ quite directly. Here the parameter ![]() $B_{20}$ may be interpreted as a measure of the depth of the magnetic well (Freidberg Reference Freidberg2014).
$B_{20}$ may be interpreted as a measure of the depth of the magnetic well (Freidberg Reference Freidberg2014).
The pressure gradient in (2.4) is somewhat deceptive. We remind ourselves that using ![]() $V''$ as a criterion is sensible only in the vacuum limit of the Mercier criterion. Thus, for a finite-
$V''$ as a criterion is sensible only in the vacuum limit of the Mercier criterion. Thus, for a finite-![]() $\beta$ equilibrium, the Mercier criterion reads, following Landreman & Jorge (Reference Landreman and Jorge2020) and taking
$\beta$ equilibrium, the Mercier criterion reads, following Landreman & Jorge (Reference Landreman and Jorge2020) and taking ![]() $B_0=1$ for simplicity,
$B_0=1$ for simplicity,
where
![]() $\kappa$ is the curvature of the magnetic axis (a function of the toroidal angle
$\kappa$ is the curvature of the magnetic axis (a function of the toroidal angle ![]() $\phi$),
$\phi$), ![]() $\sigma =Y_{11}^c/Y_{11}^s$ (see the notation of (2.1)) is related to the shaping of flux surfaces and
$\sigma =Y_{11}^c/Y_{11}^s$ (see the notation of (2.1)) is related to the shaping of flux surfaces and ![]() $\bar {\iota }_0$ is the rotational transform on axis (in the quasihelical, case
$\bar {\iota }_0$ is the rotational transform on axis (in the quasihelical, case ![]() $\iota _0-N$). The structure of the leading-order Mercier criterion is, up to the dependence on the pressure gradient, of the same form as the magnetic well, depending critically on
$\iota _0-N$). The structure of the leading-order Mercier criterion is, up to the dependence on the pressure gradient, of the same form as the magnetic well, depending critically on ![]() $B_{20}$.
$B_{20}$.
3. Case of axisymmetry
In the previous section we presented the Mercier criterion in its near-axis form following Landreman & Jorge (Reference Landreman and Jorge2020). Our goal now is to interpret (2.5) meaningfully in terms of the shaping of cross-sections. To do so, we must consider two essential points. First, we must know which choice of parameters within the near-axis description serves as a minimal, consistent parametrisation of our near-axis equilibrium. In this section, we focus on these choices for axisymmetry, leaving quasisymmetry for the next section. Second, given such a set, we need to connect them within the near-axis expansion to the most common notions of cross-section shapes such as triangularity. Once this has been achieved, we will be in a position to discuss MHD stability and its relation to the shape of the plasma cross-sections.
3.1. Parametrisation of configurations
Let us describe axisymmetric configurations uniquely within the near-axis framework. We present the most conventional choice of parameters, which we must, however, point out is not unique.
The shape of the magnetic axis is the primary ingredient in the expansion, but in the case of axisymmetry it must be a circle. We normalise its radius to ![]() $R_0=1$, as we do with the magnetic field on axis,
$R_0=1$, as we do with the magnetic field on axis, ![]() $B_0=1$, leading by Ampère's law to a poloidal current
$B_0=1$, leading by Ampère's law to a poloidal current ![]() $G_0=1$. At first order, the parameters
$G_0=1$. At first order, the parameters ![]() $\eta$ (leading-order
$\eta$ (leading-order ![]() $|\boldsymbol {B}|$ mirror ratio; see (2.2)) and
$|\boldsymbol {B}|$ mirror ratio; see (2.2)) and ![]() $\sigma$ (measure of the up–down asymmetry) describe rather explicitly elliptical flux surfaces (as we will later see). The choice of the toroidal current density on axis,
$\sigma$ (measure of the up–down asymmetry) describe rather explicitly elliptical flux surfaces (as we will later see). The choice of the toroidal current density on axis, ![]() $I_2$, then provides a finite rotational transform on axis.
$I_2$, then provides a finite rotational transform on axis.
Finally, at second order, four parameters are necessary: the pressure gradient, ![]() $p_2$, and the second-order harmonics of
$p_2$, and the second-order harmonics of ![]() $|\boldsymbol {B}|$,
$|\boldsymbol {B}|$, ![]() $B_{20}$,
$B_{20}$, ![]() $B_{22}^C$ and
$B_{22}^C$ and ![]() $B_{22}^S$. Not all choices of these natural parameters constitute valid equilibria, though. The force balance condition imposes a linear constraint, (E6), making only three of them truly independent. Different choices of independent parameters are suitable for studying different equilibrium properties. In our case, we must find the combination of natural parameters
$B_{22}^S$. Not all choices of these natural parameters constitute valid equilibria, though. The force balance condition imposes a linear constraint, (E6), making only three of them truly independent. Different choices of independent parameters are suitable for studying different equilibrium properties. In our case, we must find the combination of natural parameters ![]() $p_2$ and
$p_2$ and ![]() $|\boldsymbol {B}|$ harmonics that directly relates to the shaping of cross-sections, so that we may use them as the independent set. That is the next task. One may ask why the direct-coordinate near-axis approach was chosen if the geometry was wanted explicitly. The answer is that we want to have the capacity to constrain
$|\boldsymbol {B}|$ harmonics that directly relates to the shaping of cross-sections, so that we may use them as the independent set. That is the next task. One may ask why the direct-coordinate near-axis approach was chosen if the geometry was wanted explicitly. The answer is that we want to have the capacity to constrain ![]() $|\boldsymbol {B}|$ directly and simply, and, within these constraints, see how the geometry arises.
$|\boldsymbol {B}|$ directly and simply, and, within these constraints, see how the geometry arises.
3.2. Shapes within the inverse-coordinate near-axis framework
We must thus construct geometric notions for the cross-sections within the near-axis framework. These include concepts such as ellipticity, triangularity and up–down symmetry breaking. Although the description in this section is concerned with axisymmetry, the description of shaping presented generalises straightforwardly to the quasisymmetric case.
3.2.1. First-order shaping: ellipticity
As is well known, near the magnetic axis, flux surfaces have elliptic cross-sections. In the near-axis expansion these are described at first order in the expansion in terms of the parameters ![]() $\eta$ and
$\eta$ and ![]() $\sigma$. The shapes in the plane normal to the axis (in our tokamak, slices at constant cylindrical angle) are described as
$\sigma$. The shapes in the plane normal to the axis (in our tokamak, slices at constant cylindrical angle) are described as
where ![]() $\hat {R}$ is the unit vector in the major radius direction,
$\hat {R}$ is the unit vector in the major radius direction, ![]() $\hat {z}$ is the unit vector in the vertical cylindrical direction,
$\hat {z}$ is the unit vector in the vertical cylindrical direction, ![]() $X_{11}^c=\eta$ and
$X_{11}^c=\eta$ and ![]() $Y_{11}^s=1/\eta$ (Landreman & Sengupta Reference Landreman and Sengupta2019). In terms of the elongation (defined as the ratio of the major to the minor radius of the ellipse,
$Y_{11}^s=1/\eta$ (Landreman & Sengupta Reference Landreman and Sengupta2019). In terms of the elongation (defined as the ratio of the major to the minor radius of the ellipse, ![]() $\mathcal {E}$) and the rotation angle
$\mathcal {E}$) and the rotation angle ![]() $\vartheta$ with respect to
$\vartheta$ with respect to ![]() $\hat {\kappa }$, and defining the angle
$\hat {\kappa }$, and defining the angle ![]() $\mathcal {E}=\tan e$ (see figure 1),
$\mathcal {E}=\tan e$ (see figure 1),
For the details of how one arrives at (3.2), see Appendix B. From the above, it is clear that ![]() $\sigma$ rotates the ellipse with respect to the
$\sigma$ rotates the ellipse with respect to the ![]() $(\hat {\kappa },\hat {\tau })$Frenet–Serret frame, in the small-
$(\hat {\kappa },\hat {\tau })$Frenet–Serret frame, in the small-![]() $\sigma$ limit linearly, and thus is a measure of up–down asymmetry. However, it also affects elongation through the denominator in (3.2a). Only in the limit of
$\sigma$ limit linearly, and thus is a measure of up–down asymmetry. However, it also affects elongation through the denominator in (3.2a). Only in the limit of ![]() $\sigma =0$, for which
$\sigma =0$, for which ![]() $\vartheta =0, {\rm \pi}/2$,
$\vartheta =0, {\rm \pi}/2$, ![]() $\mathcal {E}=\eta ^2, 1/\eta ^2$ respectively, and elongation just depends on
$\mathcal {E}=\eta ^2, 1/\eta ^2$ respectively, and elongation just depends on ![]() $\eta$. This limit allows us to interpret
$\eta$. This limit allows us to interpret ![]() $\eta$ as a measure (approximate) of elongation, rigorously true in the up–down symmetric limit.
$\eta$ as a measure (approximate) of elongation, rigorously true in the up–down symmetric limit.

Figure 1. Elliptical shapes and angles. Diagram showing an ellipse framed in the normal Frenet–Serret frame where the ellipse rotation angle ![]() $\vartheta$ and elongation angle
$\vartheta$ and elongation angle ![]() $e$ are defined. These two angles uniquely characterise ellipses (up to a scale).
$e$ are defined. These two angles uniquely characterise ellipses (up to a scale).
In an up–down asymmetric scenario, the distortion of ![]() $\eta$ as a measure of elongation makes
$\eta$ as a measure of elongation makes ![]() $\vartheta$ and
$\vartheta$ and ![]() $e$ become the natural shaping parameters. Expressing the near-axis expansion in terms of these parameters yields, however, highly complicated and nonlinear expressions that necessarily require numerical tools to handle. Thus, we use
$e$ become the natural shaping parameters. Expressing the near-axis expansion in terms of these parameters yields, however, highly complicated and nonlinear expressions that necessarily require numerical tools to handle. Thus, we use ![]() $\eta$ and
$\eta$ and ![]() $\sigma$ as our parameters, capitalising on their approximate geometric meaning for interpretation.
$\sigma$ as our parameters, capitalising on their approximate geometric meaning for interpretation.
3.2.2. Second-order shaping: triangularity
In increasing order of complexity, the next family of shapes after ellipses is triangularity. Figure 2 shows cross-sections with non-zero triangularity, formally arising at second order in the near-axis expansion through ![]() $X_2=X_{20}+X_{22}^C\cos 2\chi +X_{22}^S\sin 2\chi$, and equivalently for
$X_2=X_{20}+X_{22}^C\cos 2\chi +X_{22}^S\sin 2\chi$, and equivalently for ![]() $Y_2$. Before constructing a quantitative measure of triangularity, let us first familiarise ourselves with each of these shaping coefficients at second order considering a frame-aligned ellipse at first order.
$Y_2$. Before constructing a quantitative measure of triangularity, let us first familiarise ourselves with each of these shaping coefficients at second order considering a frame-aligned ellipse at first order.

Figure 2. Examples of triangular cross-sections. The diagram shows two examples of triangular cross-sections (in black), constructed with second-order shaping with ![]() $X_{22}^C<0$ (left) and
$X_{22}^C<0$ (left) and ![]() $Y_{22}^S>0$ (right), for the same underlying elliptical shape. The stellarator literature refers to these shapes as bean and D shapes (often clearer for less elongated cross-sections), respectively. The grey contour shows how excessive shaping can lead to a pathological cross-section in which the surface self-intersects.
$Y_{22}^S>0$ (right), for the same underlying elliptical shape. The stellarator literature refers to these shapes as bean and D shapes (often clearer for less elongated cross-sections), respectively. The grey contour shows how excessive shaping can lead to a pathological cross-section in which the surface self-intersects.
Take first the ![]() $X_{22}^C\cos 2\chi$ term (see the leftmost cross-section in figure 2). The magnitude of
$X_{22}^C\cos 2\chi$ term (see the leftmost cross-section in figure 2). The magnitude of ![]() $X_{22}^C$ gives the ‘bean shape’ of the cross-section, becoming ever ‘more triangular’ as its magnitude is increased, eventually developing a characteristic dimple or indentation. Geometrically, the indentation of the bean shape appears (see figure 2) upon crossing the threshold
$X_{22}^C$ gives the ‘bean shape’ of the cross-section, becoming ever ‘more triangular’ as its magnitude is increased, eventually developing a characteristic dimple or indentation. Geometrically, the indentation of the bean shape appears (see figure 2) upon crossing the threshold ![]() $\epsilon X_{22}^C/X_{11}^C\geq 1/4$.Footnote 1 The strength of the shaping is thus measured by
$\epsilon X_{22}^C/X_{11}^C\geq 1/4$.Footnote 1 The strength of the shaping is thus measured by ![]() $\epsilon X_{22}^C/X_{11}^C$, and increases away from the axis.
$\epsilon X_{22}^C/X_{11}^C$, and increases away from the axis.
The meaning of ![]() $Y_{22}^S$ is not dissimilar and is also related to what is commonly perceived as triangularity. However, it manifests as a more D-looking shape (see the rightmost plot in figure 2). As
$Y_{22}^S$ is not dissimilar and is also related to what is commonly perceived as triangularity. However, it manifests as a more D-looking shape (see the rightmost plot in figure 2). As ![]() $\epsilon Y_{22}^S$ becomes larger, the shape becomes more and more triangular until it reaches a critical value beyond which the cross-section self intersects (see figure 2). The critical point, i.e. the first instance in which the cross-section crosses the
$\epsilon Y_{22}^S$ becomes larger, the shape becomes more and more triangular until it reaches a critical value beyond which the cross-section self intersects (see figure 2). The critical point, i.e. the first instance in which the cross-section crosses the ![]() $Y=0$ line thrice, corresponds to
$Y=0$ line thrice, corresponds to ![]() $\epsilon Y_{22}^S=Y_{11}^S/2$. The strength of the shaping is then
$\epsilon Y_{22}^S=Y_{11}^S/2$. The strength of the shaping is then ![]() $\epsilon Y_{22}^S/Y_{11}^S$, which limits the near-axis description to
$\epsilon Y_{22}^S/Y_{11}^S$, which limits the near-axis description to ![]() $\epsilon <\epsilon _{\max }=Y_{11}^S/2Y_{22}^S$. A similar limit exists for
$\epsilon <\epsilon _{\max }=Y_{11}^S/2Y_{22}^S$. A similar limit exists for ![]() $X_{22}^c$ to prevent the indentation of the bean shape from being too large so that nested surfaces touch and eventually cross each other. Both of these are a geometric interpretation of the measure
$X_{22}^c$ to prevent the indentation of the bean shape from being too large so that nested surfaces touch and eventually cross each other. Both of these are a geometric interpretation of the measure ![]() $r_c$ introduced by Landreman (Reference Landreman2021).
$r_c$ introduced by Landreman (Reference Landreman2021).
Although in different flavours, both of these components bring in triangularity. So far, we have been vague on what we mean by triangularity, and we must invoke a more rigorous definition for a quantitative consideration. We define triangularity as the relative displacement of the vertical tips of the cross-section from the cross-section mid-point divided by the width of the cross-section. It is a measure of left–right asymmetry of the cross-sections. We choose a positive value to indicate a relative displacement in the direction of ![]() $\hat {\kappa }$ (in the tokamak
$\hat {\kappa }$ (in the tokamak ![]() $-\hat {R}$). Following this definition (calculation details may be found in Appendix C), the asymptotic form of triangularity,
$-\hat {R}$). Following this definition (calculation details may be found in Appendix C), the asymptotic form of triangularity, ![]() $\delta _{\rm tok}$, may be written as
$\delta _{\rm tok}$, may be written as
which involves the shaping strength fractions previously obtained, with the negative sign being consistent with the picture in figure 2.
The same way that this notion of triangularity, ![]() $\delta _{\rm tok}$, measures the degree of left–right asymmetry, we define another geometric parameter that we call vertical triangularity,
$\delta _{\rm tok}$, measures the degree of left–right asymmetry, we define another geometric parameter that we call vertical triangularity, ![]() $\delta _y$, which measures the degree of up–down asymmetry. In this case, in terms of the shaping parameters
$\delta _y$, which measures the degree of up–down asymmetry. In this case, in terms of the shaping parameters ![]() $X_{22}^s$ and
$X_{22}^s$ and ![]() $Y_{22}^c$,
$Y_{22}^c$,
Note the sign difference from (3.3) (in fact, one can see a similar sign in (5.1) and (5.2) of Rhodes (Reference Rhodes2017)). We have taken the convention that a positive ![]() $\delta _y$ indicates an upwards bulging (meaning in the direction of the binormal to the axis).
$\delta _y$ indicates an upwards bulging (meaning in the direction of the binormal to the axis).
When the underlying elliptic shape is not frame-aligned, the description of the shaping becomes significantly more complex, as the components of ![]() $X_2$ and
$X_2$ and ![]() $Y_2$ mix together. Appendix C briefly describes how to deal with this situation by defining effective measures
$Y_2$ mix together. Appendix C briefly describes how to deal with this situation by defining effective measures ![]() $\delta _{\rm tok}$ and
$\delta _{\rm tok}$ and ![]() $\delta _y$ in the rotated frame. We give a numerical example of what this means later.
$\delta _y$ in the rotated frame. We give a numerical example of what this means later.
3.2.3. Second-order shaping: Shafranov shift
So far, we have said little regarding the relative position of flux surfaces, of which the Shafranov shift (Shafranov Reference Shafranov1963; Wesson Reference Wesson2011) is a measure. Classically, this is defined as the relative shift of the centres of circular cross-sections in the large-aspect-ratio limit of an axisymmetric configuration. In a more general stellarator, the shift becomes ambiguous, as the centre of generally shaped cross-sections (other than ellipses and circles) is non-unique. We opt to define it as
where the near-axis expansion parameters have been directly used. In an up–down symmetric configuration, ![]() $\varDelta _x$ describes the displacement of the cross-section midpoint along the up–down symmetry line from one surface to the next. The vertical portion,
$\varDelta _x$ describes the displacement of the cross-section midpoint along the up–down symmetry line from one surface to the next. The vertical portion, ![]() $\varDelta _y$, has a similar interpretation along the binormal (
$\varDelta _y$, has a similar interpretation along the binormal (![]() $Y$). Appendix D motivates the form of this definition of Shafranov shift beyond its simple geometric interpretation, following the work in Rodríguez, Sengupta & Bhattacharjee (Reference Rodríguez, Sengupta and Bhattacharjee2022c). This form of the Shafranov shift reduces to the correct tokamak definition (see Landreman Reference Landreman2021). As we are primarily concerned with the up–down symmetric form of the problem, we refer to
$Y$). Appendix D motivates the form of this definition of Shafranov shift beyond its simple geometric interpretation, following the work in Rodríguez, Sengupta & Bhattacharjee (Reference Rodríguez, Sengupta and Bhattacharjee2022c). This form of the Shafranov shift reduces to the correct tokamak definition (see Landreman Reference Landreman2021). As we are primarily concerned with the up–down symmetric form of the problem, we refer to ![]() $\varDelta _x$ as the Shafranov shift.
$\varDelta _x$ as the Shafranov shift.
3.3. Magnetohydrodynamic stability and cross-section shapes
The geometry parameters in the previous subsection constitute the appropriate shaping-related parameters in terms of which we ought to express the near-axis expansion. For simplicity, at lowest order, we choose to use parameters ![]() $\eta$ and
$\eta$ and ![]() $\sigma$ explicitly. Unless otherwise stated, we focus on up–down symmetric configurations, and so take
$\sigma$ explicitly. Unless otherwise stated, we focus on up–down symmetric configurations, and so take ![]() $\sigma =0$ and
$\sigma =0$ and ![]() $\delta _y=0$. Having the magnitude of the pressure gradient,
$\delta _y=0$. Having the magnitude of the pressure gradient, ![]() $p_2$, explicitly involved is often convenient, as it allows us to study the effect of other parameters on a configuration that needs to support a prescribed ‘pressure profile’. This leaves one of the two geometric measures, either the Shafranov shift,
$p_2$, explicitly involved is often convenient, as it allows us to study the effect of other parameters on a configuration that needs to support a prescribed ‘pressure profile’. This leaves one of the two geometric measures, either the Shafranov shift, ![]() $\varDelta _x$, or the triangularity,
$\varDelta _x$, or the triangularity, ![]() $\delta =\delta _{\rm tok}/\epsilon$, to complete the parametrisation of the near-axis configuration. Choosing one explicitly will make the other adjust self-consistently in a concealed way so that it complies with equilibrium.
$\delta =\delta _{\rm tok}/\epsilon$, to complete the parametrisation of the near-axis configuration. Choosing one explicitly will make the other adjust self-consistently in a concealed way so that it complies with equilibrium.
To express everything in terms of these parameters, we must relate them to ![]() $|\boldsymbol {B}|$ components through
$|\boldsymbol {B}|$ components through ![]() $\{X_2,Y_2\}$ coefficients. These relations form part of the near-axis expansion, and are given explicitly in Appendix E. Although algebraically involved, computational algebra may handle them straightforwardly. That way, we first present three equivalent forms of
$\{X_2,Y_2\}$ coefficients. These relations form part of the near-axis expansion, and are given explicitly in Appendix E. Although algebraically involved, computational algebra may handle them straightforwardly. That way, we first present three equivalent forms of ![]() $B_{20}$ in terms of different relevant second-order parameters, each with a different physical interpretation:
$B_{20}$ in terms of different relevant second-order parameters, each with a different physical interpretation:
Following this, the Mercier criterion, (2.5), can be written as
The effects of shaping are buried in each of the terms of these expressions, especially their sign. If the factor multiplying a particular parameter in the Mercier criterion is positive, then the geometric or physical property represented by the parameter can be said to have a stabilising effect.
Consider first (3.6c), which describes the direct effect of cross-section shaping on ![]() $B_{20}$. Because the factors multiplying both
$B_{20}$. Because the factors multiplying both ![]() $\delta$ and
$\delta$ and ![]() $\varDelta _x$ are positive, this means that positive triangularity and Shafranov shift contribute positively to
$\varDelta _x$ are positive, this means that positive triangularity and Shafranov shift contribute positively to ![]() $B_{20}$, and thus we would expect MHD stability. There is a simple geometric explanation for this behaviour. Picture an increase of
$B_{20}$, and thus we would expect MHD stability. There is a simple geometric explanation for this behaviour. Picture an increase of ![]() $\varDelta _x$ as a bunching of cross-sections on the outboard side of the configuration. As one goes from the magnetic axis outwards, each cross-section acquires more area on the inboard side compared to the outboard side. There
$\varDelta _x$ as a bunching of cross-sections on the outboard side of the configuration. As one goes from the magnetic axis outwards, each cross-section acquires more area on the inboard side compared to the outboard side. There ![]() $|\boldsymbol {B}|$ is larger, therefore
$|\boldsymbol {B}|$ is larger, therefore ![]() $B_{20}$ grows, and so does the magnetic well. Similarly, a positive triangularity brings the vertical turning points of the cross-section towards the inboard side, gathering a larger area on the high-field side. Following this logic, any shaping that does not break left–right symmetry should not affect stability.
$B_{20}$ grows, and so does the magnetic well. Similarly, a positive triangularity brings the vertical turning points of the cross-section towards the inboard side, gathering a larger area on the high-field side. Following this logic, any shaping that does not break left–right symmetry should not affect stability.
Although this geometric picture is simple, its link to stability is not as clear-cut as it may seem. When we deform the cross-sections by changing ![]() $\delta$ and
$\delta$ and ![]() $\varDelta _x$ directly, the resulting equilibrium generally supports a different pressure gradient; formally,
$\varDelta _x$ directly, the resulting equilibrium generally supports a different pressure gradient; formally, ![]() $p_2$ adjusts self-consistently in the background to satisfy
$p_2$ adjusts self-consistently in the background to satisfy ![]() $p_2/2I_2^2=-(3+\eta ^4)\varDelta _x/ (1+\eta ^4)^2 -\eta ^5\delta /(1+\eta ^4)^2+\cdots$. To discuss stability most straightforwardly we keep
$p_2/2I_2^2=-(3+\eta ^4)\varDelta _x/ (1+\eta ^4)^2 -\eta ^5\delta /(1+\eta ^4)^2+\cdots$. To discuss stability most straightforwardly we keep ![]() $p_2$ constant, and thus make it explicit as in (3.6a) and (3.6b). In such a scenario the expressions for
$p_2$ constant, and thus make it explicit as in (3.6a) and (3.6b). In such a scenario the expressions for ![]() $B_{20}$, (3.6a) and (3.6b), and those for the Mercier criterion, (3.7a) and (3.7b), are (up to a factor of
$B_{20}$, (3.6a) and (3.6b), and those for the Mercier criterion, (3.7a) and (3.7b), are (up to a factor of ![]() $1/2$) the same as far as the effects of second-order shaping are concerned. The clear geometric picture we had for (3.6c) is, however, lost. Positive triangularity and Shafranov shift no longer lead to an unequivocal increase in the magnetic well. Only vertically elongated cross-sections preserve the benefit of positive triangularity (
$1/2$) the same as far as the effects of second-order shaping are concerned. The clear geometric picture we had for (3.6c) is, however, lost. Positive triangularity and Shafranov shift no longer lead to an unequivocal increase in the magnetic well. Only vertically elongated cross-sections preserve the benefit of positive triangularity (![]() $\eta <1$), while horizontally elongated ones do so for the Shafranov shift. The reason for this difference is the hidden response of the shaping in each one of these cases. To keep the pressure constant (see before), if one increases triangularity in a configuration, then the Shafranov shift should go in the negative direction to hold the same pressure gradient (in a sense counteracting the triangular shaping). This opposite contribution to
$\eta <1$), while horizontally elongated ones do so for the Shafranov shift. The reason for this difference is the hidden response of the shaping in each one of these cases. To keep the pressure constant (see before), if one increases triangularity in a configuration, then the Shafranov shift should go in the negative direction to hold the same pressure gradient (in a sense counteracting the triangular shaping). This opposite contribution to ![]() $B_{20}$ makes (de)stabilising triangularity or Shafranov shift dominate in different situations. The stabilising effect of triangularity, for
$B_{20}$ makes (de)stabilising triangularity or Shafranov shift dominate in different situations. The stabilising effect of triangularity, for ![]() $\eta <1$, overcomes any destabilising influence of the Shafranov shift, which dominates when
$\eta <1$, overcomes any destabilising influence of the Shafranov shift, which dominates when ![]() $\eta >1$. The exact balance results in (3.6a) and (3.6b).
$\eta >1$. The exact balance results in (3.6a) and (3.6b).
The form of (3.7a) is consistent with (12.89) of Freidberg (Reference Freidberg2014). We have learnt, though, that one must be careful at offering a simple picture to explain the behaviour of stability. The simple geometric view offered by Freidberg for (3.6c) breaks down.Footnote 2 As most relevant cross-sections are elongated vertically in practice, positive triangularity (bean shaping) contributes favourably to stability. This aligns with the common wisdom of how shaping affects stability.
As is well known, increasing the pressure in a configuration leads to a deepening of the magnetic well. Here, formally, this is described by the unavoidable increase of ![]() $B_{20}$ with
$B_{20}$ with ![]() $|p_2|$, (3.6a) and (3.6b). The effect of pressure on stability is, even if
$|p_2|$, (3.6a) and (3.6b). The effect of pressure on stability is, even if ![]() $B_{20}$ increases, destabilising in the usual scenario in which triangularity is kept constant, (3.7a). This leads to the well-known (Lortz & Nührenberg Reference Lortz and Nührenberg1978; Freidberg Reference Freidberg2014) equilibrium
$B_{20}$ increases, destabilising in the usual scenario in which triangularity is kept constant, (3.7a). This leads to the well-known (Lortz & Nührenberg Reference Lortz and Nührenberg1978; Freidberg Reference Freidberg2014) equilibrium ![]() $\beta$ stability limit.Footnote 3 The Shafranov shift plays a central role in setting this limit, as can be seen by the avoidance of the
$\beta$ stability limit.Footnote 3 The Shafranov shift plays a central role in setting this limit, as can be seen by the avoidance of the ![]() $\beta$ limit for
$\beta$ limit for ![]() $\eta <1$ when fixing
$\eta <1$ when fixing ![]() $\varDelta _x$, (3.7b).
$\varDelta _x$, (3.7b).
The significance of any of the effects described is only relative to the effect of other terms in the Mercier criterion. This comparison depends on lower-order parameter choices. This is especially true for what we call the ‘intrinsic contribution’ to stability, a term that does not involve any second-order parameters directly. Its stabilising contribution grows with elongation in the horizontal direction, but it is deteriorated by current (opposite to the contribution by the pressure gradient). The behaviour with current can be understood considering the limit of very large ![]() $I_2$. In this limit, the tokamak effectively becomes a
$I_2$. In this limit, the tokamak effectively becomes a ![]() $Z$-pinch, whose instability grows like
$Z$-pinch, whose instability grows like ![]() $I_2^2$ (see chapter 11 in Freidberg Reference Freidberg2014), a classic result that in the circular-cross-section-limit becomes
$I_2^2$ (see chapter 11 in Freidberg Reference Freidberg2014), a classic result that in the circular-cross-section-limit becomes ![]() $D_{\rm Merc}\propto 1-\iota _0^2$ (Freidberg Reference Freidberg2014, chapter 12).
$D_{\rm Merc}\propto 1-\iota _0^2$ (Freidberg Reference Freidberg2014, chapter 12).
We pointed that any effect that did not break left–right symmetry at second order, namely ![]() $\delta _y$, could not affect
$\delta _y$, could not affect ![]() $B_{20}$. But we had not touched upon the effect of up–down symmetry breaking through
$B_{20}$. But we had not touched upon the effect of up–down symmetry breaking through ![]() $\sigma$. We spare the reader from the expressions one obtains in that case, which are not particularly illuminating. The procedure is, however, no different from the one we have adopted, as long as
$\sigma$. We spare the reader from the expressions one obtains in that case, which are not particularly illuminating. The procedure is, however, no different from the one we have adopted, as long as ![]() $\sigma$ is kept explicitly in the expressions. As pointed out in Appendix C, for a straightforward definition of shaping in that scenario, we redefine
$\sigma$ is kept explicitly in the expressions. As pointed out in Appendix C, for a straightforward definition of shaping in that scenario, we redefine ![]() $\delta$,
$\delta$, ![]() $\delta _y$ and
$\delta _y$ and ![]() $\varDelta _x$ in the frame of the rotated ellipse. An example of how the effect of triangularity on stability changes with the up–down symmetry breaking is shown in figure 3. As the ellipse rotates, the effect of triangularity
$\varDelta _x$ in the frame of the rotated ellipse. An example of how the effect of triangularity on stability changes with the up–down symmetry breaking is shown in figure 3. As the ellipse rotates, the effect of triangularity ![]() $\delta$ shrinks, to the point of vanishing for
$\delta$ shrinks, to the point of vanishing for ![]() $\vartheta ={\rm \pi} /2$. At that point,
$\vartheta ={\rm \pi} /2$. At that point, ![]() $\delta$ represents vertical triangularity; and as we have seen, this has no effect on stability. The behaviour of
$\delta$ represents vertical triangularity; and as we have seen, this has no effect on stability. The behaviour of ![]() $\delta _y$ in figure 3 is the reverse of that of
$\delta _y$ in figure 3 is the reverse of that of ![]() $\delta$. It goes from having no effect to having an effect which in this case surpasses the effect of
$\delta$. It goes from having no effect to having an effect which in this case surpasses the effect of ![]() $\delta$ at
$\delta$ at ![]() $\vartheta =0$. This difference in magnitude arises because the
$\vartheta =0$. This difference in magnitude arises because the ![]() $\vartheta =0, {\rm \pi}/2$ cases are geometrically different. The major or minor axes are aligned with
$\vartheta =0, {\rm \pi}/2$ cases are geometrically different. The major or minor axes are aligned with ![]() $X$ in each case, respectively.
$X$ in each case, respectively.

Figure 3. Change in the stabilising triangularity effect with up–down symmetry breaking. The plots show (left) the influence of regular and up–down triangularity on ![]() $B_{20}$ and (right) the
$B_{20}$ and (right) the ![]() $\eta$ and
$\eta$ and ![]() $\sigma$ parameters as a function of the rotation of the ellipse,
$\sigma$ parameters as a function of the rotation of the ellipse, ![]() $\theta$. The elongation of the ellipse is kept constant,
$\theta$. The elongation of the ellipse is kept constant, ![]() $\mathcal {E}=2$, and at
$\mathcal {E}=2$, and at ![]() $\theta =0$ is aligned with the vertical.
$\theta =0$ is aligned with the vertical.
4. Quasisymmetric stellarators
The discussion of MHD stability and shaping above is a renewed outlook at a problem that has long been studied (Mercier Reference Mercier1962; Solov'ev & Shafranov Reference Solov'ev and Shafranov1970; Lortz & Nührenberg Reference Lortz and Nührenberg1976). We confirmed that the behaviour in a tokamak aligns with the conventional wisdom of positive triangularity (in common elongated shapes) favouring stability, but the results are otherwise not new. The discussion above is, however, a valuable stepping stone towards dealing with the quasisymmetric problem. In quasisymmetry, like in axisymmetry, the Fourier coefficients of ![]() $|\boldsymbol {B}|$ in the near-axis expansion are constant, making most of the analysis the same.
$|\boldsymbol {B}|$ in the near-axis expansion are constant, making most of the analysis the same.
4.1. Constancy of parameters
Let us start by carefully considering the description of quasisymmetric configurations in the near-axis framework. By definition, the magnitude of the magnetic field in an equilibrium, quasisymmetric configuration (expressed in Boozer coordinates) is ![]() $|\boldsymbol {B}|=B(\psi,\chi =\theta -N\phi )$ (Boozer Reference Boozer1983; Helander Reference Helander2014; Rodríguez, Sengupta & Bhattacharjee Reference Rodríguez, Sengupta and Bhattacharjee2021). That is, the near-axis expansion of
$|\boldsymbol {B}|=B(\psi,\chi =\theta -N\phi )$ (Boozer Reference Boozer1983; Helander Reference Helander2014; Rodríguez, Sengupta & Bhattacharjee Reference Rodríguez, Sengupta and Bhattacharjee2021). That is, the near-axis expansion of ![]() $|\boldsymbol {B}|$ is precisely analogous to that of axisymmetry. Thus, we expect to find a natural parametrisation of quasisymmetric configurations analogous to that of tokamaks.
$|\boldsymbol {B}|$ is precisely analogous to that of axisymmetry. Thus, we expect to find a natural parametrisation of quasisymmetric configurations analogous to that of tokamaks.
To leading order, the shape of a magnetic axis should be chosen. For a quasisymmetric stellarator, any regular (i.e. with no vanishing curvature), closed space curve is valid, a priori, beyond a circle. The choice of axis fixes ![]() $N$, the direction of the symmetry, which corresponds to the self-linking number of the axis (Rodríguez et al. Reference Rodríguez, Sengupta and Bhattacharjee2022b). The poloidal current is then
$N$, the direction of the symmetry, which corresponds to the self-linking number of the axis (Rodríguez et al. Reference Rodríguez, Sengupta and Bhattacharjee2022b). The poloidal current is then ![]() $G_0=L/2{\rm \pi}$, where
$G_0=L/2{\rm \pi}$, where ![]() $L$ is the total length of the axis.
$L$ is the total length of the axis.
At first order, elliptical shapes are described through ![]() $\eta$ and
$\eta$ and ![]() $\sigma$, like for the tokamak. However, in general
$\sigma$, like for the tokamak. However, in general ![]() $\sigma =\sigma (\phi )$ is a function of the toroidal angle; it is the solution to a periodic first-order Riccati equation (see (A6) in Garren & Boozer (Reference Garren and Boozer1991a) or (2.14) in Landreman & Sengupta Reference Landreman and Sengupta2019) with a choice of initial condition
$\sigma =\sigma (\phi )$ is a function of the toroidal angle; it is the solution to a periodic first-order Riccati equation (see (A6) in Garren & Boozer (Reference Garren and Boozer1991a) or (2.14) in Landreman & Sengupta Reference Landreman and Sengupta2019) with a choice of initial condition ![]() $\sigma (0)$ (vanishing in stellarator symmetry). Although this makes the shape of cross-sections in a quasisymmetric stellarator depend on
$\sigma (0)$ (vanishing in stellarator symmetry). Although this makes the shape of cross-sections in a quasisymmetric stellarator depend on ![]() $\phi$, the freedom at first order truly resides on two parameters,
$\phi$, the freedom at first order truly resides on two parameters, ![]() $\eta$ and
$\eta$ and ![]() $\sigma (0)$. This underlines the special nature of quasisymmetric stellarators.
$\sigma (0)$. This underlines the special nature of quasisymmetric stellarators.
At second order in the distance from the magnetic axis we have the four parameters ![]() $p_2$,
$p_2$, ![]() $B_{20}$,
$B_{20}$, ![]() $B_{22}^C$ and
$B_{22}^C$ and ![]() $B_{22}^S$, the same number of constant parameters as in a tokamak. This is true in the ideal quasisymmetryic limit, which we assume for the analysis in this section. However, in practice, one should not forget the limitations that arise through what has come to be known as the Garren–Boozer overdetermination problem (Garren & Boozer Reference Garren and Boozer1991a). Not every axis shape and parameter choice can consistently support quasisymmetry and equilibrium simultaneously through second order. Generally one is forced to relax the strict quasisymmetric requirement on, following Landreman & Sengupta (Reference Landreman and Sengupta2019),
$B_{22}^S$, the same number of constant parameters as in a tokamak. This is true in the ideal quasisymmetryic limit, which we assume for the analysis in this section. However, in practice, one should not forget the limitations that arise through what has come to be known as the Garren–Boozer overdetermination problem (Garren & Boozer Reference Garren and Boozer1991a). Not every axis shape and parameter choice can consistently support quasisymmetry and equilibrium simultaneously through second order. Generally one is forced to relax the strict quasisymmetric requirement on, following Landreman & Sengupta (Reference Landreman and Sengupta2019), ![]() $B_{20}$, which becomes for consistency a function of the toroidal angle. Only a subset of near-axis choices (Landreman Reference Landreman2022; Rodríguez et al. Reference Rodríguez, Sengupta and Bhattacharjee2022c) have approximately constant
$B_{20}$, which becomes for consistency a function of the toroidal angle. Only a subset of near-axis choices (Landreman Reference Landreman2022; Rodríguez et al. Reference Rodríguez, Sengupta and Bhattacharjee2022c) have approximately constant ![]() $B_{20}$.Footnote 4 Thus, in practice, we can expect to find deviations between our idealised analysis and a more consistent one, driven by ‘errors’ in quasisymmetry. For deviations in the range of
$B_{20}$.Footnote 4 Thus, in practice, we can expect to find deviations between our idealised analysis and a more consistent one, driven by ‘errors’ in quasisymmetry. For deviations in the range of ![]() $\varDelta B_{20}\sim 0.01$, one may estimate deviations in
$\varDelta B_{20}\sim 0.01$, one may estimate deviations in ![]() ${\rm \Delta} V''\sim 1$. When illustrating the findings in this section with practical examples, we have to check that the idealised theory reproduces the actual near-axis configuration (see Appendix G).
${\rm \Delta} V''\sim 1$. When illustrating the findings in this section with practical examples, we have to check that the idealised theory reproduces the actual near-axis configuration (see Appendix G).
4.2. Choosing a characteristic cross-section
Although quasisymmetric configurations may be parametrised (for a given axis shape) by the same amount of parameters as a tokamak, flux surfaces are naturally asymmetric. That is, the cross-section at each angle ![]() $\phi$, described analogously to the axisymmetric caseFootnote 5 , will be generally different. This makes the notions of ellipticity, triangularity and Shafranov shift functions of
$\phi$, described analogously to the axisymmetric caseFootnote 5 , will be generally different. This makes the notions of ellipticity, triangularity and Shafranov shift functions of ![]() $\phi$. However, following the parametrisation of the axisymmetric scenario, we must be able to parametrise the whole configuration through the description of a single cross-section (and the axis shape). Given a cross-section and the axis shape, the remainder of the configuration then follows from the fulfilment of quasiymmetry and equilibrium. This simplicity is particular to quasisymmetric stellarators, but other optimised stellarators will also impose constraints on the shaping of their surfaces.
$\phi$. However, following the parametrisation of the axisymmetric scenario, we must be able to parametrise the whole configuration through the description of a single cross-section (and the axis shape). Given a cross-section and the axis shape, the remainder of the configuration then follows from the fulfilment of quasiymmetry and equilibrium. This simplicity is particular to quasisymmetric stellarators, but other optimised stellarators will also impose constraints on the shaping of their surfaces.
In principle, one could consider the geometric features of any of the cross-sections as parameters. In stellarator-symmetric stellarators, though, one cross-section is particularly simple: the up–down symmetric one. There are two such distinct cross-sections per field period, by stellarator symmetry occurring at ![]() $\phi =0, {\rm \pi}/N$, where
$\phi =0, {\rm \pi}/N$, where ![]() $N$ is the number of field periods. For simplicity we focus on the cross-section at
$N$ is the number of field periods. For simplicity we focus on the cross-section at ![]() $\phi =0$. In common quasisymmetric configurations (see later section), this often corresponds to a characteristic bean-shaped cross-section, and thus it is reasonable to consider it as representative in our discussion. For such a cross-section, the normal vector of the Frenet–Serret frame points inwards along the major radius by constructionFootnote 6 , and the configuration presents a high degree of symmetry (curvature and torsion are even functions of
$\phi =0$. In common quasisymmetric configurations (see later section), this often corresponds to a characteristic bean-shaped cross-section, and thus it is reasonable to consider it as representative in our discussion. For such a cross-section, the normal vector of the Frenet–Serret frame points inwards along the major radius by constructionFootnote 6 , and the configuration presents a high degree of symmetry (curvature and torsion are even functions of ![]() $\phi$, and
$\phi$, and ![]() $\sigma$ is odd). The task is then to connect the features of this cross-section to stability.
$\sigma$ is odd). The task is then to connect the features of this cross-section to stability.
4.3. Shaping and MHD stability in a quasisymmetric stellarator
We relate the shaping of the up–down symmetric cross-section to stability in a form similar (conceptually) to how we approached the problem in the axisymmetric case. That is, we must first find a relation between ![]() $X_2$ and
$X_2$ and ![]() $Y_2$ (in this case at
$Y_2$ (in this case at ![]() $\phi =0$) and typical shaping concepts, relate them to natural parameters of the near-axis framework and finally draw the connection to the Mercier criterion. We will, for now, ignore the changes in shape of the cross-section that occur from the projection from the plane normal to the axis to the cylindrical coordinate system. We spare the reader from the algebra, and write the Mercier criterion in the following form:
$\phi =0$) and typical shaping concepts, relate them to natural parameters of the near-axis framework and finally draw the connection to the Mercier criterion. We will, for now, ignore the changes in shape of the cross-section that occur from the projection from the plane normal to the axis to the cylindrical coordinate system. We spare the reader from the algebra, and write the Mercier criterion in the following form:
where all the interesting information lies in the forms of ![]() $\mathcal {T}$ and
$\mathcal {T}$ and ![]() $\varLambda$. Term
$\varLambda$. Term ![]() $\varLambda$, which includes the effects of the axis,
$\varLambda$, which includes the effects of the axis, ![]() $\eta$ and
$\eta$ and ![]() $\sigma$, and is important in determining the total stability of the configuration, is, however, not very illuminating (see Appendix F). Instead, we focus on the effect of triangularity, and see how the tokamak intuition and common wisdom claim holds.
$\sigma$, and is important in determining the total stability of the configuration, is, however, not very illuminating (see Appendix F). Instead, we focus on the effect of triangularity, and see how the tokamak intuition and common wisdom claim holds.
Using the appropriate relations, we obtain after significant algebra
where ![]() $\alpha =\eta ^4/\kappa (0)^4$ and
$\alpha =\eta ^4/\kappa (0)^4$ and
 \begin{equation} \bar{F}=2\left[\frac{(I_2-\tau(0))/\kappa(0)^2}{\displaystyle \int_0^{2 {\rm \pi}}\,\mathrm{d}\varphi(I_2-\tau)/\kappa^2} \frac{\displaystyle \int_0^{2{\rm \pi}}\,\mathrm{d}\varphi(1+\sigma^2 +\eta^4/\kappa^4)}{1+\eta^4/\kappa(0)^4}-1\right],\end{equation}
\begin{equation} \bar{F}=2\left[\frac{(I_2-\tau(0))/\kappa(0)^2}{\displaystyle \int_0^{2 {\rm \pi}}\,\mathrm{d}\varphi(I_2-\tau)/\kappa^2} \frac{\displaystyle \int_0^{2{\rm \pi}}\,\mathrm{d}\varphi(1+\sigma^2 +\eta^4/\kappa^4)}{1+\eta^4/\kappa(0)^4}-1\right],\end{equation}
with ![]() $\tau$ the torsion of the axis. The expression in (4.3) compares local quantities with their global average, acting as a measure of asymmetry in the stellarator. Readers familiar with the near-axis framework will recognise the averages as part of the expression for the rotational transform on axis,
$\tau$ the torsion of the axis. The expression in (4.3) compares local quantities with their global average, acting as a measure of asymmetry in the stellarator. Readers familiar with the near-axis framework will recognise the averages as part of the expression for the rotational transform on axis, ![]() $\bar {\iota }_0=2G_0\eta ^2\int [(I_2-\tau )/\kappa ^2]/\int (1+\sigma ^2+\eta ^4/\kappa ^4)$. In the axisymmetric limit, where the average and local quantities are the same,
$\bar {\iota }_0=2G_0\eta ^2\int [(I_2-\tau )/\kappa ^2]/\int (1+\sigma ^2+\eta ^4/\kappa ^4)$. In the axisymmetric limit, where the average and local quantities are the same, ![]() $\bar {F}\rightarrow 0$, and
$\bar {F}\rightarrow 0$, and ![]() $\mathcal {T}_\delta$ in (4.2) reduces to (3.7a), with
$\mathcal {T}_\delta$ in (4.2) reduces to (3.7a), with ![]() $\alpha$ generalising
$\alpha$ generalising ![]() $\eta \rightarrow \eta /\kappa (0)$. Thus, in this limit, the tokamak intuition holds: for a cross-section that is elongated in the vertical direction (
$\eta \rightarrow \eta /\kappa (0)$. Thus, in this limit, the tokamak intuition holds: for a cross-section that is elongated in the vertical direction (![]() $\alpha <1$), positive triangularity favours MHD stability. In contrast, negative triangularity contributes positively for
$\alpha <1$), positive triangularity favours MHD stability. In contrast, negative triangularity contributes positively for ![]() $\alpha >1$.
$\alpha >1$.
The presence of ![]() $\bar {F}$ does not guarantee this behaviour in a general quasisymmetric stellarator. To understand the implications of this measure of asymmetry, we consider the representation of
$\bar {F}$ does not guarantee this behaviour in a general quasisymmetric stellarator. To understand the implications of this measure of asymmetry, we consider the representation of ![]() $\mathcal {T}_\delta /3\eta$ in
$\mathcal {T}_\delta /3\eta$ in ![]() $(\alpha, \bar {F})$ space (see figure 4).Parameter
$(\alpha, \bar {F})$ space (see figure 4).Parameter ![]() $\bar {F}$ changes the stabilising implications of triangularity drastically, especially in the
$\bar {F}$ changes the stabilising implications of triangularity drastically, especially in the ![]() $\bar {F}<0$ region. Any value
$\bar {F}<0$ region. Any value ![]() $\bar {F}<(\alpha -1)/(1+\alpha )$ (of course,
$\bar {F}<(\alpha -1)/(1+\alpha )$ (of course, ![]() $\bar {F}<-1$) gives
$\bar {F}<-1$) gives ![]() $\mathcal {T}_\delta <0$, and makes negative triangularity have a stabilising effect, contrary to common wisdom. In this region, though,
$\mathcal {T}_\delta <0$, and makes negative triangularity have a stabilising effect, contrary to common wisdom. In this region, though, ![]() $0>\mathcal {T}_d>-1$, and thus the effects of triangularity are moderate. To picture the meaning of negative
$0>\mathcal {T}_d>-1$, and thus the effects of triangularity are moderate. To picture the meaning of negative ![]() $\bar {F}$, consider the limit of
$\bar {F}$, consider the limit of ![]() $\eta \sim 0$. In that case, the first fraction in the square brackets of (4.3) dominates
$\eta \sim 0$. In that case, the first fraction in the square brackets of (4.3) dominates ![]() $\bar {F}$, which for no toroidal current requires
$\bar {F}$, which for no toroidal current requires ![]() $\tau /\kappa ^2$ to have a local minimum.
$\tau /\kappa ^2$ to have a local minimum.

Figure 4. Sign of ![]() $\mathcal {T}_\delta /3\eta$ and
$\mathcal {T}_\delta /3\eta$ and ![]() $\mathcal {T}_{|p|}\bar {\iota }_0^2/4\kappa ^2$ in
$\mathcal {T}_{|p|}\bar {\iota }_0^2/4\kappa ^2$ in ![]() $(\alpha, \bar {F})$ space. The plots show
$(\alpha, \bar {F})$ space. The plots show ![]() $\mathcal {T}_\delta /3\eta$ (left) and
$\mathcal {T}_\delta /3\eta$ (left) and ![]() $\mathcal {T}_{|p|}\bar {\iota }_0^2/4\kappa ^2$ (right) in
$\mathcal {T}_{|p|}\bar {\iota }_0^2/4\kappa ^2$ (right) in ![]() $(\alpha, \bar {F})$ space. The shaded region in the left-hand plot represents the space for which
$(\alpha, \bar {F})$ space. The shaded region in the left-hand plot represents the space for which ![]() $\mathcal {T}_\delta <0$, and thus positive triangularity is detrimental to the stability of the configuration. The shadow region for
$\mathcal {T}_\delta <0$, and thus positive triangularity is detrimental to the stability of the configuration. The shadow region for ![]() $\mathcal {T}_{|p|}$ also represents a negative sign corresponding to the destabilising effect of a pressure gradient. The dotted line in the left-hand plot represents the case of the tokamak explored in the previous section, which shows the possibility of both triangularity signs being stabilising. The dashed and dotted lines in the right-hand plot correspond to the changing lower limit of the positively signed region as the magnitude of the geodesic contribution (the term with the integral
$\mathcal {T}_{|p|}$ also represents a negative sign corresponding to the destabilising effect of a pressure gradient. The dotted line in the left-hand plot represents the case of the tokamak explored in the previous section, which shows the possibility of both triangularity signs being stabilising. The dashed and dotted lines in the right-hand plot correspond to the changing lower limit of the positively signed region as the magnitude of the geodesic contribution (the term with the integral ![]() $I$) is changed from maximal (dotted line) to half its magnitude from the axisymmetric limit (labelled 0.5).
$I$) is changed from maximal (dotted line) to half its magnitude from the axisymmetric limit (labelled 0.5).
If this had a local maximum, then ![]() $\bar {F}>0$ and
$\bar {F}>0$ and ![]() $\mathcal {T}_d$ would live in the upper portion of figure 4. In that case, we see that positive triangularity will benefit stability for moderate values of
$\mathcal {T}_d$ would live in the upper portion of figure 4. In that case, we see that positive triangularity will benefit stability for moderate values of ![]() $\bar {F}$. Beyond
$\bar {F}$. Beyond ![]() $\bar {F}>(3+\alpha )/(\alpha +1)$ negative triangularity becomes once again stabilising, and in this case, strongly so. Triangularity
$\bar {F}>(3+\alpha )/(\alpha +1)$ negative triangularity becomes once again stabilising, and in this case, strongly so. Triangularity ![]() $\mathcal {T}_d$ shows a divergence at the boundary, corresponding to an unphysical Shafranov shift, indicating the breakdown of the parametrisation chosen for the configuration. In the limit
$\mathcal {T}_d$ shows a divergence at the boundary, corresponding to an unphysical Shafranov shift, indicating the breakdown of the parametrisation chosen for the configuration. In the limit ![]() $|\bar {F}|\rightarrow \infty$,
$|\bar {F}|\rightarrow \infty$, ![]() $\mathcal {T}_\delta \rightarrow -3\eta$.
$\mathcal {T}_\delta \rightarrow -3\eta$.
In summary, the common perspective on the contribution of triangularity (or bean shaping) to stability does not generally apply to quasisymmetric stellarators. For a significant asymmetry ![]() $|\bar {F}|$ the opposite is actually true. This is not a claim on the full MHD stability of a configuration, which we cannot make simply based on triangularity. Instead, it is a statement on the partial contribution of triangularity to the total MHD stability; that is, how a change in triangularity keeping the pressure, elliptic shaping, up–down symmetry and axis shape unchanged helps or worsens the stability of a configuration. Within the near-axis description this thought experiment has a precise formulation, and suggests that positive-triangularity, bean-shaped cross-sections do not necessarily improve stability.Footnote 7
$|\bar {F}|$ the opposite is actually true. This is not a claim on the full MHD stability of a configuration, which we cannot make simply based on triangularity. Instead, it is a statement on the partial contribution of triangularity to the total MHD stability; that is, how a change in triangularity keeping the pressure, elliptic shaping, up–down symmetry and axis shape unchanged helps or worsens the stability of a configuration. Within the near-axis description this thought experiment has a precise formulation, and suggests that positive-triangularity, bean-shaped cross-sections do not necessarily improve stability.Footnote 7
What does this imply in practice? Are most of the existing cases aligning or misaligning with the common wisdom? From the analytic perspective, a definitive answer should explore the value of ![]() $\bar {F}$ in quasisymmetric configurations, but we content ourselves by presenting some examples of optimised near-axis quasisymmetric configurations (see figure 5 and table 1).Footnote 8 For all the cases analysed, remarkably,
$\bar {F}$ in quasisymmetric configurations, but we content ourselves by presenting some examples of optimised near-axis quasisymmetric configurations (see figure 5 and table 1).Footnote 8 For all the cases analysed, remarkably, ![]() $\mathcal {T}_\delta <0$, a result that merits further investigation. As a result of this behaviour, the triangularity of the bean cross-section (see cross-sections in figure 5) is detrimental to MHD stability in most scenarios. Shaping contributes favourably only as an exception, of which the ‘new QH’ (Rodríguez et al. Reference Rodríguez, Sengupta and Bhattacharjee2022c) and ‘QH N4 Mercier’ (Landreman Reference Landreman2022) configurations are two examples. The author in Landreman (Reference Landreman2022) obtained the latter by optimising for quasisymmetry and a favourable Mercier criterion. Thus, finding the favourable contribution of triangular shaping is not surprising. The work here sheds some light on what appeared as a rarity in that paper. The ‘QH N4 well’ (Landreman Reference Landreman2022) presents a different scenario. This configuration presents a magnetic well, yet, according to our theory, it has the ‘wrong’ triangular shaping. This is of course not inconsistent, as the triangularity contribution can be detrimental, yet the configuration remain stable. What is more surprising is the fact that the triangularity of this configuration is stronger compared with a similar configuration that was not optimised for a magnetic well. Optimising for stability seems to drive, in this case, the wrong shaping from the perspective of our theory. The disagreement is resolved by realising that on top of triangularity the axis shape was also modified. The change in the latter is sufficient to overcome the detrimental contribution of triangularity in this case. This scenario is reminiscent of the behaviour observed in optimisation of equilibrium boundaries such as in Nührenberg & Zille (Reference Nührenberg and Zille1986) and Nührenberg (Reference Nührenberg2010), examples on which the intuition on stability and shaping was built. Once again, the variation of the surface ‘triangularity’ induces changes on the axis shape as well as other features in the equilibrium, explaining the potential disagreement. In the latter case a comparison with our theory is further complicated because of the variation of MHD stability properties throughout the volume and the necessary search for a near-axis description that adequately captures the behaviour of the global equilibrium near the axis. In any form, from the perspective of the near-axis analysis, the bean shaping we observe in most of the configurations in figure 5 is detrimental and thus cannot be directly driven by the stability requirement, as it opposes it. It is natural to believe that it is the requirement of quasisymmetry or some other property that pushes the configuration to develop such bean-like feature.
$\mathcal {T}_\delta <0$, a result that merits further investigation. As a result of this behaviour, the triangularity of the bean cross-section (see cross-sections in figure 5) is detrimental to MHD stability in most scenarios. Shaping contributes favourably only as an exception, of which the ‘new QH’ (Rodríguez et al. Reference Rodríguez, Sengupta and Bhattacharjee2022c) and ‘QH N4 Mercier’ (Landreman Reference Landreman2022) configurations are two examples. The author in Landreman (Reference Landreman2022) obtained the latter by optimising for quasisymmetry and a favourable Mercier criterion. Thus, finding the favourable contribution of triangular shaping is not surprising. The work here sheds some light on what appeared as a rarity in that paper. The ‘QH N4 well’ (Landreman Reference Landreman2022) presents a different scenario. This configuration presents a magnetic well, yet, according to our theory, it has the ‘wrong’ triangular shaping. This is of course not inconsistent, as the triangularity contribution can be detrimental, yet the configuration remain stable. What is more surprising is the fact that the triangularity of this configuration is stronger compared with a similar configuration that was not optimised for a magnetic well. Optimising for stability seems to drive, in this case, the wrong shaping from the perspective of our theory. The disagreement is resolved by realising that on top of triangularity the axis shape was also modified. The change in the latter is sufficient to overcome the detrimental contribution of triangularity in this case. This scenario is reminiscent of the behaviour observed in optimisation of equilibrium boundaries such as in Nührenberg & Zille (Reference Nührenberg and Zille1986) and Nührenberg (Reference Nührenberg2010), examples on which the intuition on stability and shaping was built. Once again, the variation of the surface ‘triangularity’ induces changes on the axis shape as well as other features in the equilibrium, explaining the potential disagreement. In the latter case a comparison with our theory is further complicated because of the variation of MHD stability properties throughout the volume and the necessary search for a near-axis description that adequately captures the behaviour of the global equilibrium near the axis. In any form, from the perspective of the near-axis analysis, the bean shaping we observe in most of the configurations in figure 5 is detrimental and thus cannot be directly driven by the stability requirement, as it opposes it. It is natural to believe that it is the requirement of quasisymmetry or some other property that pushes the configuration to develop such bean-like feature.

Figure 5. Effect of triangularity and pressure on MHD stability for some quasisymmetric stellarators. The plot shows as scatter points the factors regulating the effect of the triangularity (![]() $\mathcal {T}_\delta$) and pressure gradient (
$\mathcal {T}_\delta$) and pressure gradient (![]() $\mathcal {T}_{\vert p \vert }$) for several optimised quasisymmetric near-axis stellarators. The ‘precise’ QA and QH are from Landreman & Paul (Reference Landreman and Paul2022), the new QH corresponds to the new optimised stellarator example from Rodríguez et al. (Reference Rodríguez, Sengupta and Bhattacharjee2022c), while all others are from a recent publication (Landreman Reference Landreman2022). We chose those configurations with reduced
$\mathcal {T}_{\vert p \vert }$) for several optimised quasisymmetric near-axis stellarators. The ‘precise’ QA and QH are from Landreman & Paul (Reference Landreman and Paul2022), the new QH corresponds to the new optimised stellarator example from Rodríguez et al. (Reference Rodríguez, Sengupta and Bhattacharjee2022c), while all others are from a recent publication (Landreman Reference Landreman2022). We chose those configurations with reduced ![]() $B_{20}$ variation so that the magnetic well computation, using a constant
$B_{20}$ variation so that the magnetic well computation, using a constant ![]() $B_{20}$, showed good agreement with the full
$B_{20}$, showed good agreement with the full ![]() $V''$. The cross-sections shown correspond to the
$V''$. The cross-sections shown correspond to the ![]() $\phi =0$ cross-sections in each configuration.
$\phi =0$ cross-sections in each configuration.
Table 1. Details of the configurations in figure 5. The table includes the values of ![]() $\bar {F}$, the triangularity
$\bar {F}$, the triangularity ![]() $\delta$, the effect of triangularity
$\delta$, the effect of triangularity ![]() $\mathcal {T}_\delta$ and the magnetic well
$\mathcal {T}_\delta$ and the magnetic well ![]() $V''$ for the configurations represented in figure 5. The short labels on top refer to: PQA, precise QA; PQH, precise QH (from Landreman & Paul Reference Landreman and Paul2022); NQH, new QH (from Rodríguez et al. Reference Rodríguez, Sengupta and Bhattacharjee2022c); 22QA, 2022 Qa; N3V, N3 vacuum; N4LA, N4 long axis; N4W, N4 well; N4M, N4 Mercier; N7 and N3B, N3 beta (all these from Landreman (Reference Landreman2022)). For the latter instead of the magnetic well we show the
$V''$ for the configurations represented in figure 5. The short labels on top refer to: PQA, precise QA; PQH, precise QH (from Landreman & Paul Reference Landreman and Paul2022); NQH, new QH (from Rodríguez et al. Reference Rodríguez, Sengupta and Bhattacharjee2022c); 22QA, 2022 Qa; N3V, N3 vacuum; N4LA, N4 long axis; N4W, N4 well; N4M, N4 Mercier; N7 and N3B, N3 beta (all these from Landreman (Reference Landreman2022)). For the latter instead of the magnetic well we show the ![]() $\epsilon ^2 D_{\rm Merc}$, which shows that this finite-
$\epsilon ^2 D_{\rm Merc}$, which shows that this finite-![]() $\beta$ configuration is unstable.
$\beta$ configuration is unstable.

Besides triangularity, the effect of pressure on stability is also modified in quasisymmetric configurations from that in tokamaks. In the latter, we unavoidably encountered the equilibrium stability ![]() $\beta$ limit (see (3.7a)). For a quasisymmetric stellarator, we may write the following two equivalent forms:
$\beta$ limit (see (3.7a)). For a quasisymmetric stellarator, we may write the following two equivalent forms:
where ![]() $\mathcal {I}$ is the function introduced in (2.6), and we have written the latter in a form in which the axisymmetric limit, (3.7a), is straightforward (namely
$\mathcal {I}$ is the function introduced in (2.6), and we have written the latter in a form in which the axisymmetric limit, (3.7a), is straightforward (namely ![]() $\bar {F}\rightarrow 0$ and
$\bar {F}\rightarrow 0$ and ![]() $\mathcal {I}=\sqrt {\alpha }/(1+\sqrt {\alpha })$). The contribution of
$\mathcal {I}=\sqrt {\alpha }/(1+\sqrt {\alpha })$). The contribution of ![]() $\mathcal {I}$ is important, as it is negative and thus contributes to destabilising the stellarator for a finite plasma
$\mathcal {I}$ is important, as it is negative and thus contributes to destabilising the stellarator for a finite plasma ![]() $\beta$. Its magnitude is bounded between
$\beta$. Its magnitude is bounded between ![]() $0<[\sqrt {\alpha }/(1+\sqrt {\alpha })]_{\min }\leq \mathcal {I}<1$, and thus one may take as orientative the case in which only the first fraction in (4.4b) contributes to
$0<[\sqrt {\alpha }/(1+\sqrt {\alpha })]_{\min }\leq \mathcal {I}<1$, and thus one may take as orientative the case in which only the first fraction in (4.4b) contributes to ![]() $\mathcal {T}_{|p|}$.
$\mathcal {T}_{|p|}$.
The effect of ![]() $\bar {F}$, the measure of asymmetry, is shown in the right-hand plot of figure 4. The factor
$\bar {F}$, the measure of asymmetry, is shown in the right-hand plot of figure 4. The factor ![]() $\mathcal {T}_{|p|}$ is no longer necessarily negative. Thus, an increase in the pressure gradient that improves stability is possible; naively, there would be no
$\mathcal {T}_{|p|}$ is no longer necessarily negative. Thus, an increase in the pressure gradient that improves stability is possible; naively, there would be no ![]() $\beta$ limit. This lack of a stability limit at zero magnetic shear in a stellarator is not a new concept (see Hudson, Hegna & Nakajima Reference Hudson, Hegna and Nakajima2005). It could for instance lead to a configuration that is unstable at small plasma
$\beta$ limit. This lack of a stability limit at zero magnetic shear in a stellarator is not a new concept (see Hudson, Hegna & Nakajima Reference Hudson, Hegna and Nakajima2005). It could for instance lead to a configuration that is unstable at small plasma ![]() $\beta$, but becomes stable above some critical value, introducing the concept of a second stability regime. This would make reaching the finite
$\beta$, but becomes stable above some critical value, introducing the concept of a second stability regime. This would make reaching the finite ![]() $\beta$ equilibrium in practice difficult, but it is an attractive concept nonetheless. To picture
$\beta$ equilibrium in practice difficult, but it is an attractive concept nonetheless. To picture ![]() $\mathcal {T}_{|p|}$, the integral
$\mathcal {T}_{|p|}$, the integral ![]() $\mathcal {I}$ was largely simplified. Changing its contribution leads to changes in the region that satisfies
$\mathcal {I}$ was largely simplified. Changing its contribution leads to changes in the region that satisfies ![]() $\mathcal {T}_{|p|}>0$. That region narrows when
$\mathcal {T}_{|p|}>0$. That region narrows when ![]() $\mathcal {I}$ is larger (tending towards the ‘Max’ curve in the plot, which assumes
$\mathcal {I}$ is larger (tending towards the ‘Max’ curve in the plot, which assumes ![]() $\mathcal {I}=1$) and widens when it becomes weaker (in the limit
$\mathcal {I}=1$) and widens when it becomes weaker (in the limit ![]() $I\sim 0$ the lower bound going towards
$I\sim 0$ the lower bound going towards ![]() $\bar {F}\rightarrow -\infty$). In practice, the behaviour is more complex, as
$\bar {F}\rightarrow -\infty$). In practice, the behaviour is more complex, as ![]() $\mathcal {I}$ and
$\mathcal {I}$ and ![]() $\bar {F}$ (and even
$\bar {F}$ (and even ![]() $\alpha$) are not completely independent. Figure 5 shows
$\alpha$) are not completely independent. Figure 5 shows ![]() $\mathcal {T}_{|p|}$ for some quasisymmetric designs, showing that in all cases there appears to be a
$\mathcal {T}_{|p|}$ for some quasisymmetric designs, showing that in all cases there appears to be a ![]() $\beta$ stability limit.
$\beta$ stability limit.
5. Discussion and conclusions
In this paper, we have addressed how the shaping of poloidal cross-sections is related to the MHD stability of toroidal plasmas in order to assess the common conception of positive triangularity bean shapes being favourable. We investigated axisymmetric tokamaks and quasisymmetric stellarators through a near-axis framework.
The analysis required constructing and defining conventional shaping notions such as triangularity and Shafranov shift within the inverse-coordinate near-axis-expansion framework. The work builds on Landreman & Sengupta (Reference Landreman and Sengupta2019) and differs from the so-called direct approach by Mikhailovskii & Aburdzhaniya (Reference Mikhailovskii and Aburdzhaniya1979) (or more recent efforts like that of Kim et al. (Reference Kim, Jorge and Dorland2021)). The direct involvement of the magnetic field magnitude in our framework is convenient for discussing MHD stability beyond axisymmetry.
In the tokamak limit, we reproduce and more systematically explain existing results (Freidberg Reference Freidberg2014) on how shaping (especially triangularity) affects MHD stability through the Mercier criterion. Only for vertically elongated cross-sections is positive triangularity MHD-stabilising. This dependence on elongation is a consequence of the contribution from the Shafranov shift, which wins over the destabilising effect of negative triangularity when cross-sections are horizontally elongated. The worsening of stability with increased pressure gradients and, thus, the appearance of a ![]() $\beta$ limit were also proven.
$\beta$ limit were also proven.
We then explored the effects of shaping and pressure in stellarator-symmetric, quasisymmetric stellarators. We expressed the stability criterion in terms of the shape of a representative up–down symmetric cross-section, which together with an axis shape is sufficient to parametrise the whole configuration. The change of stability as one changes the shape of such cross-section was then studied. In practice, when the asymmetry in the problem is taken into consideration, we show that in most cases (including all the particular examples considered) negative triangularity is stabilising, contrary to current belief. The positive triangularity bean shapes most commonly encountered in quasisymmetric stellarators thus appear to oppose stability (see figure 5), even when the configurations may be overall stable. The presence of these characteristic shapes must then correspond to a different property. Note that although we show this to hold for many existing optimised near-axis configurations, the behaviour is not necessary, and it is possible to change it by tweaking the asymmetry measure ![]() $\bar {F}$; see (4.3).
$\bar {F}$; see (4.3).
This added flexibility also exists for the effect of the pressure gradient. Unlike in the axisymmetric case, finite ![]() $\beta$ corrections can lead to a more MHD-stable configuration. Such behaviour requires particular choices of magnetic axis shapes and parameters, but is not seen in the examples considered. A deeper understanding of their feasibility requires future work on
$\beta$ corrections can lead to a more MHD-stable configuration. Such behaviour requires particular choices of magnetic axis shapes and parameters, but is not seen in the examples considered. A deeper understanding of their feasibility requires future work on ![]() $\bar {F}$ and its relation to quasisymmetry and axis shapes.
$\bar {F}$ and its relation to quasisymmetry and axis shapes.
This work suggests that the relation between cross-sections and stability in a quasisymmetric stellarator is complicated and does not conform necessarily to the need of a bean-shaped cross-section for stability. Making a general statement regarding the benefit of bean-shaped cross-sections to MHD stability in a general stellarator appears to be misleading. This is worth further exploration beyond quasisymmetry.

Figure 6. Definition of the slant angle ![]() $\nu$. Diagram showing the definition of the angle
$\nu$. Diagram showing the definition of the angle ![]() $\nu$ measuring the inclination of the magnetic axis at the origin (
$\nu$ measuring the inclination of the magnetic axis at the origin (![]() $\phi =0$) with the ‘laboratory’ cylindrical coordinate system. The symbols have their usual meaning.
$\phi =0$) with the ‘laboratory’ cylindrical coordinate system. The symbols have their usual meaning.
Acknowledgements
The author would like to acknowledge fruitful discussions with C. Nührenberg, W. Sengupta, P. Helander, G. Plunk, G.R. Clark and R. Mackenbach.
Editor Peter Catto thanks the referees for their advice in evaluating this article.
Declaration of interest
The authors report no conflict of interest.
Appendix A. Mercier criterion
The Mercier criterion scalar ![]() $D_{\rm Merc}$ used in this paper can be written as
$D_{\rm Merc}$ used in this paper can be written as ![]() $D_{\rm Merc}=D_s+D_w+D_d$ (p. 23 in Bauer et al. (Reference Bauer, Betancourt and Garabedian2012) or Landreman & Jorge (Reference Landreman and Jorge2020)):
$D_{\rm Merc}=D_s+D_w+D_d$ (p. 23 in Bauer et al. (Reference Bauer, Betancourt and Garabedian2012) or Landreman & Jorge (Reference Landreman and Jorge2020)):
We reproduce this form for the sake of reference, as different forms of the Mercier criterion exist in the literature. In this case the instability criterion is ![]() $D_{\rm Merc}<0$.
$D_{\rm Merc}<0$.
Appendix B. Elliptic shaping
In this appendix, we derive in some more detail the expressions in § 3.2.1 which relate the parameters ![]() $\eta$ and
$\eta$ and ![]() $\sigma$ of the near-axis framework to the geometric properties of the elliptic cross-sections to leading order. Let us start by writing down the ellipse equation in the canonical form of a second-order polynomial. To do so we define for the leading cross-section
$\sigma$ of the near-axis framework to the geometric properties of the elliptic cross-sections to leading order. Let us start by writing down the ellipse equation in the canonical form of a second-order polynomial. To do so we define for the leading cross-section ![]() $X=\eta \cos \chi$ and
$X=\eta \cos \chi$ and ![]() $Y=(\sin \chi +\sigma \cos \chi )/\eta$, following (3.1). To construct the ellipse equation we seek expressions for
$Y=(\sin \chi +\sigma \cos \chi )/\eta$, following (3.1). To construct the ellipse equation we seek expressions for ![]() $\sin \chi$ and
$\sin \chi$ and ![]() $\cos \chi$, so that using the fundamental trigonometric relation of
$\cos \chi$, so that using the fundamental trigonometric relation of ![]() $\cos ^2\chi +\sin ^2\chi =1$,
$\cos ^2\chi +\sin ^2\chi =1$,
From this form, one may then construct the rotation angle and ellipticity of the ellipse:
 $$\begin{gather} \mathcal{E}=\frac{F}{2\eta^2}\left[1+\sqrt{1- \frac{4\eta^4}{F^2}}\right], \end{gather}$$
$$\begin{gather} \mathcal{E}=\frac{F}{2\eta^2}\left[1+\sqrt{1- \frac{4\eta^4}{F^2}}\right], \end{gather}$$ $$\begin{gather}\tan\vartheta=\frac{F-2\eta^4}{2\sigma\eta^2} \left[1+\sqrt{1+\frac{4\sigma^2\eta^4}{(F -2\eta^4)^2}}\right], \end{gather}$$
$$\begin{gather}\tan\vartheta=\frac{F-2\eta^4}{2\sigma\eta^2} \left[1+\sqrt{1+\frac{4\sigma^2\eta^4}{(F -2\eta^4)^2}}\right], \end{gather}$$
and ![]() $F=1+\sigma ^2+\eta ^4$. Here elongation is defined as the ratio of the major to the minor radius, and
$F=1+\sigma ^2+\eta ^4$. Here elongation is defined as the ratio of the major to the minor radius, and ![]() $\vartheta$ is the angle between the major radius and the positive
$\vartheta$ is the angle between the major radius and the positive ![]() $X$ direction.
$X$ direction.
The form of these expressions is reminiscent of a solution to a quadratic equation. In fact, one may rearrange (B2) in the following form:
where ![]() $\varTheta =\tan \vartheta$. Rearranging the latter and using the double-angle formula, we obtain
$\varTheta =\tan \vartheta$. Rearranging the latter and using the double-angle formula, we obtain
as used in the text. In an analogous way, and defining ![]() $\mathcal {E}=\tan e$,
$\mathcal {E}=\tan e$,
We give the geometric interpretations of the angles ![]() $\vartheta$ and
$\vartheta$ and ![]() $e$ in figure 1.
$e$ in figure 1.
We may also invert these relations to obtain a form for ![]() $\eta$ and
$\eta$ and ![]() $\sigma$ in the geometric
$\sigma$ in the geometric ![]() $\vartheta$ and
$\vartheta$ and ![]() $e$. Using (3.2a) and (3.2b):
$e$. Using (3.2a) and (3.2b):
Note that these expressions agree with what we know in the up–down symmetric limit, namely that in the limit of the major radius being aligned with the curvature direction (![]() $\vartheta \sim 0$ and
$\vartheta \sim 0$ and ![]() $\eta >1$), then
$\eta >1$), then ![]() $\eta ^2=1/\mathcal {E}$, and when aligned along the binormal,
$\eta ^2=1/\mathcal {E}$, and when aligned along the binormal, ![]() $\eta ^2=\mathcal {E}$.
$\eta ^2=\mathcal {E}$.
We remind the reader that the above is a description of the shape of the cross-section to leading order in the plane normal to the magnetic axis. In the tokamak case, this is what we call cross-sections in the ‘laboratory frame’, namely poloidal cross-sections that result from cuts of the configuration at a constant cylindrical angle. In a more general stellarator, this shape in the normal plane is not the same as in the laboratory frame. This difference reduces to a projection factor that modifies the shape of the cross-section. These changes are important to consider in the context of, for instance, quasisymmetric stellarators. With this in mind, we must consider the reinterpretation of ![]() $\eta$ as
$\eta$ as ![]() $\eta \rightarrow \eta /\kappa$ and the projection factor. Some attempts to describe the latter have been made by Landreman & Sengupta (Reference Landreman and Sengupta2018) and Rodríguez et al. (Reference Rodríguez, Sengupta and Bhattacharjee2022c), but the geometric meaning is generally obscure and complicated. In a forthcoming paper, we will present a rigorous geometric form that describes these changes. For now, we content ourselves with understanding its primary consequences, focusing on the stellarator-symmetric, quasisymmetric stellarator, particularly the cross-section at
$\eta \rightarrow \eta /\kappa$ and the projection factor. Some attempts to describe the latter have been made by Landreman & Sengupta (Reference Landreman and Sengupta2018) and Rodríguez et al. (Reference Rodríguez, Sengupta and Bhattacharjee2022c), but the geometric meaning is generally obscure and complicated. In a forthcoming paper, we will present a rigorous geometric form that describes these changes. For now, we content ourselves with understanding its primary consequences, focusing on the stellarator-symmetric, quasisymmetric stellarator, particularly the cross-section at ![]() $\phi =0$. The axis at this point has, by construction, its normal aligned with the major radius. However, generally, the magnetic axis is rotated about
$\phi =0$. The axis at this point has, by construction, its normal aligned with the major radius. However, generally, the magnetic axis is rotated about ![]() $\hat {R}$ by an angle
$\hat {R}$ by an angle ![]() $\nu$ (i.e. the angle between the binormal and the vertical
$\nu$ (i.e. the angle between the binormal and the vertical ![]() $\hat {z}$). From this inclination, the cross-section in the plane normal to the axis is re-scaled
$\hat {z}$). From this inclination, the cross-section in the plane normal to the axis is re-scaled ![]() $Y\rightarrow Y/\cos \nu$ in the laboratory frame. The ellipse thus shrinks in the vertical direction. For the most part, this is a simple adjustment that leaves
$Y\rightarrow Y/\cos \nu$ in the laboratory frame. The ellipse thus shrinks in the vertical direction. For the most part, this is a simple adjustment that leaves ![]() $\eta$ and
$\eta$ and ![]() $\sigma$ with most of their geometric interpretation.
$\sigma$ with most of their geometric interpretation.
Appendix C. Details of triangularity in the near-axis framework
In the main text, we assessed the effect of the shaping through second-harmonic modulation of the cross-sections. We did so in a geometrically intuitive form to motivate the relevant measure of the shaping strength and the final form of ![]() $\delta _{\rm tok}$. We did not, however, provide a derivation for the final expression for triangularity, (3.3). Filling that gap is the purpose of this appendix.
$\delta _{\rm tok}$. We did not, however, provide a derivation for the final expression for triangularity, (3.3). Filling that gap is the purpose of this appendix.
Let us commence by defining triangularity in an up–down symmetric tokamak. We write this definition as ![]() $\delta _{\rm tok}=(R_{\rm geo}-R_{{\rm upper}})/a$, where
$\delta _{\rm tok}=(R_{\rm geo}-R_{{\rm upper}})/a$, where ![]() $R_{\rm geo}=(R_{\min }+R_{\max })/2$,
$R_{\rm geo}=(R_{\min }+R_{\max })/2$, ![]() $a=(R_{\max }-R_{\min })/2$,
$a=(R_{\max }-R_{\min })/2$, ![]() $R_{{\rm upper}}$ is the position of the turning point in the vertical direction and
$R_{{\rm upper}}$ is the position of the turning point in the vertical direction and ![]() $R_{{\min }/{\max }}$ are the leftmost and outermost points of the cross-section along the symmetry line.Footnote 9 See the diagram in figure 7 for a depiction of these measures. Triangularity is the relative displacement of the vertical tips of the cross-section from the mid-point along the symmetry line.
$R_{{\min }/{\max }}$ are the leftmost and outermost points of the cross-section along the symmetry line.Footnote 9 See the diagram in figure 7 for a depiction of these measures. Triangularity is the relative displacement of the vertical tips of the cross-section from the mid-point along the symmetry line.

Figure 7. Basic definitions for triangularity. The diagram defines the length scales needed to compute the triangularity of an up–downsymmetric cross-section indicated for the outermost surface. The evolution of the geometric centre ![]() $R_{\rm geo}$ from one flux surface to another defines the Shafranov shift,
$R_{\rm geo}$ from one flux surface to another defines the Shafranov shift, ![]() $\varDelta _X$, with the negative sign indicating displacement outwards.
$\varDelta _X$, with the negative sign indicating displacement outwards.
To make rigorous contact with the near-axis modulation, consider ![]() $X$ and
$X$ and ![]() $Y$ (the normal and binormal directions of the cross-section) to coincide with the ‘laboratory frame’. In the tokamak context, this is, in fact, correct (taking into consideration the minus sign
$Y$ (the normal and binormal directions of the cross-section) to coincide with the ‘laboratory frame’. In the tokamak context, this is, in fact, correct (taking into consideration the minus sign ![]() $X\rightarrow -R$ following the direction in which the major radius points), a notion that needs some adjustment in the more general quasisymmetric case, which we briefly touch upon at the end of this appendix. Assuming up–down symmetry, and first only keeping
$X\rightarrow -R$ following the direction in which the major radius points), a notion that needs some adjustment in the more general quasisymmetric case, which we briefly touch upon at the end of this appendix. Assuming up–down symmetry, and first only keeping ![]() $X_{22}^C$ and
$X_{22}^C$ and ![]() $X_{20}$ shaping, we may find the various geometric quantities in
$X_{20}$ shaping, we may find the various geometric quantities in ![]() $\delta _{\rm tok}$ straightforwardly. The points
$\delta _{\rm tok}$ straightforwardly. The points ![]() $R_{\min }$ and
$R_{\min }$ and ![]() $R_{\max }$ are
$R_{\max }$ are ![]() $R_{\min /\max }=1\mp \epsilon X_{11}^C-\epsilon ^2(X_{20}+X_{22}^C)$. The turning point
$R_{\min /\max }=1\mp \epsilon X_{11}^C-\epsilon ^2(X_{20}+X_{22}^C)$. The turning point ![]() $R_{\rm upper}$ can simply be found by requiring
$R_{\rm upper}$ can simply be found by requiring ![]() $\partial _\chi Y=0$, which occurs at
$\partial _\chi Y=0$, which occurs at ![]() $\chi ={\rm \pi} /2$ asymptotically, and thus
$\chi ={\rm \pi} /2$ asymptotically, and thus ![]() $R_{\rm upper}=1-\epsilon ^2(X_{20}-X_{22}^C)$. With these results, it then follows that
$R_{\rm upper}=1-\epsilon ^2(X_{20}-X_{22}^C)$. With these results, it then follows that
for a positive ![]() $X_{11}^C$. A positive value of
$X_{11}^C$. A positive value of ![]() $X_{22}^C$ then corresponds to what is known as negative triangularity (end-points of the cross-section pointing in the direction of larger
$X_{22}^C$ then corresponds to what is known as negative triangularity (end-points of the cross-section pointing in the direction of larger ![]() $R$). We see the direct relation between
$R$). We see the direct relation between ![]() $X_{22}^C$ and triangularity through the measure of strength motivated in the main text.
$X_{22}^C$ and triangularity through the measure of strength motivated in the main text.
The effect of ![]() $Y_{22}^S$ on tokamak triangularity is analogous to that of
$Y_{22}^S$ on tokamak triangularity is analogous to that of ![]() $X_{22}^C$. In that case, we may once again compute
$X_{22}^C$. In that case, we may once again compute ![]() $R_{\rm upper}$ as the position for the turning point
$R_{\rm upper}$ as the position for the turning point ![]() $\partial _\chi Y=0$. Doing so yields an expression for
$\partial _\chi Y=0$. Doing so yields an expression for ![]() $\cos \chi$ for the turning point, which may be expanded asymptotically in
$\cos \chi$ for the turning point, which may be expanded asymptotically in ![]() $\epsilon$, as
$\epsilon$, as ![]() $\cos \chi \sim 2\epsilon Y_{22}^S/Y_{11}^S$. In this limit,
$\cos \chi \sim 2\epsilon Y_{22}^S/Y_{11}^S$. In this limit, ![]() $R_{\rm upper}\approx 1+2\epsilon ^2X_{11}^CY_{22}^S/Y_{11}^S$. With this and the symmetry line being unaffected,
$R_{\rm upper}\approx 1+2\epsilon ^2X_{11}^CY_{22}^S/Y_{11}^S$. With this and the symmetry line being unaffected, ![]() $\delta _{\rm tok}\sim 2\epsilon Y_{22}^S/Y_{11}^S$. Importantly, the term is analogous to
$\delta _{\rm tok}\sim 2\epsilon Y_{22}^S/Y_{11}^S$. Importantly, the term is analogous to ![]() $X_{22}^C$, but with the opposite sign.
$X_{22}^C$, but with the opposite sign.
Of course, in general, these two forms of ‘triangular’ shaping coincide and thus will interact in some form to result in a net triangularity. Here the asymptotic nature of the approach becomes highly valuable. In the limit ![]() $\epsilon \rightarrow 0$, each of these contributes to the total triangularity independently:Footnote 10
$\epsilon \rightarrow 0$, each of these contributes to the total triangularity independently:Footnote 10
Before concluding this appendix, we consider the case of triangularity in quasisymmetric stellarators. The derivation above holds at every toroidal angle ![]() $\phi$ in which the cross-sections are up–down symmetric.
$\phi$ in which the cross-sections are up–down symmetric.
C.1. Projection to ‘laboratory frame’
We expect the deformation of cross-sections when going from the plane normal to the axis to the cylindrical laboratory frame to affect triangularity. After careful consideration of geometry and asymptotics, we find that the triangularity in the laboratory frame of the up–down symmetric cross-section at the origin of a quasisymmetric stellarator is
 \begin{equation} \delta_{\rm lab}=\delta_{\rm tok}+\frac{\epsilon}{R_0} \left[\frac{1}{2}\left(\frac{\kappa}{\eta}\right)^3 \left(1+3\frac{\partial_\phi^2 R_0}{R_0}\right)- \frac{\eta}{\kappa}\right]\sin^2\nu, \end{equation}
\begin{equation} \delta_{\rm lab}=\delta_{\rm tok}+\frac{\epsilon}{R_0} \left[\frac{1}{2}\left(\frac{\kappa}{\eta}\right)^3 \left(1+3\frac{\partial_\phi^2 R_0}{R_0}\right)- \frac{\eta}{\kappa}\right]\sin^2\nu, \end{equation}
where ![]() $\phi$ represents the cylindrical coordinate,
$\phi$ represents the cylindrical coordinate, ![]() $R_0$ is the radial position of the magnetic axis,
$R_0$ is the radial position of the magnetic axis, ![]() $\nu$ the angle defined previously denoting the deviation of the axis binormal from
$\nu$ the angle defined previously denoting the deviation of the axis binormal from ![]() $\hat {z}$ and all quantities are evaluated at the origin
$\hat {z}$ and all quantities are evaluated at the origin ![]() $\phi =0$. Of course, in the limit of
$\phi =0$. Of course, in the limit of ![]() $\nu =0$, the triangularity is precisely that computed before,
$\nu =0$, the triangularity is precisely that computed before, ![]() $\delta _{\rm tok}$.
$\delta _{\rm tok}$.
The critical realisation is that the only difference is in an order ![]() $\sin ^2\nu$ term that shifts the value of
$\sin ^2\nu$ term that shifts the value of ![]() $\delta _{\rm tok}$. The difference depends solely on the shape of the axis and
$\delta _{\rm tok}$. The difference depends solely on the shape of the axis and ![]() $\eta$, but no other higher-order quantity. A change of triangularity in the normal plane thus directly leads to an equivalent change in the laboratory frame. No rescaling occurs because triangularity is a quantity normalised to the underlying ellipse shape, which we also learnt to be deformed. The ratio remains unchanged. Thus, with this caveat, we may mostly ignore this difference when discussing the effects of increasing or decreasing triangularity, understood as a consequence of second-order choices.
$\eta$, but no other higher-order quantity. A change of triangularity in the normal plane thus directly leads to an equivalent change in the laboratory frame. No rescaling occurs because triangularity is a quantity normalised to the underlying ellipse shape, which we also learnt to be deformed. The ratio remains unchanged. Thus, with this caveat, we may mostly ignore this difference when discussing the effects of increasing or decreasing triangularity, understood as a consequence of second-order choices.
C.2. Triangularity and up–down asymmetry
We constructed the notion of triangularity in the context of an up–down symmetric cross-section. Breaking this symmetry needs some adjustments in the analysis. The symmetry in the near-axis framework may be broken in two different ways. On the one hand, asymmetry could arise purely at second order from the modulation of ![]() $X_{22}^S$ and
$X_{22}^S$ and ![]() $Y_{22}^C$. As the main text argues, their effect is analogous to triangularity but in the vertical direction. Thus one may define
$Y_{22}^C$. As the main text argues, their effect is analogous to triangularity but in the vertical direction. Thus one may define ![]() $\delta _y$ (the vertical triangularity) as a measure of asymmetry.
$\delta _y$ (the vertical triangularity) as a measure of asymmetry.
The up–down symmetry may also be broken at first order whenever the elliptical cross-sections are not aligned with the Frenet–Serret basis. In that case, regular and up–down triangularity will no longer correspond to the expressions for ![]() $\delta _{\rm tok}$ and
$\delta _{\rm tok}$ and ![]() $\delta _y$. The rotation of the underlying ellipse mixes the shaping harmonics into a new linear combination. A reasonable way to define the geometry of such shapes is to define
$\delta _y$. The rotation of the underlying ellipse mixes the shaping harmonics into a new linear combination. A reasonable way to define the geometry of such shapes is to define ![]() $\delta _{\rm tok}$ and
$\delta _{\rm tok}$ and ![]() $\delta _y$ not in the Frenet frame but rather in the frame of the ellipse. This change requires a mapping of the shape coefficients that takes the rotation of the ellipse
$\delta _y$ not in the Frenet frame but rather in the frame of the ellipse. This change requires a mapping of the shape coefficients that takes the rotation of the ellipse ![]() $\vartheta$ into account. Defining
$\vartheta$ into account. Defining ![]() $X'$ and
$X'$ and ![]() $Y'$ as the rotated coordinates, and
$Y'$ as the rotated coordinates, and ![]() $\mathbb {C}=\cos \vartheta$ and
$\mathbb {C}=\cos \vartheta$ and ![]() $\mathbb {S}=\sin \vartheta$, where
$\mathbb {S}=\sin \vartheta$, where ![]() $\vartheta$ is the rotation angle of the ellipse as given by (3.2b), we rotate the original ellipse and define a new poloidal angle
$\vartheta$ is the rotation angle of the ellipse as given by (3.2b), we rotate the original ellipse and define a new poloidal angle ![]() $\chi '$ so that
$\chi '$ so that
This expression describes a frame-aligned ellipse, a baseline we used to define triangularity in this appendix. Here ![]() $\chi '=\chi -\varTheta$, where
$\chi '=\chi -\varTheta$, where ![]() $\tan \varTheta =-\mathbb {S}/(\eta ^2\mathbb {C}+\sigma \mathbb {S})$. We get a similar transformation for the higher order. That is, we rotate the
$\tan \varTheta =-\mathbb {S}/(\eta ^2\mathbb {C}+\sigma \mathbb {S})$. We get a similar transformation for the higher order. That is, we rotate the ![]() $X_2$ and
$X_2$ and ![]() $Y_2$ components by
$Y_2$ components by ![]() $-\vartheta$ and re-express the harmonics in
$-\vartheta$ and re-express the harmonics in ![]() $\chi =\chi '-\varTheta$ to obtain
$\chi =\chi '-\varTheta$ to obtain ![]() $X_2'$ and
$X_2'$ and ![]() $Y_2'$. Then we define using (3.3) and (3.4),
$Y_2'$. Then we define using (3.3) and (3.4), ![]() $\delta '$ and
$\delta '$ and ![]() $\delta _y'$, which will involve generally complicated linear combinations of second-order parameters. Doing so is algebraically untidy but may be accomplished using computational algebra. We do not write down the expressions here, as they do not provide much insight other than showcasing the mixing effect of the ellipse rotation. We only use some numerical examples of it in the main text.
$\delta _y'$, which will involve generally complicated linear combinations of second-order parameters. Doing so is algebraically untidy but may be accomplished using computational algebra. We do not write down the expressions here, as they do not provide much insight other than showcasing the mixing effect of the ellipse rotation. We only use some numerical examples of it in the main text.
Appendix D. Details of the generalised Shafranov shift
We introduced in the main text a definition of a generalised Shafranov shift that describes the relative displacement of cross-section centres. This generalised form was originally presented in Rodríguez et al. (Reference Rodríguez, Sengupta and Bhattacharjee2022c). The expression reduces to the axisymmetric limit as shown by Landreman & Jorge (Reference Landreman and Jorge2020). As emphasised, the arbitrariness to the centre of cross-sections extends to the definition of the Shafranov shift. This appendix will motivate the form in (3.5) taken as the definition of the Shafranov shift.
Consider a coordinate map that maps the cross-sections in the plane normal to the axis (however complicated) into circular shapes (a sort of normal form of the cross-section). Once we have performed such a mapping, we end up with circles, which have a unique centre. The transformation will generally be complicated, but it must exist, as the cross-sections are, after all, an embedding of ![]() $S^1$ in the plane.
$S^1$ in the plane.
Let us state how to achieve this at first order. The main idea will be to cast the equations describing ![]() $X$ and
$X$ and ![]() $Y$ in a form that explicitly gives
$Y$ in a form that explicitly gives ![]() $\cos \chi$ and
$\cos \chi$ and ![]() $\sin \chi$. In matrix form,
$\sin \chi$. In matrix form,
 \begin{equation} \begin{pmatrix} X \\ Y \end{pmatrix}=\epsilon\begin{pmatrix} X_{11}^C\cos\chi \\ Y_{11}^S(\sin\chi+\sigma\cos\chi) \end{pmatrix}=\epsilon\underbrace{\begin{pmatrix} X_{11}^C & 0 \\ \sigma Y_{11}^S & Y_{11}^S \end{pmatrix}}_{\mathcal{M}_{(1)}}\begin{pmatrix} \cos\chi \\ \sin\chi \end{pmatrix}. \end{equation}
\begin{equation} \begin{pmatrix} X \\ Y \end{pmatrix}=\epsilon\begin{pmatrix} X_{11}^C\cos\chi \\ Y_{11}^S(\sin\chi+\sigma\cos\chi) \end{pmatrix}=\epsilon\underbrace{\begin{pmatrix} X_{11}^C & 0 \\ \sigma Y_{11}^S & Y_{11}^S \end{pmatrix}}_{\mathcal{M}_{(1)}}\begin{pmatrix} \cos\chi \\ \sin\chi \end{pmatrix}. \end{equation}Inverting this,
and computing the norm provide the equation of a circle ![]() $(X')^2+(Y')^2=\epsilon ^2$, where
$(X')^2+(Y')^2=\epsilon ^2$, where
Note that this is the same as before when defining the ellipticity and rotation angles in the previous appendix. The ellipses become circles in the transformed space ![]() $(X',Y')$.
$(X',Y')$.
With this leading-order procedure in mind, we may construct the ‘circles’ for the second-order shaping. To do so, we use trigonometric relations of the form ![]() $\cos 2\chi =1-2\sin ^2\chi$, to
$\cos 2\chi =1-2\sin ^2\chi$, to ![]() $O(\epsilon ^2)$. With that, and multiplying through
$O(\epsilon ^2)$. With that, and multiplying through ![]() $\mathcal {M}^{(1)}$,
$\mathcal {M}^{(1)}$,
 \begin{align} &\begin{pmatrix} X' \\ Y' \end{pmatrix}-\epsilon^2\begin{pmatrix} \bar{X}_{20}+\bar{X}_{22}^C \\ \bar{Y}_{20}(1-\sigma)+\bar{Y}_{22}^C-\sigma\bar{X}_{22}^C \end{pmatrix}\nonumber\\ &\quad =\epsilon\begin{pmatrix} 1+2\epsilon\bar{X}_{22}^S\sin\chi & -2\epsilon\bar{X}_{22}^C\sin\chi \\ 2\epsilon(\bar{Y}_{22}^S-\sigma\bar{X}_{22}^S)\sin\chi & 1+2\epsilon(\sigma\bar{X}_{22}^C-\bar{Y}_{22}^C)\sin\chi \end{pmatrix}\begin{pmatrix} \cos\chi \\ \sin\chi \end{pmatrix}, \end{align}
\begin{align} &\begin{pmatrix} X' \\ Y' \end{pmatrix}-\epsilon^2\begin{pmatrix} \bar{X}_{20}+\bar{X}_{22}^C \\ \bar{Y}_{20}(1-\sigma)+\bar{Y}_{22}^C-\sigma\bar{X}_{22}^C \end{pmatrix}\nonumber\\ &\quad =\epsilon\begin{pmatrix} 1+2\epsilon\bar{X}_{22}^S\sin\chi & -2\epsilon\bar{X}_{22}^C\sin\chi \\ 2\epsilon(\bar{Y}_{22}^S-\sigma\bar{X}_{22}^S)\sin\chi & 1+2\epsilon(\sigma\bar{X}_{22}^C-\bar{Y}_{22}^C)\sin\chi \end{pmatrix}\begin{pmatrix} \cos\chi \\ \sin\chi \end{pmatrix}, \end{align}
where the overline indicates normalisation with respect to ![]() $X_{11}^C$ or
$X_{11}^C$ or ![]() $Y_{11}^S$ respectively. Inverting the matrix and keeping the relevant orders in
$Y_{11}^S$ respectively. Inverting the matrix and keeping the relevant orders in ![]() $\epsilon$, we can define a circle
$\epsilon$, we can define a circle ![]() $(X^*)^2+(Y^*)^2=\epsilon ^2$:
$(X^*)^2+(Y^*)^2=\epsilon ^2$:
 \begin{align} \begin{pmatrix} X^* \\ Y^* \end{pmatrix}&= \frac{1}{1+2\epsilon(\bar{X}_{22}^S+\sigma\bar{X}_{22}^C -\bar{Y}_{22}^C)}\nonumber\\ &\quad \begin{pmatrix} 1-2\epsilon\bar{Y}_{22}^C\sin\chi & 2\epsilon\bar{X}_{22}^C\sin\chi \\ -(\sigma+2\epsilon\bar{Y}_{22}^S\sin\chi) & 1+2\epsilon\bar{X}_{22}^S\sin\chi \end{pmatrix}\begin{pmatrix} \bar{X}-\epsilon^2(\bar{X}_{20}+\bar{X}_{22}^C) \\ \bar{Y}-\epsilon^2(\bar{Y}_{20}+Y_{22}^C) \end{pmatrix}. \end{align}
\begin{align} \begin{pmatrix} X^* \\ Y^* \end{pmatrix}&= \frac{1}{1+2\epsilon(\bar{X}_{22}^S+\sigma\bar{X}_{22}^C -\bar{Y}_{22}^C)}\nonumber\\ &\quad \begin{pmatrix} 1-2\epsilon\bar{Y}_{22}^C\sin\chi & 2\epsilon\bar{X}_{22}^C\sin\chi \\ -(\sigma+2\epsilon\bar{Y}_{22}^S\sin\chi) & 1+2\epsilon\bar{X}_{22}^S\sin\chi \end{pmatrix}\begin{pmatrix} \bar{X}-\epsilon^2(\bar{X}_{20}+\bar{X}_{22}^C) \\ \bar{Y}-\epsilon^2(\bar{Y}_{20}+Y_{22}^C) \end{pmatrix}. \end{align} Figure 8 shows an example of this transformation. The transformation matrix reduces to the ellipse map to leading order ![]() $\epsilon$. However, it is clear from this map that cross-sections have a relative shift. From that, we may read off the Shafranov shift:
$\epsilon$. However, it is clear from this map that cross-sections have a relative shift. From that, we may read off the Shafranov shift:
We refer to these as generalised Shafranov shift. It satisfies the necessary circular cross-section axisymmetric limit and holds for any ![]() $\phi$ and second-order shaping. The quantity
$\phi$ and second-order shaping. The quantity ![]() $\varDelta _x$ is directly related to the mid-point of the cross-section around the up–down symmetry line. The shift in the
$\varDelta _x$ is directly related to the mid-point of the cross-section around the up–down symmetry line. The shift in the ![]() $Y$ direction has a similar meaning but in the perpendicular direction. We emphasise that the approach presented is not unique, and the transformation
$Y$ direction has a similar meaning but in the perpendicular direction. We emphasise that the approach presented is not unique, and the transformation ![]() $(X,Y)\rightarrow (X^*,Y^*)$ could have been chosen in another way. However, those forms would not generally match the axisymmetric limit.Footnote 11
$(X,Y)\rightarrow (X^*,Y^*)$ could have been chosen in another way. However, those forms would not generally match the axisymmetric limit.Footnote 11

Figure 8. Example of the coordinate map to define the Shafranov shift. Example showing the coordinate map transformation of a second-order shape onto concentric circles. We can obtain and identify the cross-section shift from this mapping with the Shafranov shift. The deviation in ![]() $(X^*,Y^*)$ from a circle (broken line) results from higher-order effects.
$(X^*,Y^*)$ from a circle (broken line) results from higher-order effects.
To conclude this appendix, we must briefly touch on the effect of the projection to the ‘laboratory frame’ on the Shafranov shift. Focusing on the shift ![]() $\varDelta _x$, relevant for the up–down symmetric cross-section, one may show that it remains invariant. Although effectively
$\varDelta _x$, relevant for the up–down symmetric cross-section, one may show that it remains invariant. Although effectively ![]() $X_{20}$ and
$X_{20}$ and ![]() $X_{22}^C$ each have a shift from the projection, these are opposed, and thus the Shafranov shift is invariant. No scaling is involved because
$X_{22}^C$ each have a shift from the projection, these are opposed, and thus the Shafranov shift is invariant. No scaling is involved because ![]() $X$ is aligned with the major radius. Thus we expect to find a change on
$X$ is aligned with the major radius. Thus we expect to find a change on ![]() $\varDelta _y$. These changes are particularly complex, as not only does the projection involve the
$\varDelta _y$. These changes are particularly complex, as not only does the projection involve the ![]() $1/\cos \nu$ scaling, but the components of
$1/\cos \nu$ scaling, but the components of ![]() $Z_2$ are also involved. Thankfully we do not need to consider this.
$Z_2$ are also involved. Thankfully we do not need to consider this.
Appendix E. Governing near-axis equations
In order to relate the near-axis shaping to ![]() $|\boldsymbol {B}|$ harmonics and other natural near-axis elements, it is necessary to know the expressions that relate them. These come from the asymptotic expansion in powers of the distance from the magnetic axis of the magnetic field and its governing equilibrium and magnetic equations. The original works by Garren & Boozer (Reference Garren and Boozer1991a,Reference Garren and Boozerb) and Landreman & Sengupta (Reference Landreman and Sengupta2019) are good places for reference of these equations, while Rodríguez & Bhattacharjee (Reference Rodríguez and Bhattacharjee2021a) gives a more general form of the description beyond equilibria with isotropic pressure. We here use the notation in Landreman & Sengupta (Reference Landreman and Sengupta2019).
$|\boldsymbol {B}|$ harmonics and other natural near-axis elements, it is necessary to know the expressions that relate them. These come from the asymptotic expansion in powers of the distance from the magnetic axis of the magnetic field and its governing equilibrium and magnetic equations. The original works by Garren & Boozer (Reference Garren and Boozer1991a,Reference Garren and Boozerb) and Landreman & Sengupta (Reference Landreman and Sengupta2019) are good places for reference of these equations, while Rodríguez & Bhattacharjee (Reference Rodríguez and Bhattacharjee2021a) gives a more general form of the description beyond equilibria with isotropic pressure. We here use the notation in Landreman & Sengupta (Reference Landreman and Sengupta2019).
For completeness, we write down the expressions for the quasisymmetric case (which includes axisymmetry as a particular case). Following the notation of (2.1), the expansion components of position functions have the form
and similarly for ![]() $Y$ and
$Y$ and ![]() $Z$.
$Z$.
The ![]() $X_2$ components come from the requirements on
$X_2$ components come from the requirements on ![]() $|\boldsymbol {B}|$ and the Jacobian (see (A34) and (A36) in Landreman & Sengupta (Reference Landreman and Sengupta2019) or Appendix C in Rodríguez & Bhattacharjee (Reference Rodríguez and Bhattacharjee2021a)):
$|\boldsymbol {B}|$ and the Jacobian (see (A34) and (A36) in Landreman & Sengupta (Reference Landreman and Sengupta2019) or Appendix C in Rodríguez & Bhattacharjee (Reference Rodríguez and Bhattacharjee2021a)):
 \begin{align} X_{2,0}&=\frac{1}{4l'
\kappa }[l' \kappa ^2 X_{1,1}^C{}^2 +(l'\tau^2+\iota
_0^2/l') (X_{1,1}^C{}^2+Y_{1,1}^C{}^2 +Y_{1,1}^S{}{}^2)-2
\tau Y_{1,1}^C X_{1,1}^C{}'\nonumber\\ &\quad +2 \tau
X_{1,1}^C Y_{1,1}^C{}'+2 (\iota _0/l') (2l' \tau X_{1,1}^C
Y_{1,1}^S{}+Y_{1,1}^S{} Y_{1,1}^C{}'-Y_{1,1}^C
Y_{1,1}^S{}')\nonumber\\ &\quad
+X_{1,1}^C{}'{}^2+Y_{1,1}^C{}'{}^2+Y_{1,1}^S{}'{}^2 +4
Z_{20}']\nonumber\\ &\quad +\frac{1}{ B_0^3 (l')^2 \kappa }
\left[G_0^2 \left(B_{20}-\frac{3}{4} B_0 \eta ^2\right) -
B_0 G_0 (G_1+\iota_0I_1)\right],\end{align}
\begin{align} X_{2,0}&=\frac{1}{4l'
\kappa }[l' \kappa ^2 X_{1,1}^C{}^2 +(l'\tau^2+\iota
_0^2/l') (X_{1,1}^C{}^2+Y_{1,1}^C{}^2 +Y_{1,1}^S{}{}^2)-2
\tau Y_{1,1}^C X_{1,1}^C{}'\nonumber\\ &\quad +2 \tau
X_{1,1}^C Y_{1,1}^C{}'+2 (\iota _0/l') (2l' \tau X_{1,1}^C
Y_{1,1}^S{}+Y_{1,1}^S{} Y_{1,1}^C{}'-Y_{1,1}^C
Y_{1,1}^S{}')\nonumber\\ &\quad
+X_{1,1}^C{}'{}^2+Y_{1,1}^C{}'{}^2+Y_{1,1}^S{}'{}^2 +4
Z_{20}']\nonumber\\ &\quad +\frac{1}{ B_0^3 (l')^2 \kappa }
\left[G_0^2 \left(B_{20}-\frac{3}{4} B_0 \eta ^2\right) -
B_0 G_0 (G_1+\iota_0I_1)\right],\end{align}
 \begin{align}
X_{2,2}^C&=\frac{1}{4\kappa}\left[4\frac{B_{22}^C}{B_0}
-3\eta^2+\kappa^2(X_{11}^C)^2+(\tau^2-(\bar{\iota}_0/l')^2)
((X_{11}^C)^2+(Y_{11}^C)^2-(Y_{11}^S)^2)\right.\nonumber\\
&\quad +\frac{1}{(l')^2}({(X_{11}^C)'}^2+{(Y_{11}^C)'}^2
-{(Y_{11}^S)'}^2)-\frac{2\tau}{l'} Y_{11}^C{X_{11}^C}'
+\frac{2\tau}{l'} X_{11}^C{Y_{11}^C}'\nonumber\\ &\quad
+\left.\frac{2\bar{\iota}_0}{(l')^2}(Y_{11}^S{Y_{11}^C}'
+Y_{11}^C{Y_{11}^S}')+\frac{8\bar{\iota}_0}{l'}Z_{22}^S
+\frac{4}{l'}{Z_{22}^C}'\right],\end{align}
\begin{align}
X_{2,2}^C&=\frac{1}{4\kappa}\left[4\frac{B_{22}^C}{B_0}
-3\eta^2+\kappa^2(X_{11}^C)^2+(\tau^2-(\bar{\iota}_0/l')^2)
((X_{11}^C)^2+(Y_{11}^C)^2-(Y_{11}^S)^2)\right.\nonumber\\
&\quad +\frac{1}{(l')^2}({(X_{11}^C)'}^2+{(Y_{11}^C)'}^2
-{(Y_{11}^S)'}^2)-\frac{2\tau}{l'} Y_{11}^C{X_{11}^C}'
+\frac{2\tau}{l'} X_{11}^C{Y_{11}^C}'\nonumber\\ &\quad
+\left.\frac{2\bar{\iota}_0}{(l')^2}(Y_{11}^S{Y_{11}^C}'
+Y_{11}^C{Y_{11}^S}')+\frac{8\bar{\iota}_0}{l'}Z_{22}^S
+\frac{4}{l'}{Z_{22}^C}'\right],\end{align}
 \begin{align} X_{2,2}^S&=\frac{1}{2\kappa}\left[2\frac{B_{22}^S}{B_0}
+(\tau^2-(\bar{\iota}_0/l')^2)Y_{11}^CY_{11}^S-\frac{\tau}{l'}
(Y_{11}^S{X_{11}^C}'-X_{11}^C{Y_{11}^S}')\right.\nonumber\\ &\quad +\left.\frac{1}{(l')^2}{Y_{11}^S}'{Y_{11}^C}'- \frac{\bar{\iota}_0}{(l')^2}(X_{11}^C{X_{11}^C}'+Y_{11}^Y{Y_{11}^C}' -Y_{11}^S{Y_{11}^S}')+\frac{4\bar{\iota}_0}{l'}Z_{22}^C +\frac{2}{l'}{Z_{22}^S}'\right], \end{align}
\begin{align} X_{2,2}^S&=\frac{1}{2\kappa}\left[2\frac{B_{22}^S}{B_0}
+(\tau^2-(\bar{\iota}_0/l')^2)Y_{11}^CY_{11}^S-\frac{\tau}{l'}
(Y_{11}^S{X_{11}^C}'-X_{11}^C{Y_{11}^S}')\right.\nonumber\\ &\quad +\left.\frac{1}{(l')^2}{Y_{11}^S}'{Y_{11}^C}'- \frac{\bar{\iota}_0}{(l')^2}(X_{11}^C{X_{11}^C}'+Y_{11}^Y{Y_{11}^C}' -Y_{11}^S{Y_{11}^S}')+\frac{4\bar{\iota}_0}{l'}Z_{22}^C +\frac{2}{l'}{Z_{22}^S}'\right], \end{align}
where we define the pressure gradient to include the constant factor ![]() $\mu _0=4{\rm \pi} \times 10^{-7}$ often shown explicitly, and we use the shorthand
$\mu _0=4{\rm \pi} \times 10^{-7}$ often shown explicitly, and we use the shorthand ![]() $l'=\mathrm {d}l/\mathrm {d}\phi$. Here (see (A27)–(A29) in Landreman & Sengupta (Reference Landreman and Sengupta2019) or (24) in Rodríguez & Bhattacharjee (Reference Rodríguez and Bhattacharjee2021a)),
$l'=\mathrm {d}l/\mathrm {d}\phi$. Here (see (A27)–(A29) in Landreman & Sengupta (Reference Landreman and Sengupta2019) or (24) in Rodríguez & Bhattacharjee (Reference Rodríguez and Bhattacharjee2021a)),
which follow from the divergenceless and flux surface nature of the field. The shapes ![]() $\{X_2\}$ and the magnetic field harmonics
$\{X_2\}$ and the magnetic field harmonics ![]() $\{B_2\}$ are intimately related.
$\{B_2\}$ are intimately related.
Then (see (A25) and (A26) in Garren & Boozer (Reference Garren and Boozer1991a) or (27) and (28) in Rodríguez & Bhattacharjee (Reference Rodríguez and Bhattacharjee2021a)),
where ![]() $Y_{2,2}^C=Y_{2,0}+\tilde {Y}_{2,2}^C$ and (see Rodríguez & Bhattacharjee (Reference Rodríguez and Bhattacharjee2021a,Reference Rodríguez and Bhattacharjeeb) in the isotropic limit)
$Y_{2,2}^C=Y_{2,0}+\tilde {Y}_{2,2}^C$ and (see Rodríguez & Bhattacharjee (Reference Rodríguez and Bhattacharjee2021a,Reference Rodríguez and Bhattacharjeeb) in the isotropic limit)
 \begin{align} Y_{20}&=\frac{1}{2 \bar{\iota}_0 \kappa^2} \left[4l'\eta^2 (\tilde{Y}_{22}^C Z_{22}^S+Y_{22}^S ({Z}_{20}-Z_{22}^C))+\eta ^2 \tilde{Y}_{22}^C \left(2\frac{I_2}{B_0}-\tau\right) l'\right.\nonumber\\ &\quad +\eta ^2 {X_{22}^C}' -\kappa l'Z_{20} (\eta ^2-4 \kappa (X_{22}^C-\sigma X_{22}^S))-4l' \kappa^2 \sigma X_{22}^C Z_{22}^S-4l'\kappa^2 X_{20} Z_{22}^C\nonumber\\ &\quad+4l' \kappa^2 \sigma X_{20} Z_{22}^S+2 \eta ^2 \iota _0 X_{22}^S +4l'\kappa^2 \sigma X_{22}^S Z_{22}^C+\eta ^2 \kappa l' Z_{22}^C- \eta ^2 X_{20}{}'\nonumber\\ &\quad+\left.\kappa^2 \left((\sigma X_{20} - \sigma X_{22}^C- X_{22}^S) \left(2\frac{I_2}{B_0}-\tau\right)l'+ \sigma \tilde{Y}_{22}^C{}'-2 \iota _0 (\tilde{Y}_{22}^C-\sigma Y_{22}^S) + Y_{22}^S{}'\right)\right]. \end{align}
\begin{align} Y_{20}&=\frac{1}{2 \bar{\iota}_0 \kappa^2} \left[4l'\eta^2 (\tilde{Y}_{22}^C Z_{22}^S+Y_{22}^S ({Z}_{20}-Z_{22}^C))+\eta ^2 \tilde{Y}_{22}^C \left(2\frac{I_2}{B_0}-\tau\right) l'\right.\nonumber\\ &\quad +\eta ^2 {X_{22}^C}' -\kappa l'Z_{20} (\eta ^2-4 \kappa (X_{22}^C-\sigma X_{22}^S))-4l' \kappa^2 \sigma X_{22}^C Z_{22}^S-4l'\kappa^2 X_{20} Z_{22}^C\nonumber\\ &\quad+4l' \kappa^2 \sigma X_{20} Z_{22}^S+2 \eta ^2 \iota _0 X_{22}^S +4l'\kappa^2 \sigma X_{22}^S Z_{22}^C+\eta ^2 \kappa l' Z_{22}^C- \eta ^2 X_{20}{}'\nonumber\\ &\quad+\left.\kappa^2 \left((\sigma X_{20} - \sigma X_{22}^C- X_{22}^S) \left(2\frac{I_2}{B_0}-\tau\right)l'+ \sigma \tilde{Y}_{22}^C{}'-2 \iota _0 (\tilde{Y}_{22}^C-\sigma Y_{22}^S) + Y_{22}^S{}'\right)\right]. \end{align} Finally we have the self-consistent equilibrium condition which in an ideally quasisymmetric case reads (see Rodríguez Reference Rodríguez2022), using the shorthand ![]() $\tilde {\tau }=\tau -I_2/B_0$,
$\tilde {\tau }=\tau -I_2/B_0$,
where
where
 \begin{align}
\mathcal{D}_{{-}1}&={-}\frac{8\kappa^2}{G_0\eta}
\frac{\mathrm{d}}{\mathrm{d}\phi}\left\{\frac{1}{\kappa^2}
\frac{\mathrm{d}}{\mathrm{d}\phi}\left[\tilde{\tau}^2+
\frac{1}{(l')^2}\left(\frac{\kappa'}{\kappa}\right)^2
+\frac{\kappa^2}{4}\right]\right\},\end{align}
\begin{align}
\mathcal{D}_{{-}1}&={-}\frac{8\kappa^2}{G_0\eta}
\frac{\mathrm{d}}{\mathrm{d}\phi}\left\{\frac{1}{\kappa^2}
\frac{\mathrm{d}}{\mathrm{d}\phi}\left[\tilde{\tau}^2+
\frac{1}{(l')^2}\left(\frac{\kappa'}{\kappa}\right)^2
+\frac{\kappa^2}{4}\right]\right\},\end{align}
 \begin{align}
\mathcal{D}_0&=\frac{48B_{22}^S}{B_0^2}\left(\frac{\sigma\tilde{\tau}}{\eta}
+\frac{\eta\kappa'}{l'\kappa^3}\right)+\frac{48\tilde{\tau}}{B_0\eta}
\left(-\frac{B_{22}^C}{B_0}+\frac{3\eta^2}{4}\right)
+\frac{16B_{\alpha1}\tilde{\tau}}{\eta
B_{\alpha0}B_0}\nonumber\\
&\quad+\frac{8\eta}{\kappa^4B_0}\left[{-}4\kappa^4
\tilde{\tau}+3\kappa^2\tilde{\tau}^3+8\tilde{\tau}
\left(\frac{\kappa'}{l'}\right)^2-\frac{\kappa}{(l')^2}
({-}9\kappa'\tilde{\tau}'+5\tilde{\tau}\kappa'')\right.\nonumber\\
&\quad \left.-2\kappa^2
\frac{\tilde{\tau}''}{(l')^2}\right]+\frac{4\sigma}{G_0\eta\kappa^4}\left[{-}3\kappa^5\kappa'
+24\kappa\frac{(\kappa')^3}{(l')^2}-10\kappa^4\tilde{\tau}\tilde{\tau}'\right.\nonumber\\
&\quad
\left.-30\kappa^2\kappa'\frac{\kappa''}{(l')^2}-2\kappa^3
\left(\tilde{\tau}^2\kappa'-2\frac{\kappa^{(3)}}{(l')^2}\right)\right]\nonumber\\
&\quad +\frac{2I_2^2}{B_0 \eta\kappa^2} \left(-\eta^2
\tilde{\tau} +\sigma \kappa
\frac{\kappa'}{l'}\right)+\frac{4\eta I_2}{B_0 \kappa^4}
\left(- \kappa^4 + 2 \kappa^2 \tilde{\tau}^2 + 2
\frac{(\kappa')^2}{(l')^2}\right),\end{align}
\begin{align}
\mathcal{D}_0&=\frac{48B_{22}^S}{B_0^2}\left(\frac{\sigma\tilde{\tau}}{\eta}
+\frac{\eta\kappa'}{l'\kappa^3}\right)+\frac{48\tilde{\tau}}{B_0\eta}
\left(-\frac{B_{22}^C}{B_0}+\frac{3\eta^2}{4}\right)
+\frac{16B_{\alpha1}\tilde{\tau}}{\eta
B_{\alpha0}B_0}\nonumber\\
&\quad+\frac{8\eta}{\kappa^4B_0}\left[{-}4\kappa^4
\tilde{\tau}+3\kappa^2\tilde{\tau}^3+8\tilde{\tau}
\left(\frac{\kappa'}{l'}\right)^2-\frac{\kappa}{(l')^2}
({-}9\kappa'\tilde{\tau}'+5\tilde{\tau}\kappa'')\right.\nonumber\\
&\quad \left.-2\kappa^2
\frac{\tilde{\tau}''}{(l')^2}\right]+\frac{4\sigma}{G_0\eta\kappa^4}\left[{-}3\kappa^5\kappa'
+24\kappa\frac{(\kappa')^3}{(l')^2}-10\kappa^4\tilde{\tau}\tilde{\tau}'\right.\nonumber\\
&\quad
\left.-30\kappa^2\kappa'\frac{\kappa''}{(l')^2}-2\kappa^3
\left(\tilde{\tau}^2\kappa'-2\frac{\kappa^{(3)}}{(l')^2}\right)\right]\nonumber\\
&\quad +\frac{2I_2^2}{B_0 \eta\kappa^2} \left(-\eta^2
\tilde{\tau} +\sigma \kappa
\frac{\kappa'}{l'}\right)+\frac{4\eta I_2}{B_0 \kappa^4}
\left(- \kappa^4 + 2 \kappa^2 \tilde{\tau}^2 + 2
\frac{(\kappa')^2}{(l')^2}\right),\end{align}
 \begin{align}
G_0\mathcal{D}_1&=12\left(-\frac{B_{22}^C}{B_0}+\frac{3\eta^2}{4}\right)
\left(\frac{3\eta}{\kappa^2}+\frac{\kappa^2}{\eta^3}(1-\sigma^2)
\right)+\frac{4B_{\alpha1}}{G_0}\left(\frac{3\eta}{\kappa^2}-
\frac{\kappa^2}{\eta^3}(1+\sigma^2)\right)\nonumber\\
&\quad
+\frac{24\kappa^2\sigma}{\eta^3}\frac{B_{22}^S}{B_0}-
\frac{1}{\eta\kappa^6}\left[4\kappa^4
(2\kappa^4+5\eta^4)+4\kappa^2\tilde{\tau}^2
(\kappa^4+6\eta^4)\right.\nonumber\\ &\quad
+\left.12\left(\frac{\kappa'}{l'}\right)^2
(8\eta^4-5\kappa^4)+8\kappa\frac{\kappa''}{(l')^2}
(\eta^4+4\kappa^4)\right]-\frac{16\sigma\eta}{l'\kappa^3}(8\tilde{\tau}
\kappa'+\kappa\tilde{\tau}')\nonumber\\ &\quad
+\frac{8\sigma^2}{\eta\kappa^2}
\left(2\kappa^4+\kappa^2\tilde{\tau}^2+6
\left(\frac{\kappa'}{l'}\right)^2+\kappa
\frac{\kappa''}{(l')^2}\right)\nonumber\\ &\quad
-\frac{I_2^2}{ \eta \kappa^4} [2 \eta^4 + \kappa^4 ({-}1 +
2 \sigma^2)]-\frac{16\eta I_2}{\kappa^4} \left(- \eta^2
\tilde{\tau} + \sigma\kappa \frac{\kappa'}{l'}\right),\end{align}
\begin{align}
G_0\mathcal{D}_1&=12\left(-\frac{B_{22}^C}{B_0}+\frac{3\eta^2}{4}\right)
\left(\frac{3\eta}{\kappa^2}+\frac{\kappa^2}{\eta^3}(1-\sigma^2)
\right)+\frac{4B_{\alpha1}}{G_0}\left(\frac{3\eta}{\kappa^2}-
\frac{\kappa^2}{\eta^3}(1+\sigma^2)\right)\nonumber\\
&\quad
+\frac{24\kappa^2\sigma}{\eta^3}\frac{B_{22}^S}{B_0}-
\frac{1}{\eta\kappa^6}\left[4\kappa^4
(2\kappa^4+5\eta^4)+4\kappa^2\tilde{\tau}^2
(\kappa^4+6\eta^4)\right.\nonumber\\ &\quad
+\left.12\left(\frac{\kappa'}{l'}\right)^2
(8\eta^4-5\kappa^4)+8\kappa\frac{\kappa''}{(l')^2}
(\eta^4+4\kappa^4)\right]-\frac{16\sigma\eta}{l'\kappa^3}(8\tilde{\tau}
\kappa'+\kappa\tilde{\tau}')\nonumber\\ &\quad
+\frac{8\sigma^2}{\eta\kappa^2}
\left(2\kappa^4+\kappa^2\tilde{\tau}^2+6
\left(\frac{\kappa'}{l'}\right)^2+\kappa
\frac{\kappa''}{(l')^2}\right)\nonumber\\ &\quad
-\frac{I_2^2}{ \eta \kappa^4} [2 \eta^4 + \kappa^4 ({-}1 +
2 \sigma^2)]-\frac{16\eta I_2}{\kappa^4} \left(- \eta^2
\tilde{\tau} + \sigma\kappa \frac{\kappa'}{l'}\right),\end{align}
 \begin{align}
l'G_0\mathcal{D}_2&={-}\frac{16\eta\tilde{\tau}}{\kappa^2}
\left(\frac{3\eta^4}{\kappa^4}+5\right)-
\frac{32\sigma\kappa'}{l'\kappa\eta}\left(\frac{\eta^4}{\kappa^4}+1\right)-
\frac{16\eta\tilde{\tau}\sigma^2}{\kappa^2}-
\frac{64\kappa'\sigma^3}{l'\eta\kappa}\nonumber\\ &\quad
+\frac{8\eta I_2}{\kappa^6} (\eta^4 + \kappa^4 \sigma^2),
\end{align}
\begin{align}
l'G_0\mathcal{D}_2&={-}\frac{16\eta\tilde{\tau}}{\kappa^2}
\left(\frac{3\eta^4}{\kappa^4}+5\right)-
\frac{32\sigma\kappa'}{l'\kappa\eta}\left(\frac{\eta^4}{\kappa^4}+1\right)-
\frac{16\eta\tilde{\tau}\sigma^2}{\kappa^2}-
\frac{64\kappa'\sigma^3}{l'\eta\kappa}\nonumber\\ &\quad
+\frac{8\eta I_2}{\kappa^6} (\eta^4 + \kappa^4 \sigma^2),
\end{align}
The expressions for the quasisymmetric limit can be found in Landreman & Jorge (Reference Landreman and Jorge2020) explicitly.
Appendix F. Extra terms for Mercier stability in a quasisymmetric stellarator
If one was to write the form of the Mercier criterion in an ideal quasisymmetric stellarator using the pressure gradient and the triangularity shaping on the up–down symmetric cross-section at the origin as free parameters, then we may write
where ![]() $\varLambda =\varLambda _2+\varLambda _0+\varLambda _{-2}$:
$\varLambda =\varLambda _2+\varLambda _0+\varLambda _{-2}$:
 \begin{align}
\varLambda_2&=\frac{1}{\eta^2\iota_0\kappa^6(3\eta^4 +
5\kappa^4) - 4\eta^4\kappa^8(I_2-\tau)}[\iota_0^3(\eta^4 +
\kappa^4)(32\eta^8 + 11\eta^4\kappa^4-3\kappa^8)
\nonumber\\ &\quad +4\eta^2\kappa^6\tau(I_2-\tau)(
20\eta^4I_2-3(5\eta^4 + \kappa^4)\tau)
-2\eta^2\iota_0^2\kappa^2(4(16\eta^8 + 8\eta^4\kappa^4 -
3\kappa^8)I_2 \nonumber\\ &\quad -(75\eta^8 +
50\eta^4\kappa^4 - 9\kappa^8)\tau) +
\iota_0\kappa^4((201\eta^8 + 20\eta^4\kappa^4 +
3\kappa^8)\tau^2 \nonumber\\ &\quad + 20\eta^4({-}17\eta^4
+ \kappa^4)\tau I_2 + 16\eta^4(8\eta^4 -
3\kappa^4)I_2^2)], \end{align}
\begin{align}
\varLambda_2&=\frac{1}{\eta^2\iota_0\kappa^6(3\eta^4 +
5\kappa^4) - 4\eta^4\kappa^8(I_2-\tau)}[\iota_0^3(\eta^4 +
\kappa^4)(32\eta^8 + 11\eta^4\kappa^4-3\kappa^8)
\nonumber\\ &\quad +4\eta^2\kappa^6\tau(I_2-\tau)(
20\eta^4I_2-3(5\eta^4 + \kappa^4)\tau)
-2\eta^2\iota_0^2\kappa^2(4(16\eta^8 + 8\eta^4\kappa^4 -
3\kappa^8)I_2 \nonumber\\ &\quad -(75\eta^8 +
50\eta^4\kappa^4 - 9\kappa^8)\tau) +
\iota_0\kappa^4((201\eta^8 + 20\eta^4\kappa^4 +
3\kappa^8)\tau^2 \nonumber\\ &\quad + 20\eta^4({-}17\eta^4
+ \kappa^4)\tau I_2 + 16\eta^4(8\eta^4 -
3\kappa^4)I_2^2)], \end{align}
 \begin{align}
\varLambda_0&=\frac{\eta^4\iota_0^2\kappa^3({-}5\eta^4 +
\kappa^4) + 4\eta^6\iota_0\kappa^5(\tau
+3I_2)}{\eta^2\iota_0\kappa^3(\iota_0(3\eta^4 + 5\kappa^4)
+ 4\eta^2\kappa^2(\tau - I_2))} \nonumber\\ &\quad
+\frac{\iota_0({-}11\eta^8 + 46\eta^4\kappa^4 - 3\kappa^8)
+ 4\eta^2\kappa^2(11\eta^4 - 3\kappa^4)(\tau -
I_2)}{\eta^2\kappa^3(\iota_0(3\eta^4 + 5\kappa^4) +
4\eta^2\kappa^2(\tau - I_2))}\kappa'' \nonumber\\ &\quad
-\frac{32\eta^2[-\eta^2\iota_0 - \kappa^2(\tau -
I_2)]}{\iota_0(\iota_0(3\eta^4 + 5\kappa^4) +
4\eta^2\kappa^2(\tau - I_2))}\tau'', \end{align}
\begin{align}
\varLambda_0&=\frac{\eta^4\iota_0^2\kappa^3({-}5\eta^4 +
\kappa^4) + 4\eta^6\iota_0\kappa^5(\tau
+3I_2)}{\eta^2\iota_0\kappa^3(\iota_0(3\eta^4 + 5\kappa^4)
+ 4\eta^2\kappa^2(\tau - I_2))} \nonumber\\ &\quad
+\frac{\iota_0({-}11\eta^8 + 46\eta^4\kappa^4 - 3\kappa^8)
+ 4\eta^2\kappa^2(11\eta^4 - 3\kappa^4)(\tau -
I_2)}{\eta^2\kappa^3(\iota_0(3\eta^4 + 5\kappa^4) +
4\eta^2\kappa^2(\tau - I_2))}\kappa'' \nonumber\\ &\quad
-\frac{32\eta^2[-\eta^2\iota_0 - \kappa^2(\tau -
I_2)]}{\iota_0(\iota_0(3\eta^4 + 5\kappa^4) +
4\eta^2\kappa^2(\tau - I_2))}\tau'', \end{align}
and the subscript denotes the scaling with rotational transform (or similar elements such as ![]() $\tau$ and
$\tau$ and ![]() $I_2$). We write these expressions using a normalised and scaled-out version of the equations, which eases notation. In this notation, to convert to their full explicit form,
$I_2$). We write these expressions using a normalised and scaled-out version of the equations, which eases notation. In this notation, to convert to their full explicit form, ![]() $\kappa$ and
$\kappa$ and ![]() $\tau$ should be divided and
$\tau$ should be divided and ![]() $\eta$ multiplied by a factor of
$\eta$ multiplied by a factor of ![]() $\mathrm {d}l/\mathrm {d}\phi$. The current
$\mathrm {d}l/\mathrm {d}\phi$. The current ![]() $I_2$ should be divided by
$I_2$ should be divided by ![]() $\mathrm {d}l/\mathrm {d}\phi$, as we assume
$\mathrm {d}l/\mathrm {d}\phi$, as we assume ![]() $G_0=\mathrm {d}l/\mathrm {d}\phi$. The expression for
$G_0=\mathrm {d}l/\mathrm {d}\phi$. The expression for ![]() $\varLambda$ should be then divided by
$\varLambda$ should be then divided by ![]() $(\mathrm {d}l/\mathrm {d}\phi )^2$ to express it in a form consistent with the other terms in (4.1). All quantities are evaluated at
$(\mathrm {d}l/\mathrm {d}\phi )^2$ to express it in a form consistent with the other terms in (4.1). All quantities are evaluated at ![]() $\phi =0$, the location of the up–down symmetric cross-section of choice in our stellarator-symmetric configuration. Note that whenever the denominators are small, the near-axis model will be very sensitive to change.
$\phi =0$, the location of the up–down symmetric cross-section of choice in our stellarator-symmetric configuration. Note that whenever the denominators are small, the near-axis model will be very sensitive to change.
If, instead of triangularity, we were to express the Shafranov shift explicitly, then we obtain
which reduces to the axisymmetric limit when ![]() $\bar {F}\rightarrow 0$. Note that the tendency of the configuration will be for
$\bar {F}\rightarrow 0$. Note that the tendency of the configuration will be for ![]() $\mathcal {T}_\varDelta <0$, as this is the limit for a significant asymmetry
$\mathcal {T}_\varDelta <0$, as this is the limit for a significant asymmetry ![]() $\bar {F}$. Unlike in the case of triangularity, this is the typical behaviour in a tokamak with vertical elongation. Bunching of surfaces on the inboard side (that is,
$\bar {F}$. Unlike in the case of triangularity, this is the typical behaviour in a tokamak with vertical elongation. Bunching of surfaces on the inboard side (that is, ![]() $\varDelta <0$) increases stability. Of course, there is a region in
$\varDelta <0$) increases stability. Of course, there is a region in ![]() $(\alpha, \bar {F})$ space in which
$(\alpha, \bar {F})$ space in which ![]() $\mathcal {T}_\varDelta >0$. Thus, the behaviour of a tokamak for a horizontally elongated cross-section may also be, in principle, achieved with the appropriate axis and parameter combination.
$\mathcal {T}_\varDelta >0$. Thus, the behaviour of a tokamak for a horizontally elongated cross-section may also be, in principle, achieved with the appropriate axis and parameter combination.
Appendix G. Validity of ideal quasisymmetric assumption
To construct our analytic measure of stability, and understand the contribution of triangularity in quasisymmetric configurations, we took the simplifying assumption of ideal quasisymmetry. That is, we assumed ![]() $B_{20}$ to be constant. In practice, optimised quasisymmetric configurations such as those in figure 5 are not ideal. That is to say, they all have a finite variation in
$B_{20}$ to be constant. In practice, optimised quasisymmetric configurations such as those in figure 5 are not ideal. That is to say, they all have a finite variation in ![]() $B_{20}(\phi )$. As presented in the main text, this means that there will be a mismatch between the estimate of stability from the ideal analysis and the full approach.
$B_{20}(\phi )$. As presented in the main text, this means that there will be a mismatch between the estimate of stability from the ideal analysis and the full approach.
To back the validity of figure 5 we should thus provide evidence of the ideal consideration being a fair descriptor of the stability. We present in figure 9 a comparison between the magnetic well evaluated using the full near-axis form and the idealised scenario representing the stellarator by its up–down cross-section at ![]() $\phi =0$ (the cross-sections shown in figure 5, at
$\phi =0$ (the cross-sections shown in figure 5, at ![]() $\phi =0$ as defined in the relevant papers). Only cases that showed agreement were kept, as only in those cases do we expect the analysis to be trustworthy.
$\phi =0$ as defined in the relevant papers). Only cases that showed agreement were kept, as only in those cases do we expect the analysis to be trustworthy.

Figure 9. Comparison of the magnetic well criterion between the full near-axis and idealised evaluation. The plot compares the magnetic well criterion ![]() $V''$ for the configurations in figure 5 assessed using the full near-axis description (
$V''$ for the configurations in figure 5 assessed using the full near-axis description (![]() $V''$) and the idealised quasisymmetric limit (
$V''$) and the idealised quasisymmetric limit (![]() $V''_{\rm ideal}$). The plot shows excellent agreement (within 30 % in all cases).
$V''_{\rm ideal}$). The plot shows excellent agreement (within 30 % in all cases).