Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T04:10:38.207Z Has data issue: false hasContentIssue false
  • English
  • Français

Magneto-immutable turbulence in weakly collisional plasmas

Part of: Focus on Plasma Astrophysics

Published online by Cambridge University Press:  18 February 2019

J. Squire Open the ORCID record for J. Squire [Opens in a new window] ,
A. A. Schekochihin Open the ORCID record for A. A. Schekochihin [Opens in a new window] ,
E. Quataert Open the ORCID record for E. Quataert [Opens in a new window]  and
M. W. Kunz Open the ORCID record for M. W. Kunz [Opens in a new window]
J. Squire*
Affiliation:
Physics Department, University of Otago, 730 Cumberland St., Dunedin 9016, New Zealand TAPIR, Mailcode 350-17, California Institute of Technology, Pasadena, CA 91125, USA
A. A. Schekochihin
Affiliation:
The Rudolf Peierls Centre for Theoretical Physics, University of Oxford, Clarendon Laboratory, Parks Road, Oxford OX1 3P4, UK Merton College, Oxford OX1 4JD, UK
E. Quataert
Affiliation:
Astronomy Department and Theoretical Astrophysics Center, University of California, Berkeley, CA 94720, USA
M. W. Kunz
Affiliation:
Department of Astrophysical Sciences, Princeton University, Peyton Hall, Princeton, NJ 08544, USA Princeton Plasma Physics Laboratory, PO Box 451, Princeton, NJ 08543, USA
*
†Email address for correspondence: jonathan.squire@otago.ac.nz
Get access Rights & Permissions [Opens in a new window]

Abstract

We propose that pressure anisotropy causes weakly collisional turbulent plasmas to self-organize so as to resist changes in magnetic-field strength. We term this effect ‘magneto-immutability’ by analogy with incompressibility (resistance to changes in pressure). 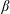The effect is important when the pressure anisotropy becomes comparable to the magnetic pressure, suggesting that in collisionless, weakly magnetized (high-$\unicode[STIX]{x1D6FD}$) plasmas its dynamical relevance is similar to that of incompressibility. Simulations of magnetized turbulence using the weakly collisional Braginskii model show that magneto-immutable turbulence is surprisingly similar, in most statistical measures, to critically balanced magnetohydrodynamic turbulence. However, in order to minimize magnetic-field variation, the flow direction becomes more constrained than in magnetohydrodynamics, and the turbulence is more strongly dominated by magnetic energy (a non-zero ‘residual energy’). These effects represent key differences between pressure-anisotropic and fluid turbulence, and should be observable in the 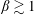$\unicode[STIX]{x1D6FD}\gtrsim 1$ turbulent solar wind.

Keywords

astrophysical plasmasplasma dynamicsspace plasma physics
Type
Research Article
Information
Journal of Plasma Physics , Volume 85 , Issue 1 , February 2019 , 905850114
Copyright
© Cambridge University Press 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bale, S. D., Kasper, J. C., Howes, G. G., Quataert, E., Salem, C. & Sundkvist, D. 2009 Magnetic fluctuation power near proton temperature anisotropy instability thresholds in the solar wind. Phys. Rev. Lett. 103, 211101.Google Scholar
Barnes, A. 1966 Collisionless damping of hydromagnetic waves. Phys. Fluids 9, 1483.Google Scholar
Barnes, A. & Hollweg, J. V. 1974 Large-amplitude hydromagnetic waves. J. Geophys. Res. 79, 2302.Google Scholar
Beresnyak, A. 2012 Basic properties of magnetohydrodynamic turbulence in the inertial range. Mon. Not. R. Astron. Soc. 422, 3495.Google Scholar
Boldyrev, S. 2006 Spectrum of magnetohydrodynamic turbulence. Phys. Rev. Lett. 96, 115002.Google Scholar
Borovsky, J. E. 2008 Flux tube texture of the solar wind: strands of the magnetic carpet at 1 AU? J. Geophys. Res.: Space Phys. 113, A08110.Google Scholar
Braginskii, S. I. 1965 Transport processes in a plasma. Rev. Plasma Phys. 1, 205.Google Scholar
Bruno, R., Carbone, V., Veltri, P., Pietropaolo, E. & Bavassano, B. 2001 Identifying intermittency events in the solar wind. Planet. Space Sci. 49, 1201–1210.Google Scholar
Chen, C. H. K. 2016 Recent progress in astrophysical plasma turbulence from solar wind observations. J. Plasma Phys. 82, 535820602.Google Scholar
Chen, C. H. K., Mallet, A., Yousef, T. A., Schekochihin, A. A. & Horbury, T. S. 2011 Anisotropy of Alfvénic turbulence in the solar wind and numerical simulations. Mon. Not. R. Astron. Soc. 415, 3219.Google Scholar
Chew, C. F., Goldberger, M. L. & Low, F. E. 1956 The Boltzmann equation and the one-fluid hydromagnetic equations in the absence of particle collisions. Proc. R. Soc. Lond. A 236, 112.Google Scholar
Goldreich, P. & Sridhar, S. 1995 Toward a theory of interstellar turbulence. Strong Alfvénic turbulence. Astrophys. J. 438, 763.Google Scholar
Goldreich, P. & Sridhar, S. 1997 Magnetohydrodynamic turbulence revisited. Astrophys. J. 485, 680.Google Scholar
Hasegawa, A. 1969 Drift mirror instability of the magnetosphere. Phys. Fluids 12, 2642.Google Scholar
Helander, P., Strumik, M. & Schekochihin, A. A. 2016 Constraints on dynamo action in plasmas. J. Plasma Phys. 82, 905820601.Google Scholar
Hellinger, P. & Trávníček, P. M. 2008 Oblique proton fire hose instability in the expanding solar wind: hybrid simulations. J. Geophys. Res.: Space Phys. 113, A10109.Google Scholar
Kasper, J. C., Lazarus, A. J. & Gary, S. P. 2002 Wind/SWE observations of firehose constraint on solar wind proton temperature anisotropy. Geophys. Res. Lett. 29 (1), 1839.Google Scholar
Kulsrud, R. M. 1983 MHD description of plasma. In Handbook of Plasma Physics (ed. Sagdeev, R. N. & Rosenbluth, M. N.). Princeton University.Google Scholar
Kunz, M. W., Schekochihin, A. A. & Stone, J. M. 2014 Firehose and mirror instabilities in a collisionless shearing plasma. Phys. Rev. Lett. 112, 205003.Google Scholar
Lesur, G. & Longaretti, P. Y. 2007 Impact of dimensionless numbers on the efficiency of magnetorotational instability induced turbulent transport. Mon. Not. R. Astron. Soc. 378, 1471.Google Scholar
Lichtenstein, B. R. & Sonett, C. P. 1980 Dynamic magnetic structure of large amplitude Alfvénic variations in the solar wind. Geophys. Res. Lett. 7, 189.Google Scholar
Mallet, A., Schekochihin, A. A. & Chandran, B. D. G. 2015 Refined critical balance in strong Alfvénic turbulence. Mon. Not. R. Astron. Soc. 449, L77–L81.Google Scholar
Mallet, A., Schekochihin, A. A., Chandran, B. D. G., Chen, C. H. K., Horbury, T. S., Wicks, R. T. & Greenan, C. C. 2016 Measures of three-dimensional anisotropy and intermittency in strong Alfvénic turbulence. Mon. Not. R. Astron. Soc. 459, 2130–2139.Google Scholar
Maron, J. & Goldreich, P. 2001 Simulations of incompressible magnetohydrodynamic turbulence. Astrophys. J. 554, 1175.Google Scholar
Matthaeus, W. H., Wan, M., Servidio, S., Greco, A., Osman, K. T., Oughton, S. & Dmitruk, P. 2015 Intermittency, nonlinear dynamics and dissipation in the solar wind and astrophysical plasmas. Proc. R. Soc. Lond. A 373, 20140154.Google Scholar
Melville, S., Schekochihin, A. A. & Kunz, M. W. 2016 Pressure-anisotropy-driven microturbulence and magnetic-field evolution in shearing, collisionless plasma. Mon. Not. R. Astron. Soc. 459, 2701.Google Scholar
Mikhailovskii, A. B. & Tsypin, V. S. 1971 Transport equations and gradient instabilities in a high pressure collisional plasma. Plasma Phys. 13, 785.Google Scholar
Pan, S. & Johnsen, E. 2017 The role of bulk viscosity on the decay of compressible, homogeneous, isotropic turbulence. J. Fluid Mech. 833, 717.Google Scholar
Perez, J. C. & Boldyrev, S. 2009 Role of cross-helicity in magnetohydrodynamic turbulence. Phys. Rev. Lett. 102, 025003.Google Scholar
Perez, J. C., Mason, J., Boldyrev, S. & Cattaneo, F. 2012 On the energy spectrum of strong magnetohydrodynamic turbulence. Phys. Rev. X 2, 041005.Google Scholar
Riley, P., Sonett, C. P., Tsurutani, B. T., Balogh, A., Forsyth, R. J. & Hoogeveen, G. W. 1996 Properties of arc-polarized Alfvén waves in the ecliptic plane: Ulysses observations. J. Geophys. Res. 101, 19987.Google Scholar
Rosenbluth, M. N.1956 The stability of the pinch. Los Alamos Sci. Lab. Rep. LA-2030.Google Scholar
Santos-Lima, R., de Gouveia Dal Pino, E. M., Kowal, G., Falceta-Gonçalves, D., Lazarian, A. & Nakwacki, M. S. 2014 Magnetic field amplification and evolution in turbulent collisionless magnetohydrodynamics: an application to the intracluster medium. Astrophys. J. 781, 84.Google Scholar
Schekochihin, A. A., Cowley, S. C., Dorland, W., Hammett, G. W., Howes, G. G., Quataert, E. & Tatsuno, T. 2009 Astrophysical gyrokinetics: kinetic and fluid turbulent cascades in magnetized weakly collisional plasmas. Astrophys. J. Suppl. 182, 310.Google Scholar
Schekochihin, A. A., Cowley, S. C., Kulsrud, R. M., Rosin, M. S. & Heinemann, T. 2008 Nonlinear growth of firehose and mirror fluctuations in astrophysical plasmas. Phys. Rev. Lett. 100, 081301.Google Scholar
Schekochihin, A. A., Cowley, S. C., Rincon, F. & Rosin, M. S. 2010 Magnetofluid dynamics of magnetized cosmic plasma: firehose and gyrothermal instabilities. Mon. Not. R. Astron. Soc. 405, 291.Google Scholar
Sharma, P., Hammett, G. W., Quataert, E. & Stone, J. M. 2006 Shearing box simulations of the MRI in a collisionless plasma. Astrophys. J. 637, 952.Google Scholar
Snyder, P. B., Hammett, G. W. & Dorland, W. 1997 Landau fluid models of collisionless magnetohydrodynamics. Phys. Plasmas 4, 3974.Google Scholar
Squire, J., Kunz, M. W., Quataert, E. & Schekochihin, A. A. 2017a Kinetic simulations of the interruption of large-amplitude shear-Alfvén waves in a high- $\unicode[STIX]{x1D6FD}$ plasma. Phys. Rev. Lett. 119, 155101.Google Scholar
Squire, J., Quataert, E. & Schekochihin, A. A. 2016 A stringent limit on the amplitude of Alfvénic perturbations in high-beta low-collisionality plasmas. Astrophys. J. Lett. 830, L25.Google Scholar
Squire, J., Schekochihin, A. A. & Quataert, E. 2017b Amplitude limits and nonlinear damping of shear-Alfvén waves in high-beta low-collisionality plasmas. New J. Phys. 19, 055005.Google Scholar
Sulem, P. L. & Passot, T. 2015 Landau fluid closures with nonlinear large-scale finite Larmor radius corrections for collisionless plasmas. J. Plasma Phys. 81, 325810103.Google Scholar
Tenerani, A. & Velli, M. 2018 Nonlinear firehose relaxation and constant-B field fluctuations. Astrophys. J. 867, L26.Google Scholar
Tsurutani, B. T., Ho, C. M., Smith, E. J., Neugebauer, M., Goldstein, B. E., Mok, J. S., Arballo, J. K., Balogh, A., Southwood, D. J. & Feldman, W. C. 1994 The relationship between interplanetary discontinuities and Alfvén waves: Ulysses observations. Geophys. Res. Lett. 21, 2267.Google Scholar
Tu, C.-Y. & Marsch, E. 1993 A model of solar wind fluctuations with two components – Alfven waves and convective structures. J. Geophys. Res. 98, 1257.Google Scholar
Vasquez, B. J. & Hollweg, J. V. 1998 Formation of spherically polarized Alfvén waves and imbedded rotational discontinuities from a small number of entirely oblique waves. J. Geophys. Res.: Space Phys. 103, 335.Google Scholar
Yang, Y., Matthaeus, W. H., Parashar, T. N., Haggerty, C. C., Roytershteyn, V., Daughton, W., Wan, M., Shi, Y. & Chen, S. 2017 Energy transfer, pressure tensor, and heating of kinetic plasma. Phys. Plasmas 24, 072306.Google Scholar
Zhdankin, V., Boldyrev, S. & Uzdensky, D. A. 2016 Scalings of intermittent structures in magnetohydrodynamic turbulence. Phys. Plasmas 23, 055705.Google Scholar