Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-10T13:32:32.757Z Has data issue: false hasContentIssue false
  • English
  • Français

Magnetorotational stability in a self-consistent three dimensional axisymmetric magnetized warm plasma equilibrium with a gravitational field

Part of: Focus on Plasma Astrophysics

Published online by Cambridge University Press:  17 October 2016

Peter J. Catto  and
Sergei I. Krasheninnikov
Peter J. Catto*
Affiliation:
Plasma Science and Fusion Center, MIT, Cambridge, MA 02139, USA
Sergei I. Krasheninnikov
Affiliation:
Mechanical and Aerospace Engineering, University of California at San Diego, La Jolla, CA 92093, USA
*
†Email address for correspondence: catto@psfc.mit.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Magnetorotational stability is revisited for self-consistent three-dimensional magnetized hot plasma equilibria in a gravitational field. The eikonal analysis presented finds that magnetorotational stability analysis must be performed with some care to retain compressibility and density gradient effects, and departures from strict Keplerian motion. Indeed, retaining these effects highlights differences between the magnetorotational instability found in the absence of gravity (Velikhov, Sov. Phys. JETP, vol. 36, 1959, pp. 995–998) and that found the presence of gravity (Balbus & Hawley, Astrophys. J., vol. 376, 1991, pp. 214–222). In the non-gravitational case, compressibility and density variation alter the stability condition, while these effects only enter for departures from strict Keplerian motion in a gravitational field. The conditions for instability are made more precise by employing recent magnetized equilibrium results (Catto et al., J. Plasma Phys., vol. 81, 2015, 515810603), rather than employing a hydrodynamic equilibrium. We focus on the stability of the 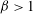$\unicode[STIX]{x1D6FD}>1$ limit for which equilibria were found in the absence of a toroidal magnetic field, where 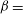$\unicode[STIX]{x1D6FD}=$  plasma/magnetic pressure.

Keywords

astrophysical plasmasplasma instabilities
Type
Research Article
Information
Journal of Plasma Physics , Volume 82 , Issue 5 , October 2016 , 905820506
Copyright
© Cambridge University Press 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Balbus, S. A. 2006 Magnetorotational instability. Scholarpedia 4 (7), 2409.CrossRefGoogle Scholar
Balbus, S. A. & Hawley, J. F. 1991 A powerful local shear instability in weakly magnetized disks. I. Linear analysis. Astrophys. J. 376, 214–222.CrossRefGoogle Scholar
Blaes, O. M. 2004 Physics fundamentals of luminous accretion disks around black holes. In Proc. LXXVIII of Les Houches Summer School, Chamonix, France (ed. Menard, F., Pelletier, G., Beskin, V. & Dalibard, J.), pp. 137–185. Springer.Google Scholar
Catto, P. J., Bernstein, I. B. & Tessarotto, M. 1987 Ion transport in toroidally rotating tokamak plasmas. Phys. Fluids 30, 2784–2795.CrossRefGoogle Scholar
Catto, P. J. & Krasheninnikov, S. I. 2015 A rotating and magnetized three-dimensional hot plasma equilibrium in a gravitational field. J. Plasma Phys. 81, 105810301, 11 pages.CrossRefGoogle Scholar
Catto, P. J., Pusztai, I. & Krasheninnikov, S. I. 2015 Axisymmetric global gravitational equilibrium for magnetized, rotating hot plasma. J. Plasma Phys. 81, 515810603, 18 pages.CrossRefGoogle Scholar
Hawley, J. F. & Balbus, S. A. 1991 A powerful local shear instability in weakly magnetized disks. II. Nonlinear evolution. Astrophys. J. 376, 223–233.CrossRefGoogle Scholar
Hawley, J. F., Gammie, C. F. & Balbus, S. A. 1995 Local three-dimensional magnetohydrodyanmic simulations of accretion disks. Astrophys. J. 440, 742–763.CrossRefGoogle Scholar
Hawley, J. F., Gammie, C. F. & Balbus, S. A. 1996 Local three-dimensional simulations of an accretion disk hydromagnetic dynamo. Astrophys. J. 464, 690–703.CrossRefGoogle Scholar
Helander, P. 2014 Theory of plasma confinement in non-axisymmetric magnetic fields. Rep. Prog. Phys. 77, 087001, 35 pages.CrossRefGoogle ScholarPubMed
Hinton, F. L. & Wong, S. K. 1985 Neoclassical ion transport in rotating axisymmetric plasmas. Phys. Fluids 28, 3082–3098.CrossRefGoogle Scholar
McNally, C. P. & Pessah, M. E. 2015 On vertically global, horizontally local models for astrophysical disks. Astrophys. J. 811:121, (22 pp).Google Scholar
Ogilvie, G. I. 1998 Waves and instabilities in a differentially rotating disc containing a poloidal magnetic field. Mon. Not. R. Astron. Soc. 297, 291–314.CrossRefGoogle Scholar
Papaloizou, J. C. B. & Pringle, J. E. 1984 The dynamical stability of differentially rotating discs with constant specific angular momentum. Mon. Not. R. Astron. Soc. 208, 721–750.CrossRefGoogle Scholar
Stone, J. M., Gammie, C. F., Balbus, S. A. & Hawley, J. F. 2000 Protostars and Planets IV (ed. Mannings, V., Boss, A. & Russell, S.), Space Science Reviews, pp. 589–611. University of Arizona.Google Scholar
Stone, J. M., Hawley, J. F., Gammie, C. F. & Balbus, S. A. 1996 Three-dimensional magnetohydrodyanmic simulations of vertically stratified accretion disks. Astrophys. J. 463, 656–673.CrossRefGoogle Scholar
Stone, J. M. & Pringle, J. E. 2001 Magnetohydrodynamic non-radiative accretion flows in two dimensions. Mon. Not. R. Astron. Soc. 322, 461–472.CrossRefGoogle Scholar
Stone, J. M., Pringle, J. E. & Begelman, M. C. 1999 Hydrodynamic non-radiative accretion flows in two dimensions. Mon. Not. R. Astron. Soc. 310, 1002–1016.CrossRefGoogle Scholar
Velikhov, E. P. 1959 Stability of an ideally conducting liquid flowing between cylinders rotating in a magnetic field. Sov. Phys. JETP 36, 995–998.Google Scholar
Wheeler, J. C. 2004 Summary of the workshop on gamma-ray burst afterglows at the 34th COSPAR meeting. Adv. Space Res. 34, 2719–2744.Google Scholar