Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-14T17:18:40.542Z Has data issue: false hasContentIssue false
  • English
  • Français

Maser gain determined by the spatial profile of work done by an average electron and the wavelength of density fluctuation driven by the maser field in multi-photon free-electron two-quantum Stark radiation

Published online by Cambridge University Press:  08 April 2015

S. H. Kim
S. H. Kim*
Affiliation:
9236 Church Road, Dallas, TX 75231, USA
*
†Email address for correspondence: kim_shang_hoon@hotmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

We find that the electron in an electron–cyclotron maser (ECM) of Nc = n1/3λ ≫ 1, where n and λ are the electron density and the maser wavelength, respectively, can only lower its energy through masing transition. From this fact and the application of Heisenberg's uncertainty principle on photon emission, we infer that until the electron energy becomes lower to pass through the width of uncertainty in the electron energy, the interval time Tint between two successive radiative transitions is zero. Hence, we find that if the number Nt of radiative transitions during the laser period T under the assumption of Tint = 0 is far larger than the number Nu of radiative transitions required to pass through the half-width ΔE of uncertainty in the electron energy, the radiation power from an electron is equal to ΔE/T. We deduce that the shift in the energy level of an average electron is predominantly produced by the density-deviation mode driven by the laser field so as to be spatially sinusoidal with period λw and amplitude 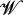$\mathcal W$. We recognize that the uncertainty in the z position of an electron emitting a laser photon through free-electron two-quantum Stark (FETQS) radiation is the wavelength λe of the electric wiggler. Thus, if λw ≪ λe, then ΔE is equal to 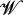$\mathcal W$. Based on the above findings, we identify electron–cyclotron masing in a high-density ECM as a gyration-driven FETQS radiation whose power is given by P = ΔE/T, where ΔE is not caused by gyration but rotation around the waveguide axis. The gain calculated based on this identification agrees with the measured one.

Type
Research Article
Information
Journal of Plasma Physics , Volume 81 , Issue 4 , August 2015 , 905810403
Copyright
Copyright © Cambridge University Press 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Alberti, S., Danly, B. G., Gulotta, G., Giguet, E., Kimura, T., Menninger, W. L., Rullier, J. L. and Temkin, R. J. 1993 Phys. Rev. Lett. 71, 2018.Google Scholar
Billardon, M. et al. 1983 Phys. Rev. Lett. 51, 1652.Google Scholar
Bratman, V. L., Denisov, G. G., Kol'chugin, B. D., Samsonov, S. V. and Volkov, A. B. 1995 Phys. Rev. Lett. 75, 3102.Google Scholar
Chen, K. W., Kim, S. H. and McKinley, M. C. 1987 Phys. Fluids 30, 3306.Google Scholar
Elias, L. R., Fairbank, W. M., Madey, J. M. J., Schwettman, H. A. and Smith, T. I. 1976 Phys. Rev. Lett. 36, 717.Google Scholar
Fedorov, M. V. 1981 Prog. Quant. Electr. 7, 73.Google Scholar
Friedman, M. and Herndon, M. 1973 Phys. Fluids 16, 1982.Google Scholar
Kim, S. H. 1993 J. Plasma Phys. 49, 181.Google Scholar
Kim, S. H. 1999 J. Phys. Soc. Japan 68, 2259.Google Scholar
Kim, S. H. 2007 J. Korean Phys. Soc. 51, 1263.Google Scholar
Kim, S. H. 2009 J. Korean Phys. Soc. 54, 2235.Google Scholar
Kim, S. H. 2012 J. Korean Phys. Soc. 60, 674.Google Scholar
Kim, S. H. 2014 J. Korean Phys. Soc. 64, 163.Google Scholar
Kim, S. H. and Wilhelm, H. E. 1971 Phys. Rev. A 4, 2308.Google Scholar
Kim, S. H. and Wilhelm, H. E. 1972 Phys. Rev. A 5, 1813.Google Scholar
Kim, S. H. and Wilhelm, H. E. 1973 J. Appl. Phys. 44, 802.Google Scholar
Levy, R. H. 1965 Phys. Fluids 8, 1288.Google Scholar
Orzechowski, T. J. et al. 1985 Phys. Rev. Lett. 54, 889.Google Scholar
Orzechowski, T. J. et al. 1986 Phys. Rev. Lett. 57, 2172.Google Scholar
Prasad, S. A. and Malmberg, J. H. 1986 Phys. Fluids 29, 2196.Google Scholar
Roberts, G. and Rostoker, N. 1985 Phys. Fluids 28, 2547.Google Scholar
Tecimer, M., Holldack, K. and Elias, L. R. 2010 Phys. Rev. ST. Accel. Beams 13, 030703.Google Scholar
Watson, J. M. 1985 IEEE Trans. Nucl. Sci. NS–32, 3363.Google Scholar