Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-10T13:09:48.283Z Has data issue: false hasContentIssue false
  • English
  • Français

Modelling the nonlinear plasma response to externally applied three-dimensional fields with the Stepped Pressure Equilibrium Code

Published online by Cambridge University Press:  17 October 2022

A.M. Wright Open the ORCID record for A.M. Wright [Opens in a new window] ,
P. Kim Open the ORCID record for P. Kim [Opens in a new window] ,
N.M. Ferraro Open the ORCID record for N.M. Ferraro [Opens in a new window]  and
S.R. Hudson Open the ORCID record for S.R. Hudson [Opens in a new window]
A.M. Wright*
Affiliation:
Princeton Plasma Physics Laboratory, Princeton, NJ 08540, USA
P. Kim
Affiliation:
Institute for Research in Electronics and Applied Physics, University of Maryland, College Park, MD 20742, USA
N.M. Ferraro
Affiliation:
Princeton Plasma Physics Laboratory, Princeton, NJ 08540, USA
S.R. Hudson
Affiliation:
Princeton Plasma Physics Laboratory, Princeton, NJ 08540, USA
*
†Email address for correspondence: awright@pppl.gov
Get access Rights & Permissions [Opens in a new window]

Abstract

Small-amplitude, symmetry-breaking magnetic field perturbations, including resonant magnetic perturbations (RMPs) and error fields, can profoundly impact plasma properties in both tokamaks and stellarators. In this work, we perform the first comparison between the Stepped Pressure Equilibrium Code (SPEC) (a comparatively fast and efficient equilibrium code based on energy-minimisation principles) and M3D-C$^{1}$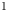 (a high-fidelity albeit computationally expensive initial-value extended-magnetohydro- dynamic (MHD) code) to assess the conditions under which SPEC can be used to model the nonlinear, non-ideal plasma response to an externally applied $(m=2,n=1)$ 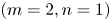RMP field in an experimentally relevant geometry. We find that SPEC is able to capture the plasma response in the weakly nonlinear regime – meaning perturbation amplitudes below the threshold for break up of the separatrix and onset of secondary magnetic island formation – when around half of the total toroidal flux is enclosed in the volume containing the $q=2$ resonant surface. The observed dependence of SPEC solutions on input parameters, including toroidal flux and the number of volumes into which the plasma is partitioned, indicates that additional exploration of the underlying Multi-Region Relaxed MHD physics model is needed to constrain the choice of parameters. Nonetheless, this work suggests promising applications of SPEC to optimisation and fusion plasma design.

Keywords

fusion plasmaplasma confinementplasma nonlinear phenomena
Type
Research Article
Information
Journal of Plasma Physics , Volume 88 , Issue 5 , October 2022 , 905880508
Check for updates
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Aleynikova, K., Hudson, S.R., Helander, P., Kumar, A., Geiger, J., Hirsch, M., Loizu, J., Nührenberg, C., Rahbarnia, K. & Qu, Z. 2021 Model for current drive induced crash cycles in W7-X. Nucl. Fusion 61 (12), 126040.CrossRefGoogle Scholar
Arnold, V.I. 1963 Proof of a theorem of A.N. Kolmogorov on the preservation of conditionally periodic motions under a small perturbation of the Hamiltonian. Russian Mathematical Surveys 18 (5), 9.CrossRefGoogle Scholar
Boozer, A.H. & Nührenberg, C. 2006 Perturbed plasma equilibria. Phys. Plasmas 13 (10), 102501.CrossRefGoogle Scholar
Callen, J.D. 2011 Effects of 3D magnetic perturbations on toroidal plasmas. Nucl. Fusion 51 (9), 094026.CrossRefGoogle Scholar
Canal, G.P., Ferraro, N.M., Evans, T.E., Osborne, T.H., Menard, J.E., Ahn, J.-W., Maingi, R., Wingen, A., Ciro, D., Frerichs, H., Schmitz, O., Soukhanoviskii, V., Waters, I. & Sabbagh, S.A. 2017 M3D-C1 simulations of the plasma response to RMPs in NSTX-U single-null and snowflake divertor configurations. Nucl. Fusion 57 (7), 076007.CrossRefGoogle Scholar
Dewar, R.L., Yoshida, Z., Bhattacharjee, A. & Hudson, S.R. 2015 Variational formulation of relaxed and multi-region relaxed magnetohydrodynamics. J. Plasma Phys. 81 (6), 515810604.CrossRefGoogle Scholar
Evans, T.E., et al. 2004 Suppression of large edge-localized modes in high-confinement DIII-D plasmas with a stochastic magnetic boundary. Phys. Rev. Lett. 92, 235003.CrossRefGoogle ScholarPubMed
Evans, T.E., et al. 2008 RMP ELM suppression in DIII-D plasmas with ITER similar shapes and collisionalities. Nucl. Fusion 48 (2), 024002.CrossRefGoogle Scholar
Evans, T.E., Moyer, R.A., Burrell, K.H., Fenstermacher, M.E., Joseph, I., Leonard, A.W., Osborne, T.H., Porter, G.D., Schaffer, M.J., Snyder, P.B., et al. 2006 Edge stability and transport control with resonant magnetic perturbations in collisionless tokamak plasmas. Nat. Phys. 2 (6), 419–423.CrossRefGoogle Scholar
Ferraro, N.M. 2012 Calculations of two-fluid linear response to non-axisymmetric fields in tokamaks. Phys. Plasmas 19 (5), 056105.CrossRefGoogle Scholar
Ferraro, N.M., Evans, T.E., Lao, L.L., Moyer, R.A., Nazikian, R., Orlov, D.M., Shafer, M.W., Unterberg, E.A., Wade, M.R. & Wingen, A. 2013 Role of plasma response in displacements of the tokamak edge due to applied non-axisymmetric fields. Nucl. Fusion 53 (7), 073042.CrossRefGoogle Scholar
Furth, H.P., Rutherford, P.H. & Selberg, H. 1973 Tearing mode in the cylindrical tokamak. Phys. Fluids 16 (7), 1054–1063.CrossRefGoogle Scholar
Hahm, T.S. & Kulsrud, R.M. 1985 Forced magnetic reconnection. Phys. Fluids 28 (8), 2412–2418.CrossRefGoogle Scholar
Hegna, C.C. 2014 Effects of a weakly 3-D equilibrium on ideal magnetohydrodynamic instabilities. Phys. Plasmas 21 (7), 072502.CrossRefGoogle Scholar
Hirshman, S.P., Sanchez, R. & Cook, C.R. 2011 SIESTA: A scalable iterative equilibrium solver for toroidal applications. Phys. Plasmas 18 (6), 062504. https://doi.org/10.1063/1.3597155CrossRefGoogle Scholar
Hirshman, S.P. & Whitson, J.C. 1983 Steepest-descent moment method for three-dimensional magnetohydrodynamic equilibria. Phys. Fluids 26 (12), 3553–3568.CrossRefGoogle Scholar
Hoelzl, M., et al. 2021 The JOREK non-linear extended MHD code and applications to large-scale instabilities and their control in magnetically confined fusion plasmas. Nucl. Fusion 61 (6), 065001.CrossRefGoogle Scholar
Hole, M.J., Hudson, S.R. & Dewar, R.L. 2006 Stepped pressure profile equilibria in cylindrical plasmas via partial Taylor relaxation. J. Plasma Phys. 72 (6), 1167–1171.CrossRefGoogle Scholar
Hole, M.J., Hudson, S.R. & Dewar, R.L. 2007 Equilibria and stability in partially relaxed plasma–vacuum systems. Nucl. Fusion 47 (8), 746–753.CrossRefGoogle Scholar
Hosking, R.J. & Dewar, R.L. 2016 Fundamental Fluid Mechanics and Magnetohydrodynamics. Springer.CrossRefGoogle Scholar
Huang, Y.-M., Hudson, S.R., Loizu, J., Zhou, Y. & Bhattacharjee, A. 2021 Numerical approach to $\delta$-function current sheets arising from resonant magnetic perturbations. arXiv:2108.09327.CrossRefGoogle Scholar
Hudson, S.R. 2009 An expression for the temperature gradient in chaotic fields. Phys. Plasmas 16 (1), 010701.CrossRefGoogle Scholar
Hudson, S.R., Dewar, R.L., Dennis, G., Hole, M.J., McGann, M., von Nessi, G. & Lazerson, S. 2012 Computation of multi-region relaxed magnetohydrodynamic equilibria. Phys. Plasmas 19 (11), 112502.CrossRefGoogle Scholar
Imbert-Gerard, L.-M., Paul, E.J. & Wright, A.M. 2020 An introduction to stellarators: from magnetic fields to symmetries and optimization. arXiv:1908.05360.Google Scholar
Izzo, V.A. & Joseph, I. 2008 RMP enhanced transport and rotational screening in simulations of DIII-D plasmas. Nucl. Fusion 48 (11), 115004.CrossRefGoogle Scholar
Jardin, S.C., Ferraro, N., Breslau, J. & Chen, J. 2012 Multiple timescale calculations of sawteeth and other global macroscopic dynamics of tokamak plasmas. Comput. Sci. Disc. 5 (1), 014002.CrossRefGoogle Scholar
Kolmogorov, A.N. 1954 On the conservation of conditionally periodic motions under small perturbation of the Hamiltonian. In Doklady Akademii Nauk SSSR, vol. 98, pp. 2–3.Google Scholar
Landreman, M., Medasani, B., Wechsung, F., Giuliani, A., Jorge, R. & Zhu, C. 2021 SIMSOPT: A flexible framework for stellarator optimization. J. Open Source Softw. 6 (65), 3525.CrossRefGoogle Scholar
Lao, L.L., John, H.S.., Stambaugh, R.D., Kellman, A.G. & Pfeiffer, W. 1985 Reconstruction of current profile parameters and plasma shapes in tokamaks. Nucl. Fusion 25 (11), 1611–1622.CrossRefGoogle Scholar
Liu, Y.Q., Bondeson, A., Fransson, C.M., Lennartson, B. & Breitholtz, C. 2000 Feedback stabilization of nonaxisymmetric resistive wall modes in tokamaks. I. Electromagnetic model. Phys. Plasmas 7 (9), 3681–3690.CrossRefGoogle Scholar
Loizu, J., Huang, Y.-M., Hudson, S.R., Baillod, A., Kumar, A. & Qu, Z.S. 2020 Direct prediction of nonlinear tearing mode saturation using a variational principle. Phys. Plasmas 27 (7), 070701.CrossRefGoogle Scholar
Loizu, J., Hudson, S., Bhattacharjee, A. & Helander, P. 2015 Magnetic islands and singular currents at rational surfaces in three-dimensional magnetohydrodynamic equilibria. Phys. Plasmas 22 (2), 022501.CrossRefGoogle Scholar
Lyons, B.C., Ferraro, N.M., Paz-Soldan, C., Nazikian, R. & Wingen, A. 2017 Effect of rotation zero-crossing on single-fluid plasma response to three-dimensional magnetic perturbations. Plasma Phys. Control. Fusion 59 (4), 044001.CrossRefGoogle Scholar
McGann, M., Hudson, S.R., Dewar, R.L. & von Nessi, G. 2010 Hamilton-Jacobi theory for continuation of magnetic field across a toroidal surface supporting a plasma pressure discontinuity. Phys. Lett. A 374 (33), 3308–3314.CrossRefGoogle Scholar
Möser, J. 1962 On invariant curves of area-preserving mappings of an annulus. In Nachrichten der Akademie der Wissenschaften in Göttingen II, pp. 1–20. Vanderhoeck & Ruprecht.Google Scholar
Nührenberg, C. & Boozer, A.H. 2003 Magnetic islands and perturbed plasma equilibria. Phys. Plasmas 10 (7), 2840–2851.CrossRefGoogle Scholar
Orain, F., Bécoulet, M., Morales, J., Huijsmans, G.T.A., Dif-Pradalier, G., Hoelzl, M., Garbet, X., Pamela, S., Nardon, E., Passeron, C., Latu, G., Fil, A. & Cahyna, P. 2014 Non-linear MHD modeling of edge localized mode cycles and mitigation by resonant magnetic perturbations. Plasma Phys. Control. Fusion 57 (1), 014020.CrossRefGoogle Scholar
Park, J.-K., Boozer, A.H. & Glasser, A.H. 2007 Computation of three-dimensional tokamak and spherical torus equilibria. Phys. Plasmas 14 (5), 052110.CrossRefGoogle Scholar
Park, J.-K. & Logan, N.C. 2017 Self-consistent perturbed equilibrium with neoclassical toroidal torque in tokamaks. Phys. Plasmas 24 (3), 032505.CrossRefGoogle Scholar
Park, W., Monticello, D.A., Strauss, H. & Manickam, J. 1986 Three-dimensional stellarator equilibrium as an ohmic steady state. Phys. Fluids 29 (4), 1171–1175.CrossRefGoogle Scholar
Piron, L., Kirk, A., Liu, Y.Q., Cunningham, G., Carr, M., Gowland, R., Katramados, I. & Martin, R. 2020 Error field correction strategies in preparation to MAST-U operation. Fusion Engng Design 161, 111932.CrossRefGoogle Scholar
Reiman, A., Ferraro, N.M., Turnbull, A., Park, J.K., Cerfon, A., Evans, T.E., Lanctot, M.J., Lazarus, E.A., Liu, Y., McFadden, G., Monticello, D. & Suzuki, Y. 2015 Tokamak plasma high field side response to an n= 3 magnetic perturbation: a comparison of 3D equilibrium solutions from seven different codes. Nucl. Fusion 55 (6), 063026.CrossRefGoogle Scholar
Reiman, A. & Greenside, H. 1986 Calculation of three-dimensional MHD equilibria with islands and stochastic regions. Comput. Phys. Commun. 43, 157.CrossRefGoogle Scholar
Singh, L., Kruger, T.G., Bader, A., Zhu, C., Hudson, S.R. & Anderson, D.T. 2020 Optimization of finite-build stellarator coils. J. Plasma Phys. 86 (4), 905860404.CrossRefGoogle Scholar
Sovinec, C.R., Gianakon, T.A., Held, E.D., Kruger, S.E. & Schnack, D.D. 2003 NIMROD: A computational laboratory for studying nonlinear fusion magnetohydrodynamics. Phys. Plasmas 10 (5), 1727–1732.CrossRefGoogle Scholar
Suzuki, Y. 2017 HINT modeling of three-dimensional tokamaks with resonant magnetic perturbation. Plasma Phys. Control. Fusion 59 (5), 054008.CrossRefGoogle Scholar
Suzuki, Y., Nakajima, N., Watanabe, K., Nakamura, Y. & Hayashi, T. 2006 Development and application of HINT2 to helical system plasmas. Nucl. Fusion 46 (11), L19–L24.CrossRefGoogle Scholar
Turnbull, A.D. 2012 Plasma response models for non-axisymmetric perturbations. Nucl. Fusion 52 (5), 054016.CrossRefGoogle Scholar
Turnbull, A.D., Ferraro, N.M., Izzo, V.A., Lazarus, E.A., Park, J.-K., Cooper, W.A., Hirshman, S.P., Lao, L.L., Lanctot, M.J., Lazerson, S., Liu, Y.Q., Reiman, A. & Turco, F. 2013 Comparisons of linear and nonlinear plasma response models for non-axisymmetric perturbations. Phys. Plasmas 20 (5), 056114.CrossRefGoogle Scholar
Wesson, J. & Campbell, D.J. 2011 Tokamaks, vol. 149. Oxford University Press.Google Scholar
Wingen, A., Ferraro, N.M., Shafer, M.W., Unterberg, E.A., Canik, J.M., Evans, T.E., Hillis, D.L., Hirshman, S.P., Seal, S.K., Snyder, P.B. & Sontag, A.C. 2015 Connection between plasma response and resonant magnetic perturbation (RMP) edge localized mode (ELM) suppression in DIII-D. Plasma Phys. Control. Fusion 57 (10), 104006.CrossRefGoogle Scholar
Zhou, Y., Ferraro, N.M., Jardin, S.C. & Strauss, H.R. 2021 Approach to nonlinear magnetohydrodynamic simulations in stellarator geometry. Nucl. Fusion 61 (8), 086015.CrossRefGoogle Scholar
Zhu, C., Gates, D.A., Hudson, S.R., Liu, H., Xu, Y., Shimizu, A. & Okamura, S. 2019 Identification of important error fields in stellarators using the hessian matrix method. Nucl. Fusion 59 (12), 126007.CrossRefGoogle Scholar
Zhu, C., Hudson, S.R., Lazerson, S.A., Song, Y. & Wan, Y. 2018 Hessian matrix approach for determining error field sensitivity to coil deviations. Plasma Phys. Control. Fusion 60 (5), 054016.CrossRefGoogle Scholar