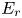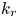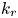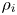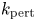1. Introduction
The geodesic acoustic mode (GAM) is a plasma oscillation observed in magnetic-confinement fusion reactors with toroidal geometry, such as tokamaks or stellarators (Winsor, Johnson & Dawson Reference Winsor, Johnson and Dawson1968). It develops because of the compressibility of the $E\times B$![]() drift velocity of the zonal flows (ZFs), where E and B denote the electric and magnetic field, respectively, which leads to $(m=\pm 1, n=0)$
drift velocity of the zonal flows (ZFs), where E and B denote the electric and magnetic field, respectively, which leads to $(m=\pm 1, n=0)$![]() pressure sidebands (where $m$
pressure sidebands (where $m$![]() and $n$
and $n$![]() are the poloidal and toroidal wavenumbers, respectively). As GAMs and ZFs satisfy charge neutrality, the perpendicular divergence of the diamagnetic current density is compensated by that of the polarization current, resulting in the GAM oscillation (Scott Reference Scott2005; Qiu, Chen & Zonca Reference Qiu, Chen and Zonca2018; Conway, Smolyakov & Ido Reference Conway, Smolyakov and Ido2021). The GAMs are thus recognized to be the non-stationary branch of the ZFs (Diamond et al. Reference Diamond, Itoh, Itoh and Hahm2005; Conway et al. Reference Conway, Smolyakov and Ido2021) and their associated electric potential is (to the leading order) an $m = n = 0$
are the poloidal and toroidal wavenumbers, respectively). As GAMs and ZFs satisfy charge neutrality, the perpendicular divergence of the diamagnetic current density is compensated by that of the polarization current, resulting in the GAM oscillation (Scott Reference Scott2005; Qiu, Chen & Zonca Reference Qiu, Chen and Zonca2018; Conway, Smolyakov & Ido Reference Conway, Smolyakov and Ido2021). The GAMs are thus recognized to be the non-stationary branch of the ZFs (Diamond et al. Reference Diamond, Itoh, Itoh and Hahm2005; Conway et al. Reference Conway, Smolyakov and Ido2021) and their associated electric potential is (to the leading order) an $m = n = 0$![]() structure. The name GAM stems from the geodesic magnetic field line curvature, which is responsible for plasma compressibility and thus a necessary condition for the emergence of the characteristic pressure mode.
structure. The name GAM stems from the geodesic magnetic field line curvature, which is responsible for plasma compressibility and thus a necessary condition for the emergence of the characteristic pressure mode.
The interaction between GAMs and turbulence is fairly complex. Nonlinear self-interactions of drift-wave (DW) turbulence are one of the main mechanisms for generating the perturbations of the electric potential, which are the origin of ZFs and GAMs (Itoh et al. Reference Itoh, Itoh, Diamond, Hahm, Fujisawa, Tynan, Yagi and Nagashima2006). Meanwhile, similarly to the ZFs, GAMs are understood to suppress DW turbulence and regulate cross-field turbulence, thus enhancing energy confinement (Conway et al. Reference Conway, Smolyakov and Ido2021). Still, their direct effect on turbulence is not clear at the moment (Smolyakov et al. Reference Smolyakov, Bashir, Efimov, Yagi and Miyato2016), as GAMs are known to deplete the energy available to ZFs and transfer part of the energy of the system back to turbulence (Scott Reference Scott2003a,Reference Scottb). This complex contribution to the turbulence dynamics makes GAMs highly interesting in current fusion research.
Prior studies have established that, as a direct consequence of nonlinear gyrokinetic theory, the GAM dynamics is well described by an equation of Schrödinger type – i.e. an equation whose linear contribution is exactly the linear Schrödinger equation, while the nonlinear dynamics necessitates an integro-differential expression, as has been discussed in § 6 of Qiu et al. (Reference Qiu, Chen and Zonca2018). Indeed, this is not surprising as it is a general result that plasma eigenmodes (more exactly, their radial envelope), arising in toroidal systems as a consequence of various types of instabilities, can be described by a nonlinear Schrödinger equation with integro-differential coefficients (Zonca & Chen Reference Zonca and Chen2014a,Reference Zonca and Chenb; Zonca et al. Reference Zonca, Chen, Briguglio, Fogaccia, Milovanov, Qiu, Vlad and Wang2015; Chen & Zonca Reference Chen and Zonca2016). For the reduced case of an isolated GAM (i.e. without interaction with other modes) a similar model equation is provided in Poli et al. (Reference Poli, Bottino, Maj, Palermo and Weber2021), where it was shown that, in the regime of moderate nonlinearity, the dynamics of undamped isolated GAM packets is well described by a cubic nonlinear Schrödinger equation (NLSE). The NLSE is a standard model (Spatschek Reference Spatschek2012) for describing nonlinear dispersive oscillations with a (linear) dispersion relation of the form
which, in the limit $k_r^2 \rho _i^2 \ll 1$![]() (where $\rho _i$
(where $\rho _i$![]() denotes the ion Larmor radius and $k_r$
denotes the ion Larmor radius and $k_r$![]() is the radial wavevector associated with the GAM radial electric field), approximates to the standard gyrokinetic GAM dispersion relation (Smolyakov, Nguyen & Garbet Reference Smolyakov, Nguyen and Garbet2008; Zonca & Chen Reference Zonca and Chen2008; Qiu, Chen & Zonca Reference Qiu, Chen and Zonca2009), as will be discussed in § 2.1. The NLSE model has been applied and studied extensively in the contexts of deep water waves, light travelling through optical fibres, Bose–Einstein condensates and others (Kuznetsov, Rubenchik & Zakharov Reference Kuznetsov, Rubenchik and Zakharov1986; Agrawal Reference Agrawal2019; Kengne, Liu & Malomed Reference Kengne, Liu and Malomed2021). Some predictions of the NLSE are well known, like the emergence of solitons, nonlinear wave breaking, the nonlinear phase shift and susceptibility to the modulational instability (MI). While some of these phenomena have already been observed in gyrokinetic simulations of GAMs in Poli et al. (Reference Poli, Bottino, Maj, Palermo and Weber2021), thus confirming the NLSE as a valid description of the dynamics, in this report the focus is set on the MI, which to the best of the authors’ knowledge has not yet been studied in the context of GAMs.
is the radial wavevector associated with the GAM radial electric field), approximates to the standard gyrokinetic GAM dispersion relation (Smolyakov, Nguyen & Garbet Reference Smolyakov, Nguyen and Garbet2008; Zonca & Chen Reference Zonca and Chen2008; Qiu, Chen & Zonca Reference Qiu, Chen and Zonca2009), as will be discussed in § 2.1. The NLSE model has been applied and studied extensively in the contexts of deep water waves, light travelling through optical fibres, Bose–Einstein condensates and others (Kuznetsov, Rubenchik & Zakharov Reference Kuznetsov, Rubenchik and Zakharov1986; Agrawal Reference Agrawal2019; Kengne, Liu & Malomed Reference Kengne, Liu and Malomed2021). Some predictions of the NLSE are well known, like the emergence of solitons, nonlinear wave breaking, the nonlinear phase shift and susceptibility to the modulational instability (MI). While some of these phenomena have already been observed in gyrokinetic simulations of GAMs in Poli et al. (Reference Poli, Bottino, Maj, Palermo and Weber2021), thus confirming the NLSE as a valid description of the dynamics, in this report the focus is set on the MI, which to the best of the authors’ knowledge has not yet been studied in the context of GAMs.
The MI is usually analysed for wave envelopes which consist of a (nearly) constant phase front that is modulated by a sinusoidal perturbation with a wavelength $\lambda _\text {pert} = 2{\rm \pi} /k_\text {pert}$![]() . One finds that this perturbation is unstable under the conditions that the NLSE is self-focusing (which for GAMs is the case when the ratio $\tau_e$
. One finds that this perturbation is unstable under the conditions that the NLSE is self-focusing (which for GAMs is the case when the ratio $\tau_e$![]() between the electron temperature $T_e$
between the electron temperature $T_e$![]() and ion temperature $T_i$
and ion temperature $T_i$![]() fulfills $\tau _e = T_e/T_i \lesssim 5.45$
fulfills $\tau _e = T_e/T_i \lesssim 5.45$![]() Smolyakov et al. Reference Smolyakov, Bashir, Efimov, Yagi and Miyato2016) and the wavevector $k_\text {pert}$
Smolyakov et al. Reference Smolyakov, Bashir, Efimov, Yagi and Miyato2016) and the wavevector $k_\text {pert}$![]() of the modulation of the envelope is within a certain range, which will be discussed in further detail in § 3. Unstable perturbations will grow exponentially at the expense of the constant envelope component until the sinusoidal modulation dominates the shape of the oscillation and saturates.
of the modulation of the envelope is within a certain range, which will be discussed in further detail in § 3. Unstable perturbations will grow exponentially at the expense of the constant envelope component until the sinusoidal modulation dominates the shape of the oscillation and saturates.
In the field of plasma physics the MI has been observed in numerous waves and oscillations (e.g. Schamel Reference Schamel1975; Murtaza & Salahuddin Reference Murtaza and Salahuddin1982). Most notable for the context of this paper are DWs, which as explained before are one of the driving mechanisms of GAMs and ZFs. The MI of DWs has been shown to spontaneously excite ZFs (Chen, Lin & White Reference Chen, Lin and White2000) or increase their amplitude (Itoh et al. Reference Itoh, Itoh, Diamond, Fujisawa, Yagi, Watari, Nagashima and Fukuyama2006). Since in this study the focus is set on isolated GAMs, where the effects of the generation mechanisms such as DWs are excluded, it is stressed here that in the present analysis the MI stems only from the self-interaction of GAMs and is not directly connected to DW MI.
After analysing the conditions for MI for the case of GAMs, the analytic predictions of the NLSE are first confirmed by numerical simulations of the NLSE and then validated against gyrokinetic simulations obtained from the global particle-in-cell code ORB5 (Bottino & Sonnendrücker Reference Bottino and Sonnendrücker2015; Lanti et al. Reference Lanti, Ohana, Tronko, Hayward-Schneider, Bottino, McMillan, Mishchenko, Scheinberg, Biancalani and Angelino2020). Details about the numerical tools are given in § 4. The results, which are presented in § 5, demonstrate that the MI does in fact appear in gyrokinetic GAM simulations, however, significant differences between the gyrokinetic and NLSE simulations are observed that can in part be explained by the (currently not included) radial dependency of the nonlinear strength $\alpha _\text {NL} = \alpha _\text {NL}(r)$![]() in the NLSE. Moreover, the radial spectra of the simulations indicate that a damping term should be included in the NLSE model in this context. The need to consider damping in the current context may at first seem surprising, since simulations are performed using a high safety factor ($q_s = 15$
in the NLSE. Moreover, the radial spectra of the simulations indicate that a damping term should be included in the NLSE model in this context. The need to consider damping in the current context may at first seem surprising, since simulations are performed using a high safety factor ($q_s = 15$![]() ) and an initial $k_r$
) and an initial $k_r$![]() spectrum for which, according to theoretical predictions by Sugama & Watanabe (Reference Sugama and Watanabe2006, Reference Sugama and Watanabe2007) and Qiu et al. (Reference Qiu, Chen and Zonca2009), it is expected that damping of GAMs is weak to negligible. However, the nonlinear evolution of the packet leads naturally to the generation of shorter and shorter wavelengths which are more efficiently damped. This effect is the nonlinear analogue of the enhanced Landau damping discussed in Palermo et al. (Reference Palermo, Biancalani, Angioni, Zonca and Bottino2016) and Biancalani et al. (Reference Biancalani, Palermo, Angioni, Bottino and Zonca2016), where the shorter wavelengths were generated by the linear dynamics in the presence of gradients.
spectrum for which, according to theoretical predictions by Sugama & Watanabe (Reference Sugama and Watanabe2006, Reference Sugama and Watanabe2007) and Qiu et al. (Reference Qiu, Chen and Zonca2009), it is expected that damping of GAMs is weak to negligible. However, the nonlinear evolution of the packet leads naturally to the generation of shorter and shorter wavelengths which are more efficiently damped. This effect is the nonlinear analogue of the enhanced Landau damping discussed in Palermo et al. (Reference Palermo, Biancalani, Angioni, Zonca and Bottino2016) and Biancalani et al. (Reference Biancalani, Palermo, Angioni, Bottino and Zonca2016), where the shorter wavelengths were generated by the linear dynamics in the presence of gradients.
In this paper, the theoretical predictions for the MI growth rate are modified with the inclusion of the damping rate derived in Qiu et al. (Reference Qiu, Chen and Zonca2009), which is appropriate in the in the underlying high safety factor $q_s$![]() and high spectral wavevectors (high $q_s, k_r$
and high spectral wavevectors (high $q_s, k_r$![]() ) regime and is furthermore consistent with the approximation of adiabatic electrons employed in the gyrokinetic (GK) simulations. Good agreement between theory and GK simulations is found if the damping rate of Qiu et al. (Reference Qiu, Chen and Zonca2009) is multiplied by a factor of approximately 2.5 (see §§ 5.3 and 5.4). This is not unexpected, as a similar discrepancy has been already reported in previous benchmarks (Biancalani et al. Reference Biancalani, Bottino, Ehrlacher, Grandgirard, Merlo, Novikau, Qiu, Sonnendrücker, Garbet and Görler2017). The following § 5.5 includes these findings in the NLSE model and compares damped NLSE simulations with the GK results, which are observed to show good agreement.
) regime and is furthermore consistent with the approximation of adiabatic electrons employed in the gyrokinetic (GK) simulations. Good agreement between theory and GK simulations is found if the damping rate of Qiu et al. (Reference Qiu, Chen and Zonca2009) is multiplied by a factor of approximately 2.5 (see §§ 5.3 and 5.4). This is not unexpected, as a similar discrepancy has been already reported in previous benchmarks (Biancalani et al. Reference Biancalani, Bottino, Ehrlacher, Grandgirard, Merlo, Novikau, Qiu, Sonnendrücker, Garbet and Görler2017). The following § 5.5 includes these findings in the NLSE model and compares damped NLSE simulations with the GK results, which are observed to show good agreement.
Sections 5.6 and 5.7 illustrate the self-focusing of a GAM with unperturbed Gaussian initial condition, which is a phenomenon closely related to the MI, and a long GAM simulation depicting breather behaviour (see e.g. Akhmediev & Korneev Reference Akhmediev and Korneev1986; Dudley et al. Reference Dudley, Genty, Dias, Kibler and Akhmediev2009) of the GAM MI.
2. Nonlinear Schrödinger equation model
2.1. Introduction
The NLSE model (Poli et al. Reference Poli, Bottino, Maj, Palermo and Weber2021) describes the dynamics of an isolated GAM packet via the complex wavefunction $\psi (r,t)$![]() , where its real part
, where its real part
represents the axisymmetric component of the GAM radial electric field $E_r(r,t)$![]() . The function $\psi$
. The function $\psi$![]() obeys the cubic NLSE given by
obeys the cubic NLSE given by
where the first two terms on the right-hand side characterize the linear GAM dispersion, while the last term introduces the contribution from nonlinear self-interactions. Their respective strengths are determined by the parameters ${\mathcal {F}}$![]() , ${\mathcal {G}}$
, ${\mathcal {G}}$![]() and $\alpha _\text {NL}$
and $\alpha _\text {NL}$![]() , which in most sections of this study will be assumed to be real values and independent of the radial coordinate $r$
, which in most sections of this study will be assumed to be real values and independent of the radial coordinate $r$![]() , which is equivalent to assuming no damping and a uniform plasma background, respectively. Damping in the NLSE will be considered later in this paper in §§ 5.2 and 5.5, and thus is discussed separately there.
, which is equivalent to assuming no damping and a uniform plasma background, respectively. Damping in the NLSE will be considered later in this paper in §§ 5.2 and 5.5, and thus is discussed separately there.
The values of the parameters ${\mathcal {F}}$![]() and ${\mathcal {G}}$
and ${\mathcal {G}}$![]() are obtained from the analytical GK result for the linear GAM dispersion relation, which according to Smolyakov et al. (Reference Smolyakov, Bashir, Efimov, Yagi and Miyato2016) is given by
are obtained from the analytical GK result for the linear GAM dispersion relation, which according to Smolyakov et al. (Reference Smolyakov, Bashir, Efimov, Yagi and Miyato2016) is given by
and holds only when $k_r^2 \rho _i^2 \ll 1$![]() . Here, $\omega _0$
. Here, $\omega _0$![]() is the dispersionless GAM frequency given by (2.5) below, $k_r$
is the dispersionless GAM frequency given by (2.5) below, $k_r$![]() is the radial wavevector of the GAM spectrum, $\rho _i$
is the radial wavevector of the GAM spectrum, $\rho _i$![]() is the ion Larmor radius and $D(\tau _e)$
is the ion Larmor radius and $D(\tau _e)$![]() is a coefficient characterizing the strength of the dispersive corrections, which depends on the electron-to-ion temperature ratio $\tau _e = T_e/T_i$
is a coefficient characterizing the strength of the dispersive corrections, which depends on the electron-to-ion temperature ratio $\tau _e = T_e/T_i$![]()

For $\omega _0$![]() the expression derived in Sugama & Watanabe (Reference Sugama and Watanabe2006) is utilized and damping is neglected
the expression derived in Sugama & Watanabe (Reference Sugama and Watanabe2006) is utilized and damping is neglected
where $v_{Ti} = \sqrt {2T_i/m_i}$![]() is the thermal ion velocity, $m_i$
is the thermal ion velocity, $m_i$![]() the ion mass, $R_0$
the ion mass, $R_0$![]() the major tokamak radius and $q_s$
the major tokamak radius and $q_s$![]() the safety factor. In order to obtain expressions for the parameters ${\mathcal {F}}$
the safety factor. In order to obtain expressions for the parameters ${\mathcal {F}}$![]() and ${\mathcal {G}}$
and ${\mathcal {G}}$![]() , the square root in the dispersion relation (2.3) is expanded using the approximation $k_r^2 \rho _i^2 \ll 1$
, the square root in the dispersion relation (2.3) is expanded using the approximation $k_r^2 \rho _i^2 \ll 1$![]() that was already assumed to hold during the derivation of the dispersion relation
that was already assumed to hold during the derivation of the dispersion relation
Here, a definition is denoted by ‘$:=$![]() ’. For the strength $\alpha _\text {NL}$
’. For the strength $\alpha _\text {NL}$![]() of the nonlinear self-interaction term there currently exists no analytical expression. As a consequence in this study the values for $\alpha _\text {NL}$
of the nonlinear self-interaction term there currently exists no analytical expression. As a consequence in this study the values for $\alpha _\text {NL}$![]() are obtained through comparisons with GK GAM simulations, which were generated with the particle-in-cell code ORB5 (Bottino & Sonnendrücker Reference Bottino and Sonnendrücker2015; Lanti et al. Reference Lanti, Ohana, Tronko, Hayward-Schneider, Bottino, McMillan, Mishchenko, Scheinberg, Biancalani and Angelino2020). The results of these comparisons are presented in Appendix A and show that the parameter is positive, $\alpha _\text {NL} > 0$
are obtained through comparisons with GK GAM simulations, which were generated with the particle-in-cell code ORB5 (Bottino & Sonnendrücker Reference Bottino and Sonnendrücker2015; Lanti et al. Reference Lanti, Ohana, Tronko, Hayward-Schneider, Bottino, McMillan, Mishchenko, Scheinberg, Biancalani and Angelino2020). The results of these comparisons are presented in Appendix A and show that the parameter is positive, $\alpha _\text {NL} > 0$![]() , increases with $\tau _e$
, increases with $\tau _e$![]() and depends approximately inversely on the ion Larmor radius, $\alpha _\text {NL} \propto 1/\rho _i$
and depends approximately inversely on the ion Larmor radius, $\alpha _\text {NL} \propto 1/\rho _i$![]() . Furthermore, $\alpha _\text {NL}$
. Furthermore, $\alpha _\text {NL}$![]() increases when approaching the centre of the plasma cross-section $r=0$
increases when approaching the centre of the plasma cross-section $r=0$![]() . No significant impact of the safety factor $q_s$
. No significant impact of the safety factor $q_s$![]() on $\alpha _\text {NL}$
on $\alpha _\text {NL}$![]() was found.
was found.
2.2. Dynamics
This section gives a short introduction to the terms in the NLSE (2.2), that will be relevant for the MI. The first term on the right-hand side, ${\mathcal {F}} \psi$![]() , is responsible for the coherent oscillation of the GAM at the dispersionless frequency ${\mathcal {F}} = \omega _0$
, is responsible for the coherent oscillation of the GAM at the dispersionless frequency ${\mathcal {F}} = \omega _0$![]() . The corresponding dynamics can be split off of the wavefunction $\psi$
. The corresponding dynamics can be split off of the wavefunction $\psi$![]() through the following transformation:
through the following transformation:
where $\hat {\psi }$![]() is the envelope of the GAM packet. This ansatz reduces the NLSE to the usually reported form
is the envelope of the GAM packet. This ansatz reduces the NLSE to the usually reported form
The second term on the right-hand side of (2.2), $-{\mathcal {G}}/2\partial _r^2 \psi$![]() (for ${\mathcal {G}} \neq {\mathcal {G}}(r)$
(for ${\mathcal {G}} \neq {\mathcal {G}}(r)$![]() ), gives the dispersive properties to the GAM dynamics. The nature of the dispersion is determined by the sign of the parameter ${\mathcal {G}}$
), gives the dispersive properties to the GAM dynamics. The nature of the dispersion is determined by the sign of the parameter ${\mathcal {G}}$![]() , which, as can be deduced from (2.4)–(2.8), depends solely on the value of the electron-to-ion temperature ratio $\tau _e$
, which, as can be deduced from (2.4)–(2.8), depends solely on the value of the electron-to-ion temperature ratio $\tau _e$![]() , with $\tau _e \approx 5.45$
, with $\tau _e \approx 5.45$![]() marking the boundary between positive and negative values of ${\mathcal {G}}$
marking the boundary between positive and negative values of ${\mathcal {G}}$![]() (Nguyen, Garbet & Smolyakov Reference Nguyen, Garbet and Smolyakov2008). The corresponding regimes are labelled as follows:
(Nguyen, Garbet & Smolyakov Reference Nguyen, Garbet and Smolyakov2008). The corresponding regimes are labelled as follows:

The full dependency of ${\mathcal {G}}$![]() on $\tau _e$
on $\tau _e$![]() is depicted in figure 1. The different kinds of dynamics corresponding to the three dispersion regimes are illustrated through NLSE simulations (without the nonlinear term) with an initial Gaussian profile in figure 2. The dispersive term broadens the width of packets as time progresses and alters the oscillation frequency of the Gaussian flanks compared with the maximum at $r = 0.5$
is depicted in figure 1. The different kinds of dynamics corresponding to the three dispersion regimes are illustrated through NLSE simulations (without the nonlinear term) with an initial Gaussian profile in figure 2. The dispersive term broadens the width of packets as time progresses and alters the oscillation frequency of the Gaussian flanks compared with the maximum at $r = 0.5$![]() (a.u.), resulting in a curvature of the phase front in $(r, t)$
(a.u.), resulting in a curvature of the phase front in $(r, t)$![]() -space. In the case of normal dispersion, the flanks oscillate faster than the packet centre, leading to convex curvature, and vice versa for anomalous dispersion.
-space. In the case of normal dispersion, the flanks oscillate faster than the packet centre, leading to convex curvature, and vice versa for anomalous dispersion.

Figure 1. Dependency of the dispersion coefficient ${\mathcal {G}}$![]() on the electron-to-ion temperature ratio $\tau _e$
on the electron-to-ion temperature ratio $\tau _e$![]() as defined in (2.4)–(2.8). The parameters were chosen as specified in table 1, with ion cyclotron frequency $\omega _{ci} \approx 1.82\times 10^8\,({\textrm {rad}}/{\textrm {s}}^{-1})$
as defined in (2.4)–(2.8). The parameters were chosen as specified in table 1, with ion cyclotron frequency $\omega _{ci} \approx 1.82\times 10^8\,({\textrm {rad}}/{\textrm {s}}^{-1})$![]() and ion Larmor radius $\rho _i/ a_\textrm {min} = 4.08\times 10^{-4}$
and ion Larmor radius $\rho _i/ a_\textrm {min} = 4.08\times 10^{-4}$![]() .
.

Figure 2. NLSE simulations illustrating the isolated impact of the dispersive term on the dynamics. The figure shows the real part $\mbox {Re}[\psi ]$![]() of the wavefunction (which for the GAM corresponds to the radial electric field $E_r$
of the wavefunction (which for the GAM corresponds to the radial electric field $E_r$![]() ) normalized to the maximum amplitude $a_0$
) normalized to the maximum amplitude $a_0$![]() of the Gaussian initial condition. The nonlinear term is disregarded ($\alpha _\textrm {NL} = 0$
of the Gaussian initial condition. The nonlinear term is disregarded ($\alpha _\textrm {NL} = 0$![]() ). The selected values of ${\mathcal {F}}$
). The selected values of ${\mathcal {F}}$![]() and ${\mathcal {G}}$
and ${\mathcal {G}}$![]() are chosen such that their relative orders of magnitude match the GAM simulations considered in the later sections. It can be observed that the coefficient ${\mathcal {F}}$
are chosen such that their relative orders of magnitude match the GAM simulations considered in the later sections. It can be observed that the coefficient ${\mathcal {F}}$![]() is responsible for the oscillation of $\mbox {Re}[\psi ]$
is responsible for the oscillation of $\mbox {Re}[\psi ]$![]() , while the dispersive term introduces a curvature in $(r,t)$
, while the dispersive term introduces a curvature in $(r,t)$![]() -space as well as an increase of the Gaussian width as time progresses.
-space as well as an increase of the Gaussian width as time progresses.
The nonlinear term introduces a shift that lowers the frequency (due to $\alpha _\textrm {NL} > 0$![]() for GAMs) proportionally to the packet amplitude squared at the location $r$
for GAMs) proportionally to the packet amplitude squared at the location $r$![]() , which for ${\mathcal {G}} = 0$
, which for ${\mathcal {G}} = 0$![]() amounts to
amounts to
This shift is illustrated in figure 3. The interaction between the nonlinear phase shift and the dispersive term creates two distinct regimes called self-defocusing regime (when ${\mathcal {G}} / \alpha _\textrm {NL} < 0$![]() , i.e. for GAMs for normal dispersion, i.e. $\tau _e \gtrsim 5.45$
, i.e. for GAMs for normal dispersion, i.e. $\tau _e \gtrsim 5.45$![]() ) and self-focusing regime (for ${\mathcal {G}} / \alpha _\textrm {NL} > 0$
) and self-focusing regime (for ${\mathcal {G}} / \alpha _\textrm {NL} > 0$![]() , i.e. vice versa) (Scott Reference Scott2006). Since the self-focusing regime is deeply connected with the formation of MI, it will be explained in further detail in the next section.
, i.e. vice versa) (Scott Reference Scott2006). Since the self-focusing regime is deeply connected with the formation of MI, it will be explained in further detail in the next section.

Figure 3. NLSE simulations illustrating the nonlinear frequency shift (in the dispersionless regime, ${\mathcal {G}} = 0$![]() ) for a Gaussian initial condition. Similarly to figure 2 the real part $\mbox {Re}[\psi ]$
) for a Gaussian initial condition. Similarly to figure 2 the real part $\mbox {Re}[\psi ]$![]() of the wavefunction is illustrated, which corresponds to the GAM radial electric field $E_r$
of the wavefunction is illustrated, which corresponds to the GAM radial electric field $E_r$![]() . Comparing the upper simulation (without nonlinearity, $\alpha _\textrm {NL} = 0$
. Comparing the upper simulation (without nonlinearity, $\alpha _\textrm {NL} = 0$![]() ) with the lower one, it is evident to see that the frequency shift as described by (2.12) is most pronounced at the centre of the Gaussian at $r=0.5$
) with the lower one, it is evident to see that the frequency shift as described by (2.12) is most pronounced at the centre of the Gaussian at $r=0.5$![]() , since there the amplitude reaches its highest value.
, since there the amplitude reaches its highest value.
3. Modulational instability
We recall in this section some known results concerning the MI. Although the material reported here can be found in textbooks (e.g. Agrawal Reference Agrawal2019), we present it to put the results of the next sections into context. The MI, also called Benjamin–Feir instability (Benjamin & Feir Reference Benjamin and Feir1967), is believed to be one of the most ubiquitous instabilities in nature (Zakharov & Ostrovsky Reference Zakharov and Ostrovsky2009). It appears not only in the NLSE, but also in other equations describing nonlinear dispersive waves, e.g. in the Withham equation and the Korteweg–de Vries equation. The instability only develops when the nonlinear and dispersive contributions to the oscillation dynamics interact such that the NLSE is self-focusing. As the name suggests, the NLSE dynamics creates a self-focusing effect of maxima in the wave packet, which is explained in further detail in Appendix B.
3.1. Introduction and behaviour
The MI is usually analysed for the case of a plane wave $A_0(t)$![]() with amplitude $a_0$
with amplitude $a_0$![]() (which can be considered to be a packet with very large width, $k_r\rightarrow 0$
(which can be considered to be a packet with very large width, $k_r\rightarrow 0$![]() ) superimposed with a radially periodic perturbation $A_1$
) superimposed with a radially periodic perturbation $A_1$![]() with a wavevector $k_\textrm {pert}$
with a wavevector $k_\textrm {pert}$![]()
When the perturbation wavevector $k_\textrm {pert}$![]() lies in the unstable range, which will be specified in § 3.2, due to the previously mentioned self-focusing effect the sinusoidal perturbation will grow exponentially (as long as the perturbation amplitude $a_1$
lies in the unstable range, which will be specified in § 3.2, due to the previously mentioned self-focusing effect the sinusoidal perturbation will grow exponentially (as long as the perturbation amplitude $a_1$![]() is small compared with the plane wave amplitude $a_0$
is small compared with the plane wave amplitude $a_0$![]() ) at the expense of the plane wave ($k_r = 0$
) at the expense of the plane wave ($k_r = 0$![]() ) component of the wave, which in the following will be called the background wave. More details on the growth process are given in Appendix B. When the perturbation has grown so large that it dominates the shape of the wave $\psi$
) component of the wave, which in the following will be called the background wave. More details on the growth process are given in Appendix B. When the perturbation has grown so large that it dominates the shape of the wave $\psi$![]() it saturates and acquires a large nonlinear phase shift (as mentioned in § 2.2) compared to the background, leading to strongly incoherent phase fronts. In this saturation phase the radial spectrum of the wave contains many high-$k_r$
it saturates and acquires a large nonlinear phase shift (as mentioned in § 2.2) compared to the background, leading to strongly incoherent phase fronts. In this saturation phase the radial spectrum of the wave contains many high-$k_r$![]() components. When the nonlinear phase shift is large enough that the perturbation has skipped an entire oscillation compared with the background, the wave front reconnects and the perturbation decreases again. Finally, the initial condition is restored and the MI process can start anew, leading to a cyclic behaviour called Akhmediev breathers (Akhmediev & Korneev Reference Akhmediev and Korneev1986). A single Akhmediev breather cycle together with the corresponding radial spectrum is shown in figure 4.
components. When the nonlinear phase shift is large enough that the perturbation has skipped an entire oscillation compared with the background, the wave front reconnects and the perturbation decreases again. Finally, the initial condition is restored and the MI process can start anew, leading to a cyclic behaviour called Akhmediev breathers (Akhmediev & Korneev Reference Akhmediev and Korneev1986). A single Akhmediev breather cycle together with the corresponding radial spectrum is shown in figure 4.

Figure 4. Single cycle of an Akhmediev breather where the initial perturbation wavevector was chosen to be $k_r = 10$![]() (a.u.). The upper figure illustrates $\mbox {Re}[\psi ]/a_0$
(a.u.). The upper figure illustrates $\mbox {Re}[\psi ]/a_0$![]() , which for the GAM corresponds to the radial electric field $E_r$
, which for the GAM corresponds to the radial electric field $E_r$![]() . As indicated by the colour bar only the positive values are drawn in the figure to emphasize the decoherent phase front at $t=4$
. As indicated by the colour bar only the positive values are drawn in the figure to emphasize the decoherent phase front at $t=4$![]() (a.u.). The bottom figure shows the evolution of the corresponding radial spectrum (i.e. the absolute value of the Fourier transform $|\mathfrak {F}[\mbox {Re}[\psi ]]|$
(a.u.). The bottom figure shows the evolution of the corresponding radial spectrum (i.e. the absolute value of the Fourier transform $|\mathfrak {F}[\mbox {Re}[\psi ]]|$![]() ). The perturbation grows exponentially until $t \approx 2.5$
). The perturbation grows exponentially until $t \approx 2.5$![]() , after which the growth slows down and at $t\approx 4$
, after which the growth slows down and at $t\approx 4$![]() the perturbation reaches its maximum value (which can be seen in the spectrum as well as in real space).
the perturbation reaches its maximum value (which can be seen in the spectrum as well as in real space).
3.2. Conditions for instability
The conditions for instability will be briefly summarized in the following (see e.g. Remoissenet Reference Remoissenet1996). By assuming that the time evolution of the perturbation $A_1(r,t)$![]() will be of the form
will be of the form
one finds that $\omega _\textrm {pert}$![]() fulfils the dispersion relation
fulfils the dispersion relation
It is immediate to see that exponential growth occurs (i.e. $\omega _\textrm {pert}$![]() is imaginary) when firstly
is imaginary) when firstly
which due to $\alpha _\textrm {NL} > 0$![]() for GAMs is equivalent to requiring anomalous dispersion (${\mathcal {G}} > 0$
for GAMs is equivalent to requiring anomalous dispersion (${\mathcal {G}} > 0$![]() , $\tau _e \lesssim 5.45$
, $\tau _e \lesssim 5.45$![]() as described in § 2.2), and secondly when the perturbation wavevector is within the range
as described in § 2.2), and secondly when the perturbation wavevector is within the range
where $k_\textrm {lim}$![]() marks the boundary between stable and unstable perturbation wavevectors. The perturbation wavevector $k^2_\textrm {pert}$
marks the boundary between stable and unstable perturbation wavevectors. The perturbation wavevector $k^2_\textrm {pert}$![]() provides the frequency mismatch of the sideband wave with respect to the background (pump) wave. The corresponding growth rate, which will be labelled $\gamma _\textrm {MI} := |\mbox {Im}\, \omega _\textrm {pert}|$
provides the frequency mismatch of the sideband wave with respect to the background (pump) wave. The corresponding growth rate, which will be labelled $\gamma _\textrm {MI} := |\mbox {Im}\, \omega _\textrm {pert}|$![]() in the following, reaches its maximum value at the wavevector $|k_\textrm {max}| := a_0 \sqrt {2 \alpha _\textrm {NL}/{\mathcal {G}}}$
in the following, reaches its maximum value at the wavevector $|k_\textrm {max}| := a_0 \sqrt {2 \alpha _\textrm {NL}/{\mathcal {G}}}$![]() . From (3.4) one finds that
. From (3.4) one finds that
The full dependency of $\gamma _\textrm {MI}$![]() on the wavevector of the initial perturbation $k_\textrm {pert}$
on the wavevector of the initial perturbation $k_\textrm {pert}$![]() is illustrated in figure 5.
is illustrated in figure 5.
4. Numerical approach
This section introduces the numerical tools employed in this paper to simulate the GAM gyrokinetically and with the NLSE model. As mentioned in the introduction, § 1, the GK results, which are obtained using the global particle-in-cell code ORB5 (Bottino & Sonnendrücker Reference Bottino and Sonnendrücker2015; Lanti et al. Reference Lanti, Ohana, Tronko, Hayward-Schneider, Bottino, McMillan, Mishchenko, Scheinberg, Biancalani and Angelino2020), are assumed to provide an accurate physical description of the GAM dynamics and are thus an adequate reference solution to validate the NLSE results and show shortcomings of this simplified model.
4.1. Split-step NLSE solver
The split-step solver (SSS) code was written by G.P. Agrawal (Agrawal Reference Agrawal2019) in MatLab and was created to solve the NLSE (2.10), which describes the dynamics of the envelope, in the context of optical fibres where it is reported. The code was modified to incorporate the originally missing oscillation term by utilizing the transformation introduced in (2.9) and adapted to make its input and output consistent with ORB5 simulations.
The split-step method states that, if the chosen numerical time step $\Delta t$![]() is small enough, the nonlinear and dispersive contributions to the NLSE dynamics (of the wave envelope $\hat {\psi }$
is small enough, the nonlinear and dispersive contributions to the NLSE dynamics (of the wave envelope $\hat {\psi }$![]() ) act (mostly) independently from each other (Faou Reference Faou2012; Agrawal Reference Agrawal2019). It follows that the solution can be approximated by alternatingly solving the two equations
) act (mostly) independently from each other (Faou Reference Faou2012; Agrawal Reference Agrawal2019). It follows that the solution can be approximated by alternatingly solving the two equations
for each time step. This approach has the significant advantage that the equations for the isolated nonlinear and isolated dispersive dynamics can each be immediately solved from an initial condition $\hat {\psi }(r,t=0)=\hat {\psi }_0$![]() using the following analytic solutions:
using the following analytic solutions:
where $\mathfrak {F}\lbrace \cdot \rbrace$![]() is the spatial Fourier transform which is calculated using the fast-Fourier-transform algorithm, $\mathfrak {F}^{-1}\lbrace \cdot \rbrace$
is the spatial Fourier transform which is calculated using the fast-Fourier-transform algorithm, $\mathfrak {F}^{-1}\lbrace \cdot \rbrace$![]() denotes the inverse Fourier transform and $\varphi _\textrm {NL}^t[\cdot ]$
denotes the inverse Fourier transform and $\varphi _\textrm {NL}^t[\cdot ]$![]() and $\varphi _{D}^t[\cdot ]$
and $\varphi _{D}^t[\cdot ]$![]() denote the exact flows (i.e. the temporal evolution starting from an initial condition $\hat \psi _0(r)$
denote the exact flows (i.e. the temporal evolution starting from an initial condition $\hat \psi _0(r)$![]() ) for the isolated nonlinear and isolated dispersive equation, respectively.
) for the isolated nonlinear and isolated dispersive equation, respectively.
The flow $\varphi _\textrm {NLSE}^t$![]() associated with the complete dynamics of the NLSE is then approximated as follows:
associated with the complete dynamics of the NLSE is then approximated as follows:
also known as the Lie splitting method, where ‘$\circ$![]() ’ denotes the concatenation of flows, $(\varphi _{D}^{\Delta t} \circ \varphi _\textrm {NL}^{\Delta t}) [\hat {\psi }_0] = \varphi _{D}^{\Delta t} [\varphi _\textrm {NL}^{\Delta t} [\hat {\psi }_0]]$
’ denotes the concatenation of flows, $(\varphi _{D}^{\Delta t} \circ \varphi _\textrm {NL}^{\Delta t}) [\hat {\psi }_0] = \varphi _{D}^{\Delta t} [\varphi _\textrm {NL}^{\Delta t} [\hat {\psi }_0]]$![]() .
.
The SSS implements a refinement of the split-step method with higher accuracy, called the symmetrized split-step Fourier method or Strang splitting scheme. In this form, the nonlinear dynamics is split into two parts of duration $\Delta t/2$![]() , with the dispersive (and thus smoothing) evolution acting in between (Faou Reference Faou2012; Agrawal Reference Agrawal2019).
, with the dispersive (and thus smoothing) evolution acting in between (Faou Reference Faou2012; Agrawal Reference Agrawal2019).
4.2. ORB5
The GK code ORB5 (Bottino & Sonnendrücker Reference Bottino and Sonnendrücker2015; Lanti et al. Reference Lanti, Ohana, Tronko, Hayward-Schneider, Bottino, McMillan, Mishchenko, Scheinberg, Biancalani and Angelino2020) is a global particle-in-cell code that simulates the plasma dynamics inside a tokamak for processes occurring on a time scale slower than that of the ion gyromotion. It can be executed with or without nonlinear plasma interactions.
The GK theory reduces the six-dimensional kinetic theory by one dimension by averaging over the gyromotion to obtain a five-dimensional problem describing the dynamics of the guiding centre distribution function $f_s$![]() of each species $s$
of each species $s$![]() . The set of GK equations describing the dynamics of $f_s$
. The set of GK equations describing the dynamics of $f_s$![]() can be constructed in different ways. The model implemented in ORB5 is derived from a GK Lagrangian describing the particle motion in a magnetic field (Brizard & Hahm Reference Brizard and Hahm2007). The time-symmetric Hamiltonian within the Lagrangian conserves energy automatically, leading to a model which is particularly useful for numerical simulations (Bottino & Sonnendrücker Reference Bottino and Sonnendrücker2015). ORB5 provides numerical results that exhibit strong agreement with other GK codes (Lanti et al. Reference Lanti, Ohana, Tronko, Hayward-Schneider, Bottino, McMillan, Mishchenko, Scheinberg, Biancalani and Angelino2020). Its recent application to the dynamics of isolated GAMs is documented in Palermo et al. (Reference Palermo, Biancalani, Angioni, Zonca and Bottino2016), Biancalani et al. (Reference Biancalani, Palermo, Angioni, Bottino and Zonca2016), Palermo et al. (Reference Palermo, Poli, Bottino, Biancalani, Conway and Scott2017), Palermo, Poli & Bottino (Reference Palermo, Poli and Bottino2020), Poli et al. (Reference Poli, Palermo, Bottino, Maj and Weber2020) and Palermo et al. (Reference Palermo, Conway, Poli and Roach2023). The interested reader is referred to these references for more details about the numerical model.
can be constructed in different ways. The model implemented in ORB5 is derived from a GK Lagrangian describing the particle motion in a magnetic field (Brizard & Hahm Reference Brizard and Hahm2007). The time-symmetric Hamiltonian within the Lagrangian conserves energy automatically, leading to a model which is particularly useful for numerical simulations (Bottino & Sonnendrücker Reference Bottino and Sonnendrücker2015). ORB5 provides numerical results that exhibit strong agreement with other GK codes (Lanti et al. Reference Lanti, Ohana, Tronko, Hayward-Schneider, Bottino, McMillan, Mishchenko, Scheinberg, Biancalani and Angelino2020). Its recent application to the dynamics of isolated GAMs is documented in Palermo et al. (Reference Palermo, Biancalani, Angioni, Zonca and Bottino2016), Biancalani et al. (Reference Biancalani, Palermo, Angioni, Bottino and Zonca2016), Palermo et al. (Reference Palermo, Poli, Bottino, Biancalani, Conway and Scott2017), Palermo, Poli & Bottino (Reference Palermo, Poli and Bottino2020), Poli et al. (Reference Poli, Palermo, Bottino, Maj and Weber2020) and Palermo et al. (Reference Palermo, Conway, Poli and Roach2023). The interested reader is referred to these references for more details about the numerical model.
In order to create GAMs in the ORB5 simulations, an electric field $E_r$![]() is initialized in ORB5 via a perturbation $\delta n_i$
is initialized in ORB5 via a perturbation $\delta n_i$![]() of the gyrocentre density of the only ion species included in the simulations. This perturbation leads through the GK Poisson equation to a potential perturbation (or equivalently to a polarization density) that ensures quasineutrality. The relevant relation between density perturbation and electric field for a (0,0) perturbation can be expressed as
of the gyrocentre density of the only ion species included in the simulations. This perturbation leads through the GK Poisson equation to a potential perturbation (or equivalently to a polarization density) that ensures quasineutrality. The relevant relation between density perturbation and electric field for a (0,0) perturbation can be expressed as
As a result, the GAM is essentially ‘dropped into’ the simulations and the formation process is not considered.
5. Simulation results
In the following simulations the (axisymmetric) GAM radial electric field is initialized in the following form:

which is similar to the initial condition discussed in (3.1) in § 3, but uses a plateau function instead of a constant background in order to avoid numerical artefacts at the boundaries of the simulation domain, i.e. $r = 0$![]() and $r = a_\textrm {min}$
and $r = a_\textrm {min}$![]() . This initial condition is depicted for different parameters in figure 6. The exponent $p$
. This initial condition is depicted for different parameters in figure 6. The exponent $p$![]() determines the steepness of the plateau edge, where $p = 1$
determines the steepness of the plateau edge, where $p = 1$![]() corresponds to a Gaussian profile and $p = 4$
corresponds to a Gaussian profile and $p = 4$![]() was chosen in the following simulations.
was chosen in the following simulations.

Figure 6. Initial condition of the GAM radial electric field $E_r = \mbox {Re}[\psi ]$![]() according to (5.1) for two values of $p$
according to (5.1) for two values of $p$![]() , compared with the usual constant background initial condition of MI described in § 3.1. Unless stated otherwise, $p=4$
, compared with the usual constant background initial condition of MI described in § 3.1. Unless stated otherwise, $p=4$![]() will be used for the packet steepness, $\textit {w}_0 = 0.35a_\textrm {min}$
will be used for the packet steepness, $\textit {w}_0 = 0.35a_\textrm {min}$![]() for the width and the centre will be placed at $r_0 = 0.6a_\textrm {min}$
for the width and the centre will be placed at $r_0 = 0.6a_\textrm {min}$![]() in subsequent simulations. The perturbation wavevector and amplitude in this example are $k_\textrm {pert} = 8({2{\rm \pi} }/{a_\textrm {min}})$
in subsequent simulations. The perturbation wavevector and amplitude in this example are $k_\textrm {pert} = 8({2{\rm \pi} }/{a_\textrm {min}})$![]() and $a_1 = 0.1$
and $a_1 = 0.1$![]() , respectively.
, respectively.
The parameters $a_0$![]() (which is related to the density perturbation amplitude $\delta n/n_0$
(which is related to the density perturbation amplitude $\delta n/n_0$![]() as discussed in Appendix A), $r_0, \textit {w}_0, a_1$
as discussed in Appendix A), $r_0, \textit {w}_0, a_1$![]() for the initial condition and $a_\textrm {min}, R_0, \tau _e, B_0, q_s, m_i$
for the initial condition and $a_\textrm {min}, R_0, \tau _e, B_0, q_s, m_i$![]() for the simulation conditions are chosen as specified in table 1, with the ion Larmor radius $\rho _i$
for the simulation conditions are chosen as specified in table 1, with the ion Larmor radius $\rho _i$![]() and the perturbation wavevector $k_\textrm {pert}$
and the perturbation wavevector $k_\textrm {pert}$![]() assuming different values in the following sections. Through the choice of $\tau _e = T_e/T_i = 3 < 5.45$
assuming different values in the following sections. Through the choice of $\tau _e = T_e/T_i = 3 < 5.45$![]() the first MI condition, (3.5), i.e. ${\mathcal {G}}>0$
the first MI condition, (3.5), i.e. ${\mathcal {G}}>0$![]() (anomalous dispersion, self-focusing NLSE) is satisfied. The geometry of the tokamak with an aspect ratio of $R_0/a_\textrm {min} = 10$
(anomalous dispersion, self-focusing NLSE) is satisfied. The geometry of the tokamak with an aspect ratio of $R_0/a_\textrm {min} = 10$![]() has a high cylindricity, which more closely resembles the NLSE model where the geometry is not considered in the equations.
has a high cylindricity, which more closely resembles the NLSE model where the geometry is not considered in the equations.
Table 1. Parameters used in the GK (ORB5) and NLSE simulations.

The GAM damping is known to decrease with rising safety factor $q_s$![]() (Palermo et al. Reference Palermo, Biancalani, Angioni, Zonca and Bottino2016). In order to fulfil the assumption of weak damping (compared with the MI growth rate $\gamma _\textrm {MI}$
(Palermo et al. Reference Palermo, Biancalani, Angioni, Zonca and Bottino2016). In order to fulfil the assumption of weak damping (compared with the MI growth rate $\gamma _\textrm {MI}$![]() , (3.8)) that was posed in § 1, the safety factor $q_s = 15$
, (3.8)) that was posed in § 1, the safety factor $q_s = 15$![]() is chosen. In this regime the damping term derived by Qiu et al. (Reference Qiu, Chen and Zonca2009) is applicable as the assumptions of $1/q_s^2 \ll k_r^2 \rho _i^2 \ll 1$
is chosen. In this regime the damping term derived by Qiu et al. (Reference Qiu, Chen and Zonca2009) is applicable as the assumptions of $1/q_s^2 \ll k_r^2 \rho _i^2 \ll 1$![]() and $\frac {1}{2} \tau _e k_r^2 \rho _i^2 \ll 1$
and $\frac {1}{2} \tau _e k_r^2 \rho _i^2 \ll 1$![]() are satisfied for all of the chosen perturbation wavevectors $k_\textrm {pert}$
are satisfied for all of the chosen perturbation wavevectors $k_\textrm {pert}$![]() (note that for $\rho _i/ a_\textrm {min} = 5.025\times 10^{-3}$
(note that for $\rho _i/ a_\textrm {min} = 5.025\times 10^{-3}$![]() and $k_r = 10 (2{\rm \pi} /a_\textrm {min})$
and $k_r = 10 (2{\rm \pi} /a_\textrm {min})$![]() the value of $\frac {1}{2}\tau _e k_r^2 \rho _i^2 \approx 0.1$
the value of $\frac {1}{2}\tau _e k_r^2 \rho _i^2 \approx 0.1$![]() and for $k_r = 14 (2{\rm \pi} /a_\textrm {min})$
and for $k_r = 14 (2{\rm \pi} /a_\textrm {min})$![]() , $\frac {1}{2}\tau _e k_r^2 \rho _i^2 \approx 0.3$
, $\frac {1}{2}\tau _e k_r^2 \rho _i^2 \approx 0.3$![]() ). We remark that GAM damping has also been studied under different approximation limits, e.g. by Sugama & Watanabe (Reference Sugama and Watanabe2006) whose expression is appropriate in the limit $k_r^2 \rho _i^2 \ll 1/q_s^2$
). We remark that GAM damping has also been studied under different approximation limits, e.g. by Sugama & Watanabe (Reference Sugama and Watanabe2006) whose expression is appropriate in the limit $k_r^2 \rho _i^2 \ll 1/q_s^2$![]() , and by Gao et al. (Reference Gao, Itoh, Sanuki and Dong2006), who employ the approximation $\tau _e \rightarrow 0$
, and by Gao et al. (Reference Gao, Itoh, Sanuki and Dong2006), who employ the approximation $\tau _e \rightarrow 0$![]() . For a detailed discussion about the damping behaviour in the transitory regime between the limits by Qiu et al. (Reference Qiu, Chen and Zonca2009), Sugama & Watanabe (Reference Sugama and Watanabe2006) and Gao et al. (Reference Gao, Itoh, Sanuki and Dong2006) the reader is referred to Zonca & Chen (Reference Zonca and Chen2008). One obtains from Qiu et al. (Reference Qiu, Chen and Zonca2009) that the unmodulated packet and wavevectors $k_r < 5 ({2{\rm \pi} }/{a_\textrm {min}})$
. For a detailed discussion about the damping behaviour in the transitory regime between the limits by Qiu et al. (Reference Qiu, Chen and Zonca2009), Sugama & Watanabe (Reference Sugama and Watanabe2006) and Gao et al. (Reference Gao, Itoh, Sanuki and Dong2006) the reader is referred to Zonca & Chen (Reference Zonca and Chen2008). One obtains from Qiu et al. (Reference Qiu, Chen and Zonca2009) that the unmodulated packet and wavevectors $k_r < 5 ({2{\rm \pi} }/{a_\textrm {min}})$![]() are undamped (see figure 10). However, damping rates of larger wavevectors, e.g. $\gamma _\textrm {Qiu}(k_r = 10 ({2{\rm \pi} }/{a_\textrm {min}})) = -6.07\times 10^{-6}\,\omega _{ci}$
are undamped (see figure 10). However, damping rates of larger wavevectors, e.g. $\gamma _\textrm {Qiu}(k_r = 10 ({2{\rm \pi} }/{a_\textrm {min}})) = -6.07\times 10^{-6}\,\omega _{ci}$![]() are of similar orders of magnitude as the MI growth rate $\gamma _\textrm {MI}(k_r = 10 ({2{\rm \pi} }/{a_\textrm {min}})) = 3.11\times 10^{-5}\omega _\textrm {ci}$
are of similar orders of magnitude as the MI growth rate $\gamma _\textrm {MI}(k_r = 10 ({2{\rm \pi} }/{a_\textrm {min}})) = 3.11\times 10^{-5}\omega _\textrm {ci}$![]() , i.e. $|\gamma _\textrm {Qiu}| \approx \frac {1}{5}|\gamma _\textrm {MI}|$
, i.e. $|\gamma _\textrm {Qiu}| \approx \frac {1}{5}|\gamma _\textrm {MI}|$![]() , which leads to the conclusion that damping may slow the growth of MI down but it is not expected to suppress MI.
, which leads to the conclusion that damping may slow the growth of MI down but it is not expected to suppress MI.
5.1. General comparison between NLSE and GK simulations
A first comparison between NLSE and GK simulations of the general GAM dynamics (without modulation of the initial condition and thus without MI) was made using the parameters in table 1. Specifically, the initial GAM electric field amplitude $a_0 = 2.5\times 10^{-4}$![]() (a.u.), sound Larmor radius $\rho _s/a_\textrm {min} = 2/375$
(a.u.), sound Larmor radius $\rho _s/a_\textrm {min} = 2/375$![]() and ion Larmor radius $\rho _i/a_\textrm {min} \approx 4.355\times 10^{-3}$
and ion Larmor radius $\rho _i/a_\textrm {min} \approx 4.355\times 10^{-3}$![]() (where $\rho _i$
(where $\rho _i$![]() and $\rho _s$
and $\rho _s$![]() are determined as described in (A1) and (A2)) were chosen as a starting point. The dispersion coefficient ${\mathcal {G}}$
are determined as described in (A1) and (A2)) were chosen as a starting point. The dispersion coefficient ${\mathcal {G}}$![]() is obtained according to (2.8) and $\alpha _\textrm {NL}$
is obtained according to (2.8) and $\alpha _\textrm {NL}$![]() is chosen as described in Appendix A (with $r=r_0=0.6a_\textrm {tok}$
is chosen as described in Appendix A (with $r=r_0=0.6a_\textrm {tok}$![]() ). Figure 7 presents the GK and NLSE simulation results.
). Figure 7 presents the GK and NLSE simulation results.

Figure 7. The GAM radial electric field $E_r$![]() in an ORB5 GK (colour contours) and NLSE (red levels) simulation of an initially unmodulated GAM. While the frequency of the oscillation matches well at the packet centre and further outward (for $r \geq 0.6 a_\textrm {min}$
in an ORB5 GK (colour contours) and NLSE (red levels) simulation of an initially unmodulated GAM. While the frequency of the oscillation matches well at the packet centre and further outward (for $r \geq 0.6 a_\textrm {min}$![]() ), differences increase when moving to smaller values of $r$
), differences increase when moving to smaller values of $r$![]() . Since the plasma parameters were chosen to be constant across the radial coordinate $r$
. Since the plasma parameters were chosen to be constant across the radial coordinate $r$![]() , these discrepancies can be attributed to an influence of the tokamak geometry on the nonlinear parameter $\alpha _\textrm {NL}$
, these discrepancies can be attributed to an influence of the tokamak geometry on the nonlinear parameter $\alpha _\textrm {NL}$![]() , which is analysed in Appendix A.
, which is analysed in Appendix A.
The comparison in figure 7 shows that, despite the uniform plasma background and thus (according to the equations introduced in § 2.1) constant values of ${\mathcal {F}}$![]() and ${\mathcal {G}}$
and ${\mathcal {G}}$![]() , the frequency of the nonlinear GAM is radially varying in the GK simulations. This major discrepancy between the NLSE and GK simulation results may be explained by a radial dependence of $\alpha _\textrm {NL}$
, the frequency of the nonlinear GAM is radially varying in the GK simulations. This major discrepancy between the NLSE and GK simulation results may be explained by a radial dependence of $\alpha _\textrm {NL}$![]() that stems from the geometry of the tokamak. This is not included in the NLSE used in this paper since, as mentioned in § 2.1, the NLSE model for GAMs has not yet been derived from analytic theory. The dependency is analysed numerically in more detail in Appendix A and will be considered in future work.
that stems from the geometry of the tokamak. This is not included in the NLSE used in this paper since, as mentioned in § 2.1, the NLSE model for GAMs has not yet been derived from analytic theory. The dependency is analysed numerically in more detail in Appendix A and will be considered in future work.
Next, an initial condition with a modulated envelope is considered. From the parameters $a_0 = 2.5\times 10^{-4}$![]() (a.u.), $\alpha _\textrm {NL}$
(a.u.), $\alpha _\textrm {NL}$![]() and ${\mathcal {G}}$
and ${\mathcal {G}}$![]() one obtains the range of unstable perturbation wavevectors $k_\textrm {pert}$
one obtains the range of unstable perturbation wavevectors $k_\textrm {pert}$![]() through (3.6) as
through (3.6) as
It follows that the wave is unstable to MI when the wavelength of the perturbation $\lambda _\textrm {pert} = 2{\rm \pi} /k_\textrm {pert}$![]() is larger than approximately 1/15th of the minor tokamak radius, and the maximum growth rate from (3.8) of $\gamma _\textrm {MI} = 3.05\times 10^{-5}\omega _{ci}$
is larger than approximately 1/15th of the minor tokamak radius, and the maximum growth rate from (3.8) of $\gamma _\textrm {MI} = 3.05\times 10^{-5}\omega _{ci}$![]() is achieved when the perturbation wavelength is approximately $a_\textrm {min}/10$
is achieved when the perturbation wavelength is approximately $a_\textrm {min}/10$![]() .
.
A comparison of an NLSE and GK simulation with $k_\textrm {pert} = 10 ({2{\rm \pi} }/{a_\textrm {min}}) \approx k_\textrm {max}$![]() and ${a_1 = 0.1}$
and ${a_1 = 0.1}$![]() is shown in figure 8. While again significant differences between the NLSE and GK simulations can be observed, the results illustrate that the MI does occur in GK GAM simulations. This is apparent since the maxima of the initial condition start to grow as time progresses and the phase skipping of the maxima (as described in § 3.1) compared with the background is observed e.g. for $t\approx 1.5 \times 10^5/\omega _{ci}$
is shown in figure 8. While again significant differences between the NLSE and GK simulations can be observed, the results illustrate that the MI does occur in GK GAM simulations. This is apparent since the maxima of the initial condition start to grow as time progresses and the phase skipping of the maxima (as described in § 3.1) compared with the background is observed e.g. for $t\approx 1.5 \times 10^5/\omega _{ci}$![]() at $r = 0.5 a_\textrm {min}$
at $r = 0.5 a_\textrm {min}$![]() and for $t\approx 2.2 \times 10^5/\omega _{ci}$
and for $t\approx 2.2 \times 10^5/\omega _{ci}$![]() at $r = 0.6 a_\textrm {min}$
at $r = 0.6 a_\textrm {min}$![]() in figure 8(b). The observed radial difference in growth rate can be explained by the radial dependency of the nonlinear parameter $\alpha _\textrm {NL}$
in figure 8(b). The observed radial difference in growth rate can be explained by the radial dependency of the nonlinear parameter $\alpha _\textrm {NL}$![]() , as from (3.4) it follows that $\gamma _\textrm {MI}$
, as from (3.4) it follows that $\gamma _\textrm {MI}$![]() increases monotonically with $\alpha _\textrm {NL}$
increases monotonically with $\alpha _\textrm {NL}$![]() , which gets larger for smaller values of $r$
, which gets larger for smaller values of $r$![]() (as determined in Appendix A). Another discrepancy is the merging of two maxima at $r=0.8 a_\textrm {min}$
(as determined in Appendix A). Another discrepancy is the merging of two maxima at $r=0.8 a_\textrm {min}$![]() and $r=0.9 a_\textrm {min}$
and $r=0.9 a_\textrm {min}$![]() in the GK simulation, which stay separated for the NLSE. This is again explained by $\alpha _\textrm {NL}$
in the GK simulation, which stay separated for the NLSE. This is again explained by $\alpha _\textrm {NL}$![]() decreasing with $r$
decreasing with $r$![]() since, according to (3.6), the wavevector with the highest growth rate depends as $k_\textrm {max} \propto \sqrt {\alpha _\textrm {NL}}$
since, according to (3.6), the wavevector with the highest growth rate depends as $k_\textrm {max} \propto \sqrt {\alpha _\textrm {NL}}$![]() . As a consequence at $r\approx 0.85 a_\textrm {min}$
. As a consequence at $r\approx 0.85 a_\textrm {min}$![]() smaller wavevectors (i.e. larger structures) will grow faster, thus favouring the merging of structures. Generally, one finds that across the whole radial space the growth rate and maximum amplitude in the GK simulation are significantly smaller compared with the NLSE simulation and theoretical predictions, as can be noticed comparing the colour bars in figure 8. This observation is further discussed in §§ 5.3 and 5.4.
smaller wavevectors (i.e. larger structures) will grow faster, thus favouring the merging of structures. Generally, one finds that across the whole radial space the growth rate and maximum amplitude in the GK simulation are significantly smaller compared with the NLSE simulation and theoretical predictions, as can be noticed comparing the colour bars in figure 8. This observation is further discussed in §§ 5.3 and 5.4.

Figure 8. Comparison of a NLSE and a GK simulation where the envelopes are modulated sinusoidally with the perturbation wavevector $k_\textrm {pert} = 10 ({2{\rm \pi} }/{a_\textrm {min}}) \approx k_\textrm {max}$![]() . The figures depict the GAM radial electric field $E_r$
. The figures depict the GAM radial electric field $E_r$![]() , which in the NLSE model is the real part of the wavefunction $\mbox {Re}[\psi ] = E_r$
, which in the NLSE model is the real part of the wavefunction $\mbox {Re}[\psi ] = E_r$![]() . While the growth of the modulation is observable in both simulations, the growth rate appears to be significantly lower in the GK result compared with the NLSE simulation. One can find further discrepancies, e.g. the two individual maxima that form in the NLSE simulation at $r=0.8 a_\textrm {min}$
. While the growth of the modulation is observable in both simulations, the growth rate appears to be significantly lower in the GK result compared with the NLSE simulation. One can find further discrepancies, e.g. the two individual maxima that form in the NLSE simulation at $r=0.8 a_\textrm {min}$![]() and $r=0.9 a_\textrm {min}$
and $r=0.9 a_\textrm {min}$![]() are seemingly merged together in the GK simulation. Panels show the (a) NLSE simulation result and (b) the GK simulation result.
are seemingly merged together in the GK simulation. Panels show the (a) NLSE simulation result and (b) the GK simulation result.
To study the aforementioned differences in further detail the radial spectra of the results are compared, as depicted in figure 9. The spectrum of the NLSE simulation contains much larger wavevectors $k_r$![]() than the GK simulation spectrum, most notably in the nonlinear saturation phase at $t\approx 1.1\times 10^5/\omega _{ci}$
than the GK simulation spectrum, most notably in the nonlinear saturation phase at $t\approx 1.1\times 10^5/\omega _{ci}$![]() (see figure 8a). Together with the lower amplitude and growth rate, these findings indicate that a damping mechanism acting preferentially on higher wavevectors is present in the GK simulations, which is not contained in the NLSE solver. As a side note it is remarked that the NLSE spectrum extends up to wavevectors larger than $30 ({2{\rm \pi} }/{a_\textrm {min}})$
(see figure 8a). Together with the lower amplitude and growth rate, these findings indicate that a damping mechanism acting preferentially on higher wavevectors is present in the GK simulations, which is not contained in the NLSE solver. As a side note it is remarked that the NLSE spectrum extends up to wavevectors larger than $30 ({2{\rm \pi} }/{a_\textrm {min}})$![]() , where the assumption $k_r^2 \rho _i^2 \ll 1$
, where the assumption $k_r^2 \rho _i^2 \ll 1$![]() posed in § 2.1 is marginally or no longer satisfied, as e.g. $k_r^2\rho _i^2 = 0.2$
posed in § 2.1 is marginally or no longer satisfied, as e.g. $k_r^2\rho _i^2 = 0.2$![]() corresponds to $k_r \approx 16 ({2{\rm \pi} }/{a_\textrm {min}})$
corresponds to $k_r \approx 16 ({2{\rm \pi} }/{a_\textrm {min}})$![]() for the current ion Larmor radius $\rho _i/a_\textrm {min} \approx 4.355\times 10^{-3}$
for the current ion Larmor radius $\rho _i/a_\textrm {min} \approx 4.355\times 10^{-3}$![]() . One can also notice in figure 9 that higher spectral components develop later in ORB5 simulations as compared with the NLSE solution. This is due to the fact that the instability develops on a slower scale in GK simulations, in particular at larger $r$
. One can also notice in figure 9 that higher spectral components develop later in ORB5 simulations as compared with the NLSE solution. This is due to the fact that the instability develops on a slower scale in GK simulations, in particular at larger $r$![]() .
.

Figure 9. Comparison of the radial spectrum of the GK and NLSE simulations reported in figure 8. The figures show the absolute value of the radial Fourier transform of the GAM radial electric field, $|\mathfrak {F}[E_r]|$![]() . It is apparent that the GK spectrum is in general more restrained to small wavevectors compared with the NLSE spectrum. This is especially noticeable in the saturation phase at $t\approx 1.1 \times 10^5/\omega _{ci}$
. It is apparent that the GK spectrum is in general more restrained to small wavevectors compared with the NLSE spectrum. This is especially noticeable in the saturation phase at $t\approx 1.1 \times 10^5/\omega _{ci}$![]() , which as described in § 3 is (according to the NLSE predictions) associated with a spectrum that contains high wavevector components. Panels show the (a) NLSE radial spectrum and (b) the GK radial spectrum.
, which as described in § 3 is (according to the NLSE predictions) associated with a spectrum that contains high wavevector components. Panels show the (a) NLSE radial spectrum and (b) the GK radial spectrum.
5.2. Damping term
This section gives a short introduction to the damping term derived in Qiu et al. (Reference Qiu, Chen and Zonca2009), which, as mentioned in § 5, can be applied to the radial GAM spectrum when electrons are considered to be adiabatic, $1/q_s^2 \ll k_r^2\rho _i^2 \ll 1$![]() and $\frac {1}{2}\tau _e k_r^2\rho _i^2 \ll 1$
and $\frac {1}{2}\tau _e k_r^2\rho _i^2 \ll 1$![]() . The condition $1/q_s^2 \ll k_r^2\rho _i^2$
. The condition $1/q_s^2 \ll k_r^2\rho _i^2$![]() is always satisfied for the chosen safety factor $q_s = 15$
is always satisfied for the chosen safety factor $q_s = 15$![]() and the wavevectors $k_\textrm {pert}$
and the wavevectors $k_\textrm {pert}$![]() of the initial perturbation. Furthermore, due to $\tau _e = 3$
of the initial perturbation. Furthermore, due to $\tau _e = 3$![]() the remaining requirements can be merged as follows:
the remaining requirements can be merged as follows:
Taking $0.3\ll 1$![]() as the boundary value for the validity of this assumption, one finds that, for the largest ion Larmor radius used in this paper, $\rho _i/ a_\textrm {min} = 5.025\times 10^{-3}$
as the boundary value for the validity of this assumption, one finds that, for the largest ion Larmor radius used in this paper, $\rho _i/ a_\textrm {min} = 5.025\times 10^{-3}$![]() , the applicability of the damping term is limited to wavevectors $k_r \lesssim 14.2 ({2{\rm \pi} }/{a_\textrm {min}})$
, the applicability of the damping term is limited to wavevectors $k_r \lesssim 14.2 ({2{\rm \pi} }/{a_\textrm {min}})$![]() . The term is given by the following expression:
. The term is given by the following expression:

where the components are defined as

This damping term describes the collisionless Landau damping of the GAM and can be applied to larger wavevectors $k_r$![]() than e.g. the term derived by Sugama & Watanabe (Reference Sugama and Watanabe2006), which is achieved by including higher-order harmonics of the ion transit resonances in the derivation. The resulting dependency is depicted in figure 10 for the parameters from table 1 (notably with $\rho _s/a_\textrm {min} = 2/375$
than e.g. the term derived by Sugama & Watanabe (Reference Sugama and Watanabe2006), which is achieved by including higher-order harmonics of the ion transit resonances in the derivation. The resulting dependency is depicted in figure 10 for the parameters from table 1 (notably with $\rho _s/a_\textrm {min} = 2/375$![]() , $\rho _i/a_\textrm {min} = 4.355\times 10^{-3}$
, $\rho _i/a_\textrm {min} = 4.355\times 10^{-3}$![]() ). It is apparent that the strength is negligible for wavevectors $k_\textrm {r} < 5({2{\rm \pi} }/{a_\textrm {min}})$
). It is apparent that the strength is negligible for wavevectors $k_\textrm {r} < 5({2{\rm \pi} }/{a_\textrm {min}})$![]() , but increases rapidly at $k\approx 10 ({2{\rm \pi} }/{a_\textrm {min}})$
, but increases rapidly at $k\approx 10 ({2{\rm \pi} }/{a_\textrm {min}})$![]() .
.

Figure 10. Damping term for the parameters given in table 1, with $\rho _s/a_\textrm {min} = 2/375$![]() , $\rho _i/a_\textrm {min} = 4.355\times 10^{-3}$
, $\rho _i/a_\textrm {min} = 4.355\times 10^{-3}$![]() . The red line illustrates the point $\frac {3}{2} k_r^2 \rho _i^2 = 0.3$
. The red line illustrates the point $\frac {3}{2} k_r^2 \rho _i^2 = 0.3$![]() beyond which the expression may not be applicable anymore. It can be observed that the slope of the damping expression changes roughly where the line is located, which can be an indicator that after this point the behaviour is unphysical. It is remarked that the high end of the perturbation wavevectors unstable to MI, i.e. for $k_\textrm {pert} = 14 ({2{\rm \pi} }/{a_\textrm {min}})$
beyond which the expression may not be applicable anymore. It can be observed that the slope of the damping expression changes roughly where the line is located, which can be an indicator that after this point the behaviour is unphysical. It is remarked that the high end of the perturbation wavevectors unstable to MI, i.e. for $k_\textrm {pert} = 14 ({2{\rm \pi} }/{a_\textrm {min}})$![]() , is very close to the damping applicability limit at $k_r \approx 16 ({2{\rm \pi} }/{a_\textrm {min}})$
, is very close to the damping applicability limit at $k_r \approx 16 ({2{\rm \pi} }/{a_\textrm {min}})$![]() .
.
5.3. Role of the perturbation wavelength
This section analyses the influence of the perturbation wavelength $\lambda _\textrm {pert} = 2{\rm \pi} /k_\textrm {pert}$![]() chosen in the initial condition of the GAM radial electric field $E_r$
chosen in the initial condition of the GAM radial electric field $E_r$![]() on MI growth (as predicted by (3.7), see figure 5). Additionally, the damping mechanism introduced in the previous section is taken into account. Similarly to the previous section, the parameters from § 5.1 are used and consequently all perturbation wavevectors $k_\textrm {pert} < 14.6 ({2{\rm \pi} }/{a_\textrm {min}}) = k_\textrm {lim}$
on MI growth (as predicted by (3.7), see figure 5). Additionally, the damping mechanism introduced in the previous section is taken into account. Similarly to the previous section, the parameters from § 5.1 are used and consequently all perturbation wavevectors $k_\textrm {pert} < 14.6 ({2{\rm \pi} }/{a_\textrm {min}}) = k_\textrm {lim}$![]() should be susceptible to MI. Thus, simulations with modulation wavevectors in the range $4-14 ({2{\rm \pi} }/{a_\textrm {min}})$
should be susceptible to MI. Thus, simulations with modulation wavevectors in the range $4-14 ({2{\rm \pi} }/{a_\textrm {min}})$![]() are analysed in this section.
are analysed in this section.
In order to obtain a quantitative measure of the growth (or damping) $\gamma$![]() of the sinusoidal perturbation, the radial Fourier transforms of the GK simulation results, $\mathfrak {F}[E_r](k_r, t)$
of the sinusoidal perturbation, the radial Fourier transforms of the GK simulation results, $\mathfrak {F}[E_r](k_r, t)$![]() , are calculated using the fast-Fourier-transform algorithm. The Fourier coefficient corresponding to the perturbation wavevector $k_\textrm {pert}$
, are calculated using the fast-Fourier-transform algorithm. The Fourier coefficient corresponding to the perturbation wavevector $k_\textrm {pert}$![]() , $\mathfrak {F}[E_r](k_r = k_\textrm {pert}, t)$
, $\mathfrak {F}[E_r](k_r = k_\textrm {pert}, t)$![]() , is then extracted and an exponential fit is applied to the region of exponential MI growth or exponential decay. Due to the fact that the growth rate depends on $\alpha _\textrm {NL}$
, is then extracted and an exponential fit is applied to the region of exponential MI growth or exponential decay. Due to the fact that the growth rate depends on $\alpha _\textrm {NL}$![]() , which in turn depends on the radial position $r$
, which in turn depends on the radial position $r$![]() , the Fourier coefficient of the whole packet would return a complex mixture of the different growth stages at the different radial positions. As a consequence, before the Fourier transform is performed, a mask is applied such that only the simulation data around each maximum of the wavefront are included. This scheme is illustrated for the example of $k_\textrm {pert} = 8 ({2{\rm \pi} }/{a_\textrm {min}})$
, the Fourier coefficient of the whole packet would return a complex mixture of the different growth stages at the different radial positions. As a consequence, before the Fourier transform is performed, a mask is applied such that only the simulation data around each maximum of the wavefront are included. This scheme is illustrated for the example of $k_\textrm {pert} = 8 ({2{\rm \pi} }/{a_\textrm {min}})$![]() in figure 11.
in figure 11.

Figure 11. Scheme for determining the growth rate $\gamma$![]() of the perturbation in the GK GAM simulations. The upper picture depicts the radial electric field of the case with $k_\textrm {pert} = 8 ({2{\rm \pi} }/{a_\textrm {min}})$
of the perturbation in the GK GAM simulations. The upper picture depicts the radial electric field of the case with $k_\textrm {pert} = 8 ({2{\rm \pi} }/{a_\textrm {min}})$![]() . The bottom picture depicts the absolute value of the Fourier coefficient at $|\mathfrak {F}[E_r](k_r = 8 ({2{\rm \pi} }/{a_\textrm {min}}),t)|$
. The bottom picture depicts the absolute value of the Fourier coefficient at $|\mathfrak {F}[E_r](k_r = 8 ({2{\rm \pi} }/{a_\textrm {min}}),t)|$![]() and the envelope of the coefficient. The exponential fit is applied only to the region where the growth rate is highest, as for the first oscillation cycles the GAM electric field is experiencing an initial transient where higher GAM harmonics that were excited by the initial ‘drop-in’ are still fading away, and for higher values of $t$
and the envelope of the coefficient. The exponential fit is applied only to the region where the growth rate is highest, as for the first oscillation cycles the GAM electric field is experiencing an initial transient where higher GAM harmonics that were excited by the initial ‘drop-in’ are still fading away, and for higher values of $t$![]() the assumption that the perturbation amplitude $a_1$
the assumption that the perturbation amplitude $a_1$![]() is small compared with the plateau amplitude $a_0$
is small compared with the plateau amplitude $a_0$![]() is not fulfilled anymore. (a) The GAM radial electric field $E_r$
is not fulfilled anymore. (a) The GAM radial electric field $E_r$![]() from a GK simulation with perturbation wavevector $k_\textrm {pert} = 8 ({2{\rm \pi} }/{a_\textrm {min}})$
from a GK simulation with perturbation wavevector $k_\textrm {pert} = 8 ({2{\rm \pi} }/{a_\textrm {min}})$![]() . The red lines show the time window where the fit was applied, the black lines indicate the radial region that was included in the calculation of the Fourier coefficient. (b) Time evolution of the absolute value of the Fourier coefficient of the perturbation wavevector $k_\textrm {pert} = 8 ({2{\rm \pi} }/{a_\textrm {min}})$
. The red lines show the time window where the fit was applied, the black lines indicate the radial region that was included in the calculation of the Fourier coefficient. (b) Time evolution of the absolute value of the Fourier coefficient of the perturbation wavevector $k_\textrm {pert} = 8 ({2{\rm \pi} }/{a_\textrm {min}})$![]() . The red lines indicate the time window where the fit was applied.
. The red lines indicate the time window where the fit was applied.
The aforementioned scheme, illustrated in figure 11, is applied to all simulations, with respective wavevectors $k_\textrm {pert} = 4, 5, \ldots, 14 ({2{\rm \pi} }/{a_\textrm {min}})$![]() . In figure 12, the MI growth rates obtained from the GK simulation data employing the method described above are compared with the theoretical results of § 3 (see figure 5 and (3.7)). The theoretical MI predictions, which do not contain damping, clearly overestimate the GK MI growth rate $\gamma$
. In figure 12, the MI growth rates obtained from the GK simulation data employing the method described above are compared with the theoretical results of § 3 (see figure 5 and (3.7)). The theoretical MI predictions, which do not contain damping, clearly overestimate the GK MI growth rate $\gamma$![]() for high perturbation wavevectors $k_\textrm {pert} > 6 ({2{\rm \pi} }/{a_\textrm {min}})$
for high perturbation wavevectors $k_\textrm {pert} > 6 ({2{\rm \pi} }/{a_\textrm {min}})$![]() . As can be seen in figure 12(a), even when the nominal damping rate following (5.4) is included the growth rate of the MI is overpredicted as compared with the GK simulations. However, after adjusting the strength of the damping amplitude by multiplying it with a factor of 2.5, the simulation results show good agreement with the theoretic predictions (figure 12b). Not only does this adjustment improve the matching of the threshold between stable and unstable perturbations at $k_\textrm {pert} \approx 11 ({2{\rm \pi} }/{a_\textrm {min}})$
. As can be seen in figure 12(a), even when the nominal damping rate following (5.4) is included the growth rate of the MI is overpredicted as compared with the GK simulations. However, after adjusting the strength of the damping amplitude by multiplying it with a factor of 2.5, the simulation results show good agreement with the theoretic predictions (figure 12b). Not only does this adjustment improve the matching of the threshold between stable and unstable perturbations at $k_\textrm {pert} \approx 11 ({2{\rm \pi} }/{a_\textrm {min}})$![]() , but it furthermore fits better to the values of the growth rates for the wavevectors in the domain $6 ({2{\rm \pi} }/{a_\textrm {min}}) \leq k_\textrm {pert} \leq 11 ({2{\rm \pi} }/{a_\textrm {min}})$
, but it furthermore fits better to the values of the growth rates for the wavevectors in the domain $6 ({2{\rm \pi} }/{a_\textrm {min}}) \leq k_\textrm {pert} \leq 11 ({2{\rm \pi} }/{a_\textrm {min}})$![]() . We remark that this correction factor is also in line with the benchmark in Biancalani et al. (Reference Biancalani, Bottino, Ehrlacher, Grandgirard, Merlo, Novikau, Qiu, Sonnendrücker, Garbet and Görler2017) (see figure 4(b) in this reference), where a similar difference between numeric simulations and theoretical prediction has been observed.
. We remark that this correction factor is also in line with the benchmark in Biancalani et al. (Reference Biancalani, Bottino, Ehrlacher, Grandgirard, Merlo, Novikau, Qiu, Sonnendrücker, Garbet and Görler2017) (see figure 4(b) in this reference), where a similar difference between numeric simulations and theoretical prediction has been observed.

Figure 12. The GAM perturbation growth and damping rates $\gamma$![]() in GK simulations where the initial condition was modulated with different perturbation wavevectors $k_\textrm {pert}$
in GK simulations where the initial condition was modulated with different perturbation wavevectors $k_\textrm {pert}$![]() . The GK results were obtained via the method illustrated in figure 11. The left figure shows the comparison of the simulation results with the theoretical predictions for the analytic MI growth rate $\gamma _\textrm {MI}$
. The GK results were obtained via the method illustrated in figure 11. The left figure shows the comparison of the simulation results with the theoretical predictions for the analytic MI growth rate $\gamma _\textrm {MI}$![]() (3.4), and the damping $\gamma _\textrm {Qiu}$
(3.4), and the damping $\gamma _\textrm {Qiu}$![]() (5.4). The theoretical predictions are found to overestimate the growth rate significantly, as seen in figure 12(a). The right figure establishes that, when the damping term is amplified by a factor of 2.5, data for the wavevectors in the region $6 ({2{\rm \pi} }/{a_\textrm {min}}) \leq k_\textrm {pert} \leq 11 ({2{\rm \pi} }/{a_\textrm {min}})$
(5.4). The theoretical predictions are found to overestimate the growth rate significantly, as seen in figure 12(a). The right figure establishes that, when the damping term is amplified by a factor of 2.5, data for the wavevectors in the region $6 ({2{\rm \pi} }/{a_\textrm {min}}) \leq k_\textrm {pert} \leq 11 ({2{\rm \pi} }/{a_\textrm {min}})$![]() more closely match the theoretical predictions. (a) Unmodified damping according to $\gamma _\textrm {Qiu}$
more closely match the theoretical predictions. (a) Unmodified damping according to $\gamma _\textrm {Qiu}$![]() . (b) Damping multiplied by a factor of 2.5.
. (b) Damping multiplied by a factor of 2.5.
In contrast to the well-matching growth rates at medium wavevectors, the matching becomes poorer at larger and smaller $k_\textrm {pert}$![]() , as is apparent in figure 12(b). For wavevectors $k_\textrm {pert} > 11 ({2{\rm \pi} }/{a_\textrm {min}})$
, as is apparent in figure 12(b). For wavevectors $k_\textrm {pert} > 11 ({2{\rm \pi} }/{a_\textrm {min}})$![]() , the MI is damped in GK simulations and its time behaviour is more prone to fitting errors due to the initial transient process. Additionally, these values are close to the applicability limit $\frac {3}{2} k_r^2\rho _i^2 \ll 1$
, the MI is damped in GK simulations and its time behaviour is more prone to fitting errors due to the initial transient process. Additionally, these values are close to the applicability limit $\frac {3}{2} k_r^2\rho _i^2 \ll 1$![]() of the damping term. On the other hand, the growth rates obtained from the GK simulations at the lower end, with $k_\textrm {pert} < 6 ({2{\rm \pi} }/{a_\textrm {min}})$
of the damping term. On the other hand, the growth rates obtained from the GK simulations at the lower end, with $k_\textrm {pert} < 6 ({2{\rm \pi} }/{a_\textrm {min}})$![]() , are too high compared with theory. Further investigations regarding this discrepancy are needed.
, are too high compared with theory. Further investigations regarding this discrepancy are needed.
5.4. Role of the ion Larmor radius
The last section established that the small scales (high wavevectors) are more strongly affected by damping and that the analytical term from Qiu et al. (Reference Qiu, Chen and Zonca2009), when adjusted by a factor 2.5, gives a good approximation to the observations. This section tests this hypothesis further by analysing the impact of a change of the ion Larmor radius $\rho _i$![]() on the damping scale, where the values $\rho _{i1}/a_\textrm {min} = 3.842\times 10^{-3}$
on the damping scale, where the values $\rho _{i1}/a_\textrm {min} = 3.842\times 10^{-3}$![]() , $\rho _{i2}/a_\textrm {min} = 4.355\times 10^{-3}$
, $\rho _{i2}/a_\textrm {min} = 4.355\times 10^{-3}$![]() (same value as in the previous sections) and $\rho _{i3}/a_\textrm {min} = 5.025\times 10^{-3}$
(same value as in the previous sections) and $\rho _{i3}/a_\textrm {min} = 5.025\times 10^{-3}$![]() were chosen for the comparison. The changes of $\rho _i$
were chosen for the comparison. The changes of $\rho _i$![]() are achieved by adjusting the ion thermal velocity $v_{Ti}$
are achieved by adjusting the ion thermal velocity $v_{Ti}$![]() , which in the simulations is determined according to (A1) and (A2). The analytic damping term $\gamma _\textrm {Qiu}$
, which in the simulations is determined according to (A1) and (A2). The analytic damping term $\gamma _\textrm {Qiu}$![]() predicts that, for smaller Larmor radii, smaller scales i.e. higher wavevectors $k_\textrm {pert}$
predicts that, for smaller Larmor radii, smaller scales i.e. higher wavevectors $k_\textrm {pert}$![]() should be less damped.
should be less damped.
A change of $\rho _i$![]() (via $v_{Ti}$
(via $v_{Ti}$![]() ) influences both ${\mathcal {G}}$
) influences both ${\mathcal {G}}$![]() and $\alpha _\textrm {NL}$
and $\alpha _\textrm {NL}$![]() , meaning that the range of unstable wavevectors $k_\textrm {pert} < k_\textrm {lim} = 2 a_0 \sqrt {\alpha _\textrm {NL}/{\mathcal {G}}}$
, meaning that the range of unstable wavevectors $k_\textrm {pert} < k_\textrm {lim} = 2 a_0 \sqrt {\alpha _\textrm {NL}/{\mathcal {G}}}$![]() from (3.6) may change. To decorrelate the change of $\rho _i$
from (3.6) may change. To decorrelate the change of $\rho _i$![]() from the change of the unstable MI wavevectors, the parameter $a_0$
from the change of the unstable MI wavevectors, the parameter $a_0$![]() is selected depending on $\rho _i$
is selected depending on $\rho _i$![]() to ensure that the range of the unstable MI wavevectors stays the same. Precisely, due to ${\mathcal {G}} \propto \rho _i^3$
to ensure that the range of the unstable MI wavevectors stays the same. Precisely, due to ${\mathcal {G}} \propto \rho _i^3$![]() (see (2.8) with $v_{Ti} \propto \rho _i$
(see (2.8) with $v_{Ti} \propto \rho _i$![]() ) and $\alpha _\textrm {NL} \propto 1/\rho _i$
) and $\alpha _\textrm {NL} \propto 1/\rho _i$![]() (see Appendix A) one finds from (3.6) that in order to keep the unstable range constant $a_0$
(see Appendix A) one finds from (3.6) that in order to keep the unstable range constant $a_0$![]() needs to be adjusted as
needs to be adjusted as

In order to obtain the same $k_\textrm {lim} = 14.5 ({2{\rm \pi} }/{a_\textrm {min}})$![]() as in the previous sections the corresponding amplitudes are $a_{01} \approx 1.99\times 10^{-4}$
as in the previous sections the corresponding amplitudes are $a_{01} \approx 1.99\times 10^{-4}$![]() (a.u.), $a_{02} \approx 2.56\times 10^{-4}$
(a.u.), $a_{02} \approx 2.56\times 10^{-4}$![]() (a.u.) and $a_{03} \approx 3.40\times 10^{-4}$
(a.u.) and $a_{03} \approx 3.40\times 10^{-4}$![]() (a.u.) for $\rho _{i1}, \rho _{i2}$
(a.u.) for $\rho _{i1}, \rho _{i2}$![]() and $\rho _{i3}$
and $\rho _{i3}$![]() , respectively. The simulations were analysed with the scheme introduced in the last section with the corresponding growth and damping rates presented in figure 13.
, respectively. The simulations were analysed with the scheme introduced in the last section with the corresponding growth and damping rates presented in figure 13.

Figure 13. The GAM MI growth and damping rates in GK simulations with different perturbation wavevectors $k_\textrm {pert}$![]() and ion Larmor radii $\rho _i$
and ion Larmor radii $\rho _i$![]() ($\rho _{i1}/a_\textrm {min} = 3.842\times 10^{-3}$
($\rho _{i1}/a_\textrm {min} = 3.842\times 10^{-3}$![]() , $\rho _{i2}/a_\textrm {min} = 4.355\times 10^{-3}$
, $\rho _{i2}/a_\textrm {min} = 4.355\times 10^{-3}$![]() and $\rho _{i3}/a_\textrm {min} = 5.025\times 10^{-3}$
and $\rho _{i3}/a_\textrm {min} = 5.025\times 10^{-3}$![]() ) compared with the theoretical predictions from the analytic MI growth rate $\gamma _\textrm {MI}$
) compared with the theoretical predictions from the analytic MI growth rate $\gamma _\textrm {MI}$![]() , (3.4) and the analytic GAM damping $\gamma _\textrm {Qiu}$
, (3.4) and the analytic GAM damping $\gamma _\textrm {Qiu}$![]() , (5.4). The difference in the maxima of the growth rates stems mainly from the different packet background amplitudes that were chosen according to (5.11).
, (5.4). The difference in the maxima of the growth rates stems mainly from the different packet background amplitudes that were chosen according to (5.11).
The results confirm the findings of the previous section that the adjustment by a factor of 2.5 of the amplitude of the damping term does reproduce the observed damping rate. Additionally, the theoretical predictions for the change of growth rates from $\gamma _\textrm {MI}$![]() due to the changing amplitude is in good agreement with the simulation results. However, similarly to figure 12(b) the damping rate is overestimated in the region where the simulations are damped and the growth rate results for $k_\textrm {pert} < 6 ({2{\rm \pi} }/{a_\textrm {min}})$
due to the changing amplitude is in good agreement with the simulation results. However, similarly to figure 12(b) the damping rate is overestimated in the region where the simulations are damped and the growth rate results for $k_\textrm {pert} < 6 ({2{\rm \pi} }/{a_\textrm {min}})$![]() are again higher than the theoretical prediction.
are again higher than the theoretical prediction.
5.5. NLSE simulations including damping
We now include the findings regarding the damping term of the previous two sections in the NLSE solver and compare a damped NLSE simulation with a GK simulation. The damping given by (5.4) is amplified by a factor 2.5 and included in the numerical solver at the point where the dispersive term is applied, i.e. (4.4) in § 4.1. However, as shown in figure 9(a), during the MI saturation phase large wavevectors ($k_r > 20 ({2{\rm \pi} }/{a_\textrm {min}})$![]() ) appear in the spectrum which, due to the condition $({\tau _e}/{2}) k_r^2 \rho _i^2 \ll 1$
) appear in the spectrum which, due to the condition $({\tau _e}/{2}) k_r^2 \rho _i^2 \ll 1$![]() from § 5.2, lie outside of the applicability range of $\gamma _\textrm {Qiu}$
from § 5.2, lie outside of the applicability range of $\gamma _\textrm {Qiu}$![]() . From the GK simulations, see figure 9(b), it is clear that these high wavevectors should be strongly suppressed, which was achieved by applying $\gamma = -4\times 10^{-4}\omega _{ci}$
. From the GK simulations, see figure 9(b), it is clear that these high wavevectors should be strongly suppressed, which was achieved by applying $\gamma = -4\times 10^{-4}\omega _{ci}$![]() to all wavevectors fulfilling $({\tau _e}/{2}) k_r^2 \rho _i^2 \geq 0.3$
to all wavevectors fulfilling $({\tau _e}/{2}) k_r^2 \rho _i^2 \geq 0.3$![]() .
.
The (undamped) NLSE simulation presented in figure 8(a) is now repeated with the inclusion of the above described damping scheme. The damped result is reported in figure 14 together with the corresponding spectrum. A clear improvement in regards to multiple aspects can be discerned when comparing damped and undamped NLSE simulations with the related GK result from figure 8(b). First of all, the point in time at which the MI saturation phase appears in the simulations matches much better, with $t^\textrm {NLSE damp.}_\textrm {sat.} \approx 1.8\times 10^5\,1/\omega _i$![]() and $t^\textrm {GK}_\textrm {sat.} \approx 2.2\times 10^5\,1/\omega _i$
and $t^\textrm {GK}_\textrm {sat.} \approx 2.2\times 10^5\,1/\omega _i$![]() (at the packet centre $r = r_0 = 0.6 a_\textrm {tok}$
(at the packet centre $r = r_0 = 0.6 a_\textrm {tok}$![]() ), compared with the undamped NLSE simulation from figure 8(a) with $t^\textrm {NLSE undamp.}_\textrm {sat.} \approx 1.1\times 10^5\,1/\omega _i$
), compared with the undamped NLSE simulation from figure 8(a) with $t^\textrm {NLSE undamp.}_\textrm {sat.} \approx 1.1\times 10^5\,1/\omega _i$![]() . Furthermore, the maximal amplitude at the centre $r=r_0$
. Furthermore, the maximal amplitude at the centre $r=r_0$![]() is in better agreement, with $E^\textrm {NLSE damp.}_\textrm {max} = 1.31 a_0$
is in better agreement, with $E^\textrm {NLSE damp.}_\textrm {max} = 1.31 a_0$![]() and $E^\textrm {GK}_\textrm {max} \approx 1.26 a_0$
and $E^\textrm {GK}_\textrm {max} \approx 1.26 a_0$![]() , compared with $E^\textrm {NLSE undamp.}_\textrm {max} = 2.43 a_0$
, compared with $E^\textrm {NLSE undamp.}_\textrm {max} = 2.43 a_0$![]() . The growth rate is $\gamma ^\textrm {NLSE damp.} \approx 1.48\times 10^{-5} \omega _{ci}$
. The growth rate is $\gamma ^\textrm {NLSE damp.} \approx 1.48\times 10^{-5} \omega _{ci}$![]() , which is very similar to the value obtained for the GK simulation with $\gamma ^\textrm {GK} \approx 1.41\times 10^{-5} \omega _{ci}$
, which is very similar to the value obtained for the GK simulation with $\gamma ^\textrm {GK} \approx 1.41\times 10^{-5} \omega _{ci}$![]() . However, a spectral comparison between figures 14 and 9(b) illustrates significant differences, notably that the GK spectrum is much more complex, with more interactions of the different wavevectors. This may in part stem from the radial dependence of the value of $\alpha _\textrm {NL}$
. However, a spectral comparison between figures 14 and 9(b) illustrates significant differences, notably that the GK spectrum is much more complex, with more interactions of the different wavevectors. This may in part stem from the radial dependence of the value of $\alpha _\textrm {NL}$![]() , which leads to incoherent phase fronts in the GK simulations and is not included in the NLSE simulation (see also discussion in § 5.1), on the other hand, it may also be a consequence of the generally reduced complexity of the NLSE model.
, which leads to incoherent phase fronts in the GK simulations and is not included in the NLSE simulation (see also discussion in § 5.1), on the other hand, it may also be a consequence of the generally reduced complexity of the NLSE model.

Figure 14. Repetition of the NLSE simulation reported in figure 8(a), where now the damping scheme described at the beginning of this section is included. The figure shows the time evolution of the GAM radial electric field $E_r$![]() (left) as well as the corresponding radial spectrum (right), i.e. the absolute value of the radial Fourier transform of the GAM radial electric field, $|\mathfrak {F}[E_r]|$
(left) as well as the corresponding radial spectrum (right), i.e. the absolute value of the radial Fourier transform of the GAM radial electric field, $|\mathfrak {F}[E_r]|$![]() .
.
5.6. Self-focusing of Gaussian packets
This section illustrates the self-focusing effect of the NLSE on an unmodulated initial condition where for the envelope a Gaussian packet is chosen. As detailed in § 2.2, self-focusing is observed for anomalous dispersion, i.e. ${\mathcal {G}} > 0$![]() and $\tau _e \lesssim 5.45$
and $\tau _e \lesssim 5.45$![]() . The resulting comparison between a GK, an undamped NLSE and a damped NLSE (as specified in § 5.2) simulation is presented in figure 15.
. The resulting comparison between a GK, an undamped NLSE and a damped NLSE (as specified in § 5.2) simulation is presented in figure 15.

Figure 15. Comparison of the evolution of the GAM radial electric field $E_r$![]() with an unperturbed Gaussian initial condition according to the undamped NLSE, damped NLSE and GK theory. The plasma background parameters of the simulations are $\tau _e = 2$
with an unperturbed Gaussian initial condition according to the undamped NLSE, damped NLSE and GK theory. The plasma background parameters of the simulations are $\tau _e = 2$![]() , $q_s = 11$
, $q_s = 11$![]() , $\rho _i/a_\textrm {min} = 3.784\times 10^{-3}$
, $\rho _i/a_\textrm {min} = 3.784\times 10^{-3}$![]() , the initial condition is given by (5.1) with $a_0 = 3\times 10^{-4}$
, the initial condition is given by (5.1) with $a_0 = 3\times 10^{-4}$![]() (a.u.), $a_1 = 0$
(a.u.), $a_1 = 0$![]() , $\textit {w}_0 = 0.1 a_\textrm {min}$
, $\textit {w}_0 = 0.1 a_\textrm {min}$![]() and $p = 1$
and $p = 1$![]() . (a) The NLSE simulation result. (b) The GK simulation result. (c) The damped NLSE simulation result.
. (a) The NLSE simulation result. (b) The GK simulation result. (c) The damped NLSE simulation result.
One can observe that, in all three simulations, the Gaussian packet experiences self-focusing, resulting in an increase of the maximal amplitude and a phase skip of the Gaussian centre compared with the packet edges. It is apparent that this behaviour is very similar to the MI, while it in contrast does not require an initial modulation of the envelope. We should note at this point that, differently from the standard scenario of the MI presented in § 3.1, the background wave is not a plane wave but a packet with a finite spectrum. Hence, it contains also higher spectral components, which can act as a seed for MI. Indeed, a spectral analysis, which for the sake of brevity is not reported here, reveals exponential growth of the wavevectors $k_r = 3 ({2{\rm \pi} }/{a_\textrm {min}})$![]() , $4 ({2{\rm \pi} }/{a_\textrm {min}})$
, $4 ({2{\rm \pi} }/{a_\textrm {min}})$![]() and $5 ({2{\rm \pi} }/{a_\textrm {min}})$
and $5 ({2{\rm \pi} }/{a_\textrm {min}})$![]() . This observation suggests an interpretation of this behaviour as an MI, whereas the observed unstable wavevectors are not necessarily the ones with the strongest growth rates but also depend on the initial conditions of the packet. We should add that the generation of higher spectral components is an inherent part of the nonlinear dynamics of the GAM, which might contribute to the observed spectral behaviour on top of the MI.
. This observation suggests an interpretation of this behaviour as an MI, whereas the observed unstable wavevectors are not necessarily the ones with the strongest growth rates but also depend on the initial conditions of the packet. We should add that the generation of higher spectral components is an inherent part of the nonlinear dynamics of the GAM, which might contribute to the observed spectral behaviour on top of the MI.
Similarly to § 5.2 it is observed that, with damping included in the NLSE model, the maximum amplitude of the GK simulation is more closely reproduced. Furthermore one finds better agreement for the width and steepness of the focused packet, i.e. in the GK and damped NLSE simulations at $t \approx 1.1\times 10^5\,1/\omega _i$![]() compared with the undamped NLSE at $t \approx 0.8\times 10^5\,1/\omega _i$
compared with the undamped NLSE at $t \approx 0.8\times 10^5\,1/\omega _i$![]() . The radial asymmetry that develops in the GK simulation is not found in the NLSE simulations and can be explained by the radial dependence of $\alpha _\textrm {NL}$
. The radial asymmetry that develops in the GK simulation is not found in the NLSE simulations and can be explained by the radial dependence of $\alpha _\textrm {NL}$![]() that was introduced in § 5.1 and is explored further in Appendix A.
that was introduced in § 5.1 and is explored further in Appendix A.
5.7. Breather simulations
In this section the phenomenon of the Akhmediev breather is studied in GK simulations. Akhmediev breathers (ABs) (Akhmediev & Korneev Reference Akhmediev and Korneev1986) are special types of MI solutions to the NLSE which predict that after the saturation phase, the MI initial condition is restored, as illustrated in figure 4, and new MI growth should be observable. This phenomenon is hard to observe in GK simulations as e.g. the dependency of $\alpha _\textrm {NL}$![]() breaks the packet apart and hinders the return to the initial condition after the first saturation phase. As a consequence, we concentrate on the region $r> 0.6 a_\textrm {min}$
breaks the packet apart and hinders the return to the initial condition after the first saturation phase. As a consequence, we concentrate on the region $r> 0.6 a_\textrm {min}$![]() , where the results from Appendix A predict only small changes of $\alpha _\textrm {NL}$
, where the results from Appendix A predict only small changes of $\alpha _\textrm {NL}$![]() . A GK simulation with a breather solution is depicted in figure 16.
. A GK simulation with a breather solution is depicted in figure 16.

Figure 16. Gyrokinetic simulation of a GAM which shows the breather behaviour of the MI. The upper figure shows the radial electric field $E_r$![]() with its radial shape, the bottom figure shows the value of $E_r$
with its radial shape, the bottom figure shows the value of $E_r$![]() along the lines shown in the upper figure, which follow the maxima. The red curve shows two MI saturation phases, the first at $t\approx 1.7\times 10^5\,1/\omega _{ci}$
along the lines shown in the upper figure, which follow the maxima. The red curve shows two MI saturation phases, the first at $t\approx 1.7\times 10^5\,1/\omega _{ci}$![]() and the second one at $t\approx 3.3\times 10^5\,1/\omega _{ci}$
and the second one at $t\approx 3.3\times 10^5\,1/\omega _{ci}$![]() . The black curve shows the start of a second MI growth phase at the end of the simulation. The parameters are chosen as specified in table 1, with $\rho _{i3}/a_\textrm {min} = 5.025\times 10^{-3}$
. The black curve shows the start of a second MI growth phase at the end of the simulation. The parameters are chosen as specified in table 1, with $\rho _{i3}/a_\textrm {min} = 5.025\times 10^{-3}$![]() , $a_0 = 3.4\times 10^{-4}$
, $a_0 = 3.4\times 10^{-4}$![]() and $k_\textrm {pert} = 8 ({2{\rm \pi} }/{a_\textrm {min}})$
and $k_\textrm {pert} = 8 ({2{\rm \pi} }/{a_\textrm {min}})$![]() .
.
The maximum at $r_2\approx 0.87 a_\textrm {min}$![]() experiences two saturation phases, the first one at $t\approx 1.5\times 10^5 \omega _{ci}^{-1}$
experiences two saturation phases, the first one at $t\approx 1.5\times 10^5 \omega _{ci}^{-1}$![]() and the second at $t\approx 3.3\times 10^5 \omega _{ci}^{-1}$
and the second at $t\approx 3.3\times 10^5 \omega _{ci}^{-1}$![]() , thus demonstrating the AB phenomenon for a GAM packet in a GK simulation. Comparable behaviour happens for the maximum at $r\approx 0.71$
, thus demonstrating the AB phenomenon for a GAM packet in a GK simulation. Comparable behaviour happens for the maximum at $r\approx 0.71$![]() , however, the growth is slower and not as pronounced. The impact of the damping mechanism and the differences in the nonlinear coefficient $\alpha _\textrm {NL}$
, however, the growth is slower and not as pronounced. The impact of the damping mechanism and the differences in the nonlinear coefficient $\alpha _\textrm {NL}$![]() are again present in the simulations: for example, the second saturation phase at $t\approx 3.3\times 10^5 \omega _{ci}^{-1}$
are again present in the simulations: for example, the second saturation phase at $t\approx 3.3\times 10^5 \omega _{ci}^{-1}$![]() of the maximum centred around $r_2$
of the maximum centred around $r_2$![]() is observed to have a maximum amplitude of $1.44 a_0$
is observed to have a maximum amplitude of $1.44 a_0$![]() , which is significantly lower than the value of $1.74 a_0$
, which is significantly lower than the value of $1.74 a_0$![]() found in the first saturation phase, whereas an undamped AB would under ideal conditions yield the same maximum value in both saturation phases.
found in the first saturation phase, whereas an undamped AB would under ideal conditions yield the same maximum value in both saturation phases.
While more complex patterns of the AB are possible under ideal conditions, such as the appearance of growth phases of other unstable wavevectors in between the saturation phases of the initial perturbation wavevector $k_\textrm {pert}$![]() , see e.g. Copie, Randoux & Suret (Reference Copie, Randoux and Suret2020), the deviations from a pure NLSE-like behaviour due to the mechanisms introduced in the previous sections make the possibility of such observations highly unlikely.
, see e.g. Copie, Randoux & Suret (Reference Copie, Randoux and Suret2020), the deviations from a pure NLSE-like behaviour due to the mechanisms introduced in the previous sections make the possibility of such observations highly unlikely.
6. Summary and conclusions
The results of this paper show that geodesic-acoustic oscillations (GAMs) are susceptible to modulational instability (MI) under the conditions predicted by the nonlinear Schrödinger equation (NLSE) model. However, the high wavevectors that are part of the nonlinear saturation phase and important for the MI cycle (and MI breathers, see § 5.7) do not develop in gyrokinetic (GK) simulations due to the Landau damping which was characterized in detail in §§ 5.2–5.5. For the parameters considered in this study the aforementioned damping effect hinders the MI process significantly from developing to its full extent and is strong enough to stabilize some of the (according to the undamped NLSE model) unstable wavevectors, as was illustrated in figure 13 for $k \gtrsim 12 ({2{\rm \pi} }/{a_\textrm {min}})$![]() . A second significant shortcoming of the NLSE model was the assumption that $\alpha _\textrm {NL}$
. A second significant shortcoming of the NLSE model was the assumption that $\alpha _\textrm {NL}$![]() is independent of the radial coordinate $r$
is independent of the radial coordinate $r$![]() . The GK simulations of this paper establish the radial variation of the nonlinear coefficient $\alpha _\textrm {NL} = \alpha _\textrm {NL}(r)$
. The GK simulations of this paper establish the radial variation of the nonlinear coefficient $\alpha _\textrm {NL} = \alpha _\textrm {NL}(r)$![]() of the NLSE model for GAMs, which was not evident in the prior study on this topic (Poli et al. Reference Poli, Bottino, Maj, Palermo and Weber2021), due to the relatively narrow Gaussian packets that were considered there.
of the NLSE model for GAMs, which was not evident in the prior study on this topic (Poli et al. Reference Poli, Bottino, Maj, Palermo and Weber2021), due to the relatively narrow Gaussian packets that were considered there.
One can conclude from the theoretical descriptions of the MI and the damping mechanism ((3.7) and (5.4), respectively) that GAM MI is more likely to be observable for high safety factors and small Larmor radii (i.e. low ion temperatures $T_i$![]() and thermal velocities $v_{Ti}$
and thermal velocities $v_{Ti}$![]() ). Theory further suggests that the tokamak aspect ratio $A = R_0 / a_\textrm {min}$
). Theory further suggests that the tokamak aspect ratio $A = R_0 / a_\textrm {min}$![]() may have an impact on the GAM MI growth rate, however, further investigations on the dependency of the nonlinear coefficient $\alpha _\textrm {NL}$
may have an impact on the GAM MI growth rate, however, further investigations on the dependency of the nonlinear coefficient $\alpha _\textrm {NL}$![]() on the geometric parameters are needed to confirm this prediction.
on the geometric parameters are needed to confirm this prediction.
The observed significance of damping in the GK simulation results might seem surprising as the initial spectrum of the packet lies in a range for which theory predicts negligible damping. This enhanced damping observed in the GK simulations is akin to the phenomenon analysed in detail in Palermo et al. (Reference Palermo, Biancalani, Angioni, Zonca and Bottino2016) and Biancalani et al. (Reference Biancalani, Palermo, Angioni, Bottino and Zonca2016). There, the generation of higher wavevectors through linear processes due to the presence of radially non-uniform profiles was found to increase GAM damping significantly, leading to the inclusion of a ‘phase-mixing damping adjustment’. Similarly to these findings, as was discussed in § 3.1, the MI process is associated with the (in our case nonlinear) generation of high wavevector components in the radial GAM spectrum. This interpretation of the simulation results is confirmed by the good agreement they exhibit with an NLSE model corrected with the inclusion of the damping rate derived in Qiu et al. (Reference Qiu, Chen and Zonca2009), as is presented in § 5.5. The overall correction factor adopted here to achieve a quantitative matching with the GK simulations is in line with previous findings (Biancalani et al. Reference Biancalani, Bottino, Ehrlacher, Grandgirard, Merlo, Novikau, Qiu, Sonnendrücker, Garbet and Görler2017).
While the NLSE model proved to give accurate predictions of the general GAM behaviour, the exact dynamics shows significant differences. An improvement of the model, putting it on a more firm theoretical ground, requires a derivation of the NLSE equation for GAMs from first principles, which should be addressed in the near future. Predictive capability to other parameter regimes is limited and will only improve with further studies on the unknown variable $\alpha _\textrm {NL}$![]() .
.
Altogether, the results indicate that (without considering interactions with other plasma modes) the possibility and impact of an MI on the GAM dynamics will be small. This conclusion becomes more evident by the fact that in this study, electrons were treated adiabatically in simulations and in the damping term, while recent research suggests that a kinetic treatment of the electrons will increase damping, thus decreasing the likeliness of MI even further (Zhang & Lin Reference Zhang and Lin2010; Ehrlacher et al. Reference Ehrlacher, Garbet, Grandgirard, Sarazin, Donnel, Caschera, Ghendrih and Zarzoso2018). On the other hand, the self-focusing behaviour associated with the MI formation process is omnipresent in the regime of anomalous dispersion (${\mathcal {G}} > 0$![]() , $\tau _e \lesssim 5.45$
, $\tau _e \lesssim 5.45$![]() ) and may be observable in other simulations similarly to the case presented in § 5.6. The main reason behind this is the size of the involved structures and unstable wavevectors $k_r$
) and may be observable in other simulations similarly to the case presented in § 5.6. The main reason behind this is the size of the involved structures and unstable wavevectors $k_r$![]() : while the self-focusing effect only requires that a local maximum is present in the packet envelope, which can be of any size (or even simply the packet itself), MI formation requires that the maximum is ‘on top of’ a relatively constant packet, thus demanding much finer structures and higher wavevectors. This is not only a much more unlikely initial condition to spontaneously develop in a tokamak, but is also much more significantly affected by the damping process illustrated in §§ 5.2–5.4. However, this conclusion is only valid in the absence of interaction with other plasma modes.
: while the self-focusing effect only requires that a local maximum is present in the packet envelope, which can be of any size (or even simply the packet itself), MI formation requires that the maximum is ‘on top of’ a relatively constant packet, thus demanding much finer structures and higher wavevectors. This is not only a much more unlikely initial condition to spontaneously develop in a tokamak, but is also much more significantly affected by the damping process illustrated in §§ 5.2–5.4. However, this conclusion is only valid in the absence of interaction with other plasma modes.
Acknowledgements
We thank Professor Dr Z. Qiu (University of Zhejiang) for his support and fruitful discussions concerning the damping term derived in Qiu et al. (Reference Qiu, Chen and Zonca2009). We thank Professor Dr F. Zonca for helpful discussions.
Editor Per Helander thanks the referees for their advice in evaluating this article.
Funding
This work has been carried out within the framework of the EUROfusion Consortium, funded by the European Union via the Euratom Research and Training Programme (Grant Agreement No 101052200 – EUROfusion). Views and opinions expressed are, however, those of the author(s) only and do not necessarily reflect those of the European Union or the European Commission. Neither the European Union nor the European Commission can be held responsible for them.
Declaration of interests
The authors report no conflict of interest.
Data availability statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Appendix A. Determination of $\alpha _\textrm {NL}$
In order to make meaningful predictions about the MI behaviour and growth rates $\gamma _\textrm {MI}$![]() (see (3.7)), it is necessary to assess the magnitude of the strength $\alpha _\textrm {NL}$
(see (3.7)), it is necessary to assess the magnitude of the strength $\alpha _\textrm {NL}$![]() of the nonlinear term. Since an analytical expression for this parameter has currently not yet been derived, as was already mentioned in § 2.1, its value is in this study determined by comparing NLSE results with GK simulations of isolated GAMs obtained with the code ORB5. The axisymmetric component of the GAM radial electric field is initialized as described in § 4.2, where the NLSE evolves an initial electric field perturbation, while in ORB5 the electric field is generated from an initial perturbation $\delta n$
of the nonlinear term. Since an analytical expression for this parameter has currently not yet been derived, as was already mentioned in § 2.1, its value is in this study determined by comparing NLSE results with GK simulations of isolated GAMs obtained with the code ORB5. The axisymmetric component of the GAM radial electric field is initialized as described in § 4.2, where the NLSE evolves an initial electric field perturbation, while in ORB5 the electric field is generated from an initial perturbation $\delta n$![]() of the ion density.
of the ion density.
To obtain the exact value of the initial electric field perturbation from the initial density perturbation amplitude $\delta n / n_0$![]() one would have to evaluate the proportionality constant of the relation in (4.6). Since the exact physical values of the electric field do not matter for the results of this study and to simplify comparisons between the NLSE and GK simulations, we define a normalized amplitude of the electric field simply as $a_0 = \delta n / n_0$
one would have to evaluate the proportionality constant of the relation in (4.6). Since the exact physical values of the electric field do not matter for the results of this study and to simplify comparisons between the NLSE and GK simulations, we define a normalized amplitude of the electric field simply as $a_0 = \delta n / n_0$![]() . As a consequence, the parameter $\alpha _\textrm {NL}$
. As a consequence, the parameter $\alpha _\textrm {NL}$![]() is given here in units related to the amplitude of the relative density perturbation $\delta n / n_0$
is given here in units related to the amplitude of the relative density perturbation $\delta n / n_0$![]() .
.
For the comparison of NLSE and GK simulations an unperturbed Gaussian envelope (i.e. $a_1 = 0$![]() , $p = 1$
, $p = 1$![]() in (5.1)) was chosen for the initial condition. The dependency of $\alpha _\textrm {NL}$
in (5.1)) was chosen for the initial condition. The dependency of $\alpha _\textrm {NL}$![]() on the electron-to-ion temperature ratio $\tau _e = T_e/T_i$
on the electron-to-ion temperature ratio $\tau _e = T_e/T_i$![]() , the safety factor $q_s$
, the safety factor $q_s$![]() , the radial position $r_0$
, the radial position $r_0$![]() of the GAM and the ion Larmor radius $\rho _i$
of the GAM and the ion Larmor radius $\rho _i$![]() was determined. The ion Larmor radius is set in ORB5 by the choice of the parameter $L_x$
was determined. The ion Larmor radius is set in ORB5 by the choice of the parameter $L_x$![]() , which is defined through the following relations:
, which is defined through the following relations:
This subsequently also affects the value of the ion temperature. The remaining parameters $a_\textrm {min}, R_0, B_0, m_i$![]() were chosen as specified in table 1. The results for the dependencies on $\tau _e$
were chosen as specified in table 1. The results for the dependencies on $\tau _e$![]() , $\rho _i$
, $\rho _i$![]() (i.e. $L_x$
(i.e. $L_x$![]() ) and $r_0$
) and $r_0$![]() are depicted in figures 17–19, respectively. The respective error bars illustrate the range of values of $\alpha _\textrm {NL}$
are depicted in figures 17–19, respectively. The respective error bars illustrate the range of values of $\alpha _\textrm {NL}$![]() in which the NLSE simulations matched GK results within one quarter of the oscillation period $1/4 T_\textrm {GAM}$
in which the NLSE simulations matched GK results within one quarter of the oscillation period $1/4 T_\textrm {GAM}$![]() at the end of the simulation.
at the end of the simulation.
From figure 17 one finds that $\alpha _\textrm {NL}(\tau _e)$![]() increases nearly linearly with $\tau _e$
increases nearly linearly with $\tau _e$![]() , but with different slopes in the regime of anomalous ($\tau _e \lesssim 5.45$
, but with different slopes in the regime of anomalous ($\tau _e \lesssim 5.45$![]() ) and normal ($\tau _e \gtrsim 5.45$
) and normal ($\tau _e \gtrsim 5.45$![]() ) dispersion. The error bars in the regime of anomalous dispersion are higher due to the self-focusing effect of Gaussian packets, which is discussed in § 5.6 and complicated comparisons. From figure 18 as a first approximation the proportionality $\alpha _\textrm {NL} \propto 1/\rho _i$
) dispersion. The error bars in the regime of anomalous dispersion are higher due to the self-focusing effect of Gaussian packets, which is discussed in § 5.6 and complicated comparisons. From figure 18 as a first approximation the proportionality $\alpha _\textrm {NL} \propto 1/\rho _i$![]() is obtained. The radial position of the GAM is found to heavily influence the strength of the nonlinear parameter as seen in figure 19, most notably when $r_0$
is obtained. The radial position of the GAM is found to heavily influence the strength of the nonlinear parameter as seen in figure 19, most notably when $r_0$![]() is below $0.4 a_\textrm {min}$
is below $0.4 a_\textrm {min}$![]() . For the safety factor $q_s$
. For the safety factor $q_s$![]() it was found that the value of $\alpha _\textrm {NL}$
it was found that the value of $\alpha _\textrm {NL}$![]() does not change significantly in the range $q_s = 1 \dots 15$
does not change significantly in the range $q_s = 1 \dots 15$![]() considered in this paper.
considered in this paper.

Figure 17. Dependency of the nonlinear parameter $\alpha _\textrm {NL}$![]() on the electron-to-ion temperature ratio $\tau _e$
on the electron-to-ion temperature ratio $\tau _e$![]() . The remaining parameters were chosen as specified in table 1, with $\rho _i/a_\textrm {min} = 3.842\times 10^{-3}$
. The remaining parameters were chosen as specified in table 1, with $\rho _i/a_\textrm {min} = 3.842\times 10^{-3}$![]() , $q_s = 5$
, $q_s = 5$![]() and $r_0 = 0.5a_\textrm {min}$
and $r_0 = 0.5a_\textrm {min}$![]() .
.

Figure 18. Dependency of the nonlinear parameter $\alpha _\textrm {NL}$![]() on the ion Larmor radius $\rho _i$
on the ion Larmor radius $\rho _i$![]() . The remaining parameters were chosen as specified in table 1, with $\tau _e = 4$
. The remaining parameters were chosen as specified in table 1, with $\tau _e = 4$![]() , $q_s = 5$
, $q_s = 5$![]() and $r_0 = 0.5 a_\textrm {min}$
and $r_0 = 0.5 a_\textrm {min}$![]() .
.

Figure 19. Dependency of the nonlinear parameter $\alpha _\textrm {NL}$![]() on the position $r_0$
on the position $r_0$![]() of the GAM in the minor tokamak radius. This dependency was not included in the NLSE simulation dynamics. The remaining parameters were chosen as specified in table 1, with $\tau _e = 4$
of the GAM in the minor tokamak radius. This dependency was not included in the NLSE simulation dynamics. The remaining parameters were chosen as specified in table 1, with $\tau _e = 4$![]() , $\rho _i/a_\textrm {min} = 3.842\times 10^{-3}$
, $\rho _i/a_\textrm {min} = 3.842\times 10^{-3}$![]() and $q_s = 5$
and $q_s = 5$![]() .
.
Appendix B. Qualitative picture for the self-focusing NLSE and MI
This section presents a qualitative explanation for the MI formation process in terms of an interaction of the between the effects of the nonlinear and the dispersive term, which were introduced in § 2.2. Although the MI is meanwhile a well-known phenomenon, we believe that the summary of this simple interpretation might be useful, in particular to interpret the results of this paper.
As depicted in figure 2, the effect of the dispersive term (without nonlinearity, $\alpha _\textrm {NL} = 0$![]() ) on a ‘flat’ phase front at $t=0$
) on a ‘flat’ phase front at $t=0$![]() is an increase in width and the appearance of (in the case of anomalous dispersion concave) curvature as time progresses. When considering a packet with initial curvature opposite to what is generated by the dispersive term, one can observe that during the process of reducing the phase-front curvature, the packet width decreases until the phase front is flat, as shown in figure 20. After this point one finds the usual dispersive broadening. This is the well-known behaviour of a Gaussian pulse in optics (but with the roles of time and space reversed), see e.g. Hecht (Reference Hecht2012). One can conclude that, in the regime of anomalous dispersion, as long as the packet curvature is convex in $(r,t)$
is an increase in width and the appearance of (in the case of anomalous dispersion concave) curvature as time progresses. When considering a packet with initial curvature opposite to what is generated by the dispersive term, one can observe that during the process of reducing the phase-front curvature, the packet width decreases until the phase front is flat, as shown in figure 20. After this point one finds the usual dispersive broadening. This is the well-known behaviour of a Gaussian pulse in optics (but with the roles of time and space reversed), see e.g. Hecht (Reference Hecht2012). One can conclude that, in the regime of anomalous dispersion, as long as the packet curvature is convex in $(r,t)$![]() -space, the width and curvature of the packet will decrease while the amplitude of the maximum increases. For normal dispersion one will observe the same effect for an initially concave packet.
-space, the width and curvature of the packet will decrease while the amplitude of the maximum increases. For normal dispersion one will observe the same effect for an initially concave packet.

Figure 20. An NLSE simulation of the GAM electric field $E_r = \mbox {Re}[\psi ]$![]() for a Gaussian with an initial convex curvature in $(r,t)$
for a Gaussian with an initial convex curvature in $(r,t)$![]() -space. The anomalous dispersion reduces the width of the Gaussian while increasing its amplitude until the phase front is flat at $t\approx 3.5$
-space. The anomalous dispersion reduces the width of the Gaussian while increasing its amplitude until the phase front is flat at $t\approx 3.5$![]() . After this point one observes the usual dispersive broadening and increase of concave curvature.
. After this point one observes the usual dispersive broadening and increase of concave curvature.
As mentioned in § 2.2 the nonlinear term introduces a phase shift, described by (2.12), in regions where the amplitude is higher, which gives maxima in the packet a convex curvature, as seen in figure 3. It follows that, when both the nonlinear and (anomalous) dispersive contributions to the dynamics are considered, the dispersive term acts to reduce the curvature from the nonlinear phase shift and decreases the width of the packet. As long as the strength of the nonlinear phase shift is stronger than the effect of the dispersive term, the packet stays convexly curved. As a result, the width of the region around the maximum will decrease while its amplitude rises. This competition between the nonlinear and the dispersive term is represented mathematically by second condition for MI growth stated in the previous section (3.6), which can be rewritten to
Here, the left-hand side is the strength of the phase shift of a local sinusoidal maximum due to the dispersive term, while the right-hand side is the nonlinear phase-shift of the maximum relative to its surrounding background.