Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T04:46:24.824Z Has data issue: false hasContentIssue false
  • English
  • Français

Multiscale structures and noise in magnetized plasmas line-tied at conducting surfaces

Published online by Cambridge University Press:  28 March 2019

A. B. Hassam  and
Yi-Min Huang
A. B. Hassam*
Affiliation:
Department of Physics, University of Maryland, College Park, Maryland, 20742, USA
Yi-Min Huang
Affiliation:
Department of Astrophysical Sciences, Princeton University, Princeton, New Jersey, 08544, USA
*
†Email address for correspondence: hassam@umd.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

In magnetized plasma situations where magnetic fields intersect massive conducting boundaries, ‘line-tied’ boundary conditions are often used, analytically and in numerical simulations. For ideal magnetohydrodynamic (MHD) plasmas, these conditions are arrived at given the relatively long time scales for magnetic fields penetrating resistively into good conductors. Under line-tied boundary conditions, numerical simulations often exhibit what could be construed as numerical ‘noise’ emanating from the boundaries. We show here that this ‘noise’ is real. By combining numerical and analytical methods, we highlight the existence of sharp spatial structures near the conductors and confirm the appearance of short wavelength structures riding on long wavelength modes. We conclude that, for numerical fidelity, the short multiscale structures need to be resolved. Generally, the short structure widths scale as the square root of the plasma 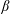$\unicode[STIX]{x1D6FD}$.

Keywords

astrophysical plasmasfusion plasmaplasma simulation
Type
Research Article
Information
Journal of Plasma Physics , Volume 85 , Issue 2 , April 2019 , 905850206
Copyright
© Cambridge University Press 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antiochos, S. K. 1987 The topology of force-free magnetic fields and its implications for coronal activity. Astrophys. J. 312, 886–894.Google Scholar
Bender, C. M. & Orszag, S. A. 1999 Advanced Mathematical Methods for Scientists and Engineers. Springer.Google Scholar
Gresho, P. M. & Lee, R. L. 1981 Don’t suppress the wiggles – they’re telling you something! Comput. Fluids 9 (2), 223–253.Google Scholar
Guzdar, P. N., Drake, J. F., McCarthy, D., Hassam, A. B. & Liu, C. S. 1993 Three-dimensional fluid simulations of the nonlinear driftresistive ballooning modes in tokamak edge plasmas. Phys. Fluids B 5, 3712–3727.Google Scholar
Hood, A. W. 1986 Photospheric line-tying conditions for the stability of coronal magnetic fields. Solar Phys. 105, 307–312.Google Scholar
Hood, A. W. & Priest, E. R. 1979 Kink instability of solar coronal loops as the cause of solar flares. Solar Phys. 64, 303–321.Google Scholar
Huang, Yi-Min, Zweibel, E. G. & Sovinec, C. R. 2006 $m=1$ ideal internal kink modes in a line-tied screw pinch. Phys. Plasmas 13, 092102.Google Scholar
Lionello, R., Velli, M., Einaudi, G. & Mikić, Z. 1998 Nonlinear magnetohydrodynamic evolution of line-tied coronal loops. Astrophys. J. 494, 840–850.Google Scholar
Parker, E. N. 1972 Topological dissipation and the small-scale fields in turbulent gases. Astrophys. J. 174, 499–510.Google Scholar
Parker, E. N. 1979 Cosmical Magnetic Fields. Oxford University Press.Google Scholar
Priest, E. 2014 Magnetohydrodynamics of the Sun. Cambridge University Press.Google Scholar
Scheper, R. A. & Hassam, A. B. 1999 Line-tying and reduced equations of magnetohydrodynamics. Astrophys. J. 511, 976–980.Google Scholar
Strauss, H. R. 1976 Nonlinear, three-dimensional magnetohydrodynamics of noncircular tokamaks. Phys. Fluids 19 (1), 134–140.Google Scholar
Trefethen, Lloyd N. 2000 Spectral Methods in Matlab. SIAM.Google Scholar