1 Introduction
Energy principles provide a powerful tool to assess the linear stability of plasmas within different theoretical frameworks. In particular, the energy principles for the fluid models of ideal magnetohydrodynamics (MHD) and the double-adiabatic theory of Chew, Goldberger & Low (Reference Chew, Goldberger and Low1956) yield a necessary and sufficient condition for stability (Bernstein et al.
Reference Bernstein, Frieman, Kruskal and Kurlsrud1958; Laval, Mercier & Pellat Reference Laval, Mercier and Pellat1965). The original work that formulated the hybrid fluid–kinetic theory of a zero-Larmor-radius collisionless plasma with one ion species, known as kinetic magnetohydrodynamics (KMHD) (Kruskal & Oberman Reference Kruskal and Oberman1958; Rosenbluth & Rostoker Reference Rosenbluth and Rostoker1959), showed that, like in the other conservative theories, a potential energy functional which depends only on the state of the system exists also in KMHD. In this case, the state of a linear perturbation about a static equilibrium is specified by the fluid displacement vector
![]() $\unicode[STIX]{x1D743}$
and the convection-subtracted (Lagrangian) perturbations of the ion and electron distribution functions, to be denoted by
$\unicode[STIX]{x1D743}$
and the convection-subtracted (Lagrangian) perturbations of the ion and electron distribution functions, to be denoted by
![]() $\hat{f}_{s}$
with
$\hat{f}_{s}$
with
![]() $s$
the species index. The incremental potential energy functional is the sum of fluid plus kinetic terms,
$s$
the species index. The incremental potential energy functional is the sum of fluid plus kinetic terms,
Here,
![]() $\unicode[STIX]{x1D6FF}W_{\bot }^{F}[\unicode[STIX]{x1D743}_{\bot }]$
is the incremental potential energy in ‘perpendicular ideal MHD’, namely the ideal-MHD model closed with the ‘convection only’ pressure evolution equation
$\unicode[STIX]{x1D6FF}W_{\bot }^{F}[\unicode[STIX]{x1D743}_{\bot }]$
is the incremental potential energy in ‘perpendicular ideal MHD’, namely the ideal-MHD model closed with the ‘convection only’ pressure evolution equation
![]() $\text{d}p/\,\text{d}t=\unicode[STIX]{x2202}p/\unicode[STIX]{x2202}t+\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735}p=0$
, which depends only on the component of the fluid displacement perpendicular to the equilibrium magnetic field
$\text{d}p/\,\text{d}t=\unicode[STIX]{x2202}p/\unicode[STIX]{x2202}t+\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735}p=0$
, which depends only on the component of the fluid displacement perpendicular to the equilibrium magnetic field
![]() $\unicode[STIX]{x1D743}_{\bot }$
. The Lagrangian distribution function perturbations
$\unicode[STIX]{x1D743}_{\bot }$
. The Lagrangian distribution function perturbations
![]() $\hat{f}_{s}$
are related to the fixed-point (Eulerian) perturbations
$\hat{f}_{s}$
are related to the fixed-point (Eulerian) perturbations
![]() $f_{s1}$
through
$f_{s1}$
through
![]() $\hat{f}_{s}=f_{s1}+\unicode[STIX]{x1D743}\boldsymbol{\cdot }\unicode[STIX]{x2202}f_{s0}/\unicode[STIX]{x2202}\boldsymbol{x}$
and
$\hat{f}_{s}=f_{s1}+\unicode[STIX]{x1D743}\boldsymbol{\cdot }\unicode[STIX]{x2202}f_{s0}/\unicode[STIX]{x2202}\boldsymbol{x}$
and
![]() $f_{s0}$
stands for the equilibrium distribution functions, which are uniform in the direction of the equilibrium magnetic field and monotonically decreasing with the phase-space energy
$f_{s0}$
stands for the equilibrium distribution functions, which are uniform in the direction of the equilibrium magnetic field and monotonically decreasing with the phase-space energy
![]() $\unicode[STIX]{x1D700}$
, so
$\unicode[STIX]{x1D700}$
, so
![]() $\unicode[STIX]{x1D6FF}W^{K}[\hat{f}_{s}]$
is positive definite. In (1.1) and throughout the present work, the equilibrium distribution functions are also assumed to be isotropic in velocity space, so the equilibrium pressures
$\unicode[STIX]{x1D6FF}W^{K}[\hat{f}_{s}]$
is positive definite. In (1.1) and throughout the present work, the equilibrium distribution functions are also assumed to be isotropic in velocity space, so the equilibrium pressures
![]() $p_{s0}$
are scalars.
$p_{s0}$
are scalars.
The existence of a potential energy functional allows us immediately to establish sufficient conditions for stability in KMHD. Clearly, if
![]() $\unicode[STIX]{x1D6FF}W$
is a positive definite functional of
$\unicode[STIX]{x1D6FF}W$
is a positive definite functional of
![]() $(\unicode[STIX]{x1D743},\hat{f}_{s})$
, energy conservation implies that the kinetic energy must remain bounded in time for any possible dynamical evolution, hence the system is stable. Since
$(\unicode[STIX]{x1D743},\hat{f}_{s})$
, energy conservation implies that the kinetic energy must remain bounded in time for any possible dynamical evolution, hence the system is stable. Since
![]() $\unicode[STIX]{x1D6FF}W^{K}[\hat{f}_{s}]$
is positive definite, the most obvious sufficient condition for KMHD stability is that
$\unicode[STIX]{x1D6FF}W^{K}[\hat{f}_{s}]$
is positive definite, the most obvious sufficient condition for KMHD stability is that
![]() $\unicode[STIX]{x1D6FF}W_{\bot }^{F}[\unicode[STIX]{x1D743}_{\bot }]$
be positive definite, or equivalently that the system be stable according to ‘perpendicular ideal MHD’. Tighter sufficient conditions for stability can be obtained by imposing physical constraints on
$\unicode[STIX]{x1D6FF}W_{\bot }^{F}[\unicode[STIX]{x1D743}_{\bot }]$
be positive definite, or equivalently that the system be stable according to ‘perpendicular ideal MHD’. Tighter sufficient conditions for stability can be obtained by imposing physical constraints on
![]() $\hat{f}_{s}$
instead of just using
$\hat{f}_{s}$
instead of just using
![]() $\hat{f}_{s}^{2}\geqslant 0$
. The perturbed distribution functions must be such that their density moments are equal to the fluid perturbed density, which (assuming ions of unit electric charge) must be the same for the two species in order to satisfy charge neutrality and must fulfil the linearized fluid continuity equation,
$\hat{f}_{s}^{2}\geqslant 0$
. The perturbed distribution functions must be such that their density moments are equal to the fluid perturbed density, which (assuming ions of unit electric charge) must be the same for the two species in order to satisfy charge neutrality and must fulfil the linearized fluid continuity equation,
![]() $\int \text{d}^{3}\boldsymbol{v}f_{s1}=-\unicode[STIX]{x1D743}\boldsymbol{\cdot }\unicode[STIX]{x1D735}n_{0}-n_{0}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D743}$
, or equivalently
$\int \text{d}^{3}\boldsymbol{v}f_{s1}=-\unicode[STIX]{x1D743}\boldsymbol{\cdot }\unicode[STIX]{x1D735}n_{0}-n_{0}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D743}$
, or equivalently
![]() $\int \text{d}^{3}\boldsymbol{v}\hat{f}_{s}=-n_{0}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D743}$
, where
$\int \text{d}^{3}\boldsymbol{v}\hat{f}_{s}=-n_{0}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D743}$
, where
![]() $n_{0}$
is the equilibrium particle density. Now, minimizing
$n_{0}$
is the equilibrium particle density. Now, minimizing
![]() $\unicode[STIX]{x1D6FF}W$
subject to the constraint
$\unicode[STIX]{x1D6FF}W$
subject to the constraint
![]() $\int \text{d}^{3}\boldsymbol{v}~\hat{f}_{s}=-n_{0}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D743}$
yields
$\int \text{d}^{3}\boldsymbol{v}~\hat{f}_{s}=-n_{0}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D743}$
yields
so
![]() $\unicode[STIX]{x1D6FF}W[\unicode[STIX]{x1D743},\hat{f}_{s}]$
is bounded from below by the incremental potential energy in the isothermal ideal-MHD model closed with the pressure evolution equation
$\unicode[STIX]{x1D6FF}W[\unicode[STIX]{x1D743},\hat{f}_{s}]$
is bounded from below by the incremental potential energy in the isothermal ideal-MHD model closed with the pressure evolution equation
![]() $d(pn^{-1})/\,\text{d}t=0$
, and stability according to isothermal ideal MHD is a sufficient condition for KMHD stability. Yet another sufficient condition for stability may be obtained by considering the Rosenbluth–Rostoker form of the KMHD potential energy, which results from specializing
$d(pn^{-1})/\,\text{d}t=0$
, and stability according to isothermal ideal MHD is a sufficient condition for KMHD stability. Yet another sufficient condition for stability may be obtained by considering the Rosenbluth–Rostoker form of the KMHD potential energy, which results from specializing
![]() $\unicode[STIX]{x1D6FF}W^{K}[\hat{f}_{s}]$
to the distribution functions of a zero-frequency normal mode, defined as an unstable normal mode with zero real frequency and infinitesimally small growth rate. The solution for these zero-frequency normal modes, to be denoted by
$\unicode[STIX]{x1D6FF}W^{K}[\hat{f}_{s}]$
to the distribution functions of a zero-frequency normal mode, defined as an unstable normal mode with zero real frequency and infinitesimally small growth rate. The solution for these zero-frequency normal modes, to be denoted by
![]() $\hat{f}_{s}^{\unicode[STIX]{x1D714}=0}$
, was derived in Rosenbluth & Rostoker (Reference Rosenbluth and Rostoker1959) and was expressed in terms of
$\hat{f}_{s}^{\unicode[STIX]{x1D714}=0}$
, was derived in Rosenbluth & Rostoker (Reference Rosenbluth and Rostoker1959) and was expressed in terms of
![]() $\unicode[STIX]{x1D743}_{\bot }$
and equilibrium quantities only, hence the following form of KMHD potential energy could be defined as a functional of
$\unicode[STIX]{x1D743}_{\bot }$
and equilibrium quantities only, hence the following form of KMHD potential energy could be defined as a functional of
![]() $\unicode[STIX]{x1D743}_{\bot }$
$\unicode[STIX]{x1D743}_{\bot }$
With the condition that the particle orbits be periodic or nearly periodic, upper and lower bounds for
![]() $\unicode[STIX]{x1D6FF}W^{RR}[\unicode[STIX]{x1D743}_{\bot }]$
, known as comparison theorems, were also derived (Kruskal & Oberman Reference Kruskal and Oberman1958; Rosenbluth & Rostoker Reference Rosenbluth and Rostoker1959). The lower bound is
$\unicode[STIX]{x1D6FF}W^{RR}[\unicode[STIX]{x1D743}_{\bot }]$
, known as comparison theorems, were also derived (Kruskal & Oberman Reference Kruskal and Oberman1958; Rosenbluth & Rostoker Reference Rosenbluth and Rostoker1959). The lower bound is
where
![]() $\langle \cdots \rangle =\int \text{d}l\,(\cdots \,)B^{-1}/\int \text{d}l\,B^{-1}$
is the magnetic flux tube average, so
$\langle \cdots \rangle =\int \text{d}l\,(\cdots \,)B^{-1}/\int \text{d}l\,B^{-1}$
is the magnetic flux tube average, so
![]() $\unicode[STIX]{x1D6FF}W^{RR}[\unicode[STIX]{x1D743}_{\bot }]$
is bounded from below by the incremental potential energy in the adiabatic ideal-MHD model closed with the pressure evolution equation
$\unicode[STIX]{x1D6FF}W^{RR}[\unicode[STIX]{x1D743}_{\bot }]$
is bounded from below by the incremental potential energy in the adiabatic ideal-MHD model closed with the pressure evolution equation
![]() $d(pn^{-5/3})/\,\text{d}t=0$
, after minimization with respect to
$d(pn^{-5/3})/\,\text{d}t=0$
, after minimization with respect to
![]() $\unicode[STIX]{x1D709}_{\Vert }$
. This is usually accepted as proof that stability according to adiabatic ideal MHD is a sufficient condition for stability in KMHD although, strictly speaking, equations (1.3) and (1.4) mean only that, if an equilibrium admits a KMHD zero-frequency normal mode, it is either marginal or unstable in adiabatic ideal MHD. In any case, even if these two statements happened not to be equivalent, one always has the result that stability in isothermal ideal MHD is sufficient for stability in KMHD, a result that is slightly more pessimistic but is rigorous and has the advantage of not requiring the periodic orbit assumption.
$\unicode[STIX]{x1D709}_{\Vert }$
. This is usually accepted as proof that stability according to adiabatic ideal MHD is a sufficient condition for stability in KMHD although, strictly speaking, equations (1.3) and (1.4) mean only that, if an equilibrium admits a KMHD zero-frequency normal mode, it is either marginal or unstable in adiabatic ideal MHD. In any case, even if these two statements happened not to be equivalent, one always has the result that stability in isothermal ideal MHD is sufficient for stability in KMHD, a result that is slightly more pessimistic but is rigorous and has the advantage of not requiring the periodic orbit assumption.
The situation is different when it comes to proving necessary conditions for KMHD stability, and rigorous results regarding this more difficult problem have turned out to be elusive. The upper bound for the Rosenbluth–Rostoker potential energy is
where
![]() $\unicode[STIX]{x1D6FF}W^{DA}$
is the incremental potential energy in the Chew–Goldberger–Low, double-adiabatic fluid theory, with
$\unicode[STIX]{x1D6FF}W^{DA}$
is the incremental potential energy in the Chew–Goldberger–Low, double-adiabatic fluid theory, with
![]() $\unicode[STIX]{x1D73F}_{0}$
the equilibrium magnetic curvature vector. This implies that, if an equilibrium is unstable according to the double-adiabatic theory to a fluid displacement perturbation with zero parallel component, then a KMHD trial perturbation can be constructed that makes the KMHD potential energy negative. One may be tempted to argue that, by analogy with the mechanical systems with finite degrees of freedom or the simpler ideal-MHD and double-adiabatic fluid theories, this also implies a KMHD instability. However, actually proving it is neither immediate nor easy due to the fact that, as shown explicitly in Ramos (Reference Ramos2015b
), KMHD does not have a self-adjointness property. The standard approaches to prove that an unstable growth follows when a trial perturbation that makes the potential energy negative is used as initial condition, do not work in KMHD because of its lack of self-adjointness. There are two such standard approaches. In the first one, the initial condition is expanded as a superposition of normal modes and it is argued that, in order to make the potential energy negative, at least one of the normal modes must have a positive growth rate which will cause an exponential growth of the perturbation. The validity of this method requires of course that a complete basis of normal modes exists and this has not been proved for KMHD (even allowing for a continuum of singular modes) because the KMHD normal modes are not eigenfunctions of a self-adjoint operator. The second approach, which does not rely on the expansion in normal modes, is the one put forward in the rigorous proof of the necessary condition for ideal-MHD stability of Laval et al. (Reference Laval, Mercier and Pellat1965). However, this method requires that the ‘force-times-displacement’ functional
$\unicode[STIX]{x1D73F}_{0}$
the equilibrium magnetic curvature vector. This implies that, if an equilibrium is unstable according to the double-adiabatic theory to a fluid displacement perturbation with zero parallel component, then a KMHD trial perturbation can be constructed that makes the KMHD potential energy negative. One may be tempted to argue that, by analogy with the mechanical systems with finite degrees of freedom or the simpler ideal-MHD and double-adiabatic fluid theories, this also implies a KMHD instability. However, actually proving it is neither immediate nor easy due to the fact that, as shown explicitly in Ramos (Reference Ramos2015b
), KMHD does not have a self-adjointness property. The standard approaches to prove that an unstable growth follows when a trial perturbation that makes the potential energy negative is used as initial condition, do not work in KMHD because of its lack of self-adjointness. There are two such standard approaches. In the first one, the initial condition is expanded as a superposition of normal modes and it is argued that, in order to make the potential energy negative, at least one of the normal modes must have a positive growth rate which will cause an exponential growth of the perturbation. The validity of this method requires of course that a complete basis of normal modes exists and this has not been proved for KMHD (even allowing for a continuum of singular modes) because the KMHD normal modes are not eigenfunctions of a self-adjoint operator. The second approach, which does not rely on the expansion in normal modes, is the one put forward in the rigorous proof of the necessary condition for ideal-MHD stability of Laval et al. (Reference Laval, Mercier and Pellat1965). However, this method requires that the ‘force-times-displacement’ functional
be equal to the incremental potential energy, which is defined as
where
![]() $\unicode[STIX]{x1D70C}_{0}$
is the equilibrium mass density and
$\unicode[STIX]{x1D70C}_{0}$
is the equilibrium mass density and
![]() $K=1/2\int \text{d}^{3}\boldsymbol{x}\,\unicode[STIX]{x1D70C}_{0}|\unicode[STIX]{x2202}\unicode[STIX]{x1D743}/\unicode[STIX]{x2202}t|^{2}$
is the kinetic energy. The equality
$K=1/2\int \text{d}^{3}\boldsymbol{x}\,\unicode[STIX]{x1D70C}_{0}|\unicode[STIX]{x2202}\unicode[STIX]{x1D743}/\unicode[STIX]{x2202}t|^{2}$
is the kinetic energy. The equality
![]() $U=\unicode[STIX]{x1D6FF}W$
holds when the force operator
$U=\unicode[STIX]{x1D6FF}W$
holds when the force operator
![]() $\boldsymbol{F}$
is self-adjoint so that
$\boldsymbol{F}$
is self-adjoint so that
![]() $\text{d}(\int \text{d}^{3}\boldsymbol{x}~\unicode[STIX]{x1D743}\boldsymbol{\cdot }\boldsymbol{F})/\text{d}t=2\int \text{d}^{3}\boldsymbol{x}(\unicode[STIX]{x2202}\unicode[STIX]{x1D743}/\unicode[STIX]{x2202}t)\boldsymbol{\cdot }\boldsymbol{F}$
, but it does not hold in KMHD whose force operator does not have this property.
$\text{d}(\int \text{d}^{3}\boldsymbol{x}~\unicode[STIX]{x1D743}\boldsymbol{\cdot }\boldsymbol{F})/\text{d}t=2\int \text{d}^{3}\boldsymbol{x}(\unicode[STIX]{x2202}\unicode[STIX]{x1D743}/\unicode[STIX]{x2202}t)\boldsymbol{\cdot }\boldsymbol{F}$
, but it does not hold in KMHD whose force operator does not have this property.
This paper investigates the KMHD initial-value problem with the aim of establishing stability criteria whose derivation does not use the classic comparison theorems and does not require the self-adjointness of the force operator or the existence of a complete basis of normal modes. The analysis uses the KMHD formulation of Ramos (Reference Ramos2015a
,Reference Ramos
b
) based on drift-kinetic equations in the reference frame of the complete macroscopic fluid velocity, in which the electric field is eliminated algebraically and the quasineutrality condition is satisfied automatically at all times if it is satisfied by the initial condition. This formulation does not rely on solutions of the kinetic equations by integration along particle orbits and does not require that such orbits be periodic or nearly periodic. Time-dependent solutions of the initial-value problem for the linear KMHD system are considered, hence all quantities are real and generally do not have a separable time dependence. For these physical solutions, the incremental potential energy
![]() $\unicode[STIX]{x1D6FF}W$
and the ‘force-times-displacement’
$\unicode[STIX]{x1D6FF}W$
and the ‘force-times-displacement’
![]() $U$
functionals are evaluated explicitly. They are shown to be different in general, which corroborates the claim that the KMHD force operator is not self-adjoint. A special class of such solutions of the KMHD initial-value problem makes the difference
$U$
functionals are evaluated explicitly. They are shown to be different in general, which corroborates the claim that the KMHD force operator is not self-adjoint. A special class of such solutions of the KMHD initial-value problem makes the difference
![]() $\unicode[STIX]{x1D6FF}W-U$
particularly simple albeit not zero and, for these, the initial values of the KMHD potential energy
$\unicode[STIX]{x1D6FF}W-U$
particularly simple albeit not zero and, for these, the initial values of the KMHD potential energy
![]() $\unicode[STIX]{x1D6FF}W[\unicode[STIX]{x1D743}(0),\hat{f}_{s}(0)]$
and the double-adiabatic potential energy
$\unicode[STIX]{x1D6FF}W[\unicode[STIX]{x1D743}(0),\hat{f}_{s}(0)]$
and the double-adiabatic potential energy
![]() $\unicode[STIX]{x1D6FF}W^{DA}[\unicode[STIX]{x1D743}(0)]$
are equal. Accounting for their still non-zero
$\unicode[STIX]{x1D6FF}W^{DA}[\unicode[STIX]{x1D743}(0)]$
are equal. Accounting for their still non-zero
![]() $\unicode[STIX]{x1D6FF}W-U$
, these special KMHD perturbations are then used to obtain a condition under which they can be proved to grow in time without bound if the equilibrium is unstable in the double-adiabatic theory. That condition pertains a sufficiently regular behaviour of the oscillations about stable equilibria at long times (such that the squared amplitudes of the distribution function perturbations do not undergo short bursts with large deviations from their time averages) and its validity would guarantee that stability according to the double-adiabatic fluid theory is a necessary condition for KMHD stability.
$\unicode[STIX]{x1D6FF}W-U$
, these special KMHD perturbations are then used to obtain a condition under which they can be proved to grow in time without bound if the equilibrium is unstable in the double-adiabatic theory. That condition pertains a sufficiently regular behaviour of the oscillations about stable equilibria at long times (such that the squared amplitudes of the distribution function perturbations do not undergo short bursts with large deviations from their time averages) and its validity would guarantee that stability according to the double-adiabatic fluid theory is a necessary condition for KMHD stability.
2 The general KMHD system and its conservation laws
The KMHD theory describes a collisionless, quasineutral plasma with a single ion species (of unit charge for simplicity), in the strong magnetization limit of zero Larmor radii where particles are perfectly tied to the magnetic field lines. The kinetic pressures of each species are formally taken as comparable to the magnetic pressure (so the skin depths are of the order of the Larmor radii) and the macroscopic flow velocities are formally taken as comparable to the sound speed. Thus, the Hall and other two-fluid effects become negligible in the leading order as the Larmor radii tend to zero, in which limit the two species share a common, single-fluid macroscopic velocity
![]() $\boldsymbol{u}$
. The quasineutrality condition implies that they share also a common particle density
$\boldsymbol{u}$
. The quasineutrality condition implies that they share also a common particle density
![]() $n$
. The result is a hybrid model, whereby a system of single-fluid, dissipation-free, hydromagnetic equations is closed with a pressure tensor which is the sum of ion and electron contributions determined kinetically:
$n$
. The result is a hybrid model, whereby a system of single-fluid, dissipation-free, hydromagnetic equations is closed with a pressure tensor which is the sum of ion and electron contributions determined kinetically:
where
![]() $\unicode[STIX]{x1D70C}=(m_{i}+m_{e})n$
denotes the mass density and the ion and electron pressure tensors have the zero-Larmor-radius collisionless form (Chew et al.
Reference Chew, Goldberger and Low1956)
$\unicode[STIX]{x1D70C}=(m_{i}+m_{e})n$
denotes the mass density and the ion and electron pressure tensors have the zero-Larmor-radius collisionless form (Chew et al.
Reference Chew, Goldberger and Low1956)
with
![]() $\boldsymbol{b}=\boldsymbol{B}/B$
denoting the magnetic unit vector and
$\boldsymbol{b}=\boldsymbol{B}/B$
denoting the magnetic unit vector and
![]() $\unicode[STIX]{x1D644}$
denoting the identity tensor. The parallel and perpendicular pressures are the corresponding moments of the distribution functions of each species,
$\unicode[STIX]{x1D644}$
denoting the identity tensor. The parallel and perpendicular pressures are the corresponding moments of the distribution functions of each species,
and the phase-space velocity variable
![]() $\boldsymbol{w}$
is the random velocity in the reference frame of the macroscopic flow,
$\boldsymbol{w}$
is the random velocity in the reference frame of the macroscopic flow,
![]() $\boldsymbol{w}=\boldsymbol{v}-\boldsymbol{u}$
. The distribution functions are independent of the gyrophase angle and satisfy a zero-Larmor-radius drift-kinetic equation. It is most advantageous to refer this drift-kinetic equation to the shifted velocity variable
$\boldsymbol{w}=\boldsymbol{v}-\boldsymbol{u}$
. The distribution functions are independent of the gyrophase angle and satisfy a zero-Larmor-radius drift-kinetic equation. It is most advantageous to refer this drift-kinetic equation to the shifted velocity variable
![]() $\boldsymbol{w}$
so that its solution,
$\boldsymbol{w}$
so that its solution,
![]() $f_{s}=f_{s}(w_{\Vert },w_{\bot },\boldsymbol{x},t)$
, can be used directly in the evaluation of the pressure moments (2.6), without having to subtract any components of the macroscopic velocity. The transformation to this reference frame of the macroscopic flow allows also to eliminate exactly the electric field from the drift-kinetic equation, which becomes (Ramos Reference Ramos2008)
$f_{s}=f_{s}(w_{\Vert },w_{\bot },\boldsymbol{x},t)$
, can be used directly in the evaluation of the pressure moments (2.6), without having to subtract any components of the macroscopic velocity. The transformation to this reference frame of the macroscopic flow allows also to eliminate exactly the electric field from the drift-kinetic equation, which becomes (Ramos Reference Ramos2008)
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}t}+\left(\boldsymbol{u}+w_{\Vert }\boldsymbol{b}\right)\boldsymbol{\cdot }\frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\boldsymbol{x}}\Bigg|_{w_{\Vert },w_{\bot }}+\frac{w_{\bot }}{2}\left[(\boldsymbol{b}\boldsymbol{b}-\unicode[STIX]{x1D644})\boldsymbol{ : }(\unicode[STIX]{x1D735}\boldsymbol{u})+w_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\ln B\right]\frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}w_{\bot }}\nonumber\\ \displaystyle & & \displaystyle \quad +\left[\frac{\boldsymbol{b}\boldsymbol{\cdot }\left(\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D617}_{s}\right)}{m_{s}n}-w_{\Vert }(\boldsymbol{b}\boldsymbol{b})\boldsymbol{ : }(\unicode[STIX]{x1D735}\boldsymbol{u})-\frac{w_{\bot }^{2}}{2}\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\ln B\right]\frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}w_{\Vert }}=0.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}t}+\left(\boldsymbol{u}+w_{\Vert }\boldsymbol{b}\right)\boldsymbol{\cdot }\frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\boldsymbol{x}}\Bigg|_{w_{\Vert },w_{\bot }}+\frac{w_{\bot }}{2}\left[(\boldsymbol{b}\boldsymbol{b}-\unicode[STIX]{x1D644})\boldsymbol{ : }(\unicode[STIX]{x1D735}\boldsymbol{u})+w_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\ln B\right]\frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}w_{\bot }}\nonumber\\ \displaystyle & & \displaystyle \quad +\left[\frac{\boldsymbol{b}\boldsymbol{\cdot }\left(\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D617}_{s}\right)}{m_{s}n}-w_{\Vert }(\boldsymbol{b}\boldsymbol{b})\boldsymbol{ : }(\unicode[STIX]{x1D735}\boldsymbol{u})-\frac{w_{\bot }^{2}}{2}\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\ln B\right]\frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}w_{\Vert }}=0.\end{eqnarray}$$
The closed system of (2.1)–(2.7) (which has been written without any explicit reference to the electric field but has taken it properly into account) is the formulation of the KMHD theoretical model that will be investigated in this work. This general, nonlinear system has several exact conservation properties. The continuity equation (2.3) is in the form of conservation law for the number of particles and the equation of motion (2.4) combined with (2.3) can be expressed as the conservation law for momentum,
The drift-kinetic equation (2.7) upholds these two conservation laws. For consistency with particle conservation and quasineutrality, the ‘kinetically defined’ particle densities
![]() $n_{s}^{kin}\equiv \int \text{d}^{3}\boldsymbol{w}~f_{s}$
should always be the same for both species and equal to the solution
$n_{s}^{kin}\equiv \int \text{d}^{3}\boldsymbol{w}~f_{s}$
should always be the same for both species and equal to the solution
![]() $n$
of the fluid continuity equation (2.3). Since the momentum conservation equation was subtracted from the kinetic equation when transforming it to the macroscopic flow frame and eliminating the electric field, the
$n$
of the fluid continuity equation (2.3). Since the momentum conservation equation was subtracted from the kinetic equation when transforming it to the macroscopic flow frame and eliminating the electric field, the
![]() $w_{\Vert }$
moment of (2.7) is not redundant with the parallel component of (2.4). Instead, the
$w_{\Vert }$
moment of (2.7) is not redundant with the parallel component of (2.4). Instead, the
![]() $w_{\Vert }$
moment of
$w_{\Vert }$
moment of
![]() $f_{s}$
should by definition be always zero. Now, calling
$f_{s}$
should by definition be always zero. Now, calling
![]() $c_{s\Vert }\equiv \int \text{d}^{3}\boldsymbol{w}~w_{\Vert }f_{s}$
, the
$c_{s\Vert }\equiv \int \text{d}^{3}\boldsymbol{w}~w_{\Vert }f_{s}$
, the
![]() $1$
and
$1$
and
![]() $w_{\Vert }$
moments of the drift-kinetic equation (2.7) combined with the continuity equation (2.3) yield
$w_{\Vert }$
moments of the drift-kinetic equation (2.7) combined with the continuity equation (2.3) yield
This is a homogeneous system for
![]() $(n_{s}^{kin}-n)$
and
$(n_{s}^{kin}-n)$
and
![]() $c_{s\Vert }$
, which guarantees that the required constraints
$c_{s\Vert }$
, which guarantees that the required constraints
![]() $n_{s}^{kin}-n=0$
and
$n_{s}^{kin}-n=0$
and
![]() $c_{s\Vert }=0$
are satisfied at all times provided they are satisfied by the initial condition. Finally, the KMHD system has an energy conservation law. Combining equation (2.1) dotted with
$c_{s\Vert }=0$
are satisfied at all times provided they are satisfied by the initial condition. Finally, the KMHD system has an energy conservation law. Combining equation (2.1) dotted with
![]() $\boldsymbol{B}$
, equation (2.4) dotted with
$\boldsymbol{B}$
, equation (2.4) dotted with
![]() $\boldsymbol{u}$
, equation (2.3) and the
$\boldsymbol{u}$
, equation (2.3) and the
![]() $w^{2}$
moment of equation (2.7), one gets
$w^{2}$
moment of equation (2.7), one gets
 $$\begin{eqnarray}\displaystyle & & \displaystyle \hspace{-10.00002pt}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}\left[\frac{\unicode[STIX]{x1D70C}u^{2}}{2}+\frac{B^{2}}{2}+\frac{1}{2}\mathop{\sum }_{s=i,e}\left(p_{s\Vert }+2p_{s\bot }\right)\right]\nonumber\\ \displaystyle & & \displaystyle \quad +\,\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left\{\frac{\unicode[STIX]{x1D70C}u^{2}}{2}\boldsymbol{u}-(\boldsymbol{u}\times \boldsymbol{B})\times \boldsymbol{B}+\mathop{\sum }_{s=i,e}\left[\frac{1}{2}\left(p_{s\Vert }+2p_{s\bot }\right)\boldsymbol{u}+\unicode[STIX]{x1D617}_{s}\boldsymbol{\cdot }\boldsymbol{u}+q_{s\Vert }\boldsymbol{b}\right]\right\}=0,\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \hspace{-10.00002pt}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}\left[\frac{\unicode[STIX]{x1D70C}u^{2}}{2}+\frac{B^{2}}{2}+\frac{1}{2}\mathop{\sum }_{s=i,e}\left(p_{s\Vert }+2p_{s\bot }\right)\right]\nonumber\\ \displaystyle & & \displaystyle \quad +\,\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left\{\frac{\unicode[STIX]{x1D70C}u^{2}}{2}\boldsymbol{u}-(\boldsymbol{u}\times \boldsymbol{B})\times \boldsymbol{B}+\mathop{\sum }_{s=i,e}\left[\frac{1}{2}\left(p_{s\Vert }+2p_{s\bot }\right)\boldsymbol{u}+\unicode[STIX]{x1D617}_{s}\boldsymbol{\cdot }\boldsymbol{u}+q_{s\Vert }\boldsymbol{b}\right]\right\}=0,\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
where
![]() $q_{s\Vert }=m_{s}/2\int \text{d}^{3}\boldsymbol{w}w_{\Vert }w^{2}f_{s}$
is the parallel heat flux. In order to streamline the exposition, this paper will assume that the plasma domain is bounded by a rigid and perfectly conducting wall where the normal components of
$q_{s\Vert }=m_{s}/2\int \text{d}^{3}\boldsymbol{w}w_{\Vert }w^{2}f_{s}$
is the parallel heat flux. In order to streamline the exposition, this paper will assume that the plasma domain is bounded by a rigid and perfectly conducting wall where the normal components of
![]() $\boldsymbol{u}$
and
$\boldsymbol{u}$
and
![]() $\boldsymbol{B}$
vanish. As indicated by the normal-mode analysis of Ramos (Reference Ramos2015b
), the results can be generalized to the case where the plasma domain is surrounded by a vacuum region and the plasma–vacuum interface is a closed magnetic surface where the density drops continuously to zero, but the details of this generalization will be skipped here. Thus, for the purposes of the present paper, the global version of the energy conservation law is
$\boldsymbol{B}$
vanish. As indicated by the normal-mode analysis of Ramos (Reference Ramos2015b
), the results can be generalized to the case where the plasma domain is surrounded by a vacuum region and the plasma–vacuum interface is a closed magnetic surface where the density drops continuously to zero, but the details of this generalization will be skipped here. Thus, for the purposes of the present paper, the global version of the energy conservation law is
and the space integral
![]() $\int \text{d}^{3}\boldsymbol{x}$
extends over the plasma domain.
$\int \text{d}^{3}\boldsymbol{x}$
extends over the plasma domain.
3 Linearized KMHD system and specification of initial conditions
The linear stability problem that this work will address concerns small-amplitude perturbations about a static equilibrium, and the subscripts
![]() $0$
and
$0$
and
![]() $1$
will be used to denote respectively equilibrium and first-order perturbation variables. The equilibrium distribution functions will be assumed here to be isotropic Maxwellians,
$1$
will be used to denote respectively equilibrium and first-order perturbation variables. The equilibrium distribution functions will be assumed here to be isotropic Maxwellians,
with density and temperatures that are uniform in the direction of the equilibrium magnetic field,
and satisfy the force balance equation
so that, with a vanishing macroscopic flow,
![]() $\boldsymbol{u}_{0}=0$
, this constitutes a time-independent solution of the KMHD system (2.1)–(2.7). The Maxwellian equilibrium distribution function is a preferred choice on physical grounds, but the analysis is equally applicable to other equilibrium distribution functions that are constant along the magnetic field, isotropic in velocity space and monotonically decreasing with
$\boldsymbol{u}_{0}=0$
, this constitutes a time-independent solution of the KMHD system (2.1)–(2.7). The Maxwellian equilibrium distribution function is a preferred choice on physical grounds, but the analysis is equally applicable to other equilibrium distribution functions that are constant along the magnetic field, isotropic in velocity space and monotonically decreasing with
![]() $w^{2}$
.
$w^{2}$
.
The first-order perturbation satisfies the linearized KMHD system
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}f_{s1}}{\unicode[STIX]{x2202}t}+w_{\Vert }\boldsymbol{b}_{0}\boldsymbol{\cdot }\frac{\unicode[STIX]{x2202}f_{s1}}{\unicode[STIX]{x2202}\boldsymbol{x}}\Bigg|_{w_{\Vert },w_{\bot }}+~\frac{w_{\bot }}{2}(\boldsymbol{b}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\ln B_{0})\left(w_{\Vert }\frac{\unicode[STIX]{x2202}f_{s1}}{\unicode[STIX]{x2202}w_{\bot }}-w_{\bot }\frac{\unicode[STIX]{x2202}f_{s1}}{\unicode[STIX]{x2202}w_{\Vert }}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad +\left(\boldsymbol{u}_{1}+w_{\Vert }\boldsymbol{b}_{1}\right)\boldsymbol{\cdot }\frac{\unicode[STIX]{x2202}f_{Ms0}}{\unicode[STIX]{x2202}\boldsymbol{x}}\Bigg|_{w_{\Vert },w_{\bot }}+~\frac{w_{\bot }}{2}[(\boldsymbol{b}_{0}\boldsymbol{b}_{0}-\unicode[STIX]{x1D644})\boldsymbol{ : }(\unicode[STIX]{x1D735}\boldsymbol{u}_{1})]\frac{\unicode[STIX]{x2202}f_{Ms0}}{\unicode[STIX]{x2202}w_{\bot }}\nonumber\\ \displaystyle & & \displaystyle \qquad +\left[\frac{\boldsymbol{b}_{0}\boldsymbol{\cdot }(\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D617}_{s1})+\boldsymbol{b}_{1}\boldsymbol{\cdot }(\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D617}_{s0})}{m_{s}n_{0}}-w_{\Vert }(\boldsymbol{b}_{0}\boldsymbol{b}_{0})\boldsymbol{ : }(\unicode[STIX]{x1D735}\boldsymbol{u}_{1})\right]\frac{\unicode[STIX]{x2202}f_{Ms0}}{\unicode[STIX]{x2202}w_{\Vert }}=0.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}f_{s1}}{\unicode[STIX]{x2202}t}+w_{\Vert }\boldsymbol{b}_{0}\boldsymbol{\cdot }\frac{\unicode[STIX]{x2202}f_{s1}}{\unicode[STIX]{x2202}\boldsymbol{x}}\Bigg|_{w_{\Vert },w_{\bot }}+~\frac{w_{\bot }}{2}(\boldsymbol{b}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\ln B_{0})\left(w_{\Vert }\frac{\unicode[STIX]{x2202}f_{s1}}{\unicode[STIX]{x2202}w_{\bot }}-w_{\bot }\frac{\unicode[STIX]{x2202}f_{s1}}{\unicode[STIX]{x2202}w_{\Vert }}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad +\left(\boldsymbol{u}_{1}+w_{\Vert }\boldsymbol{b}_{1}\right)\boldsymbol{\cdot }\frac{\unicode[STIX]{x2202}f_{Ms0}}{\unicode[STIX]{x2202}\boldsymbol{x}}\Bigg|_{w_{\Vert },w_{\bot }}+~\frac{w_{\bot }}{2}[(\boldsymbol{b}_{0}\boldsymbol{b}_{0}-\unicode[STIX]{x1D644})\boldsymbol{ : }(\unicode[STIX]{x1D735}\boldsymbol{u}_{1})]\frac{\unicode[STIX]{x2202}f_{Ms0}}{\unicode[STIX]{x2202}w_{\bot }}\nonumber\\ \displaystyle & & \displaystyle \qquad +\left[\frac{\boldsymbol{b}_{0}\boldsymbol{\cdot }(\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D617}_{s1})+\boldsymbol{b}_{1}\boldsymbol{\cdot }(\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D617}_{s0})}{m_{s}n_{0}}-w_{\Vert }(\boldsymbol{b}_{0}\boldsymbol{b}_{0})\boldsymbol{ : }(\unicode[STIX]{x1D735}\boldsymbol{u}_{1})\right]\frac{\unicode[STIX]{x2202}f_{Ms0}}{\unicode[STIX]{x2202}w_{\Vert }}=0.\end{eqnarray}$$
The initial-value solution of this system requires specification of the initial conditions
![]() $\boldsymbol{B}_{1}(0)$
,
$\boldsymbol{B}_{1}(0)$
,
![]() $n_{1}(0)$
,
$n_{1}(0)$
,
![]() $\boldsymbol{u}_{1}(0)$
and
$\boldsymbol{u}_{1}(0)$
and
![]() $f_{s1}(0)$
, subject to the constraints
$f_{s1}(0)$
, subject to the constraints
![]() $\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{B}_{1}(0)=0$
,
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{B}_{1}(0)=0$
,
![]() $\int \text{d}^{3}\boldsymbol{w}~f_{s1}(0)=n_{1}(0)$
and
$\int \text{d}^{3}\boldsymbol{w}~f_{s1}(0)=n_{1}(0)$
and
![]() $\int \text{d}^{3}\boldsymbol{w}~w_{\Vert }f_{s1}(0)=0$
. The zero-divergence constraint on
$\int \text{d}^{3}\boldsymbol{w}~w_{\Vert }f_{s1}(0)=0$
. The zero-divergence constraint on
![]() $\boldsymbol{B}_{1}(0)$
leaves it with only two independent components, so the initial conditions for
$\boldsymbol{B}_{1}(0)$
leaves it with only two independent components, so the initial conditions for
![]() $\boldsymbol{B}_{1}$
and
$\boldsymbol{B}_{1}$
and
![]() $n_{1}$
can be implemented in terms of a three-component vector
$n_{1}$
can be implemented in terms of a three-component vector
![]() $\unicode[STIX]{x1D743}(0)=\unicode[STIX]{x1D709}_{\Vert }(0)\boldsymbol{b}_{0}+\unicode[STIX]{x1D743}_{\bot }(0)$
, through
$\unicode[STIX]{x1D743}(0)=\unicode[STIX]{x1D709}_{\Vert }(0)\boldsymbol{b}_{0}+\unicode[STIX]{x1D743}_{\bot }(0)$
, through
![]() $\boldsymbol{B}_{1}(0)=\unicode[STIX]{x1D735}\times [\unicode[STIX]{x1D743}_{\bot }(0)\times \boldsymbol{B}_{0}]$
and
$\boldsymbol{B}_{1}(0)=\unicode[STIX]{x1D735}\times [\unicode[STIX]{x1D743}_{\bot }(0)\times \boldsymbol{B}_{0}]$
and
![]() $n_{1}(0)=-\unicode[STIX]{x1D743}_{\bot }(0)\boldsymbol{\cdot }\unicode[STIX]{x1D735}n_{0}-n_{0}~\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D743}(0)$
. Now, defining the time-dependent displacement vector
$n_{1}(0)=-\unicode[STIX]{x1D743}_{\bot }(0)\boldsymbol{\cdot }\unicode[STIX]{x1D735}n_{0}-n_{0}~\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D743}(0)$
. Now, defining the time-dependent displacement vector
equations (3.4) and (3.6) can be integrated to get the relationships
valid at all times, which allow us to eliminate
![]() $\boldsymbol{B}_{1}$
,
$\boldsymbol{B}_{1}$
,
![]() $\boldsymbol{j}_{1}$
and
$\boldsymbol{j}_{1}$
and
![]() $n_{1}$
in favour of
$n_{1}$
in favour of
![]() $\unicode[STIX]{x1D743}$
in the dynamical system. The dynamical displacement vector
$\unicode[STIX]{x1D743}$
in the dynamical system. The dynamical displacement vector
![]() $\unicode[STIX]{x1D743}$
also serves to define the convection-subtracted (Lagrangian) perturbations of the distribution functions,
$\unicode[STIX]{x1D743}$
also serves to define the convection-subtracted (Lagrangian) perturbations of the distribution functions,
so the pressure tensors become
with
and the parallel and perpendicular components of
![]() $-\unicode[STIX]{x1D735}\boldsymbol{\cdot }\hat{\unicode[STIX]{x1D617}}_{s}$
are the following functionals of
$-\unicode[STIX]{x1D735}\boldsymbol{\cdot }\hat{\unicode[STIX]{x1D617}}_{s}$
are the following functionals of
![]() $\hat{f}_{s}$
:
$\hat{f}_{s}$
:
and
where
![]() $\unicode[STIX]{x1D73F}_{0}=(\boldsymbol{b}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\boldsymbol{b}_{0}$
is the equilibrium magnetic curvature. Then, recalling that the force operator in ‘perpendicular ideal MHD’ is the functional of
$\unicode[STIX]{x1D73F}_{0}=(\boldsymbol{b}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\boldsymbol{b}_{0}$
is the equilibrium magnetic curvature. Then, recalling that the force operator in ‘perpendicular ideal MHD’ is the functional of
![]() $\unicode[STIX]{x1D743}_{\bot }$
$\unicode[STIX]{x1D743}_{\bot }$
with
![]() $\boldsymbol{B}_{1}$
and
$\boldsymbol{B}_{1}$
and
![]() $\boldsymbol{j}_{1}$
given respectively by (3.12) and (3.5), and that, as a consequence of (3.3) and (3.12) the parallel component of
$\boldsymbol{j}_{1}$
given respectively by (3.12) and (3.5), and that, as a consequence of (3.3) and (3.12) the parallel component of
![]() $(\boldsymbol{j}_{0}\times \boldsymbol{B}_{1})+\unicode[STIX]{x1D735}[\unicode[STIX]{x1D743}_{\bot }\boldsymbol{\cdot }\unicode[STIX]{x1D735}(n_{0}T_{i0}+n_{0}T_{e0})]$
vanishes, the linearized momentum equation (3.7) can be written as
$(\boldsymbol{j}_{0}\times \boldsymbol{B}_{1})+\unicode[STIX]{x1D735}[\unicode[STIX]{x1D743}_{\bot }\boldsymbol{\cdot }\unicode[STIX]{x1D735}(n_{0}T_{i0}+n_{0}T_{e0})]$
vanishes, the linearized momentum equation (3.7) can be written as
The transformation of the linearized drift-kinetic equation (3.10) to the variable
![]() $\hat{f}_{s}$
yields
$\hat{f}_{s}$
yields
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}\hat{f}_{s}}{\unicode[STIX]{x2202}t}+w_{\Vert }\boldsymbol{b}_{0}\boldsymbol{\cdot }\frac{\unicode[STIX]{x2202}\hat{f}_{s}}{\unicode[STIX]{x2202}\boldsymbol{x}}\Bigg|_{w_{\Vert },w_{\bot }}+\frac{w_{\bot }}{2}(\boldsymbol{b}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\ln B_{0})\left(w_{\Vert }\frac{\unicode[STIX]{x2202}\hat{f}_{s}}{\unicode[STIX]{x2202}w_{\bot }}-w_{\bot }\frac{\unicode[STIX]{x2202}\hat{f}_{s}}{\unicode[STIX]{x2202}w_{\Vert }}\right)\nonumber\\ \displaystyle & & \displaystyle \quad +\left[\frac{w_{\Vert }\hat{F}_{s\Vert }}{m_{s}n_{0}}+\frac{w_{\bot }^{2}}{2}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}_{1}+\left(w_{\Vert }^{2}-\frac{w_{\bot }^{2}}{2}\right)(\boldsymbol{b}_{0}\boldsymbol{b}_{0})\boldsymbol{ : }(\unicode[STIX]{x1D735}\boldsymbol{u}_{1})\right]\frac{m_{s}f_{Ms0}}{T_{s0}}=0,\quad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}\hat{f}_{s}}{\unicode[STIX]{x2202}t}+w_{\Vert }\boldsymbol{b}_{0}\boldsymbol{\cdot }\frac{\unicode[STIX]{x2202}\hat{f}_{s}}{\unicode[STIX]{x2202}\boldsymbol{x}}\Bigg|_{w_{\Vert },w_{\bot }}+\frac{w_{\bot }}{2}(\boldsymbol{b}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\ln B_{0})\left(w_{\Vert }\frac{\unicode[STIX]{x2202}\hat{f}_{s}}{\unicode[STIX]{x2202}w_{\bot }}-w_{\bot }\frac{\unicode[STIX]{x2202}\hat{f}_{s}}{\unicode[STIX]{x2202}w_{\Vert }}\right)\nonumber\\ \displaystyle & & \displaystyle \quad +\left[\frac{w_{\Vert }\hat{F}_{s\Vert }}{m_{s}n_{0}}+\frac{w_{\bot }^{2}}{2}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}_{1}+\left(w_{\Vert }^{2}-\frac{w_{\bot }^{2}}{2}\right)(\boldsymbol{b}_{0}\boldsymbol{b}_{0})\boldsymbol{ : }(\unicode[STIX]{x1D735}\boldsymbol{u}_{1})\right]\frac{m_{s}f_{Ms0}}{T_{s0}}=0,\quad\end{eqnarray}$$
subject to the initial-value constraints
![]() $\int \text{d}^{3}\boldsymbol{w}~\hat{f}_{s}(0)=-n_{0}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D743}(0)$
and
$\int \text{d}^{3}\boldsymbol{w}~\hat{f}_{s}(0)=-n_{0}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D743}(0)$
and
![]() $\int \text{d}^{3}\boldsymbol{w}~w_{\Vert }\hat{f}_{s}(0)=0$
. Now, equations (3.17)–(3.21) constitute the sought-after formulation of the linearized KMHD system that uses
$\int \text{d}^{3}\boldsymbol{w}~w_{\Vert }\hat{f}_{s}(0)=0$
. Now, equations (3.17)–(3.21) constitute the sought-after formulation of the linearized KMHD system that uses
![]() $(\unicode[STIX]{x1D743},\hat{f}_{s})$
as the primary dynamical variables.
$(\unicode[STIX]{x1D743},\hat{f}_{s})$
as the primary dynamical variables.
It is convenient to express
![]() $\hat{f}_{s}$
as the sum
$\hat{f}_{s}$
as the sum
![]() $\hat{f}_{s}^{even}+\hat{f}_{s}^{odd}$
of its even and odd parts with respect to
$\hat{f}_{s}^{even}+\hat{f}_{s}^{odd}$
of its even and odd parts with respect to
![]() $w_{\Vert }$
and split equation (3.21) into a system for
$w_{\Vert }$
and split equation (3.21) into a system for
![]() $\hat{f}_{s}^{even}$
and
$\hat{f}_{s}^{even}$
and
![]() $\hat{f}_{s}^{odd}$
. Also, it is useful to change the phase-space coordinates from
$\hat{f}_{s}^{odd}$
. Also, it is useful to change the phase-space coordinates from
![]() $(w_{\Vert },w_{\bot })$
to the coordinates
$(w_{\Vert },w_{\bot })$
to the coordinates
![]() $w=(w_{\Vert }^{2}+w_{\bot }^{2})^{1/2}$
and
$w=(w_{\Vert }^{2}+w_{\bot }^{2})^{1/2}$
and
![]() $\unicode[STIX]{x1D706}=w_{\bot }^{2}/(w^{2}B_{0})$
related to the kinetic energy and the magnetic moment. Denoting the phase-space parallel derivative at constant
$\unicode[STIX]{x1D706}=w_{\bot }^{2}/(w^{2}B_{0})$
related to the kinetic energy and the magnetic moment. Denoting the phase-space parallel derivative at constant
![]() $w$
and
$w$
and
![]() $\unicode[STIX]{x1D706}$
simply by
$\unicode[STIX]{x1D706}$
simply by
![]() $\boldsymbol{b}_{0}\boldsymbol{\cdot }\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\boldsymbol{x}$
and defining the
$\boldsymbol{b}_{0}\boldsymbol{\cdot }\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\boldsymbol{x}$
and defining the
![]() $Q$
operator
$Q$
operator
one obtains
Several useful identities involving the parallel derivative
![]() $\boldsymbol{b}_{0}\boldsymbol{\cdot }\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\boldsymbol{x}$
at constant
$\boldsymbol{b}_{0}\boldsymbol{\cdot }\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\boldsymbol{x}$
at constant
![]() $w$
and
$w$
and
![]() $\unicode[STIX]{x1D706}$
are listed in appendix A. By virtue of (A 4), the functional
$\unicode[STIX]{x1D706}$
are listed in appendix A. By virtue of (A 4), the functional
![]() $\hat{F}_{s\Vert }[\hat{f}_{s}]$
(3.17) reduces to
$\hat{F}_{s\Vert }[\hat{f}_{s}]$
(3.17) reduces to
Then, the
![]() $w_{\Vert }$
moment of (3.24) yields
$w_{\Vert }$
moment of (3.24) yields
and, using (A 3), the
![]() $1$
moment of (3.23) yields
$1$
moment of (3.23) yields
Thus, as expected from the general nonlinear result (2.9) and (2.10), the linearized drift-kinetic equation (3.21) also preserves the constraints
![]() $\int \text{d}^{3}\boldsymbol{w}~\hat{f}_{s}=-n_{0}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D743}$
and
$\int \text{d}^{3}\boldsymbol{w}~\hat{f}_{s}=-n_{0}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D743}$
and
![]() $\int \text{d}^{3}\boldsymbol{w}~w_{\Vert }\hat{f}_{s}=0$
at all times, once they are imposed on the initial condition.
$\int \text{d}^{3}\boldsymbol{w}~w_{\Vert }\hat{f}_{s}=0$
at all times, once they are imposed on the initial condition.
4 The potential energy functional
The first term of the nonlinearly conserved energy (2.12) is the kinetic energy of the macroscopic flow,
![]() $K=\int \text{d}^{3}\boldsymbol{x}~\unicode[STIX]{x1D70C}u^{2}/2$
. One may call the remainder a ‘potential energy
$K=\int \text{d}^{3}\boldsymbol{x}~\unicode[STIX]{x1D70C}u^{2}/2$
. One may call the remainder a ‘potential energy
![]() $W$
’ and state the energy conservation law as
$W$
’ and state the energy conservation law as
![]() $\text{d}(K+W)/\text{d}t=0$
. Within the context of small-amplitude perturbations about a static equilibrium, it can be shown that such
$\text{d}(K+W)/\text{d}t=0$
. Within the context of small-amplitude perturbations about a static equilibrium, it can be shown that such
![]() $W$
agrees with the physical definition of potential energy as the integral along a dynamic trajectory of the force times the infinitesimal displacement, the result of which is a functional of the final state independent of the details of the trajectory leading to it. For the considered small-amplitude perturbations about a static equilibrium, the kinetic energy is quadratic in the perturbation. Therefore, retaining quantities to the second perturbative order, one has
$W$
agrees with the physical definition of potential energy as the integral along a dynamic trajectory of the force times the infinitesimal displacement, the result of which is a functional of the final state independent of the details of the trajectory leading to it. For the considered small-amplitude perturbations about a static equilibrium, the kinetic energy is quadratic in the perturbation. Therefore, retaining quantities to the second perturbative order, one has
and
![]() $W=W_{0}+W_{1}+W_{2}$
, where
$W=W_{0}+W_{1}+W_{2}$
, where
Since
![]() $K$
is a second-order quantity, energy conservation implies that
$K$
is a second-order quantity, energy conservation implies that
![]() $W_{1}$
must be independent of time like
$W_{1}$
must be independent of time like
![]() $W_{0}$
. This is also a consequence of the equilibrium condition (3.3), as shown in appendix B. Moreover, instead of using (4.4) that involves the second-order perturbation of the magnetic field and the pressures,
$W_{0}$
. This is also a consequence of the equilibrium condition (3.3), as shown in appendix B. Moreover, instead of using (4.4) that involves the second-order perturbation of the magnetic field and the pressures,
![]() $W_{2}$
can be inferred from the energy conservation law. Thus, up to a constant
$W_{2}$
can be inferred from the energy conservation law. Thus, up to a constant
![]() $C$
independent of time, one can write
$C$
independent of time, one can write
![]() $W(t)=W_{0}+W_{1}+W_{2}(t)=C+\unicode[STIX]{x1D6FF}W(t)$
, with
$W(t)=W_{0}+W_{1}+W_{2}(t)=C+\unicode[STIX]{x1D6FF}W(t)$
, with
The linearized momentum equation (3.20) implies that
![]() $\unicode[STIX]{x1D6FF}W$
is the sum of a fluid term plus a kinetic term,
$\unicode[STIX]{x1D6FF}W$
is the sum of a fluid term plus a kinetic term,
![]() $\unicode[STIX]{x1D6FF}W=\unicode[STIX]{x1D6FF}W_{\bot }^{F}+\unicode[STIX]{x1D6FF}W^{K}$
, given by
$\unicode[STIX]{x1D6FF}W=\unicode[STIX]{x1D6FF}W_{\bot }^{F}+\unicode[STIX]{x1D6FF}W^{K}$
, given by
and
The ‘perpendicular ideal-MHD’ force operator
![]() $\boldsymbol{F}_{\bot }^{F}[\unicode[STIX]{x1D743}_{\bot }]$
is known to be self-adjoint (Bernstein et al.
Reference Bernstein, Frieman, Kruskal and Kurlsrud1957, Reference Bernstein, Frieman, Kruskal and Kurlsrud1958), therefore
$\boldsymbol{F}_{\bot }^{F}[\unicode[STIX]{x1D743}_{\bot }]$
is known to be self-adjoint (Bernstein et al.
Reference Bernstein, Frieman, Kruskal and Kurlsrud1957, Reference Bernstein, Frieman, Kruskal and Kurlsrud1958), therefore
and (4.6) can be integrated to express
![]() $\unicode[STIX]{x1D6FF}W_{\bot }^{F}$
as the functional of
$\unicode[STIX]{x1D6FF}W_{\bot }^{F}$
as the functional of
![]() $\unicode[STIX]{x1D743}_{\bot }$
$\unicode[STIX]{x1D743}_{\bot }$
It will be shown next that, for physical trajectories that are solutions of the linearized KMHD system, equation (4.7) can also be integrated to get an expression of
![]() $\unicode[STIX]{x1D6FF}W^{K}$
as a functional of
$\unicode[STIX]{x1D6FF}W^{K}$
as a functional of
![]() $\hat{f}_{s}$
only. Substituting (3.25) and (3.18) for
$\hat{f}_{s}$
only. Substituting (3.25) and (3.18) for
![]() $\hat{F}_{s\Vert }$
and
$\hat{F}_{s\Vert }$
and
![]() $\hat{F}_{s\bot }$
, integrating by parts and using the identity (A 3), one obtains
$\hat{F}_{s\bot }$
, integrating by parts and using the identity (A 3), one obtains
 $$\begin{eqnarray}\displaystyle & & \displaystyle \hspace{-10.00002pt}\frac{\text{d}\unicode[STIX]{x1D6FF}\,W^{K}}{\text{d}t}=\mathop{\sum }_{s=i,e}m_{s}\int \text{d}^{3}\boldsymbol{x}~\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left[\int \text{d}^{3}\boldsymbol{w}~\hat{f}_{s}^{even}\left(w_{\Vert }^{2}u_{1\Vert }\boldsymbol{b}_{0}+\frac{w_{\bot }^{2}}{2}\boldsymbol{u}_{1\bot }\right)\right]\nonumber\\ \displaystyle & & \displaystyle \hspace{-10.00002pt}\quad -\mathop{\sum }_{s=i,e}m_{s}\int \text{d}^{3}\boldsymbol{x}\int \text{d}^{3}\boldsymbol{w}\,\hat{f}_{s}^{even}\left[w_{\Vert }\boldsymbol{b}_{0}\boldsymbol{\cdot }\frac{\unicode[STIX]{x2202}(w_{\Vert }u_{1\Vert })}{\unicode[STIX]{x2202}\boldsymbol{x}}+\frac{w_{\bot }^{2}}{2}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}_{1\bot }-\left(w_{\Vert }^{2}-\frac{w_{\bot }^{2}}{2}\right)\boldsymbol{u}_{1\bot }\boldsymbol{\cdot }\unicode[STIX]{x1D73F}_{0}\right].\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \hspace{-10.00002pt}\frac{\text{d}\unicode[STIX]{x1D6FF}\,W^{K}}{\text{d}t}=\mathop{\sum }_{s=i,e}m_{s}\int \text{d}^{3}\boldsymbol{x}~\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left[\int \text{d}^{3}\boldsymbol{w}~\hat{f}_{s}^{even}\left(w_{\Vert }^{2}u_{1\Vert }\boldsymbol{b}_{0}+\frac{w_{\bot }^{2}}{2}\boldsymbol{u}_{1\bot }\right)\right]\nonumber\\ \displaystyle & & \displaystyle \hspace{-10.00002pt}\quad -\mathop{\sum }_{s=i,e}m_{s}\int \text{d}^{3}\boldsymbol{x}\int \text{d}^{3}\boldsymbol{w}\,\hat{f}_{s}^{even}\left[w_{\Vert }\boldsymbol{b}_{0}\boldsymbol{\cdot }\frac{\unicode[STIX]{x2202}(w_{\Vert }u_{1\Vert })}{\unicode[STIX]{x2202}\boldsymbol{x}}+\frac{w_{\bot }^{2}}{2}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}_{1\bot }-\left(w_{\Vert }^{2}-\frac{w_{\bot }^{2}}{2}\right)\boldsymbol{u}_{1\bot }\boldsymbol{\cdot }\unicode[STIX]{x1D73F}_{0}\right].\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
The first term of this expression vanishes by virtue of Green’s divergence theorem and the ideal wall boundary conditions, and the second term can be rewritten using the identity (A 5) and the definition (3.22). The result is
and, substituting the drift-kinetic evolution equation for
![]() $\hat{f}_{s}^{even}$
(3.23),
$\hat{f}_{s}^{even}$
(3.23),
Further integration by parts with a vanishing boundary term yields
and, substituting the drift-kinetic equation for
![]() $\hat{f}_{s}^{odd}$
(3.24),
$\hat{f}_{s}^{odd}$
(3.24),
Finally, recalling
![]() $\int \text{d}^{3}\boldsymbol{w}~w_{\Vert }\hat{f}_{s}^{odd}=0$
, this becomes
$\int \text{d}^{3}\boldsymbol{w}~w_{\Vert }\hat{f}_{s}^{odd}=0$
, this becomes
which can be integrated to arrive at the desired result
In summary, adding its fluid and kinetic terms, the KMHD incremental potential energy functional is
which is equivalent to the expression advanced in (1.1) since, for the equilibrium Maxwellian distribution functions,
![]() $\unicode[STIX]{x2202}f_{Ms0}/\unicode[STIX]{x2202}\unicode[STIX]{x1D700}=-f_{Ms0}/T_{s0}$
. The second-order energy conservation law becomes
$\unicode[STIX]{x2202}f_{Ms0}/\unicode[STIX]{x2202}\unicode[STIX]{x1D700}=-f_{Ms0}/T_{s0}$
. The second-order energy conservation law becomes
with the
![]() $K$
and
$K$
and
![]() $\unicode[STIX]{x1D6FF}W$
functionals given respectively by (4.1) and (4.17). The relationship between this energy conservation law and the quadratic form for normal modes derived in Ramos (Reference Ramos2015b
) is discussed in appendix C.
$\unicode[STIX]{x1D6FF}W$
functionals given respectively by (4.1) and (4.17). The relationship between this energy conservation law and the quadratic form for normal modes derived in Ramos (Reference Ramos2015b
) is discussed in appendix C.
The criterion that a positive definite
![]() $\unicode[STIX]{x1D6FF}W[\unicode[STIX]{x1D743},\hat{f}_{s}]$
is sufficient for KMHD stability is an immediate consequence of the second-order energy conservation law because then, for any dynamical evolution,
$\unicode[STIX]{x1D6FF}W[\unicode[STIX]{x1D743},\hat{f}_{s}]$
is sufficient for KMHD stability is an immediate consequence of the second-order energy conservation law because then, for any dynamical evolution,
and
![]() $K(t)$
would be a bounded function of time. The Cauchy–Schwarz inequality and the particle conservation constraint yield
$K(t)$
would be a bounded function of time. The Cauchy–Schwarz inequality and the particle conservation constraint yield
which implies the lower bound (1.2) for the KMHD incremental potential energy, hence the result that stability in isothermal ideal MHD is a sufficient condition for stability in KMHD.
5 The ‘force-times-displacement’ functional
The search for a necessary condition for KMHD stability will involve the ‘force-times-displacement’ functional
![]() $U$
defined in (1.6). From the linearized momentum equation (3.20) and the expression for the ‘perpendicular ideal-MHD’ potential energy (4.9), this functional is
$U$
defined in (1.6). From the linearized momentum equation (3.20) and the expression for the ‘perpendicular ideal-MHD’ potential energy (4.9), this functional is
![]() $U=\unicode[STIX]{x1D6FF}W_{\bot }^{F}+U^{K}$
with
$U=\unicode[STIX]{x1D6FF}W_{\bot }^{F}+U^{K}$
with
Unlike the fluid part of
![]() $U$
that equals
$U$
that equals
![]() $\unicode[STIX]{x1D6FF}W_{\bot }^{F}$
, and as a consequence of the lack of self-adjointness in the kinetic part of the force operator,
$\unicode[STIX]{x1D6FF}W_{\bot }^{F}$
, and as a consequence of the lack of self-adjointness in the kinetic part of the force operator,
![]() $U^{K}$
is in general different from
$U^{K}$
is in general different from
![]() $\unicode[STIX]{x1D6FF}W^{K}$
and an explicit evaluation of
$\unicode[STIX]{x1D6FF}W^{K}$
and an explicit evaluation of
![]() $U^{K}$
is necessary. This can be carried out along the lines of the evaluation of
$U^{K}$
is necessary. This can be carried out along the lines of the evaluation of
![]() $\unicode[STIX]{x1D6FF}W^{K}$
in the previous section. In complete analogy with the procedure followed to arrive at (4.11), one obtains
$\unicode[STIX]{x1D6FF}W^{K}$
in the previous section. In complete analogy with the procedure followed to arrive at (4.11), one obtains
The next step is to substitute the drift-kinetic evolution equation for
![]() $\hat{f}_{s}^{even}$
. However, what is needed here is not (3.23) but its integrated form with respect to time,
$\hat{f}_{s}^{even}$
. However, what is needed here is not (3.23) but its integrated form with respect to time,
After substituting this time-integrated form, (5.2) becomes
 $$\begin{eqnarray}\displaystyle U^{K} & = & \displaystyle \frac{1}{2}\mathop{\sum }_{s=i,e}\int \text{d}^{3}\boldsymbol{x}\int \text{d}^{3}\boldsymbol{w}\,\frac{T_{s0}}{f_{Ms0}}~\hat{f}_{s}^{even}\left[\hat{f}_{s}^{even}-\hat{f}_{s}^{even}(0)+w_{\Vert }\boldsymbol{b}_{0}\boldsymbol{\cdot }\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\boldsymbol{x}}\int _{0}^{t}\,\text{d}t^{\prime }\,\hat{f}_{s}^{odd}(t^{\prime })\right]\nonumber\\ \displaystyle & & \displaystyle -\,\frac{1}{2}\mathop{\sum }_{s=i,e}m_{s}\int \text{d}^{3}\boldsymbol{x}\int \text{d}^{3}\boldsymbol{w}~\hat{f}_{s}^{even}w^{2}Q[\unicode[STIX]{x1D743}(0)]\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle U^{K} & = & \displaystyle \frac{1}{2}\mathop{\sum }_{s=i,e}\int \text{d}^{3}\boldsymbol{x}\int \text{d}^{3}\boldsymbol{w}\,\frac{T_{s0}}{f_{Ms0}}~\hat{f}_{s}^{even}\left[\hat{f}_{s}^{even}-\hat{f}_{s}^{even}(0)+w_{\Vert }\boldsymbol{b}_{0}\boldsymbol{\cdot }\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\boldsymbol{x}}\int _{0}^{t}\,\text{d}t^{\prime }\,\hat{f}_{s}^{odd}(t^{\prime })\right]\nonumber\\ \displaystyle & & \displaystyle -\,\frac{1}{2}\mathop{\sum }_{s=i,e}m_{s}\int \text{d}^{3}\boldsymbol{x}\int \text{d}^{3}\boldsymbol{w}~\hat{f}_{s}^{even}w^{2}Q[\unicode[STIX]{x1D743}(0)]\end{eqnarray}$$
and, after integration by parts with a vanishing boundary term,
 $$\begin{eqnarray}\displaystyle U^{K} & = & \displaystyle \frac{1}{2}\mathop{\sum }_{s=i,e}\int \text{d}^{3}\boldsymbol{x}\int \text{d}^{3}\boldsymbol{w}~\frac{T_{s0}}{f_{Ms0}}\left[(\hat{f}_{s}^{even})^{2}-\left(w_{\Vert }\boldsymbol{b}_{0}\boldsymbol{\cdot }\frac{\unicode[STIX]{x2202}\hat{f}_{s}^{even}}{\unicode[STIX]{x2202}\boldsymbol{x}}\right)~\int _{0}^{t}\,\text{d}t^{\prime }\,\hat{f}_{s}^{odd}(t^{\prime })\right]\nonumber\\ \displaystyle & & \displaystyle -\,\frac{1}{2}\mathop{\sum }_{s=i,e}m_{s}\int \text{d}^{3}\boldsymbol{x}\int \text{d}^{3}\boldsymbol{w}~\hat{f}_{s}^{even}\left\{\frac{T_{s0}}{m_{s}f_{Ms0}}\hat{f}_{s}^{even}(0)+w^{2}Q[\unicode[STIX]{x1D743}(0)]\right\}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle U^{K} & = & \displaystyle \frac{1}{2}\mathop{\sum }_{s=i,e}\int \text{d}^{3}\boldsymbol{x}\int \text{d}^{3}\boldsymbol{w}~\frac{T_{s0}}{f_{Ms0}}\left[(\hat{f}_{s}^{even})^{2}-\left(w_{\Vert }\boldsymbol{b}_{0}\boldsymbol{\cdot }\frac{\unicode[STIX]{x2202}\hat{f}_{s}^{even}}{\unicode[STIX]{x2202}\boldsymbol{x}}\right)~\int _{0}^{t}\,\text{d}t^{\prime }\,\hat{f}_{s}^{odd}(t^{\prime })\right]\nonumber\\ \displaystyle & & \displaystyle -\,\frac{1}{2}\mathop{\sum }_{s=i,e}m_{s}\int \text{d}^{3}\boldsymbol{x}\int \text{d}^{3}\boldsymbol{w}~\hat{f}_{s}^{even}\left\{\frac{T_{s0}}{m_{s}f_{Ms0}}\hat{f}_{s}^{even}(0)+w^{2}Q[\unicode[STIX]{x1D743}(0)]\right\}.\end{eqnarray}$$
Finally, substituting the drift-kinetic equation for
![]() $\hat{f}_{s}^{odd}$
(3.24) and using again
$\hat{f}_{s}^{odd}$
(3.24) and using again
![]() $\int \text{d}^{3}\boldsymbol{w}\,w_{\Vert }\hat{f}_{s}^{odd}=0$
,
$\int \text{d}^{3}\boldsymbol{w}\,w_{\Vert }\hat{f}_{s}^{odd}=0$
,
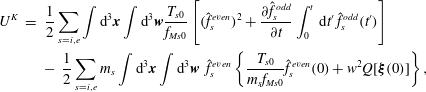 $$\begin{eqnarray}\displaystyle U^{K} & = & \displaystyle \frac{1}{2}\mathop{\sum }_{s=i,e}\int \text{d}^{3}\boldsymbol{x}\int \text{d}^{3}\boldsymbol{w}\frac{T_{s0}}{f_{Ms0}}\left[(\hat{f}_{s}^{even})^{2}+\frac{\unicode[STIX]{x2202}\hat{f}_{s}^{odd}}{\unicode[STIX]{x2202}t}\int _{0}^{t}\,\text{d}t^{\prime }\,\hat{f}_{s}^{odd}(t^{\prime })\right]\nonumber\\ \displaystyle & & \displaystyle -~\frac{1}{2}\mathop{\sum }_{s=i,e}m_{s}\int \text{d}^{3}\boldsymbol{x}\int \text{d}^{3}\boldsymbol{w}~\hat{f}_{s}^{even}\left\{\frac{T_{s0}}{m_{s}f_{Ms0}}\hat{f}_{s}^{even}(0)+w^{2}Q[\unicode[STIX]{x1D743}(0)]\right\},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle U^{K} & = & \displaystyle \frac{1}{2}\mathop{\sum }_{s=i,e}\int \text{d}^{3}\boldsymbol{x}\int \text{d}^{3}\boldsymbol{w}\frac{T_{s0}}{f_{Ms0}}\left[(\hat{f}_{s}^{even})^{2}+\frac{\unicode[STIX]{x2202}\hat{f}_{s}^{odd}}{\unicode[STIX]{x2202}t}\int _{0}^{t}\,\text{d}t^{\prime }\,\hat{f}_{s}^{odd}(t^{\prime })\right]\nonumber\\ \displaystyle & & \displaystyle -~\frac{1}{2}\mathop{\sum }_{s=i,e}m_{s}\int \text{d}^{3}\boldsymbol{x}\int \text{d}^{3}\boldsymbol{w}~\hat{f}_{s}^{even}\left\{\frac{T_{s0}}{m_{s}f_{Ms0}}\hat{f}_{s}^{even}(0)+w^{2}Q[\unicode[STIX]{x1D743}(0)]\right\},\end{eqnarray}$$
hence
 $$\begin{eqnarray}\displaystyle U^{K} & = & \displaystyle \unicode[STIX]{x1D6FF}W^{K}-\frac{1}{2}\mathop{\sum }_{s=i,e}\int \text{d}^{3}\boldsymbol{x}\int \text{d}^{3}\boldsymbol{w}\,\frac{T_{s0}}{f_{Ms0}}\left[(\hat{f}_{s}^{odd})^{2}-\frac{\unicode[STIX]{x2202}\hat{f}_{s}^{odd}}{\unicode[STIX]{x2202}t}\,\int _{0}^{t}\,\text{d}t^{\prime }\,\hat{f}_{s}^{odd}(t^{\prime })\right]\nonumber\\ \displaystyle & & \displaystyle -\,\frac{1}{2}\mathop{\sum }_{s=i,e}m_{s}\int \text{d}^{3}\boldsymbol{x}\int \text{d}^{3}\boldsymbol{w}~\hat{f}_{s}^{even}\left\{\frac{T_{s0}}{m_{s}f_{Ms0}}\hat{f}_{s}^{even}(0)+w^{2}Q[\unicode[STIX]{x1D743}(0)]\right\}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle U^{K} & = & \displaystyle \unicode[STIX]{x1D6FF}W^{K}-\frac{1}{2}\mathop{\sum }_{s=i,e}\int \text{d}^{3}\boldsymbol{x}\int \text{d}^{3}\boldsymbol{w}\,\frac{T_{s0}}{f_{Ms0}}\left[(\hat{f}_{s}^{odd})^{2}-\frac{\unicode[STIX]{x2202}\hat{f}_{s}^{odd}}{\unicode[STIX]{x2202}t}\,\int _{0}^{t}\,\text{d}t^{\prime }\,\hat{f}_{s}^{odd}(t^{\prime })\right]\nonumber\\ \displaystyle & & \displaystyle -\,\frac{1}{2}\mathop{\sum }_{s=i,e}m_{s}\int \text{d}^{3}\boldsymbol{x}\int \text{d}^{3}\boldsymbol{w}~\hat{f}_{s}^{even}\left\{\frac{T_{s0}}{m_{s}f_{Ms0}}\hat{f}_{s}^{even}(0)+w^{2}Q[\unicode[STIX]{x1D743}(0)]\right\}.\end{eqnarray}$$
This result provides an explicit formula for the difference
![]() $\unicode[STIX]{x1D6FF}W-U$
which, due to the lack of KMHD self-adjointness, is not zero in general, as anticipated.
$\unicode[STIX]{x1D6FF}W-U$
which, due to the lack of KMHD self-adjointness, is not zero in general, as anticipated.
A special class of perturbations make the difference
![]() $\unicode[STIX]{x1D6FF}W-U$
particularly simple, albeit not zero. They are those for which the initial value of the distribution functions is
$\unicode[STIX]{x1D6FF}W-U$
particularly simple, albeit not zero. They are those for which the initial value of the distribution functions is
that satisfies the constraints
![]() $\int \text{d}^{3}\boldsymbol{w}~\hat{f}_{s}(0)=-n_{0}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D743}(0)$
and
$\int \text{d}^{3}\boldsymbol{w}~\hat{f}_{s}(0)=-n_{0}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D743}(0)$
and
![]() $\int \text{d}^{3}\boldsymbol{w}~w_{\Vert }\hat{f}_{s}(0)=0$
, and makes the last term of (5.7) vanish. For this special class, the ‘force-times-displacement’ functional reduces to
$\int \text{d}^{3}\boldsymbol{w}~w_{\Vert }\hat{f}_{s}(0)=0$
, and makes the last term of (5.7) vanish. For this special class, the ‘force-times-displacement’ functional reduces to
![]() $U=\unicode[STIX]{x1D6FF}W-R/2$
, with
$U=\unicode[STIX]{x1D6FF}W-R/2$
, with
and the initial value of the kinetic term of the potential energy functional is
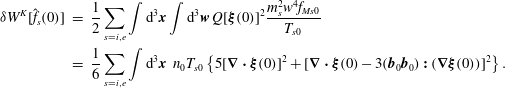 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}W^{K}[\hat{f}_{s}(0)] & = & \displaystyle \frac{1}{2}\mathop{\sum }_{s=i,e}\int \text{d}^{3}\boldsymbol{x}\int \text{d}^{3}\boldsymbol{w}\,Q[\unicode[STIX]{x1D743}(0)]^{2}\frac{m_{s}^{2}w^{4}f_{Ms0}}{T_{s0}}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{6}\mathop{\sum }_{s=i,e}\int \text{d}^{3}\boldsymbol{x}~n_{0}T_{s0}\left\{5[\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D743}(0)]^{2}+[\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D743}(0)-3(\boldsymbol{b}_{0}\boldsymbol{b}_{0})\boldsymbol{ : }(\unicode[STIX]{x1D735}\unicode[STIX]{x1D743}(0))]^{2}\right\}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}W^{K}[\hat{f}_{s}(0)] & = & \displaystyle \frac{1}{2}\mathop{\sum }_{s=i,e}\int \text{d}^{3}\boldsymbol{x}\int \text{d}^{3}\boldsymbol{w}\,Q[\unicode[STIX]{x1D743}(0)]^{2}\frac{m_{s}^{2}w^{4}f_{Ms0}}{T_{s0}}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{6}\mathop{\sum }_{s=i,e}\int \text{d}^{3}\boldsymbol{x}~n_{0}T_{s0}\left\{5[\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D743}(0)]^{2}+[\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D743}(0)-3(\boldsymbol{b}_{0}\boldsymbol{b}_{0})\boldsymbol{ : }(\unicode[STIX]{x1D735}\unicode[STIX]{x1D743}(0))]^{2}\right\}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
Thus, for this class of perturbations, the initial value of the KMHD incremental potential energy is equal to that of the double-adiabatic fluid theory (Chew et al. Reference Chew, Goldberger and Low1956; Bernstein et al. Reference Bernstein, Frieman, Kruskal and Kurlsrud1958),
where
![]() $\unicode[STIX]{x1D6FF}W^{DA}[\unicode[STIX]{x1D743}(0)]$
includes the contribution of the parallel displacement
$\unicode[STIX]{x1D6FF}W^{DA}[\unicode[STIX]{x1D743}(0)]$
includes the contribution of the parallel displacement
![]() $\unicode[STIX]{x1D709}_{\Vert }(0)$
. This choice of initial condition will be used next in the investigation of a necessary condition for KMHD stability.
$\unicode[STIX]{x1D709}_{\Vert }(0)$
. This choice of initial condition will be used next in the investigation of a necessary condition for KMHD stability.
6 Necessary condition for KMHD stability
The energy principle provides a necessary and sufficient condition for stability in the double-adiabatic fluid theory (Bernstein et al.
Reference Bernstein, Frieman, Kruskal and Kurlsrud1958; Laval et al.
Reference Laval, Mercier and Pellat1965). This means that, if an equilibrium is unstable in the double-adiabatic theory, a trial fluid displacement
![]() $\unicode[STIX]{x1D743}^{tr}$
exists such that
$\unicode[STIX]{x1D743}^{tr}$
exists such that
![]() $\unicode[STIX]{x1D6FF}W^{DA}[\unicode[STIX]{x1D743}^{tr}]<0$
. Such a trial fluid displacement may have a non-zero parallel component. Consider then the following initial condition for the KMHD system:
$\unicode[STIX]{x1D6FF}W^{DA}[\unicode[STIX]{x1D743}^{tr}]<0$
. Such a trial fluid displacement may have a non-zero parallel component. Consider then the following initial condition for the KMHD system:
This perturbation belongs to the special class discussed in the previous section, therefore the initial value of the KMHD incremental potential energy is
and the initial value of the kinetic energy is
![]() $K(0)=0$
. Defining the time-dependent fluid displacement norm,
$K(0)=0$
. Defining the time-dependent fluid displacement norm,
its time derivatives are
The considered perturbation belongs to the class for which
![]() $U(t)=\unicode[STIX]{x1D6FF}W(t)-R(t)/2$
and energy conservation implies
$U(t)=\unicode[STIX]{x1D6FF}W(t)-R(t)/2$
and energy conservation implies
![]() $\unicode[STIX]{x1D6FF}W(t)+K(t)=\unicode[STIX]{x1D6FF}W(0)+K(0)=\unicode[STIX]{x1D6FF}W(0)$
, hence
$\unicode[STIX]{x1D6FF}W(t)+K(t)=\unicode[STIX]{x1D6FF}W(0)+K(0)=\unicode[STIX]{x1D6FF}W(0)$
, hence
with
![]() $R(t)$
as defined in (5.9). The initial condition
$R(t)$
as defined in (5.9). The initial condition
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D743}(0)/\unicode[STIX]{x2202}t=0$
implies
$\unicode[STIX]{x2202}\unicode[STIX]{x1D743}(0)/\unicode[STIX]{x2202}t=0$
implies
![]() $\text{d}N\,(0)/\text{d}t=0$
. Then, after time integration,
$\text{d}N\,(0)/\text{d}t=0$
. Then, after time integration,
with
A general lower bound for
![]() $N_{R}(t)$
can be derived. Calling
$N_{R}(t)$
can be derived. Calling
one has
Simple integration by parts yields
 $$\begin{eqnarray}\displaystyle \int _{0}^{t}\,\text{d}t^{\prime }\int _{0}^{t^{\prime }}\,\text{d}t^{\prime \prime }\,g_{s}(t^{\prime \prime }) & = & \displaystyle 2\int _{0}^{t}\,\text{d}t^{\prime }\int _{0}^{t^{\prime }}\,\text{d}t^{\prime \prime }\,[\hat{f}_{s}^{odd}(t^{\prime \prime })]^{2}-\int _{0}^{t}\,\text{d}t^{\prime }\,\hat{f}_{s}^{odd}(t^{\prime })\int _{0}^{t^{\prime }}\,\text{d}t^{\prime \prime }\,\hat{f}_{s}^{odd}(t^{\prime \prime })\nonumber\\ \displaystyle & = & \displaystyle 2\int _{0}^{t}\,\text{d}t^{\prime }\,(t-t^{\prime })[\hat{f}_{s}^{odd}(t^{\prime })]^{2}-\frac{1}{2}\left[\int _{0}^{t}\,\text{d}t^{\prime }\,\hat{f}_{s}^{odd}(t^{\prime })\right]^{2}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{0}^{t}\,\text{d}t^{\prime }\int _{0}^{t^{\prime }}\,\text{d}t^{\prime \prime }\,g_{s}(t^{\prime \prime }) & = & \displaystyle 2\int _{0}^{t}\,\text{d}t^{\prime }\int _{0}^{t^{\prime }}\,\text{d}t^{\prime \prime }\,[\hat{f}_{s}^{odd}(t^{\prime \prime })]^{2}-\int _{0}^{t}\,\text{d}t^{\prime }\,\hat{f}_{s}^{odd}(t^{\prime })\int _{0}^{t^{\prime }}\,\text{d}t^{\prime \prime }\,\hat{f}_{s}^{odd}(t^{\prime \prime })\nonumber\\ \displaystyle & = & \displaystyle 2\int _{0}^{t}\,\text{d}t^{\prime }\,(t-t^{\prime })[\hat{f}_{s}^{odd}(t^{\prime })]^{2}-\frac{1}{2}\left[\int _{0}^{t}\,\text{d}t^{\prime }\,\hat{f}_{s}^{odd}(t^{\prime })\right]^{2}\end{eqnarray}$$
and, by virtue of the Cauchy–Schwarz inequality
one obtains
This yields the lower bound for
![]() $N_{R}(t)$
$N_{R}(t)$
where
Since
![]() $K(t)\geqslant 0$
, this implies also the lower bound for
$K(t)\geqslant 0$
, this implies also the lower bound for
![]() $N(t)$
$N(t)$
The considered perturbation has
![]() $\unicode[STIX]{x1D6FF}W(0)=\unicode[STIX]{x1D6FF}W^{DA}(0)<0$
, so
$\unicode[STIX]{x1D6FF}W(0)=\unicode[STIX]{x1D6FF}W^{DA}(0)<0$
, so
![]() $-\unicode[STIX]{x1D6FF}W(0)t^{2}$
grows in time without bound. If the equilibrium under consideration is KMHD stable, the norm
$-\unicode[STIX]{x1D6FF}W(0)t^{2}$
grows in time without bound. If the equilibrium under consideration is KMHD stable, the norm
![]() $N(t)$
must be a bounded function of time and (6.17) implies that this can only happen if
$N(t)$
must be a bounded function of time and (6.17) implies that this can only happen if
![]() $\unicode[STIX]{x1D6F7}_{s}(t)$
becomes negative and not negligible as
$\unicode[STIX]{x1D6F7}_{s}(t)$
becomes negative and not negligible as
![]() $t\rightarrow \infty$
. Therefore, if it were possible to prove that for any KMHD-stable equilibrium the long-time behaviour of
$t\rightarrow \infty$
. Therefore, if it were possible to prove that for any KMHD-stable equilibrium the long-time behaviour of
![]() $\hat{f}_{s}^{odd}(t)$
is such that, as
$\hat{f}_{s}^{odd}(t)$
is such that, as
![]() $t\rightarrow \infty$
,
$t\rightarrow \infty$
,
![]() $\unicode[STIX]{x1D6F7}_{s}(t)$
either stays non-negative or tends to zero, the double-adiabatic unstable equilibrium under consideration must be KMHD unstable and that would complete the proof that stability according to the double-adiabatic fluid theory is a necessary condition for KMHD stability. The KMHD theory is time reversible and dissipationless, but includes the possible Landau damping of initial-value solutions as a consequence of the mixing of the phases of different spectral components. It would then seem reasonable to expect that, for perturbations about a KMHD-stable equilibrium, the long-time behaviour of
$\unicode[STIX]{x1D6F7}_{s}(t)$
either stays non-negative or tends to zero, the double-adiabatic unstable equilibrium under consideration must be KMHD unstable and that would complete the proof that stability according to the double-adiabatic fluid theory is a necessary condition for KMHD stability. The KMHD theory is time reversible and dissipationless, but includes the possible Landau damping of initial-value solutions as a consequence of the mixing of the phases of different spectral components. It would then seem reasonable to expect that, for perturbations about a KMHD-stable equilibrium, the long-time behaviour of
![]() $[\hat{f}_{s}^{odd}(t)]^{2}$
is such that it either tends to a time-independent limit or oscillates about some time-independent average, with deviations of finite amplitude evenly distributed above and below the average. If one characterizes such a behaviour by the condition that the limit
$[\hat{f}_{s}^{odd}(t)]^{2}$
is such that it either tends to a time-independent limit or oscillates about some time-independent average, with deviations of finite amplitude evenly distributed above and below the average. If one characterizes such a behaviour by the condition that the limit
exists and
![]() $0\leqslant [\hat{f}_{s}^{odd}(t\rightarrow \infty )]^{2}\leqslant 2(\hat{f}_{\infty s}^{odd})^{2}$
, then the lemma given in appendix D guarantees that, as
$0\leqslant [\hat{f}_{s}^{odd}(t\rightarrow \infty )]^{2}\leqslant 2(\hat{f}_{\infty s}^{odd})^{2}$
, then the lemma given in appendix D guarantees that, as
![]() $t\rightarrow \infty$
,
$t\rightarrow \infty$
,
![]() $\unicode[STIX]{x1D6F7}_{s}(t)$
either stays non-negative or tends to zero. Actually, appendix D shows that this is guaranteed by the weaker condition that
$\unicode[STIX]{x1D6F7}_{s}(t)$
either stays non-negative or tends to zero. Actually, appendix D shows that this is guaranteed by the weaker condition that
![]() $\hat{f}_{s}^{odd}(t)$
be bounded and, for sufficiently large values of
$\hat{f}_{s}^{odd}(t)$
be bounded and, for sufficiently large values of
![]() $t$
,
$t$
,
regardless of the existence of the limit (6.18). The validity of this condition means that linear KMHD would not allow the possibility that, after a sufficiently long time has elapsed,
![]() $[\hat{f}_{s}^{odd}(t)]^{2}$
underwent short bursts during which it would reach large values relative to the prevalent, time-averaged ones. Such bursty time variation, reminiscent of the so-called ‘rogue wave’ phenomenon, is precluded by the condition (6.19). In conclusion, if the long-time behaviour of oscillations about a KMHD-stable equilibrium satisfies the condition (6.19), it has been demonstrated that stability in the double-adiabatic fluid theory would be a necessary condition for stability in KMHD.
$[\hat{f}_{s}^{odd}(t)]^{2}$
underwent short bursts during which it would reach large values relative to the prevalent, time-averaged ones. Such bursty time variation, reminiscent of the so-called ‘rogue wave’ phenomenon, is precluded by the condition (6.19). In conclusion, if the long-time behaviour of oscillations about a KMHD-stable equilibrium satisfies the condition (6.19), it has been demonstrated that stability in the double-adiabatic fluid theory would be a necessary condition for stability in KMHD.
The form of the initial condition for the distribution functions (6.2) used here is related to that of the zero-frequency normal modes, although it is not the same. The distribution functions of the zero-frequency normal mode solution of Rosenbluth & Rostoker (Reference Rosenbluth and Rostoker1959) are given in terms of the corresponding fluid displacement eigenvector
![]() $\unicode[STIX]{x1D743}$
by
$\unicode[STIX]{x1D743}$
by
where
![]() $\langle \cdots \rangle _{\unicode[STIX]{x1D70F}}$
is the transit-bounce average
$\langle \cdots \rangle _{\unicode[STIX]{x1D70F}}$
is the transit-bounce average
These contour integrals are taken along one period of the particle phase-space trajectories that follow the magnetic field lines at constant
![]() $w$
and
$w$
and
![]() $\unicode[STIX]{x1D706}$
, under the assumption that such orbits are periodic (trapped particles or passing particles on closed magnetic loops) or nearly periodic (passing particles on ergodic magnetic lines, with the argument that such lines approximately close on themselves). As a consequence of the identity (A 5), the contribution of
$\unicode[STIX]{x1D706}$
, under the assumption that such orbits are periodic (trapped particles or passing particles on closed magnetic loops) or nearly periodic (passing particles on ergodic magnetic lines, with the argument that such lines approximately close on themselves). As a consequence of the identity (A 5), the contribution of
![]() $\unicode[STIX]{x1D709}_{\Vert }$
to
$\unicode[STIX]{x1D709}_{\Vert }$
to
![]() $\langle Q[\unicode[STIX]{x1D743}]\rangle _{\unicode[STIX]{x1D70F}}$
vanishes, so the zero-frequency normal-mode distribution functions depend only on the perpendicular displacement,
$\langle Q[\unicode[STIX]{x1D743}]\rangle _{\unicode[STIX]{x1D70F}}$
vanishes, so the zero-frequency normal-mode distribution functions depend only on the perpendicular displacement,
![]() $\langle Q[\unicode[STIX]{x1D743}]\rangle _{\unicode[STIX]{x1D70F}}=\langle Q[\unicode[STIX]{x1D743}_{\bot }]\rangle _{\unicode[STIX]{x1D70F}}$
. The classic comparison theorem (1.5) (Kruskal & Oberman Reference Kruskal and Oberman1958; Rosenbluth & Rostoker Reference Rosenbluth and Rostoker1959) applies to a generic perpendicular displacement
$\langle Q[\unicode[STIX]{x1D743}]\rangle _{\unicode[STIX]{x1D70F}}=\langle Q[\unicode[STIX]{x1D743}_{\bot }]\rangle _{\unicode[STIX]{x1D70F}}$
. The classic comparison theorem (1.5) (Kruskal & Oberman Reference Kruskal and Oberman1958; Rosenbluth & Rostoker Reference Rosenbluth and Rostoker1959) applies to a generic perpendicular displacement
![]() $\unicode[STIX]{x1D743}_{\bot }$
and can be stated as
$\unicode[STIX]{x1D743}_{\bot }$
and can be stated as
but, in order to prove the inequality, one needs the periodic or nearly periodic orbit assumption. The present study uses the initial distribution functions
![]() $\hat{f}_{s}(0)=-Q[\unicode[STIX]{x1D743}(0)]~m_{s}w^{2}T_{s0}^{-1}f_{Ms0}$
with an initial
$\hat{f}_{s}(0)=-Q[\unicode[STIX]{x1D743}(0)]~m_{s}w^{2}T_{s0}^{-1}f_{Ms0}$
with an initial
![]() $\unicode[STIX]{x1D743}(0)$
that can have a non-zero parallel component and makes
$\unicode[STIX]{x1D743}(0)$
that can have a non-zero parallel component and makes
![]() $\unicode[STIX]{x1D6FF}W^{DA}[\unicode[STIX]{x1D743}(0)]$
negative. Therefore, the initial KMHD incremental potential energy is known to be negative irrespective of orbit periodicity considerations and the analysis is equally valid for non-periodic passing particles. The argument of near periodicity on ergodic magnetic lines is not needed here. Besides, the present study looked for a proof of instability by actually demonstrating that the chosen initial condition would result in an unbounded growth of the perturbation, not just that the incremental potential energy would become negative.
$\unicode[STIX]{x1D6FF}W^{DA}[\unicode[STIX]{x1D743}(0)]$
negative. Therefore, the initial KMHD incremental potential energy is known to be negative irrespective of orbit periodicity considerations and the analysis is equally valid for non-periodic passing particles. The argument of near periodicity on ergodic magnetic lines is not needed here. Besides, the present study looked for a proof of instability by actually demonstrating that the chosen initial condition would result in an unbounded growth of the perturbation, not just that the incremental potential energy would become negative.
7 Summary
This work has investigated the linear stability properties of KMHD from the initial-value point of view. The analysis has been based on the formulation introduced in Ramos (Reference Ramos2015a ,Reference Ramos b ) to study the KMHD normal modes. This formulation uses drift-kinetic equations in the reference frame of the complete macroscopic fluid velocity, eliminates the electric field and guarantees that the quasineutrality condition is satisfied automatically at all times if it is satisfied by the initial condition. Moreover, it does not solve the kinetic equations by integration along characteristics and does not require that the particle orbits be periodic or nearly periodic. Such a formulation is unconventional compared with more traditional approaches, so the article was written as a self-contained presentation and §§ 2 and 3 were devoted to the detailed introduction of the adopted KMHD description, both in its nonlinear and linearized versions. The derivation of the KMHD potential energy functional within this framework was then given in § 4. The main new results are in §§ 5 and 6. Section 5 evaluated explicitly the ‘force-times-displacement’ functional, emphasizing the fact that it is different from the potential energy in KMHD, a result that can be taken as an independent proof that the KMHD force operator is not self-adjoint. Finally, § 6 looked for a proof that stability according to the double-adiabatic fluid theory is a necessary condition for KMHD stability by studying the possibility that, if an isotropic-pressure static equilibrium is double-adiabatic unstable, an appropriately chosen KMHD initial condition would grow in time without bound. This was demonstrated with the proviso that the long-time behaviour of oscillations about KMHD-stable equilibria satisfies the condition (6.19).
The two results regarding KMHD stability that this work has arrived at, namely that stability in isothermal ideal MHD is sufficient for stability in KMHD and that, provided the condition (6.19) holds, stability in the Chew–Goldberger–Low double-adiabatic theory including the variation of the parallel fluid displacement would be necessary for stability in KMHD, do not rely on the classic comparison theorems of Kruskal & Oberman (Reference Kruskal and Oberman1958), Rosenbluth & Rostoker (Reference Rosenbluth and Rostoker1959). They do not require the periodicity or near periodicity of particle orbits and are equally valid for non-periodic passing particles. In addition, the necessary condition analysis does not require the self-adjointness of the force operator or the existence of a complete basis of normal modes, which are properties that have not been proved for KMHD. However, the necessary condition result hinges on the validity of the hypothesis (6.19) on the long-time behaviour of oscillations about KMHD-stable equilibria. This is a reasonable assumption but remains a yet to be proved mathematical conjecture, which underscores the difficulty of finding a completely rigorous proof of a necessary condition for KMHD stability.
Acknowledgements
The author thanks A. Cerfon, J. Freidberg and J. Hastie for their motivation and helpful discussions. This work was sponsored by the U.S. Department of Energy under grants nos DEFG02-91ER54109 and DEFC02-08ER54969 at the Massachusetts Institute of Technology and as part of the author’s participation in the Center for Extended MHD Modeling (CEMM).
Appendix A. Some identities involving the phase-space parallel derivative at constant magnetic moment
When taking the phase-space parallel derivative
![]() $\boldsymbol{b}_{0}\boldsymbol{\cdot }\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\boldsymbol{x}$
at constant
$\boldsymbol{b}_{0}\boldsymbol{\cdot }\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\boldsymbol{x}$
at constant
![]() $w$
and
$w$
and
![]() $\unicode[STIX]{x1D706}$
,
$\unicode[STIX]{x1D706}$
,
![]() $w_{\bot }$
and
$w_{\bot }$
and
![]() $w_{\Vert }$
must be considered as the functions
$w_{\Vert }$
must be considered as the functions
Also, the Jacobian of the coordinate transformation from
![]() $(w_{\bot },w_{\Vert })$
to
$(w_{\bot },w_{\Vert })$
to
![]() $(w,\unicode[STIX]{x1D706})$
is
$(w,\unicode[STIX]{x1D706})$
is
Then, it is a simple exercise to verify the following identities: If
![]() $f^{odd}$
is a continuous function of phase space that is odd with respect to
$f^{odd}$
is a continuous function of phase space that is odd with respect to
![]() $w_{\Vert }$
and therefore vanishes at
$w_{\Vert }$
and therefore vanishes at
![]() $w_{\Vert }=0$
,
$w_{\Vert }=0$
,
If
![]() $f^{even}$
is a function of phase space that is even with respect to
$f^{even}$
is a function of phase space that is even with respect to
![]() $w_{\Vert }$
,
$w_{\Vert }$
,
If
![]() $\unicode[STIX]{x1D702}_{\Vert }\boldsymbol{b}_{0}$
is a parallel vector function of
$\unicode[STIX]{x1D702}_{\Vert }\boldsymbol{b}_{0}$
is a parallel vector function of
![]() $\boldsymbol{x}$
,
$\boldsymbol{x}$
,
Appendix B. The first-order potential energy
Energy conservation implies that the first-order potential energy
![]() $W_{1}$
must be independent of time. Here it is shown how this is also a consequence of the equilibrium force balance condition. Substituting (3.12) for
$W_{1}$
must be independent of time. Here it is shown how this is also a consequence of the equilibrium force balance condition. Substituting (3.12) for
![]() $\boldsymbol{B}_{1}$
in (4.3) and differentiating with respect to time,
$\boldsymbol{B}_{1}$
in (4.3) and differentiating with respect to time,
and, using vector identities along with (3.9), (3.14),
From the drift-kinetic equation for
![]() $\hat{f}_{s}^{even}$
(3.23) and the identity (A 3), one gets
$\hat{f}_{s}^{even}$
(3.23) and the identity (A 3), one gets
 $$\begin{eqnarray}\displaystyle -\frac{m_{s}}{2}\int \text{d}^{3}\boldsymbol{w}\,w^{2}\frac{\unicode[STIX]{x2202}\hat{f}_{s}^{even}}{\unicode[STIX]{x2202}t} & = & \displaystyle \frac{m_{s}}{2}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left[\left(\int \text{d}^{3}\boldsymbol{w}\,w_{\Vert }w^{2}\hat{f}_{s}^{odd}\right)\boldsymbol{b}_{0}\right]+\frac{m_{s}^{2}}{2}\int \text{d}^{3}\boldsymbol{w}~\frac{w^{4}f_{Ms0}}{T_{s0}}Q[\boldsymbol{u}_{1}]\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }(q_{s\Vert 1}\boldsymbol{b}_{0})+\frac{5n_{0}T_{s0}}{2}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}_{1}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle -\frac{m_{s}}{2}\int \text{d}^{3}\boldsymbol{w}\,w^{2}\frac{\unicode[STIX]{x2202}\hat{f}_{s}^{even}}{\unicode[STIX]{x2202}t} & = & \displaystyle \frac{m_{s}}{2}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left[\left(\int \text{d}^{3}\boldsymbol{w}\,w_{\Vert }w^{2}\hat{f}_{s}^{odd}\right)\boldsymbol{b}_{0}\right]+\frac{m_{s}^{2}}{2}\int \text{d}^{3}\boldsymbol{w}~\frac{w^{4}f_{Ms0}}{T_{s0}}Q[\boldsymbol{u}_{1}]\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }(q_{s\Vert 1}\boldsymbol{b}_{0})+\frac{5n_{0}T_{s0}}{2}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}_{1}\end{eqnarray}$$
so, bringing this result to (B 2), integrating by parts and using Green’s divergence theorem with a vanishing boundary term,
which is equal to zero by virtue of the equilibrium relation (3.3).
Appendix C. Relationship between the second-order energy conservation law and the normal-mode quadratic form
KMHD normal modes are
![]() $(\unicode[STIX]{x1D743},\hat{f}_{s})$
solutions of the linearized KMHD system that can be factorized as the product of a time-dependent exponential,
$(\unicode[STIX]{x1D743},\hat{f}_{s})$
solutions of the linearized KMHD system that can be factorized as the product of a time-dependent exponential,
![]() $\exp (-i\unicode[STIX]{x1D714}t)$
, and a time-independent eigenfunction which may now be complex. For the proper normal modes that are square-integrable functions of
$\exp (-i\unicode[STIX]{x1D714}t)$
, and a time-independent eigenfunction which may now be complex. For the proper normal modes that are square-integrable functions of
![]() $(\boldsymbol{x},\boldsymbol{w})$
, the following quadratic form was derived in Ramos (Reference Ramos2015b
):
$(\boldsymbol{x},\boldsymbol{w})$
, the following quadratic form was derived in Ramos (Reference Ramos2015b
):
where
 $$\begin{eqnarray}{\mathcal{P}}=\mathop{\sum }_{s=i,e}\int \text{d}^{3}\boldsymbol{x}\left(\int \text{d}^{3}\boldsymbol{w}~\frac{T_{s0}w_{\Vert }^{2}}{f_{Ms0}}~\left|\boldsymbol{b}_{0}\boldsymbol{\cdot }\frac{\unicode[STIX]{x2202}\hat{f}_{s}^{even}}{\unicode[STIX]{x2202}\boldsymbol{x}}\right|^{2}-\frac{m_{s}}{n_{0}}~\left|\int \text{d}^{3}\boldsymbol{w}~w_{\Vert }^{2}~\boldsymbol{b}_{0}\boldsymbol{\cdot }\frac{\unicode[STIX]{x2202}\hat{f}_{s}^{even}}{\unicode[STIX]{x2202}\boldsymbol{x}}\right|^{2}\right).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{P}}=\mathop{\sum }_{s=i,e}\int \text{d}^{3}\boldsymbol{x}\left(\int \text{d}^{3}\boldsymbol{w}~\frac{T_{s0}w_{\Vert }^{2}}{f_{Ms0}}~\left|\boldsymbol{b}_{0}\boldsymbol{\cdot }\frac{\unicode[STIX]{x2202}\hat{f}_{s}^{even}}{\unicode[STIX]{x2202}\boldsymbol{x}}\right|^{2}-\frac{m_{s}}{n_{0}}~\left|\int \text{d}^{3}\boldsymbol{w}~w_{\Vert }^{2}~\boldsymbol{b}_{0}\boldsymbol{\cdot }\frac{\unicode[STIX]{x2202}\hat{f}_{s}^{even}}{\unicode[STIX]{x2202}\boldsymbol{x}}\right|^{2}\right).\end{eqnarray}$$
The notation used in Ramos (Reference Ramos2015a
,Reference Ramos
b
) defined the forces
![]() $\boldsymbol{F}_{\bot }^{F}$
,
$\boldsymbol{F}_{\bot }^{F}$
,
![]() $\hat{F}_{s\Vert }$
and
$\hat{F}_{s\Vert }$
and
![]() $\hat{\boldsymbol{F}}_{s\bot }$
with a sign opposite to the definitions used here, but (C 1) has been written following the standard sign convention adopted in the present paper. This quadratic form, together with the self-adjointness of
$\hat{\boldsymbol{F}}_{s\bot }$
with a sign opposite to the definitions used here, but (C 1) has been written following the standard sign convention adopted in the present paper. This quadratic form, together with the self-adjointness of
![]() $\boldsymbol{F}_{\bot }^{F}$
, implies that the squared KMHD eigenfrequencies
$\boldsymbol{F}_{\bot }^{F}$
, implies that the squared KMHD eigenfrequencies
![]() $\unicode[STIX]{x1D714}^{2}$
are real. The term
$\unicode[STIX]{x1D714}^{2}$
are real. The term
![]() ${\mathcal{P}}$
is positive because of the Cauchy–Schwarz inequality and, recalling (3.25), it can also be written as
${\mathcal{P}}$
is positive because of the Cauchy–Schwarz inequality and, recalling (3.25), it can also be written as
 $$\begin{eqnarray}{\mathcal{P}}=\mathop{\sum }_{s=i,e}\int \text{d}^{3}\boldsymbol{x}\left(\int \text{d}^{3}\boldsymbol{w}~\frac{T_{s0}}{f_{Ms0}}~\left|w_{\Vert }\boldsymbol{b}_{0}\boldsymbol{\cdot }\frac{\unicode[STIX]{x2202}\hat{f}_{s}^{even}}{\unicode[STIX]{x2202}\boldsymbol{x}}\right|^{2}-\frac{|\hat{F}_{s\Vert }|^{2}}{m_{s}n_{0}}\right).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{P}}=\mathop{\sum }_{s=i,e}\int \text{d}^{3}\boldsymbol{x}\left(\int \text{d}^{3}\boldsymbol{w}~\frac{T_{s0}}{f_{Ms0}}~\left|w_{\Vert }\boldsymbol{b}_{0}\boldsymbol{\cdot }\frac{\unicode[STIX]{x2202}\hat{f}_{s}^{even}}{\unicode[STIX]{x2202}\boldsymbol{x}}\right|^{2}-\frac{|\hat{F}_{s\Vert }|^{2}}{m_{s}n_{0}}\right).\end{eqnarray}$$
The normal-mode drift-kinetic equation for
![]() $\hat{f}_{s}^{odd}$
(3.24) yields
$\hat{f}_{s}^{odd}$
(3.24) yields
and, using the property
![]() $\int \text{d}^{3}\boldsymbol{w}~w_{\Vert }~\hat{f}_{s}^{odd}=0$
,
$\int \text{d}^{3}\boldsymbol{w}~w_{\Vert }~\hat{f}_{s}^{odd}=0$
,
therefore
Since
![]() $\unicode[STIX]{x1D714}^{2}$
is real,
$\unicode[STIX]{x1D714}^{2}$
is real,
![]() $|\unicode[STIX]{x1D714}|^{4}=\unicode[STIX]{x1D714}^{4}$
. Then, substituting (C 6) in (C 1) and dividing by
$|\unicode[STIX]{x1D714}|^{4}=\unicode[STIX]{x1D714}^{4}$
. Then, substituting (C 6) in (C 1) and dividing by
![]() $\unicode[STIX]{x1D714}^{2}$
, one obtains the following equivalent version of the normal-mode quadratic form
$\unicode[STIX]{x1D714}^{2}$
, one obtains the following equivalent version of the normal-mode quadratic form
 $$\begin{eqnarray}\displaystyle & & \displaystyle -\!\int \text{d}^{3}\boldsymbol{x}~\unicode[STIX]{x1D743}_{\bot }\boldsymbol{\cdot }\boldsymbol{F}_{\bot }^{F}[\unicode[STIX]{x1D743}_{\bot }^{\ast }]+\mathop{\sum }_{s=i,e}\int \text{d}^{3}\boldsymbol{x}\int \text{d}^{3}\boldsymbol{w}\,\frac{T_{s0}}{f_{Ms0}}\left(|\hat{f}_{s}^{even}|^{2}-\frac{|\unicode[STIX]{x1D714}|^{2}}{\unicode[STIX]{x1D714}^{2}}~|\hat{f}_{s}^{odd}|^{2}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D714}^{2}\int \text{d}^{3}\boldsymbol{x}~\unicode[STIX]{x1D70C}_{0}~\unicode[STIX]{x1D743}\boldsymbol{\cdot }\unicode[STIX]{x1D743}^{\ast }.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle -\!\int \text{d}^{3}\boldsymbol{x}~\unicode[STIX]{x1D743}_{\bot }\boldsymbol{\cdot }\boldsymbol{F}_{\bot }^{F}[\unicode[STIX]{x1D743}_{\bot }^{\ast }]+\mathop{\sum }_{s=i,e}\int \text{d}^{3}\boldsymbol{x}\int \text{d}^{3}\boldsymbol{w}\,\frac{T_{s0}}{f_{Ms0}}\left(|\hat{f}_{s}^{even}|^{2}-\frac{|\unicode[STIX]{x1D714}|^{2}}{\unicode[STIX]{x1D714}^{2}}~|\hat{f}_{s}^{odd}|^{2}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D714}^{2}\int \text{d}^{3}\boldsymbol{x}~\unicode[STIX]{x1D70C}_{0}~\unicode[STIX]{x1D743}\boldsymbol{\cdot }\unicode[STIX]{x1D743}^{\ast }.\end{eqnarray}$$
A single normal mode can also be a real solution of the initial-value problem (of the kind considered in the main body of this paper) if it is a growing or damped mode, so that its time dependence is
![]() $\exp (\unicode[STIX]{x1D6FE}t)$
with a real
$\exp (\unicode[STIX]{x1D6FE}t)$
with a real
![]() $\unicode[STIX]{x1D6FE}=-i\unicode[STIX]{x1D714}$
and a real eigenfunction. In this case
$\unicode[STIX]{x1D6FE}=-i\unicode[STIX]{x1D714}$
and a real eigenfunction. In this case
![]() $\unicode[STIX]{x1D743}=\unicode[STIX]{x1D743}^{\ast }$
,
$\unicode[STIX]{x1D743}=\unicode[STIX]{x1D743}^{\ast }$
,
![]() $\hat{f}_{s}=\hat{f}_{s}^{\ast }$
and
$\hat{f}_{s}=\hat{f}_{s}^{\ast }$
and
![]() $\unicode[STIX]{x1D714}^{2}=-|\unicode[STIX]{x1D714}|^{2}$
, besides
$\unicode[STIX]{x1D714}^{2}=-|\unicode[STIX]{x1D714}|^{2}$
, besides
![]() $\unicode[STIX]{x1D714}\unicode[STIX]{x1D743}=i\unicode[STIX]{x2202}\unicode[STIX]{x1D743}/\unicode[STIX]{x2202}t$
, so the quadratic form (C 7) becomes
$\unicode[STIX]{x1D714}\unicode[STIX]{x1D743}=i\unicode[STIX]{x2202}\unicode[STIX]{x1D743}/\unicode[STIX]{x2202}t$
, so the quadratic form (C 7) becomes
which, divided by 2, is the second-order energy conservation law (4.18)
Appendix D. An auxiliary lemma
Let
![]() $\unicode[STIX]{x1D719}(t)$
be a differentiable real function of the real variable
$\unicode[STIX]{x1D719}(t)$
be a differentiable real function of the real variable
![]() $t$
, bounded by
$t$
, bounded by
![]() $0\leqslant \unicode[STIX]{x1D719}(t)\leqslant \unicode[STIX]{x1D719}_{max}$
that, for
$0\leqslant \unicode[STIX]{x1D719}(t)\leqslant \unicode[STIX]{x1D719}_{max}$
that, for
![]() $t\geqslant t_{c}\geqslant 0$
, satisfies
$t\geqslant t_{c}\geqslant 0$
, satisfies
It is to be proved next, that the behaviour as
![]() $t\rightarrow \infty$
of the function
$t\rightarrow \infty$
of the function
is such that it either stays non-negative or tends to zero.
Differentiating with respect to
![]() $t$
,
$t$
,
and, integrating by parts with respect to
![]() $\unicode[STIX]{x1D708}$
,
$\unicode[STIX]{x1D708}$
,
hence
The condition (D1) implies that, for
![]() $t\geqslant t_{c}$
,
$t\geqslant t_{c}$
,
and the bound
![]() $0\leqslant \unicode[STIX]{x1D719}(t)\leqslant \unicode[STIX]{x1D719}_{max}$
implies that
$0\leqslant \unicode[STIX]{x1D719}(t)\leqslant \unicode[STIX]{x1D719}_{max}$
implies that
![]() $\unicode[STIX]{x1D6F7}(t)$
is bounded by
$\unicode[STIX]{x1D6F7}(t)$
is bounded by
![]() $-\unicode[STIX]{x1D719}_{max}/8\leqslant \unicode[STIX]{x1D6F7}(t)\leqslant 9\unicode[STIX]{x1D719}_{max}/8$
. Since
$-\unicode[STIX]{x1D719}_{max}/8\leqslant \unicode[STIX]{x1D6F7}(t)\leqslant 9\unicode[STIX]{x1D719}_{max}/8$
. Since
![]() $\unicode[STIX]{x1D6F7}(t)$
is bounded, it either oscillates or tends to a limit as
$\unicode[STIX]{x1D6F7}(t)$
is bounded, it either oscillates or tends to a limit as
![]() $t\rightarrow \infty$
. If it oscillates, it must stay non-negative because otherwise there would be intervals at arbitrarily large values of
$t\rightarrow \infty$
. If it oscillates, it must stay non-negative because otherwise there would be intervals at arbitrarily large values of
![]() $t$
where
$t$
where
![]() $\unicode[STIX]{x1D6F7}(t)<0$
and
$\unicode[STIX]{x1D6F7}(t)<0$
and
![]() $\text{d}\unicode[STIX]{x1D6F7}(t)/\text{d}t<0$
, contradicting (D 6). If it tends to a limit, such limit must be positive or zero because otherwise
$\text{d}\unicode[STIX]{x1D6F7}(t)/\text{d}t<0$
, contradicting (D 6). If it tends to a limit, such limit must be positive or zero because otherwise
![]() $\lim _{t\rightarrow \infty }\unicode[STIX]{x1D6F7}(t)<0$
and
$\lim _{t\rightarrow \infty }\unicode[STIX]{x1D6F7}(t)<0$
and
![]() $\lim _{t\rightarrow \infty }t\,\text{d}\unicode[STIX]{x1D6F7}(t)/\text{d}t=0$
, contradicting again (D 6).
$\lim _{t\rightarrow \infty }t\,\text{d}\unicode[STIX]{x1D6F7}(t)/\text{d}t=0$
, contradicting again (D 6).


