1 Introduction
Large-angle collisions are associated with large momentum transfers, but their influence can often be ignored in plasma physics, as the cumulative effect of many small-angle deflections are larger by a factor of the Coulomb logarithm,
![]() $\ln \unicode[STIX]{x1D6EC}$
(Rosenbluth, MacDonald & Judd Reference Rosenbluth, MacDonald and Judd1957; Trubnikov Reference Trubnikov1965). In many plasmas, e.g. magnetic fusion plasmas and astrophysical plasmas,
$\ln \unicode[STIX]{x1D6EC}$
(Rosenbluth, MacDonald & Judd Reference Rosenbluth, MacDonald and Judd1957; Trubnikov Reference Trubnikov1965). In many plasmas, e.g. magnetic fusion plasmas and astrophysical plasmas,
![]() $\ln \unicode[STIX]{x1D6EC}$
is typically of the order of 10–30. This allows collisions to be accurately accounted for using a Fokker–Planck equation, originally derived for Coulomb interactions by Landau as the small-momentum-transfer limit of the Boltzmann equation (Landau Reference Landau and Ter Haar1965).
$\ln \unicode[STIX]{x1D6EC}$
is typically of the order of 10–30. This allows collisions to be accurately accounted for using a Fokker–Planck equation, originally derived for Coulomb interactions by Landau as the small-momentum-transfer limit of the Boltzmann equation (Landau Reference Landau and Ter Haar1965).
A unique situation occurs in runaway acceleration of electrons, where large-angle collisions can play a dominant role even for large
![]() $\ln \unicode[STIX]{x1D6EC}$
, as they cause an exponential growth of the runaway density – a runaway avalanche (Sokolov Reference Sokolov1979). Runaway is the acceleration of particles in the presence of an electric field which exceeds the critical field
$\ln \unicode[STIX]{x1D6EC}$
, as they cause an exponential growth of the runaway density – a runaway avalanche (Sokolov Reference Sokolov1979). Runaway is the acceleration of particles in the presence of an electric field which exceeds the critical field
![]() $E_{\text{c}}=n_{\text{e}}\ln \unicode[STIX]{x1D6EC}e^{3}(4\unicode[STIX]{x03C0}\unicode[STIX]{x1D700}_{0}^{2}m_{\text{e}}c^{2})^{-1}$
(Connor & Hastie Reference Connor and Hastie1975), where
$E_{\text{c}}=n_{\text{e}}\ln \unicode[STIX]{x1D6EC}e^{3}(4\unicode[STIX]{x03C0}\unicode[STIX]{x1D700}_{0}^{2}m_{\text{e}}c^{2})^{-1}$
(Connor & Hastie Reference Connor and Hastie1975), where
![]() $n_{\text{e}}$
is the electron density,
$n_{\text{e}}$
is the electron density,
![]() $e$
is the elementary charge,
$e$
is the elementary charge,
![]() $\unicode[STIX]{x1D700}_{0}$
is the vacuum permittivity,
$\unicode[STIX]{x1D700}_{0}$
is the vacuum permittivity,
![]() $m_{\text{e}}$
is the electron rest mass and
$m_{\text{e}}$
is the electron rest mass and
![]() $c$
is the speed of light. Since the collisional drag for superthermal electrons is given by
$c$
is the speed of light. Since the collisional drag for superthermal electrons is given by
![]() $F_{\text{c}}=eE_{\text{c}}(v/c)^{-2}$
, any electrons with speed greater than the critical speed
$F_{\text{c}}=eE_{\text{c}}(v/c)^{-2}$
, any electrons with speed greater than the critical speed
![]() $v_{\text{c}}=c\sqrt{E_{\text{c}}/E}$
will be accelerated indefinitely, and are hence referred to as runaway electrons (Wilson Reference Wilson1925). Electron runaway occurs in a wide range of plasmas, e.g. in atmospheric discharges (Gurevich, Milikh & Roussel-Dupre Reference Gurevich, Milikh and Roussel-Dupre1992), in solar flares (Holman Reference Holman1985) and in tokamak disruptions when the plasma current changes quickly and a strong electric field is induced (Gill Reference Gill1993; Jaspers Reference Jaspers1993). Due to the large plasma current they would carry, reactor-scale tokamaks such as ITER will be particularly susceptible to the conversion of plasma current to relativistic runaway-electron current by large-angle collisions during disruptions (Rosenbluth & Putvinski Reference Rosenbluth and Putvinski1997). The subsequent uncontrolled loss of a runaway-electron beam could damage plasma-facing components, and the runaways therefore pose a critical threat to the viability of nuclear fusion for energy production (Hollmann et al.
Reference Hollmann, Aleynikov, Fülöp, Humphreys, Izzo, Lehnen, Loarte, Lukash, Papp and Parks2015).
$v_{\text{c}}=c\sqrt{E_{\text{c}}/E}$
will be accelerated indefinitely, and are hence referred to as runaway electrons (Wilson Reference Wilson1925). Electron runaway occurs in a wide range of plasmas, e.g. in atmospheric discharges (Gurevich, Milikh & Roussel-Dupre Reference Gurevich, Milikh and Roussel-Dupre1992), in solar flares (Holman Reference Holman1985) and in tokamak disruptions when the plasma current changes quickly and a strong electric field is induced (Gill Reference Gill1993; Jaspers Reference Jaspers1993). Due to the large plasma current they would carry, reactor-scale tokamaks such as ITER will be particularly susceptible to the conversion of plasma current to relativistic runaway-electron current by large-angle collisions during disruptions (Rosenbluth & Putvinski Reference Rosenbluth and Putvinski1997). The subsequent uncontrolled loss of a runaway-electron beam could damage plasma-facing components, and the runaways therefore pose a critical threat to the viability of nuclear fusion for energy production (Hollmann et al.
Reference Hollmann, Aleynikov, Fülöp, Humphreys, Izzo, Lehnen, Loarte, Lukash, Papp and Parks2015).
In a plasma, runaways are mainly generated by two separate mechanisms. When the electrons in the runaway region
![]() $v>v_{c}$
are being accelerated, collisional velocity-space diffusion will feed thermal electrons into the runaway region at a steady rate. This primary runaway generation, or Dreicer mechanism (Dreicer Reference Dreicer1960), generates new runaways at a rate which is exponentially sensitive to the electric field. The runaway population growth rate was derived in Connor & Hastie (Reference Connor and Hastie1975), Cohen (Reference Cohen1976) and is
$v>v_{c}$
are being accelerated, collisional velocity-space diffusion will feed thermal electrons into the runaway region at a steady rate. This primary runaway generation, or Dreicer mechanism (Dreicer Reference Dreicer1960), generates new runaways at a rate which is exponentially sensitive to the electric field. The runaway population growth rate was derived in Connor & Hastie (Reference Connor and Hastie1975), Cohen (Reference Cohen1976) and is
where the undetermined constant factor
![]() $\unicode[STIX]{x1D705}$
is of order unity. Here
$\unicode[STIX]{x1D705}$
is of order unity. Here
![]() $n_{\text{RE}}$
is the number density of runaways,
$n_{\text{RE}}$
is the number density of runaways,
![]() $\unicode[STIX]{x1D70F}_{\text{c}}=4\unicode[STIX]{x03C0}\unicode[STIX]{x1D700}_{0}^{2}m_{\text{e}}^{2}c^{3}/(n_{\text{e}}e^{4}\ln \unicode[STIX]{x1D6EC})$
is the relativistic-electron collision time,
$\unicode[STIX]{x1D70F}_{\text{c}}=4\unicode[STIX]{x03C0}\unicode[STIX]{x1D700}_{0}^{2}m_{\text{e}}^{2}c^{3}/(n_{\text{e}}e^{4}\ln \unicode[STIX]{x1D6EC})$
is the relativistic-electron collision time,
![]() $E_{\text{D}}=m_{\text{e}}^{2}c^{3}/(e\unicode[STIX]{x1D70F}_{\text{c}}T_{\text{e}})$
is the so-called Dreicer field and
$E_{\text{D}}=m_{\text{e}}^{2}c^{3}/(e\unicode[STIX]{x1D70F}_{\text{c}}T_{\text{e}})$
is the so-called Dreicer field and
![]() $Z_{\text{eff}}=\sum _{i}n_{i}Z_{i}^{2}/\sum _{i}n_{i}Z_{i}$
is the effective ion charge (with the sum taken over all ion species
$Z_{\text{eff}}=\sum _{i}n_{i}Z_{i}^{2}/\sum _{i}n_{i}Z_{i}$
is the effective ion charge (with the sum taken over all ion species
![]() $i$
). The parameters
$i$
). The parameters
![]() $h$
,
$h$
,
![]() $\unicode[STIX]{x1D706}$
and
$\unicode[STIX]{x1D706}$
and
![]() $\unicode[STIX]{x1D702}$
(not given here) depend on
$\unicode[STIX]{x1D702}$
(not given here) depend on
![]() $E/E_{\text{c}}$
and approach unity as
$E/E_{\text{c}}$
and approach unity as
![]() $E/E_{\text{c}}$
becomes large (in the non-relativistic limit), and ensure that the growth rate vanishes as
$E/E_{\text{c}}$
becomes large (in the non-relativistic limit), and ensure that the growth rate vanishes as
![]() $E\rightarrow E_{\text{c}}$
.
$E\rightarrow E_{\text{c}}$
.
A secondary runaway generation mechanism is provided by large-angle collisions, whereby an electron with kinetic energy
![]() $\unicode[STIX]{x1D716}=(\unicode[STIX]{x1D6FE}-1)m_{\text{e}}c^{2}>2\unicode[STIX]{x1D716}_{\text{c}}$
can send a stationary target electron into the runaway region in a single collision event while remaining a runaway itself, where
$\unicode[STIX]{x1D716}=(\unicode[STIX]{x1D6FE}-1)m_{\text{e}}c^{2}>2\unicode[STIX]{x1D716}_{\text{c}}$
can send a stationary target electron into the runaway region in a single collision event while remaining a runaway itself, where
![]() $\unicode[STIX]{x1D716}_{\text{c}}$
is the kinetic energy corresponding to the critical speed. Secondary generation, also referred to as avalanche generation due to the resulting exponential growth of the runaway population, generates new runaways at a rate calculated by Rosenbluth & Putvinski (Reference Rosenbluth and Putvinski1997) to be approximately
$\unicode[STIX]{x1D716}_{\text{c}}$
is the kinetic energy corresponding to the critical speed. Secondary generation, also referred to as avalanche generation due to the resulting exponential growth of the runaway population, generates new runaways at a rate calculated by Rosenbluth & Putvinski (Reference Rosenbluth and Putvinski1997) to be approximately
The function
![]() $C=C(E,\,Z_{\text{eff}})$
was shown to be
$C=C(E,\,Z_{\text{eff}})$
was shown to be
![]() $C=1$
when collisional diffusion is neglected (formally by setting
$C=1$
when collisional diffusion is neglected (formally by setting
![]() $Z_{\text{eff}}=-1$
).
$Z_{\text{eff}}=-1$
).
While the avalanche growth rate is formally of order
![]() $1/\text{ln}\unicode[STIX]{x1D6EC}$
smaller than the primary generation rate, the more favourable scaling with electric field makes it the dominant source of new runaways for sufficiently large runaway populations
$1/\text{ln}\unicode[STIX]{x1D6EC}$
smaller than the primary generation rate, the more favourable scaling with electric field makes it the dominant source of new runaways for sufficiently large runaway populations
![]() $n_{\text{RE}}$
or sufficiently small
$n_{\text{RE}}$
or sufficiently small
![]() $E/E_{\text{D}}$
, i.e. at low temperature. In the presence of a constant electric field
$E/E_{\text{D}}$
, i.e. at low temperature. In the presence of a constant electric field
![]() $E$
, with no initial runaway population (apart from a small primary seed), the secondary generation rate will exceed the primary one after approximately one avalanche e-folding time
$E$
, with no initial runaway population (apart from a small primary seed), the secondary generation rate will exceed the primary one after approximately one avalanche e-folding time
![]() $t_{\text{ava}}\approx 2\ln \unicode[STIX]{x1D6EC}m_{\text{e}}c/[Ce(E-E_{\text{c}})]$
. This corresponds to the time for an initially slow electron to be accelerated to a kinetic energy
$t_{\text{ava}}\approx 2\ln \unicode[STIX]{x1D6EC}m_{\text{e}}c/[Ce(E-E_{\text{c}})]$
. This corresponds to the time for an initially slow electron to be accelerated to a kinetic energy
![]() $E_{\text{k}}\approx \ln \unicode[STIX]{x1D6EC}/C$
MeV (Jayakumar, Fleischmann & Zweben Reference Jayakumar, Fleischmann and Zweben1993) (neglecting the weak electric-field dependence of
$E_{\text{k}}\approx \ln \unicode[STIX]{x1D6EC}/C$
MeV (Jayakumar, Fleischmann & Zweben Reference Jayakumar, Fleischmann and Zweben1993) (neglecting the weak electric-field dependence of
![]() $C$
). Numerically,
$C$
). Numerically,
![]() $t_{\text{ava}}\approx 3.4\ln \unicode[STIX]{x1D6EC}/[C(E-E_{\text{c}})]~\text{ms}$
, with
$t_{\text{ava}}\approx 3.4\ln \unicode[STIX]{x1D6EC}/[C(E-E_{\text{c}})]~\text{ms}$
, with
![]() $E$
and
$E$
and
![]() $E_{\text{c}}$
in
$E_{\text{c}}$
in
![]() $\text{V}~\text{m}^{-1}$
. If the electric field decreases in magnitude with time, avalanche will become important even earlier. In many practical runaway scenarios, the runaway process will last for multiple
$\text{V}~\text{m}^{-1}$
. If the electric field decreases in magnitude with time, avalanche will become important even earlier. In many practical runaway scenarios, the runaway process will last for multiple
![]() $t_{\text{ava}}$
(Gurevich, Milikh & Roussel-Dupre Reference Gurevich, Milikh and Roussel-Dupre1994; Gurevich & Zybin Reference Gurevich and Zybin2001; Helander, Eriksson & Andersson Reference Helander, Eriksson and Andersson2002), and secondary generation will therefore be the dominant runaway mechanism.
$t_{\text{ava}}$
(Gurevich, Milikh & Roussel-Dupre Reference Gurevich, Milikh and Roussel-Dupre1994; Gurevich & Zybin Reference Gurevich and Zybin2001; Helander, Eriksson & Andersson Reference Helander, Eriksson and Andersson2002), and secondary generation will therefore be the dominant runaway mechanism.
In this work we derive a conservative large-angle (also known as ‘close’ or ‘knock-on’) collision model from the high-energy limit of the linearized relativistic Boltzmann collision integral. We will show how the operators used to model large-angle collisions in previous studies are obtained through various approximations of the Boltzmann collision operator, and how our more general operator resolves issues with previous models and allows the study of new physical effects. In particular, we resolve the issue of double counting of large-angle and small-angle collisions, and show that this development is essential to accurately capture the dynamics. We find that the change to the runaway growth rate due to the new operator is largest during the early stages of the runaway acceleration process, and the likelihood of a given runaway seed transforming into a serious runaway beam can thus potentially be affected. Furthermore, we consider the effect of the inverse knock-on process, where a runaway is slowed down in a single large-angle collision. This effect was recently shown by Aleynikov & Breizman (Reference Aleynikov and Breizman2015) to be significant for runaway in a near-threshold electric field.
The rest of the paper is organized as follows. In § 2 we introduce the theoretical models describing the large-angle collisions. After giving an overview of the existing models, we present a derivation of the new conservative operator. In § 3 we investigate the effect of the new operator on the runaway growth rate numerically, using the kinetic equation solver CODE (Landreman, Stahl & Fülöp Reference Landreman, Stahl and Fülöp2014; Stahl et al. Reference Stahl, Embréus, Papp, Landreman and Fülöp2016). Finally, we summarize our conclusions in § 4.
2 Theoretical models for runaway generation due to large-angle collisions
One of the earliest models for avalanche runaway generation was introduced by Rosenbluth & Putvinski (Reference Rosenbluth and Putvinski1997). Due to its simple form, suitable for analytical development, it has been widely used to study the dynamics of an avalanching runaway population (Eriksson & Helander Reference Eriksson and Helander2003; Smith et al. Reference Smith, Helander, Eriksson and Fülöp2005; Fülöp et al. Reference Fülöp, Pokol, Helander and Lisak2006; Nilsson et al. Reference Nilsson, Decker, Peysson, Granetz, Saint-Laurent and Vlainic2015). Rosenbluth and Putvinski proposed a kinetic equation for the electron distribution of the form
where
![]() $\text{d}f_{\text{e}}/\text{d}t$
represents the advective part of the motion,
$\text{d}f_{\text{e}}/\text{d}t$
represents the advective part of the motion,
![]() $C_{\text{FP}}$
is the Fokker–Planck collision operator and
$C_{\text{FP}}$
is the Fokker–Planck collision operator and
![]() $S$
a source term representing ‘secondary high-energy electrons knocked out of their orbits by close collisions of a primary relativistic electron with low-energy electrons from the background plasma’ (Rosenbluth & Putvinski Reference Rosenbluth and Putvinski1997). Assuming all existing runaways to be infinitely energetic and having zero pitch angle, they obtained (here adapting their more general result to a homogeneous plasma)
$S$
a source term representing ‘secondary high-energy electrons knocked out of their orbits by close collisions of a primary relativistic electron with low-energy electrons from the background plasma’ (Rosenbluth & Putvinski Reference Rosenbluth and Putvinski1997). Assuming all existing runaways to be infinitely energetic and having zero pitch angle, they obtained (here adapting their more general result to a homogeneous plasma)
where
![]() $\unicode[STIX]{x1D709}=\cos \unicode[STIX]{x1D703}=p_{\Vert }/p$
is the pitch-angle cosine,
$\unicode[STIX]{x1D709}=\cos \unicode[STIX]{x1D703}=p_{\Vert }/p$
is the pitch-angle cosine,
![]() $\unicode[STIX]{x1D6FE}=\sqrt{1+(p/m_{\text{e}}c)^{2}}$
is the Lorentz factor,
$\unicode[STIX]{x1D6FE}=\sqrt{1+(p/m_{\text{e}}c)^{2}}$
is the Lorentz factor,
![]() $\unicode[STIX]{x1D709}_{0}=\sqrt{(\unicode[STIX]{x1D6FE}-1)/(\unicode[STIX]{x1D6FE}+1)}$
and the momentum-space volume element is
$\unicode[STIX]{x1D709}_{0}=\sqrt{(\unicode[STIX]{x1D6FE}-1)/(\unicode[STIX]{x1D6FE}+1)}$
and the momentum-space volume element is
![]() $p^{2}\,\text{d}p\,\text{d}\unicode[STIX]{x1D709}\,\text{d}\unicode[STIX]{x1D711}$
, with
$p^{2}\,\text{d}p\,\text{d}\unicode[STIX]{x1D709}\,\text{d}\unicode[STIX]{x1D711}$
, with
![]() $\unicode[STIX]{x1D711}$
the azimuthal angle of the momentum (the gyroangle). The delta function ensures that secondary electrons are only born on the parabola
$\unicode[STIX]{x1D711}$
the azimuthal angle of the momentum (the gyroangle). The delta function ensures that secondary electrons are only born on the parabola
![]() $p_{\bot }^{2}=2p_{\Vert }m_{\text{e}}c$
in momentum space. In the non-relativistic limit,
$p_{\bot }^{2}=2p_{\Vert }m_{\text{e}}c$
in momentum space. In the non-relativistic limit,
![]() $p\ll m_{\text{e}}c$
, secondaries are born at perpendicular angles,
$p\ll m_{\text{e}}c$
, secondaries are born at perpendicular angles,
![]() $p_{\Vert }\approx 0$
, and are prone to trapping in an inhomogeneous magnetic field (Rosenbluth & Putvinski Reference Rosenbluth and Putvinski1997). Away from the magnetic axis of a tokamak, this can lead to a strong reduction in the avalanche growth rate, as recently also demonstrated in detailed numerical simulations by Nilsson et al. (Reference Nilsson, Decker, Peysson, Granetz, Saint-Laurent and Vlainic2015).
$p_{\Vert }\approx 0$
, and are prone to trapping in an inhomogeneous magnetic field (Rosenbluth & Putvinski Reference Rosenbluth and Putvinski1997). Away from the magnetic axis of a tokamak, this can lead to a strong reduction in the avalanche growth rate, as recently also demonstrated in detailed numerical simulations by Nilsson et al. (Reference Nilsson, Decker, Peysson, Granetz, Saint-Laurent and Vlainic2015).
A more general model was later described by Chiu et al. (Reference Chiu, Rosenbluth, Harvey and Chan1998) (from now on referred to as the Chiu–Harvey operator), which has also been used in runaway studies (Chiu et al. Reference Chiu, Rosenbluth, Harvey and Chan1998; Harvey et al. Reference Harvey, Chan, Chiu, Evans and Rosenbluth2000; Stahl et al. Reference Stahl, Embréus, Papp, Landreman and Fülöp2016). Allowing runaway-electron energies to be finite but assuming the runaway pitch angle to be zero, they obtained a knock-on source term
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F4}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}_{1}) & = & \displaystyle \frac{\unicode[STIX]{x1D6FE}_{1}^{2}}{(\unicode[STIX]{x1D6FE}_{1}^{2}-1)(\unicode[STIX]{x1D6FE}-1)^{2}(\unicode[STIX]{x1D6FE}_{1}-\unicode[STIX]{x1D6FE})^{2}}\left((\unicode[STIX]{x1D6FE}_{1}-1)^{2}-\frac{(\unicode[STIX]{x1D6FE}-1)(\unicode[STIX]{x1D6FE}_{1}-\unicode[STIX]{x1D6FE})}{\unicode[STIX]{x1D6FE}_{1}^{2}}\right.\nonumber\\ \displaystyle & & \displaystyle \left.\times \,[2\unicode[STIX]{x1D6FE}_{1}^{2}+2\unicode[STIX]{x1D6FE}_{1}-1-(\unicode[STIX]{x1D6FE}-1)(\unicode[STIX]{x1D6FE}_{1}-\unicode[STIX]{x1D6FE})]\vphantom{\frac{(\unicode[STIX]{x1D6FE}-1)(\unicode[STIX]{x1D6FE}_{1}-\unicode[STIX]{x1D6FE})}{\unicode[STIX]{x1D6FE}_{1}^{2}}}\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F4}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}_{1}) & = & \displaystyle \frac{\unicode[STIX]{x1D6FE}_{1}^{2}}{(\unicode[STIX]{x1D6FE}_{1}^{2}-1)(\unicode[STIX]{x1D6FE}-1)^{2}(\unicode[STIX]{x1D6FE}_{1}-\unicode[STIX]{x1D6FE})^{2}}\left((\unicode[STIX]{x1D6FE}_{1}-1)^{2}-\frac{(\unicode[STIX]{x1D6FE}-1)(\unicode[STIX]{x1D6FE}_{1}-\unicode[STIX]{x1D6FE})}{\unicode[STIX]{x1D6FE}_{1}^{2}}\right.\nonumber\\ \displaystyle & & \displaystyle \left.\times \,[2\unicode[STIX]{x1D6FE}_{1}^{2}+2\unicode[STIX]{x1D6FE}_{1}-1-(\unicode[STIX]{x1D6FE}-1)(\unicode[STIX]{x1D6FE}_{1}-\unicode[STIX]{x1D6FE})]\vphantom{\frac{(\unicode[STIX]{x1D6FE}-1)(\unicode[STIX]{x1D6FE}_{1}-\unicode[STIX]{x1D6FE})}{\unicode[STIX]{x1D6FE}_{1}^{2}}}\right),\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6F4}=(2\unicode[STIX]{x03C0}r_{0}^{2})^{-1}\,\text{d}\unicode[STIX]{x1D70E}/\text{d}\unicode[STIX]{x1D6FE}$
is the normalized Møller differential cross-section for free–free electron–electron scattering (Møller Reference Møller1932),
$\unicode[STIX]{x1D6F4}=(2\unicode[STIX]{x03C0}r_{0}^{2})^{-1}\,\text{d}\unicode[STIX]{x1D70E}/\text{d}\unicode[STIX]{x1D6FE}$
is the normalized Møller differential cross-section for free–free electron–electron scattering (Møller Reference Møller1932),
![]() $r_{0}=e^{2}/(4\unicode[STIX]{x03C0}\unicode[STIX]{x1D700}_{0}m_{\text{e}}c^{2})$
is the classical electron radius and
$r_{0}=e^{2}/(4\unicode[STIX]{x03C0}\unicode[STIX]{x1D700}_{0}m_{\text{e}}c^{2})$
is the classical electron radius and
![]() $\unicode[STIX]{x1D6FE}_{1}$
is connected to
$\unicode[STIX]{x1D6FE}_{1}$
is connected to
![]() $p$
and
$p$
and
![]() $\unicode[STIX]{x1D709}$
by the relation
$\unicode[STIX]{x1D709}$
by the relation
where a misprint in the original paper incorrectly replaced the
![]() $\unicode[STIX]{x1D6FE}-1$
factor with
$\unicode[STIX]{x1D6FE}-1$
factor with
![]() $\unicode[STIX]{x1D6FE}_{1}$
. Since the authors work under the assumption that the runaway pitch angles are negligible, the distribution only appears in the angle-averaged form
$\unicode[STIX]{x1D6FE}_{1}$
. Since the authors work under the assumption that the runaway pitch angles are negligible, the distribution only appears in the angle-averaged form
Both models for large-angle collisions presented above suffer from several defects. In particular, they do not conserve particle number, energy or momentum. In addition, the Rosenbluth–Putvinski model assumes that the incoming particle momentum is infinite, which has the consequence that particles can be created with an energy higher than any of the existing runaways. This assumption is not made in the model derived by Chiu et al. (Reference Chiu, Rosenbluth, Harvey and Chan1998), where the electron energy distribution is properly taken into account, but all incident runaways are still assumed to have zero pitch angle. The magnitudes of both sources (
![]() $S_{\text{RP}}$
and
$S_{\text{RP}}$
and
![]() $S_{\text{CH}}$
) increase rapidly with decreasing momenta and the sources are thus sensitive to the choice of cutoff momentum (introduced to avoid double counting of small-angle collisions).
$S_{\text{CH}}$
) increase rapidly with decreasing momenta and the sources are thus sensitive to the choice of cutoff momentum (introduced to avoid double counting of small-angle collisions).
In the following we will derive a knock-on collision model from the Boltzmann collision integral. As we will show, the model takes into account the full momentum dependence of the primary distribution, and conserves particle number, momentum and energy, while also consistently distinguishing between small- and large-angle collisions, therefore avoiding double counting.
2.1 The Boltzmann collision integral and the Fokker–Planck limit
The Boltzmann collision operator gives the time rate of change of the distribution function due to binary collisions, described by an arbitrary differential cross-section. It can be derived with the following heuristic argument (Montgomery & Tidman Reference Montgomery and Tidman1964; Cercignani & Kremer Reference Cercignani and Kremer2002). The collision operator can be defined as
![]() $C_{ab}(f_{a})=(\text{d}n_{a})_{\text{c},ab}/\text{d}t\,\text{d}\boldsymbol{p}$
, where
$C_{ab}(f_{a})=(\text{d}n_{a})_{\text{c},ab}/\text{d}t\,\text{d}\boldsymbol{p}$
, where
![]() $(\text{d}n_{a})_{\text{c},ab}$
is the differential change in the density of a species
$(\text{d}n_{a})_{\text{c},ab}$
is the differential change in the density of a species
![]() $a$
due to collisions with species
$a$
due to collisions with species
![]() $b$
, and is defined in terms of the differential cross-section
$b$
, and is defined in terms of the differential cross-section
![]() $\text{d}\unicode[STIX]{x1D70E}$
by Lifshitz & Pitaevski (Reference Lifshitz and Pitaevski1981) and Cercignani & Kremer (Reference Cercignani and Kremer2002)
$\text{d}\unicode[STIX]{x1D70E}$
by Lifshitz & Pitaevski (Reference Lifshitz and Pitaevski1981) and Cercignani & Kremer (Reference Cercignani and Kremer2002)
The first term on the right-hand side, the gain term, describes the rate at which particles
![]() $a$
of momentum
$a$
of momentum
![]() $\boldsymbol{p}_{1}$
will scatter to momentum
$\boldsymbol{p}_{1}$
will scatter to momentum
![]() $\boldsymbol{p}$
. The second term, the loss term, is the rate at which particles
$\boldsymbol{p}$
. The second term, the loss term, is the rate at which particles
![]() $a$
scatter away from momentum
$a$
scatter away from momentum
![]() $\boldsymbol{p}$
. Here, we introduced the Møller relative speed
$\boldsymbol{p}$
. Here, we introduced the Møller relative speed![]() and the differential cross-section
and the differential cross-section
![]() $\text{d}\unicode[STIX]{x1D70E}_{ab}$
for scattering events
$\text{d}\unicode[STIX]{x1D70E}_{ab}$
for scattering events
![]() $\boldsymbol{p}$
,
$\boldsymbol{p}$
,
![]() $\boldsymbol{p}^{\prime }\rightarrow \boldsymbol{p}_{1}$
,
$\boldsymbol{p}^{\prime }\rightarrow \boldsymbol{p}_{1}$
,
![]() $\boldsymbol{p}_{2}$
. The barred quantities are defined likewise, but with
$\boldsymbol{p}_{2}$
. The barred quantities are defined likewise, but with
![]() $\boldsymbol{p}$
exchanged for
$\boldsymbol{p}$
exchanged for
![]() $\boldsymbol{p}_{1}$
and
$\boldsymbol{p}_{1}$
and
![]() $\boldsymbol{p}^{\prime }$
for
$\boldsymbol{p}^{\prime }$
for
![]() $\boldsymbol{p}_{2}$
. Since the interactions are viewed as instantaneous, the time labels of the distribution functions have been suppressed for clarity of notation.
$\boldsymbol{p}_{2}$
. Since the interactions are viewed as instantaneous, the time labels of the distribution functions have been suppressed for clarity of notation.
The elastic differential cross-section satisfies the symmetry property ![]() (known as the principle of detailed balance (Weinberg Reference Weinberg2005)), allowing the collision operator to be cast in the commonly adopted symmetric form
(known as the principle of detailed balance (Weinberg Reference Weinberg2005)), allowing the collision operator to be cast in the commonly adopted symmetric form
where
![]() $\boldsymbol{p}_{1}$
and
$\boldsymbol{p}_{1}$
and
![]() $\boldsymbol{p}_{2}$
(six degrees of freedom) are uniquely determined in terms of
$\boldsymbol{p}_{2}$
(six degrees of freedom) are uniquely determined in terms of
![]() $\boldsymbol{p}$
and
$\boldsymbol{p}$
and
![]() $\boldsymbol{p}^{\prime }$
by two scattering angles and four constraints by the conservation of momentum and energy,
$\boldsymbol{p}^{\prime }$
by two scattering angles and four constraints by the conservation of momentum and energy,
From this collision operator, the Fokker–Planck operator, which is often used in plasma physics, can be obtained by a Taylor expansion to second order in the momentum transfer
![]() $\unicode[STIX]{x0394}\boldsymbol{p}=\boldsymbol{p}_{1}-\boldsymbol{p}$
(Landau Reference Landau1936; Akama Reference Akama1970), motivated by the fact that the cross-section for Coulomb collisions is singular for small deflections. It is then seen that the contribution of small-angle collisions is larger than those of large-angle collisions by a factor of the Coulomb logarithm,
$\unicode[STIX]{x0394}\boldsymbol{p}=\boldsymbol{p}_{1}-\boldsymbol{p}$
(Landau Reference Landau1936; Akama Reference Akama1970), motivated by the fact that the cross-section for Coulomb collisions is singular for small deflections. It is then seen that the contribution of small-angle collisions is larger than those of large-angle collisions by a factor of the Coulomb logarithm,
where the maximum centre-of-mass deflection angle for self-collisions is
![]() $\unicode[STIX]{x1D703}_{\max }=\unicode[STIX]{x03C0}/2$
(not
$\unicode[STIX]{x1D703}_{\max }=\unicode[STIX]{x03C0}/2$
(not
![]() $\unicode[STIX]{x03C0}$
as it is for unlike-species collisions, or collisions would be double counted) and
$\unicode[STIX]{x03C0}$
as it is for unlike-species collisions, or collisions would be double counted) and
![]() $\unicode[STIX]{x1D703}_{\min }$
is a cutoff required to regularize the expression, typically chosen as the scattering angle corresponding to impact parameters of order the Debye length,Footnote
1
beyond which particles will not interact because of Debye screening.
$\unicode[STIX]{x1D703}_{\min }$
is a cutoff required to regularize the expression, typically chosen as the scattering angle corresponding to impact parameters of order the Debye length,Footnote
1
beyond which particles will not interact because of Debye screening.
Note that by using a total collision operator
![]() $C_{\text{FP}}+C_{\text{Boltz}}$
as prescribed by (2.1), the Boltzmann operator has effectively been added twice, although different approximations are used to evaluate the two terms. A subset of collisions will therefore be double counted. One way to resolve this issue is to apply the Fokker–Planck operator only to collision angles smaller than some
$C_{\text{FP}}+C_{\text{Boltz}}$
as prescribed by (2.1), the Boltzmann operator has effectively been added twice, although different approximations are used to evaluate the two terms. A subset of collisions will therefore be double counted. One way to resolve this issue is to apply the Fokker–Planck operator only to collision angles smaller than some
![]() $\unicode[STIX]{x1D703}_{\text{m}}$
, and the knock-on (Boltzmann) operator for
$\unicode[STIX]{x1D703}_{\text{m}}$
, and the knock-on (Boltzmann) operator for
![]() $\unicode[STIX]{x1D703}>\unicode[STIX]{x1D703}_{\text{m}}$
. The Coulomb logarithm used in the Fokker–Planck operator then ought to be changed from (2.11) to
$\unicode[STIX]{x1D703}>\unicode[STIX]{x1D703}_{\text{m}}$
. The Coulomb logarithm used in the Fokker–Planck operator then ought to be changed from (2.11) to
When an incident electron of momentum
![]() $p$
knocks a stationary electron to momentum
$p$
knocks a stationary electron to momentum
![]() $p_{\text{m}}$
, the corresponding centre-of-mass scattering angle
$p_{\text{m}}$
, the corresponding centre-of-mass scattering angle
![]() $\unicode[STIX]{x1D703}_{\text{m}}$
is given by
$\unicode[STIX]{x1D703}_{\text{m}}$
is given by
By using this energy-dependent modification to the Coulomb logarithm, no collisions will be double counted. Indeed, by taking the energy moment of the test-particle collision operator (the sum of Fokker–Planck and Boltzmann), it can be verified that with this choice, the average energy loss rate experienced by a test particle becomes independent of the cutoff
![]() $p_{\text{m}}$
, when
$p_{\text{m}}$
, when
![]() $p_{\text{m}}\ll m_{\text{e}}c$
.
$p_{\text{m}}\ll m_{\text{e}}c$
.
The number of collisions that are double counted can often be significant when this effect is unaccounted for. Assuming
![]() $v_{\text{m}}/c\sim \sqrt{E_{\text{c}}/E}$
to be located at a non-relativistic energy (that is, we assume
$v_{\text{m}}/c\sim \sqrt{E_{\text{c}}/E}$
to be located at a non-relativistic energy (that is, we assume
![]() $E\gg E_{\text{c}}$
), the modification to the Coulomb logarithm is approximately given by
$E\gg E_{\text{c}}$
), the modification to the Coulomb logarithm is approximately given by
![]() $\ln \sqrt{2(E/E_{c})(\unicode[STIX]{x1D6FE}-1)}$
. For highly energetic electrons with
$\ln \sqrt{2(E/E_{c})(\unicode[STIX]{x1D6FE}-1)}$
. For highly energetic electrons with
![]() $\unicode[STIX]{x1D6FE}\sim 50$
and
$\unicode[STIX]{x1D6FE}\sim 50$
and
![]() $E/E_{\text{c}}\sim 100$
, this corresponds to a change of approximately 5, which – depending on plasma parameters – typically constitutes a relative change to the Coulomb logarithm of 25–50 %.
$E/E_{\text{c}}\sim 100$
, this corresponds to a change of approximately 5, which – depending on plasma parameters – typically constitutes a relative change to the Coulomb logarithm of 25–50 %.
In principle, as
![]() $\unicode[STIX]{x1D703}_{\text{m}}$
approaches the cutoff imposed by Debye screening (or the binding energy of atoms in the case of electrons in neutral media), the Boltzmann operator will account for all collisions and
$\unicode[STIX]{x1D703}_{\text{m}}$
approaches the cutoff imposed by Debye screening (or the binding energy of atoms in the case of electrons in neutral media), the Boltzmann operator will account for all collisions and
![]() $\overline{\ln \unicode[STIX]{x1D6EC}}=0$
. However, this corresponds to a cutoff momentum smaller than thermal,
$\overline{\ln \unicode[STIX]{x1D6EC}}=0$
. However, this corresponds to a cutoff momentum smaller than thermal,
![]() $p_{\text{m}}\ll p_{\text{Te}}$
, and the assumption of stationary targets is violated when evaluating the operator in the bulk region. In addition, to numerically resolve the Boltzmann operator in a finite-difference scheme, the grid spacing in momentum must be much smaller than
$p_{\text{m}}\ll p_{\text{Te}}$
, and the assumption of stationary targets is violated when evaluating the operator in the bulk region. In addition, to numerically resolve the Boltzmann operator in a finite-difference scheme, the grid spacing in momentum must be much smaller than
![]() $p_{\text{m}}$
, and it is therefore desirable to choose
$p_{\text{m}}$
, and it is therefore desirable to choose
![]() $p_{\text{m}}$
as large as allowed while having a well converged description of the secondary generation rate. The sensitivity of the result to the choice of
$p_{\text{m}}$
as large as allowed while having a well converged description of the secondary generation rate. The sensitivity of the result to the choice of
![]() $p_{\text{m}}$
is investigated in the next section.
$p_{\text{m}}$
is investigated in the next section.
In the following we will find it more useful not to work with the symmetric form of the Boltzmann operator given by (2.8), but instead use the alternative given directly from (2.7),
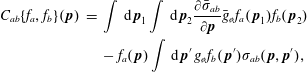
where
![]() $\unicode[STIX]{x1D70E}_{ab}(\,\boldsymbol{p},\boldsymbol{p}^{\prime })=\int \,\text{d}\,\boldsymbol{p}_{1}\unicode[STIX]{x2202}\unicode[STIX]{x1D70E}_{ab}/\unicode[STIX]{x2202}\boldsymbol{p}_{1}$
is the total cross-section.
$\unicode[STIX]{x1D70E}_{ab}(\,\boldsymbol{p},\boldsymbol{p}^{\prime })=\int \,\text{d}\,\boldsymbol{p}_{1}\unicode[STIX]{x2202}\unicode[STIX]{x1D70E}_{ab}/\unicode[STIX]{x2202}\boldsymbol{p}_{1}$
is the total cross-section.
2.2 Derivation of a conservative knock-on operator
For the avalanche problem, one is concerned with the electron–electron Boltzmann operator. We consider the scenario where a small runaway population has been accelerated by an electric field (or other mechanism), leaving a largely intact thermal bulk population. We may then write our electron distribution as
![]() $f_{\text{e}}(\,\boldsymbol{p})=f_{\text{Me}}(\,\boldsymbol{p})+\unicode[STIX]{x1D6FF}f_{\text{e}}(\,\boldsymbol{p})$
, where the runaway distribution
$f_{\text{e}}(\,\boldsymbol{p})=f_{\text{Me}}(\,\boldsymbol{p})+\unicode[STIX]{x1D6FF}f_{\text{e}}(\,\boldsymbol{p})$
, where the runaway distribution
![]() $\unicode[STIX]{x1D6FF}f_{\text{e}}$
is much smaller than the bulk distribution
$\unicode[STIX]{x1D6FF}f_{\text{e}}$
is much smaller than the bulk distribution
![]() $f_{\text{Me}}$
,
$f_{\text{Me}}$
,
![]() $\Vert \unicode[STIX]{x1D6FF}f_{\text{e}}\Vert \ll \Vert f_{\text{Me}}\Vert$
(for example in terms of number densities
$\Vert \unicode[STIX]{x1D6FF}f_{\text{e}}\Vert \ll \Vert f_{\text{Me}}\Vert$
(for example in terms of number densities
![]() $n_{\text{RE}}\ll n_{\text{e}}$
). We may then linearize the bilinear Boltzmann operator by ignoring terms quadratic in
$n_{\text{RE}}\ll n_{\text{e}}$
). We may then linearize the bilinear Boltzmann operator by ignoring terms quadratic in
![]() $\unicode[STIX]{x1D6FF}f_{\text{e}}$
, obtaining
$\unicode[STIX]{x1D6FF}f_{\text{e}}$
, obtaining
where terms
![]() $C_{\text{ee}}\{f_{\text{Me}},f_{\text{Me}}\}$
vanish since
$C_{\text{ee}}\{f_{\text{Me}},f_{\text{Me}}\}$
vanish since
![]() $f_{\text{Me}}$
is chosen as an equilibrium distribution. The first term, the test-particle term, describes the effect of large-angle collisions on the runaway electrons as they collide with the thermal population. The second term, the field-particle term, describes the reaction of the bulk electrons as they are being struck by the runaways. Intuitively, one could expect this field-particle term to constitute the avalanche knock-on source. We shall show below that this is indeed the case.
$f_{\text{Me}}$
is chosen as an equilibrium distribution. The first term, the test-particle term, describes the effect of large-angle collisions on the runaway electrons as they collide with the thermal population. The second term, the field-particle term, describes the reaction of the bulk electrons as they are being struck by the runaways. Intuitively, one could expect this field-particle term to constitute the avalanche knock-on source. We shall show below that this is indeed the case.
Before giving the explicit forms of the collision operator, we will make one final approximation. We assume that both the incident and outgoing electrons in the large-angle collisions are significantly faster than the thermal speed
![]() $v_{\text{Te}}=\sqrt{2T_{\text{e}}/m_{\text{e}}}$
, so that we may approximate the bulk population with a Dirac delta function:
$v_{\text{Te}}=\sqrt{2T_{\text{e}}/m_{\text{e}}}$
, so that we may approximate the bulk population with a Dirac delta function:
![]() $f_{\text{Me}}(\,\boldsymbol{p})\approx n_{\text{e}}\unicode[STIX]{x1D6FF}(\,\boldsymbol{p})$
. The collision operator then takes the form
$f_{\text{Me}}(\,\boldsymbol{p})\approx n_{\text{e}}\unicode[STIX]{x1D6FF}(\,\boldsymbol{p})$
. The collision operator then takes the form
The total cross-section
![]() $\unicode[STIX]{x1D70E}_{\text{ee}}(\,\boldsymbol{p})$
is given in (A 9) in appendix A. The limiting momenta
$\unicode[STIX]{x1D70E}_{\text{ee}}(\,\boldsymbol{p})$
is given in (A 9) in appendix A. The limiting momenta
![]() $q^{\ast }$
and
$q^{\ast }$
and
![]() $q_{0}$
are determined from constraints imposed by conservation laws. For the gain term, i.e. the first term in each equation, energy conservation in each collision reads
$q_{0}$
are determined from constraints imposed by conservation laws. For the gain term, i.e. the first term in each equation, energy conservation in each collision reads
![]() $\unicode[STIX]{x1D6FE}_{1}=\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D6FE}^{\prime }-1$
, where
$\unicode[STIX]{x1D6FE}_{1}=\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D6FE}^{\prime }-1$
, where
![]() $\unicode[STIX]{x1D6FE}$
and
$\unicode[STIX]{x1D6FE}$
and
![]() $\unicode[STIX]{x1D6FE}^{\prime }$
are the Lorentz factors of the two electrons after the collision. The conditions
$\unicode[STIX]{x1D6FE}^{\prime }$
are the Lorentz factors of the two electrons after the collision. The conditions
![]() $\unicode[STIX]{x1D6FE}^{\prime }>\unicode[STIX]{x1D6FE}$
or
$\unicode[STIX]{x1D6FE}^{\prime }>\unicode[STIX]{x1D6FE}$
or
![]() $\unicode[STIX]{x1D6FE}^{\prime }<\unicode[STIX]{x1D6FE}$
determines whether
$\unicode[STIX]{x1D6FE}^{\prime }<\unicode[STIX]{x1D6FE}$
determines whether
![]() $\unicode[STIX]{x1D6FE}$
refers to the bulk particle or runaway particle after the collision, respectively (note that the electrons are in fact indistinguishable, but an artificial distinction like this must be performed in order to avoid double counting). We therefore obtain
$\unicode[STIX]{x1D6FE}$
refers to the bulk particle or runaway particle after the collision, respectively (note that the electrons are in fact indistinguishable, but an artificial distinction like this must be performed in order to avoid double counting). We therefore obtain
![]() $q^{\ast }$
from setting
$q^{\ast }$
from setting
![]() $\unicode[STIX]{x1D6FE}^{\prime }=\unicode[STIX]{x1D6FE}$
in the conservation law, giving
$\unicode[STIX]{x1D6FE}^{\prime }=\unicode[STIX]{x1D6FE}$
in the conservation law, giving
![]() $\unicode[STIX]{x1D6FE}^{\ast }=2\unicode[STIX]{x1D6FE}-1$
, which corresponds to
$\unicode[STIX]{x1D6FE}^{\ast }=2\unicode[STIX]{x1D6FE}-1$
, which corresponds to
![]() $q^{\ast }=m_{\text{e}}c\sqrt{\unicode[STIX]{x1D6FE}^{\ast 2}-1}$
.
$q^{\ast }=m_{\text{e}}c\sqrt{\unicode[STIX]{x1D6FE}^{\ast 2}-1}$
.
Similarly, we cannot account for all collisions, since we have assumed the bulk particles to be much slower than the outgoing particles. We therefore choose to account only for those collisions where incident and outgoing particles have momenta larger than some
![]() $p=p_{\text{m}}\gg p_{\text{Te}}$
. Setting
$p=p_{\text{m}}\gg p_{\text{Te}}$
. Setting
![]() $\unicode[STIX]{x1D6FE}^{\prime }=\unicode[STIX]{x1D6FE}_{\text{m}}$
then yields the lower limit
$\unicode[STIX]{x1D6FE}^{\prime }=\unicode[STIX]{x1D6FE}_{\text{m}}$
then yields the lower limit
![]() $\unicode[STIX]{x1D6FE}_{0}=\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D6FE}_{\text{m}}-1$
, corresponding to
$\unicode[STIX]{x1D6FE}_{0}=\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D6FE}_{\text{m}}-1$
, corresponding to
![]() $q_{0}=m_{\text{e}}c\sqrt{\unicode[STIX]{x1D6FE}_{0}^{2}-1}$
. Note that for the total operator
$q_{0}=m_{\text{e}}c\sqrt{\unicode[STIX]{x1D6FE}_{0}^{2}-1}$
. Note that for the total operator
![]() $C_{\text{Boltz}}$
, the two gain terms in (2.16) and (2.17) combine into one integral, taken over all momenta
$C_{\text{Boltz}}$
, the two gain terms in (2.16) and (2.17) combine into one integral, taken over all momenta
![]() $p_{1}>q_{0}$
. The full expression is thus independent of the parameter
$p_{1}>q_{0}$
. The full expression is thus independent of the parameter
![]() $q^{\ast }$
which distinguishes the two outgoing particles (as is expected, since the distinction is not physically relevant for scattering of identical particles).
$q^{\ast }$
which distinguishes the two outgoing particles (as is expected, since the distinction is not physically relevant for scattering of identical particles).
We can now derive explicit expressions for the collision operator. Since there are only two degrees of freedom in the scattering process (for example two independent scattering angles), the differential cross-section
![]() $\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D70E}}_{\text{ee}}/\unicode[STIX]{x2202}\boldsymbol{p}$
will invariably contain a delta function. In Møller scattering (relativistic electron–electron scattering), the cross-section is azimuthally symmetric (assuming the electrons to be spin unpolarized) and takes the form
$\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D70E}}_{\text{ee}}/\unicode[STIX]{x2202}\boldsymbol{p}$
will invariably contain a delta function. In Møller scattering (relativistic electron–electron scattering), the cross-section is azimuthally symmetric (assuming the electrons to be spin unpolarized) and takes the form
where
![]() $\unicode[STIX]{x1D703}_{\text{s}}$
is the deflection angle,
$\unicode[STIX]{x1D703}_{\text{s}}$
is the deflection angle,
![]() $\unicode[STIX]{x1D6F4}$
is defined in (2.4) and
$\unicode[STIX]{x1D6F4}$
is defined in (2.4) and
![]() $\unicode[STIX]{x1D709}^{\ast }$
is defined in (2.5). The delta function enforces the relation between scattering angle and energy transfer that follows from the conservation of 4-momentum. The gain term then takes the form
$\unicode[STIX]{x1D709}^{\ast }$
is defined in (2.5). The delta function enforces the relation between scattering angle and energy transfer that follows from the conservation of 4-momentum. The gain term then takes the form
 $$\begin{eqnarray}\displaystyle n_{\text{e}}\int \,\text{d}\,\boldsymbol{p}_{1}\,v_{1}\frac{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D70E}}_{\text{ee}}}{\unicode[STIX]{x2202}\boldsymbol{p}}f_{\text{e}}(\,\boldsymbol{p}_{1}) & = & \displaystyle \frac{1}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70F}_{\text{c}}\ln \unicode[STIX]{x1D6EC}}\frac{1}{p\unicode[STIX]{x1D6FE}}\int \,\text{d}p_{1}\frac{p_{1}^{3}}{\unicode[STIX]{x1D6FE}_{1}}\unicode[STIX]{x1D6F4}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}_{1})\nonumber\\ \displaystyle & & \displaystyle \times \,\int \,\text{d}\unicode[STIX]{x1D709}_{1}\,\text{d}\unicode[STIX]{x1D711}_{1}\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D709}_{s}-\unicode[STIX]{x1D709}^{\ast })f_{\text{e}}(\,\boldsymbol{p}_{1}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle n_{\text{e}}\int \,\text{d}\,\boldsymbol{p}_{1}\,v_{1}\frac{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D70E}}_{\text{ee}}}{\unicode[STIX]{x2202}\boldsymbol{p}}f_{\text{e}}(\,\boldsymbol{p}_{1}) & = & \displaystyle \frac{1}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70F}_{\text{c}}\ln \unicode[STIX]{x1D6EC}}\frac{1}{p\unicode[STIX]{x1D6FE}}\int \,\text{d}p_{1}\frac{p_{1}^{3}}{\unicode[STIX]{x1D6FE}_{1}}\unicode[STIX]{x1D6F4}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}_{1})\nonumber\\ \displaystyle & & \displaystyle \times \,\int \,\text{d}\unicode[STIX]{x1D709}_{1}\,\text{d}\unicode[STIX]{x1D711}_{1}\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D709}_{s}-\unicode[STIX]{x1D709}^{\ast })f_{\text{e}}(\,\boldsymbol{p}_{1}).\end{eqnarray}$$
This expression (when choosing integration limits appropriate for the field-particle term) is the generalized ‘knock-on source term’
![]() $S$
, which reduces to the expressions given by Rosenbluth & Putvinski (Reference Rosenbluth and Putvinski1997) and Chiu et al. (Reference Chiu, Rosenbluth, Harvey and Chan1998) – (2.2) and (2.3), respectively – using appropriate approximations, as shown in appendix B. This connection has not been acknowledged in previous studies, to the degree that Chiu et al. (Reference Chiu, Rosenbluth, Harvey and Chan1998) incorrectly ascribe the discrepancy between their result and that of Besedin & Pankratov (Reference Besedin and Pankratov1986) by the fact that ‘The present expressions are simply a statement of the total rate at which electrons in different velocity-space elements of primary electrons knock a collection of cold bulk electrons into velocity-space elements of the secondary electrons. The expression in (Besedin & Pankratov Reference Besedin and Pankratov1986) uses a Boltzmann-like integral operator’. In fact, as we show in appendix B, the approaches are completely equivalent, and the discrepancy is the result of an error in the calculation of Besedin & Pankratov (Reference Besedin and Pankratov1986).
$S$
, which reduces to the expressions given by Rosenbluth & Putvinski (Reference Rosenbluth and Putvinski1997) and Chiu et al. (Reference Chiu, Rosenbluth, Harvey and Chan1998) – (2.2) and (2.3), respectively – using appropriate approximations, as shown in appendix B. This connection has not been acknowledged in previous studies, to the degree that Chiu et al. (Reference Chiu, Rosenbluth, Harvey and Chan1998) incorrectly ascribe the discrepancy between their result and that of Besedin & Pankratov (Reference Besedin and Pankratov1986) by the fact that ‘The present expressions are simply a statement of the total rate at which electrons in different velocity-space elements of primary electrons knock a collection of cold bulk electrons into velocity-space elements of the secondary electrons. The expression in (Besedin & Pankratov Reference Besedin and Pankratov1986) uses a Boltzmann-like integral operator’. In fact, as we show in appendix B, the approaches are completely equivalent, and the discrepancy is the result of an error in the calculation of Besedin & Pankratov (Reference Besedin and Pankratov1986).
There are multiple ways of carrying out the integration over the delta function; if we assume a distribution function independent of gyroangle,
![]() $f_{\text{e}}(\,\boldsymbol{p}_{1})=f_{\text{e}}(p_{1},\cos \unicode[STIX]{x1D703}_{1})$
, a few convenient expressions are given by
$f_{\text{e}}(\,\boldsymbol{p}_{1})=f_{\text{e}}(p_{1},\cos \unicode[STIX]{x1D703}_{1})$
, a few convenient expressions are given by
 $$\begin{eqnarray}\displaystyle \int _{-1}^{1}\,\text{d}\unicode[STIX]{x1D709}_{1}\int _{0}^{2\unicode[STIX]{x03C0}}\,\text{d}\unicode[STIX]{x1D711}_{1}\,\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D709}_{s}-\unicode[STIX]{x1D709}^{\ast })f_{\text{e}}(p_{1},\unicode[STIX]{x1D709}_{1}) & = & \displaystyle \int _{0}^{2\unicode[STIX]{x03C0}}\,\text{d}\unicode[STIX]{x1D711}_{\text{s}}\,\,f_{\text{e}}(p_{1},\unicode[STIX]{x1D709}_{1})\nonumber\\ \displaystyle & = & \displaystyle 2\int _{\cos (\unicode[STIX]{x1D703}+\unicode[STIX]{x1D703}^{\ast })}^{\cos (\unicode[STIX]{x1D703}-\unicode[STIX]{x1D703}^{\ast })}\,\text{d}\unicode[STIX]{x1D709}_{1}\frac{f_{\text{e}}(p_{1},\unicode[STIX]{x1D709}_{1})}{\sqrt{1-\unicode[STIX]{x1D709}^{\ast 2}-\unicode[STIX]{x1D709}_{1}^{2}-\unicode[STIX]{x1D709}^{2}+2\unicode[STIX]{x1D709}^{\ast }\unicode[STIX]{x1D709}_{1}\unicode[STIX]{x1D709}}}\nonumber\\ \displaystyle & = & \displaystyle 2\unicode[STIX]{x03C0}\mathop{\sum }_{L}f_{L}(p_{1})P_{L}(\unicode[STIX]{x1D709})P_{L}(\unicode[STIX]{x1D709}^{\ast }),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{-1}^{1}\,\text{d}\unicode[STIX]{x1D709}_{1}\int _{0}^{2\unicode[STIX]{x03C0}}\,\text{d}\unicode[STIX]{x1D711}_{1}\,\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D709}_{s}-\unicode[STIX]{x1D709}^{\ast })f_{\text{e}}(p_{1},\unicode[STIX]{x1D709}_{1}) & = & \displaystyle \int _{0}^{2\unicode[STIX]{x03C0}}\,\text{d}\unicode[STIX]{x1D711}_{\text{s}}\,\,f_{\text{e}}(p_{1},\unicode[STIX]{x1D709}_{1})\nonumber\\ \displaystyle & = & \displaystyle 2\int _{\cos (\unicode[STIX]{x1D703}+\unicode[STIX]{x1D703}^{\ast })}^{\cos (\unicode[STIX]{x1D703}-\unicode[STIX]{x1D703}^{\ast })}\,\text{d}\unicode[STIX]{x1D709}_{1}\frac{f_{\text{e}}(p_{1},\unicode[STIX]{x1D709}_{1})}{\sqrt{1-\unicode[STIX]{x1D709}^{\ast 2}-\unicode[STIX]{x1D709}_{1}^{2}-\unicode[STIX]{x1D709}^{2}+2\unicode[STIX]{x1D709}^{\ast }\unicode[STIX]{x1D709}_{1}\unicode[STIX]{x1D709}}}\nonumber\\ \displaystyle & = & \displaystyle 2\unicode[STIX]{x03C0}\mathop{\sum }_{L}f_{L}(p_{1})P_{L}(\unicode[STIX]{x1D709})P_{L}(\unicode[STIX]{x1D709}^{\ast }),\end{eqnarray}$$
where we have introduced the quantities
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\cos \unicode[STIX]{x1D711}_{\text{s}}={\displaystyle \frac{\unicode[STIX]{x1D709}_{1}-\unicode[STIX]{x1D709}^{\ast }\unicode[STIX]{x1D709}}{\sqrt{1-\unicode[STIX]{x1D709}^{\ast 2}}\sqrt{1-\unicode[STIX]{x1D709}^{2}}}},\\ f_{L}(p)={\displaystyle \frac{2L+1}{2}}\displaystyle \int _{-1}^{1}\,\text{d}\unicode[STIX]{x1D709}\,f_{\text{e}}(p,\unicode[STIX]{x1D709})P_{L}(\unicode[STIX]{x1D709}).\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\cos \unicode[STIX]{x1D711}_{\text{s}}={\displaystyle \frac{\unicode[STIX]{x1D709}_{1}-\unicode[STIX]{x1D709}^{\ast }\unicode[STIX]{x1D709}}{\sqrt{1-\unicode[STIX]{x1D709}^{\ast 2}}\sqrt{1-\unicode[STIX]{x1D709}^{2}}}},\\ f_{L}(p)={\displaystyle \frac{2L+1}{2}}\displaystyle \int _{-1}^{1}\,\text{d}\unicode[STIX]{x1D709}\,f_{\text{e}}(p,\unicode[STIX]{x1D709})P_{L}(\unicode[STIX]{x1D709}).\end{array}\right\}\end{eqnarray}$$
In particular the form involving Legendre polynomials
![]() $P_{L}$
is a powerful result, as it demonstrates that the linearized Boltzmann operator is diagonal in
$P_{L}$
is a powerful result, as it demonstrates that the linearized Boltzmann operator is diagonal in
![]() $L$
, in the sense that if
$L$
, in the sense that if
![]() $C_{\text{Boltz}}(\,\boldsymbol{p})=\sum _{L}C_{L}(p)P_{L}(\cos \unicode[STIX]{x1D703})$
, then
$C_{\text{Boltz}}(\,\boldsymbol{p})=\sum _{L}C_{L}(p)P_{L}(\cos \unicode[STIX]{x1D703})$
, then
![]() $C_{L}$
depends only on
$C_{L}$
depends only on
![]() $f_{L}$
(and not other
$f_{L}$
(and not other
![]() $f_{l}$
with
$f_{l}$
with
![]() $l\neq L$
). This behaviour exhibits the spherical symmetry inherent in scattering on stationary targets. Utilizing this property leads to significant practical gains in terms of numerical computation times. Analogous expressions in terms of Legendre polynomials and the integration over
$l\neq L$
). This behaviour exhibits the spherical symmetry inherent in scattering on stationary targets. Utilizing this property leads to significant practical gains in terms of numerical computation times. Analogous expressions in terms of Legendre polynomials and the integration over
![]() $\unicode[STIX]{x1D711}_{\text{s}}$
were also found by Gurevich & Zybin (Reference Gurevich and Zybin2001) for the so-called ionization integral in neutral gases. The form of the integral taken over
$\unicode[STIX]{x1D711}_{\text{s}}$
were also found by Gurevich & Zybin (Reference Gurevich and Zybin2001) for the so-called ionization integral in neutral gases. The form of the integral taken over
![]() $\unicode[STIX]{x1D709}_{1}$
was obtained by Helander, Lisak & Ryutov (Reference Helander, Lisak and Ryutov1993) in the analogous problem of elastic nucleon–nucleon scattering, and equivalent formulations were also recently given by Aleynikov et al. (Reference Aleynikov, Aleynikova, Breizman, Huijsmans, Konovalov, Putvinski and Zhogolev2014) and Boozer (Reference Boozer2015).
$\unicode[STIX]{x1D709}_{1}$
was obtained by Helander, Lisak & Ryutov (Reference Helander, Lisak and Ryutov1993) in the analogous problem of elastic nucleon–nucleon scattering, and equivalent formulations were also recently given by Aleynikov et al. (Reference Aleynikov, Aleynikova, Breizman, Huijsmans, Konovalov, Putvinski and Zhogolev2014) and Boozer (Reference Boozer2015).
The Legendre modes of the collision operator are explicitly given by
 $$\begin{eqnarray}\displaystyle C_{L}\{f_{\text{e}},f_{\text{Me}}\} & = & \displaystyle \frac{(m_{\text{e}}c)^{-3}}{2\unicode[STIX]{x1D70F}_{\text{c}}\ln \unicode[STIX]{x1D6EC}}\frac{1}{\unicode[STIX]{x1D6FE}p}\int _{q_{0}}^{q^{\ast }}\,\text{d}p_{1}\frac{p_{1}^{3}}{\unicode[STIX]{x1D6FE}_{1}}f_{L}(p_{1})P_{L}(\unicode[STIX]{x1D709}^{\ast })\unicode[STIX]{x1D6F4}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}_{1})\nonumber\\ \displaystyle & & \displaystyle -\,\frac{1}{4\unicode[STIX]{x1D70F}_{\text{c}}\ln \unicode[STIX]{x1D6EC}}\frac{v}{c}f_{L}(p)\int _{\unicode[STIX]{x1D6FE}_{\text{m}}}^{\unicode[STIX]{x1D6FE}+1-\unicode[STIX]{x1D6FE}_{\text{m}}}\,\text{d}\unicode[STIX]{x1D6FE}_{1}\unicode[STIX]{x1D6F4}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle C_{L}\{f_{\text{e}},f_{\text{Me}}\} & = & \displaystyle \frac{(m_{\text{e}}c)^{-3}}{2\unicode[STIX]{x1D70F}_{\text{c}}\ln \unicode[STIX]{x1D6EC}}\frac{1}{\unicode[STIX]{x1D6FE}p}\int _{q_{0}}^{q^{\ast }}\,\text{d}p_{1}\frac{p_{1}^{3}}{\unicode[STIX]{x1D6FE}_{1}}f_{L}(p_{1})P_{L}(\unicode[STIX]{x1D709}^{\ast })\unicode[STIX]{x1D6F4}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}_{1})\nonumber\\ \displaystyle & & \displaystyle -\,\frac{1}{4\unicode[STIX]{x1D70F}_{\text{c}}\ln \unicode[STIX]{x1D6EC}}\frac{v}{c}f_{L}(p)\int _{\unicode[STIX]{x1D6FE}_{\text{m}}}^{\unicode[STIX]{x1D6FE}+1-\unicode[STIX]{x1D6FE}_{\text{m}}}\,\text{d}\unicode[STIX]{x1D6FE}_{1}\unicode[STIX]{x1D6F4}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}),\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle C_{L}\{f_{\text{Me}},f_{\text{e}}\} & = & \displaystyle \frac{(m_{\text{e}}c)^{-3}}{2\unicode[STIX]{x1D70F}_{\text{c}}\ln \unicode[STIX]{x1D6EC}}\frac{1}{\unicode[STIX]{x1D6FE}p}\int _{q^{\ast }}^{\infty }\,\text{d}p_{1}\frac{p_{1}^{3}}{\unicode[STIX]{x1D6FE}_{1}}f_{L}(p_{1})P_{L}(\unicode[STIX]{x1D709}^{\ast })\unicode[STIX]{x1D6F4}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}_{1})\nonumber\\ \displaystyle & & \displaystyle -\,\frac{(m_{\text{e}}c)^{-1}}{4\unicode[STIX]{x1D70F}_{\text{c}}\ln \unicode[STIX]{x1D6EC}}\unicode[STIX]{x1D6FF}_{L,0}\frac{\unicode[STIX]{x1D6FF}(p)}{p^{2}}\int _{q_{0}(p_{\text{m}})}^{\infty }\,\text{d}p^{\prime }\frac{{p^{\prime }}^{3}}{\unicode[STIX]{x1D6FE}^{\prime }}f_{0}(p^{\prime })\int _{\unicode[STIX]{x1D6FE}_{\text{m}}}^{\unicode[STIX]{x1D6FE}^{\prime }+1-\unicode[STIX]{x1D6FE}_{\text{m}}}\,\text{d}\unicode[STIX]{x1D6FE}_{1}\unicode[STIX]{x1D6F4}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}^{\prime }).\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle C_{L}\{f_{\text{Me}},f_{\text{e}}\} & = & \displaystyle \frac{(m_{\text{e}}c)^{-3}}{2\unicode[STIX]{x1D70F}_{\text{c}}\ln \unicode[STIX]{x1D6EC}}\frac{1}{\unicode[STIX]{x1D6FE}p}\int _{q^{\ast }}^{\infty }\,\text{d}p_{1}\frac{p_{1}^{3}}{\unicode[STIX]{x1D6FE}_{1}}f_{L}(p_{1})P_{L}(\unicode[STIX]{x1D709}^{\ast })\unicode[STIX]{x1D6F4}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}_{1})\nonumber\\ \displaystyle & & \displaystyle -\,\frac{(m_{\text{e}}c)^{-1}}{4\unicode[STIX]{x1D70F}_{\text{c}}\ln \unicode[STIX]{x1D6EC}}\unicode[STIX]{x1D6FF}_{L,0}\frac{\unicode[STIX]{x1D6FF}(p)}{p^{2}}\int _{q_{0}(p_{\text{m}})}^{\infty }\,\text{d}p^{\prime }\frac{{p^{\prime }}^{3}}{\unicode[STIX]{x1D6FE}^{\prime }}f_{0}(p^{\prime })\int _{\unicode[STIX]{x1D6FE}_{\text{m}}}^{\unicode[STIX]{x1D6FE}^{\prime }+1-\unicode[STIX]{x1D6FE}_{\text{m}}}\,\text{d}\unicode[STIX]{x1D6FE}_{1}\unicode[STIX]{x1D6F4}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}^{\prime }).\qquad\end{eqnarray}$$
Note further that since we only consider those collisions where both the incident and outgoing particles have momenta
![]() $p>p_{\text{m}}$
, the gain terms must only be applied for
$p>p_{\text{m}}$
, the gain terms must only be applied for
![]() $\unicode[STIX]{x1D6FE}>\unicode[STIX]{x1D6FE}_{\text{m}}$
, while the test-particle loss term is applied for
$\unicode[STIX]{x1D6FE}>\unicode[STIX]{x1D6FE}_{\text{m}}$
, while the test-particle loss term is applied for
![]() $\unicode[STIX]{x1D6FE}>2\unicode[STIX]{x1D6FE}_{\text{m}}-1$
. In appendix A it is explicitly demonstrated that this collision operator conserves density, momentum and energy.
$\unicode[STIX]{x1D6FE}>2\unicode[STIX]{x1D6FE}_{\text{m}}-1$
. In appendix A it is explicitly demonstrated that this collision operator conserves density, momentum and energy.

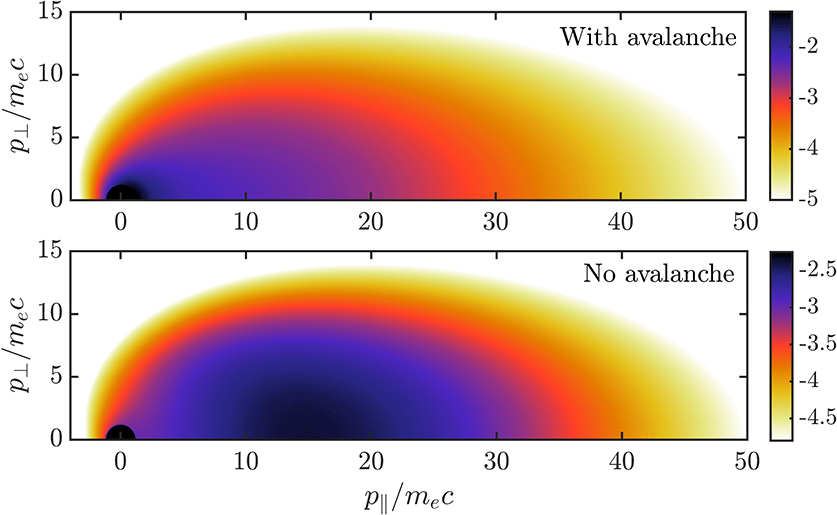
Figure 1. Illustration of the large-angle collision operators investigated in this study. Darker colours represent larger amplitudes (in arbitrary units), where white and black are separated by 3 orders of magnitude. (a) The distribution function
![]() $\log f_{\text{e}}$
with which we evaluate the large-angle collision operator; (c) the Chiu–Harvey operator
$\log f_{\text{e}}$
with which we evaluate the large-angle collision operator; (c) the Chiu–Harvey operator
![]() $\log C_{\text{CH}}$
; (d) the full field-particle operator
$\log C_{\text{CH}}$
; (d) the full field-particle operator
![]() $\log C_{\text{boltz}}^{\text{(fp)}}$
(dashed: the line
$\log C_{\text{boltz}}^{\text{(fp)}}$
(dashed: the line
![]() $\unicode[STIX]{x1D709}=\sqrt{(\unicode[STIX]{x1D6FE}-1)/(\unicode[STIX]{x1D6FE}+1)}$
, where the Rosenbluth–Putvinski operator creates knock-ons); (b) the magnitude of the full test-particle operator
$\unicode[STIX]{x1D709}=\sqrt{(\unicode[STIX]{x1D6FE}-1)/(\unicode[STIX]{x1D6FE}+1)}$
, where the Rosenbluth–Putvinski operator creates knock-ons); (b) the magnitude of the full test-particle operator
![]() $\log |C_{\text{boltz}}^{\text{(tp)}}|$
, where the dotted line separates the region of negative contributions (to the right) from the positive contributions (to the left).
$\log |C_{\text{boltz}}^{\text{(tp)}}|$
, where the dotted line separates the region of negative contributions (to the right) from the positive contributions (to the left).
A qualitative illustration of the large-angle collision operators discussed here is shown in figure 1. A test runaway distribution (figure 1
a) was generated by applying a constant electric field
![]() $E=15E_{\text{c}}$
for a short time
$E=15E_{\text{c}}$
for a short time
![]() $t\approx 0.5\unicode[STIX]{x1D70F}_{\text{c}}$
with
$t\approx 0.5\unicode[STIX]{x1D70F}_{\text{c}}$
with
![]() $Z_{\text{eff}}=5$
, and the large-angle collision operators were evaluated in the final time step. The figures show a snapshot of where large-angle collisions between runaways and bulk particles create or remove electrons in phase space; comparing 1(c) and 1(d) shows that the Chiu–Harvey operator creates secondary runaways in a significantly smaller region in momentum space than the full field-particle operator, however the total number of secondary runaways created is equal between the models. Figure 1(b) shows the Boltzmann test-particle operator, illustrating the reaction of the already present runaways: they are removed at small pitch angles where the runaway distribution is largest, and placed at larger pitch angles and lower energy. The sum of figure 1(b,d) is the full Boltzmann operator which conserves particle number, momentum and energy.
$Z_{\text{eff}}=5$
, and the large-angle collision operators were evaluated in the final time step. The figures show a snapshot of where large-angle collisions between runaways and bulk particles create or remove electrons in phase space; comparing 1(c) and 1(d) shows that the Chiu–Harvey operator creates secondary runaways in a significantly smaller region in momentum space than the full field-particle operator, however the total number of secondary runaways created is equal between the models. Figure 1(b) shows the Boltzmann test-particle operator, illustrating the reaction of the already present runaways: they are removed at small pitch angles where the runaway distribution is largest, and placed at larger pitch angles and lower energy. The sum of figure 1(b,d) is the full Boltzmann operator which conserves particle number, momentum and energy.
Note finally that all of the knock-on models described in this paper share the assumption of a stationary bulk, which means that the operators can only be evaluated at speeds much larger than the thermal speed
![]() $v_{\text{Te}}$
. Since the sources must be applied for speeds smaller than the critical speed
$v_{\text{Te}}$
. Since the sources must be applied for speeds smaller than the critical speed
![]() $v_{c}$
in order to accurately capture the runaway rate, the condition
$v_{c}$
in order to accurately capture the runaway rate, the condition
![]() $v_{\text{Te}}\ll v_{c}$
limits the electric-field values to
$v_{\text{Te}}\ll v_{c}$
limits the electric-field values to
![]() $\sqrt{E}\ll \sqrt{E_{\text{D}}/2}$
(effectively forming a lower limit in density and an upper limit in temperature for a given
$\sqrt{E}\ll \sqrt{E_{\text{D}}/2}$
(effectively forming a lower limit in density and an upper limit in temperature for a given
![]() $E$
). As a consequence, avalanche generation in electric fields large enough for Dreicer generation to be significant is not accessible by the models used here. This limitation would be resolved by accounting for the velocity distribution of the target population in (2.7), resulting in a significantly more complicated operator. However, in many scenarios of interest this is not an issue; the critical velocity tends to be significantly larger than thermal, or is comparable only for a relatively short period of time during which a runaway seed is generated, which then proceeds to grow primarily by avalanche generation.
$E$
). As a consequence, avalanche generation in electric fields large enough for Dreicer generation to be significant is not accessible by the models used here. This limitation would be resolved by accounting for the velocity distribution of the target population in (2.7), resulting in a significantly more complicated operator. However, in many scenarios of interest this is not an issue; the critical velocity tends to be significantly larger than thermal, or is comparable only for a relatively short period of time during which a runaway seed is generated, which then proceeds to grow primarily by avalanche generation.
3 Numerical study of the effect of large-angle collisions
We use the kinetic equation solver CODE (Landreman et al.
Reference Landreman, Stahl and Fülöp2014; Stahl et al.
Reference Stahl, Embréus, Papp, Landreman and Fülöp2016) to compare the various models for the knock-on collision operator. We use CODE to solve the relativistic 0D
![]() $+$
2P kinetic equation for the electron distribution
$+$
2P kinetic equation for the electron distribution
where
![]() $\boldsymbol{F}_{L}$
is the Lorentz force, and
$\boldsymbol{F}_{L}$
is the Lorentz force, and
![]() $\boldsymbol{F}_{S}$
is the radiation reaction force associated with synchrotron radiation and the brackets denote averaging over the azimuthal (gyro) angle.
$\boldsymbol{F}_{S}$
is the radiation reaction force associated with synchrotron radiation and the brackets denote averaging over the azimuthal (gyro) angle.
![]() $C_{\text{ei}}$
and
$C_{\text{ei}}$
and
![]() $C_{\text{ee}}$
are the gyroaveraged Fokker–Planck collision operators for electron–ion and electron–electron collisions, respectively. The thermal bulk population is resolved in the simulations, as well as the relativistic runaway tail. The collision operator
$C_{\text{ee}}$
are the gyroaveraged Fokker–Planck collision operators for electron–ion and electron–electron collisions, respectively. The thermal bulk population is resolved in the simulations, as well as the relativistic runaway tail. The collision operator
![]() $C_{\text{ei}}+C_{\text{ee}}$
and the numerical scheme used are described in Landreman et al. (Reference Landreman, Stahl and Fülöp2014). In the numerical solutions of (3.1) a Dirichlet boundary condition
$C_{\text{ei}}+C_{\text{ee}}$
and the numerical scheme used are described in Landreman et al. (Reference Landreman, Stahl and Fülöp2014). In the numerical solutions of (3.1) a Dirichlet boundary condition
![]() $f_{e}=0$
is imposed at the upper boundary
$f_{e}=0$
is imposed at the upper boundary
![]() $p_{\max }$
in momentum. The boundary is chosen large enough for the results to be insensitive to variations in
$p_{\max }$
in momentum. The boundary is chosen large enough for the results to be insensitive to variations in
![]() $p_{\max }$
or details of the boundary condition; the value of the distribution is naturally negligibly small near the boundary, since it asymptotically tends to decrease exponentially with energy.
$p_{\max }$
or details of the boundary condition; the value of the distribution is naturally negligibly small near the boundary, since it asymptotically tends to decrease exponentially with energy.
First, we will study the sensitivity of the avalanche dynamics to the arbitrary cutoff parameter
![]() $p_{\text{m}}$
and investigate the effects of adding the test-particle Boltzmann operator, which restores conservation laws in the knock-on collisions. We then focus on two scenarios: (i) we revisit the classical calculation of the steady-state avalanche growth rate in a constant electric field, (ii) we calculate the runaway growth rate in the near-critical field, accounting for synchrotron energy loss.
$p_{\text{m}}$
and investigate the effects of adding the test-particle Boltzmann operator, which restores conservation laws in the knock-on collisions. We then focus on two scenarios: (i) we revisit the classical calculation of the steady-state avalanche growth rate in a constant electric field, (ii) we calculate the runaway growth rate in the near-critical field, accounting for synchrotron energy loss.
3.1 Sensitivity to the cutoff parameter
 $p_{\text{m}}$
$p_{\text{m}}$
We will now demonstrate that our complete knock-on model satisfies the essential property that the solutions to the kinetic equation are independent of the arbitrary cutoff momentum
![]() $p_{m}$
, as long as it is chosen small enough. To determine the sensitivity of the solutions to
$p_{m}$
, as long as it is chosen small enough. To determine the sensitivity of the solutions to
![]() $p_{\text{m}}$
, we will consider the instantaneous runaway growth rate when the primary runaway population is described by a shifted Maxwellian runaway distribution
$p_{\text{m}}$
, we will consider the instantaneous runaway growth rate when the primary runaway population is described by a shifted Maxwellian runaway distribution
![]() $f_{\text{RE}}\propto \exp [-(\,\boldsymbol{p}-\boldsymbol{p}_{0})^{2}/q^{2}]$
. For this test we have chosen the momentum
$f_{\text{RE}}\propto \exp [-(\,\boldsymbol{p}-\boldsymbol{p}_{0})^{2}/q^{2}]$
. For this test we have chosen the momentum
![]() $p_{0}\approx 6m_{\text{e}}c$
in the parallel direction, with width
$p_{0}\approx 6m_{\text{e}}c$
in the parallel direction, with width
![]() $q\approx 0.6m_{\text{e}}c$
. Two electric-field strengths are investigated, a low-field case where
$q\approx 0.6m_{\text{e}}c$
. Two electric-field strengths are investigated, a low-field case where
![]() $E=3E_{\text{c}}$
and a high-field case
$E=3E_{\text{c}}$
and a high-field case
![]() $E=100E_{\text{c}}$
. The resulting growth rates are shown in figure 2, as a function of the cutoff
$E=100E_{\text{c}}$
. The resulting growth rates are shown in figure 2, as a function of the cutoff
![]() $p_{\text{m}}$
after a short time
$p_{\text{m}}$
after a short time
![]() $0.03\unicode[STIX]{x1D70F}_{\text{c}}$
. The growth rate obtained using the field-particle operator alone is nearly independent of
$0.03\unicode[STIX]{x1D70F}_{\text{c}}$
. The growth rate obtained using the field-particle operator alone is nearly independent of
![]() $p_{\text{m}}$
as long as it is smaller than
$p_{\text{m}}$
as long as it is smaller than
![]() $p_{c}$
, indicating that secondary particles created with momentum
$p_{c}$
, indicating that secondary particles created with momentum
![]() $p<p_{c}$
are unlikely to run away. For the Rosenbluth–Putvinski operator, this behaviour was also observed by Nilsson et al. (Reference Nilsson, Decker, Peysson, Granetz, Saint-Laurent and Vlainic2015).
$p<p_{c}$
are unlikely to run away. For the Rosenbluth–Putvinski operator, this behaviour was also observed by Nilsson et al. (Reference Nilsson, Decker, Peysson, Granetz, Saint-Laurent and Vlainic2015).
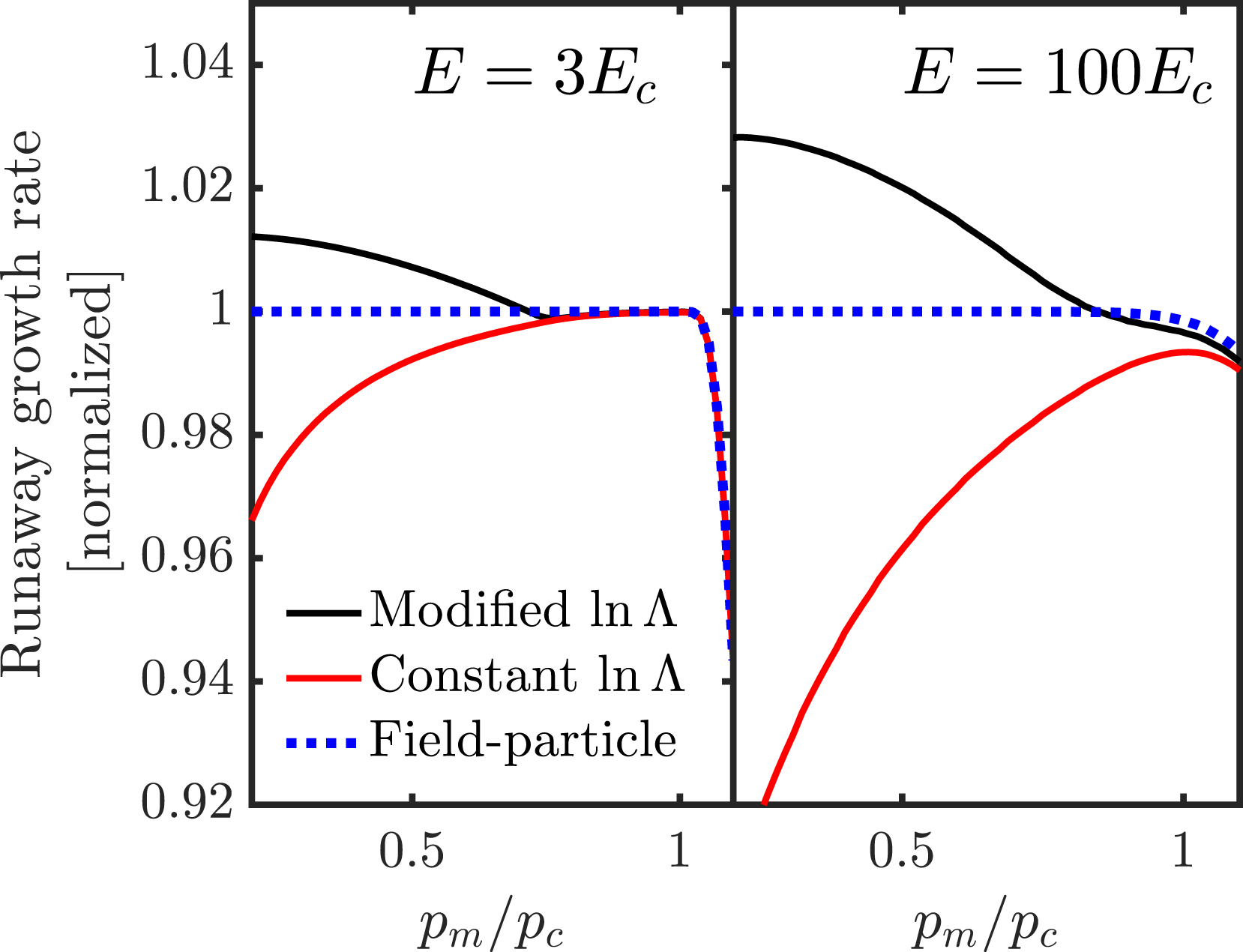
Figure 2. Runaway growth rate as function of momentum cutoff parameter
![]() $p_{\text{m}}$
for two different electric fields, normalized to the field-particle
$p_{\text{m}}$
for two different electric fields, normalized to the field-particle
![]() $p_{m}=0$
value. Lines correspond to (dotted blue) the field-particle Boltzmann operator, equation (2.24) and (solid) the full operator including the test-particle operator when (red)
$p_{m}=0$
value. Lines correspond to (dotted blue) the field-particle Boltzmann operator, equation (2.24) and (solid) the full operator including the test-particle operator when (red)
![]() $\ln \unicode[STIX]{x1D6EC}$
is held fixed or (black) modified according to (2.12), which is the physically most correct model. Plasma parameters: thermal electron density
$\ln \unicode[STIX]{x1D6EC}$
is held fixed or (black) modified according to (2.12), which is the physically most correct model. Plasma parameters: thermal electron density
![]() $n_{\text{e}}=10^{20}~\text{m}^{-3}$
; temperature
$n_{\text{e}}=10^{20}~\text{m}^{-3}$
; temperature
![]() $T_{\text{e}}=100~\text{eV}$
.
$T_{\text{e}}=100~\text{eV}$
.
When the test-particle operator is added, but the Coulomb logarithm
![]() $\ln \unicode[STIX]{x1D6EC}$
is left unmodified, the growth rate is decreased. This can be understood from the fact that the test-particle operator represents a source of energy loss for the runaways, which diverges logarithmically as
$\ln \unicode[STIX]{x1D6EC}$
is left unmodified, the growth rate is decreased. This can be understood from the fact that the test-particle operator represents a source of energy loss for the runaways, which diverges logarithmically as
![]() $p_{\text{m}}\rightarrow 0$
. When
$p_{\text{m}}\rightarrow 0$
. When
![]() $\ln \unicode[STIX]{x1D6EC}$
is modified (black line in figure 2, representing the most physically accurate model), the mean energy loss rate of a runaway becomes independent of
$\ln \unicode[STIX]{x1D6EC}$
is modified (black line in figure 2, representing the most physically accurate model), the mean energy loss rate of a runaway becomes independent of
![]() $p_{\text{m}}$
. The growth rate, however, is found to increase with decreasing
$p_{\text{m}}$
. The growth rate, however, is found to increase with decreasing
![]() $p_{\text{m}}$
, settling to a constant value in the limit
$p_{\text{m}}$
, settling to a constant value in the limit
![]() $p_{\text{m}}\rightarrow 0$
. The underlying mechanism for this behaviour is that a fraction of all collisions are now accounted for with a Boltzmann operator rather than with a Fokker–Planck operator. This leads to an increase in the runaway probability for particles with
$p_{\text{m}}\rightarrow 0$
. The underlying mechanism for this behaviour is that a fraction of all collisions are now accounted for with a Boltzmann operator rather than with a Fokker–Planck operator. This leads to an increase in the runaway probability for particles with
![]() $p<p_{c}$
, since the Boltzmann operator fully captures the stochastic nature of the collisions; instead of continuously experiencing the average energy loss, an electron is accelerated freely until it undergoes a collision, by which point it may have gained enough energy to enter the runaway region (
$p<p_{c}$
, since the Boltzmann operator fully captures the stochastic nature of the collisions; instead of continuously experiencing the average energy loss, an electron is accelerated freely until it undergoes a collision, by which point it may have gained enough energy to enter the runaway region (
![]() $p>p_{c}$
). Note that this effect only appears to modify the growth rate with a few per cent, the effect being weaker for smaller electric fields. The effect is, however, directly proportional to
$p>p_{c}$
). Note that this effect only appears to modify the growth rate with a few per cent, the effect being weaker for smaller electric fields. The effect is, however, directly proportional to
![]() $1/\ln \unicode[STIX]{x1D6EC}$
, as it depends on the relative importance of small- and large-angle collisions. This implies that for higher-density or lower-temperature plasmas, the effect can be expected to be more pronounced.
$1/\ln \unicode[STIX]{x1D6EC}$
, as it depends on the relative importance of small- and large-angle collisions. This implies that for higher-density or lower-temperature plasmas, the effect can be expected to be more pronounced.
It should be remarked that the field-particle knock-on operator uses a constant Coulomb logarithm in the Fokker–Planck operator, yet is still well behaved when
![]() $p_{m}$
becomes small. We have pointed out that the field-particle knock-on operators, like those used in previous runaway avalanche studies, double count collisions with the Fokker–Planck operator. However, they do so only with the field-particle Fokker–Planck operator, and not the test-particle operator which describes the friction on runaways. Therefore, only the Coulomb logarithm in the field-particle operator should be modified when using such models. The field-particle Fokker–Planck operator is essential when considering the dynamics of the bulk population, however it does not significantly affect the avalanche growth rate, thereby explaining the insensitivity to
$p_{m}$
becomes small. We have pointed out that the field-particle knock-on operators, like those used in previous runaway avalanche studies, double count collisions with the Fokker–Planck operator. However, they do so only with the field-particle Fokker–Planck operator, and not the test-particle operator which describes the friction on runaways. Therefore, only the Coulomb logarithm in the field-particle operator should be modified when using such models. The field-particle Fokker–Planck operator is essential when considering the dynamics of the bulk population, however it does not significantly affect the avalanche growth rate, thereby explaining the insensitivity to
![]() $p_{m}$
for
$p_{m}$
for
![]() $p_{m}\lesssim p_{c}$
.
$p_{m}\lesssim p_{c}$
.
3.2 Steady-state avalanche growth rate at moderate electric fields
The steady-state avalanche growth rate in a constant electric field is a classical result; Rosenbluth and Putvinski derived the growth rate formula (1.2) in 1997. After an initial transient, the distribution function tends to approach the asymptotic quasi-steady-state behaviour
![]() $f(t,p,\unicode[STIX]{x1D709})\sim n_{\text{RE}}(t)\bar{f}(p,\unicode[STIX]{x1D709})$
, where
$f(t,p,\unicode[STIX]{x1D709})\sim n_{\text{RE}}(t)\bar{f}(p,\unicode[STIX]{x1D709})$
, where
![]() $\int \bar{f}\,\text{d}\,\boldsymbol{p}=1$
. The kinetic equation, being linear in the runaway distribution, then prescribes that the runaway population will grow with a constant growth rate
$\int \bar{f}\,\text{d}\,\boldsymbol{p}=1$
. The kinetic equation, being linear in the runaway distribution, then prescribes that the runaway population will grow with a constant growth rate
In figure 3 we show the growth rate
![]() $\unicode[STIX]{x1D6E4}$
obtained from numerical solutions of the kinetic equation using various models for the knock-on operator, for moderate electric fields ranging from
$\unicode[STIX]{x1D6E4}$
obtained from numerical solutions of the kinetic equation using various models for the knock-on operator, for moderate electric fields ranging from
![]() $E=1.5E_{\text{c}}$
to
$E=1.5E_{\text{c}}$
to
![]() $E=30E_{\text{c}}$
and
$E=30E_{\text{c}}$
and
![]() $Z_{\text{eff}}=1$
. We see that using the Rosenbluth–Putvinski knock-on operator leads to a significant error compared to the more accurate models when the electric field is near the critical – of order 30 % at
$Z_{\text{eff}}=1$
. We see that using the Rosenbluth–Putvinski knock-on operator leads to a significant error compared to the more accurate models when the electric field is near the critical – of order 30 % at
![]() $1.5E_{\text{c}}$
. At larger electric fields the error is insignificant. Interestingly, the full Boltzmann operator (solid black line) yields a correction of only a few per cent compared to the field-particle operator alone. This means that the test-particle part of the operator does not influence the growth rate significantly. This result is robust; it is not affected by changes in thermal electron density and temperature, and only slightly modified by changes in the effective charge. Note that a significant error is obtained if one fails to account for the double counting of small-angle collisions – the size of this error is sensitive to the cutoff
$1.5E_{\text{c}}$
. At larger electric fields the error is insignificant. Interestingly, the full Boltzmann operator (solid black line) yields a correction of only a few per cent compared to the field-particle operator alone. This means that the test-particle part of the operator does not influence the growth rate significantly. This result is robust; it is not affected by changes in thermal electron density and temperature, and only slightly modified by changes in the effective charge. Note that a significant error is obtained if one fails to account for the double counting of small-angle collisions – the size of this error is sensitive to the cutoff
![]() $p_{\text{m}}$
, diverging logarithmically as it approaches zero, and the result is included primarily for illustrative purposes.
$p_{\text{m}}$
, diverging logarithmically as it approaches zero, and the result is included primarily for illustrative purposes.

Figure 3. Steady-state runaway growth rate normalized to the diffusion-free result
![]() $\unicode[STIX]{x1D6E4}_{0}=(E/E_{\text{c}}-1)/2\ln \unicode[STIX]{x1D6EC}$
, equation (1.2), in the presence of a constant electric field, neglecting radiation losses. The red dot-dashed line represents the theoretical prediction, Rosenbluth & Putvinski (Reference Rosenbluth and Putvinski1997, equation (18)). Plasma parameters: thermal electron density
$\unicode[STIX]{x1D6E4}_{0}=(E/E_{\text{c}}-1)/2\ln \unicode[STIX]{x1D6EC}$
, equation (1.2), in the presence of a constant electric field, neglecting radiation losses. The red dot-dashed line represents the theoretical prediction, Rosenbluth & Putvinski (Reference Rosenbluth and Putvinski1997, equation (18)). Plasma parameters: thermal electron density
![]() $n_{\text{e}}=10^{20}~\text{m}^{-3}$
; temperature
$n_{\text{e}}=10^{20}~\text{m}^{-3}$
; temperature
![]() $T_{\text{e}}=100~\text{eV}$
; effective charge
$T_{\text{e}}=100~\text{eV}$
; effective charge
![]() $Z_{\text{eff}}=1$
.
$Z_{\text{eff}}=1$
.
3.3 Avalanche generation in a near-threshold electric field with synchrotron radiation losses
In tokamaks, the runaway dynamics in electric fields near the runaway generation threshold is of particular interest. Due to the large self-inductance of tokamaks, after a transient phase during which the ohmic current of the background is dissipated, the electric field will tend towards that value
![]() $E_{a}$
– the threshold field – for which the runaway growth rate vanishes,
$E_{a}$
– the threshold field – for which the runaway growth rate vanishes,
![]() $\unicode[STIX]{x1D6E4}(E_{a})=0$
(Breizman Reference Breizman2014).
$\unicode[STIX]{x1D6E4}(E_{a})=0$
(Breizman Reference Breizman2014).
At these low electric fields, radiation losses have a large impact, and cannot be ignored in the calculation of the runaway growth rate. In this section, we will include the effect of synchrotron radiation losses and investigate runaway generation when
![]() $E\sim E_{a}$
. A model for this was recently presented by Aleynikov & Breizman (Reference Aleynikov and Breizman2015) (referred to as A&B), using a simplified kinetic equation following a method used by Lehtinen, Bell & Inan (Reference Lehtinen, Bell and Inan1999). An interesting prediction by the A&B model was that reverse knock-on can have a significant effect on the growth rate, where for electric fields
$E\sim E_{a}$
. A model for this was recently presented by Aleynikov & Breizman (Reference Aleynikov and Breizman2015) (referred to as A&B), using a simplified kinetic equation following a method used by Lehtinen, Bell & Inan (Reference Lehtinen, Bell and Inan1999). An interesting prediction by the A&B model was that reverse knock-on can have a significant effect on the growth rate, where for electric fields
![]() $E\lesssim E_{a}$
, existing runaways will be slowed down to
$E\lesssim E_{a}$
, existing runaways will be slowed down to
![]() $v<v_{c}$
in single large-angle collision events. This leads to a negative avalanche growth rate, which previous large-angle collision models are incapable of describing, as this process is inherently a large-angle test-particle effect. Using the knock-on operator presented in this work, we will now assess the magnitude of the reverse knock-on effect, as well as determine the threshold field
$v<v_{c}$
in single large-angle collision events. This leads to a negative avalanche growth rate, which previous large-angle collision models are incapable of describing, as this process is inherently a large-angle test-particle effect. Using the knock-on operator presented in this work, we will now assess the magnitude of the reverse knock-on effect, as well as determine the threshold field
![]() $E_{a}$
and the growth rate when
$E_{a}$
and the growth rate when
![]() $E\sim E_{a}$
, accounting for radiation losses.
$E\sim E_{a}$
, accounting for radiation losses.
In figure 4 we show how the quasi-steady-state growth rate
![]() $\unicode[STIX]{x1D6E4}$
depends on the electric-field strength, similar to figure 4 of A&B. We use the same plasma parameters
$\unicode[STIX]{x1D6E4}$
depends on the electric-field strength, similar to figure 4 of A&B. We use the same plasma parameters
![]() $Z_{\text{eff}}=5$
and
$Z_{\text{eff}}=5$
and
![]() $\unicode[STIX]{x1D70F}_{r}=3m_{\text{e}}n_{\text{e}}\ln \unicode[STIX]{x1D6EC}/(2\unicode[STIX]{x1D700}_{0}B^{2})=70$
(corresponding to
$\unicode[STIX]{x1D70F}_{r}=3m_{\text{e}}n_{\text{e}}\ln \unicode[STIX]{x1D6EC}/(2\unicode[STIX]{x1D700}_{0}B^{2})=70$
(corresponding to
![]() $B\approx 1.81~\text{T}$
at
$B\approx 1.81~\text{T}$
at
![]() $n_{\text{e}}=10^{20}~\text{m}^{-3}$
), although a slight discrepancy occurs due to our
$n_{\text{e}}=10^{20}~\text{m}^{-3}$
), although a slight discrepancy occurs due to our
![]() $\ln \unicode[STIX]{x1D6EC}=14.9$
– consistent with the background parameters chosen – compared to their
$\ln \unicode[STIX]{x1D6EC}=14.9$
– consistent with the background parameters chosen – compared to their
![]() $\ln \unicode[STIX]{x1D6EC}=18$
. In this scenario, the A&B threshold electric field is
$\ln \unicode[STIX]{x1D6EC}=18$
. In this scenario, the A&B threshold electric field is
![]() $E_{a}\approx 1.71E_{c}$
. Several models for the knock-on operator are included in the comparison, in addition to the no-avalanche case since we are now interested in the sub-threshold dynamics. The simulations are run for approximately 300 relativistic collision times
$E_{a}\approx 1.71E_{c}$
. Several models for the knock-on operator are included in the comparison, in addition to the no-avalanche case since we are now interested in the sub-threshold dynamics. The simulations are run for approximately 300 relativistic collision times
![]() $\unicode[STIX]{x1D70F}_{c}$
, upon which the growth rates have settled to the asymptotic steady-state value, corresponding to approximately 6 s with the plasma parameters given above.
$\unicode[STIX]{x1D70F}_{c}$
, upon which the growth rates have settled to the asymptotic steady-state value, corresponding to approximately 6 s with the plasma parameters given above.

Figure 4. Steady-state runaway growth rate in the presence of a constant electric field, accounting for synchrotron radiation losses and using various models for the large-angle collision operator: the Rosenbluth–Putvinski operator, equation (2.2) (green, dashed); the Boltzmann operator equations (2.23)–(2.24) (black, solid) and without any large-angle collision operator (black, dash-dotted). For comparison we have included equation (11) of Aleynikov & Breizman (Reference Aleynikov and Breizman2015) (blue, dotted). In (b), the avalanche-free growth rate (black, dotted line in (a)) has been subtracted to yield a pure ‘avalanche growth rate’
![]() $\unicode[STIX]{x1D6E4}_{\text{ava}}$
. Plasma parameters: thermal electron density
$\unicode[STIX]{x1D6E4}_{\text{ava}}$
. Plasma parameters: thermal electron density
![]() $n_{\text{e}}=10^{20}~\text{m}^{-3}$
; temperature
$n_{\text{e}}=10^{20}~\text{m}^{-3}$
; temperature
![]() $T_{\text{e}}=1~\text{keV}$
; effective charge
$T_{\text{e}}=1~\text{keV}$
; effective charge
![]() $Z_{\text{eff}}=5$
,
$Z_{\text{eff}}=5$
,
![]() $B=1.81~\text{T}$
.
$B=1.81~\text{T}$
.
It is interesting to observe that the test-particle operator, which allows runaways to be thermalized in a single large-angle collision, does not significantly modify the dynamics, in contrast to the theoretical prediction by Aleynikov & Breizman (Reference Aleynikov and Breizman2015). Unlike the A&B model, which predicts a significant negative growth rate due to this effect when
![]() $E\lesssim E_{a}$
, we find that the large-angle collision operator always adds a positive contribution to the total growth rate compared to the no-avalanche case (see figure 4(b) where the no-avalanche growth rate has been subtracted). It can be concluded that the negative growth rates in the sub-threshold regime is a result primarily of the Fokker–Planck dynamics, rather than of large-angle collisions. The reason for this discrepancy to the A&B model can be understood by considering the behaviour of the distribution shape functions
$E\lesssim E_{a}$
, we find that the large-angle collision operator always adds a positive contribution to the total growth rate compared to the no-avalanche case (see figure 4(b) where the no-avalanche growth rate has been subtracted). It can be concluded that the negative growth rates in the sub-threshold regime is a result primarily of the Fokker–Planck dynamics, rather than of large-angle collisions. The reason for this discrepancy to the A&B model can be understood by considering the behaviour of the distribution shape functions
![]() $\bar{f}=f/n$
, defined before (3.2), which are illustrated in figures 5 and 6. A&B predicted the distribution to be a delta function in momentum, located at the point of force balance,
$\bar{f}=f/n$
, defined before (3.2), which are illustrated in figures 5 and 6. A&B predicted the distribution to be a delta function in momentum, located at the point of force balance,
![]() $p_{\max }$
. When this occurs near the critical speed
$p_{\max }$
. When this occurs near the critical speed
![]() $v_{c}$
, runaways cannot produce knock-ons with sufficient energy to become runaway. Large-angle collisions then act only to slow down the existing population. In numerical solutions of the full kinetic equation, conversely, it is found that the runaway population takes on a wide energy spectrum, and there will always be sufficiently many runaways with the energy required to produce new runaways to counter the reverse knock-on effect.
$v_{c}$
, runaways cannot produce knock-ons with sufficient energy to become runaway. Large-angle collisions then act only to slow down the existing population. In numerical solutions of the full kinetic equation, conversely, it is found that the runaway population takes on a wide energy spectrum, and there will always be sufficiently many runaways with the energy required to produce new runaways to counter the reverse knock-on effect.
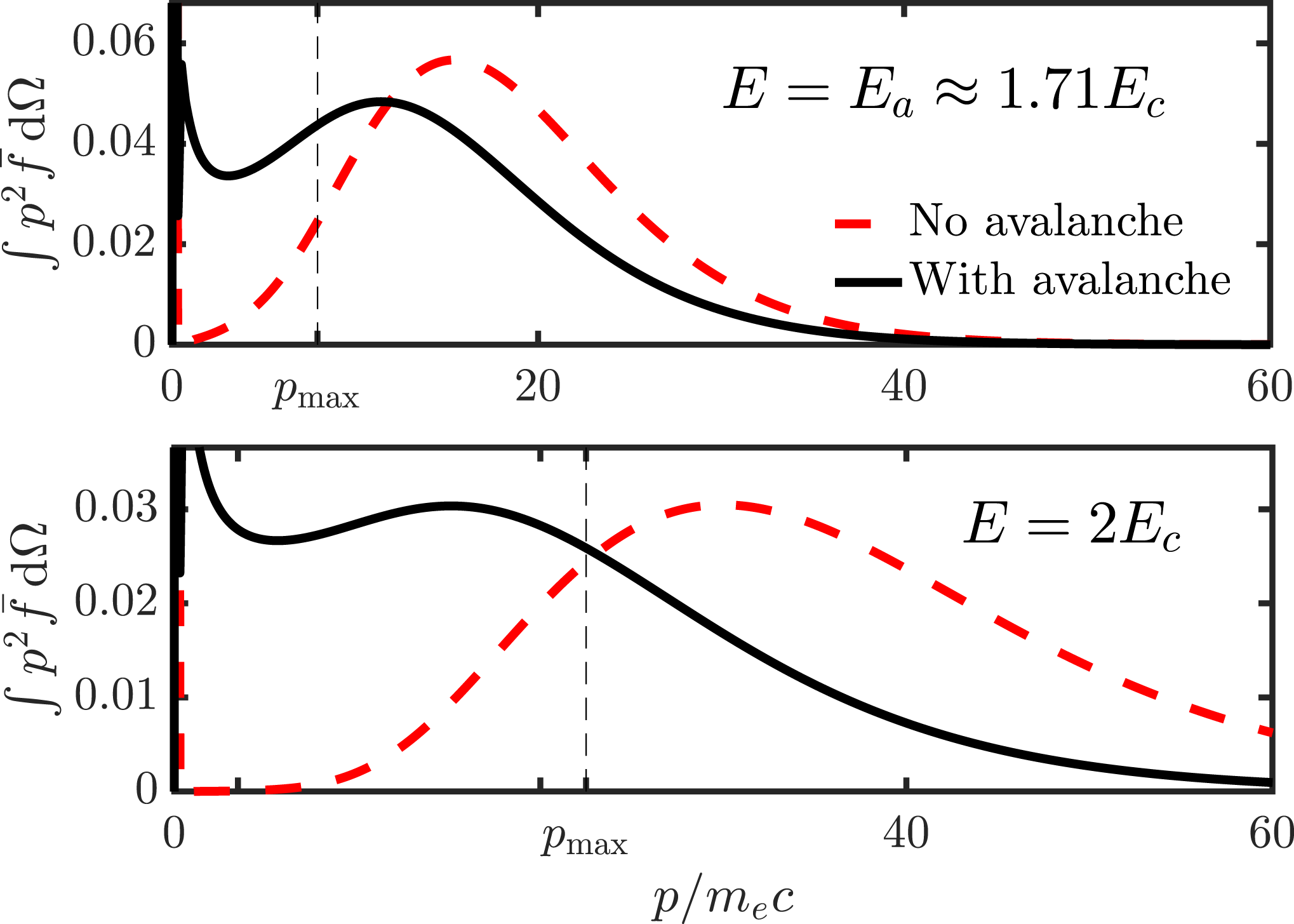
Figure 5. Steady-state runaway momentum distributions
![]() $\int p^{2}\bar{f}\,\text{d}\unicode[STIX]{x1D6FA}$
(defined to have unit area under the shown curves). Included in the panels is the maximum runaway momentum
$\int p^{2}\bar{f}\,\text{d}\unicode[STIX]{x1D6FA}$
(defined to have unit area under the shown curves). Included in the panels is the maximum runaway momentum
![]() $p_{\max }$
predicted by Aleynikov & Breizman (Reference Aleynikov and Breizman2015). Plasma parameters: background electron density
$p_{\max }$
predicted by Aleynikov & Breizman (Reference Aleynikov and Breizman2015). Plasma parameters: background electron density
![]() $n_{\text{e}}=10^{20}~\text{m}^{-3}$
; temperature
$n_{\text{e}}=10^{20}~\text{m}^{-3}$
; temperature
![]() $T_{\text{e}}=1~\text{keV}$
; effective charge
$T_{\text{e}}=1~\text{keV}$
; effective charge
![]() $Z_{\text{eff}}=5$
,
$Z_{\text{eff}}=5$
,
![]() $B=1.81~\text{T}$
.
$B=1.81~\text{T}$
.
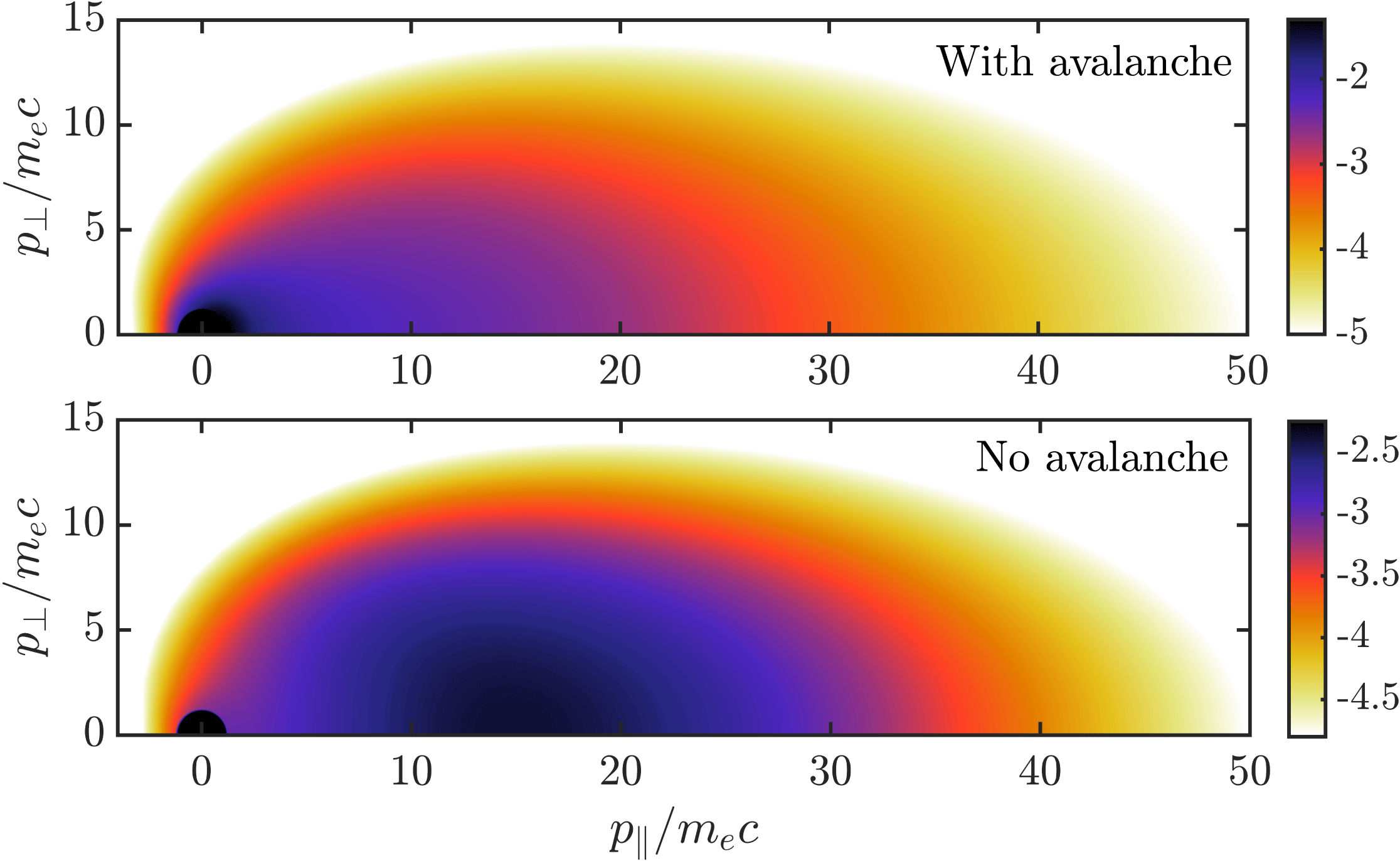
Figure 6. Steady-state normalized runaway momentum distributions
![]() $\log _{10}\bar{f}$
from the
$\log _{10}\bar{f}$
from the
![]() $E=E_{a}$
case of figure 5.
$E=E_{a}$
case of figure 5.
A notable difference between the A&B model and full solutions of the kinetic equation considered here, which can play an important role when considering the decay of the runaway current in tokamaks, is that the growth rate is not as sensitive to variations in electric field close to (but below) the effective critical field
![]() $E_{a}$
as predicted by A&B. It is known that the decay rate is determined primarily by the value of the effective critical field
$E_{a}$
as predicted by A&B. It is known that the decay rate is determined primarily by the value of the effective critical field
![]() $E_{a}$
when the self-inductance can be considered large (roughly when the total runaway current is much larger than
$E_{a}$
when the self-inductance can be considered large (roughly when the total runaway current is much larger than
![]() ${\sim}200~\text{kA}$
) (Breizman Reference Breizman2014). Since the threshold field
${\sim}200~\text{kA}$
) (Breizman Reference Breizman2014). Since the threshold field
![]() $E_{a}$
given by the A&B model is reasonably accurate in many cases, it is likely that it may be used to describe runaway current decay in large-current scenarios. However, for moderate runaway currents in the range of hundreds of kA, the overall shape of
$E_{a}$
given by the A&B model is reasonably accurate in many cases, it is likely that it may be used to describe runaway current decay in large-current scenarios. However, for moderate runaway currents in the range of hundreds of kA, the overall shape of
![]() $\unicode[STIX]{x1D6E4}(E)$
will determine its evolution, which previous theoretical models fail to describe – particularly for electric fields
$\unicode[STIX]{x1D6E4}(E)$
will determine its evolution, which previous theoretical models fail to describe – particularly for electric fields
![]() $E\lesssim E_{a}$
.
$E\lesssim E_{a}$
.
Finally, we show the effective critical field
![]() $E_{a}$
calculated numerically by CODE for a wide range of
$E_{a}$
calculated numerically by CODE for a wide range of
![]() $Z_{\text{eff}}$
and magnetic-field strength parameters
$Z_{\text{eff}}$
and magnetic-field strength parameters
![]() $\unicode[STIX]{x1D70F}_{\text{r}}=6\unicode[STIX]{x03C0}\unicode[STIX]{x1D716}_{0}^{2}m_{e}^{2}c^{3}/e^{4}B^{2}\unicode[STIX]{x1D70F}_{c}$
. This is shown in figure 7, along with the values given by the A&B model by determining the roots of their equation (11). It is seen that the predictions of Aleynikov & Breizman (Reference Aleynikov and Breizman2015) are typically accurate unless the effective charge is very large, and are most accurate for sufficiently small or large
$\unicode[STIX]{x1D70F}_{\text{r}}=6\unicode[STIX]{x03C0}\unicode[STIX]{x1D716}_{0}^{2}m_{e}^{2}c^{3}/e^{4}B^{2}\unicode[STIX]{x1D70F}_{c}$
. This is shown in figure 7, along with the values given by the A&B model by determining the roots of their equation (11). It is seen that the predictions of Aleynikov & Breizman (Reference Aleynikov and Breizman2015) are typically accurate unless the effective charge is very large, and are most accurate for sufficiently small or large
![]() $B$
. The observed trend in the accuracy of their model is unexpected, since they have utilized fast pitch-angle equilibration time (large
$B$
. The observed trend in the accuracy of their model is unexpected, since they have utilized fast pitch-angle equilibration time (large
![]() $Z_{\text{eff}}$
) and weak magnetic field (large
$Z_{\text{eff}}$
) and weak magnetic field (large
![]() $\unicode[STIX]{x1D70F}_{\text{r}}$
) in order to reduce the kinetic equation to a tractable form.
$\unicode[STIX]{x1D70F}_{\text{r}}$
) in order to reduce the kinetic equation to a tractable form.
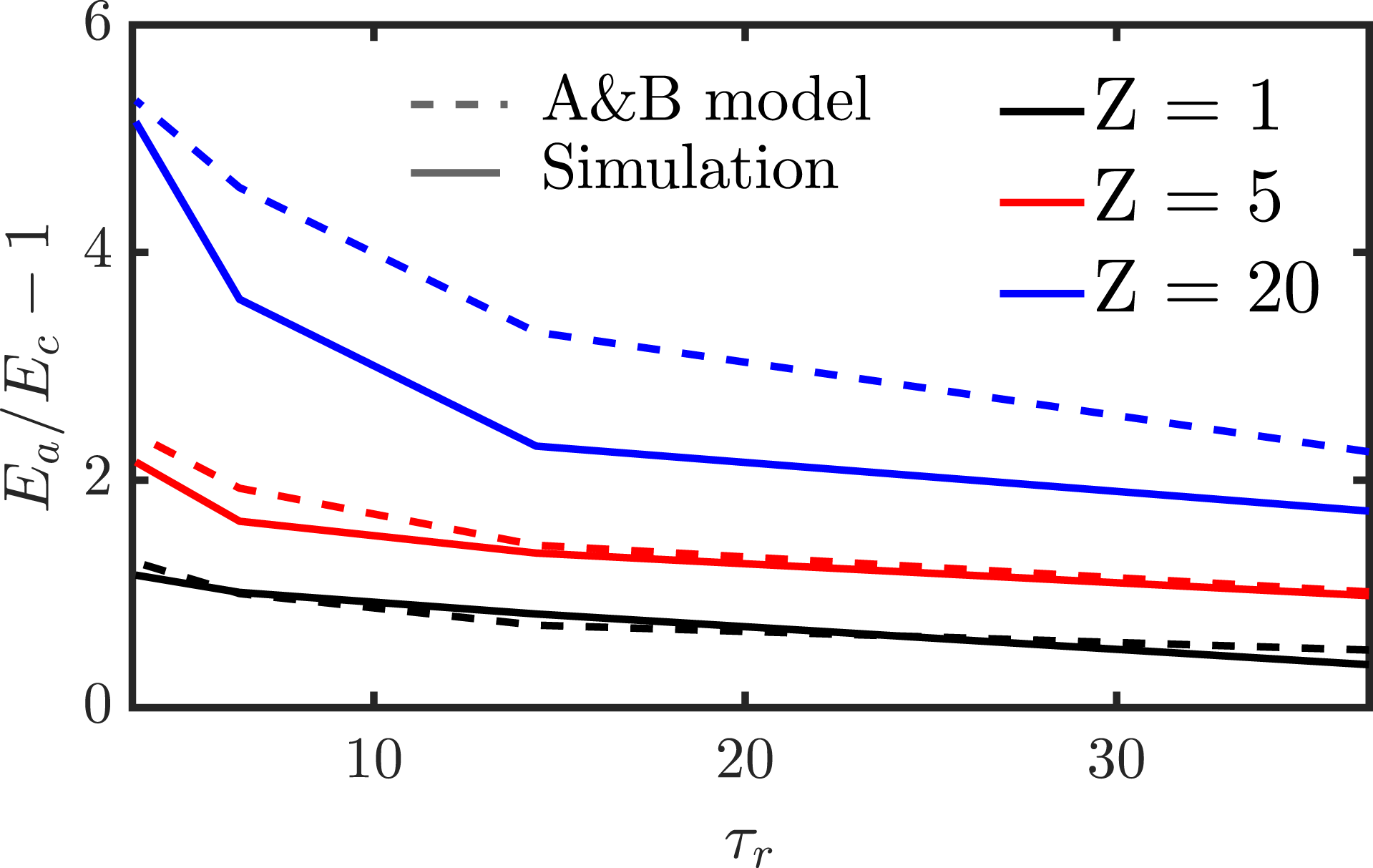
Figure 7. Threshold electric field determined numerically from solutions of the kinetic equation, as a function of normalized magnetic-field strength
![]() $\unicode[STIX]{x1D70F}_{\text{r}}$
for various values of the effective charge. Predictions by the theoretical model of Aleynikov & Breizman (Reference Aleynikov and Breizman2015) are included for comparison.
$\unicode[STIX]{x1D70F}_{\text{r}}$
for various values of the effective charge. Predictions by the theoretical model of Aleynikov & Breizman (Reference Aleynikov and Breizman2015) are included for comparison.
4 Conclusions
Predictions indicate that a major part of the initial plasma current in large tokamaks can be converted to runaway-electron current. This is partly due to the large plasma size limiting the loss of runaway-electron seeds, but more importantly, it is due to the avalanche mechanism which leads to an exponential growth of runaways. The runaway-electron growth rate due to avalanching is exponentially sensitive to the plasma current, and avalanche runaway generation is therefore expected to be a serious issue in ITER and other high-current reactor-scale tokamaks. As the plasma current in present devices cannot be increased above a few megaamperes, full experimental simulation of high-current tokamak disruptions is not possible. Therefore it is very important to develop accurate theoretical models from first principles, to test the validity of approximative models.
In this paper we have developed a fully conservative knock-on collision operator derived from the relativistic Boltzmann operator, and compared it to existing models. Close to the critical electric field, the new model leads to behaviour significantly different from that of the widely used Rosenbluth & Putvinski (Reference Rosenbluth and Putvinski1997) avalanche model. This influences the predictions for the transformation of a runaway seed to an avalanching population; fortunately the new operator predicts a lower growth rate than Rosenbluth & Putvinski (Reference Rosenbluth and Putvinski1997) and therefore the implications for ITER should be positive, although the difference between models is marginal for high electric fields. We have also described how to resolve the issue of double counting the small- and large-angle collisions, and have illustrated the importance of this issue. The new operator includes both the test-particle and field-particle parts of the collision operator, however we have shown that the test-particle part does not influence the growth rate significantly.
Using kinetic simulations we have performed a careful study of the runaway growth rate in the presence of synchrotron radiation losses and several different avalanche operators. Again, we find a significant difference in runaway rates close to the critical field, however, the effective critical field appears to be well reproduced by simplified models unless the effective charge is very large.
Acknowledgements
The authors would like to thank L. Hesslow, I. Pusztai, E. Hirvijoki, J. Connor, G. Papp and M. Landreman for constructive discussions. This work was supported by the Swedish Research Council (Dnr. 2014-5510) and the European Research Council (ERC-2014-CoG grant 647121). This work has been carried out within the framework of the EUROfusion Consortium and has received funding from the Euratom research and training programme 2014–2018 under grant agreement no. 633053. The views and opinions expressed herein do not necessarily reflect those of the European Commission.
Appendix A. Density, momentum and energy conservation
The full electron–electron Boltzmann operator
![]() $C$
is known to satisfy conservation of density, momentum and energy, expressed by the relations
$C$
is known to satisfy conservation of density, momentum and energy, expressed by the relations
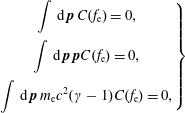 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \int \,\text{d}\,\boldsymbol{p}\,C(f_{\text{e}})=0,\\ \displaystyle \int \,\text{d}\,\boldsymbol{p}\,\boldsymbol{p}C(f_{\text{e}})=0,\\ \displaystyle \int \,\text{d}\,\boldsymbol{p}\,m_{\text{e}}c^{2}(\unicode[STIX]{x1D6FE}-1)C(f_{\text{e}})=0,\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \int \,\text{d}\,\boldsymbol{p}\,C(f_{\text{e}})=0,\\ \displaystyle \int \,\text{d}\,\boldsymbol{p}\,\boldsymbol{p}C(f_{\text{e}})=0,\\ \displaystyle \int \,\text{d}\,\boldsymbol{p}\,m_{\text{e}}c^{2}(\unicode[STIX]{x1D6FE}-1)C(f_{\text{e}})=0,\end{array}\right\}\end{eqnarray}$$
or in our case of a cylindrically symmetric plasma, in terms of the Legendre modes of the collision operator,
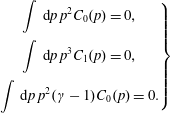 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \int \,\text{d}p\,p^{2}C_{0}(p)=0,\\ \displaystyle \int \,\text{d}p\,p^{3}C_{1}(p)=0,\\ \displaystyle \int \,\text{d}p\,p^{2}(\unicode[STIX]{x1D6FE}-1)C_{0}(p)=0.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \int \,\text{d}p\,p^{2}C_{0}(p)=0,\\ \displaystyle \int \,\text{d}p\,p^{3}C_{1}(p)=0,\\ \displaystyle \int \,\text{d}p\,p^{2}(\unicode[STIX]{x1D6FE}-1)C_{0}(p)=0.\end{array}\right\}\end{eqnarray}$$
We will show that our explicit form of the knock-on operator, accounting only for collisions involving electrons with momenta
![]() $p>p_{\text{m}}$
, satisfies the same conservation laws. Taking the full operator
$p>p_{\text{m}}$
, satisfies the same conservation laws. Taking the full operator
![]() $C_{L}=C_{L}\{f_{\text{e}},f_{\text{Me}}\}+C_{L}\{f_{\text{Me}},f_{\text{e}}\}$
from (2.23)–(2.24), noting that the gain term only applies for
$C_{L}=C_{L}\{f_{\text{e}},f_{\text{Me}}\}+C_{L}\{f_{\text{Me}},f_{\text{e}}\}$
from (2.23)–(2.24), noting that the gain term only applies for
![]() $\unicode[STIX]{x1D6FE}>\unicode[STIX]{x1D6FE}_{\text{m}}$
and the loss term for
$\unicode[STIX]{x1D6FE}>\unicode[STIX]{x1D6FE}_{\text{m}}$
and the loss term for
![]() $\unicode[STIX]{x1D6FE}>2\unicode[STIX]{x1D6FE}_{\text{m}}-1$
, we find upon integration (changing momentum integrals to energy integrals by
$\unicode[STIX]{x1D6FE}>2\unicode[STIX]{x1D6FE}_{\text{m}}-1$
, we find upon integration (changing momentum integrals to energy integrals by
![]() $v\,\text{d}p=m_{\text{e}}c^{2}\,\text{d}\unicode[STIX]{x1D6FE}$
)
$v\,\text{d}p=m_{\text{e}}c^{2}\,\text{d}\unicode[STIX]{x1D6FE}$
)
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}_{L}\{h\} & = & \displaystyle \int _{0}^{\infty }\,\text{d}p\,p^{2}h(p)C_{L}(p)\nonumber\\ \displaystyle & = & \displaystyle \frac{m_{\text{e}}c}{2\unicode[STIX]{x1D70F}_{\text{c}}\ln \unicode[STIX]{x1D6EC}}\int _{\unicode[STIX]{x1D6FE}_{\text{m}}}^{\infty }\,\text{d}\unicode[STIX]{x1D6FE}\,h(p)\int _{\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D6FE}_{\text{m}}-1}^{\infty }\,\text{d}\unicode[STIX]{x1D6FE}_{1}\,p_{1}^{2}\unicode[STIX]{x1D6F4}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}_{1})P_{L}(\unicode[STIX]{x1D709}^{\ast })f_{L}(p_{1})\nonumber\\ \displaystyle & & \displaystyle -\,\frac{m_{\text{e}}c}{4\unicode[STIX]{x1D70F}_{\text{c}}\ln \unicode[STIX]{x1D6EC}}\int _{2\unicode[STIX]{x1D6FE}_{\text{m}}-1}^{\infty }\,\text{d}\unicode[STIX]{x1D6FE}\,p^{2}h(p)f_{L}(p)\int _{\unicode[STIX]{x1D6FE}_{\text{m}}}^{\unicode[STIX]{x1D6FE}+1-\unicode[STIX]{x1D6FE}_{\text{m}}}\,\text{d}\unicode[STIX]{x1D6FE}_{1}\,\unicode[STIX]{x1D6F4}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE})\nonumber\\ \displaystyle & & \displaystyle -\frac{m_{\text{e}}ch(0)}{4\unicode[STIX]{x1D70F}_{\text{c}}\ln \unicode[STIX]{x1D6EC}}\unicode[STIX]{x1D6FF}_{L,0}\int _{2\unicode[STIX]{x1D6FE}_{\text{m}}-1}^{\infty }\,\text{d}\unicode[STIX]{x1D6FE}\,p^{2}f_{0}(p)\int _{\unicode[STIX]{x1D6FE}_{\text{m}}}^{\unicode[STIX]{x1D6FE}+1-\unicode[STIX]{x1D6FE}_{\text{m}}}\,\text{d}\unicode[STIX]{x1D6FE}_{1}\unicode[STIX]{x1D6F4}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}_{L}\{h\} & = & \displaystyle \int _{0}^{\infty }\,\text{d}p\,p^{2}h(p)C_{L}(p)\nonumber\\ \displaystyle & = & \displaystyle \frac{m_{\text{e}}c}{2\unicode[STIX]{x1D70F}_{\text{c}}\ln \unicode[STIX]{x1D6EC}}\int _{\unicode[STIX]{x1D6FE}_{\text{m}}}^{\infty }\,\text{d}\unicode[STIX]{x1D6FE}\,h(p)\int _{\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D6FE}_{\text{m}}-1}^{\infty }\,\text{d}\unicode[STIX]{x1D6FE}_{1}\,p_{1}^{2}\unicode[STIX]{x1D6F4}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}_{1})P_{L}(\unicode[STIX]{x1D709}^{\ast })f_{L}(p_{1})\nonumber\\ \displaystyle & & \displaystyle -\,\frac{m_{\text{e}}c}{4\unicode[STIX]{x1D70F}_{\text{c}}\ln \unicode[STIX]{x1D6EC}}\int _{2\unicode[STIX]{x1D6FE}_{\text{m}}-1}^{\infty }\,\text{d}\unicode[STIX]{x1D6FE}\,p^{2}h(p)f_{L}(p)\int _{\unicode[STIX]{x1D6FE}_{\text{m}}}^{\unicode[STIX]{x1D6FE}+1-\unicode[STIX]{x1D6FE}_{\text{m}}}\,\text{d}\unicode[STIX]{x1D6FE}_{1}\,\unicode[STIX]{x1D6F4}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE})\nonumber\\ \displaystyle & & \displaystyle -\frac{m_{\text{e}}ch(0)}{4\unicode[STIX]{x1D70F}_{\text{c}}\ln \unicode[STIX]{x1D6EC}}\unicode[STIX]{x1D6FF}_{L,0}\int _{2\unicode[STIX]{x1D6FE}_{\text{m}}-1}^{\infty }\,\text{d}\unicode[STIX]{x1D6FE}\,p^{2}f_{0}(p)\int _{\unicode[STIX]{x1D6FE}_{\text{m}}}^{\unicode[STIX]{x1D6FE}+1-\unicode[STIX]{x1D6FE}_{\text{m}}}\,\text{d}\unicode[STIX]{x1D6FE}_{1}\unicode[STIX]{x1D6F4}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}).\end{eqnarray}$$
In the first term, the integration order can be interchanged by using
Exchanging the names of the dummy variables
![]() $\unicode[STIX]{x1D6FE}_{1}$
and
$\unicode[STIX]{x1D6FE}_{1}$
and
![]() $\unicode[STIX]{x1D6FE}$
in this term then yields
$\unicode[STIX]{x1D6FE}$
in this term then yields
 $$\begin{eqnarray}\displaystyle \frac{2\unicode[STIX]{x1D70F}_{\text{c}}\ln \unicode[STIX]{x1D6EC}}{m_{\text{e}}c}\unicode[STIX]{x1D6E4}_{L}\{h\} & = & \displaystyle \int _{2\unicode[STIX]{x1D6FE}_{\text{m}}-1}^{\infty }\,\text{d}\unicode[STIX]{x1D6FE}p^{2}f_{L}(p)\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{\unicode[STIX]{x1D6FE}_{\text{m}}}^{\unicode[STIX]{x1D6FE}+1-\unicode[STIX]{x1D6FE}_{\text{m}}}\,\text{d}\unicode[STIX]{x1D6FE}_{1}\left[h(p_{1})P_{L}\left(\frac{\unicode[STIX]{x1D6FE}+1}{\unicode[STIX]{x1D6FE}_{1}+1}\frac{p_{1}}{p}\right)-\frac{h(p)+\unicode[STIX]{x1D6FF}_{L,0}h(0)}{2}\right]\unicode[STIX]{x1D6F4}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}).\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{2\unicode[STIX]{x1D70F}_{\text{c}}\ln \unicode[STIX]{x1D6EC}}{m_{\text{e}}c}\unicode[STIX]{x1D6E4}_{L}\{h\} & = & \displaystyle \int _{2\unicode[STIX]{x1D6FE}_{\text{m}}-1}^{\infty }\,\text{d}\unicode[STIX]{x1D6FE}p^{2}f_{L}(p)\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{\unicode[STIX]{x1D6FE}_{\text{m}}}^{\unicode[STIX]{x1D6FE}+1-\unicode[STIX]{x1D6FE}_{\text{m}}}\,\text{d}\unicode[STIX]{x1D6FE}_{1}\left[h(p_{1})P_{L}\left(\frac{\unicode[STIX]{x1D6FE}+1}{\unicode[STIX]{x1D6FE}_{1}+1}\frac{p_{1}}{p}\right)-\frac{h(p)+\unicode[STIX]{x1D6FF}_{L,0}h(0)}{2}\right]\unicode[STIX]{x1D6F4}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}).\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
The conservation of density, momentum and energy correspond to the conditions
![]() $0=\unicode[STIX]{x1D6E4}_{0}\{1\}=\unicode[STIX]{x1D6E4}_{1}\{p\}=\unicode[STIX]{x1D6E4}_{0}\{\unicode[STIX]{x1D6FE}-1\}$
, respectively. With
$0=\unicode[STIX]{x1D6E4}_{0}\{1\}=\unicode[STIX]{x1D6E4}_{1}\{p\}=\unicode[STIX]{x1D6E4}_{0}\{\unicode[STIX]{x1D6FE}-1\}$
, respectively. With
![]() $L=0$
and
$L=0$
and
![]() $h=1$
, the bracket term in the
$h=1$
, the bracket term in the
![]() $\unicode[STIX]{x1D6FE}_{1}$
-integral vanishes identically; therefore the knock-on operator will conserve density independently of the differential cross-section
$\unicode[STIX]{x1D6FE}_{1}$
-integral vanishes identically; therefore the knock-on operator will conserve density independently of the differential cross-section
![]() $\unicode[STIX]{x1D6F4}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE})=(2\unicode[STIX]{x03C0}r_{0}^{2})^{-1}\unicode[STIX]{x2202}\unicode[STIX]{x1D70E}/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FE}$
. For the other two conditions, one finds
$\unicode[STIX]{x1D6F4}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE})=(2\unicode[STIX]{x03C0}r_{0}^{2})^{-1}\unicode[STIX]{x2202}\unicode[STIX]{x1D70E}/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FE}$
. For the other two conditions, one finds
 $$\begin{eqnarray}\displaystyle 2\unicode[STIX]{x1D70F}_{\text{c}}\ln \unicode[STIX]{x1D6EC}\unicode[STIX]{x1D6E4}_{1}\{p\} & = & \displaystyle (m_{\text{e}}c)^{2}\int _{2\unicode[STIX]{x1D6FE}_{\text{m}}-1}^{\infty }\,\text{d}\unicode[STIX]{x1D6FE}\,p(\unicode[STIX]{x1D6FE}+1)f_{1}(p)\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{\unicode[STIX]{x1D6FE}_{\text{m}}}^{\unicode[STIX]{x1D6FE}+1-\unicode[STIX]{x1D6FE}_{\text{m}}}\,\text{d}\unicode[STIX]{x1D6FE}_{1}\left[\unicode[STIX]{x1D6FE}_{1}-1-\frac{\unicode[STIX]{x1D6FE}-1}{2}\right]\unicode[STIX]{x1D6F4}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 2\unicode[STIX]{x1D70F}_{\text{c}}\ln \unicode[STIX]{x1D6EC}\unicode[STIX]{x1D6E4}_{1}\{p\} & = & \displaystyle (m_{\text{e}}c)^{2}\int _{2\unicode[STIX]{x1D6FE}_{\text{m}}-1}^{\infty }\,\text{d}\unicode[STIX]{x1D6FE}\,p(\unicode[STIX]{x1D6FE}+1)f_{1}(p)\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{\unicode[STIX]{x1D6FE}_{\text{m}}}^{\unicode[STIX]{x1D6FE}+1-\unicode[STIX]{x1D6FE}_{\text{m}}}\,\text{d}\unicode[STIX]{x1D6FE}_{1}\left[\unicode[STIX]{x1D6FE}_{1}-1-\frac{\unicode[STIX]{x1D6FE}-1}{2}\right]\unicode[STIX]{x1D6F4}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}),\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle 2\unicode[STIX]{x1D70F}_{\text{c}}\ln \unicode[STIX]{x1D6EC}\unicode[STIX]{x1D6E4}_{0}\{\unicode[STIX]{x1D6FE}-1\} & = & \displaystyle m_{\text{e}}c\int _{2\unicode[STIX]{x1D6FE}_{\text{m}}-1}^{\infty }\,\text{d}\unicode[STIX]{x1D6FE}\,p^{2}f_{0}(p)\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{\unicode[STIX]{x1D6FE}_{\text{m}}}^{\unicode[STIX]{x1D6FE}+1-\unicode[STIX]{x1D6FE}_{\text{m}}}\,\text{d}\unicode[STIX]{x1D6FE}_{1}\left[\unicode[STIX]{x1D6FE}_{1}-1-\frac{\unicode[STIX]{x1D6FE}-1}{2}\right]\unicode[STIX]{x1D6F4}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 2\unicode[STIX]{x1D70F}_{\text{c}}\ln \unicode[STIX]{x1D6EC}\unicode[STIX]{x1D6E4}_{0}\{\unicode[STIX]{x1D6FE}-1\} & = & \displaystyle m_{\text{e}}c\int _{2\unicode[STIX]{x1D6FE}_{\text{m}}-1}^{\infty }\,\text{d}\unicode[STIX]{x1D6FE}\,p^{2}f_{0}(p)\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{\unicode[STIX]{x1D6FE}_{\text{m}}}^{\unicode[STIX]{x1D6FE}+1-\unicode[STIX]{x1D6FE}_{\text{m}}}\,\text{d}\unicode[STIX]{x1D6FE}_{1}\left[\unicode[STIX]{x1D6FE}_{1}-1-\frac{\unicode[STIX]{x1D6FE}-1}{2}\right]\unicode[STIX]{x1D6F4}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}).\end{eqnarray}$$
The integrals over
![]() $\unicode[STIX]{x1D6FE}_{1}$
will vanish for all cross-sections that respect the indistinguishability of the electrons, i.e. for which
$\unicode[STIX]{x1D6FE}_{1}$
will vanish for all cross-sections that respect the indistinguishability of the electrons, i.e. for which
![]() $\unicode[STIX]{x1D6F4}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE})=\unicode[STIX]{x1D6F4}(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D6FE})$
where
$\unicode[STIX]{x1D6F4}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE})=\unicode[STIX]{x1D6F4}(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D6FE})$
where
![]() $\unicode[STIX]{x1D6FE}_{2}=\unicode[STIX]{x1D6FE}+1-\unicode[STIX]{x1D6FE}_{1}$
. This follows directly from the observation that
$\unicode[STIX]{x1D6FE}_{2}=\unicode[STIX]{x1D6FE}+1-\unicode[STIX]{x1D6FE}_{1}$
. This follows directly from the observation that
confirming that our operator indeed satisfies the conservation laws.
A.1 Total cross-section
For our case of the Møller cross-section, the differential cross-section of (2.4) can be integrated analytically to produce the total cross-section. One obtains
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70E}(p) & = & \displaystyle \int _{\unicode[STIX]{x1D6FE}_{\text{m}}}^{\unicode[STIX]{x1D6FE}+1-\unicode[STIX]{x1D6FE}_{\text{m}}}\,\text{d}\unicode[STIX]{x1D6FE}_{1}\,2\unicode[STIX]{x03C0}r_{0}^{2}\unicode[STIX]{x1D6F4}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE})\nonumber\\ \displaystyle & = & \displaystyle \frac{2\unicode[STIX]{x03C0}r_{0}^{2}}{\unicode[STIX]{x1D6FE}^{2}-1}\left[\left(\frac{\unicode[STIX]{x1D6FE}+1}{2}-\unicode[STIX]{x1D6FE}_{\text{m}}\right)\left(1+\frac{2\unicode[STIX]{x1D6FE}^{2}}{(\unicode[STIX]{x1D6FE}-\unicode[STIX]{x1D6FE}_{\text{m}})(\unicode[STIX]{x1D6FE}_{\text{m}}-1)}\right)-\frac{2\unicode[STIX]{x1D6FE}-1}{\unicode[STIX]{x1D6FE}-1}\ln \frac{\unicode[STIX]{x1D6FE}-\unicode[STIX]{x1D6FE}_{\text{m}}}{\unicode[STIX]{x1D6FE}_{\text{m}}-1}\right].\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70E}(p) & = & \displaystyle \int _{\unicode[STIX]{x1D6FE}_{\text{m}}}^{\unicode[STIX]{x1D6FE}+1-\unicode[STIX]{x1D6FE}_{\text{m}}}\,\text{d}\unicode[STIX]{x1D6FE}_{1}\,2\unicode[STIX]{x03C0}r_{0}^{2}\unicode[STIX]{x1D6F4}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE})\nonumber\\ \displaystyle & = & \displaystyle \frac{2\unicode[STIX]{x03C0}r_{0}^{2}}{\unicode[STIX]{x1D6FE}^{2}-1}\left[\left(\frac{\unicode[STIX]{x1D6FE}+1}{2}-\unicode[STIX]{x1D6FE}_{\text{m}}\right)\left(1+\frac{2\unicode[STIX]{x1D6FE}^{2}}{(\unicode[STIX]{x1D6FE}-\unicode[STIX]{x1D6FE}_{\text{m}})(\unicode[STIX]{x1D6FE}_{\text{m}}-1)}\right)-\frac{2\unicode[STIX]{x1D6FE}-1}{\unicode[STIX]{x1D6FE}-1}\ln \frac{\unicode[STIX]{x1D6FE}-\unicode[STIX]{x1D6FE}_{\text{m}}}{\unicode[STIX]{x1D6FE}_{\text{m}}-1}\right].\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
Appendix B. The Chiu–Harvey and Rosenbluth–Putvinski models
We derive the Chiu–Harvey source by assuming runaways to have a negligible perpendicular velocity component, i.e. that
![]() $f_{\text{e}}$
is well described by a delta function in pitch angle,
$f_{\text{e}}$
is well described by a delta function in pitch angle,
![]() $f_{\text{e}}(p_{1},\cos \unicode[STIX]{x1D703}_{1})=F(p_{1})\unicode[STIX]{x1D6FF}(\cos \unicode[STIX]{x1D703}_{1}-1)/(2\unicode[STIX]{x03C0}p_{1}^{2})$
with
$f_{\text{e}}(p_{1},\cos \unicode[STIX]{x1D703}_{1})=F(p_{1})\unicode[STIX]{x1D6FF}(\cos \unicode[STIX]{x1D703}_{1}-1)/(2\unicode[STIX]{x03C0}p_{1}^{2})$
with
![]() $F(p_{1})=2\unicode[STIX]{x03C0}\int _{-1}^{1}\text{d}\cos \unicode[STIX]{x1D703}_{1}p_{1}^{2}\,f_{\text{e}}(p_{1},\cos \unicode[STIX]{x1D703}_{1})$
. From (2.20) we then find
$F(p_{1})=2\unicode[STIX]{x03C0}\int _{-1}^{1}\text{d}\cos \unicode[STIX]{x1D703}_{1}p_{1}^{2}\,f_{\text{e}}(p_{1},\cos \unicode[STIX]{x1D703}_{1})$
. From (2.20) we then find
 $$\begin{eqnarray}\displaystyle S_{\text{CH}} & = & \displaystyle \frac{1}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70F}_{\text{c}}\ln \unicode[STIX]{x1D6EC}}\frac{1}{p\unicode[STIX]{x1D6FE}}\int _{q^{\ast }}^{\infty }\,\text{d}p_{1}\frac{p_{1}}{\unicode[STIX]{x1D6FE}_{1}}F(p_{1})\unicode[STIX]{x1D6F4}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}_{1})\int _{-1}^{1}\,\text{d}\unicode[STIX]{x1D709}_{1}\,\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D709}_{s}-\unicode[STIX]{x1D709}^{\ast })\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D709}_{1}-1)\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70F}_{\text{c}}\ln \unicode[STIX]{x1D6EC}}\frac{1}{p\unicode[STIX]{x1D6FE}}\int _{q^{\ast }}^{\infty }\,\text{d}p_{1}\,\frac{p_{1}}{\unicode[STIX]{x1D6FE}_{1}}F(p_{1})\unicode[STIX]{x1D6F4}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}_{1})\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D709}-\unicode[STIX]{x1D709}^{\ast })\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70F}_{\text{c}}\ln \unicode[STIX]{x1D6EC}}\frac{p_{1}^{2}}{p\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D709}}F(p_{1})\unicode[STIX]{x1D6F4}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}_{1})H(p_{1}-q^{\ast }),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle S_{\text{CH}} & = & \displaystyle \frac{1}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70F}_{\text{c}}\ln \unicode[STIX]{x1D6EC}}\frac{1}{p\unicode[STIX]{x1D6FE}}\int _{q^{\ast }}^{\infty }\,\text{d}p_{1}\frac{p_{1}}{\unicode[STIX]{x1D6FE}_{1}}F(p_{1})\unicode[STIX]{x1D6F4}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}_{1})\int _{-1}^{1}\,\text{d}\unicode[STIX]{x1D709}_{1}\,\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D709}_{s}-\unicode[STIX]{x1D709}^{\ast })\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D709}_{1}-1)\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70F}_{\text{c}}\ln \unicode[STIX]{x1D6EC}}\frac{1}{p\unicode[STIX]{x1D6FE}}\int _{q^{\ast }}^{\infty }\,\text{d}p_{1}\,\frac{p_{1}}{\unicode[STIX]{x1D6FE}_{1}}F(p_{1})\unicode[STIX]{x1D6F4}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}_{1})\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D709}-\unicode[STIX]{x1D709}^{\ast })\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70F}_{\text{c}}\ln \unicode[STIX]{x1D6EC}}\frac{p_{1}^{2}}{p\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D709}}F(p_{1})\unicode[STIX]{x1D6F4}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}_{1})H(p_{1}-q^{\ast }),\end{eqnarray}$$
where
![]() $H(x)$
denotes the Heaviside step function, and we used
$H(x)$
denotes the Heaviside step function, and we used
We also utilized
![]() $\cos \unicode[STIX]{x1D703}_{\text{s}}=\cos \unicode[STIX]{x1D703}$
when
$\cos \unicode[STIX]{x1D703}_{\text{s}}=\cos \unicode[STIX]{x1D703}$
when
![]() $\cos \unicode[STIX]{x1D703}_{1}=1$
, and kinematics constrain the incident momentum
$\cos \unicode[STIX]{x1D703}_{1}=1$
, and kinematics constrain the incident momentum
![]() $p_{1}$
according to (2.5). This result agrees exactly with the Chiu–Harvey source
$p_{1}$
according to (2.5). This result agrees exactly with the Chiu–Harvey source
![]() $S_{\text{CH}}$
of (2.3). In terms of an expansion in Legendre polynomials, the Chiu–Harvey avalanche source is obtained from the general field-particle operator in (2.24) simply by replacing
$S_{\text{CH}}$
of (2.3). In terms of an expansion in Legendre polynomials, the Chiu–Harvey avalanche source is obtained from the general field-particle operator in (2.24) simply by replacing
![]() $f_{L}(p)$
by
$f_{L}(p)$
by
![]() $(2L+1)f_{0}(p)$
, corresponding to the delta function approximation. In this representation, however, the approximation holds limited appeal as it does not provide a significant simplification of the collision operator; indeed, compared to the full operator it requires a larger number of Legendre polynomials to be retained since the true
$(2L+1)f_{0}(p)$
, corresponding to the delta function approximation. In this representation, however, the approximation holds limited appeal as it does not provide a significant simplification of the collision operator; indeed, compared to the full operator it requires a larger number of Legendre polynomials to be retained since the true
![]() $f_{L}$
decreases rapidly with
$f_{L}$
decreases rapidly with
![]() $L$
for sufficiently large
$L$
for sufficiently large
![]() $L$
.
$L$
.
By the addition of the sink terms in (2.23) and (2.24), and extending the integration limit down from
![]() $q^{\ast }$
to
$q^{\ast }$
to
![]() $q_{0}$
, the Chiu–Harvey operator can be made conservative. However, the delta function assumption in pitch angle causes incorrect momentum dynamics, and the total momentum of the distribution will not be conserved in this treatment. This can be corrected by treating the
$q_{0}$
, the Chiu–Harvey operator can be made conservative. However, the delta function assumption in pitch angle causes incorrect momentum dynamics, and the total momentum of the distribution will not be conserved in this treatment. This can be corrected by treating the
![]() $L=1$
mode exactly, corresponding to a total conservative knock-on operator in the Chiu–Harvey approximation of the form
$L=1$
mode exactly, corresponding to a total conservative knock-on operator in the Chiu–Harvey approximation of the form
 $$\begin{eqnarray}\displaystyle C_{\text{CH}}^{\text{(cons)}} & = & \displaystyle \bar{S}_{\text{CH}}-\frac{1}{4\unicode[STIX]{x1D70F}_{\text{c}}\ln \unicode[STIX]{x1D6EC}}vf_{\text{e}}(\,\boldsymbol{p})\unicode[STIX]{x1D70E}(p)-\frac{\unicode[STIX]{x1D6FF}(\,\boldsymbol{p})}{4\unicode[STIX]{x1D70F}_{\text{c}}\ln \unicode[STIX]{x1D6EC}}\int _{p^{\prime }>q_{0}(p_{\text{m}})}\,\text{d}\,\boldsymbol{p}^{\prime }v^{\prime }f_{\text{e}}(\,\boldsymbol{p}^{\prime })\unicode[STIX]{x1D70E}(p^{\prime })\nonumber\\ \displaystyle & & \displaystyle -\,\frac{3(m_{\text{e}}c)^{-3}}{8\unicode[STIX]{x03C0}\unicode[STIX]{x1D70F}_{\text{c}}\ln \unicode[STIX]{x1D6EC}}\frac{\unicode[STIX]{x1D709}}{\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D6FE}+1)}\int _{p_{1}>q_{0}}\,\text{d}\,\boldsymbol{p}_{1}\frac{\unicode[STIX]{x1D6FE}_{1}+1}{\unicode[STIX]{x1D6FE}_{1}}\unicode[STIX]{x1D6F4}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}_{1})(1-\unicode[STIX]{x1D709}_{1})f_{\text{e}}(\,\boldsymbol{p}_{1})\nonumber\\ \displaystyle & & \displaystyle +\,\frac{3}{8\unicode[STIX]{x1D70F}_{\text{c}}\ln \unicode[STIX]{x1D6EC}}\unicode[STIX]{x1D709}v\unicode[STIX]{x1D70E}(p)\int _{-1}^{1}\,\text{d}\unicode[STIX]{x1D709}_{1}(1-\unicode[STIX]{x1D709}_{1})f_{\text{e}}(p,\unicode[STIX]{x1D709}_{1}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle C_{\text{CH}}^{\text{(cons)}} & = & \displaystyle \bar{S}_{\text{CH}}-\frac{1}{4\unicode[STIX]{x1D70F}_{\text{c}}\ln \unicode[STIX]{x1D6EC}}vf_{\text{e}}(\,\boldsymbol{p})\unicode[STIX]{x1D70E}(p)-\frac{\unicode[STIX]{x1D6FF}(\,\boldsymbol{p})}{4\unicode[STIX]{x1D70F}_{\text{c}}\ln \unicode[STIX]{x1D6EC}}\int _{p^{\prime }>q_{0}(p_{\text{m}})}\,\text{d}\,\boldsymbol{p}^{\prime }v^{\prime }f_{\text{e}}(\,\boldsymbol{p}^{\prime })\unicode[STIX]{x1D70E}(p^{\prime })\nonumber\\ \displaystyle & & \displaystyle -\,\frac{3(m_{\text{e}}c)^{-3}}{8\unicode[STIX]{x03C0}\unicode[STIX]{x1D70F}_{\text{c}}\ln \unicode[STIX]{x1D6EC}}\frac{\unicode[STIX]{x1D709}}{\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D6FE}+1)}\int _{p_{1}>q_{0}}\,\text{d}\,\boldsymbol{p}_{1}\frac{\unicode[STIX]{x1D6FE}_{1}+1}{\unicode[STIX]{x1D6FE}_{1}}\unicode[STIX]{x1D6F4}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}_{1})(1-\unicode[STIX]{x1D709}_{1})f_{\text{e}}(\,\boldsymbol{p}_{1})\nonumber\\ \displaystyle & & \displaystyle +\,\frac{3}{8\unicode[STIX]{x1D70F}_{\text{c}}\ln \unicode[STIX]{x1D6EC}}\unicode[STIX]{x1D709}v\unicode[STIX]{x1D70E}(p)\int _{-1}^{1}\,\text{d}\unicode[STIX]{x1D709}_{1}(1-\unicode[STIX]{x1D709}_{1})f_{\text{e}}(p,\unicode[STIX]{x1D709}_{1}),\end{eqnarray}$$
where
![]() $\bar{S}_{\text{CH}}$
equals (B 1) with
$\bar{S}_{\text{CH}}$
equals (B 1) with
![]() $q^{\ast }$
changed to
$q^{\ast }$
changed to
![]() $q_{0}$
, and the last two momentum-correcting terms are small when the runaway population consists predominantly of electrons with small pitch-angle,
$q_{0}$
, and the last two momentum-correcting terms are small when the runaway population consists predominantly of electrons with small pitch-angle,
![]() $1-\unicode[STIX]{x1D709}_{1}\ll 1$
. Unlike the Chiu–Harvey model, this operator depends not only on the angle-averaged distribution
$1-\unicode[STIX]{x1D709}_{1}\ll 1$
. Unlike the Chiu–Harvey model, this operator depends not only on the angle-averaged distribution
![]() $\int f_{\text{e}}\,\text{d}\unicode[STIX]{x1D709}$
, but also on
$\int f_{\text{e}}\,\text{d}\unicode[STIX]{x1D709}$
, but also on
![]() $\int (1-\unicode[STIX]{x1D709})f_{\text{e}}\,\text{d}\unicode[STIX]{x1D709}$
.
$\int (1-\unicode[STIX]{x1D709})f_{\text{e}}\,\text{d}\unicode[STIX]{x1D709}$
.
Note that the issue of double counting is important only in the test-particle part of the operator. In the Chiu–Harvey approach, when the test-particle part is neglected, only field-particle collisions would be double counted, and for those the small-angle collisions have negligible impact on runaway generation.
The Rosenbluth–Putvinski result is obtained under the assumptions that the primary electrons not only have small pitch angle, but also large energy. Therefore, in the second line of (B 1),
![]() $(p_{1}/\unicode[STIX]{x1D6FE}_{1})\unicode[STIX]{x1D6F4}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}_{1})\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D709}-\unicode[STIX]{x1D709}^{\ast })$
can be replaced by
$(p_{1}/\unicode[STIX]{x1D6FE}_{1})\unicode[STIX]{x1D6F4}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}_{1})\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D709}-\unicode[STIX]{x1D709}^{\ast })$
can be replaced by
![]() $m_{\text{e}}c\unicode[STIX]{x1D6F4}(\unicode[STIX]{x1D6FE},\infty )\unicode[STIX]{x1D6FF}$
$m_{\text{e}}c\unicode[STIX]{x1D6F4}(\unicode[STIX]{x1D6FE},\infty )\unicode[STIX]{x1D6FF}$
![]() $(\unicode[STIX]{x1D709}-\unicode[STIX]{x1D709}_{0})$
with an error of order
$(\unicode[STIX]{x1D709}-\unicode[STIX]{x1D709}_{0})$
with an error of order
![]() $1/\unicode[STIX]{x1D6FE}_{1}$
, where
$1/\unicode[STIX]{x1D6FE}_{1}$
, where
![]() $\unicode[STIX]{x1D709}_{0}=\lim _{\unicode[STIX]{x1D6FE}_{1}\rightarrow \infty }\unicode[STIX]{x1D709}^{\ast }=\sqrt{(\unicode[STIX]{x1D6FE}-1)/(\unicode[STIX]{x1D6FE}+1)}$
. Under this assumption, the source term reduces to
$\unicode[STIX]{x1D709}_{0}=\lim _{\unicode[STIX]{x1D6FE}_{1}\rightarrow \infty }\unicode[STIX]{x1D709}^{\ast }=\sqrt{(\unicode[STIX]{x1D6FE}-1)/(\unicode[STIX]{x1D6FE}+1)}$
. Under this assumption, the source term reduces to
where the last step follows by replacing the integral over
![]() $F$
by the runaway number density
$F$
by the runaway number density
![]() $n_{\text{RE}}$
, valid when
$n_{\text{RE}}$
, valid when
![]() $\unicode[STIX]{x1D6FE}^{\ast }=\sqrt{(q^{\ast }/m_{\text{e}}c)^{2}+1}=2\unicode[STIX]{x1D6FE}-1$
is small compared to typical runaway energies. This result agrees exactly with
$\unicode[STIX]{x1D6FE}^{\ast }=\sqrt{(q^{\ast }/m_{\text{e}}c)^{2}+1}=2\unicode[STIX]{x1D6FE}-1$
is small compared to typical runaway energies. This result agrees exactly with
![]() $S_{\text{RP}}$
in (2.2). Note that this final approximation allows secondary electrons to be created with momentum and energy larger than that of any present primary electron. In fact, when integrated over all momenta the Rosenbluth–Putvinski source term is found to create energy and momentum at an infinite rate.
$S_{\text{RP}}$
in (2.2). Note that this final approximation allows secondary electrons to be created with momentum and energy larger than that of any present primary electron. In fact, when integrated over all momenta the Rosenbluth–Putvinski source term is found to create energy and momentum at an infinite rate.