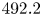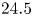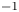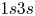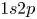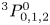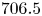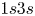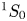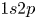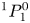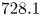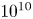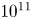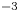1. Introduction
Atmospheric pressure plasma jets (APPJs) have been widely studied in recent decades. Their low gas temperature and abundance of highly reactive chemical species make them ideal candidates for a number of particular applications such as medical (Park et al. Reference Park, Park, Choi, Koo, Byun, Hong, Sim, Collins and Lee2012), surface sterilization (Laroussi et al. Reference Laroussi, Kong, Morfill and Stolz2012) and agricultural (Attri et al. Reference Attri, Ishikawa, Okumura, Koga and Shiratani2020). Operating at atmospheric pressure provides many benefits such as a lower cost plus simplicity and flexibility to set up, as there is no need for the vacuum systems commonly needed for low pressure plasmas. However, this makes understanding the plasma chemistry much more difficult as the surrounding environment is no longer controlled and collisional reactions with ambient air now play a dominant role. To optimize the performance of APPJs to suit the particular application, it is important to know the properties of the plasma such as the reactive species density, electron density and temperature and in particular how varying controllable parameters such as the gas flow and applied voltage may affect these properties.
One of the most important properties from the point of view of biological applications is the electric field produced by the plasma jet. If the field is high enough, cell electroporation may be achieved, temporarily creating pore-like openings in the cell membrane. This makes it much easier for reactive species produced by the plasma jet source to successfully penetrate the membrane and enter the cell (Kim et al. Reference Kim, Chung, Bae and Leem2010; Zhang et al. Reference Zhang, Zhuang, von Woedtke, Kolb, Zhang, Fang and Weltmann2014). One study of HL-$60$![]() cells indicates that a threshold of $30$
cells indicates that a threshold of $30$![]() kV cm$^{-1}$
kV cm$^{-1}$![]() for $60$
for $60$![]() ns duration is sufficient to achieve cell electroporation (Beebe et al. Reference Beebe, Blackmore, White, Joshi and Schoenbach2004). Another study conducted on skin tumour cells, investigated the application of nanosecond pulsed electric fields of greater than $20$
ns duration is sufficient to achieve cell electroporation (Beebe et al. Reference Beebe, Blackmore, White, Joshi and Schoenbach2004). Another study conducted on skin tumour cells, investigated the application of nanosecond pulsed electric fields of greater than $20$![]() kV cm$^{-1}$
kV cm$^{-1}$![]() and found that the cell nuclei shrunk and caused blood flow to the tumours to stop (Nuccitelli et al. Reference Nuccitelli, Pliquett, Chen, Ford, Swanson, Beebe, Kolb and Schoenbach2006). This magnitude of electric field is obtainable for the plasma jet source discussed in this work. Previous biological studies conducted using our plasma jet device exhibit its potential applications for the sterilization of bacteria cells (Flynn et al. Reference Flynn, Busetti, Wielogorska, Chevallier, Elliott, Laverty, Gorman, Graham and Gilmore2016) and the detoxification of maize (Wielogorska et al. Reference Wielogorska, Ahmed, Meneely, Graham, Elliott and Gilmore2019), which provides a strong motivation to study the physical conditions within our particular jet. Many of the APPJs studied in the literature have different geometries, electrode configurations and power delivery, hence direct reproducibility between plasma jets cannot always be made. Having a combined knowledge of both the physical and biological nature of these individually unique APPJs can therefore help further expand the existing knowledge.
and found that the cell nuclei shrunk and caused blood flow to the tumours to stop (Nuccitelli et al. Reference Nuccitelli, Pliquett, Chen, Ford, Swanson, Beebe, Kolb and Schoenbach2006). This magnitude of electric field is obtainable for the plasma jet source discussed in this work. Previous biological studies conducted using our plasma jet device exhibit its potential applications for the sterilization of bacteria cells (Flynn et al. Reference Flynn, Busetti, Wielogorska, Chevallier, Elliott, Laverty, Gorman, Graham and Gilmore2016) and the detoxification of maize (Wielogorska et al. Reference Wielogorska, Ahmed, Meneely, Graham, Elliott and Gilmore2019), which provides a strong motivation to study the physical conditions within our particular jet. Many of the APPJs studied in the literature have different geometries, electrode configurations and power delivery, hence direct reproducibility between plasma jets cannot always be made. Having a combined knowledge of both the physical and biological nature of these individually unique APPJs can therefore help further expand the existing knowledge.
For all applications of these types of plasma jet sources, the plasma plume interacts with some form of target. This could be a metallic surface being treated/decontaminated or a wound being disinfected. It is now well known that any object in close vicinity of the plasma plume will change the dynamics of the plasma (Akishev et al. Reference Akishev, Karalnik, Medvedev, Petryakov, Trushkin and Shafikov2017; Kovačević et al. Reference Kovačević, Sretenović, Slikboer, Guaitella, Sobota and Kuraica2018; Sobota et al. Reference Sobota, Guaitella, Sretenović, Kovačević, Slikboer, Krstić, Obradović and Kuraica2019). The addition of a target has already been shown to increase helium metastable densities (Urabe et al. Reference Urabe, Morita, Tachibana and Ganguly2010; Zaplotnik et al. Reference Zaplotnik, Bišćan, Popović, Mozetič and Milošević2016) and electron densities in close proximity to the target (Klarenaar et al. Reference Klarenaar, Guaitella, Engeln and Sobota2018; Hofmans et al. Reference Hofmans, Viegas, van Rooij, Klarenaar, Guaitella, Bourdon and Sobota2020; Viegas et al. Reference Viegas, Hofmans, van Rooij, Obrusník, Klarenaar, Bonaventura, Guaitella, Sobota and Bourdon2020). It is therefore essential to study the plasma under different target conditions similar to those of their particular application to get a better understanding of the typical plasma behaviour and properties. This work highlights the sensitivity of the axial electric field along the plasma plume to changes of the parameters such as the helium gas flow rate, target properties and the separation between the target and tube exit.
Another important property of APPJs is their ability to produce a wide variety of reactive and excited species. One of the primary goals for APPJs within this decade has been to develop diagnostic methods capable of measuring densities of excited species, metastable states and reactive species (Lu et al. Reference Lu, Naidis, Laroussi and Ostrikov2014). Concentrations of reactive species such as O, OH and NO can be determined experimentally through the use of one- or two-photon laser-induced fluorescence spectroscopy and optical absorption spectroscopy (van Gessel, Alards & Bruggeman Reference van Gessel, Alards and Bruggeman2013; Pei et al. Reference Pei, Wu, Xian, Lu and Pan2014; Yonemori & Ono Reference Yonemori and Ono2014; Xiong, Yang & Bruggeman Reference Xiong, Yang and Bruggeman2015; Schröter et al. Reference Schröter, Bredin, Gibson, West, Dedrick, Wagenaars, Niemi, Gans and O'Connell2020; Steuer et al. Reference Steuer, Korolov, Chur, Schulze, Schulz-von der Gathen, Golda and Böke2021). However, few experimental studies have focused on measuring the density of excited species. This work estimates excited state densities within the plasma directly from plasma emission without the need for a laser and complex optics, hence making it a cheaper and simpler method. By spectrally isolating emission through the use of a bandpass filter coupled to a calibrated intensified CCD (iCCD) camera, images of the plasma bullets can be analysed and used to determine temporal and spatially resolved excited state densities. One advantage of this compact experimental configuration is that it provides the capability of having multi-diagnostic measurements. For example, electric field measurements and excited state density measurements could be conducted simultaneously, assuming one has access to two iCCD cameras, although this was not the case for the work presented here. The ability to make multi-diagnostic measurements can be a very useful tool due to the sensitivity of APPJs where streamer propagation and the plasma bullets temporal and spatial position is not always completely reproducible (Xian et al. Reference Xian, Lu, Cao, Yang, Xiong, Jiang and Pan2009; Wu, Lu & Pan Reference Wu, Lu and Pan2013; Lu et al. Reference Lu, Naidis, Laroussi and Ostrikov2014).
2. Experimental set-up
The plasma jet used in this study is a form of dielectric barrier discharge produced by our custom built apparatus, the plasma jet source. The plasma jet source consists of two copper ring electrodes, each $5$![]() mm wide and $100$
mm wide and $100$![]() $\mathrm {\mu }$
$\mathrm {\mu }$![]() m thick, wrapped externally around a cylindrical quartz tube (inner diameter: $4$
m thick, wrapped externally around a cylindrical quartz tube (inner diameter: $4$![]() mm outer diameter: $6$
mm outer diameter: $6$![]() mm) vertically orientated as depicted in figure 1(a). The powered electrode is fixed at a distance of $20$
mm) vertically orientated as depicted in figure 1(a). The powered electrode is fixed at a distance of $20$![]() mm from the exit nozzle of the tube and remains separated from the grounded electrode at a distance of $25$
mm from the exit nozzle of the tube and remains separated from the grounded electrode at a distance of $25$![]() mm. To ignite the plasma, a high voltage ($1$
mm. To ignite the plasma, a high voltage ($1$![]() –$12$
–$12$![]() kV) pulsed power supply (Haiden PHF-2 K) with repetition rates in the $1$
kV) pulsed power supply (Haiden PHF-2 K) with repetition rates in the $1$![]() –$100$
–$100$![]() kHz range is applied between the two electrodes and helium gas (99.9 % purity) is passed through the tube and a stream of plasma bullets are produced. The plasma plume extends into open air at atmospheric pressure and room temperature. The applied voltage is measured using a Tekronix P6015A high voltage probe and two Pearson probes monitor the current in both the powered and grounded cable. The voltage pulse is attenuated by the probe by 1000x before being viewed via a GHz digital oscilloscope (Tektronix TDS5104). Typical voltage and current waveforms are shown in figure 2 for a supplied voltage of $6$
kHz range is applied between the two electrodes and helium gas (99.9 % purity) is passed through the tube and a stream of plasma bullets are produced. The plasma plume extends into open air at atmospheric pressure and room temperature. The applied voltage is measured using a Tekronix P6015A high voltage probe and two Pearson probes monitor the current in both the powered and grounded cable. The voltage pulse is attenuated by the probe by 1000x before being viewed via a GHz digital oscilloscope (Tektronix TDS5104). Typical voltage and current waveforms are shown in figure 2 for a supplied voltage of $6$![]() kV at a repetition frequency of $20$
kV at a repetition frequency of $20$![]() kHz and a helium flow rate of $2$
kHz and a helium flow rate of $2$![]() standard litres per minute (slm). The spike in the ground current at approximately $3$
standard litres per minute (slm). The spike in the ground current at approximately $3$![]() $\mathrm {\mu }$
$\mathrm {\mu }$![]() s corresponds to the plasma breakdown. Plasma bullets are generated only in this first positive half-cycle of the voltage waveform and last several hundreds of nanoseconds, reaching peak velocities of up to $100$
s corresponds to the plasma breakdown. Plasma bullets are generated only in this first positive half-cycle of the voltage waveform and last several hundreds of nanoseconds, reaching peak velocities of up to $100$![]() km s$^{-1}$
km s$^{-1}$![]() .
.

Figure 1. (a) Schematic of the plasma jet source used in this work. The jet is vertically orientated with the helium gas flow represented by the arrow and (b) typical spectrum of the excited species produced by this plasma jet source taken along the plume at $1$![]() mm from the tube exit.
mm from the tube exit.

Figure 2. Waveform profiles of the applied voltage (blue) and current (orange) flowing through the powered electrode, and the current flowing through the ground electrode (green) (6 kV, 2 slm, 20 kHz).
An example of the excited species produced by the plasma is presented in figure 1(b). This spectrum was taken along the plume at $1$![]() mm from the tube exit using an Ocean Optics broadband USB spectrometer. Several helium lines are identified, the most intense being the helium $706.5$
mm from the tube exit using an Ocean Optics broadband USB spectrometer. Several helium lines are identified, the most intense being the helium $706.5$![]() nm line, which is an indication of high energy electrons (Walsh et al. Reference Walsh, Iza, Janson, Law and Kong2010). The presence of atomic oxygen can be seen from emission at the $777.4$
nm line, which is an indication of high energy electrons (Walsh et al. Reference Walsh, Iza, Janson, Law and Kong2010). The presence of atomic oxygen can be seen from emission at the $777.4$![]() nm triplet and $844.7$
nm triplet and $844.7$![]() nm singlet and is often desirable for plasma related biomedical applications due to its effective sterilization ability (Moreau, Orange & Feuilloley Reference Moreau, Orange and Feuilloley2008; Kong et al. Reference Kong, Kroesen, Morfill, Nosenko, Shimizu, van Dijk and Zimmermann2009; Georgescu et al. Reference Georgescu, Lungu, Lupu and Osiac2010). Multiple nitrogen lines are also present, with strong emission from the excited ions, ${\rm N}_{2}^{+}$
nm singlet and is often desirable for plasma related biomedical applications due to its effective sterilization ability (Moreau, Orange & Feuilloley Reference Moreau, Orange and Feuilloley2008; Kong et al. Reference Kong, Kroesen, Morfill, Nosenko, Shimizu, van Dijk and Zimmermann2009; Georgescu et al. Reference Georgescu, Lungu, Lupu and Osiac2010). Multiple nitrogen lines are also present, with strong emission from the excited ions, ${\rm N}_{2}^{+}$![]() , produced predominately by Penning ionization between ground state nitrogen and helium metastables (Sretenovic et al. Reference Sretenovic, Krstic, Kovacevic, Obradovic and Kuraica2012).
, produced predominately by Penning ionization between ground state nitrogen and helium metastables (Sretenovic et al. Reference Sretenovic, Krstic, Kovacevic, Obradovic and Kuraica2012).
3. Results and discussion
3.1. Electric field measurements
A non-perturbing spectroscopic method was used to measure the electric field strength along the plasma plume. This method is based on the Stark shifting of the helium $492.2$![]() nm ($4^{1} D$
nm ($4^{1} D$![]() –$2^{1} P$
–$2^{1} P$![]() ) allowed line and its forbidden component ($4^{1} F$
) allowed line and its forbidden component ($4^{1} F$![]() –$2^{1} P$
–$2^{1} P$![]() ) developed by Kuraica & Konjević (Reference Kuraica and Konjević1997) as adaptions of calculations by Foster (Reference Foster1927). The separation between the allowed and forbidden peak, $\Delta \lambda _{pp}$
) developed by Kuraica & Konjević (Reference Kuraica and Konjević1997) as adaptions of calculations by Foster (Reference Foster1927). The separation between the allowed and forbidden peak, $\Delta \lambda _{pp}$![]() , can be used to obtain a value for the electric field using (3.1) (Cvetanović et al. Reference Cvetanović, Martinović, Obradović and Kuraica2015). This equation is valid for electric field values in the range 3–100 kV cm$^{-1}$
, can be used to obtain a value for the electric field using (3.1) (Cvetanović et al. Reference Cvetanović, Martinović, Obradović and Kuraica2015). This equation is valid for electric field values in the range 3–100 kV cm$^{-1}$![]() .
.
where $\Delta \lambda _{pp}$![]() is in nm. A schematic of the optical set-up used is shown in figure 3. The apparatus used four lenses in order to reduce vignetting and achieve a clear $1$
is in nm. A schematic of the optical set-up used is shown in figure 3. The apparatus used four lenses in order to reduce vignetting and achieve a clear $1$![]() :$1$
:$1$![]() object–image projection of the emitted light from the plasma plume onto the slit of a double grating spectrometer (SPEX $750$
object–image projection of the emitted light from the plasma plume onto the slit of a double grating spectrometer (SPEX $750$![]() ) which contains $2 \times 1200$
) which contains $2 \times 1200$![]() l mm$^{-1}$
l mm$^{-1}$![]() gratings. The slit width was set at $50$
gratings. The slit width was set at $50$![]() $\mathrm {\mu }$
$\mathrm {\mu }$![]() m, corresponding to a measured instrumental broadening of $0.029$
m, corresponding to a measured instrumental broadening of $0.029$![]() nm. A periscope assembly rotated the image presented to the spectrometer so that the resulting spatial information represented a radial sample across the plasma plume. A linear polarizer was placed before the entrance of the spectrometer allowing only ${\rm \pi}$
nm. A periscope assembly rotated the image presented to the spectrometer so that the resulting spatial information represented a radial sample across the plasma plume. A linear polarizer was placed before the entrance of the spectrometer allowing only ${\rm \pi}$![]() -polarized light to be transmitted, hence only the axial electric field is measured. An iCCD camera (Andor iStar) with $1024\times 1024$
-polarized light to be transmitted, hence only the axial electric field is measured. An iCCD camera (Andor iStar) with $1024\times 1024$![]() pixels, of $13$
pixels, of $13$![]() $\mathrm {\mu }$
$\mathrm {\mu }$![]() m pixel dimension, was used to capture the spectrum. The achieved spectral dispersion was $7.41$
m pixel dimension, was used to capture the spectrum. The achieved spectral dispersion was $7.41$![]() pm pixel$^{-1}$
pm pixel$^{-1}$![]() and the spatial resolution was $100$
and the spatial resolution was $100$![]() $\mathrm {\mu }$
$\mathrm {\mu }$![]() m. The iCCD gate was triggered by the rising edge of the voltage pulse with a tuneable delay and adjusted to capture the plasma bullets in the field of view. Each measurement consists of $150$
m. The iCCD gate was triggered by the rising edge of the voltage pulse with a tuneable delay and adjusted to capture the plasma bullets in the field of view. Each measurement consists of $150$![]() accumulations, each with $2\times 10^{7}$
accumulations, each with $2\times 10^{7}$![]() gates of $25$
gates of $25$![]() ns duration. The plasma jet source was moved vertically upwards in $1$
ns duration. The plasma jet source was moved vertically upwards in $1$![]() mm increments using a motorized controller and the timing adjusted accordingly to follow the plasma bullets along the plasma plume.
mm increments using a motorized controller and the timing adjusted accordingly to follow the plasma bullets along the plasma plume.

Figure 3. Schematic of the experimental apparatus used for obtaining axial electric field measurements of the plasma plume. A polarizer is placed in front of the spectrometer to allow only ${\rm \pi}$![]() -polarized light to be transmitted.
-polarized light to be transmitted.
For each of the recorded spectra at the imaged plume positions, a lineout along the same region of interest was taken. This lineout was taken centrally along the $z=0$![]() axis of the plume and had a spatial size of $0.8$
axis of the plume and had a spatial size of $0.8$![]() mm. The electric field values measured in this way correspond to those at the luminous head of the plasma bullet along this central region of interest, hence they represent the average electric field measured and do not contain information regarding its radial profile. Upon exiting the tube, it is known that the plasma bullets electric field profile is initially annular and becomes spherical further along the plume due to air diffusion into the helium gas flow (Sretenović et al. Reference Sretenović, Krstić, Kovačević, Obradović and Kuraica2011; Naidis Reference Naidis2012). This annular bullet profile is initially evident in the recorded spectrum upon exiting the tube, however, it typically changes 2–5 mm after the tube exit into a spherical profile, depending on the helium flow rate.
mm. The electric field values measured in this way correspond to those at the luminous head of the plasma bullet along this central region of interest, hence they represent the average electric field measured and do not contain information regarding its radial profile. Upon exiting the tube, it is known that the plasma bullets electric field profile is initially annular and becomes spherical further along the plume due to air diffusion into the helium gas flow (Sretenović et al. Reference Sretenović, Krstić, Kovačević, Obradović and Kuraica2011; Naidis Reference Naidis2012). This annular bullet profile is initially evident in the recorded spectrum upon exiting the tube, however, it typically changes 2–5 mm after the tube exit into a spherical profile, depending on the helium flow rate.
A typical output spectrum taken from a lineout of the iCCD image is shown in figure 4. There are 3 main contributions; the $492.2$![]() nm allowed line, its forbidden component and emission from a molecular nitrogen second positive system transition (SPS) at $491.7$
nm allowed line, its forbidden component and emission from a molecular nitrogen second positive system transition (SPS) at $491.7$![]() nm. Transitions of both the helium and nitrogen (SPS) appear predominantly through excitation by energetic electrons (Sretenovic et al. Reference Sretenovic, Krstic, Kovacevic, Obradovic and Kuraica2012). All of these peaks must be accounted for in the fitting process to allow an accurate value of $\Delta \lambda _{pp}$
nm. Transitions of both the helium and nitrogen (SPS) appear predominantly through excitation by energetic electrons (Sretenovic et al. Reference Sretenovic, Krstic, Kovacevic, Obradovic and Kuraica2012). All of these peaks must be accounted for in the fitting process to allow an accurate value of $\Delta \lambda _{pp}$![]() to be obtained. Typically, instrumental broadening and Doppler broadening have a Gaussian profile whereas Stark broadening and van der Waals broadening are Lorentzian, so an overall Voigt line profile is expected. Since the jet operates at atmospheric pressure, Doppler broadening due to high temperature discharges are unlikely and can be neglected. Each line was fitted with a pseudo-Voigt profile taking into account the instrumental broadening. The separation, $\Delta \lambda _{pp}$
to be obtained. Typically, instrumental broadening and Doppler broadening have a Gaussian profile whereas Stark broadening and van der Waals broadening are Lorentzian, so an overall Voigt line profile is expected. Since the jet operates at atmospheric pressure, Doppler broadening due to high temperature discharges are unlikely and can be neglected. Each line was fitted with a pseudo-Voigt profile taking into account the instrumental broadening. The separation, $\Delta \lambda _{pp}$![]() , between the allowed and forbidden peaks was then substituted into (3.1) to calculate the corresponding field strength.
, between the allowed and forbidden peaks was then substituted into (3.1) to calculate the corresponding field strength.

Figure 4. Data taken from a lineout across the inset (top left) with all contributing components fitted with pseudo-Voigt profiles. The grey dotted line represents separation between the allowed and forbidden peaks, $\Delta \lambda _{pp}$![]() .
.
Figure 5 shows the axial electric field measured for different gas flow rates along the length of the plasma plume at a supplied voltage of $6$![]() kV. The jet can be seen in the laboratory to extend a few mm further than the maximum distances shown in the figure, however, there is insufficient emitted light intensity in this region for useful measurements. The visible tip of the plume also experiences turbulence, causing the length of the plume to fluctuate in the mm range and making measurements in this region impractical. The strength of the electric field is shown to increase gradually as a function of distance along the plume length. The general behaviour of increasing electric field remains the same for all gas flows, with the main difference being that, at lower flows, the electric field rises at a quicker rate along the plume in comparison with higher flows with the overall range of the electric field profile being similar in magnitude. This relationship of increasing electric field strength with increasing distance along the plume has been observed for similar plasma jets (Sretenović et al. Reference Sretenović, Krstić, Kovačević, Obradović and Kuraica2014; Sobota et al. Reference Sobota, Guaitella, Sretenović, Krstić, Kovačević, Obrusník, Nguyen, Zajíčková, Obradović and Kuraica2016; Kovačević et al. Reference Kovačević, Sretenović, Slikboer, Guaitella, Sobota and Kuraica2018; Hofmans & Sobota Reference Hofmans and Sobota2019). This gradual increase seen for all flows comes partly as a result of the radial size of the plasma bullet decreasing with distance. This causes an increase in charge density resulting in a higher electric field. Experiments and numerical simulations have demonstrated that the electron density increases along the path of the plume consistent with the increasing electric field values (Naidis Reference Naidis2012; Klarenaar et al. Reference Klarenaar, Guaitella, Engeln and Sobota2018; Kovačević et al. Reference Kovačević, Sretenović, Slikboer, Guaitella, Sobota and Kuraica2018; Hofmans et al. Reference Hofmans, Viegas, van Rooij, Klarenaar, Guaitella, Bourdon and Sobota2020). The difference for the rate of increase of electric field strength seen for the different gas flows comes largely due to gas mixing of the helium with the surrounding air. To further demonstrate this gas mixing, schlieren imaging was used to visually investigate the fluid dynamics between the pure flowing helium and surrounding air. The optical arrangement consisted of two $300$
kV. The jet can be seen in the laboratory to extend a few mm further than the maximum distances shown in the figure, however, there is insufficient emitted light intensity in this region for useful measurements. The visible tip of the plume also experiences turbulence, causing the length of the plume to fluctuate in the mm range and making measurements in this region impractical. The strength of the electric field is shown to increase gradually as a function of distance along the plume length. The general behaviour of increasing electric field remains the same for all gas flows, with the main difference being that, at lower flows, the electric field rises at a quicker rate along the plume in comparison with higher flows with the overall range of the electric field profile being similar in magnitude. This relationship of increasing electric field strength with increasing distance along the plume has been observed for similar plasma jets (Sretenović et al. Reference Sretenović, Krstić, Kovačević, Obradović and Kuraica2014; Sobota et al. Reference Sobota, Guaitella, Sretenović, Krstić, Kovačević, Obrusník, Nguyen, Zajíčková, Obradović and Kuraica2016; Kovačević et al. Reference Kovačević, Sretenović, Slikboer, Guaitella, Sobota and Kuraica2018; Hofmans & Sobota Reference Hofmans and Sobota2019). This gradual increase seen for all flows comes partly as a result of the radial size of the plasma bullet decreasing with distance. This causes an increase in charge density resulting in a higher electric field. Experiments and numerical simulations have demonstrated that the electron density increases along the path of the plume consistent with the increasing electric field values (Naidis Reference Naidis2012; Klarenaar et al. Reference Klarenaar, Guaitella, Engeln and Sobota2018; Kovačević et al. Reference Kovačević, Sretenović, Slikboer, Guaitella, Sobota and Kuraica2018; Hofmans et al. Reference Hofmans, Viegas, van Rooij, Klarenaar, Guaitella, Bourdon and Sobota2020). The difference for the rate of increase of electric field strength seen for the different gas flows comes largely due to gas mixing of the helium with the surrounding air. To further demonstrate this gas mixing, schlieren imaging was used to visually investigate the fluid dynamics between the pure flowing helium and surrounding air. The optical arrangement consisted of two $300$![]() mm focal length lenses, a white light source, a razor blade and an iCCD camera. The blade was positioned vertically at the focal point of the second lens. A final lens was placed in front of the camera to improve image quality. The exposure time of each image was $50$
mm focal length lenses, a white light source, a razor blade and an iCCD camera. The blade was positioned vertically at the focal point of the second lens. A final lens was placed in front of the camera to improve image quality. The exposure time of each image was $50$![]() $\mathrm {\mu }$
$\mathrm {\mu }$![]() s. Figure 6 shows images captured of the helium flow. As can be seen, there is a clear difference in the flowing helium shape and in its mixing with the ambient air for the two helium flow rates. At $2$
s. Figure 6 shows images captured of the helium flow. As can be seen, there is a clear difference in the flowing helium shape and in its mixing with the ambient air for the two helium flow rates. At $2$![]() slm, the helium flow is almost completely laminar across the region imaged, whereas at $1$
slm, the helium flow is almost completely laminar across the region imaged, whereas at $1$![]() slm, the helium gas expands radially with distance along the plume and diffuses into the air. Since the plasma discharge propagates along a helium–air channel upon exiting the tube, more mixing of the helium with the surrounding air will result in a higher molar fraction of air along the propagation channel. At $10$
slm, the helium gas expands radially with distance along the plume and diffuses into the air. Since the plasma discharge propagates along a helium–air channel upon exiting the tube, more mixing of the helium with the surrounding air will result in a higher molar fraction of air along the propagation channel. At $10$![]() mm from the tube exit, the measured electric field at $1$
mm from the tube exit, the measured electric field at $1$![]() slm is $3.2$
slm is $3.2$![]() kV cm$^{-1}$
kV cm$^{-1}$![]() greater than that measured at $2$
greater than that measured at $2$![]() slm. The greater helium–air mixing for a $1$
slm. The greater helium–air mixing for a $1$![]() slm flow rate is readily visible at the position of the dashed line in figure 6. The value of the first Townsend ionization coefficient for discharge propagation is lower for a helium–air channel in comparison with pure helium, therefore, a greater fraction of air in the helium flow will reduce this coefficient, resulting in an increased electric field (Sobota et al. Reference Sobota, Guaitella, Sretenović, Krstić, Kovačević, Obrusník, Nguyen, Zajíčková, Obradović and Kuraica2016; Kovačević et al. Reference Kovačević, Sretenović, Slikboer, Guaitella, Sobota and Kuraica2018), as also observed in numerical simulations (Naidis Reference Naidis2012; Hofmans et al. Reference Hofmans, Viegas, van Rooij, Klarenaar, Guaitella, Bourdon and Sobota2020).
slm flow rate is readily visible at the position of the dashed line in figure 6. The value of the first Townsend ionization coefficient for discharge propagation is lower for a helium–air channel in comparison with pure helium, therefore, a greater fraction of air in the helium flow will reduce this coefficient, resulting in an increased electric field (Sobota et al. Reference Sobota, Guaitella, Sretenović, Krstić, Kovačević, Obrusník, Nguyen, Zajíčková, Obradović and Kuraica2016; Kovačević et al. Reference Kovačević, Sretenović, Slikboer, Guaitella, Sobota and Kuraica2018), as also observed in numerical simulations (Naidis Reference Naidis2012; Hofmans et al. Reference Hofmans, Viegas, van Rooij, Klarenaar, Guaitella, Bourdon and Sobota2020).

Figure 5. Variation of the axial electric field along the plume for different helium flow rates. ($6$![]() kV, $20$
kV, $20$![]() kHz).
kHz).

Figure 6. Schlieren images of the helium flow upon exiting the quartz tube for flow rates of $1$![]() and $2$
and $2$![]() slm. The red dashed line represents a distance of $10$
slm. The red dashed line represents a distance of $10$![]() mm from the tube exit. The measured axial electric field values at these planes are shown.
mm from the tube exit. The measured axial electric field values at these planes are shown.
Since the applications of the plasma jet requires it to be impacting on a target, it is important to know what changes this will have on the dynamics of the jet. Any object in the close vicinity of the plasma plume will have an effect on it because it will divert the gas flow and interact electrically with the plasma. For example, if an object is placed slightly beyond the visible plume length of the plasma, the plume will extend further to make contact with the surface of the object. To get a better understanding of targets and how their dielectric or conductive properties plus their distance from the tube exit influences the plasma, the electric field profile along the jet was studied for two different targets; plastic and water. Three distances between the tube exit and target were investigated; $8$![]() , $14$
, $14$![]() and $16$
and $16$![]() mm, as shown in figure 7. Neither target was grounded for these measurements. For both targets, there are minimal changes in the measured electric field except at a few mm directly above the target where a clear enhancement can be observed. The magnitude of this increase is strongly dependent on the distance between the tube exit and the target. When the target was placed $8$
mm, as shown in figure 7. Neither target was grounded for these measurements. For both targets, there are minimal changes in the measured electric field except at a few mm directly above the target where a clear enhancement can be observed. The magnitude of this increase is strongly dependent on the distance between the tube exit and the target. When the target was placed $8$![]() mm from the tube exit, an increase of $0.9$
mm from the tube exit, an increase of $0.9$![]() kV cm$^{-1}$
kV cm$^{-1}$![]() (relative increase of $6$
(relative increase of $6$![]() %) is measured for plastic and $1.5$
%) is measured for plastic and $1.5$![]() kV cm$^{-1}$
kV cm$^{-1}$![]() (relative increase of $10$
(relative increase of $10$![]() %) for water in comparison with that measured for a freely expanding jet at the same position. However, when the target distance was extended to $14$
%) for water in comparison with that measured for a freely expanding jet at the same position. However, when the target distance was extended to $14$![]() mm, an increase of $4.0$
mm, an increase of $4.0$![]() kV cm$^{-1}$
kV cm$^{-1}$![]() (relative increase of $16$
(relative increase of $16$![]() %) is measured for plastic and $6.8$
%) is measured for plastic and $6.8$![]() kV cm$^{-1}$
kV cm$^{-1}$![]() (relative increase of $28$
(relative increase of $28$![]() %) for water. When the target distance was extended another $2$
%) for water. When the target distance was extended another $2$![]() mm from the tube exit, the electric field increased further, reaching as high as $31.2 \pm 2.3$
mm from the tube exit, the electric field increased further, reaching as high as $31.2 \pm 2.3$![]() kV cm$^{-1}$
kV cm$^{-1}$![]() for plastic and $32.1 \pm 1.6$
for plastic and $32.1 \pm 1.6$![]() kV cm$^{-1}$
kV cm$^{-1}$![]() for water. Whilst no electric field measurement was taken at this distance for the freely expanding jet due to low signal, from figure 7(c), a notable increase can already be seen for both targets at $14$
for water. Whilst no electric field measurement was taken at this distance for the freely expanding jet due to low signal, from figure 7(c), a notable increase can already be seen for both targets at $14$![]() mm, therefore, we postulate that the electric field measured for both targets at $15$
mm, therefore, we postulate that the electric field measured for both targets at $15$![]() and $16$
and $16$![]() mm is greater than that for a freely expanding jet.
mm is greater than that for a freely expanding jet.

Figure 7. Comparison of the axial electric field profile along the plasma plume for a freely expanding jet and for the jet interacting with a target of plastic and water placed at a distance of (a) $8$![]() mm, (b) $14$
mm, (b) $14$![]() mm and (c) $16$
mm and (c) $16$![]() mm. (d) Target positions overlayed on schlieren image of the helium flowing at 1 slm (no plasma ignited).
mm. (d) Target positions overlayed on schlieren image of the helium flowing at 1 slm (no plasma ignited).
This behaviour of additional electric field enhancement depending on the target position is again partly related to the fraction of air due to mixing, outlined previously. Figure 7(d), displays the targets positions overlayed on a schlieren image of the helium flow when no plasma was ignited. There is a greater diffusion of helium into the surrounding air along the planes (b,c) in comparison with plane (a). This means greater gas mixing at these planes resulting in a higher molar fraction of air present and hence a higher electric field. Another contributing factor leading to the electric field enhancement is due to the compression of charge on striking the target surface. Figure 8 shows images of the plasma plume interacting with the plastic and water target at the measured positions. It can be seen that the larger the separation between the tube exit and target, the more constricted the plasma plume becomes at the surface of the target, which would lead to compression of charge and hence a higher electric field. One main difference between the two targets is a radial spreading of the plasma on the surface of the plastic target covering a much larger surface area of the target in comparison with water. The slight additional enhancement of the electric field for the water target may partially be due to charging of the surface on impact. Numerical simulations of a similar gas jet interacting with targets of varying permittivities showed that higher permittivity targets resulted in more positive charge build up on the target surface (Viegas & Bourdon Reference Viegas and Bourdon2020). This behaviour of different targets only inducing enhanced peak electric fields near the target has been seen both experimentally (Klarenaar et al. Reference Klarenaar, Guaitella, Engeln and Sobota2018; Sobota et al. Reference Sobota, Guaitella, Sretenović, Kovačević, Slikboer, Krstić, Obradović and Kuraica2019) and numerically (Norberg, Johnsen & Kushner Reference Norberg, Johnsen and Kushner2015; Wang, Zheng & Jia Reference Wang, Zheng and Jia2016; Ji et al. Reference Ji, Yan, Xia and Liu2018; Schweigert et al. Reference Schweigert, Vagapov, Lin and Keidar2019). Thomson scattering measurements of a similar gas jet impacting upon different targets also show the electron density increasing with distance from the tube exit, reaching a higher maximum electron density immediately before the target (Klarenaar et al. Reference Klarenaar, Guaitella, Engeln and Sobota2018), with a larger increase in electron density for conducting targets of copper and water in comparison with glass. This increase in electron density would result in a higher electric field. Therefore the additional increase in density measured for conducting targets would explain why our electric field magnitude is on average greater for water compared with plastic.

Figure 8. Images of the plasma–target interaction at different target positions for (a) plastic and (b) water.
3.2. Fast two-dimensional monochromatic imaging
In order to estimate excited state densities within the plasma jet, a fast two-dimensional (2-D) monochromatic imaging configuration was utilized to measure emission from the plasma source quartz tube. This required imaging the plasma bullets with an appropriate bandpass filter attached to the iCCD to isolate emission from single states. A $200$![]() mm focal length lens was used and an appropriate filter mounted to the iCCD. The camera was triggered by the rising edge of the voltage pulse in a similar manner to that described in § 3.1. The gate time used was $20$
mm focal length lens was used and an appropriate filter mounted to the iCCD. The camera was triggered by the rising edge of the voltage pulse in a similar manner to that described in § 3.1. The gate time used was $20$![]() ns and each exposure resulted in an accumulation of $10$
ns and each exposure resulted in an accumulation of $10$![]() bullets per image. The propagation of the plasma bullets were recorded at $50$
bullets per image. The propagation of the plasma bullets were recorded at $50$![]() ns intervals. Due to the strong emission intensity of helium lines shown in figure 1(b), the helium $^{3}$
ns intervals. Due to the strong emission intensity of helium lines shown in figure 1(b), the helium $^{3}$![]() S at $706.5$
S at $706.5$![]() nm and $^{1}$
nm and $^{1}$![]() S at $728.1$
S at $728.1$![]() nm were chosen to investigate. Sample images of the plasma bullets within the source can be seen in figure 9(a). These are 2-D images of 3-D plasma bullets, however, assuming the bullet is an optically thin plasma, the signal in each pixel corresponds to the line integrated emission from excited helium states in a column extending from the pixel through the plasma bullet to infinity. The emission value recorded at each pixel is therefore the emission integrated along a column with face area equal to the pixel width squared, $w^{2}_{{\rm px}}$
nm were chosen to investigate. Sample images of the plasma bullets within the source can be seen in figure 9(a). These are 2-D images of 3-D plasma bullets, however, assuming the bullet is an optically thin plasma, the signal in each pixel corresponds to the line integrated emission from excited helium states in a column extending from the pixel through the plasma bullet to infinity. The emission value recorded at each pixel is therefore the emission integrated along a column with face area equal to the pixel width squared, $w^{2}_{{\rm px}}$![]() . For each image, a lineout along the bullet region was taken, as shown in figure 9(b). The measured profile is reasonably approximated, for our purposes, by a Gaussian. If each pixel corresponds to the total emission from helium states in a long column extending through that pixel, we can relate the maximum signal, $C_{p}$
. For each image, a lineout along the bullet region was taken, as shown in figure 9(b). The measured profile is reasonably approximated, for our purposes, by a Gaussian. If each pixel corresponds to the total emission from helium states in a long column extending through that pixel, we can relate the maximum signal, $C_{p}$![]() , per bullet, taken here as the amplitude of the Gaussian fit divided by the number of bullets accumulated on the camera, to the total number of emitters, $N_{{\rm em}}$
, per bullet, taken here as the amplitude of the Gaussian fit divided by the number of bullets accumulated on the camera, to the total number of emitters, $N_{{\rm em}}$![]() , in that column using (3.2)
, in that column using (3.2)
Here, ${\rm iCCD}_{{\rm res}}$![]() , is the response of the iCCD and has units of counts/eV, $E_{\gamma }$
, is the response of the iCCD and has units of counts/eV, $E_{\gamma }$![]() is the photon energy of the transition being observed and QE is the quantum efficiency of the iCCD, i.e. the fraction of photons incident on the CCD that are absorbed and contribute to the pixel signal. Also, $T$
is the photon energy of the transition being observed and QE is the quantum efficiency of the iCCD, i.e. the fraction of photons incident on the CCD that are absorbed and contribute to the pixel signal. Also, $T$![]() is the total transmission of the imaging system and is dominated by the transmission of the bandpass filter and $\varOmega$
is the total transmission of the imaging system and is dominated by the transmission of the bandpass filter and $\varOmega$![]() is the solid angle subtended by the first lens in the imaging system. The response of the iCCD was initially calibrated for each bandpass filter before taking any measurements. The bandpass filters used were $700$
is the solid angle subtended by the first lens in the imaging system. The response of the iCCD was initially calibrated for each bandpass filter before taking any measurements. The bandpass filters used were $700$![]() and $730$
and $730$![]() nm (Thorlabs FB$700$
nm (Thorlabs FB$700$![]() -$10$
-$10$![]() and FL$730$
and FL$730$![]() -$10$
-$10$![]() ), both having a full width at half-maximum (FWHM) of $10\pm 2$
), both having a full width at half-maximum (FWHM) of $10\pm 2$![]() nm, thus allowing emission from $^{3}$
nm, thus allowing emission from $^{3}$![]() S and $^{1}$
S and $^{1}$![]() S states to pass through the given filter. Transmission profiles over the wavelength range of the filters were provided by the supplier, however, due to the uncertainty of the central wavelength of each filter, ${\pm }2$
S states to pass through the given filter. Transmission profiles over the wavelength range of the filters were provided by the supplier, however, due to the uncertainty of the central wavelength of each filter, ${\pm }2$![]() nm, the quoted transmissions were experimentally verified. The numerical values used in the analysis are tabulated in table 1.
nm, the quoted transmissions were experimentally verified. The numerical values used in the analysis are tabulated in table 1.

Figure 9. (a) Sample images of the plasma bullets at 3 different time delays when the $700$![]() nm bandpass filter was present. The powered electrode extends from $25$
nm bandpass filter was present. The powered electrode extends from $25$![]() to $30$
to $30$![]() mm and the ground electrode from $-5$
mm and the ground electrode from $-5$![]() to $0$
to $0$![]() mm. (b) Data taken from a lineout across the plasma bullet region (inset) fitted using a Gaussian profile with $\chi ^{2} = 2.2$
mm. (b) Data taken from a lineout across the plasma bullet region (inset) fitted using a Gaussian profile with $\chi ^{2} = 2.2$![]() .
.
Table 1. Values used to calculate the excited state densities of the helium $^{3}$![]() S and $^{1}$
S and $^{1}$![]() S states.
S states.

The radial density profile of the excited helium states corresponding to the transition we are observing, $n_{{\rm He}}(r)$![]() , must firstly be obtained. The shape of this profile will be the Abel inversion of the profile projected onto the camera, i.e. the lineout along the region of interest. Since this is well fitted by a Gaussian, we can take the Abel inversion to also be a Gaussian with the same FWHM. Assuming that the density does not significantly vary during the exposure time, $t$
, must firstly be obtained. The shape of this profile will be the Abel inversion of the profile projected onto the camera, i.e. the lineout along the region of interest. Since this is well fitted by a Gaussian, we can take the Abel inversion to also be a Gaussian with the same FWHM. Assuming that the density does not significantly vary during the exposure time, $t$![]() , for any single bullet the number of emitters is approximated by (3.3)
, for any single bullet the number of emitters is approximated by (3.3)
where $A_{ul}$![]() , is the rate at which the excited states emit. The $A$
, is the rate at which the excited states emit. The $A$![]() rates are transition dependent and since the $706$
rates are transition dependent and since the $706$![]() nm helium state has a degeneracy of $g=3$
nm helium state has a degeneracy of $g=3$![]() , the sum of the three $A$
, the sum of the three $A$![]() rates was used. The values of the $A$
rates was used. The values of the $A$![]() rates were taken from NIST Atomic Spectra Database (Kramida et al. Reference Kramida, Ralchenko and Reader2021) and are also tabulated in table 1. The time is dictated by the camera acquisition and was $20$
rates were taken from NIST Atomic Spectra Database (Kramida et al. Reference Kramida, Ralchenko and Reader2021) and are also tabulated in table 1. The time is dictated by the camera acquisition and was $20$![]() ns for all images. In figure 9(a), two distinct sets of plasma bullets can be seen in each image, one of the bullets travelling upwards starting from the powered electrode towards the ground electrode, and the other again starting from the powered electrode but travelling downwards towards the open end of the quartz tube with little emission being detected outside of the tube. Figure 10 compares the excited state densities of the $^{3}$
ns for all images. In figure 9(a), two distinct sets of plasma bullets can be seen in each image, one of the bullets travelling upwards starting from the powered electrode towards the ground electrode, and the other again starting from the powered electrode but travelling downwards towards the open end of the quartz tube with little emission being detected outside of the tube. Figure 10 compares the excited state densities of the $^{3}$![]() S and $^{1}$
S and $^{1}$![]() S helium states. For both states and bullet propagation directions, the excited state density is lowest at the point of creation (the powered electrode) and shows an increase with distance from the powered electrode before decreasing again. The measured excited state density for the $^{3}$
S helium states. For both states and bullet propagation directions, the excited state density is lowest at the point of creation (the powered electrode) and shows an increase with distance from the powered electrode before decreasing again. The measured excited state density for the $^{3}$![]() S state is on average much larger than the $^{1}$
S state is on average much larger than the $^{1}$![]() S state, reaching a maximum density of up to $(9.0\pm 0.8)\times 10^{10}$
S state, reaching a maximum density of up to $(9.0\pm 0.8)\times 10^{10}$![]() cm$^{-3}$
cm$^{-3}$![]() for the $^{3}$
for the $^{3}$![]() S state and $(3.4\pm 0.3)\times 10^{10}$
S state and $(3.4\pm 0.3)\times 10^{10}$![]() cm$^{-3}$
cm$^{-3}$![]() for the $^{1}$
for the $^{1}$![]() S state. For both states there was little to no detection of emission along the plume upon exiting the tube. This most likely comes as a result of helium quenching through Penning ionization from the increased fraction of oxygen outside of the tube. One study conducted on a helium radio frequency-driven APPJ using a collisional–radiative model to estimate helium and oxygen excited state densities as a function of relative air concentration showed that both the $^{3}$
S state. For both states there was little to no detection of emission along the plume upon exiting the tube. This most likely comes as a result of helium quenching through Penning ionization from the increased fraction of oxygen outside of the tube. One study conducted on a helium radio frequency-driven APPJ using a collisional–radiative model to estimate helium and oxygen excited state densities as a function of relative air concentration showed that both the $^{3}$![]() S and $^{1}$
S and $^{1}$![]() S helium excited state densities decreased rapidly for air concentrations above 0.1 % (Petrova et al. Reference Petrova, Boris, Hinshelwood, Johnson, Gillman and Walton2020).
S helium excited state densities decreased rapidly for air concentrations above 0.1 % (Petrova et al. Reference Petrova, Boris, Hinshelwood, Johnson, Gillman and Walton2020).

Figure 10. Excited state densities of the $^{3}$![]() S at $706$
S at $706$![]() nm and $^{1}$
nm and $^{1}$![]() S at $728$
S at $728$![]() nm helium states as a function of distance from the grounded electrode. The brown dashed rectangle represents the position of the powered electrode.
nm helium states as a function of distance from the grounded electrode. The brown dashed rectangle represents the position of the powered electrode.
4. Conclusions
Several optical diagnostics were utilized to investigate the behaviour of a kHz APPJ source. Electric field measurements made along the length of the plume showed that the electric field increases with distance from the tube exit. These values ranged from 4 to 25 kV cm$^{-1}$![]() . This increase comes as a result of the plasma bullets radially decreasing in size as a function of distance from the tube exit meaning the field lines will also be compressed. The rate of increase has been shown to be dependent on the helium gas flow rate, with lower gas flows showing a sharper increase with distance in comparison with larger flow rates with the typical values measured remaining within the same range. Schlieren imaging was used to demonstrate this difference by showing that a greater fraction of air mixed in the helium flow resulted in a higher electric field. The presence of a target was shown to influence the magnitude of the electric field in close proximity to the target. The magnitude of this increase is strongly dependent on the distance between the tube exit and the target, with larger separation causing a greater relative change in the measured electric field. The relative increase measured was on average higher for the conducting target of water compared with plastic. A cheap minimal equipment optical measurement configuration, termed here as fast 2-D monochromatic imaging, was introduced as a tool for measuring excited state densities within the plasma jet source. Using this method, estimates for the excited helium $^{3}$
. This increase comes as a result of the plasma bullets radially decreasing in size as a function of distance from the tube exit meaning the field lines will also be compressed. The rate of increase has been shown to be dependent on the helium gas flow rate, with lower gas flows showing a sharper increase with distance in comparison with larger flow rates with the typical values measured remaining within the same range. Schlieren imaging was used to demonstrate this difference by showing that a greater fraction of air mixed in the helium flow resulted in a higher electric field. The presence of a target was shown to influence the magnitude of the electric field in close proximity to the target. The magnitude of this increase is strongly dependent on the distance between the tube exit and the target, with larger separation causing a greater relative change in the measured electric field. The relative increase measured was on average higher for the conducting target of water compared with plastic. A cheap minimal equipment optical measurement configuration, termed here as fast 2-D monochromatic imaging, was introduced as a tool for measuring excited state densities within the plasma jet source. Using this method, estimates for the excited helium $^{3}$![]() S and $^{1}$
S and $^{1}$![]() S states inside the source were found to be of the order of $10^{10}$
S states inside the source were found to be of the order of $10^{10}$![]() –$10^{11}$
–$10^{11}$![]() cm$^{-3}$
cm$^{-3}$![]() .
.
Acknowledgements
We would like to acknowledge Dr C.M.O. Mahony for his useful feedback on this manuscript and the referees for their remarks and advice.
Editor Edward Thomas, Jr. thanks the referees for their advice in evaluating this article.
Funding
This research was funded by Engineering and Physical Sciences Research Council (EPSRC), grant number EP/P026079/1.
Declaration of interests
The author report no conflict of interest.