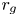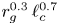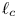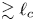1 Introduction
The transport of high-energy charged particles in magnetized, collisionless turbulence is central to many topics of high-energy astrophysics and space plasma physics, e.g. it governs the phenomenology of cosmic rays of all energies and on all scales (Berezinskii et al. Reference Berezinskii, Bulanov, Dogiel and Ptuskin1990; Zweibel Reference Zweibel2017; Amato & Blasi Reference Amato and Blasi2018, and references therein), including that of solar energetic particles (Oughton & Engelbrecht Reference Oughton and Engelbrecht2021, and references therein), just as it controls the acceleration rate of particles in Fermi-type processes (Blandford & Eichler Reference Blandford and Eichler1987, and references therein) or dictates the spatial profile of high-energy radiation around powerful sources (HESS Collaboration et al. Reference Abramowski, Aharonian, Benkhali, Akhperjanian, Angüner, Backes, Balzer, Becherini, Tjus and Berge2016; López-Coto et al. Reference López-Coto, de Oña Wilhelmi, Aharonian, Amato and Hinton2022; Liu Reference Liu2022, and references therein). Most of the phenomenology in those fields has relied on the use of a quasilinear theory (QLT) description (Jokipii Reference Jokipii1966; Hall & Sturrock Reference Hall and Sturrock1967; Kulsrud & Pearce Reference Kulsrud and Pearce1969; Schlickeiser Reference Schlickeiser2002) and its nonlinear extensions, e.g. Shalchi (Reference Shalchi2009) and references therein. While attractive in its convenience and its phenomenological success when compared with solar wind data (Bieber et al. Reference Bieber, Matthaeus, Smith, Wanner, Kallenrode and Wibberenz1994; Bieber, Wanner & Matthaeus Reference Bieber, Wanner and Matthaeus1996) or to numerical simulations of test particle propagation in synthetic wave turbulence (Giacalone & Jokipii Reference Giacalone and Jokipii1999; Casse, Lemoine & Pelletier Reference Casse, Lemoine and Pelletier2002; Dundovic et al. Reference Dundovic, Pezzi, Blasi, Evoli and Matthaeus2020; Mertsch Reference Mertsch2020; Reichherzer et al. Reference Reichherzer, Becker Tjus, Zweibel, Merten and Pueschel2020), this general picture is known to be impaired by a number of issues.
Within the wave turbulence paradigm, it is recognized that the inherent anisotropy of MHD turbulence (Goldreich & Sridhar Reference Goldreich and Sridhar1995, Reference Goldreich and Sridhar1997) leads to the erasure of most wave–particle resonances (Chandran Reference Chandran2000b), with the exception of those associated with fast compressive modes (Yan & Lazarian Reference Yan and Lazarian2002; Cho & Lazarian Reference Cho and Lazarian2003; Beresnyak, Yan & Lazarian Reference Beresnyak, Yan and Lazarian2011), although this last statement has itself been recently disputed (Kempski & Quataert Reference Kempski and Quataert2022). Furthermore, recent large-scale numerical simulations point to a picture in which most of the fluctuation power is not concentrated in compressive eigenmodes but rather, in low-frequency structures (Fu et al. Reference Fu, Li, Gan, Du and Steinberg2022; Gan et al. Reference Gan, Li, Fu and Du2022; Du et al. Reference Du, Li, Gan and Fu2023), see also Grošelj et al. (Reference Grošelj, Chen, Mallet, Samtaney, Schneider and Jenko2019).
More importantly, developed MHD turbulence cannot be epitomized by a sum of linear plane waves (e.g. Matthaeus et al. Reference Matthaeus, Wan, Servidio, Greco, Osman, Oughton and Dmitruk2015; Vlahos & Isliker Reference Vlahos and Isliker2023), as is implicit to the quasilinear framework and to the numerical simulations of synthetic wave turbulence that seek to test it. One particular, key assumption that must be called into question is that of random phased fluctuations. Figure 18 of Maron & Goldreich (Reference Maron and Goldreich2001) provides a vivid illustration of that problem by comparing a snapshot extracted from a simulation of incompressible MHD turbulence with its quasilinear analogue, namely that obtained by switching to Fourier space, then randomizing the phases of the Fourier modes, then switching back to configuration space. That exercise washes out the conspicuous coherent structures of the MHD snapshot; for good reason too, as the rise of phase coherence, which builds up through nonlinear interactions, the emergence of structures and the development of intermittency are regarded as three symbiotic features of turbulence. Measurements conducted in the solar wind support that picture, just as they reveal non-zero phase coherence among the fluctuations (Hada, Koga & Yamamoto Reference Hada, Koga and Yamamoto2003; Koga et al. Reference Koga, Chian, Miranda and Rempel2007, Reference Koga, Chian, Hada and Rempel2008; Sahraoui Reference Sahraoui2008; Nakanotani, Zhao & Zank Reference Nakanotani, Zhao and Zank2023). Finally, because intermittency increases toward small scales, the random phase approximation likely becomes worse for low-energy (small gyroradius) particles.
Those observations bring into question the role that such structures can play with regards to spatial transport.Footnote 1 The present study seeks to examine this issue and it argues, in particular, that the sharp bends of magnetic field lines, which – see below – abound on all scales in MHD turbulence, can provide an efficient source of pitch-angle scattering. The argument is in itself rather simple and it can be formulated as follows. As recalled in § 2, a particle of gyroradius $r_{g}$![]() crossing a bend of the magnetic field with curvature radius $\lesssim r_{g}$
crossing a bend of the magnetic field with curvature radius $\lesssim r_{g}$![]() sees its magnetic moment vary by an order of unity, entailing a comparable change in the pitch angle. That effect has received a lot of attention in magnetospheric plasma physics, see e.g. Gray & Lee (Reference Gray and Lee1982), Birmingham (Reference Birmingham1984), Chen & Palmadesso (Reference Chen and Palmadesso1986), Whipple, Northrop & Birmingham (Reference Whipple, Northrop and Birmingham1986), Büchner & Zelenyi (Reference Büchner and Zelenyi1986), Anderson et al. (Reference Anderson, Decker, Paschalidis and Sarris1997), Delcourt, Zelenyi & Sauvaud (Reference Delcourt, Zelenyi and Sauvaud2000) or Artemyev et al. (Reference Artemyev, Orlova, Mourenas, Agapitov and Krasnoselskikh2013), where it is often referred to as ‘magnetic field line curvature scattering.’ Interestingly, magnetic moment violation through localized interactions with regions of weak, tangled magnetic fields has also recently been observed in a numerical model of a tokamak (Escande & Sattin Reference Escande and Sattin2021). In a turbulent plasma, if one were to rely on the scaling of two-point functions only, e.g. the magnetic power spectrum, one could argue that such structures do not exist on the relevant scales (as discussed further below). However, such fluctuations are strongly intermittent, so much so in fact that the extended power-law tails of their probability distribution functions (p.d.f.s) provide sufficiently many structures to sustain scattering. This is demonstrated here through direct sampling in a numerical simulation of incompressible MHD without a mean field (§ 3). These results are summarized and discussed further in § 4.
sees its magnetic moment vary by an order of unity, entailing a comparable change in the pitch angle. That effect has received a lot of attention in magnetospheric plasma physics, see e.g. Gray & Lee (Reference Gray and Lee1982), Birmingham (Reference Birmingham1984), Chen & Palmadesso (Reference Chen and Palmadesso1986), Whipple, Northrop & Birmingham (Reference Whipple, Northrop and Birmingham1986), Büchner & Zelenyi (Reference Büchner and Zelenyi1986), Anderson et al. (Reference Anderson, Decker, Paschalidis and Sarris1997), Delcourt, Zelenyi & Sauvaud (Reference Delcourt, Zelenyi and Sauvaud2000) or Artemyev et al. (Reference Artemyev, Orlova, Mourenas, Agapitov and Krasnoselskikh2013), where it is often referred to as ‘magnetic field line curvature scattering.’ Interestingly, magnetic moment violation through localized interactions with regions of weak, tangled magnetic fields has also recently been observed in a numerical model of a tokamak (Escande & Sattin Reference Escande and Sattin2021). In a turbulent plasma, if one were to rely on the scaling of two-point functions only, e.g. the magnetic power spectrum, one could argue that such structures do not exist on the relevant scales (as discussed further below). However, such fluctuations are strongly intermittent, so much so in fact that the extended power-law tails of their probability distribution functions (p.d.f.s) provide sufficiently many structures to sustain scattering. This is demonstrated here through direct sampling in a numerical simulation of incompressible MHD without a mean field (§ 3). These results are summarized and discussed further in § 4.
Shortly after the present paper was submitted, similar considerations regarding the role of magnetic bends on particle transport have been reported by Kempski et al. (Reference Kempski, Fielding, Quataert, Galishnikova, Kunz, Philippov and Ripperda2023).
2 Particle transport in intermittent turbulence
2.1 Perturbations along field lines
Throughout, the particle gyroradius $r_{g}$![]() is regarded as small compared with the coherence scale $\ell _{c}$
is regarded as small compared with the coherence scale $\ell _{c}$![]() of the turbulence and the turbulence is assumed magnetostatic, meaning that the characteristic eddy velocity $\langle \delta u^2\rangle ^{1/2}\ll v$
of the turbulence and the turbulence is assumed magnetostatic, meaning that the characteristic eddy velocity $\langle \delta u^2\rangle ^{1/2}\ll v$![]() , with $v=|\boldsymbol {v}\vert$
, with $v=|\boldsymbol {v}\vert$![]() the particle velocity. To describe transport in a turbulence of structures, it is best to break the cascade into three different intervals of length scales $l$
the particle velocity. To describe transport in a turbulence of structures, it is best to break the cascade into three different intervals of length scales $l$![]() , as commonly done: the short-scale modes $l \ll r_{g}$
, as commonly done: the short-scale modes $l \ll r_{g}$![]() , the large-scale ones $l \gg r_{g}$
, the large-scale ones $l \gg r_{g}$![]() and the resonant modes $l \sim r_{g}$
and the resonant modes $l \sim r_{g}$![]() . Short-scale modes will be found to exert a negligible influence, while large-scale modes both regulate adiabatically the evolution of the pitch angle of particles through mirroring effects (Cesarsky & Kulsrud Reference Cesarsky and Kulsrud1973; Chandran Reference Chandran2000a; Malyshkin & Kulsrud Reference Malyshkin and Kulsrud2001; Xu & Lazarian Reference Xu and Lazarian2020; Lazarian & Xu Reference Lazarian and Xu2021) and contribute to global transport through the random motion of field lines (e.g. Jokipii Reference Jokipii1971; Bykov & Toptygin Reference Bykov and Toptygin1993; Chuvilgin & Ptuskin Reference Chuvilgin and Ptuskin1993). The resonant modes with $l\sim r_{g}$
. Short-scale modes will be found to exert a negligible influence, while large-scale modes both regulate adiabatically the evolution of the pitch angle of particles through mirroring effects (Cesarsky & Kulsrud Reference Cesarsky and Kulsrud1973; Chandran Reference Chandran2000a; Malyshkin & Kulsrud Reference Malyshkin and Kulsrud2001; Xu & Lazarian Reference Xu and Lazarian2020; Lazarian & Xu Reference Lazarian and Xu2021) and contribute to global transport through the random motion of field lines (e.g. Jokipii Reference Jokipii1971; Bykov & Toptygin Reference Bykov and Toptygin1993; Chuvilgin & Ptuskin Reference Chuvilgin and Ptuskin1993). The resonant modes with $l\sim r_{g}$![]() will provide a source of non-adiabaticity that leads to pitch-angle scattering. Here, the notion of ‘resonant’ means that the mode length scale $l\sim r_{g}$
will provide a source of non-adiabaticity that leads to pitch-angle scattering. Here, the notion of ‘resonant’ means that the mode length scale $l\sim r_{g}$![]() and nothing else; in particular, no gyroresonance to a plane wave.
and nothing else; in particular, no gyroresonance to a plane wave.
In general terms, as a particle propagates along a field line, it experiences magnetic perturbations of the form
where $\boldsymbol {b}\equiv \boldsymbol {B}/B$![]() ($B\equiv \vert \boldsymbol {B}\vert$
($B\equiv \vert \boldsymbol {B}\vert$![]() ) represents the unit vector along the (total) magnetic field B. Together with $\boldsymbol {b}$
) represents the unit vector along the (total) magnetic field B. Together with $\boldsymbol {b}$![]() , to which it is orthogonal, the unit vector $\boldsymbol {n}$
, to which it is orthogonal, the unit vector $\boldsymbol {n}$![]() spans the osculating plane of the field line. Both scalars $\kappa$
spans the osculating plane of the field line. Both scalars $\kappa$![]() and $m$
and $m$![]() carry the dimension of an inverse length scale; $m\equiv B^{-1}\,\boldsymbol {b}\boldsymbol {\cdot }(\boldsymbol {b}\boldsymbol {\cdot } \boldsymbol {\nabla })\boldsymbol {B}$
carry the dimension of an inverse length scale; $m\equiv B^{-1}\,\boldsymbol {b}\boldsymbol {\cdot }(\boldsymbol {b}\boldsymbol {\cdot } \boldsymbol {\nabla })\boldsymbol {B}$![]() characterizes the mirror force, while $\kappa \equiv B^{-1}\vert \boldsymbol {b}\times (\boldsymbol {b}\boldsymbol {\cdot } \boldsymbol {\nabla })\boldsymbol {B}\vert$
characterizes the mirror force, while $\kappa \equiv B^{-1}\vert \boldsymbol {b}\times (\boldsymbol {b}\boldsymbol {\cdot } \boldsymbol {\nabla })\boldsymbol {B}\vert$![]() measures the local curvature of the magnetic field line.
measures the local curvature of the magnetic field line.
The influence of large-scale modes $l\gg r_{g}$![]() can be followed in a guiding-centre description. It then reduces to the mirror force in a magnetostatic turbulence, $\partial _t \mu = - v (1-\mu ^2) m/2$
can be followed in a guiding-centre description. It then reduces to the mirror force in a magnetostatic turbulence, $\partial _t \mu = - v (1-\mu ^2) m/2$![]() , where $\mu \equiv \boldsymbol {v}\boldsymbol {\cdot }\boldsymbol {b}/v$
, where $\mu \equiv \boldsymbol {v}\boldsymbol {\cdot }\boldsymbol {b}/v$![]() denotes the pitch-angle cosine of the particle. The particle momentum $p$
denotes the pitch-angle cosine of the particle. The particle momentum $p$![]() is exactly conserved in the magnetostatic approximation, while the magnetic moment $M\,\equiv \,(1-\mu ^2)p^2/2B$
is exactly conserved in the magnetostatic approximation, while the magnetic moment $M\,\equiv \,(1-\mu ^2)p^2/2B$![]() is conserved to order $\mathcal {O}(r_{g}/l)$
is conserved to order $\mathcal {O}(r_{g}/l)$![]() . The mirror forces influence $\mu$
. The mirror forces influence $\mu$![]() in an adiabatic manner, decreasing it in regions of increasing magnetic field strength and vice versa. The overall process can lead to spatial diffusion, but it should not lead by itself to a scaling of the mean free path with $r_{g}$
in an adiabatic manner, decreasing it in regions of increasing magnetic field strength and vice versa. The overall process can lead to spatial diffusion, but it should not lead by itself to a scaling of the mean free path with $r_{g}$![]() , given that the dominant effect is tied to the largest length scales on which most of the turbulent power is concentrated.
, given that the dominant effect is tied to the largest length scales on which most of the turbulent power is concentrated.
Unlike mirror-type fluctuations, field line curvature $\kappa$![]() is absent of both QLT and guiding-centre formalisms, at least for magnetostatic turbulence. Finite-$\kappa$
is absent of both QLT and guiding-centre formalisms, at least for magnetostatic turbulence. Finite-$\kappa$![]() effects are contained to some degree in a wave description, yet the magnitude of $\kappa$
effects are contained to some degree in a wave description, yet the magnitude of $\kappa$![]() as predicted by QLT turns out too modest on the scales of interest (namely $l\sim r_{g}$
as predicted by QLT turns out too modest on the scales of interest (namely $l\sim r_{g}$![]() ) to play any role, see below. In the guiding-centre picture, $\kappa$
) to play any role, see below. In the guiding-centre picture, $\kappa$![]() contributes to perpendicular drifts leaving the pitch angle unaffected because the corresponding modes on scales $l \gg r_{g}$
contributes to perpendicular drifts leaving the pitch angle unaffected because the corresponding modes on scales $l \gg r_{g}$![]() mostly renormalize the mean magnetic field that a particle then follows adiabatically, see § 2.2 below. However, it has long been recognized in the community of magnetospheric plasma physics that regions of sufficiently large curvature can lead to abrupt pitch-angle deflection (e.g. Speiser Reference Speiser1965; Gray & Lee Reference Gray and Lee1982; Birmingham Reference Birmingham1984; Büchner & Zelenyi Reference Büchner and Zelenyi1986, Reference Büchner and Zelenyi1989; Chen & Palmadesso Reference Chen and Palmadesso1986; Whipple et al. Reference Whipple, Northrop and Birmingham1986; Anderson et al. Reference Anderson, Decker, Paschalidis and Sarris1997; Delcourt et al. Reference Delcourt, Zelenyi and Sauvaud2000; Artemyev et al. Reference Artemyev, Orlova, Mourenas, Agapitov and Krasnoselskikh2013). That association with reconnecting current sheets provides an explicit connection to structures and intermittency.
mostly renormalize the mean magnetic field that a particle then follows adiabatically, see § 2.2 below. However, it has long been recognized in the community of magnetospheric plasma physics that regions of sufficiently large curvature can lead to abrupt pitch-angle deflection (e.g. Speiser Reference Speiser1965; Gray & Lee Reference Gray and Lee1982; Birmingham Reference Birmingham1984; Büchner & Zelenyi Reference Büchner and Zelenyi1986, Reference Büchner and Zelenyi1989; Chen & Palmadesso Reference Chen and Palmadesso1986; Whipple et al. Reference Whipple, Northrop and Birmingham1986; Anderson et al. Reference Anderson, Decker, Paschalidis and Sarris1997; Delcourt et al. Reference Delcourt, Zelenyi and Sauvaud2000; Artemyev et al. Reference Artemyev, Orlova, Mourenas, Agapitov and Krasnoselskikh2013). That association with reconnecting current sheets provides an explicit connection to structures and intermittency.
Further below, it will be argued that such regions of large enough curvature exist in sufficient numbers to sustain parallel transport. Those regions emerge out of the non-Gaussian, power-law tails of the p.d.f. of the curvature strength and they are therefore directly related to the intermittent nature of the fluctuations. Being localized in space, they act sporadically on the particle trajectory. To capture their influence, one must therefore consider their p.d.f.s in their integrity, as measured in terms of strength and length scale; see Lemoine (Reference Lemoine2022) for similar developments in the context of particle acceleration. For the sake of simplicity, the discussion that follows focusses on such localized regions of high curvature, leaving aside the possible role of small-scale mirrors. As both mirrors and bends compose the perturbations seen along a field line – (2.1) above – the random fields $\kappa (\boldsymbol {x})$![]() and $m(\boldsymbol {x})$
and $m(\boldsymbol {x})$![]() are likely correlated, so that, by tracing the regions of large curvature, we will also trace those of intense, small-scale mirrors. As a matter of fact, regions of large $\kappa$
are likely correlated, so that, by tracing the regions of large curvature, we will also trace those of intense, small-scale mirrors. As a matter of fact, regions of large $\kappa$![]() are commonly associated with low magnetic field strength, i.e. $\kappa \propto B^{-2}$
are commonly associated with low magnetic field strength, i.e. $\kappa \propto B^{-2}$![]() approximately (Yang et al. Reference Yang, Wan, Matthaeus, Shi, Parashar, Lu and Chen2019; Yuen & Lazarian Reference Yuen and Lazarian2020). The true physical cause responsible for jumps in the magnetic moment associated with a loss of adiabaticity is that the particle crosses a region in which the magnetic field is tangled on scales smaller than the particle gyroradius and this likely occurs in a region where both $\kappa$
approximately (Yang et al. Reference Yang, Wan, Matthaeus, Shi, Parashar, Lu and Chen2019; Yuen & Lazarian Reference Yuen and Lazarian2020). The true physical cause responsible for jumps in the magnetic moment associated with a loss of adiabaticity is that the particle crosses a region in which the magnetic field is tangled on scales smaller than the particle gyroradius and this likely occurs in a region where both $\kappa$![]() and $m$
and $m$![]() are significant. A key difference between $\kappa$
are significant. A key difference between $\kappa$![]() and $m$
and $m$![]() , however, is that the former is always positive, while the latter can take positive or negative values. As a particle crosses a wavepacket of mirror fluctuations, both positive and negative contributions tend to cancel each other, weakening the overall influence exerted on the particle. By contrast, a sharp bend of the magnetic field line will impart a net effect on the particle trajectory. The detailed contribution of magnetic mirrors on scales $l\sim r_{g}$
, however, is that the former is always positive, while the latter can take positive or negative values. As a particle crosses a wavepacket of mirror fluctuations, both positive and negative contributions tend to cancel each other, weakening the overall influence exerted on the particle. By contrast, a sharp bend of the magnetic field line will impart a net effect on the particle trajectory. The detailed contribution of magnetic mirrors on scales $l\sim r_{g}$![]() and their interplay with curved magnetic fields is thus deferred to a future study.
and their interplay with curved magnetic fields is thus deferred to a future study.
We make use of the short-hand notation $\kappa _l(\boldsymbol {x})$![]() , which characterizes the value of the $\kappa$
, which characterizes the value of the $\kappa$![]() field on scale $l$
field on scale $l$![]() at point $\boldsymbol {x}$
at point $\boldsymbol {x}$![]() and which corresponds to the value that would be measured at $\boldsymbol {x}$
and which corresponds to the value that would be measured at $\boldsymbol {x}$![]() by coarse graining the turbulence on scale $l$
by coarse graining the turbulence on scale $l$![]() , meaning filtering out the scales $< l$
, meaning filtering out the scales $< l$![]() . In practice, we define $\boldsymbol {\kappa }(\boldsymbol {x})\equiv \boldsymbol {b}\boldsymbol {\cdot }\boldsymbol {\nabla }\boldsymbol {b}$
. In practice, we define $\boldsymbol {\kappa }(\boldsymbol {x})\equiv \boldsymbol {b}\boldsymbol {\cdot }\boldsymbol {\nabla }\boldsymbol {b}$![]() and $\boldsymbol {\kappa _l}(\boldsymbol {x})=G_l\star \boldsymbol {\kappa }$
and $\boldsymbol {\kappa _l}(\boldsymbol {x})=G_l\star \boldsymbol {\kappa }$![]() , where the $\star$
, where the $\star$![]() symbol stands for spatial convolution and $G_l(\boldsymbol {x})=(2{\rm \pi} l^2)^{-3/2}\exp (-x^2/2l^2)$
symbol stands for spatial convolution and $G_l(\boldsymbol {x})=(2{\rm \pi} l^2)^{-3/2}\exp (-x^2/2l^2)$![]() represents the coarse-graining kernel. In weak turbulence, the power spectrum $\mathcal {P}_{\kappa _l}$
represents the coarse-graining kernel. In weak turbulence, the power spectrum $\mathcal {P}_{\kappa _l}$![]() of $\boldsymbol {\kappa _l}$
of $\boldsymbol {\kappa _l}$![]() can then be written to first order in the perturbations in terms of the power spectrum of magnetic fluctuations $\mathcal {P}_B$
can then be written to first order in the perturbations in terms of the power spectrum of magnetic fluctuations $\mathcal {P}_B$![]() through
through
Here, $B$![]() stands for the mean field strength on scales $\gg l$
stands for the mean field strength on scales $\gg l$![]() . The power spectra are normalized via $(2{\rm \pi} )^{-3}\int \,{\rm d}\boldsymbol {k} \mathcal {P}_B(\boldsymbol {k}) = \langle \delta B^2\rangle$
. The power spectra are normalized via $(2{\rm \pi} )^{-3}\int \,{\rm d}\boldsymbol {k} \mathcal {P}_B(\boldsymbol {k}) = \langle \delta B^2\rangle$![]() , with $\langle \delta B^2\rangle$
, with $\langle \delta B^2\rangle$![]() the variance of magnetic field fluctuations, and $(2{\rm \pi} )^{-3}\int \,{\rm d}\boldsymbol {k} \mathcal {P}_{\kappa _l}(\boldsymbol {k})=\langle \boldsymbol {\kappa _l}^2\rangle$
the variance of magnetic field fluctuations, and $(2{\rm \pi} )^{-3}\int \,{\rm d}\boldsymbol {k} \mathcal {P}_{\kappa _l}(\boldsymbol {k})=\langle \boldsymbol {\kappa _l}^2\rangle$![]() . The parallel wavenumber is defined as $k_\parallel = \boldsymbol {k}\boldsymbol {\cdot }\boldsymbol {B}/B$
. The parallel wavenumber is defined as $k_\parallel = \boldsymbol {k}\boldsymbol {\cdot }\boldsymbol {B}/B$![]() . In the following, we write $\langle \kappa _l\rangle \equiv \langle \boldsymbol {\kappa _l}^2\rangle ^{1/2}$
. In the following, we write $\langle \kappa _l\rangle \equiv \langle \boldsymbol {\kappa _l}^2\rangle ^{1/2}$![]() for simplicity. The general scaling of the characteristic curvature strength $\langle \kappa _l\rangle$
for simplicity. The general scaling of the characteristic curvature strength $\langle \kappa _l\rangle$![]() as a function of scale $l$
as a function of scale $l$![]() can then be obtained through direct integration of (2.2). For a Goldreich–Sridhar spectrum of the form $P_B(\boldsymbol {k}) \propto k_\perp ^{-10/3}g(k_\parallel /k_\perp ^{2/3}k_{\rm min}^{1/3})$
can then be obtained through direct integration of (2.2). For a Goldreich–Sridhar spectrum of the form $P_B(\boldsymbol {k}) \propto k_\perp ^{-10/3}g(k_\parallel /k_\perp ^{2/3}k_{\rm min}^{1/3})$![]() , with $g(x)$
, with $g(x)$![]() a function concentrated in $x\in [-1,+1]$
a function concentrated in $x\in [-1,+1]$![]() and of integral unity over ${\mathbb {R}}$
and of integral unity over ${\mathbb {R}}$![]() (Goldreich & Sridhar Reference Goldreich and Sridhar1995, Reference Goldreich and Sridhar1997), one obtains
(Goldreich & Sridhar Reference Goldreich and Sridhar1995, Reference Goldreich and Sridhar1997), one obtains

up to a prefactor of the order of unity. One would obtain a similar result for the mirror term on scale $l$![]() , $\langle m_l\rangle$
, $\langle m_l\rangle$![]() . Those quantities are here written to first order in the perturbations, neglecting intermittency effects. One nevertheless expects the above scaling $\langle \kappa _l\rangle \propto l^{-1/3}$
. Those quantities are here written to first order in the perturbations, neglecting intermittency effects. One nevertheless expects the above scaling $\langle \kappa _l\rangle \propto l^{-1/3}$![]() to remain approximately correct in the limit of large-amplitude turbulence, with the rescaling $B\rightarrow \langle B^2\rangle ^{1/2}$
to remain approximately correct in the limit of large-amplitude turbulence, with the rescaling $B\rightarrow \langle B^2\rangle ^{1/2}$![]() , the latter quantity representing the total mean field on large scales.
, the latter quantity representing the total mean field on large scales.
This definition of the perturbation introduces two length scales, one being $l$![]() of course, the other $\kappa _l^{-1}$
of course, the other $\kappa _l^{-1}$![]() or $m_l^{-1}$
or $m_l^{-1}$![]() ($m_l$
($m_l$![]() mirror term on scale $l$
mirror term on scale $l$![]() ). Here, $l$
). Here, $l$![]() is understood as the characteristic length scale over which those scalars depart from zero in some region of space. The dimensionless number $m_l l$
is understood as the characteristic length scale over which those scalars depart from zero in some region of space. The dimensionless number $m_l l$![]() then characterizes the magnitude of the magnetic field perturbation at that point, while $\kappa _l l$
then characterizes the magnitude of the magnetic field perturbation at that point, while $\kappa _l l$![]() is related to the ratio of the curvature radius of the perturbed magnetic field line to the length scale over which the perturbation exists. A value $\kappa _l l \ll 1$
is related to the ratio of the curvature radius of the perturbed magnetic field line to the length scale over which the perturbation exists. A value $\kappa _l l \ll 1$![]() indicates a weak perturbation of the field line, while $\kappa _l l \gg 1$
indicates a weak perturbation of the field line, while $\kappa _l l \gg 1$![]() rather corresponds to a sharp cusp. The outcome of an interaction of a particle of gyroradius $r_{g}$
rather corresponds to a sharp cusp. The outcome of an interaction of a particle of gyroradius $r_{g}$![]() with a bend of the magnetic field line thus depends on the relative hierarchy of the three length scales $r_{g}$
with a bend of the magnetic field line thus depends on the relative hierarchy of the three length scales $r_{g}$![]() , $\kappa _l^{-1}$
, $\kappa _l^{-1}$![]() and $l$
and $l$![]() . Given that the characteristic fluctuation $\langle {\kappa _l}\rangle$
. Given that the characteristic fluctuation $\langle {\kappa _l}\rangle$![]() increases with decreasing scale, and that particles are sensitive to modes with $l\gtrsim r_{g}$
increases with decreasing scale, and that particles are sensitive to modes with $l\gtrsim r_{g}$![]() but insensitive to scales $l\ll r_{g}$
but insensitive to scales $l\ll r_{g}$![]() , one can already anticipate that the maximum effect will result from interactions at $l\sim r_{g}$
, one can already anticipate that the maximum effect will result from interactions at $l\sim r_{g}$![]() .
.
In the following, we focus on the evolution in time of the magnetic moment $M(t)$![]() , rather than that of the pitch-angle cosine $\mu (t)$
, rather than that of the pitch-angle cosine $\mu (t)$![]() , because this allows us to isolate the contribution of small-scale structures, which affect both $M$
, because this allows us to isolate the contribution of small-scale structures, which affect both $M$![]() and $\mu$
and $\mu$![]() , from that of large-scale mirrors, which influence $\mu$
, from that of large-scale mirrors, which influence $\mu$![]() only (Kunz, Schekochihin & Stone Reference Kunz, Schekochihin and Stone2014). At constant $B$
only (Kunz, Schekochihin & Stone Reference Kunz, Schekochihin and Stone2014). At constant $B$![]() , $\Delta M/M = -\mu \,\Delta \mu /(1-\mu ^2)$
, $\Delta M/M = -\mu \,\Delta \mu /(1-\mu ^2)$![]() , therefore magnetic moment violation evinces pitch-angle scattering, of course. Determining the mean free path to order-unity violation of $M$
, therefore magnetic moment violation evinces pitch-angle scattering, of course. Determining the mean free path to order-unity violation of $M$![]() thus provides a means to determine the mean free path to scattering by those regions of high curvature.
thus provides a means to determine the mean free path to scattering by those regions of high curvature.
2.2 Interaction of a particle with a localized bend of the field line
To capture the role of curvature and coarse-graining scale, consider first the geometry of a magnetic reversal across a current sheet, characterized by a Harris profile $\boldsymbol {B}=B_0\{\kappa l_< {\rm tanh}(z/l_<),0,1\}$![]() , including here a guide field along $z$
, including here a guide field along $z$![]() (e.g. Büchner & Zelenyi Reference Büchner and Zelenyi1986, Reference Büchner and Zelenyi1989; Chen & Palmadesso Reference Chen and Palmadesso1986). The curvature takes its maximum value $\kappa$
(e.g. Büchner & Zelenyi Reference Büchner and Zelenyi1986, Reference Büchner and Zelenyi1989; Chen & Palmadesso Reference Chen and Palmadesso1986). The curvature takes its maximum value $\kappa$![]() at $z=0$
at $z=0$![]() and vanishes away from the current sheet on scales $\gg l_<$
and vanishes away from the current sheet on scales $\gg l_<$![]() . Yet, in such a profile, the magnetic field line direction rotates by a finite angle $\theta$
. Yet, in such a profile, the magnetic field line direction rotates by a finite angle $\theta$![]() across the sheet, with $\cos \theta = (1- \kappa ^2 l_<^2)/(1 + \kappa ^2 l_<^2)$
across the sheet, with $\cos \theta = (1- \kappa ^2 l_<^2)/(1 + \kappa ^2 l_<^2)$![]() , so that the influence of the curvature persists on large length scales $\gg l_<$
, so that the influence of the curvature persists on large length scales $\gg l_<$![]() , i.e. the perturbation takes the form of a kink rather than a cusp. In effect, coarse graining of the profile through a convolution with a Gaussian kernel of width $l\gg l_<$
, i.e. the perturbation takes the form of a kink rather than a cusp. In effect, coarse graining of the profile through a convolution with a Gaussian kernel of width $l\gg l_<$![]() – nothing changes if $l\ll l_<$
– nothing changes if $l\ll l_<$![]() – does not modify the overall profile substantially, but renormalizes the length scales according to the substitutions $l_< \rightarrow l$
– does not modify the overall profile substantially, but renormalizes the length scales according to the substitutions $l_< \rightarrow l$![]() and $\kappa \rightarrow \kappa l_< /l $
and $\kappa \rightarrow \kappa l_< /l $![]() .
.
In § 3 below, we extract the statistics of field line curvature from a numerical simulation of incompressible MHD turbulence and categorize those statistics according to the coarse-graining scale $l$![]() . The presence of current sheets of width $l_<$
. The presence of current sheets of width $l_<$![]() with a profile similar to the above will be properly recorded on all scales $l \gg l_<$
with a profile similar to the above will be properly recorded on all scales $l \gg l_<$![]() with a coarse-grained curvature properly rescaled. For the time being, however, we focus on a bend laid on a single scale $l$
with a coarse-grained curvature properly rescaled. For the time being, however, we focus on a bend laid on a single scale $l$![]() . The above Harris profile can be modified to this effect, e.g. $\boldsymbol {B}=B_0\{1 + \kappa _l l({z}/{l} - 1) {\rm e}^{-({z^2}/{2 l^2})},0,1\}$
. The above Harris profile can be modified to this effect, e.g. $\boldsymbol {B}=B_0\{1 + \kappa _l l({z}/{l} - 1) {\rm e}^{-({z^2}/{2 l^2})},0,1\}$![]() . Here, the curvature vanishes on (parallel) length scales $\gg l$
. Here, the curvature vanishes on (parallel) length scales $\gg l$![]() , while at $z=0$
, while at $z=0$![]() , it takes value $\kappa _l$
, it takes value $\kappa _l$![]() . Integrating the motion of particles in such a magnetic geometry gives a behaviour illustrated in figure 1. We emphasize that this figure is a sketch, presented for illustrative purposes only. The form and the shape of the bend may vary, but to the extent that the physics is captured by the two scales $\kappa _l^{-1}$
. Integrating the motion of particles in such a magnetic geometry gives a behaviour illustrated in figure 1. We emphasize that this figure is a sketch, presented for illustrative purposes only. The form and the shape of the bend may vary, but to the extent that the physics is captured by the two scales $\kappa _l^{-1}$![]() and $l$
and $l$![]() , it captures the generic behaviour. Namely, for $l/r_{g}\ll 1$
, it captures the generic behaviour. Namely, for $l/r_{g}\ll 1$![]() (case a), the particle crosses the perturbation ballistically, without suffering significant deflection, while in the opposite limit $l\gg r_{g}$
(case a), the particle crosses the perturbation ballistically, without suffering significant deflection, while in the opposite limit $l\gg r_{g}$![]() (case c), the particle follows the field line adiabatically. In both cases, the normalized magnetic moment $\hat M(t)\equiv M(t)/M(0)$
(case c), the particle follows the field line adiabatically. In both cases, the normalized magnetic moment $\hat M(t)\equiv M(t)/M(0)$![]() remains approximately constant. On the contrary, when $l\sim r_{g}$
remains approximately constant. On the contrary, when $l\sim r_{g}$![]() and $\kappa _l r_{g} \gtrsim 1$
and $\kappa _l r_{g} \gtrsim 1$![]() , the interaction becomes non-adiabatic and $\vert \Delta \hat M\vert \sim \mathcal {O}(1)$
, the interaction becomes non-adiabatic and $\vert \Delta \hat M\vert \sim \mathcal {O}(1)$![]() .
.

Figure 1. Simple cartoon illustrating the interaction of a particle (trajectory in blue) with a localized bend of the magnetic field line (in black), for three different cases: (a) small-scale mode $l\ll r_{g}$![]() ; (b) near-resonant mode $l\sim r_{g}$
; (b) near-resonant mode $l\sim r_{g}$![]() and $\kappa _l r_{g}\gtrsim 1$
and $\kappa _l r_{g}\gtrsim 1$![]() ; (c) large-scale bend $l\gg r_{g}$
; (c) large-scale bend $l\gg r_{g}$![]() and $\kappa _l r_{g}\ll 1$
and $\kappa _l r_{g}\ll 1$![]() . In (a), the particle crosses the perturbation ballistically while, in (c), the particle follows the bend adiabatically; in both cases, the magnetic moment is approximately conserved, $\vert \Delta \hat M\vert \equiv \vert M(t)/M(0)-1\vert \ll 1$
. In (a), the particle crosses the perturbation ballistically while, in (c), the particle follows the bend adiabatically; in both cases, the magnetic moment is approximately conserved, $\vert \Delta \hat M\vert \equiv \vert M(t)/M(0)-1\vert \ll 1$![]() ; in (b), the interaction gives rise to substantial non-adiabatic evolution of $M$
; in (b), the interaction gives rise to substantial non-adiabatic evolution of $M$![]() , with $\vert \Delta \hat M\vert \sim \mathcal {O}(1)$
, with $\vert \Delta \hat M\vert \sim \mathcal {O}(1)$![]() .
.
The variation of the magnetic moment of a particle that crosses a region of high curvature $\kappa$![]() , independently of the evolution of magnetic field lines on scales $\gg 1/\kappa$
, independently of the evolution of magnetic field lines on scales $\gg 1/\kappa$![]() , is captured by the analysis of Birmingham (Reference Birmingham1984) in the limit $r_{g}< l$
, is captured by the analysis of Birmingham (Reference Birmingham1984) in the limit $r_{g}< l$![]() . The strength of the interaction depends critically on the parameter $\max (\kappa r_{g})$
. The strength of the interaction depends critically on the parameter $\max (\kappa r_{g})$![]() , because the magnetic moment changes by an amount
, because the magnetic moment changes by an amount
with $\alpha$![]() , $\beta$
, $\beta$![]() coefficients determined in (21) of that reference, and $\varPhi$
coefficients determined in (21) of that reference, and $\varPhi$![]() the particle gyrophase at the location where $B$
the particle gyrophase at the location where $B$![]() finds its minimum. The interaction thus becomes non-adiabatic whenever $\max (\kappa r_{g})\gtrsim 0.1$
finds its minimum. The interaction thus becomes non-adiabatic whenever $\max (\kappa r_{g})\gtrsim 0.1$![]() and it can either reduce or increase the magnetic moment, depending on the sign of the cosine factor. The exact value of the curvature does not play a significant role provided it exceeds that threshold.
and it can either reduce or increase the magnetic moment, depending on the sign of the cosine factor. The exact value of the curvature does not play a significant role provided it exceeds that threshold.
As will be shown in § 3, regions with curvature $\kappa _l l \gtrsim 1$![]() are rare, all the more so at small scales $l\ll \ell _{c}$
are rare, all the more so at small scales $l\ll \ell _{c}$![]() , since $\langle \kappa _l l \rangle \propto l^{2/3}$
, since $\langle \kappa _l l \rangle \propto l^{2/3}$![]() (2.3). Ignoring the statistics beyond the root-mean-square (r.m.s.) $\langle \kappa _l \rangle$
(2.3). Ignoring the statistics beyond the root-mean-square (r.m.s.) $\langle \kappa _l \rangle$![]() as one would do in a quasilinear context, one would conclude that $\kappa _l r_{g} \lesssim (l/r_{g})^{-1/3}(r_{g}/\ell _{c})^{2/3}\ll 1$
as one would do in a quasilinear context, one would conclude that $\kappa _l r_{g} \lesssim (l/r_{g})^{-1/3}(r_{g}/\ell _{c})^{2/3}\ll 1$![]() for all $l\gtrsim r_{g}$
for all $l\gtrsim r_{g}$![]() , hence that curvature is everywhere weak and negligible. However, once we consider the full extent of the statistics of $\kappa _l$
, hence that curvature is everywhere weak and negligible. However, once we consider the full extent of the statistics of $\kappa _l$![]() (§ 3), we find a non-vanishing probability of observing $\kappa _l r_{g}\gtrsim 1$
(§ 3), we find a non-vanishing probability of observing $\kappa _l r_{g}\gtrsim 1$![]() , with a maximum for $l\sim r_{g}$
, with a maximum for $l\sim r_{g}$![]() . Regarding small scales $l\ll r_{g}$
. Regarding small scales $l\ll r_{g}$![]() , their contribution can be ignored, because the gyromotion of the particle leads to an effective coarse graining on scales $r_{g}$
, their contribution can be ignored, because the gyromotion of the particle leads to an effective coarse graining on scales $r_{g}$![]() .
.
To model the influence of high-curvature regions, we consider in the following a simplified version of (2.4), namely $\Delta M/M = \pm 1$![]() for particles such that $\max (\kappa _l r_{g})\gtrsim 1$
for particles such that $\max (\kappa _l r_{g})\gtrsim 1$![]() , and $\Delta M/M = 0$
, and $\Delta M/M = 0$![]() otherwise. Since the local value of the gyroradius is what matters, in particular its maximum at maximum curvature, it proves important to distinguish $r_{g}$
otherwise. Since the local value of the gyroradius is what matters, in particular its maximum at maximum curvature, it proves important to distinguish $r_{g}$![]() from its mean value $\bar {r}_{g}$
from its mean value $\bar {r}_{g}$![]() measured in the r.m.s. magnetic field strength $\langle B^2\rangle ^{1/2}$
measured in the r.m.s. magnetic field strength $\langle B^2\rangle ^{1/2}$![]() . To this effect, we introduce a renormalized curvature that incorporates the dependence on the local strength of the magnetic field, as follows:
. To this effect, we introduce a renormalized curvature that incorporates the dependence on the local strength of the magnetic field, as follows:
Hence, for a particle of average gyroradius $\bar {r}_{g}$![]() , defined with respect to the r.m.s. $\langle B^2 \rangle ^{1/2}$
, defined with respect to the r.m.s. $\langle B^2 \rangle ^{1/2}$![]() , the product $\max (\kappa _l r_{g}) \simeq \bar {r}_{g} \max (\hat \kappa _l)$
, the product $\max (\kappa _l r_{g}) \simeq \bar {r}_{g} \max (\hat \kappa _l)$![]() .
.
3 Analysis of a direct numerical simulation of incompressible MHD
This section extracts and analyses the statistics of field line curvature from a direct numerical simulation of incompressible MHD without guide field. This simulation (hereafter referred to as JHU-MHD) is that made available for public use from the Johns Hopkins University Turbulence DatabaseFootnote 2 (Eyink et al. Reference Eyink, Vishniac, Lalescu, Aluie, Kanov, Bürger, Burns, Meneveau and Szalay2013). Its spatial resolution reaches $1\,024^3$![]() , for a ratio of the coherence scale $\ell _{c}$
, for a ratio of the coherence scale $\ell _{c}$![]() to the box size $L_{\rm box}$
to the box size $L_{\rm box}$![]() of $\ell _{c}/L_{\rm box} \simeq 0.14$
of $\ell _{c}/L_{\rm box} \simeq 0.14$![]() . In the absence of a mean field $B$
. In the absence of a mean field $B$![]() , such a simulation effectively mimics large-amplitude, nonlinear turbulence with $\langle \delta B^2\rangle ^{1/2} \gtrsim \text {a few }\times \,B$
, such a simulation effectively mimics large-amplitude, nonlinear turbulence with $\langle \delta B^2\rangle ^{1/2} \gtrsim \text {a few }\times \,B$![]() , since in each coherence volume, the random component defines an effective large-scale field that governs the physics on smaller scales. Clearly, additional simulations sampling compressive driving, lower amplitude $\delta B/B$
, since in each coherence volume, the random component defines an effective large-scale field that governs the physics on smaller scales. Clearly, additional simulations sampling compressive driving, lower amplitude $\delta B/B$![]() and moderate or low $\beta$
and moderate or low $\beta$![]() cases are warranted to gain a better grasp of the dependence of the curvature statistics on particular physical conditions. Nonetheless, the apparent mild dependence of the statistics of field line curvature on the physical set-up, recalled further below, suggests that the present simulation suffices for the present discussion. The turbulence in that simulation develops a strong cascade in the sense of Goldreich & Sridhar (Reference Goldreich and Sridhar1995), as velocity and magnetic perturbations are comparable on the outer scale. We may therefore expect the scaling $\langle \kappa _l\rangle \sim l^{-1/3}\ell _{c}^{-2/3}$
cases are warranted to gain a better grasp of the dependence of the curvature statistics on particular physical conditions. Nonetheless, the apparent mild dependence of the statistics of field line curvature on the physical set-up, recalled further below, suggests that the present simulation suffices for the present discussion. The turbulence in that simulation develops a strong cascade in the sense of Goldreich & Sridhar (Reference Goldreich and Sridhar1995), as velocity and magnetic perturbations are comparable on the outer scale. We may therefore expect the scaling $\langle \kappa _l\rangle \sim l^{-1/3}\ell _{c}^{-2/3}$![]() to hold, at least approximately. A sample of $24\,000$
to hold, at least approximately. A sample of $24\,000$![]() particles have been tracked in a single time snapshot of the simulation volume to follow the evolution of their pitch-angle cosine $\mu$
particles have been tracked in a single time snapshot of the simulation volume to follow the evolution of their pitch-angle cosine $\mu$![]() and magnetic moment $M$
and magnetic moment $M$![]() in magnetostatic turbulence. Those particles have been injected at random places in the simulation volume, with a single $\mu (0)=0.5$
in magnetostatic turbulence. Those particles have been injected at random places in the simulation volume, with a single $\mu (0)=0.5$![]() , gyroradius $\bar {r}_{g} = 0.016\ell _{c}$
, gyroradius $\bar {r}_{g} = 0.016\ell _{c}$![]() and velocity $v\simeq c$
and velocity $v\simeq c$![]() . This gyroradius has been chosen to be as small as possible, while remaining in the inertial range. The pitch-angle cosine $\mu (t)$
. This gyroradius has been chosen to be as small as possible, while remaining in the inertial range. The pitch-angle cosine $\mu (t)$![]() is defined with respect to the local magnetic field $\boldsymbol {B}(\boldsymbol {x})$
is defined with respect to the local magnetic field $\boldsymbol {B}(\boldsymbol {x})$![]() measured at each point along the particle trajectory, not with respect to some reference magnetic field.
measured at each point along the particle trajectory, not with respect to some reference magnetic field.
3.1 Particle trajectories
Figure 2 presents a selection of four different histories of $\mu (t)$![]() , $\hat M(t)$
, $\hat M(t)$![]() and $\hat \kappa (t)$
and $\hat \kappa (t)$![]() measured along particle trajectories. Those examples have been chosen because they are illustrative of the different types of histories that can be observed in that simulation. That sample is not meant to be representative, in the sense that one type of trajectories shown here may be encountered more frequently than another. Figure 2(a) shows one example in which $\mu (t)$
measured along particle trajectories. Those examples have been chosen because they are illustrative of the different types of histories that can be observed in that simulation. That sample is not meant to be representative, in the sense that one type of trajectories shown here may be encountered more frequently than another. Figure 2(a) shows one example in which $\mu (t)$![]() hardly evolves in time over 3 coherence lengths of the turbulence. The normalized curvature $\hat \kappa$
hardly evolves in time over 3 coherence lengths of the turbulence. The normalized curvature $\hat \kappa$![]() (orange line) does not take values larger than $\simeq 0.2$
(orange line) does not take values larger than $\simeq 0.2$![]() here, and its variation takes place on scales of the order of the coherence scale $\ell _{c}$
here, and its variation takes place on scales of the order of the coherence scale $\ell _{c}$![]() . The absence of noticeable variation of $\hat M$
. The absence of noticeable variation of $\hat M$![]() is thus of no surprise. In panel (b), $\hat \kappa$
is thus of no surprise. In panel (b), $\hat \kappa$![]() undergoes excursions up to values slightly larger than unity, yet on scales $\gtrsim 0.2\ell _{c}$
undergoes excursions up to values slightly larger than unity, yet on scales $\gtrsim 0.2\ell _{c}$![]() (judging from the full width at half-maximum), significantly larger than $\bar {r}_{g}$
(judging from the full width at half-maximum), significantly larger than $\bar {r}_{g}$![]() . Those excursions do not impact $\hat M$
. Those excursions do not impact $\hat M$![]() significantly, up to a slight quiver during the interaction. Nonetheless, $\mu (t)$
significantly, up to a slight quiver during the interaction. Nonetheless, $\mu (t)$![]() evolves strongly, if adiabatically ($\Delta M/M\sim 0$
evolves strongly, if adiabatically ($\Delta M/M\sim 0$![]() ) between the points of maximum $\hat \kappa$
) between the points of maximum $\hat \kappa$![]() , which are likely associated with large-scale magnetic mirrors. Panels (c,d) show particles crossing more active regions. In (c), the magnetic moment undergoes two abrupt jumps, each of approximately ${\sim }20\,\%$
, which are likely associated with large-scale magnetic mirrors. Panels (c,d) show particles crossing more active regions. In (c), the magnetic moment undergoes two abrupt jumps, each of approximately ${\sim }20\,\%$![]() , at respectively $ct/\ell _{c} = 1.1$
, at respectively $ct/\ell _{c} = 1.1$![]() and $2.6$
and $2.6$![]() . Interestingly, the variation in magnetic moment occurs over a few gyroradii, as indicated by the oscillations, at locations where $\hat \kappa$
. Interestingly, the variation in magnetic moment occurs over a few gyroradii, as indicated by the oscillations, at locations where $\hat \kappa$![]() reaches values $\sim 10$
reaches values $\sim 10$![]() . At those points, the conditions guaranteeing non-adiabaticity, see (2.4), $l\sim \bar {r}_{g}$
. At those points, the conditions guaranteeing non-adiabaticity, see (2.4), $l\sim \bar {r}_{g}$![]() , $\hat \kappa \bar {r}_{g}>1$
, $\hat \kappa \bar {r}_{g}>1$![]() are fulfilled. Outside of those regions, the particle seems to be influenced, here as well, by large-scale mirrors. Finally, in panel (d), the particle undergoes one localized violent interaction that leads to a large jump in magnetic moment, $\Delta M/M\sim 1$
are fulfilled. Outside of those regions, the particle seems to be influenced, here as well, by large-scale mirrors. Finally, in panel (d), the particle undergoes one localized violent interaction that leads to a large jump in magnetic moment, $\Delta M/M\sim 1$![]() . Not visible in this figure, the largest value of $\hat \kappa$
. Not visible in this figure, the largest value of $\hat \kappa$![]() is here of the order of $3\times 10^3$
is here of the order of $3\times 10^3$![]() and the interaction takes place over a few gyroradii, ensuring a non-adiabatic transition.
and the interaction takes place over a few gyroradii, ensuring a non-adiabatic transition.

Figure 2. Examples of histories of the pitch-angle cosine $\mu (t)$![]() (solid purple) as a function of time, drawn from the numerical simulation of incompressible MHD discussed in the text. In green solid line, the variation of the normalized magnetic moment $\hat M(t)-1\equiv M(t)/M(0)-1$
(solid purple) as a function of time, drawn from the numerical simulation of incompressible MHD discussed in the text. In green solid line, the variation of the normalized magnetic moment $\hat M(t)-1\equiv M(t)/M(0)-1$![]() ; in orange, the $\log _{10}$
; in orange, the $\log _{10}$![]() of the normalized curvature $\hat \kappa (\boldsymbol {x})\equiv \kappa (\boldsymbol {x}) \langle B^2\rangle ^{1/2}/B(\boldsymbol {x})$
of the normalized curvature $\hat \kappa (\boldsymbol {x})\equiv \kappa (\boldsymbol {x}) \langle B^2\rangle ^{1/2}/B(\boldsymbol {x})$![]() measured at each point along the trajectories of those four particles. The gyroradius is such that $2{\rm \pi} \bar {r}_{g}/\ell _{c} = 0.1$
measured at each point along the trajectories of those four particles. The gyroradius is such that $2{\rm \pi} \bar {r}_{g}/\ell _{c} = 0.1$![]() .
.
3.2 Statistics of the field line curvature
In numerical simulations, the curvature $\kappa$![]() – as calculated without coarse graining – is observed to be distributed as a broken power law (Schekochihin et al. Reference Schekochihin, Cowley, Maron and Malyshkin2001; Yang et al. Reference Yang, Wan, Matthaeus, Shi, Parashar, Lu and Chen2019; Yuen & Lazarian Reference Yuen and Lazarian2020) with an index $s_\kappa \sim 2\rightarrow 2.5$
– as calculated without coarse graining – is observed to be distributed as a broken power law (Schekochihin et al. Reference Schekochihin, Cowley, Maron and Malyshkin2001; Yang et al. Reference Yang, Wan, Matthaeus, Shi, Parashar, Lu and Chen2019; Yuen & Lazarian Reference Yuen and Lazarian2020) with an index $s_\kappa \sim 2\rightarrow 2.5$![]() at large values of $\kappa$
at large values of $\kappa$![]() , for a p.d.f. ${ {\mathsf {p}}}_\kappa \propto \kappa ^{-s_\kappa }$
, for a p.d.f. ${ {\mathsf {p}}}_\kappa \propto \kappa ^{-s_\kappa }$![]() . Interestingly, these studies have been performed in rather diverse conditions: Yang et al. (Reference Yang, Wan, Matthaeus, Shi, Parashar, Lu and Chen2019) discuss two- and three-dimensional incompressible MHD as well as two-dimensional kinetic simulations of large-amplitude turbulence ($\langle \delta B^2\rangle ^{1/2}/B\sim 1$
. Interestingly, these studies have been performed in rather diverse conditions: Yang et al. (Reference Yang, Wan, Matthaeus, Shi, Parashar, Lu and Chen2019) discuss two- and three-dimensional incompressible MHD as well as two-dimensional kinetic simulations of large-amplitude turbulence ($\langle \delta B^2\rangle ^{1/2}/B\sim 1$![]() ), which yield $s_\kappa \simeq 2$
), which yield $s_\kappa \simeq 2$![]() in two dimensions and $s_\kappa \simeq 2.5$
in two dimensions and $s_\kappa \simeq 2.5$![]() in three dimensions; Yuen & Lazarian (Reference Yuen and Lazarian2020) investigate compressible MHD turbulence with varying amplitudes to observe a trend of slightly softer spectra with decreasing turbulence level; finally, Schekochihin et al. (Reference Schekochihin, Cowley, Maron and Malyshkin2001) examines a wholly different configuration, i.e. the sub-viscous range of high-Pm turbulence, where the weak, small-scale magnetic field is stirred by a large-scale velocity field; the observed index, $s_\kappa \simeq 2$
in three dimensions; Yuen & Lazarian (Reference Yuen and Lazarian2020) investigate compressible MHD turbulence with varying amplitudes to observe a trend of slightly softer spectra with decreasing turbulence level; finally, Schekochihin et al. (Reference Schekochihin, Cowley, Maron and Malyshkin2001) examines a wholly different configuration, i.e. the sub-viscous range of high-Pm turbulence, where the weak, small-scale magnetic field is stirred by a large-scale velocity field; the observed index, $s_\kappa \simeq 2$![]() , agrees nicely with the theoretical model developed therein. Quite remarkably, recent in situ measurements of the statistics of field line curvature in the magnetosheath confirm those findings, in particular $s_\kappa \simeq 2.5$
, agrees nicely with the theoretical model developed therein. Quite remarkably, recent in situ measurements of the statistics of field line curvature in the magnetosheath confirm those findings, in particular $s_\kappa \simeq 2.5$![]() at large curvature (Bandyopadhyay et al. Reference Bandyopadhyay, Yang, Matthaeus, Chasapis, Parashar, Russell, Strangeway, Torbert, Giles and Gershman2020; Huang et al. Reference Huang, Zhang, Sahraoui, Yuan, Deng, Jiang, Xu, Wei, He and Zhang2020). That property thus appears robust.
at large curvature (Bandyopadhyay et al. Reference Bandyopadhyay, Yang, Matthaeus, Chasapis, Parashar, Russell, Strangeway, Torbert, Giles and Gershman2020; Huang et al. Reference Huang, Zhang, Sahraoui, Yuan, Deng, Jiang, Xu, Wei, He and Zhang2020). That property thus appears robust.
The coarse-grained variables $\kappa _l$![]() span a family of distributions ${ {\mathsf {p}}}_{\kappa _l}$
span a family of distributions ${ {\mathsf {p}}}_{\kappa _l}$![]() , each characterized by the coarse-graining scale $l$
, each characterized by the coarse-graining scale $l$![]() . These distributions, more precisely the p.d.f.s of the dimensionless quantities $\kappa _l\,l$
. These distributions, more precisely the p.d.f.s of the dimensionless quantities $\kappa _l\,l$![]() (${ {\mathsf {p}}}_{\kappa _ll}$
(${ {\mathsf {p}}}_{\kappa _ll}$![]() ) and $\hat \kappa _ll$
) and $\hat \kappa _ll$![]() (${ {\mathsf {p}}}_{\hat \kappa _ll}$
(${ {\mathsf {p}}}_{\hat \kappa _ll}$![]() ) are displayed in figure 3. They have been obtained by direct sampling in the JHU-MHD simulation of incompressible turbulence, as follows: for a given coarse-graining scale $l$
) are displayed in figure 3. They have been obtained by direct sampling in the JHU-MHD simulation of incompressible turbulence, as follows: for a given coarse-graining scale $l$![]() , we extract at most $(L_{\rm box}/l)^3$
, we extract at most $(L_{\rm box}/l)^3$![]() data points and at each point $\boldsymbol {x}$
data points and at each point $\boldsymbol {x}$![]() , we compute $\kappa _l^{\rm num}(\boldsymbol {x}) = \vert \boldsymbol {b_l}\times \boldsymbol {b_l}\boldsymbol {\cdot }\boldsymbol {\nabla }\boldsymbol {B_l}\vert /\vert \boldsymbol {B_l}\vert$
, we compute $\kappa _l^{\rm num}(\boldsymbol {x}) = \vert \boldsymbol {b_l}\times \boldsymbol {b_l}\boldsymbol {\cdot }\boldsymbol {\nabla }\boldsymbol {B_l}\vert /\vert \boldsymbol {B_l}\vert$![]() where $\boldsymbol {B_l}(\boldsymbol {x})$
where $\boldsymbol {B_l}(\boldsymbol {x})$![]() denotes the coarse-grained magnetic field on scale $l$
denotes the coarse-grained magnetic field on scale $l$![]() at $\boldsymbol {x}$
at $\boldsymbol {x}$![]() ; that quantity can be directly accessed using the numerical tools of the database. Sampling variance implies that data on $l\sim \ell _{c}$
; that quantity can be directly accessed using the numerical tools of the database. Sampling variance implies that data on $l\sim \ell _{c}$![]() (red points in figure 3) display a substantial level of shot noise. The grid size $\Delta x$
(red points in figure 3) display a substantial level of shot noise. The grid size $\Delta x$![]() also affects the estimate, by introducing an effective maximal curvature scale $\kappa _l \sim 1/\Delta x$
also affects the estimate, by introducing an effective maximal curvature scale $\kappa _l \sim 1/\Delta x$![]() at all values of $l$
at all values of $l$![]() .
.

Figure 3. (a) Statistics of the curvature $\kappa _l$![]() coarse grained on scale $l$
coarse grained on scale $l$![]() (multiplied by $l$
(multiplied by $l$![]() ), as measured through direct sampling in the JHU-MHD simulation, for various coarse-graining scales, as indicated. Note that the $y-$
), as measured through direct sampling in the JHU-MHD simulation, for various coarse-graining scales, as indicated. Note that the $y-$![]() axis shows $x { {\mathsf {p}}}_{\kappa _l l}(x)$
axis shows $x { {\mathsf {p}}}_{\kappa _l l}(x)$![]() where $x\equiv \kappa _l l$
where $x\equiv \kappa _l l$![]() . The dotted line shows a scaling ${ {\mathsf {p}}}_{\kappa _ll}(x)\propto x^{-2.5}$
. The dotted line shows a scaling ${ {\mathsf {p}}}_{\kappa _ll}(x)\propto x^{-2.5}$![]() , for reference. (b) Same, for the normalized curvature $\hat \kappa _l \, l$
, for reference. (b) Same, for the normalized curvature $\hat \kappa _l \, l$![]() . The dotted line shows a scaling ${ {\mathsf {p}}}_{\hat \kappa _ll}(x)\propto x^{-2.0}$
. The dotted line shows a scaling ${ {\mathsf {p}}}_{\hat \kappa _ll}(x)\propto x^{-2.0}$![]() , for reference. See text for details.
, for reference. See text for details.
On scales $l\sim \ell _{c}$![]() , the distribution of $p_{\kappa _l l}$
, the distribution of $p_{\kappa _l l}$![]() can be approximately described as Gaussian, with a mean value $\langle \kappa _l l \rangle \sim 1$
can be approximately described as Gaussian, with a mean value $\langle \kappa _l l \rangle \sim 1$![]() , as could be expected on dimensional grounds. On smaller length scales, the p.d.f.s develop power-law tails, signalling intermittency. For such broken power-law distributions, the value of $x=\kappa _l l$
, as could be expected on dimensional grounds. On smaller length scales, the p.d.f.s develop power-law tails, signalling intermittency. For such broken power-law distributions, the value of $x=\kappa _l l$![]() , where $x\,{ {\mathsf {p}}}_{\kappa _ll}(x)$
, where $x\,{ {\mathsf {p}}}_{\kappa _ll}(x)$![]() , finds its peak value provides a fair estimate of $\langle \kappa _l l\rangle$
, finds its peak value provides a fair estimate of $\langle \kappa _l l\rangle$![]() . That quantity is observed to scale approximately as predicted by (2.3), i.e. $(l/\ell _{c})^{2/3}$
. That quantity is observed to scale approximately as predicted by (2.3), i.e. $(l/\ell _{c})^{2/3}$![]() . That mean value would provide a faithful description of the p.d.f. if the latter were Gaussian, but it is not, and if one were to measure higher-order moments, they would depart sharply from Gaussian scalings. At large values, the statistics of $\kappa _l l$
. That mean value would provide a faithful description of the p.d.f. if the latter were Gaussian, but it is not, and if one were to measure higher-order moments, they would depart sharply from Gaussian scalings. At large values, the statistics of $\kappa _l l$![]() indeed follow an approximate power law $p_{\kappa _ll}\propto (\kappa _ll)^{-2.5}$
indeed follow an approximate power law $p_{\kappa _ll}\propto (\kappa _ll)^{-2.5}$![]() , while that of the normalized curvature $\hat \kappa _ll$
, while that of the normalized curvature $\hat \kappa _ll$![]() is harder, roughly $p_{\hat \kappa _ll}\propto (\hat \kappa _ll)^{-2.0}$
is harder, roughly $p_{\hat \kappa _ll}\propto (\hat \kappa _ll)^{-2.0}$![]() . This is not surprising because $\hat \kappa _l \equiv \kappa _l \langle B^2\rangle ^{1/2}/B$
. This is not surprising because $\hat \kappa _l \equiv \kappa _l \langle B^2\rangle ^{1/2}/B$![]() , and $B$
, and $B$![]() and $\kappa _l$
and $\kappa _l$![]() are anti-correlated (Yang et al. Reference Yang, Wan, Matthaeus, Shi, Parashar, Lu and Chen2019; Yuen & Lazarian Reference Yuen and Lazarian2020). This anti-correlation between $\kappa _l$
are anti-correlated (Yang et al. Reference Yang, Wan, Matthaeus, Shi, Parashar, Lu and Chen2019; Yuen & Lazarian Reference Yuen and Lazarian2020). This anti-correlation between $\kappa _l$![]() and $B$
and $B$![]() formalizes the intuition that magnetic field tension opposes the stretching and folding motions that would push the curvature to large values, i.e. that it is easier to bend a weak magnetic field than a strong one. More quantitatively, from $\kappa _l \propto B^{-2}$
formalizes the intuition that magnetic field tension opposes the stretching and folding motions that would push the curvature to large values, i.e. that it is easier to bend a weak magnetic field than a strong one. More quantitatively, from $\kappa _l \propto B^{-2}$![]() and $p_{\kappa _ll}\propto (\kappa _ll)^{-2.5}$
and $p_{\kappa _ll}\propto (\kappa _ll)^{-2.5}$![]() , one derives $\hat \kappa _l \propto \kappa _l/B \propto \kappa _l^{3/2}$
, one derives $\hat \kappa _l \propto \kappa _l/B \propto \kappa _l^{3/2}$![]() , hence $p_{\hat \kappa _ll}\propto (\hat \kappa _ll)^{-2.0}$
, hence $p_{\hat \kappa _ll}\propto (\hat \kappa _ll)^{-2.0}$![]() indeed.
indeed.
This observation finds a particular importance when one recalls that $\hat \kappa _l$![]() , not $\kappa _l$
, not $\kappa _l$![]() , is the quantity that governs the strength of the interaction of a particle of mean gyroradius $\bar {r}_{g}$
, is the quantity that governs the strength of the interaction of a particle of mean gyroradius $\bar {r}_{g}$![]() with a sharp bend of the magnetic field line. The apparent anti-correlation between $\kappa$
with a sharp bend of the magnetic field line. The apparent anti-correlation between $\kappa$![]() and $B$
and $B$![]() implies that particles see their gyroradius enlarged by a factor of a few or more when interacting with a localized bend of the magnetic field, which relaxes the constraint to achieve non-adiabatic interactions, $\hat \kappa _l l \gtrsim 1$
implies that particles see their gyroradius enlarged by a factor of a few or more when interacting with a localized bend of the magnetic field, which relaxes the constraint to achieve non-adiabatic interactions, $\hat \kappa _l l \gtrsim 1$![]() at $l\sim \bar {r}_{g}$
at $l\sim \bar {r}_{g}$![]() , see (2.4).
, see (2.4).
Finally, those $\hat \kappa _l$![]() statistics allow us to calculate the mean free path to magnetic moment violation, by noting that the cumulative distribution function $P_{\hat \kappa _l l}(>x )$
statistics allow us to calculate the mean free path to magnetic moment violation, by noting that the cumulative distribution function $P_{\hat \kappa _l l}(>x )$![]() provides the filling fraction of space where values $\hat \kappa _l l> x$
provides the filling fraction of space where values $\hat \kappa _l l> x$![]() can be found. Accordingly, the quantity $l/P_{\hat \kappa _l}(>x )$
can be found. Accordingly, the quantity $l/P_{\hat \kappa _l}(>x )$![]() defines the mean free path to interaction with one such region. Hence
defines the mean free path to interaction with one such region. Hence
determines the mean free path $\lambda _{s}$![]() to interaction with order-of-unity variation of the magnetic moment according to (2.4). That mean free path, which is measured along the field line, neglects the influence of perpendicular drifts which, if sufficiently strong, might move the particle out of the region on a crossing time $\sim l/v$
to interaction with order-of-unity variation of the magnetic moment according to (2.4). That mean free path, which is measured along the field line, neglects the influence of perpendicular drifts which, if sufficiently strong, might move the particle out of the region on a crossing time $\sim l/v$![]() . This appears reasonable, as the magnitude of the drift velocity is $v_{D}\sim v r_{g}/(3L)$
. This appears reasonable, as the magnitude of the drift velocity is $v_{D}\sim v r_{g}/(3L)$![]() for a mode on length scale $L> r_{g}$
for a mode on length scale $L> r_{g}$![]() , so that the corresponding perpendicular displacement is of order $\sim (l/L)\,r_{g}/3$
, so that the corresponding perpendicular displacement is of order $\sim (l/L)\,r_{g}/3$![]() with $l\sim r_{g}< L$
with $l\sim r_{g}< L$![]() . Such drifts nevertheless offer a potentially interesting source of perpendicular transport on long time scales.
. Such drifts nevertheless offer a potentially interesting source of perpendicular transport on long time scales.
In the present description, the global transport of the particles is controlled by a complex interplay of phenomena acting on different scales, in particular, confinement by large-scale mirrors, magnetic diffusivity associated with the meandering motion of field lines and scattering on highly curved regions. While the former two do not depend on particle rigidity, the latter becomes increasingly important at low rigidities, suggesting that those localized interactions that violate $M$![]() and thus regulate parallel transport will also regulate the general transport properties at sufficiently small rigidities. In effect, approximating ${ {\mathsf {p}}}_{\hat \kappa _l l}$
and thus regulate parallel transport will also regulate the general transport properties at sufficiently small rigidities. In effect, approximating ${ {\mathsf {p}}}_{\hat \kappa _l l}$![]() via
via
with $\alpha _{\hat \kappa } \sim 2$![]() at $x\gg \langle \hat \kappa _l l \rangle$
at $x\gg \langle \hat \kappa _l l \rangle$![]() , one obtains
, one obtains
The first equality derives from the power-law approximation of ${ {\mathsf {p}}}_{\hat \kappa _l l}$![]() , while the second makes use of (2.3) and the third further assumes $\alpha \simeq 2$
, while the second makes use of (2.3) and the third further assumes $\alpha \simeq 2$![]() . This scaling is written as $r_{g}^{0.3}$
. This scaling is written as $r_{g}^{0.3}$![]() and not $r_{g}^{1/3}$
and not $r_{g}^{1/3}$![]() to emphasize the uncertainty related to the value of $\alpha$
to emphasize the uncertainty related to the value of $\alpha$![]() . A rigorous evaluation of $\lambda _{s}$
. A rigorous evaluation of $\lambda _{s}$![]() , based on its definition (3.1) and the statistics measured in the JHU-MHD simulations (figure 3) confirms the above approximate scaling $\lambda _{s}\propto r_{g}^{0.3}$
, based on its definition (3.1) and the statistics measured in the JHU-MHD simulations (figure 3) confirms the above approximate scaling $\lambda _{s}\propto r_{g}^{0.3}$![]() , see figure 4. It should be clear that the above result has nothing to do with the usual quasilinear result $\lambda _{s} \propto \bar {r}_{g} [k \langle \vert \delta B_k\vert ^2\rangle ]^{-1}$
, see figure 4. It should be clear that the above result has nothing to do with the usual quasilinear result $\lambda _{s} \propto \bar {r}_{g} [k \langle \vert \delta B_k\vert ^2\rangle ]^{-1}$![]() at $k\sim \bar {r}_{g}^{-1}$
at $k\sim \bar {r}_{g}^{-1}$![]() and $\langle \vert \delta B_k\vert ^2\rangle \propto k^{-5/3}$
and $\langle \vert \delta B_k\vert ^2\rangle \propto k^{-5/3}$![]() (Berezinskii et al. Reference Berezinskii, Bulanov, Dogiel and Ptuskin1990), even though it shares a similar scaling with momentum.Footnote 3 Interestingly, in the conditions of incompressible, strong turbulence of the JHU-MHD simulation, the quasilinear calculation predicts a very mild scaling of $\lambda _{s}$
(Berezinskii et al. Reference Berezinskii, Bulanov, Dogiel and Ptuskin1990), even though it shares a similar scaling with momentum.Footnote 3 Interestingly, in the conditions of incompressible, strong turbulence of the JHU-MHD simulation, the quasilinear calculation predicts a very mild scaling of $\lambda _{s}$![]() with momentum (Chandran Reference Chandran2000b; Yan & Lazarian Reference Yan and Lazarian2002).
with momentum (Chandran Reference Chandran2000b; Yan & Lazarian Reference Yan and Lazarian2002).

Figure 4. Numerical evaluation of the mean free path for order-of-unity violations of the magnetic moment through scattering, as defined in (3.1) and using the statistics of $\hat \kappa _l l$![]() extracted from the JHU-MHD simulation. This mean free path, written here in units of $\ell _{c}$
extracted from the JHU-MHD simulation. This mean free path, written here in units of $\ell _{c}$![]() , is plotted as a function of rigidity $2{\rm \pi} r_{g}/\ell _{c}$
, is plotted as a function of rigidity $2{\rm \pi} r_{g}/\ell _{c}$![]() , using the correspondence $l\sim r_{g}$
, using the correspondence $l\sim r_{g}$![]() in defining the threshold beyond which $\hat M$
in defining the threshold beyond which $\hat M$![]() can change by an order-of-unity factor, as expressed by (2.4). The dotted grey line indicates a scaling $\propto \bar {r}_{g}^{0.3}$
can change by an order-of-unity factor, as expressed by (2.4). The dotted grey line indicates a scaling $\propto \bar {r}_{g}^{0.3}$![]() for reference.
for reference.
It must also be emphasized that figure 4 does not constitute a measurement of the mean free path to scattering vs rigidity by itself. It rather indicates what scaling one would expect on the basis of the theoretical model proposed in § 2.2, given the p.d.f. of the normalized curvature extracted from the JHU-MHD simulation. The following section extracts, however, this mean free path for one value of the rigidity through particle tracking in that same simulation.
3.3 Magnetic moment diffusion
Figure 5 presents the p.d.f. of $\hat M$![]() , as measured from the sample of particles propagated through the turbulence volume. As indicated earlier, those particles have all been injected with a unique pitch-angle cosine $\mu (0)=0.5$
, as measured from the sample of particles propagated through the turbulence volume. As indicated earlier, those particles have all been injected with a unique pitch-angle cosine $\mu (0)=0.5$![]() , a unique rigidity $2{\rm \pi} \bar {r}_{g}/\ell _{c}=0.1$
, a unique rigidity $2{\rm \pi} \bar {r}_{g}/\ell _{c}=0.1$![]() , albeit at different locations drawn at random; all particles are relativistic with $v\simeq c$
, albeit at different locations drawn at random; all particles are relativistic with $v\simeq c$![]() . The trajectory of those particles has been followed for $3\ell _{c}/c$
. The trajectory of those particles has been followed for $3\ell _{c}/c$![]() by integrating the equation of motion using a Boris pusher, see Lemoine (Reference Lemoine2022) for details. Recalling that the length of the simulation volume is $L_{\rm box}\simeq 7 \ell _{c}$
by integrating the equation of motion using a Boris pusher, see Lemoine (Reference Lemoine2022) for details. Recalling that the length of the simulation volume is $L_{\rm box}\simeq 7 \ell _{c}$![]() , the particles cannot cross the simulation box during the integration. Periodic boundary conditions are applied on all three sides of the simulation cube.
, the particles cannot cross the simulation box during the integration. Periodic boundary conditions are applied on all three sides of the simulation cube.

Figure 5. (a) The p.d.f. of the normalized magnetic moment $\hat M$![]() (times $\hat M$
(times $\hat M$![]() ) at various times, as measured from the sample of particles propagated through the turbulence volume. All particles are injected with a same pitch-angle cosine $\mu (0)=0.5$
) at various times, as measured from the sample of particles propagated through the turbulence volume. All particles are injected with a same pitch-angle cosine $\mu (0)=0.5$![]() and rigidity $2{\rm \pi} r_{g}/\ell _{c}=0.1$
and rigidity $2{\rm \pi} r_{g}/\ell _{c}=0.1$![]() . Although the sampling noise becomes substantial at large excursions of $\hat M$
. Although the sampling noise becomes substantial at large excursions of $\hat M$![]() , the overall trend can be properly captured thanks to the large number of bins. (b) Cumulativedistribution function for $\vert \Delta \hat M\vert = \vert \hat M-1\vert$
, the overall trend can be properly captured thanks to the large number of bins. (b) Cumulativedistribution function for $\vert \Delta \hat M\vert = \vert \hat M-1\vert$![]() , emphasizing the deviations of $\hat M$
, emphasizing the deviations of $\hat M$![]() from its initial value ($=1$
from its initial value ($=1$![]() ). This cumulative distribution function shows that, by $c t/\ell _{c}\simeq 2$
). This cumulative distribution function shows that, by $c t/\ell _{c}\simeq 2$![]() , approximately 20 %–30 % of particles have seen their magnetic moment change by an order of unity or more. The slight glitch apparent at $\vert \Delta \hat M\vert =1$
, approximately 20 %–30 % of particles have seen their magnetic moment change by an order of unity or more. The slight glitch apparent at $\vert \Delta \hat M\vert =1$![]() results from the fact that $\hat M$
results from the fact that $\hat M$![]() is a positive quantity, which makes $\Delta \hat M$
is a positive quantity, which makes $\Delta \hat M$![]() bounded from below by $1$
bounded from below by $1$![]() .
.
The p.d.f. shown in figure 5(a) broadens in time through the development of a power-law tail. This signals encounters with intermittent, localized regions of high curvature. These power-law tails are indeed reminiscent of those observed in the momentum distribution of particles accelerated in strong turbulence, for which it was shown, on the basis of a large deviation argument, that rare interactions of substantial energy gain generically lead to power-law behaviour for the distribution, quite unlike a Brownian motion characterized by frequent interactions of modest energy change, which rather lead to Gaussian type distributions (Lemoine Reference Lemoine2021).
Figure 5(b) presents the cumulative distribution function of $\vert \Delta \hat M\vert \equiv \vert \hat M-1\vert$![]() , to offer a closer look on the statistics of the deviations of $\hat M$
, to offer a closer look on the statistics of the deviations of $\hat M$![]() . The connection between the p.d.f. shown in the left panel and the cumulative distribution function is not straightforward, because the p.d.f. derives from the sample of values of $\hat M$
. The connection between the p.d.f. shown in the left panel and the cumulative distribution function is not straightforward, because the p.d.f. derives from the sample of values of $\hat M$![]() at a given time, while the cumulative distribution measures the fraction of particles that have experienced a change of $\hat M$
at a given time, while the cumulative distribution measures the fraction of particles that have experienced a change of $\hat M$![]() by a given amount in the time interval $[0,t]$
by a given amount in the time interval $[0,t]$![]() . This cumulative distribution function shows that, by $ct/\ell _{c}\simeq 1$
. This cumulative distribution function shows that, by $ct/\ell _{c}\simeq 1$![]() , approximately $15\,\%$
, approximately $15\,\%$![]() of particles have suffered a order-of-unity change in $\hat M$
of particles have suffered a order-of-unity change in $\hat M$![]() ; this fraction increases up to ${\simeq }25\,\%$
; this fraction increases up to ${\simeq }25\,\%$![]() at $ct/\ell _{c}\simeq 2$
at $ct/\ell _{c}\simeq 2$![]() .
.
Finally,figure 6 displays the evolution in time of the variance of the distribution shown in figure 5(a), to probe the possible diffusive regime of $\hat M$![]() . While the values at early times are dominated by numerical noise, associated with the narrow core of the distribution of $\hat M$
. While the values at early times are dominated by numerical noise, associated with the narrow core of the distribution of $\hat M$![]() , a clear diffusive regime sets in at $ct/\ell _{c}\gtrsim 0.1$
, a clear diffusive regime sets in at $ct/\ell _{c}\gtrsim 0.1$![]() with a scaling regime $\langle \Delta \hat M^2\rangle \simeq 0.8 ct/\ell _{c}\gtrsim 0.1$
with a scaling regime $\langle \Delta \hat M^2\rangle \simeq 0.8 ct/\ell _{c}\gtrsim 0.1$![]() , corresponding to a diffusion coefficient $D_{\hat M}\simeq 0.4 c/\ell _{c}$
, corresponding to a diffusion coefficient $D_{\hat M}\simeq 0.4 c/\ell _{c}$![]() . When translated into a mean free path to $\hat M$
. When translated into a mean free path to $\hat M$![]() -violation, as $\lambda _{s}$
-violation, as $\lambda _{s}$![]() , the corresponding value is $2.5\ell _{c}$
, the corresponding value is $2.5\ell _{c}$![]() , i.e. a factor of a few larger than the theoretical value shown in figure 4 for that rigidity $2{\rm \pi} \bar {r}_{g}/\ell _{c}=0.1$
, i.e. a factor of a few larger than the theoretical value shown in figure 4 for that rigidity $2{\rm \pi} \bar {r}_{g}/\ell _{c}=0.1$![]() . This lends overall consistency to the picture presented here.
. This lends overall consistency to the picture presented here.

Figure 6. Evolution of the variance of $\Delta \hat M$![]() in time, as measured from the sample of tracked particles through the turbulence volume. The values at $ct/\ell _{c}\lesssim 0.1$
in time, as measured from the sample of tracked particles through the turbulence volume. The values at $ct/\ell _{c}\lesssim 0.1$![]() are dominated by numerical noise, whose magnitude is of the order of $\sim 0.1$
are dominated by numerical noise, whose magnitude is of the order of $\sim 0.1$![]() , while the transition to a diffusive regime at $ct/\ell _{c}\gtrsim 0.1$
, while the transition to a diffusive regime at $ct/\ell _{c}\gtrsim 0.1$![]() is manifest. The dotted line in that region indicates a linear (diffusive) scaling $\langle \Delta \hat M^2\rangle \simeq 0.8 ct/\ell _{c}$
is manifest. The dotted line in that region indicates a linear (diffusive) scaling $\langle \Delta \hat M^2\rangle \simeq 0.8 ct/\ell _{c}$![]() .
.
4 Summary and discussion
The present paper has examined the possibility that localized, intermittent regions of highly tangled magnetic fields, in particular sharp bends of the magnetic field lines characterized by the curvature $\kappa \equiv B^{-1} \vert \boldsymbol {b}\times (\boldsymbol {b}\boldsymbol {\cdot } \boldsymbol {\nabla })\boldsymbol {B}\vert$![]() , can contribute to the scattering of particles with gyroradius $\bar {r}_{g}<\ell _{c}$
, can contribute to the scattering of particles with gyroradius $\bar {r}_{g}<\ell _{c}$![]() ($\ell _{c}$
($\ell _{c}$![]() is coherence scale). The argument relies on the observations that (i) a bend of large curvature $\kappa _l > 1/r_{g}$
is coherence scale). The argument relies on the observations that (i) a bend of large curvature $\kappa _l > 1/r_{g}$![]() ($r_{g}$
($r_{g}$![]() is the local gyroradius) laid on a spatial scale $l\sim \bar {r}_{g}$
is the local gyroradius) laid on a spatial scale $l\sim \bar {r}_{g}$![]() can induce an order-of-unity change in the magnetic moment of particles and that (ii) the extended (non-Gaussian) distributions of $\kappa _l$
can induce an order-of-unity change in the magnetic moment of particles and that (ii) the extended (non-Gaussian) distributions of $\kappa _l$![]() on all scales $l < \ell _{c}$
on all scales $l < \ell _{c}$![]() , characteristics of the sharp gradients and coherent structures of MHD turbulence, guarantee that such regions exist and abound. The statistics of $\kappa _l$
, characteristics of the sharp gradients and coherent structures of MHD turbulence, guarantee that such regions exist and abound. The statistics of $\kappa _l$![]() (more precisely $\hat \kappa _l$
(more precisely $\hat \kappa _l$![]() , see text), which have been extracted from a simulation of incompressible MHD turbulence without a guide field, display a hard power-law tail ${ {\mathsf {p}}}_{\hat \kappa _l l}\propto (\hat \kappa _l l)^{-2.0}$
, see text), which have been extracted from a simulation of incompressible MHD turbulence without a guide field, display a hard power-law tail ${ {\mathsf {p}}}_{\hat \kappa _l l}\propto (\hat \kappa _l l)^{-2.0}$![]() . When combined with (i), this predicts a mean free path $\lambda _{s}$
. When combined with (i), this predicts a mean free path $\lambda _{s}$![]() to magnetic moment violation of the form $\lambda _{s}\sim \ell _{c}^{0.7}\bar {r}_{g}^{0.3}$
to magnetic moment violation of the form $\lambda _{s}\sim \ell _{c}^{0.7}\bar {r}_{g}^{0.3}$![]() (for $\langle \delta B^2\rangle ^{1/2}/\langle B^2\rangle ^{1/2} \sim 1$
(for $\langle \delta B^2\rangle ^{1/2}/\langle B^2\rangle ^{1/2} \sim 1$![]() ). Net diffusion of the magnetic moment $M$
). Net diffusion of the magnetic moment $M$![]() has been demonstrated by tracking particles for one value of the rigidity in the MHD simulation and the inferred scattering frequency agrees, within a factor of a few, with the above. In this picture, the pitch-angle cosine of particles ($\mu$
has been demonstrated by tracking particles for one value of the rigidity in the MHD simulation and the inferred scattering frequency agrees, within a factor of a few, with the above. In this picture, the pitch-angle cosine of particles ($\mu$![]() ) evolves under the conjunct influence of large-scale mirrors, which can modify $\mu$
) evolves under the conjunct influence of large-scale mirrors, which can modify $\mu$![]() by order unity on scales ${\sim }\ell _{c}$
by order unity on scales ${\sim }\ell _{c}$![]() while leaving $M$
while leaving $M$![]() unchanged, and of localized, violent interactions with sharp bends of the magnetic field lines on scales $\sim \bar {r}_{g}$
unchanged, and of localized, violent interactions with sharp bends of the magnetic field lines on scales $\sim \bar {r}_{g}$![]() , which affect both. The latter can be regarded as ‘resonant’, in the sense that they are maximized at $l\sim \bar {r}_{g}$
, which affect both. The latter can be regarded as ‘resonant’, in the sense that they are maximized at $l\sim \bar {r}_{g}$![]() , however, nowhere do we make reference to a resonance with a travelling wave.
, however, nowhere do we make reference to a resonance with a travelling wave.
The main result of the present paper is thus to demonstrate that coherent structures, in particular regions of high curvature, can play a key role in mediating particle diffusion in magnetized turbulence. This provides ample motivation to extend the present model toward a theory of transport based on interactions with intermittent structures, and more work appears to be needed in that regard. In particular, one should explore the statistics of $\hat \kappa _l$![]() and related quantities in simulations of compressible turbulence with varying amplitudes to better connect them to the main characteristics of the turbulence, better characterize the topology of regions of large curvature as well as repeat the above exercise of particle tracking using very high resolution simulations following e.g. Cohet & Marcowith (Reference Cohet and Marcowith2016). The present description of particle scattering also bears important consequences for perpendicular transport, notably because the apparent anti-correlation between large curvature and weak magnetic field strength implies that, while suffering magnetic moment violating interactions, the particles are more likely to jump to a neighbouring field line. Additionally, the strong perpendicular drifts imparted by those structures on scales $> r_{g}$
and related quantities in simulations of compressible turbulence with varying amplitudes to better connect them to the main characteristics of the turbulence, better characterize the topology of regions of large curvature as well as repeat the above exercise of particle tracking using very high resolution simulations following e.g. Cohet & Marcowith (Reference Cohet and Marcowith2016). The present description of particle scattering also bears important consequences for perpendicular transport, notably because the apparent anti-correlation between large curvature and weak magnetic field strength implies that, while suffering magnetic moment violating interactions, the particles are more likely to jump to a neighbouring field line. Additionally, the strong perpendicular drifts imparted by those structures on scales $> r_{g}$![]() provide a new source of transport whose role deserves close scrutiny.
provide a new source of transport whose role deserves close scrutiny.
With respect to phenomenological applications, it is interesting to note that the stochastic process that describes pitch-angle evolution departs markedly from a Brownian motion, and indeed, visual inspection of individual particle trajectories suggests that this is the case; see for instance figure 2, which illustrates vastly different histories for different particles over several $\ell _{c}$![]() . On asymptotic time scales, however, the process will eventually converge to central-limit behaviour, meaning that the intermittency effects will eventually blend in, leaving $\lambda _{s}\propto \bar {r}_{g}^{0.3}$
. On asymptotic time scales, however, the process will eventually converge to central-limit behaviour, meaning that the intermittency effects will eventually blend in, leaving $\lambda _{s}\propto \bar {r}_{g}^{0.3}$![]() as the sole parameter governing the random walk. This appears of direct interest to cosmic-ray phenomenology, which infers a similar mean free path from the observed chemical composition, just as the former observation of non-Brownian transport on short length scales may directly impact the phenomenology of cosmic-ray halos around sources and their radiative signatures.
as the sole parameter governing the random walk. This appears of direct interest to cosmic-ray phenomenology, which infers a similar mean free path from the observed chemical composition, just as the former observation of non-Brownian transport on short length scales may directly impact the phenomenology of cosmic-ray halos around sources and their radiative signatures.
Acknowledgements
It is a pleasure to acknowledge insightful discussions with A. Marcowith, S. Xu and E. Zweibel and to thank the referees for their detailed reports. The possibility to use the resources of the JH Turbulence Database (JHTDB), which is developed as an open resource by the Johns Hopkins University, under the sponsorship of the National Science Foundation, is gratefully acknowledged.
Editor A. Schekochihin thanks the referees for their advice in evaluating this article.
Funding
This work has been supported by the ANR (UnRIP project, Grant No. ANR-20- CE30-0030).
Declaration of interests
The author reports no conflict of interest.